Spectral Method in Epidemic Time Series: Application to COVID-19 Pandemic
Abstract
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Identification of the Model

2.2. Phenomenological Model to Fit the Cumulative and the Daily Numbers of Reported Case Data
| Phenomenological model for the cumulative numbers of reported cases with |
| We start with a first eigenvalue , for some . The phenomenological model used to fit the cumulative numbers of reported cases has the following form
For discrete times, it is equivalent to say that By computing the first derivative of , we obtain a model for the daily number of cases of the following form |
| Phenomenological model for the cumulative numbers of reported cases with |
| Assume that the eigenvalues are two conjugated complex numbers , for some and . The phenomenological model used to fit the cumulative numbers of reported cases has the following form
For discrete times, it is equivalent to say that By computing the first derivative of , we obtain a model for the daily number of cases of the following form |
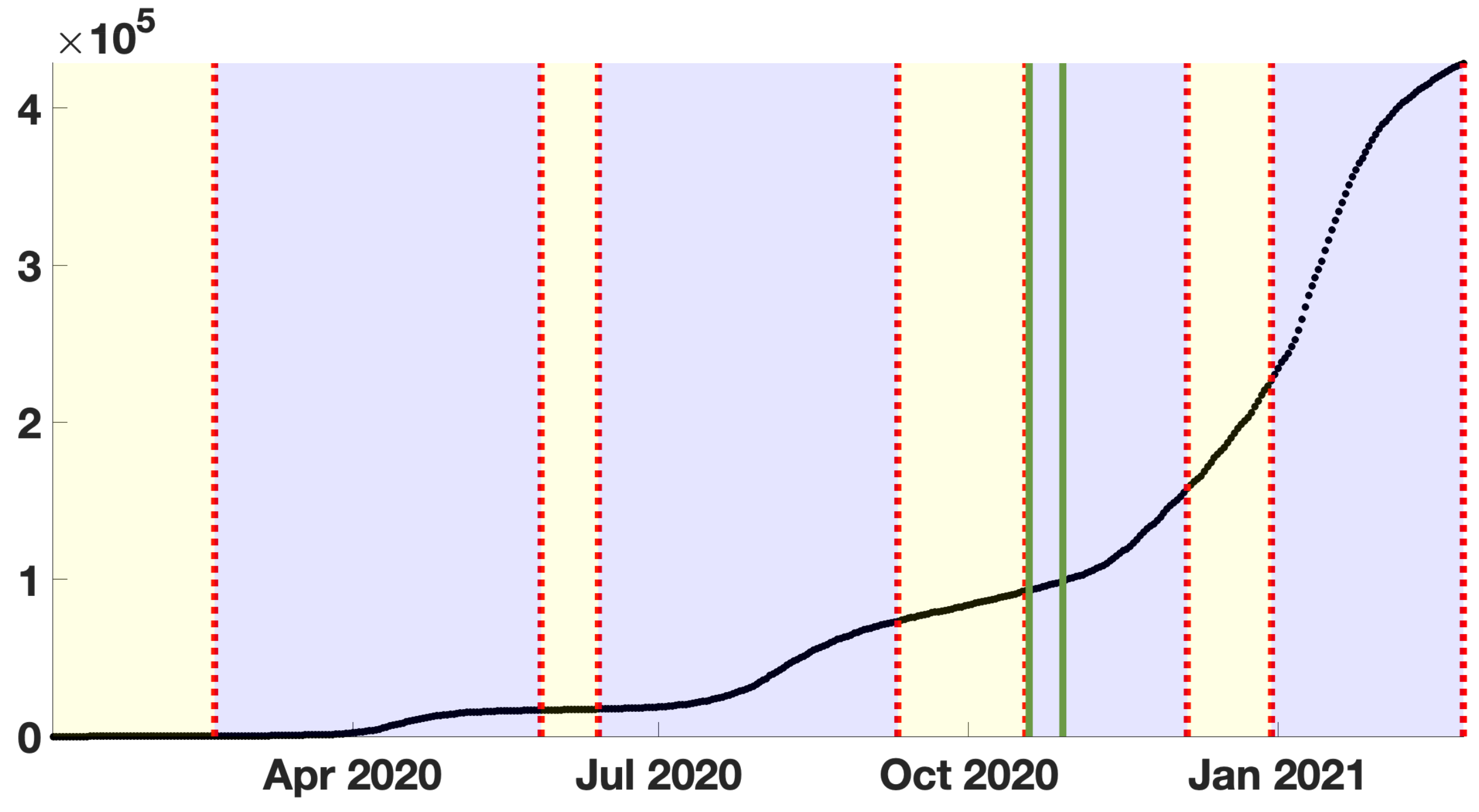
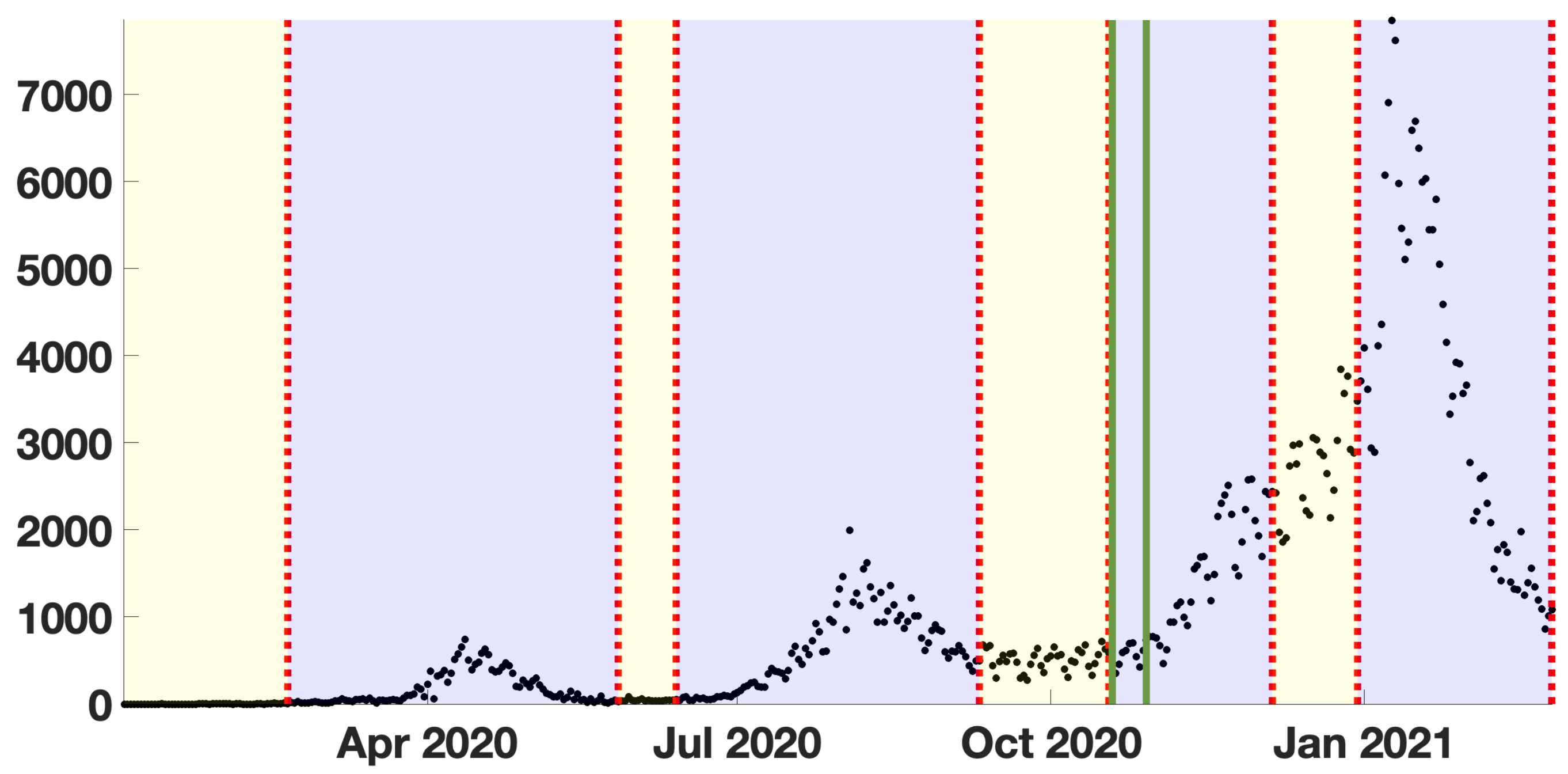
2.3. Cumulative and Daily Number of Reported Cases for COVID-19 in Japan
3. Results
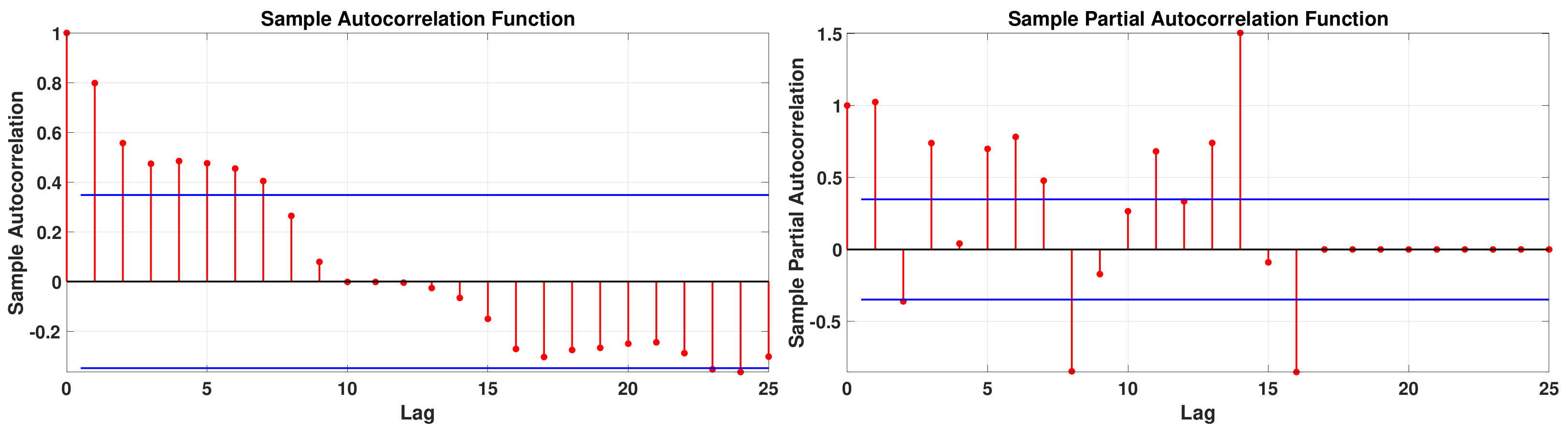
3.1. Methods Applied to Ten Days Data
- Step 1:
- Step 2:
- Next, we consider the residual left after the previous fit,
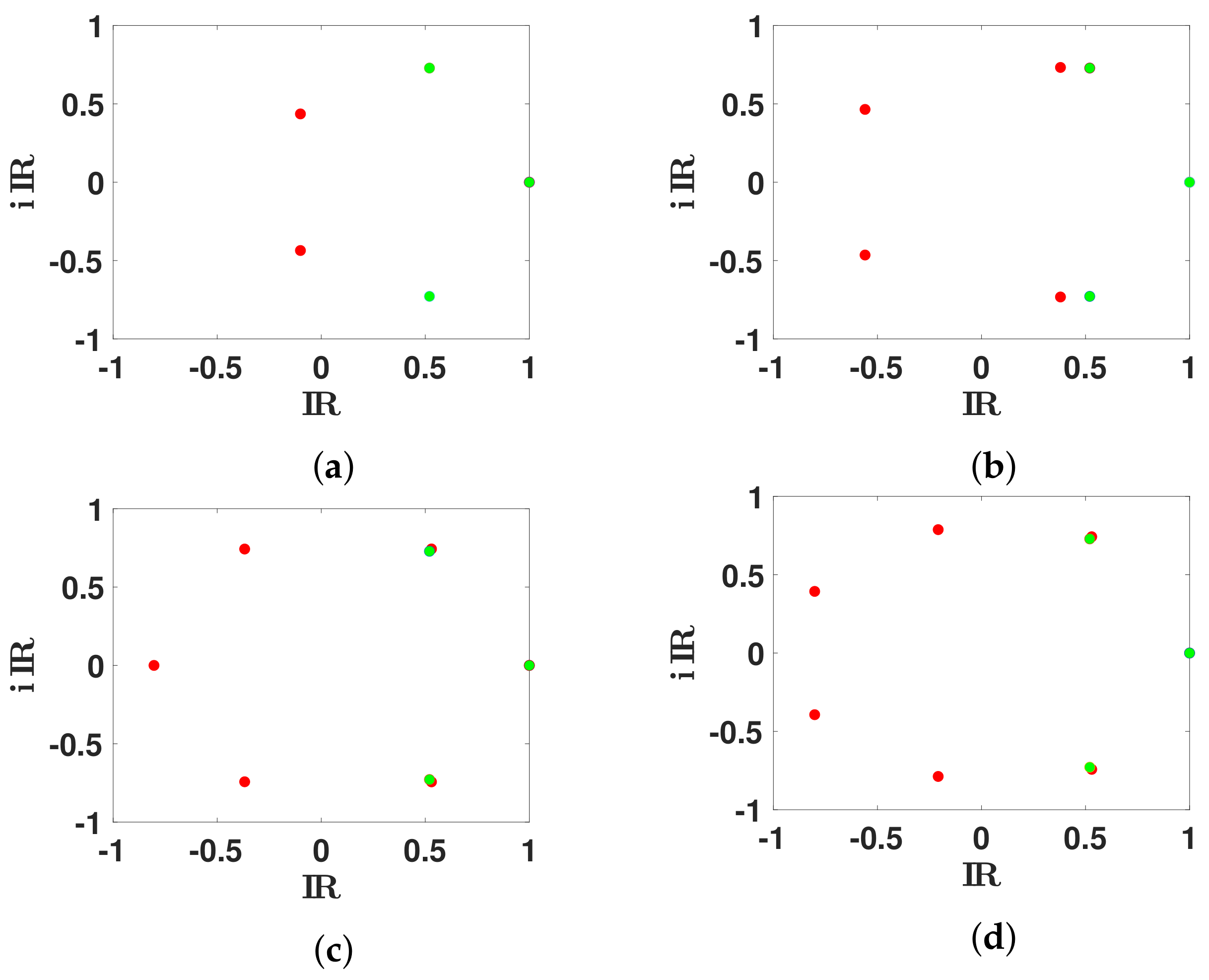
3.2. Spectral Truncation Method Applied to Ten Days Data
3.2.1. Re-Normalizing Procedure
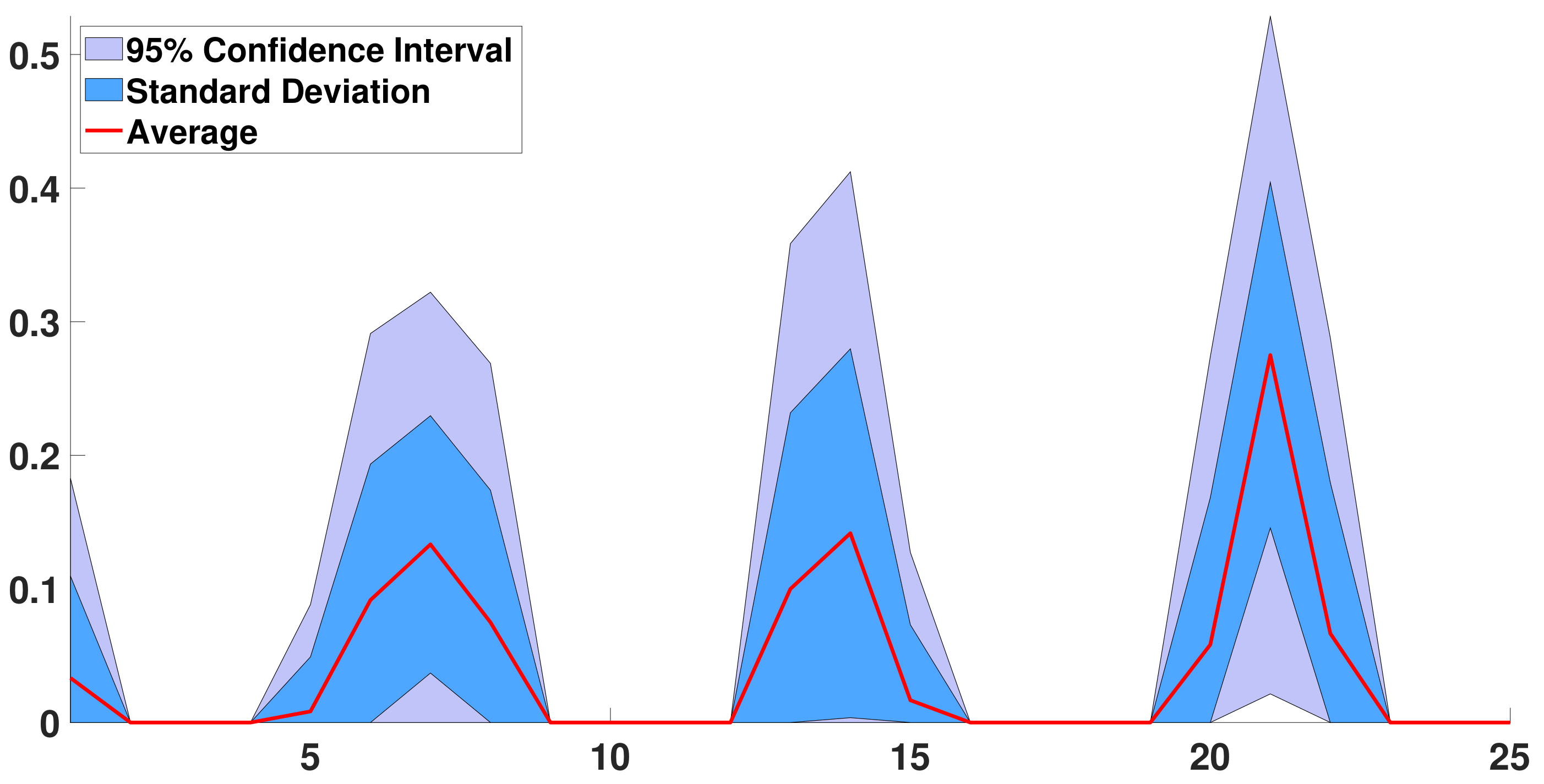
3.2.2. Daily Basic Reproduction Numbers
3.2.3. Applying the Model to Daily Number of Reported Cases
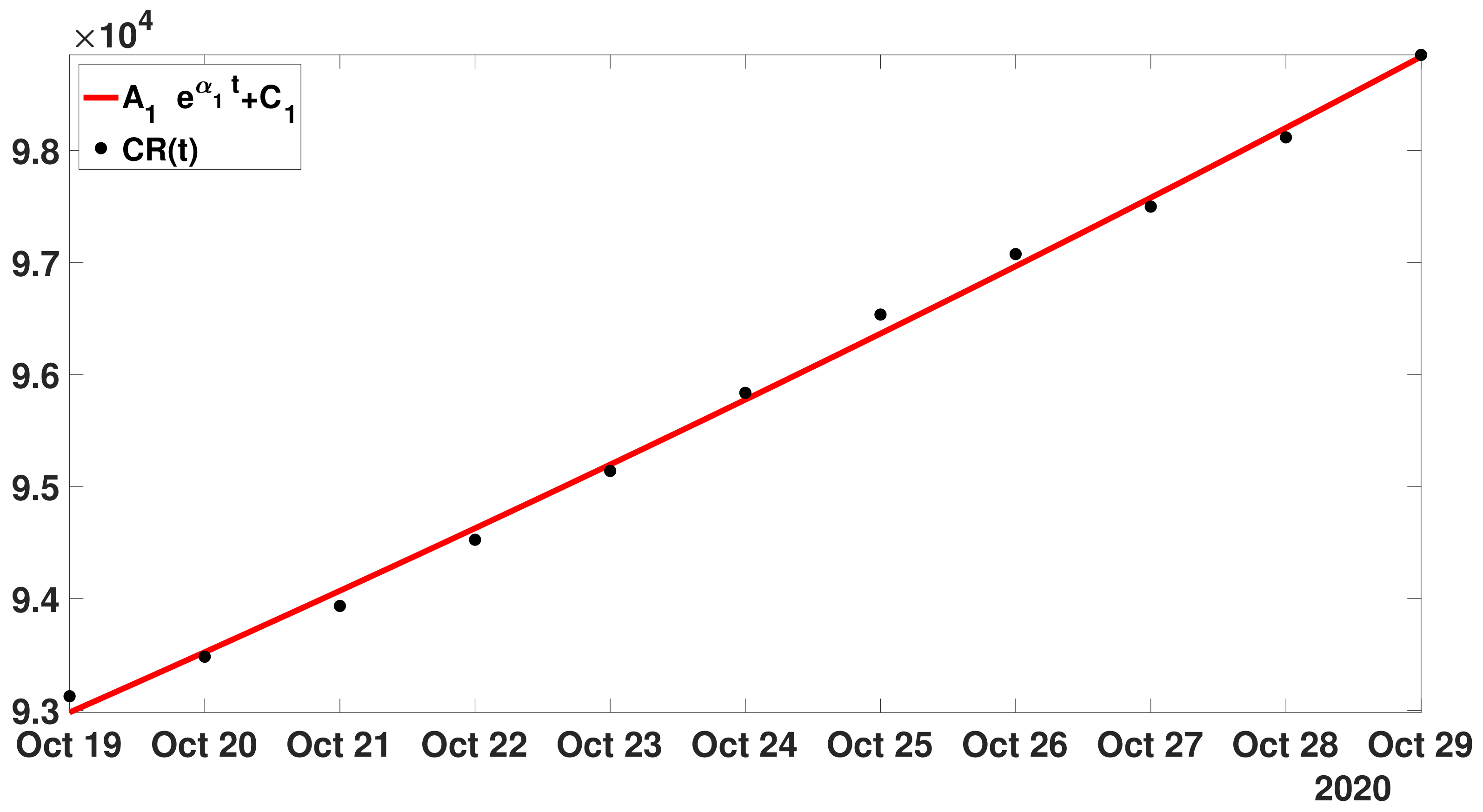
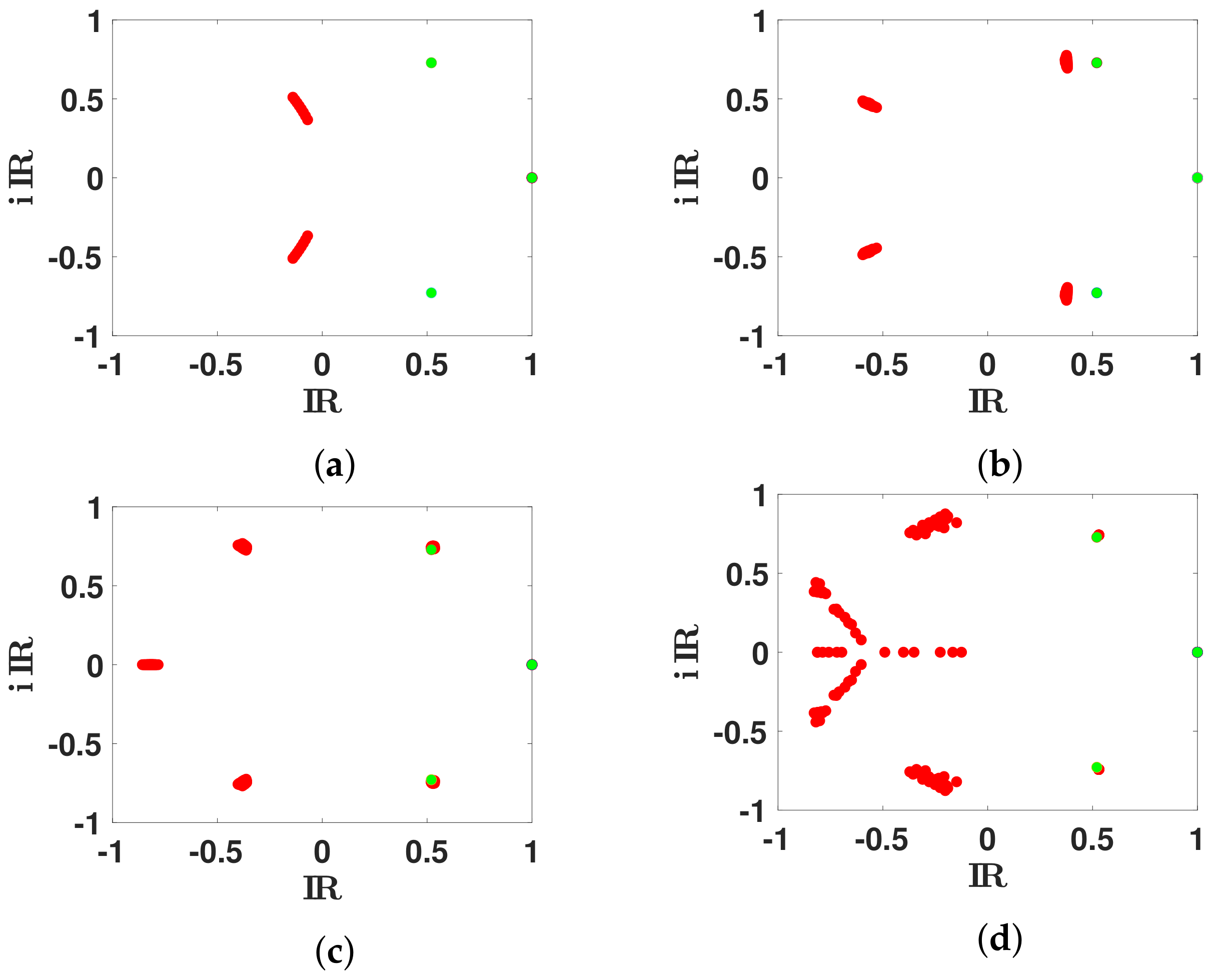
3.3. Extension of the Spectral Truncation Method over One Month
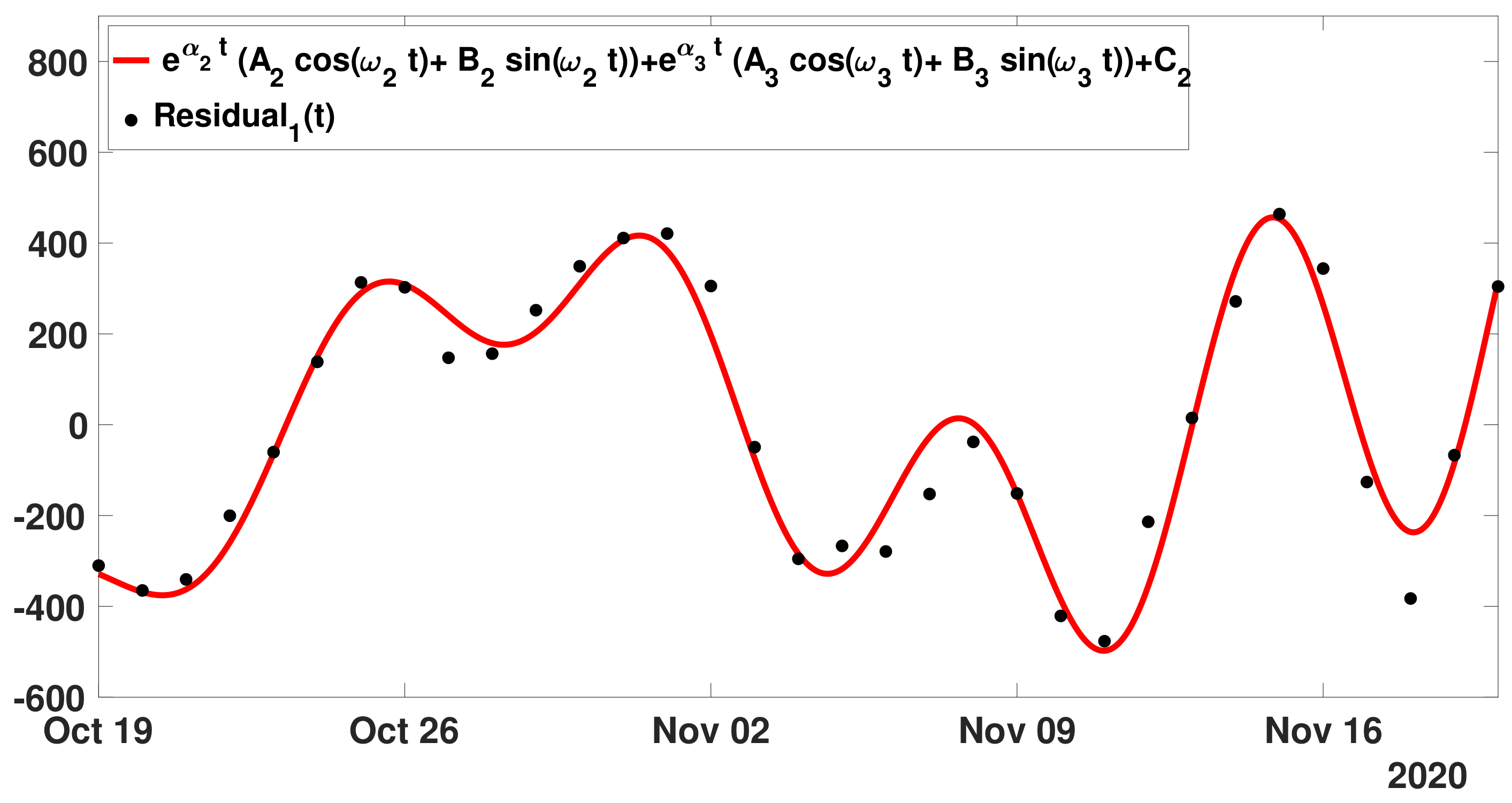
- Step 1: In Figure 13, we fit the modelwith the cumulative number of reported cases data between 19 October and 19 November 2020.
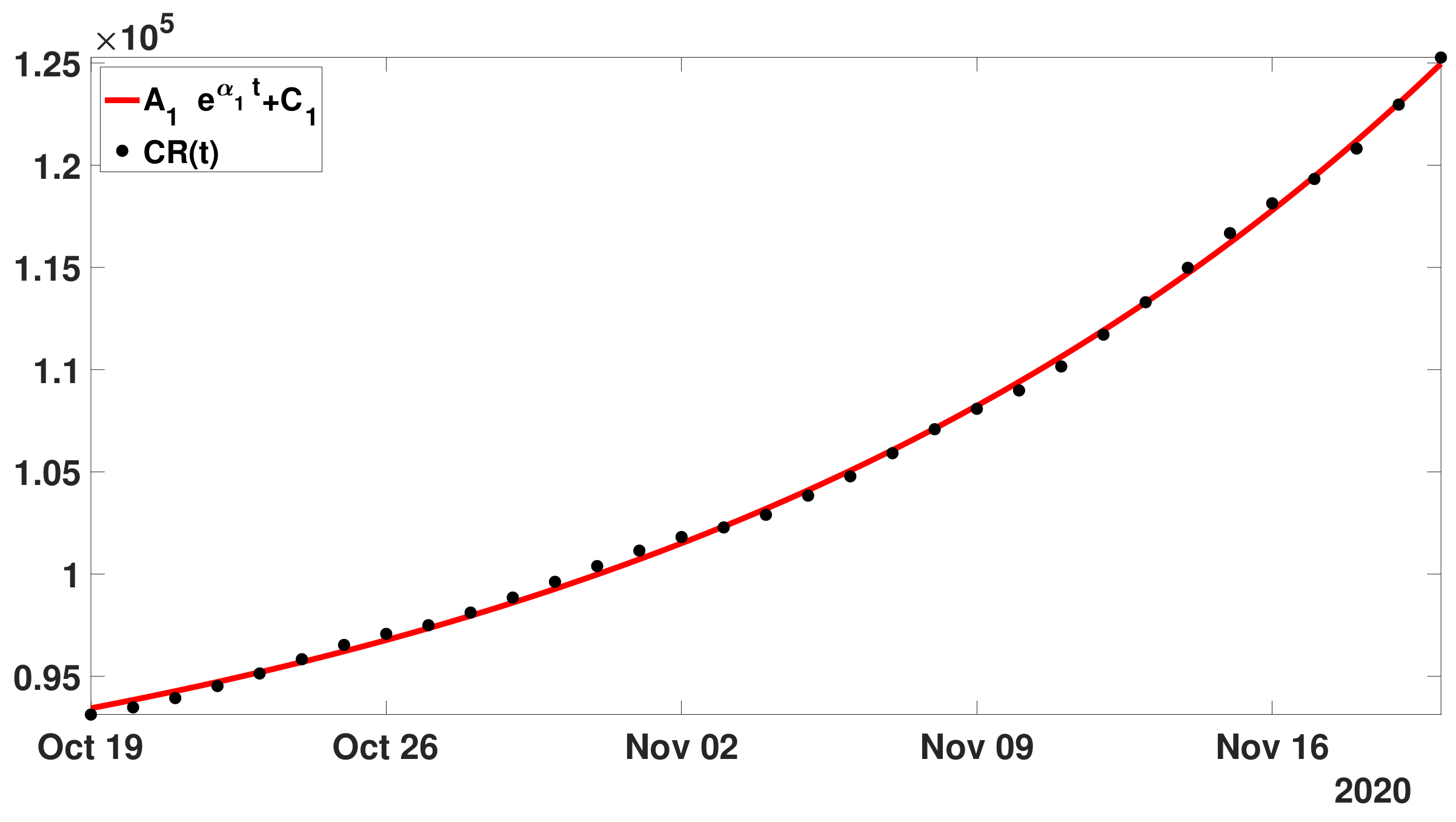
- Step 2: Next we define as before the first residualand we fit the with the model
4. Discussion
4.1. Data over Ten Days
4.2. Data over One Month
4.3. Perspectives and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Non Identifiability Result
Appendix B. Identifiability Result

Appendix C. Identification of the Phenomenological Model
Appendix D. About Residual 2 (t) in Section 3.3

References
- Demongeot, J.; Griette, Q.; Maday, Y.; Magal, P. Kermack-McKendrick model with age of infection starting from a single or multiple cohorts of infected patients. arXiv 2022, arXiv:2205.15634. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics: II. Proc. R. Soc. Lond. Ser. B 1932, 138, 55–83. [Google Scholar]
- Chao, D.L.; Halloran, M.E.; Obenchain, V.J.; Longini, I.M., Jr. FluTE, a publicly available stochastic influenza epidemic simulation model. PLoS Comput. Biol. 2010, 6, e1000656. [Google Scholar] [CrossRef] [PubMed]
- Itoh, Y.; Shichinohe, S.; Nakayama, M.; Igarashi, M.; Ishii, A.; Ishigaki, H.; Ishida, H.; Kitagawa, N.; Sasamura, T.; Shiohara, M.; et al. Emergence of H7N9 Influenza A Virus Resistant to Neuraminidase Inhibitors in Nonhuman Primates. Antimicrob. Agents Chemother. 2015, 59, 4962–4973. [Google Scholar] [PubMed]
- Alvarez, L.; Colom, M.; Morel, J.D.; Morel, J.M. Computing the daily reproduction number of COVID-19 by inverting the renewal equation using a variational technique. Proc. Natl. Acad. Sci. USA 2021, 118, e2105112118. [Google Scholar] [PubMed]
- Alvarez, L.; Morel, J.-D.; Morel, J.-M. Modeling COVID-19 incidence by the renewal equation after removal of administrative bias and noise. Biology 2022, 11, 540. [Google Scholar]
- Demongeot, J.; Griette, Q.; Magal, P. SI epidemic model applied to COVID-19 data in mainland China. R. Soc. Open Sci. 2020, 7, 201878. [Google Scholar] [CrossRef]
- Griette, Q.; Demongeot, J.; Magal, P. What can we learn from COVID-19 data by using epidemic models with unidentified infectious cases? Math. Biosci. Eng. 2021, 19, 537–594. [Google Scholar] [CrossRef]
- Griette, Q.; Demongeot, J.; Magal, P. A robust phenomenological approach to investigate COVID-19 data for France. Math. Appl. Sci. Eng. 2021, 2, 149–218. [Google Scholar]
- Nishiura, H. Time variations in the transmissibility of pandemic influenza in Prussia, Germany, from 1918–19. Theor. Biol. Med. Model. 2007, 4, 20. [Google Scholar] [CrossRef]
- Nishiura, H.; Chowell, G. The Effective Reproduction Number as a Prelude to Statistical Estimation of Time-Dependent Epidemic Trends. In Mathematical and Statistical Estimation Approaches; Epidemiology, G., Chowell, J.M., Hyman, L.M., Bettencourt, A., Castillo-Chavez, C., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 103–121. [Google Scholar]
- Bakhta, A.; Boiveau, T.; Maday, Y.; Mula, O. Epidemiological forecasting with model reduction of compartmental models. application to the COVID-19 pandemic. Biology 2020, 10, 22. [Google Scholar] [CrossRef] [PubMed]
- Waku, J.; Oshinubi, K.; Demongeot, J. Maximal reproduction number estimation and identification of transmission rate from the first inflection point of new infectious cases waves: COVID-19 outbreak example. Math. Comput. Simul. 2022, 198, 47–64. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.M.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef] [PubMed]
- Whittle, P. Hypothesis Testing in Time Series Analysis. Almquist Wicksell 1951.
- Whittle, P. Prediction and Regulation; English Universities Press: London, UK, 1963. [Google Scholar]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; MIT Press: Cambridge, MA, USA, 1949. [Google Scholar]
- Chan, K.S.; Tong, H. A note on certain integral equations associated with non-linear time series analysis. Probab. Th. Rel. Fields 1986, 73, 153–158. [Google Scholar]
- Lim, K.S.; Tong, H. A statistical approach to difference-delay equation modelling in ecology—Two case studies. J. Time Ser. Anal. 1983, 4, 239–267. [Google Scholar] [CrossRef]
- Priestley, M.B. Spectral Analysis and Time Series; Academic Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Ramsay, J.O. Monotone Regression Splines in Action. Stat. Sci. 1988, 3, 425–441. [Google Scholar] [CrossRef]
- Ramsay, J.; Hooker, G. Dynamic Data Analysis: Modeling Data with Differential Equations; Springer: New York, NY, USA, 2017. [Google Scholar]
- Tong, H. Non-Linear Time Series: A Dynamical System Approach; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Tuan, P.D. The estimation of parameters for autoregressive moving average models. J. Time Ser. Anal. 1984, 5, 53–68. [Google Scholar]
- Priestley, M.B. Evolutionary spectra and non-stationary processes. J. R. Stat. Soc. Ser. 1965, 27, 204–229. [Google Scholar] [CrossRef]
- Malthus, T.R. An Essay on the Principle of Population as It Affects the Future Improvement of Society, with Remarks on the Speculations of Mr. Godwin, M. Condorcet, and Other Writers; J. Johnson: London, UK, 1798. [Google Scholar]
- Fisher, R.A. The Wave of Advance of Advantageous Genes. Ann. Eugen. 1937, 7, 353–369. [Google Scholar] [CrossRef]
- Lambert, J.H. Beytrage Zum Gebrauche Der Mathematik Und Deren Anwendung; Verlage des Buchladens der Realschule: Berlin, Germany, 1765; p. 72. [Google Scholar]
- Euler, L. Recherches générales sur la mortalité et la multiplication du genre humain. MéMoires L’AcadéMie Des Sci. Berl. 1767, 16, 144–164. [Google Scholar]
- Lotka, A.J. Relation between birth rates and death rates. Science 1907, 26, 121–130. [Google Scholar] [CrossRef]
- Leslie, P.H. On the use of matrices in certain population mathematics. Biometrika 1945, 33, 183–212. [Google Scholar] [CrossRef] [PubMed]
- Hahn, G.M. Mammalian cell populations. Math. Biosci. 1970, 6, 295–315. [Google Scholar] [CrossRef]
- Cazelles, B.; Chavez, M.; Magny, G.C.D.; Guégan, J.F.; Hales, S. Time-dependent spectral analysis of epidemiological time-series with wavelets. J. R. Soc. Interface 2007, 4, 625–636. [Google Scholar] [CrossRef]
- Robinson, E.A. Predictive deconvolution of time series with application to seismic exploration. Geophysics 1967, 32, 418–484. [Google Scholar] [CrossRef]
- Peacock, K.L.; Treitel, S. Predictive deconvolution: Theory and practice. Geophysics 1969, 34, 155–169. [Google Scholar] [CrossRef]
- Robinson, E.A.; Treitel, S. Geophysical Signal Analysis; Prentice-Hill, Inc.: Englewood Cliffs, NJ, USA, 1980. [Google Scholar]
- Walden, A.T.; Hosken, J.W.J. The nature of non-Gaussianity of primary reflection coefficients and its significance for deconvolution. Geophys. Prosp. 1986, 34, 1038–1066. [Google Scholar] [CrossRef]
- Vinod, D.; Cherstvy, A.G.; Wang, W.; Metzler, R.; Sokolov, I.M. Nonergodicity of reset geometric Brownian motion. Phys. Rev. E 2022, 105, L012106. [Google Scholar] [CrossRef]
- Ritschel, S.; Cherstvy, A.G.; Metzler, R. Universality of delay-time averages for financial time series: Analytical results, computer simulations, and analysis of historical stock-market prices. J. Phys. Complex. 2021, 2, 045003. [Google Scholar] [CrossRef]
- Data from WHO. Available online: https://COVID19.who.int/WHO-COVID-19-global-data.csv (accessed on 20 July 2022).
- Demongeot, J.; Oshinubi, K.; Rachdi, M.; Seligmann, H.; Thuderoz, F.; Waku, J. Estimation of Daily Reproduction Numbers during the COVID-19 Outbreak. Computation 2021, 9, 109. [Google Scholar] [CrossRef]
- Powered by the Institute of Global Health, Faculty of Medicine, University of Geneva and the Swiss Data Science Center, ETH Zürich-EPFL. Available online: https://renkulab.shinyapps.io/COVID-19-Epidemic-Forecasting/_w_850fb011/?tab=jhu_pred&country=Japan (accessed on 20 July 2022).
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef] [PubMed]
- Scire, J.; Nadeau, S.; Vaughan, T.; Brupbacher, G.; Fuchs, S.; Sommer, J.; Koch, K.N.; Misteli, R.; Mundorff, L.; Götz, T.; et al. Reproductive number of the COVID-19 epidemic in Switzerland with a focus on the Cantons of Basel-Stadt and Basel-Landschaft. Swiss Med. Wkly. 2020, 150, w20271. [Google Scholar] [PubMed]
- Kawasuji, H.; Takegoshi, Y.; Kaneda, M.; Ueno, A.; Miyajima, Y.; Kawago, K.; Fukui, Y.; Yoshida, Y.; Kimura, M.; Yamada, H.; et al. Transmissibility of COVID-19 depends on the viral load around onset in adult and symptomatic patients. PLoS ONE 2020, 15, e0243597. [Google Scholar] [CrossRef]
- Kim, S.E.; Jeong, H.S.; Yu, Y.; Shin, S.U.; Kim, S.; Oh, T.H.; Kim, U.J.; Kang, S.J.; Jang, H.C.; Jung, S.I.; et al. Viral kinetics of SARS-CoV-2 in asymptomatic carriers and presymptomatic patients. Int. J. Infect. Dis. 2020, 95, 441–443. [Google Scholar] [CrossRef]
- Ioannidis, J.P.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2022, 38, 423–438. [Google Scholar] [CrossRef]
- Ducrot, A.; Griette, Q.; Liu, Z.; Magal, P. Differential Equations and Population Dynamics I: Introductory Approaches; Springer Nature: Berlin, Germany, 2022. [Google Scholar]
- Kirkland, S. On the spectrum of a Leslie matrix with a near-periodic fecundity pattern. Linear Algebra Its Appl. 1993, 178, 261–279. [Google Scholar] [CrossRef]


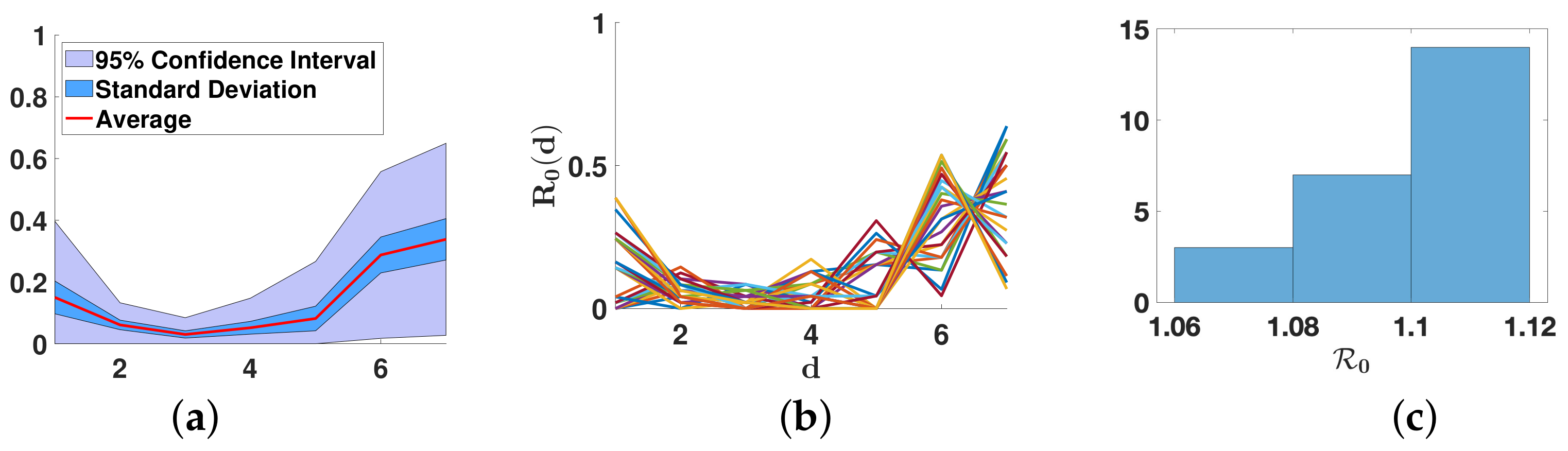
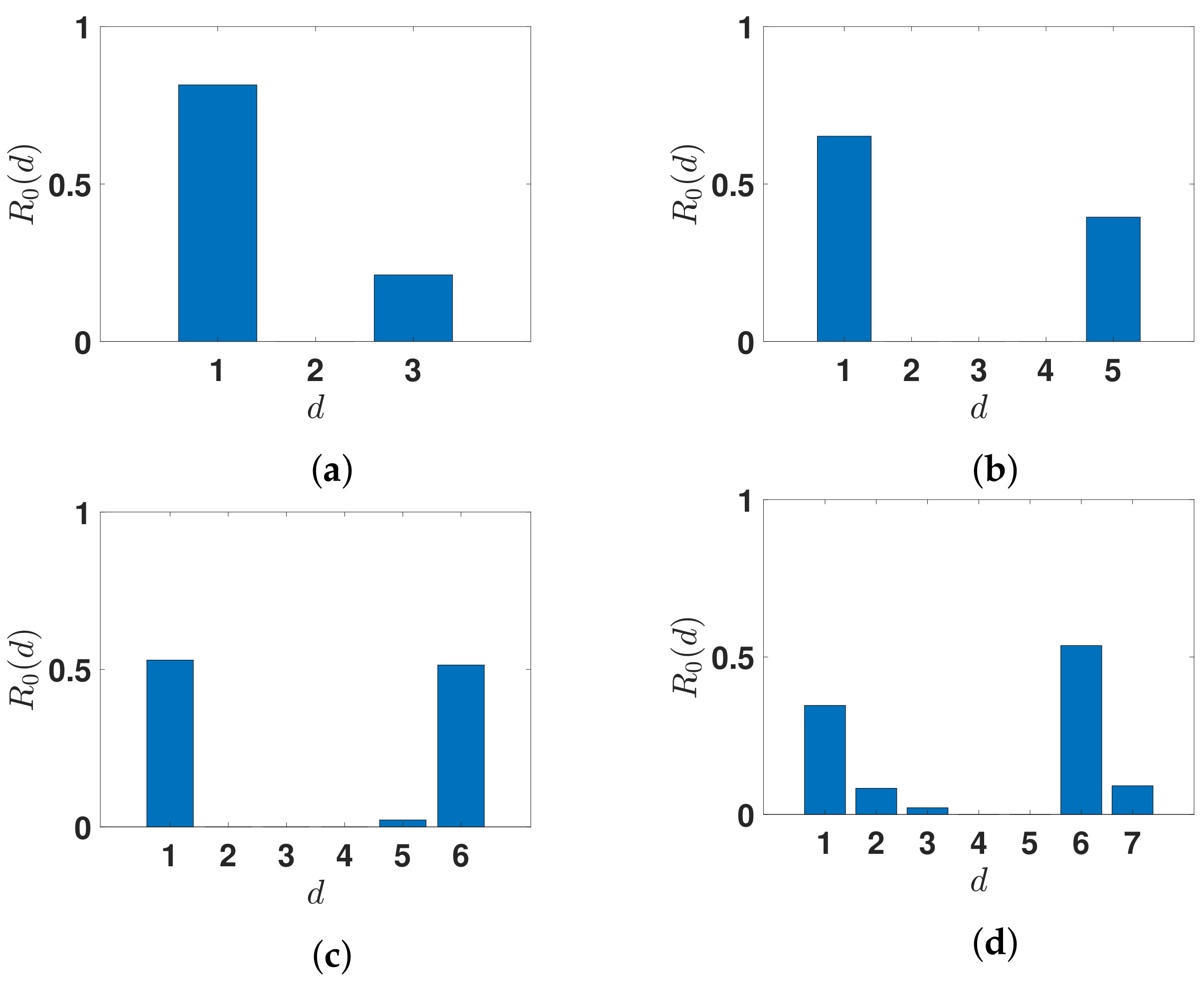



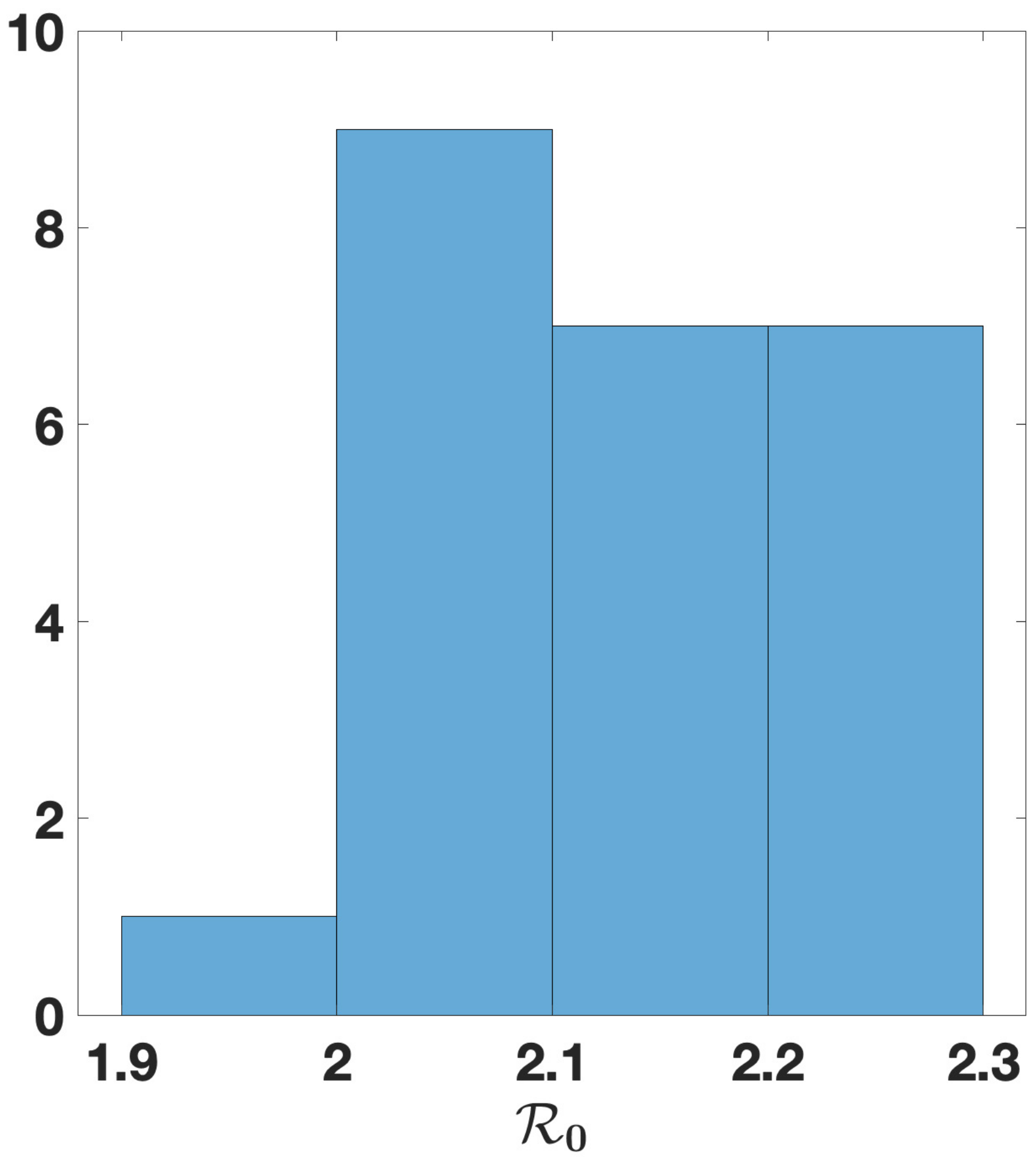

| n | 3 | 5 | 6 | 7 |
|---|---|---|---|---|
| 1.02 | 1.04 | 1.06 | 1.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demongeot, J.; Magal, P. Spectral Method in Epidemic Time Series: Application to COVID-19 Pandemic. Biology 2022, 11, 1825. https://doi.org/10.3390/biology11121825
Demongeot J, Magal P. Spectral Method in Epidemic Time Series: Application to COVID-19 Pandemic. Biology. 2022; 11(12):1825. https://doi.org/10.3390/biology11121825
Chicago/Turabian StyleDemongeot, Jacques, and Pierre Magal. 2022. "Spectral Method in Epidemic Time Series: Application to COVID-19 Pandemic" Biology 11, no. 12: 1825. https://doi.org/10.3390/biology11121825
APA StyleDemongeot, J., & Magal, P. (2022). Spectral Method in Epidemic Time Series: Application to COVID-19 Pandemic. Biology, 11(12), 1825. https://doi.org/10.3390/biology11121825








