Genome-Wide Study of Colocalization between Genomic Stretches: A Method and Applications to the Regulation of Gene Expression
Simple Summary
Abstract
1. Introduction
2. Theory and Methods
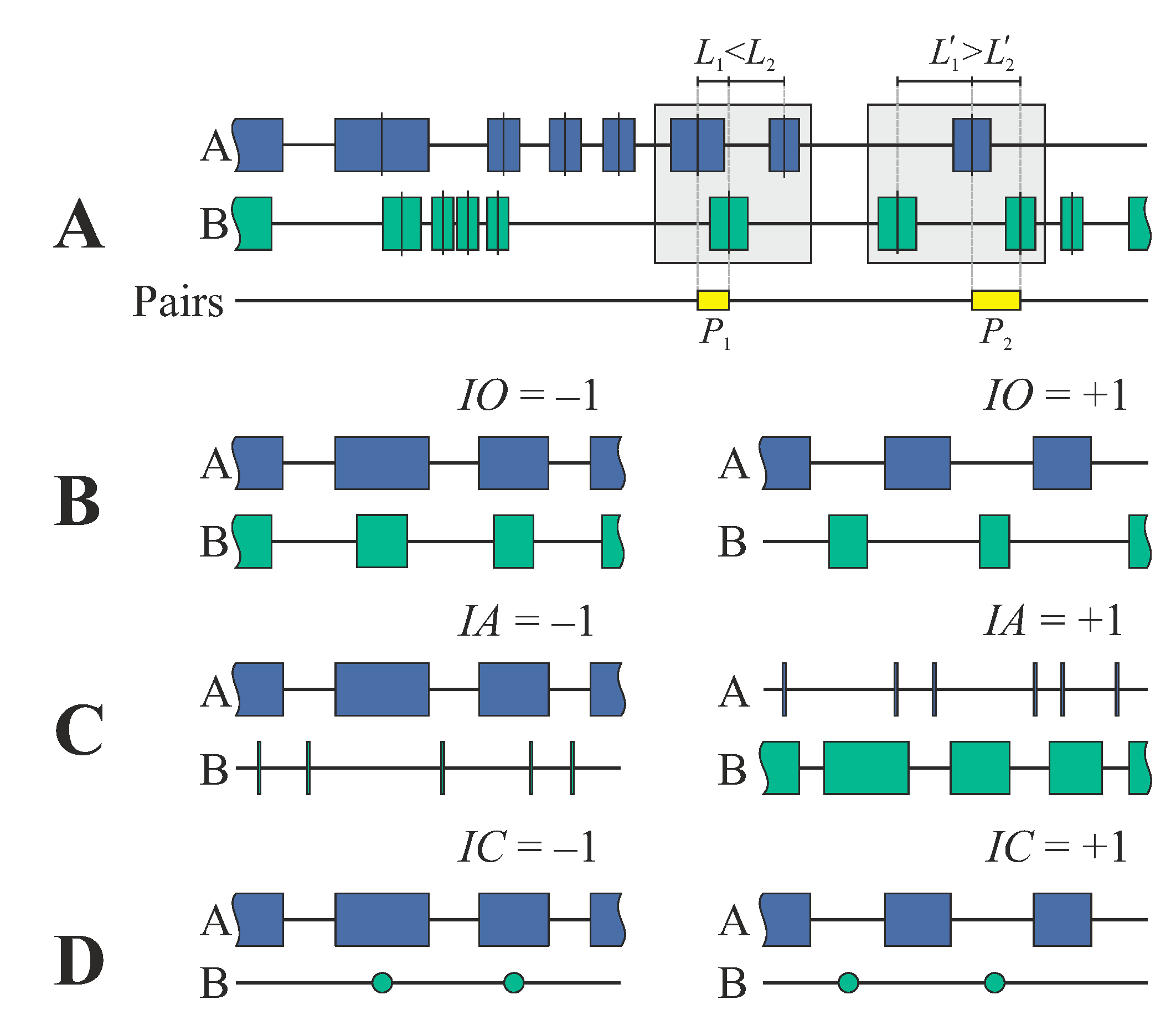
2.1. Characterizing Stretch–Stretch and Stretch–Point Characteristics by Sets of Indices
- (i)
- The index of overlapping (IO) characterizes mutual stretch–stretch colocalization and is defined as:where k refers to the k-th pair of the nearest neighbors, and denote the sites of stretch centers over the genome, is the distance between the centers of neighboring stretches, and ak and bk denote the lengths of the stretches.
- (ii)
- The index of asymmetry (IA) characterizes the skewness between the lengths of the k-th nearest neighbors:
- (iii)
- The index of coverage (IC) characterizes the mutual colocalization between stretches (A) and points (B):
2.2. Statistical Criteria
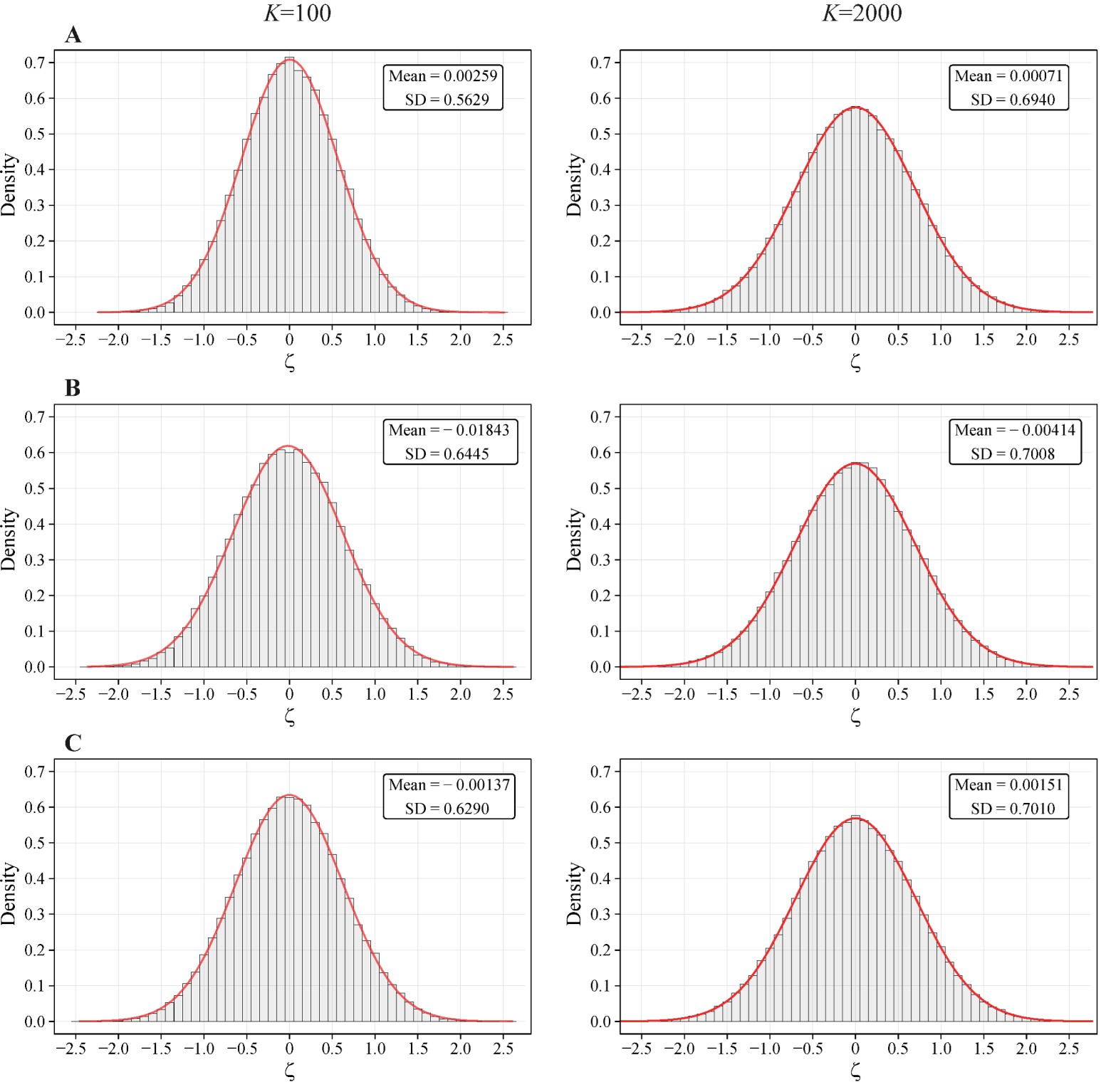
2.3. Simulations
2.4. Extension to AABB/BBAA Patterns
3. Results
3.1. Test: Colocalization between Exons and Random Stretches
- If structural entropy criterion for each of the stretch sets (that means the centers of stretches for both sets are distributed non-randomly), then Equation (7) is applied.
- If the positions of centers for one of the stretch sets are distributed non-randomly (), whereas the other centers are distributed randomly (), the general colocalization should be assessed via either criterion (6a) or (6b) (and the respective ) for the random set.
- If the positions of centers for both stretch sets are random ( for each set), then Equation (7) is applied again.
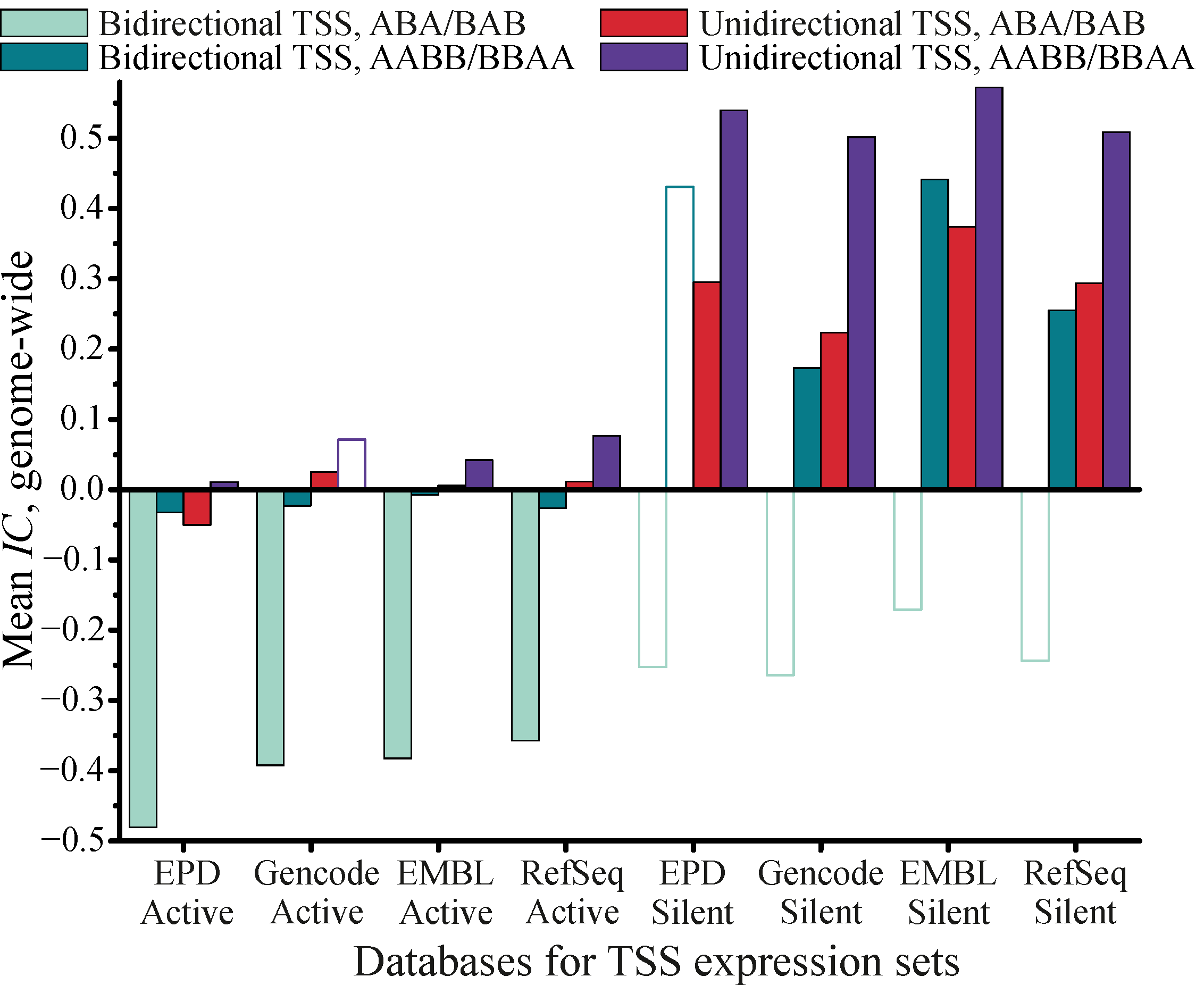
3.2. Colocalization between Stretches and Gene Expression
3.2.1. Strong Colocalization between CpG Islands and Exons Suggests a Role of CGI in Transcription
3.2.2. Strong Colocalization between CpG Islands and Transcription Start Sites Confirms CGIs Take Part in Transcription Regulation
3.2.3. Strong Colocalization between CpG Islands and DNAseI Hypersensitivity Sites Suggests That CGIs Often Correspond to Open Chromatin Regions
3.2.4. Genome-Wide Study of Colocalization between Promoters and Histone Mark H2A.Z (Isoform H2AFZ) for Cell Line K562
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kappelmann-Fenzl, M. Next Generation Sequencing and Data Analysis; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Davis, C.A.; Hitz, B.C.; Sloan, C.A.; Chan, E.T.; Davidson, J.M.; Gabdank, I.; Hilton, J.A.; Jain, K.; Baymuradov, U.K.; Narayanan, A.K.; et al. The encyclopedia of DNA elements (ENCODE): Data portal update. Nucleic. Acids Res. 2018, 46, D794–D801. [Google Scholar] [CrossRef]
- Dreos, R.; Ambrosini, G.; Groux, R.; Cavin Perier, R.; Bucher, P. The eukaryotic promoter database in its 30th year: Focus on non-vertebrate organisms. Nucleic. Acids Res. 2017, 45, D51–D55. [Google Scholar] [CrossRef]
- Frankish, A.; Diekhans, M.; Ferreira, A.M.; Johnson, R.; Jungreis, I.; Loveland, J.; Mudge, J.M.; Sisu, C.; Wright, J.; Armstrong, J.; et al. GENCODE reference annotation for the human and mouse genomes. Nucleic. Acids Res. 2019, 47, D766–D773. [Google Scholar] [CrossRef]
- Barrett, T.; Wilhite, S.E.; Ledoux, P.; Evangelista, C.; Kim, I.F.; Tomashevsky, M.; Marshall, K.A.; Phillippy, K.H.; Sherman, P.M.; Holko, M.; et al. NCBI GEO: Archive for functional genomics data sets--update. Nucleic. Acids Res. 2013, 41, D991–D995. [Google Scholar] [CrossRef]
- Andersson, R.; Gebhard, C.; Miguel-Escalada, I.; Hoof, I.; Bornholdt, J.; Boyd, M.; Chen, Y.; Zhao, X.; Schmidl, C.; Suzuki, T.; et al. An atlas of active enhancers across human cell types and tissues. Nature 2014, 507, 455–461. [Google Scholar] [CrossRef]
- Ranganathan, S.; Gribskov, M.R.; Nakai, K.; Schönbach, C. Encyclopedia of Bioinformatics and Computational Biology: ABC of Bioinformatics, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2019; Volume 1–3, p. 3284. [Google Scholar]
- Kravatsky, Y.V.; Chechetkin, V.R.; Tchurikov, N.A.; Kravatskaya, G.I. Genome-wide study of correlations between genomic features and their relationship with the regulation of gene expression. DNA Res. 2015, 22, 109–119. [Google Scholar] [CrossRef]
- Favorov, A.; Mularoni, L.; Cope, L.M.; Medvedeva, Y.; Mironov, A.A.; Makeev, V.J.; Wheelan, S.J. Exploring massive, genome scale datasets with the GenometriCorr package. PLoS Comput. Biol. 2012, 8, e1002529. [Google Scholar] [CrossRef]
- Heger, A.; Webber, C.; Goodson, M.; Ponting, C.P.; Lunter, G. GAT: A simulation framework for testing the association of genomic intervals. Bioinformatics 2013, 29, 2046–2048. [Google Scholar] [CrossRef]
- Gel, B.; Diez-Villanueva, A.; Serra, E.; Buschbeck, M.; Peinado, M.A.; Malinverni, R. RegioneR: An R/Bioconductor package for the association analysis of genomic regions based on permutation tests. Bioinformatics 2016, 32, 289–291. [Google Scholar] [CrossRef]
- Sheffield, N.C.; Bock, C. LOLA: Enrichment analysis for genomic region sets and regulatory elements in R and Bioconductor. Bioinformatics 2016, 32, 587–589. [Google Scholar] [CrossRef]
- Layer, R.M.; Pedersen, B.S.; DiSera, T.; Marth, G.T.; Gertz, J.; Quinlan, A.R. GIGGLE: A search engine for large-scale integrated genome analysis. Nat. Methods 2018, 15, 123–126. [Google Scholar] [CrossRef]
- Guo, Y.F.; Li, J.; Chen, Y.; Zhang, L.S.; Deng, H.W. A new permutation strategy of pathway-based approach for genome-wide association study. BMC Bioinform. 2009, 10, 429. [Google Scholar] [CrossRef]
- De, S.; Pedersen, B.S.; Kechris, K. The dilemma of choosing the ideal permutation strategy while estimating statistical significance of genome-wide enrichment. Brief. Bioinform. 2014, 15, 919–928. [Google Scholar] [CrossRef]
- Che, R.; Jack, J.R.; Motsinger-Reif, A.A.; Brown, C.C. An adaptive permutation approach for genome-wide association study: Evaluation and recommendations for use. BioData Min. 2014, 7, 9. [Google Scholar] [CrossRef]
- Stavrovskaya, E.D.; Niranjan, T.; Fertig, E.J.; Wheelan, S.J.; Favorov, A.V.; Mironov, A.A. StereoGene: Rapid estimation of genome-wide correlation of continuous or interval feature data. Bioinformatics 2017, 33, 3158–3165. [Google Scholar] [CrossRef]
- Simovski, B.; Kanduri, C.; Gundersen, S.; Titov, D.; Domanska, D.; Bock, C.; Bossini-Castillo, L.; Chikina, M.; Favorov, A.; Layer, R.M.; et al. Coloc-Stats: A unified web interface to perform colocalization analysis of genomic features. Nucleic. Acids Res. 2018, 46, W186–W193. [Google Scholar] [CrossRef]
- Chechetkin, V.R. Statistics of genome architecture. Phys. Lett. A 2013, 377, 3312–3316. [Google Scholar] [CrossRef]
- Krinner, S.; Heitzer, A.P.; Diermeier, S.D.; Obermeier, I.; Langst, G.; Wagner, R. CpG domains downstream of TSSs promote high levels of gene expression. Nucleic. Acids Res. 2014, 42, 3551–3564. [Google Scholar] [CrossRef]
- Wu, H.; Caffo, B.; Jaffee, H.A.; Irizarry, R.A.; Feinberg, A.P. Redefining CpG islands using hidden Markov models. Biostatistics 2010, 11, 499–514. [Google Scholar] [CrossRef]
- Illingworth, R.S.; Bird, A.P. CpG islands–‘a rough guide’. FEBS Lett. 2009, 583, 1713–1720. [Google Scholar] [CrossRef]
- Bell, C.G.; Wilson, G.A.; Butcher, L.M.; Roos, C.; Walter, L.; Beck, S. Human-specific CpG "beacons" identify loci associated with human-specific traits and disease. Epigenetcs 2012, 7, 1188–1199. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.M.; Zhou, P.; Wang, L.Y.; Li, Z.H.; Zhang, Y.N.; Zhang, Y.X. Correlation between DNAse I hypersensitive site distribution and gene expression in HeLa S3 cells. PLoS ONE 2012, 7, e42414. [Google Scholar] [CrossRef]
- Mercer, T.R.; Edwards, S.L.; Clark, M.B.; Neph, S.J.; Wang, H.; Stergachis, A.B.; John, S.; Sandstrom, R.; Li, G.; Sandhu, K.S.; et al. DNAse I-hypersensitive exons colocalize with promoters and distal regulatory elements. Nat. Genet 2013, 45, 852–859. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, J.; Noh, K.M.; Choi, W.Y.; Jeon, S.; Oh, G.T.; Kim-Ha, J.; Jin, Y.; Cho, S.W.; Kim, Y.J. Intragenic CpG islands play important roles in bivalent chromatin assembly of developmental genes. Proc. Natl. Acad. Sci. USA 2017, 114, E1885–E1894. [Google Scholar] [CrossRef] [PubMed]
- Sarda, S.; Hannenhalli, S. Orphan CpG islands as alternative promoters. Transcription 2018, 9, 171–176. [Google Scholar] [CrossRef]
- Deaton, A.M.; Bird, A. CpG islands and the regulation of transcription. Genes Dev. 2011, 25, 1010–1022. [Google Scholar] [CrossRef] [PubMed]
- Tchurikov, N.A.; Kretova, O.V.; Moiseeva, E.D.; Sosin, D.V. Evidence for RNA synthesis in the intergenic region between enhancer and promoter and its inhibition by insulators in Drosophila Melanogaster. Nucleic. Acids Res. 2009, 37, 111–122. [Google Scholar] [CrossRef][Green Version]
- Kim, T.K.; Hemberg, M.; Gray, J.M.; Costa, A.M.; Bear, D.M.; Wu, J.; Harmin, D.A.; Laptewicz, M.; Barbara-Haley, K.; Kuersten, S.; et al. Widespread transcription at neuronal activity-regulated enhancers. Nature 2010, 465, 182–187. [Google Scholar] [CrossRef]
- Richard, P.; Manley, J.L. How bidirectional becomes unidirectional. Nat. Struct. Mol. Biol. 2013, 20, 1022–1024. [Google Scholar] [CrossRef]
- Tchurikov, N.A.; Alembekov, I.R.; Klushevskaya, E.S.; Kretova, A.N.; Keremet, A.M.; Sidorova, A.E.; Meilakh, P.B.; Chechetkin, V.R.; Kravatskaya, G.I.; Kravatsky, Y.V. Genes possessing the most frequent DNA DSBs are highly associated with development and cancers, and essentially overlap with the rDNA-contacting genes. Int. J. Mol. Sci. 2022, 23, 7201. [Google Scholar] [CrossRef]
- Scruggs, B.S.; Gilchrist, D.A.; Nechaev, S.; Muse, G.W.; Burkholder, A.; Fargo, D.C.; Adelman, K. Bidirectional transcription arises from two distinct hubs of transcription factor binding and active chromatin. Mol. Cell 2015, 58, 1101–1112. [Google Scholar] [CrossRef] [PubMed]
- Santisteban, M.S.; Hang, M.; Smith, M.M. Histone variant H2A.Z and RNA–polymerase II transcription elongation. Mol. Cell Biol. 2011, 31, 1848–1860. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Roberts, D.N.; Cairns, B.R. Genome-wide dynamics of Htz1, a histone H2A variant that poises repressed/basal promoters for activation through histone loss. Cell 2005, 123, 219–231. [Google Scholar] [CrossRef] [PubMed]
- Wan, Y.; Saleem, R.A.; Ratushny, A.V.; Roda, O.; Smith, J.J.; Lin, C.H.; Chiang, J.H.; Aitchison, J.D. Role of the histone variant H2A.Z/Htz1p in TBP recruitment, chromatin dynamics, and regulated expression of oleate-responsive genes. Mol. Cell Biol. 2009, 29, 2346–2358. [Google Scholar] [CrossRef] [PubMed]
- Raisner, R.M.; Hartley, P.D.; Meneghini, M.D.; Bao, M.Z.; Liu, C.L.; Schreiber, S.L.; Rando, O.J.; Madhani, H.D. Histone variant H2A.Z marks the 5′ ends of both active and inactive genes in euchromatin. Cell 2005, 123, 233–248. [Google Scholar] [CrossRef] [PubMed]
- Guillemette, B.; Bataille, A.R.; Gevry, N.; Adam, M.; Blanchette, M.; Robert, F.; Gaudreau, L. Variant histone H2A.Z is globally localized to the promoters of inactive yeast genes and regulates nucleosome positioning. PLoS Biol. 2005, 3, e384. [Google Scholar] [CrossRef]
- Li, A.; Eirin-Lopez, J.M.; Ausio, J. H2AX: Tailoring histone H2A for chromatin-dependent genomic integrity. Biochem Cell Biol. 2005, 83, 505–515. [Google Scholar] [CrossRef]
- Albert, I.; Mavrich, T.N.; Tomsho, L.P.; Qi, J.; Zanton, S.J.; Schuster, S.C.; Pugh, B.F. Translational and rotational settings of H2A.Z nucleosomes across the Saccharomyces Cerevisiae genome. Nature 2007, 446, 572–576. [Google Scholar] [CrossRef]
- Barski, A.; Cuddapah, S.; Cui, K.; Roh, T.Y.; Schones, D.E.; Wang, Z.; Wei, G.; Chepelev, I.; Zhao, K. High-resolution profiling of histone methylations in the human genome. Cell 2007, 129, 823–837. [Google Scholar] [CrossRef]
- Jin, C.; Felsenfeld, G. Nucleosome stability mediated by histone variants H3.3 and H2A.Z. Genes Dev 2007, 21, 1519–1529. [Google Scholar] [CrossRef]
- Schones, D.E.; Cui, K.; Cuddapah, S.; Roh, T.Y.; Barski, A.; Wang, Z.; Wei, G.; Zhao, K. Dynamic regulation of nucleosome positioning in the human genome. Cell 2008, 132, 887–898. [Google Scholar] [PubMed]
- Giaimo, B.D.; Ferrante, F.; Herchenrother, A.; Hake, S.B.; Borggrefe, T. The histone variant H2A.Z in gene regulation. Epigenetics Chromatin 2019, 12, 37. [Google Scholar] [CrossRef] [PubMed]
- Rangasamy, D.; Berven, L.; Ridgway, P.; Tremethick, D.J. Pericentric heterochromatin becomes enriched with H2A.Z during early mammalian development. EMBO J. 2003, 22, 1599–1607. [Google Scholar] [CrossRef] [PubMed]
- Rangasamy, D.; Greaves, I.; Tremethick, D.J. RNA interference demonstrates a novel role for H2A.Z in chromosome segregation. Nat. Struct. Mol. Biol. 2004, 11, 650–655. [Google Scholar] [CrossRef]
- Ridgway, P.; Rangasamy, D.; Berven, L.; Svensson, U.; Tremethick, D.J. Analysis of histone variant H2A.Z localization and expression during early development. Methods Enzym. 2004, 375, 239–252. [Google Scholar]
- Xu, Y.; Ayrapetov, M.K.; Xu, C.; Gursoy-Yuzugullu, O.; Hu, Y.; Price, B.D. Histone H2A.Z controls a critical chromatin remodeling step required for DNA double-strand break repair. Mol. Cell 2012, 48, 723–733. [Google Scholar] [CrossRef]
- Talbert, P.B.; Henikoff, S. Histone variants on the move: Substrates for chromatin dynamics. Nat. Rev. Mol. Cell Biol. 2017, 18, 115–126. [Google Scholar] [CrossRef]
- Rudnizky, S.; Bavly, A.; Malik, O.; Pnueli, L.; Melamed, P.; Kaplan, A. H2A.Z controls the stability and mobility of nucleosomes to regulate expression of the LH genes. Nat. Commun. 2016, 7, 12958. [Google Scholar] [CrossRef]
- Chen, Z.; Gabizon, R.; Brown, A.I.; Lee, A.; Song, A.; Diaz-Celis, C.; Kaplan, C.D.; Koslover, E.F.; Yao, T.; Bustamante, C. High-resolution and high-accuracy topographic and transcriptional maps of the nucleosome barrier. Elife 2019, 8, e48281. [Google Scholar] [CrossRef]
- O’Leary, N.A.; Wright, M.W.; Brister, J.R.; Ciufo, S.; Haddad, D.; McVeigh, R.; Rajput, B.; Robbertse, B.; Smith-White, B.; Ako-Adjei, D.; et al. Reference sequence (RefSeq) database at NCBI: Current status, taxonomic expansion, and functional annotation. Nucleic. Acids Res. 2016, 44, D733–D745. [Google Scholar] [CrossRef]
- Horikoshi, N.; Kujirai, T.; Sato, K.; Kimura, H.; Kurumizaka, H. Structure-based design of an H2A.Z.1 mutant stabilizing a nucleosome in vitro and in vivo. Biochem. Biophys. Res. Commun. 2019, 515, 719–724. [Google Scholar] [CrossRef] [PubMed]
- Bargaje, R.; Alam, M.P.; Patowary, A.; Sarkar, M.; Ali, T.; Gupta, S.; Garg, M.; Singh, M.; Purkanti, R.; Scaria, V.; et al. Proximity of H2A.Z containing nucleosome to the transcription start site influences gene expression levels in the mammalian liver and brain. Nucleic. Acids. Res. 2012, 40, 8965–8978. [Google Scholar] [CrossRef] [PubMed]
- Chechetkin, V.R.; Lobzin, V.V. Evolving ribonucleocapsid assembly/packaging signals in the genomes of the human and animal coronaviruses: Targeting, transmission and evolution. J. Biomol. Struct. Dyn. 2021, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Chechetkin, V.; Lobzin, V. Combining detection and reconstruction of correlational and periodic motifs in viral genomic sequences with transitional genome mapping: Application to COVID-19. J. Integr. OMICS 2021, 11, 26–36. [Google Scholar] [CrossRef]




| Fraction of Events with Predicted p < 0.05 per 1000 MC Realizations | Benchmark, Time per 1 Run | |||
|---|---|---|---|---|
| Option | Pairs ≈ 50 | Pairs ≈ 500 | Pairs ≈ 5000 | Pairs ≈ 500 |
| regioneR [11] | ||||
| overlapPermTest p-value, exons–set A; random–set B | 0.024 | 0.082 | 0.093 | 543.6 s |
| region distance p-value, exons–set A; random–set B | 0.871 | 0.772 | 1.000 | |
| overlapPermTest p-value, random–set A; exons–set B | 0.026 | 0.080 | 0.051 | 543.6 s |
| region distance p-value, random–set A; exons–set B | 0.092 | 0.100 | 0.056 | |
| GenometriCorr [9] | ||||
| projection test p-value, exons–reference; random–query | 0.081 | 0.120 | 0.072 | 72.94 s |
| Jaccard test p-value, exons– reference; random–query | 0.065 | 0.105 | 0.074 | |
| projection test p-value, random–reference; exons–query | 0.090 | 0.088 | 0.098 | 72.94 s |
| Jaccard test p-value, random–reference; exons–query | 0.066 | 0.106 | 0.091 | |
| Genomic Association Tester [10] | ||||
| gat-run.py p-value, exons–annotation; random–segment | 0.067 | 0.108 | 0.080 | 24.96 s |
| gat-run.py p-value, random–annotation; exons–segment | 0.068 | 0.109 | 0.093 | 106.56 s |
| StereoGene [17] | ||||
| Mann Z-criterion, exons–reference; random–query, wSize = 5000 | 0.046 | 0.050 | 0.050 | 0.235 s |
| Mann Z-criterion, random–reference; exons–query, wSize = 5000 | 0.046 | 0.047 | 0.053 | 0.235 s |
| Genome Colocalization Track Analyzer | ||||
| United ζ-criterion, Equations (6), (7) and (15) | 0.049 | 0.052 | 0.050 | 0.233 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kravatsky, Y.V.; Chechetkin, V.R.; Tchurikov, N.A.; Kravatskaya, G.I. Genome-Wide Study of Colocalization between Genomic Stretches: A Method and Applications to the Regulation of Gene Expression. Biology 2022, 11, 1422. https://doi.org/10.3390/biology11101422
Kravatsky YV, Chechetkin VR, Tchurikov NA, Kravatskaya GI. Genome-Wide Study of Colocalization between Genomic Stretches: A Method and Applications to the Regulation of Gene Expression. Biology. 2022; 11(10):1422. https://doi.org/10.3390/biology11101422
Chicago/Turabian StyleKravatsky, Yuri V., Vladimir R. Chechetkin, Nickolai A. Tchurikov, and Galina I. Kravatskaya. 2022. "Genome-Wide Study of Colocalization between Genomic Stretches: A Method and Applications to the Regulation of Gene Expression" Biology 11, no. 10: 1422. https://doi.org/10.3390/biology11101422
APA StyleKravatsky, Y. V., Chechetkin, V. R., Tchurikov, N. A., & Kravatskaya, G. I. (2022). Genome-Wide Study of Colocalization between Genomic Stretches: A Method and Applications to the Regulation of Gene Expression. Biology, 11(10), 1422. https://doi.org/10.3390/biology11101422





