Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
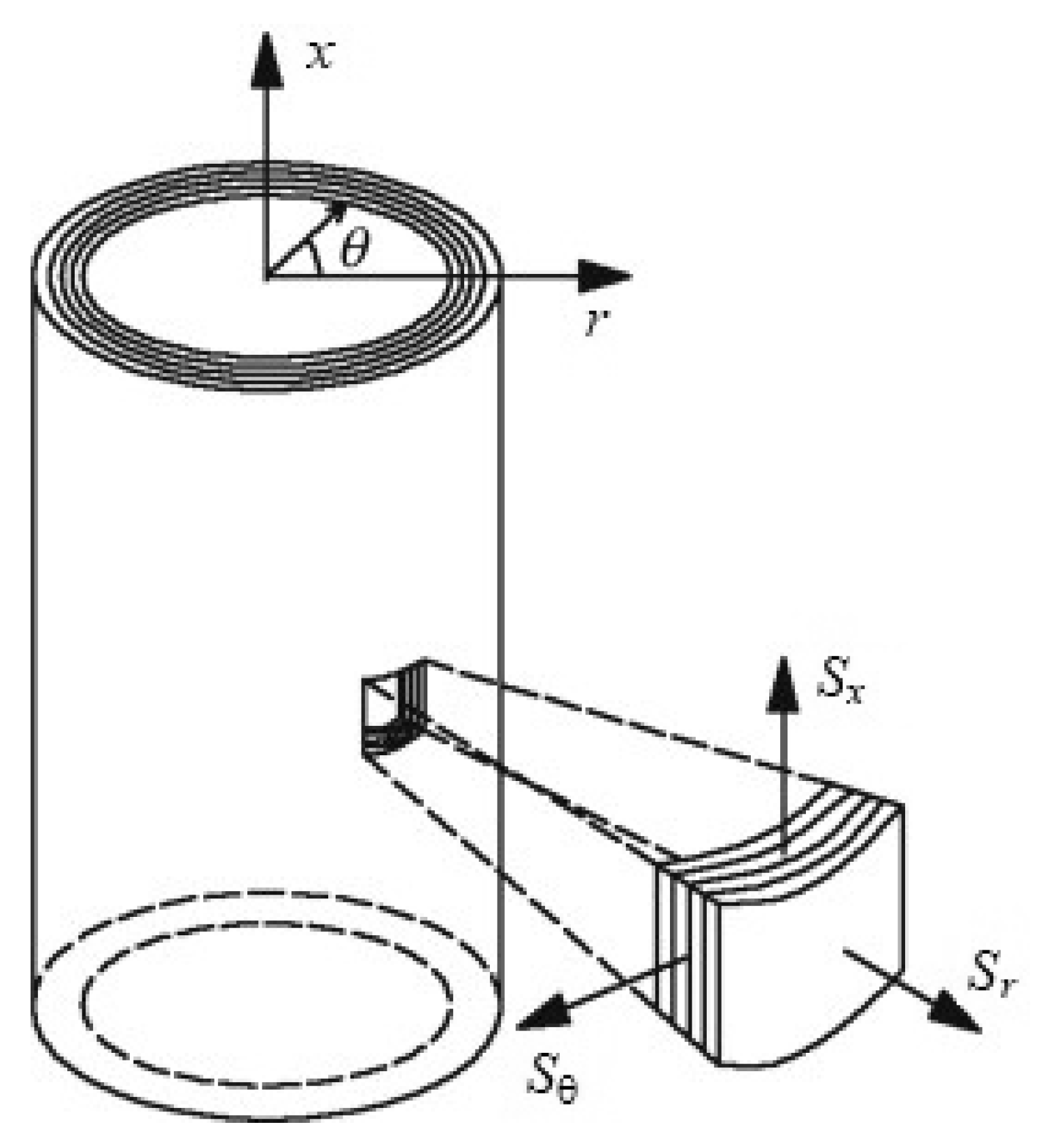
2.1. Material and Specimen Preparation
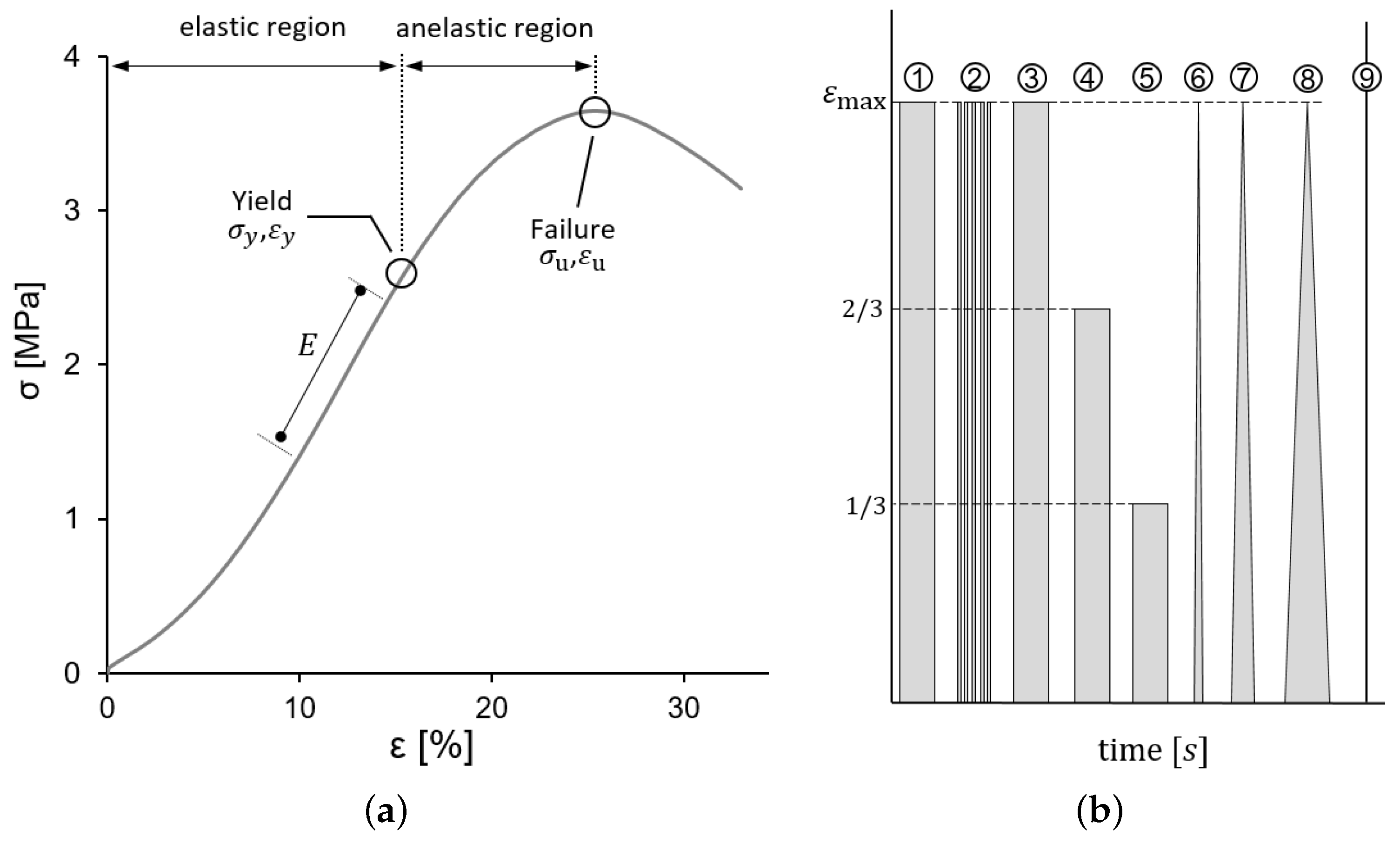
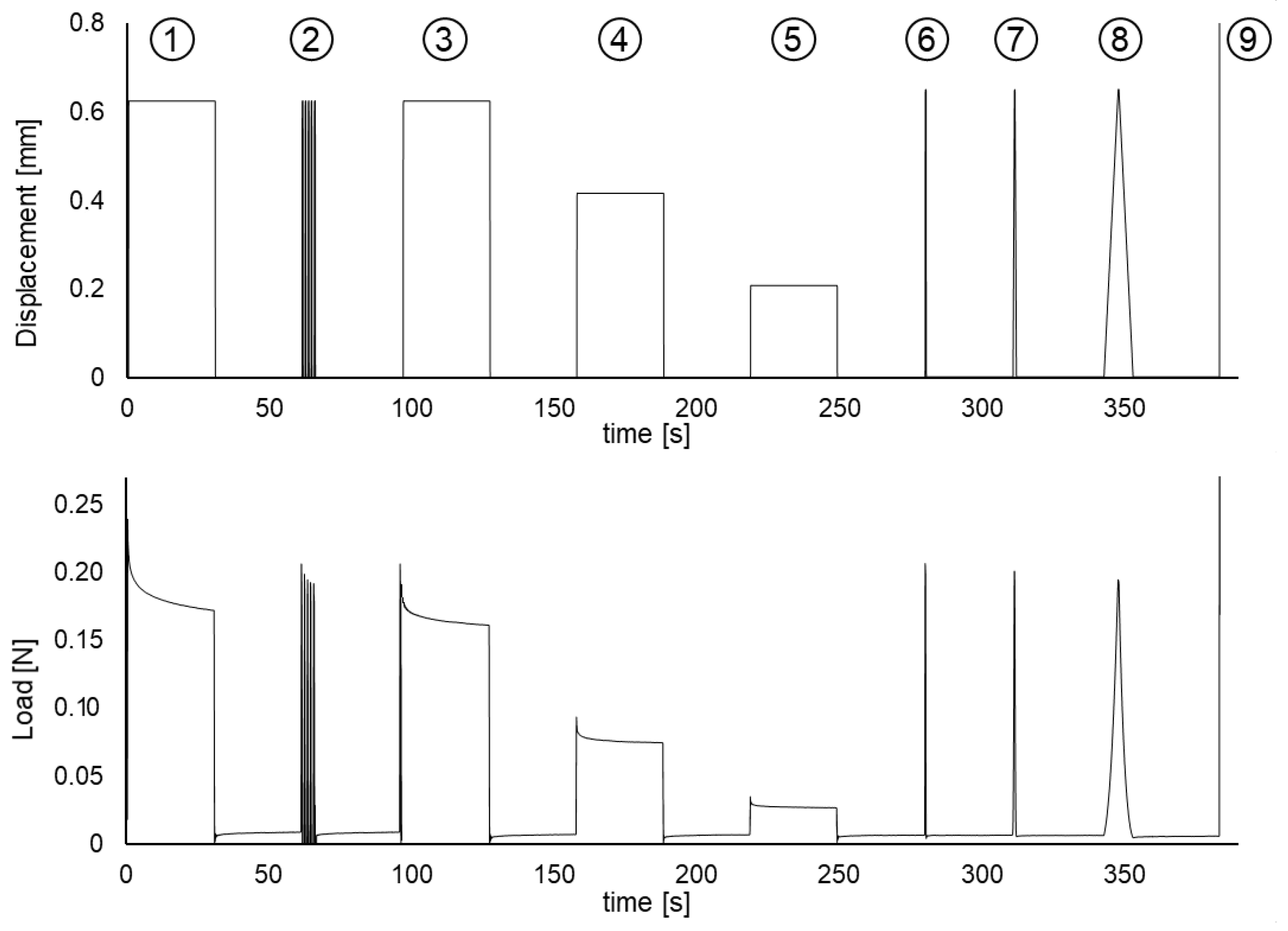
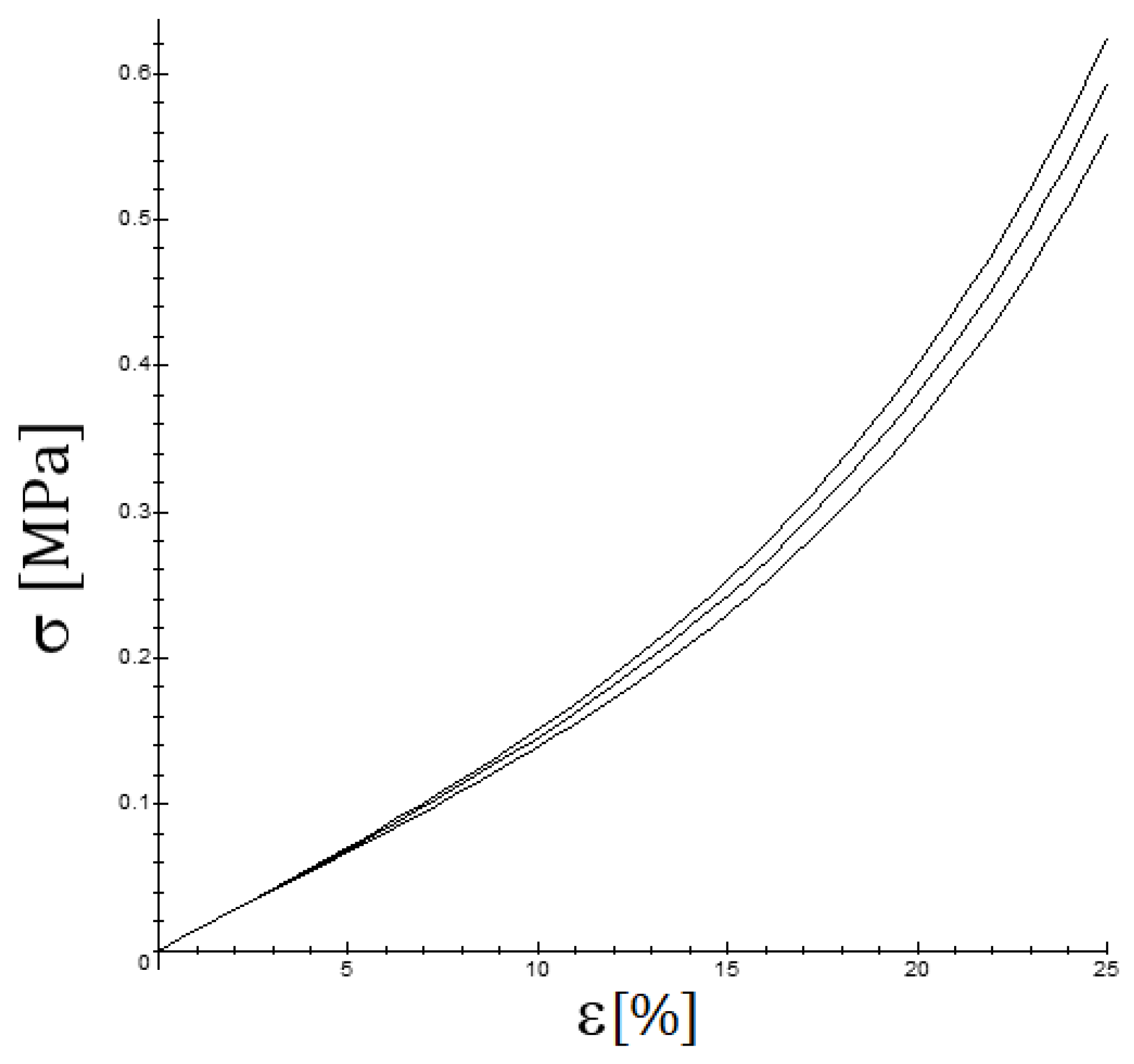
2.2. Mechanical Tests, Measures of Strain and Stress
2.3. Fung Models for Elastic and Viscoelastic Behavior
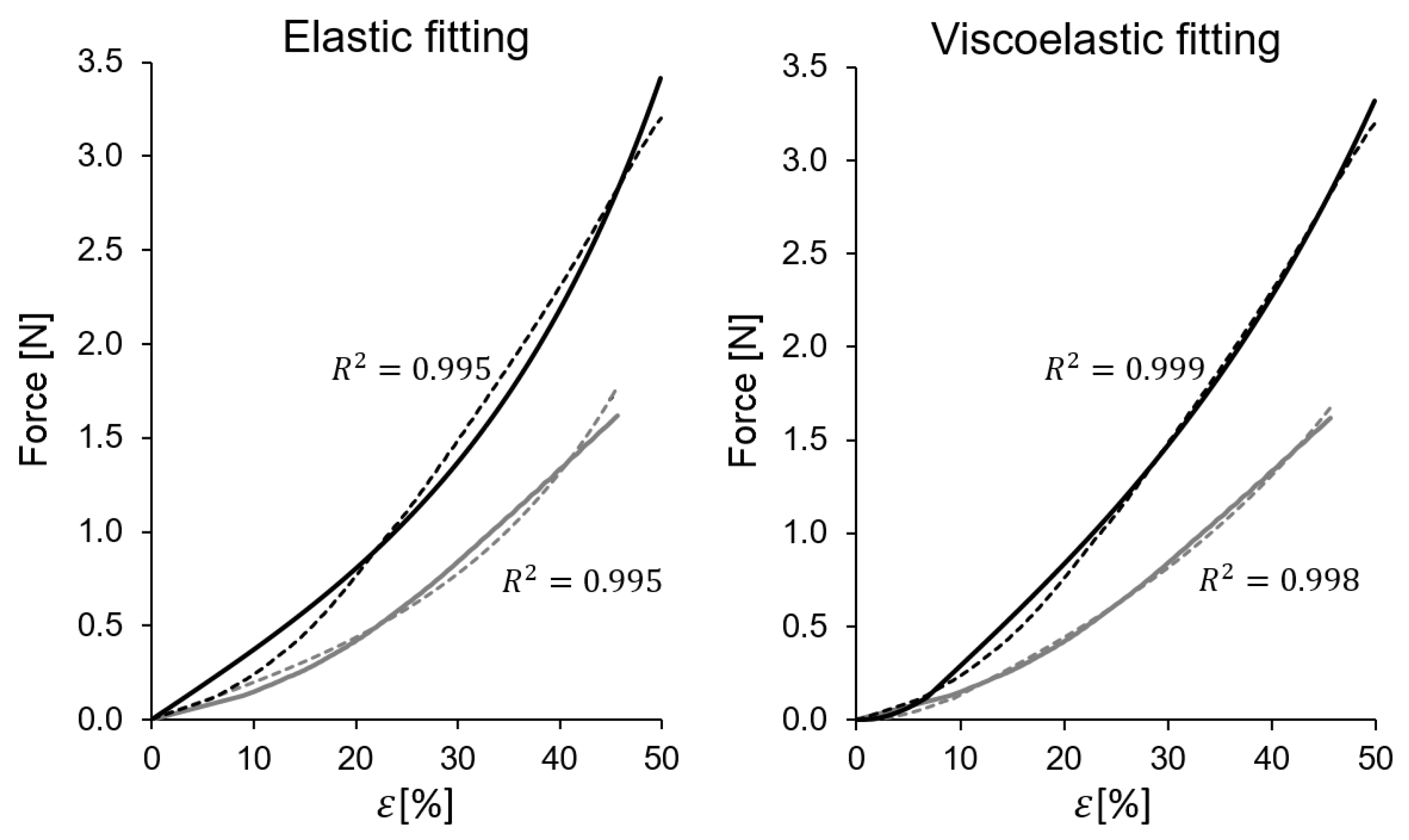
2.3.1. Elastic Fung Model
2.3.2. Viscoelastic Fung Model
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CBV(s) | Cerebral Bridging Vein(s) |
| FEHM | Finite Element Head Model |
| PMHS(s) | Post Mortem Human Subject(s) |
| QLVE | Quasi-Linear Viscoelastic |
| SDH | Subdural Hematoma |
| SEDF | Strain Energy Density Function |
| TBI | Traumatic Brain Injury |
| UTM | Universal Test Machine |
| VC | Viscoelastic Contribution |
| YM | Young’s modulus |
Appendix A. Viscoelastic Computations
References
- Dewan, M.C.; Rattani, A.; Gupta, S.; Baticulon, R.E.; Hung, Y.C.; Punchak, M.; Agrawal, A.; Adeleye, A.O.; Shrime, M.G.; Rubiano, A.M.; et al. Estimating the global incidence of traumatic brain injury. J. Neurosurg. 2018, 130, 1080–1097. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Graham, D.I.; Adams, J.H.; Nicoll, J.A.R.; Maxwell, W.L.; Gennarelli, T.A. The nature, distribution and causes of traumatic brain injury. Brain Pathol. 1995, 5, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Monea, A.G.; Baeck, K.; Verbeken, E.; Verpoest, I.; Vander Sloten, J.; Goffin, J.; Depreitere, B. The biomechanical behaviour of the bridging vein–superior sagittal sinus complex with implications for the mechanopathology of acute subdural haematoma. J. Mech. Behav. Biomed. Mater. 2014, 32, 155–165. [Google Scholar] [CrossRef]
- Depreitere, B.; Van Lierde, C.; Vander Sloten, J.; Van Audekercke, R.; Van Der Perre, G.; Plets, C.; Goffin, J. Mechanics of acute subdural hematomas resulting from bridging vein rupture. J. Neurosurg. 2006, 104, 950–956. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chauhan, N.B. Chronic neurodegenerative consequences of traumatic brain injury. Restor. Neurol. Neurosci. 2014, 32, 337–365. [Google Scholar] [CrossRef] [PubMed]
- Padula, W.V.; Capo-Aponte, J.E.; Padula, W.V.; Singman, E.L.; Jenness, J. The consequence of spatial visual processing dysfunction caused by traumatic brain injury (TBI). Brain Inj. 2017, 31, 589–600. [Google Scholar] [CrossRef]
- Jourdan, C.; Azouvi, P.; Genêt, F.; Selly, N.; Josseran, L.; Schnitzler, A. Disability and health consequences of traumatic brain injury: National prevalence. Am. J. Phys. Med. Rehabil. 2018, 97, 323–331. [Google Scholar] [CrossRef]
- Konda, S.; Tiesman, H.M.; Reichard, A.A. Fatal traumatic brain injuries in the construction industry, 2003–2010. Am. J. Ind. Med. 2016, 59, 212–220. [Google Scholar] [CrossRef]
- Monson, K.L.; Converse, M.I.; Manley, G.T. Cerebral blood vessel damage in traumatic brain injury. Clin. Biomech. 2019, 64, 98–113. [Google Scholar] [CrossRef]
- Delteil, C.; Kolopp, M.; Torrents, J.; Hedouin, V.; Fanton, L.; Leonetti, G.; Tuchtan, L.; Piercecchi, M.D. Descriptive data on intracranial hemorrhage related to fatal non-accidental head injury in a pediatric population. Revue Médecine Légale 2020, 11, 68–73. [Google Scholar] [CrossRef]
- Porto, L.; Bartels, M.B.; Zwaschka, J.; You, S.J.; Polkowski, C.; Luetkens, J.; Endler, C.; Kieslich, M.; Hattingen, E. Abusive head trauma: Experience improves diagnosis. Neuroradiology 2021, 63, 417–430. [Google Scholar] [CrossRef]
- Lee, K.S. Chronic subdural hematoma in the aged, trauma or degeneration? J. Korean Neurosurg. Soc. 2016, 59, 1–5. [Google Scholar] [CrossRef]
- Oehmichen, M.; Auer, R.N.; König, H.G. Forensic Neuropathology and Associated Neurology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; ISBN 978-1-28-041343-8. [Google Scholar]
- Sokolowski, S.; Fabian, F. On the Problem of the Mechanical Resistance of Cerebral Bridge Veins. Rocz. Pomor. Akad. Med. Gen. Karola Swierczewskiego Szczecinie 1961, 7, 301–308. [Google Scholar]
- Lodi, C.A.; Ursine, M.; Minassian, A.T.; Beydon, L. A Mathematical Model of Intracranial Pressure and Cerebral Hemodynamics Response to CO2 Changes. WIT Trans. Biomed. Health 1997, 4. [Google Scholar] [CrossRef]
- Famaey, N.; Cui, Z.Y.; Musigazi, G.U.; Ivens, J.; Depreitere, B.; Verbeken, E.; Van der Sloten, J. Structural and mechanical characterisation of bridging veins: A review. J. Mech. Behav. Biomed. Mater. 2015, 41, 222–240. [Google Scholar] [CrossRef]
- Lee, M.C.; Haut, R.C. Insensitivity of tensile failure properties of human bridging veins to strain rate: Implications in biomechanics of subdural hematoma. J. Biomech. 1989, 22, 537–542. [Google Scholar] [CrossRef]
- Monson, K.L.; Goldsmith, W.; Barbaro, N.M.; Manley, G.T. Axial mechanical properties of fresh human cerebral blood vessels. J. Biomech. Eng. 2003, 125, 288–294. [Google Scholar] [CrossRef]
- Monson, K.L.; Goldsmith, W.; Barbaro, N.M.; Manley, G.T. Significance of source and size in the mechanical response of human cerebral blood vessels. J. Biomech. 2005, 38, 737–744. [Google Scholar] [CrossRef]
- Delye, H.; Goffin, J.; Verschueren, P.; Van der Sloten, J.; Van der Perre, G.; Alaerts, H.; Verpoest, I.; Berckmans, D. Biomechanical Properties of the Superior Sagittal Sinus-Bridging Vein Complex. Stapp Car Crash J. 2006, 50, 625–636. [Google Scholar] [PubMed]
- Lee, M.C.; Haut, R.C. Strain rate effects on tensile failure properties of the common carotid artery and jugular veins of ferrets. J. Biomech. 1992, 25, 925–927. [Google Scholar] [CrossRef]
- Barrett, J.M.; Fewster, K.M.; Cudlip, A.C.; Dickerson, C.R.; Callaghan, J.P. The rate of tendon failure in a collagen fibre recruitment-based model. J. Mech. Behav. Biomed. Mater. 2021, 115, 104273. [Google Scholar] [CrossRef]
- Holzapfel, A.G. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; John Wiley & Sons: Chichester, UK, 2000; ISBN 0-471-82319-8. [Google Scholar]
- Funk, J.R.; Hall, G.W.; Crandall, J.R.; Pilkey, W.D. Linear and quasi-linear viscoelastic characterization of ankle ligaments. J. Biomech. Eng. 2000, 122, 15–22. [Google Scholar] [CrossRef]
- Deng, S.X.; Tomioka, J.; Debes, J.C.; Fung, Y.C. New experiments on shear modulus of elasticity of arteries. Am. J.-Physiol.-Heart Circ. Physiol. 1994, 266, H1–H10. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Zhao, J.; Liao, D.; Gregersen, H. Biomechanical properties of the layered oesophagus and its remodelling in experimental type-1 diabetes. J. Biomech. 2006, 39, 894–904. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar]
- Kroon, M.; Holzapfel, G.A. A new constitutive model for multi-layered collagenous tissues. J. Biomech. 2008, 41, 2766–2771. [Google Scholar] [CrossRef]
- Natali, A.N.; Carniel, E.L.; Gregersen, H. Biomechanical behaviour of oesophageal tissues: Material and structural configuration, experimental data and constitutive analysis. Med. Eng. Phys. 2009, 31, 1056–1062. [Google Scholar] [CrossRef] [PubMed]
- Sánchez Molina, D. A Constitutive Model of Human Esophagus Tissue with Application for the Treatment of Stenosis. Ph.D. Dissertation, UPC, Barcelona, Spain, 2013. [Google Scholar]
- Ho, J.; Kleiven, S. Dynamic response of the brain with vasculature: A three-dimensional computational study. J. Biomech. 2007, 40, 3006–3012. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics. Mechanical Properties of Living Tissues; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Holzapfel, G.A. Collagen in arterial walls: Biomechanical aspects. In Collagen; Springer: Boston, MA, USA, 2008; pp. 285–324. [Google Scholar]
- Davis, F.M.; De Vita, R. A nonlinear constitutive model for stress relaxation in ligaments and tendons. Ann. Biomed. Eng. 2012, 40, 2541–2550. [Google Scholar] [CrossRef]
- Han, H.; Tao, W.; Zhang, M. The dural entrance of cerebral bridging veins into the superior sagittal sinus: An anatomical comparison between cadavers and digital subtraction angiography. Neuroradiology 2007, 49, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Wayne Chen, W.; Jane Wang, Q.; Huan, Z.; Luo, X. Semi-analytical viscoelastic contact modeling of polymer-based materials. J. Tribol. 2011, 133, 041404. [Google Scholar] [CrossRef]
- Morro, A. Modelling of viscoelastic materials and creep behaviour. Meccanica 2017, 52, 3015–3021. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Martínez-Sáez, L.; Llumà, J.; Velázquez-Ameijide, J.; Arregui-Dalmases, C. A strain rate dependent model with decreasing Young’s Modulus for cortical human bone. 2021; preprint. [Google Scholar]
- Takhounts, E.G.; Eppinger, R.H.; Campbell, J.Q.; Tannous, R.E.; Power, E.D.; Shook, L.S. On the Development of the SIMon Finite Element Head Model. Stapp Car Crash J. 2003, 47, 107–133. [Google Scholar]
- Sanchez-Molina, D.; Velazquez-Ameijide, J.; Arregui-Dalmases, C.; Crandall, J.R.; Untaroiu, C.D. Minimization of analytical injury metrics for head impact injuries. Traffic Inj. Prev. 2012, 13, 278–285. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Molina, D.; Arregui-Dalmases, C.; Velázquez-Ameijide, J.; Angelini, M.; Kerrigan, J.; Crandall, J. Traumatic brain injury in pedestrian—Vehicle collisions: Convexity and suitability of some functionals used as injury metrics. Comput. Methods Programs Biomed. 2016, 136, 55–64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takhounts, E.G.; Ridella, S.A.; Hasija, V.; Tannous, R.E.; Campbell, J.Q.; Malone, D.; Duma, S. Investigation of Traumatic Brain Injuries Using the Next Generation of Simulated Injury Monitor (SIMon) Finite Element Head Model. Stapp Car Crash J. 2008, 52, 1–31. [Google Scholar]
- Fernandes, F.A.; Sousa, R.J.A.D. Head injury predictors in sports trauma—A state-of-the-art review. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2015, 229, 592–608. [Google Scholar] [CrossRef]
- Raul, J.S.; Roth, S.; Ludes, B.; Willinger, R. Influence of the benign enlargement of the subarachnoid space on the bridging veins strain during a shaking event: A finite element study. Int. J. Leg. Med. 2008, 122, 337–340. [Google Scholar] [CrossRef]
- Kleiven, S. Predictors for Traumatic Brain Injuries Evaluated through Accident Reconstructions. Stapp Car Crash J. 2007, 51, 81–114. [Google Scholar]
- Doorly, M.C. Investigations into Head Injury Criteria Using Numerical Reconstruction of Real Life Accident Cases. Ph.D. Dissertation, University College Dublin, Dublin, Ireland, 2007. [Google Scholar]
- Yan, W.; Pangestu, O.D. A modified human head model for the study of impact head injury. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 1049–1057. [Google Scholar] [CrossRef]
- Viano, D.C.; Casson, I.R.; Pellman, E.J.; Zhang, L.; King, A.I.; Yang, K.H. Concussion in professional football: Brain responses by finite element analysis: Part 9. Neurosurgery 2005, 57, 891–916. [Google Scholar] [CrossRef]
- Zoghi-Moghadam, M.; Sadegh, A.M. Global/local head models to analyse cerebral blood vessel rupture leading to ASDH and SAH. Comput. Methods Biomech. Biomed. Eng. 2009, 12, 1–12. [Google Scholar] [CrossRef]
- Fernandes, F.A.; Tchepel, D.; de Sousa, R.J.A.; Ptak, M. Development and validation of a new finite element human head model: Yet another head model (YEAHM). Eng. Comput. 2018, 35, 477–496. [Google Scholar] [CrossRef]
- Subramaniam, D.R.; Unnikrishnan, G.; Sundaramurthy, A.; Rubio, J.E.; Kote, V.B.; Reifman, J. The importance of modeling the human cerebral vasculature in blunt trauma. Biomed. Eng. Online 2021, 20, 1–19. [Google Scholar] [CrossRef]
- Zhao, W.; Ji, S. Incorporation of vasculature in a head injury model lowers local mechanical strains in dynamic impact. J. Biomech. 2020, 104, 109732. [Google Scholar] [CrossRef]
- Costa, J.M.; Fernandes, F.A.; de Sousa, R.J.A. Prediction of subdural haematoma based on a detailed numerical model of the cerebral bridging veins. J. Mech. Behav. Biomed. Mater. 2020, 111, 103976. [Google Scholar] [CrossRef]
- Sánchez-Molina, D.; García-Vilana, S.; Velázquez-Ameijide, J.; Arregui-Dalmases, C. Probabilistic assessment for clavicle fracture under compression loading: Rate-dependent behavior. Biomed. Eng. Appl. Basis Commun. 2020, 32, 2050040. [Google Scholar] [CrossRef]
- Nørlund, N.E. Hypergeometric functions. Acta Math. 1955, 94, 289–349. [Google Scholar] [CrossRef]
- Luo, M.J.; Milovanovic, G.V.; Agarwal, P. Some results on the extended beta and extended hypergeometric functions. Appl. Math. Comput. 2014, 248, 631–651. [Google Scholar] [CrossRef]



| Specimen | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Identifier | (MPa) | (MPa) | (N) | (MPa) | (%) | (N) | (MPa) | (%) | () |
| 2628A | 4.56 | 6.60 | 1.036 | 3.73 | 42.0 | 0.650 | 2.34 | 26.7 | 0.950 |
| 2628B | 2.10 | 2.37 | 0.612 | 3.38 | 64.6 | 0.405 | 2.24 | 45.6 | 1.196 |
| 2628C | 3.18 | 4.29 | 0.643 | 3.95 | 52.2 | 0.383 | 2.35 | 31.9 | 0.922 |
| 2629A | 5.03 | 6.51 | 0.791 | 4.44 | 46.9 | 0.426 | 2.39 | 27.7 | 0.723 |
| 2629B | 4.88 | 7.02 | 0.746 | 4.06 | 39.0 | 0.479 | 2.60 | 27.4 | 0.708 |
| 2629C | 5.11 | 6.36 | 0.680 | 3.89 | 37.9 | 0.533 | 3.05 | 31.7 | 0.799 |
| 2630A | 3.66 | 5.60 | 0.513 | 2.17 | 32.8 | 0.349 | 1.47 | 23.6 | 0.566 |
| 2630B | 4.74 | 8.57 | 1.814 | 5.00 | 52.7 | 0.902 | 2.49 | 24.3 | 0.686 |
| 2632A | 5.63 | 6.80 | 0.378 | 2.32 | 31.8 | 0.378 | 2.32 | 31.8 | 0.721 |
| 2634A | 6.10 | — | 0.278 | 0.65 | 16.3 | 0.204 | 0.47 | 13.3 | 0.389 |
| 2634B | 2.59 | 2.83 | 1.060 | 3.17 | 55.0 | 1.036 | 3.10 | 51.2 | 1.145 |
| 2640A | 5.94 | 6.95 | 0.876 | 5.17 | 52.8 | 0.581 | 3.43 | 32.9 | 0.897 |
| 2836B | 2.05 | 3.18 | 0.175 | 1.08 | 32.5 | 0.108 | 0.66 | 21.7 | 0.001 |
| 2836C | 4.02 | 6.65 | 0.091 | 0.79 | 18.3 | 0.091 | 0.79 | 18.3 | 0.004 |
| 2836D | 3.80 | 6.09 | 0.493 | 3.03 | 41.0 | 0.241 | 1.48 | 22.9 | 0.171 |
| 3636A | 4.48 | 4.86 | 0.470 | 1.34 | 24.3 | 0.313 | 0.89 | 17.4 | 0.137 |
| 3636B | 4.92 | 5.43 | 0.357 | 1.60 | 32.6 | 0.238 | 1.07 | 19.1 | 0.020 |
| 3636C | 6.61 | — | 0.293 | 0.93 | 18.7 | 0.213 | 0.68 | 11.3 | 0.020 |
| 647A | — | — | 0.125 | 0.70 | 11.7 | 0.081 | 0.45 | 8.10 | 0.002 |
| 647B | 3.10 | 6.36 | 0.262 | 1.01 | 24.3 | 0.164 | 0.63 | 17.2 | 0.019 |
| Elastic Model | Viscoelastic Model | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Specimen | g | VC | |||||||||
| Identifier | (s) | (–) | (N) | (MPa) | (–) | (N) | (NPa) | (–) | (%) | ||
| 2836B | 0.001 | 14.92 | 0.015 | 0.091 | 0.991 | 14.92 | 0.015 | 0.091 | 0.000 | 0.991 | 0.04 |
| 2836C | 0.004 | 17.70 | 0.016 | 0.140 | 0.997 | 17.70 | 0.016 | 0.141 | 0.000 | 0.997 | 0.00 |
| 647B | 0.019 | 28.66 | 0.013 | 0.051 | 0.991 | 23.61 | 0.012 | 0.045 | 0.144 | 0.995 | 7.36 |
| 3636C | 0.020 | 13.11 | 0.110 | 0.350 | 0.999 | 13.11 | 0.110 | 0.350 | 0.005 | 0.999 | 1.29 |
| 3636B | 0.020 | 2.770 | 0.365 | 1.637 | 0.992 | 1.847 | 0.466 | 2.091 | 0.047 | 0.994 | 7.40 |
| 3636A | 0.137 | 2.301 | 0.636 | 1.817 | 0.992 | 1.727 | 0.827 | 2.363 | 0.018 | 0.995 | 6.66 |
| 2836D | 0.171 | 16.33 | 0.024 | 0.149 | 0.993 | 14.69 | 0.023 | 0.143 | 0.044 | 0.994 | 8.75 |
| 2634A | 0.389 | 23.33 | 0.061 | 0.141 | 0.995 | 13.72 | 0.078 | 0.180 | 0.194 | 0.999 | 38.6 |
| 2630A | 0.566 | 14.32 | 0.041 | 0.172 | 0.997 | 11.63 | 0.040 | 0.169 | 0.090 | 0.999 | 17.7 |
| 2630B | 0.686 | 21.76 | 0.044 | 0.122 | 0.981 | 14.81 | 0.012 | 0.032 | 0.514 | 0.993 | 54.6 |
| 2629B | 0.708 | 11.93 | 0.054 | 0.293 | 0.977 | 5.896 | 0.049 | 0.265 | 0.217 | 0.995 | 42.3 |
| 2632A | 0.721 | 5.616 | 0.139 | 0.852 | 0.992 | 3.728 | 0.150 | 0.923 | 0.065 | 0.995 | 23.5 |
| 2629A | 0.723 | 7.926 | 0.090 | 0.506 | 0.992 | 4.706 | 0.098 | 0.551 | 0.111 | 0.999 | 30.5 |
| 2629C | 0.799 | 6.579 | 0.112 | 0.643 | 0.990 | 4.614 | 0.095 | 0.544 | 0.120 | 0.997 | 33.2 |
| 2640A | 0.897 | 4.567 | 0.193 | 1.139 | 0.996 | 4.995 | 0.215 | 1.270 | 0.008 | 0.996 | 33.0 |
| 2628C | 0.922 | 9.487 | 0.042 | 0.256 | 0.985 | 5.531 | 0.043 | 0.261 | 0.148 | 0.997 | 25.8 |
| 2628A | 0.950 | 12.12 | 0.074 | 0.268 | 0.993 | 10.61 | 0.053 | 0.189 | 0.121 | 0.995 | 27.8 |
| 2634B | 1.145 | 2.554 | 0.314 | 0.940 | 0.984 | 1.225 | 0.146 | 0.435 | 0.366 | 0.998 | 44.3 |
| 2628B | 1.196 | 3.425 | 0.100 | 0.554 | 0.987 | 1.742 | 0.121 | 0.670 | 0.143 | 0.998 | 20.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez-Molina, D.; García-Vilana, S.; Llumà, J.; Galtés, I.; Velázquez-Ameijide, J.; Rebollo-Soria, M.C.; Arregui-Dalmases, C. Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions. Biology 2021, 10, 831. https://doi.org/10.3390/biology10090831
Sánchez-Molina D, García-Vilana S, Llumà J, Galtés I, Velázquez-Ameijide J, Rebollo-Soria MC, Arregui-Dalmases C. Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions. Biology. 2021; 10(9):831. https://doi.org/10.3390/biology10090831
Chicago/Turabian StyleSánchez-Molina, David, Silvia García-Vilana, Jordi Llumà, Ignasi Galtés, Juan Velázquez-Ameijide, Mari Carmen Rebollo-Soria, and Carlos Arregui-Dalmases. 2021. "Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions" Biology 10, no. 9: 831. https://doi.org/10.3390/biology10090831
APA StyleSánchez-Molina, D., García-Vilana, S., Llumà, J., Galtés, I., Velázquez-Ameijide, J., Rebollo-Soria, M. C., & Arregui-Dalmases, C. (2021). Mechanical Behavior of Blood Vessels: Elastic and Viscoelastic Contributions. Biology, 10(9), 831. https://doi.org/10.3390/biology10090831






