Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics
Abstract
Simple Summary
Abstract
1. Introduction
1.1. Fluid–Structure Interaction Analyses
1.2. Biomedical FSI Applications
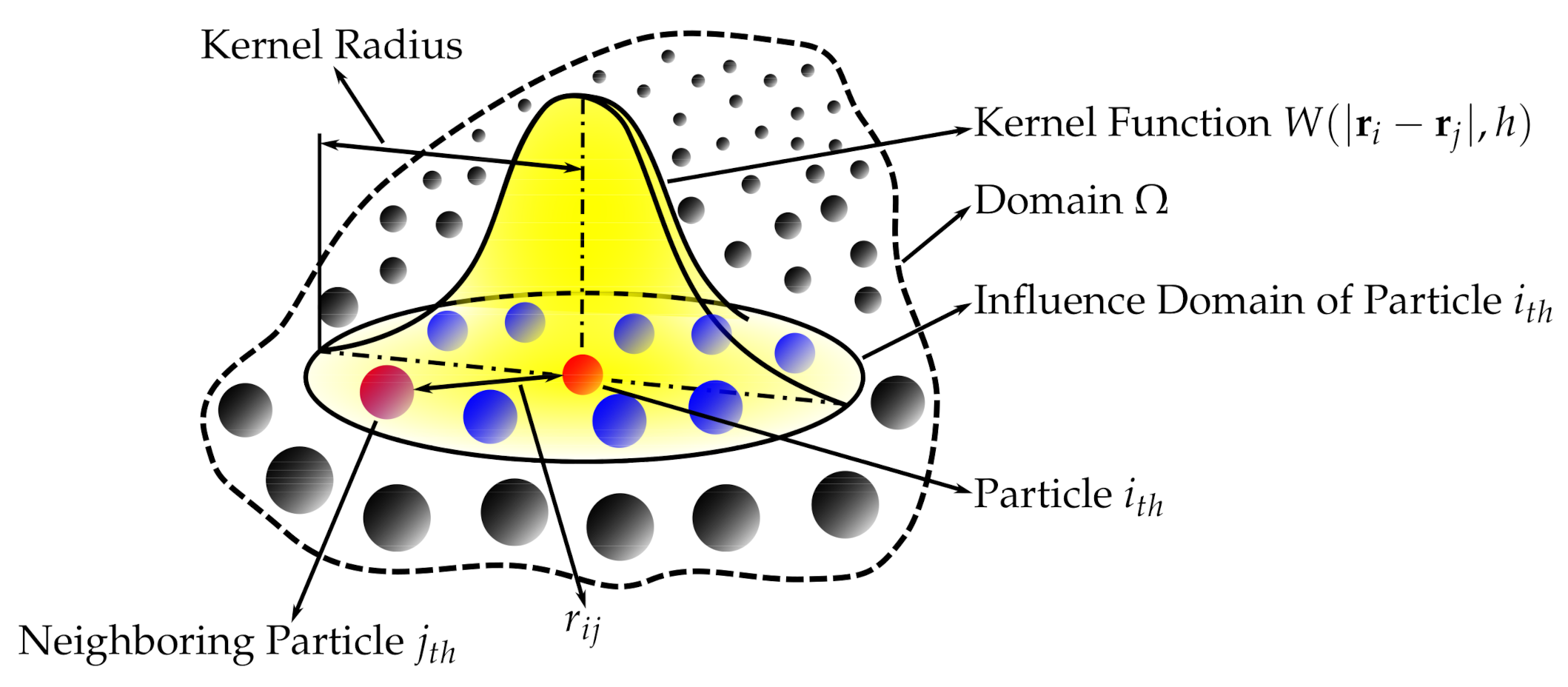
2. Smoothed-Particle Hydrodynamics
3. Applications
3.1. Blood Flow in Arteries
3.2. Blood Flow’s Interaction with Heart
3.3. Cerebrospinal Fluid’s Interaction with the Brain
3.4. Other Applications
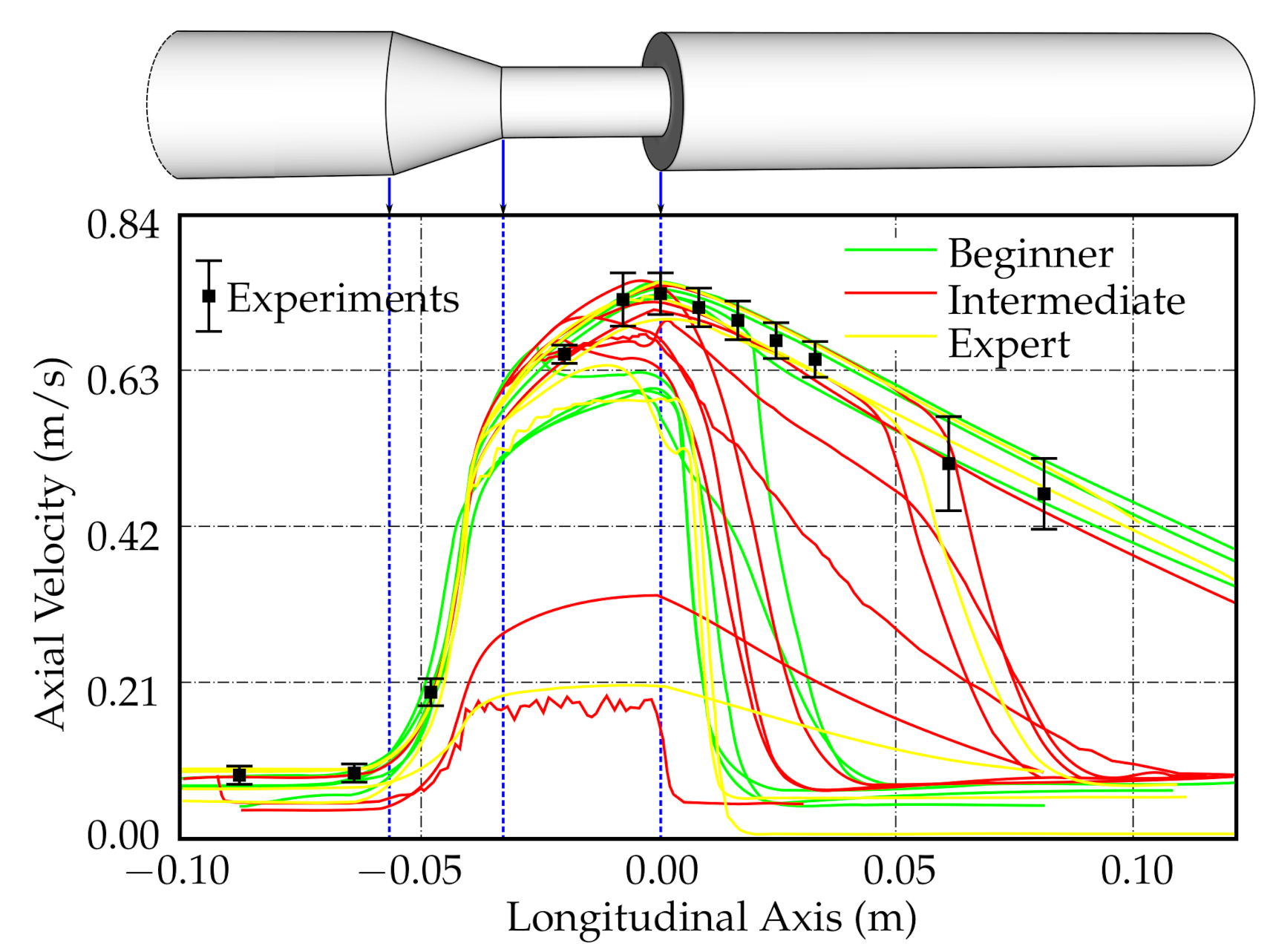
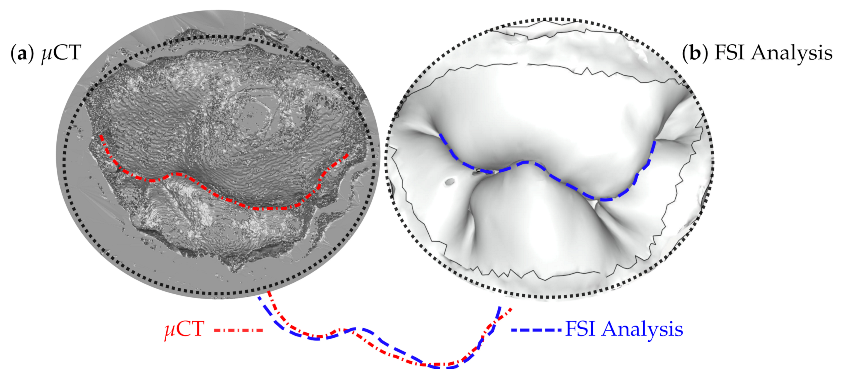
4. Validation
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FSI | Fluid–structure interaction |
| SPH | Smoothed-particle hydrodynamics |
| FDA | U.S. Food and Drug Administration |
| PIV | particle image velocimetry |
| ALE | Artitrary Lagrangian–Euletian |
| CT | Computed tomography |
| IB | Immersed boundary |
| GPU | Graphics processing unit |
| CPU | Central processing unit |
| LBFS | Lattice Boltzman flux solver |
| CFD | Computational fluid dynamics |
| MMD | Moyamoya disease |
| FPM | Finite particle method |
| CSPM | Corrective particle method |
| KGF-SPH | Kernel gradient-free SPH |
| DFPM | Decoupled finite element method |
References
- Trusty, P.; Slesnick, T.; Wei, Z.; Rossignac, J.; Kanter, K.; Fogel, M.; Yoganathan, A. Fontan Surgical Planning: Previous Accomplishments, Current Challenges, and Future Directions. J. Cardiovasc. Trans. Res. 2018, 11, 133–144. [Google Scholar] [CrossRef]
- Shi, W.; Zheng, M.; Liu, P. Virtual surgical bleeding simulation with navier-stokes equation and modified smooth particle hydrodynamics method. In Proceedings of the 2017 IEEE International Conference on Information and Automation (ICIA), Macao, China, 18–20 July 2017; pp. 276–281. [Google Scholar] [CrossRef]
- Fernandez, J.W.; Das, R.; Cleary, P.W.; Hunter, P.J.; Thomas, C.D.L.; Clement, J.G. Using smooth particle hydrodynamics to investigate femoral cortical bone remodelling at the Haversian level. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 129–143. [Google Scholar] [CrossRef]
- Toma, M.; Dehesa-Baeza, A.; Chan-Akeley, R.; Nguyen, P.; Zwibel, H. Cerebrospinal Fluid Interaction with Cerebral Cortex during Pediatric Abusive Head Trauma. J. Pediatr. Neurol. 2020, 18, 223–230. [Google Scholar] [CrossRef]
- Toma, M.; Lu, Y.; Zhou, H.; Garcia, J. Thresholding Segmentation Errors and Uncertainty with Patient-Specific Geometries. J. Biomed. Phys. Eng. 2021, 11, 115–122. [Google Scholar] [CrossRef]
- Toma, M.; Oshima, M.; Takagi, S. Decomposition and parallelization of strongly coupled fluid-structure interaction linear subsystems based on the Q1/P0 discretization. J. Comput. Struct. 2016, 173, 84–94. [Google Scholar] [CrossRef]
- Manenti, S.; Panizzo, A.; Ruol, P.; Martinelli, L. SPH simulation of a floating body forced by regular waves. In Proceedings of the 3rd SPHERIC Workshop, Lausanne, Switzerland, 4–6 June 2008; pp. 38–41. [Google Scholar]
- Peskin, C. Flow patterns around heart valves: A numerical method. J. Comput. Phys. 1972, 10, 252–271. [Google Scholar] [CrossRef]
- Griffith, B.; Xiaoyu, L. Hybrid finite difference/finite element immersed boundary method. Int. J. Numer. Methods Biomed. Eng. 2017, 33, 12. [Google Scholar] [CrossRef] [PubMed]
- Mittal, R.; Iaccarino, G. Immersed Boundary Method. Annu. Rev. Fluid Mech. 2004, 37, 239–261. [Google Scholar] [CrossRef]
- Bandringa, H. Immersed Boundary Methods. Master’s Thesis, University of Gronigen, Gronigen, The Netherlands, 2010. [Google Scholar]
- Tian, F.; Young, J.; Lai, J. Immersed Boundary Method and its Applications in a Variety of Complex Flow Problems. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Harikrishnan, B.; Chen, Z.; Shu, C. A New Explicit Immersed Boundary Method for Simulation of Fluid-Solid Interactions. Adv. Appl. Math. Mech. 2020, 13, 261–284. [Google Scholar] [CrossRef]
- Peskin, C.; Lai, M. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comput. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef]
- De Rosis, A.; Ubertini, S.; Ubertini, F. A partitioned approach for two-dimensional fluid–structure interaction problems by a coupled lattice Boltzmann-finite element method with immersed boundary. J. Fluid Struct. 2014, 45, 202–215. [Google Scholar] [CrossRef]
- Chen, Y.; Cai, Q.; Xia, Z.; Wang, M.; Chen, S. Momentum-exchange method in lattice Boltzmann simulations of particle-fluid interactions. Phys. Rev. E 2013, 88. [Google Scholar] [CrossRef] [PubMed]
- Peskin, C. Numerical Analysis of Blood Flow in the Heart. J. Comput. Phys. 1977, 25, 220–252. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Kobayashi, S.; Zheng, J.; Vito, R. Effect of stenosis asymmetry on blood flow and artery compression: A three-dimensional fluid-structure interaction model. Ann. Biomed. Eng. 2003, 31, 1182–1193. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.; Fong, F.; Wang, D. Computational evaluation of smoothed particle hydrodynamics for implementing blood flow modelling through CT reconstructed arteries. J.-Ray Sci. Technol. 2017, 25, 213–232. [Google Scholar] [CrossRef]
- Nasar, A. Eulerian and Lagrangian Smoothed Particle Hydrodynamics as Models for the Interaction of Fluids and Flexible Structures in Biomedical Flows. Ph.D. Thesis, The University of Manchester (United Kingdom), PQDT-UK & Ireland, Manchester, UK, 2016. [Google Scholar]
- Hron, J.; Madlik, M. Fluid-structure interaction with applications in biomechanics. Nonlinear Anal. Real World Appl. 2007, 8, 1431–1458. [Google Scholar] [CrossRef]
- Al-Saad, M.; Suarez, C.; Obeidat, A.; Bordas, S.; Kulasegaram, S. Application of Smooth Particle Hydrodynamics Method for Modelling Blood Flow with Thrombus Formation. Comput. Model. Eng. Sci. 2020, 122, 831–862. [Google Scholar] [CrossRef]
- Frissane, H.; Taddei, L.; Lebaal, N.; Roth, S. SPH modeling of high velocity impact into ballistic gelatin. Development of an axis-symmetrical formulation. Mech. Adv. Mater. Struct. 2019, 26, 1881–1888. [Google Scholar] [CrossRef]
- Lucy, L. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gingold, R.; Monaghan, J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Ye, T.; Pan, D.; Huang, C.; Liu, M. Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 2019, 31, 011301. [Google Scholar] [CrossRef]
- Zhang, L.; Ademiloye, A.; Liew, K. Meshfree and Particle Methods in Biomechanics: Prospects and Challenges. Arch. Comput. Methods Eng. 2019, 26, 1547–1576. [Google Scholar] [CrossRef]
- Toma, M. The Emerging Use of SPH in Biomedical Applications. Signif. Bioeng. Biosci. 2017, 1, SBB.000502. [Google Scholar] [CrossRef]
- Durrwachter, J. Hemodynamics of the Left Ventricle: Validation of a Smoothed—Particle Hydrodynamics Fluid-Structure Interaction Model. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2016. [Google Scholar]
- Toma, M.; Einstein, D.; Bloodworth, C.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid-Structure Interaction and Structural Analyses using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2815. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Rezavand, M.; Hu, X. A Multi-Resolution SPH Method for Fluid-Structure Interactions. J. Comput. Phys. 2021, 429. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Kobayashi, S.; Ku, D. Steady flow and wall compression in stenotic arteries: A three-dimensional thick-wall model with fluid–wall interactions. J. Biomech. Eng. 2001, 123, 548–557. [Google Scholar] [CrossRef]
- Downing, J.M.; Ku, D.N. Effects of Frictional Losses and Pulsatile Flow on the Collapse of Stenotic Arteries. J. Biomech. Eng. 1997, 119, 317–324. [Google Scholar] [CrossRef]
- Yamaguchi, T.; Kobayashi, T.; Liu, H. Fluid-wall interactions in the collapse and ablation of an atheromatous plaque in coronary arteries. In Proceedings of the Third World Congress of Biomechanics, Sapporo, Japan, 2–8 August 1998; p. 20b. [Google Scholar]
- Yamaguchi, T.; Furuta, N.; Nakayama, T.; Kobayashi, T. Computations of the fluid and wall mechanical interactions in arterial diseases. In Proceedings of the 1995 ASME International Mechanical Congress and Exposition, San Francisco, CA, USA, 12–17 November 1995; pp. 197–198. [Google Scholar]
- Yamaguchi, T.; Nakayama, T.; Kobayashi, T. Computations of the wall mechanical response under unsteady flows in arterial diseases. Adv. Bioeng. 1996, 33, 369–370. [Google Scholar]
- Bathe, M.; Kamm, R. A fluid-structure interaction finite element analysis of pulsatile blood flow through a compliant stenotic artery. J. Biomech. Eng. 1999, 121, 361–369. [Google Scholar] [CrossRef]
- Yang, C.; Tang, D.; Atluri, S. Patient-specific carotid plaque progression simulation using 3D meshless generalized finite difference models with fluid–structure interactions based on serial in vivo MRI data. Comput. Model. Eng. Sci. 2011, 72, 53–77. [Google Scholar] [CrossRef] [PubMed]
- Chui, Y.P.; Heng, P.A. A meshless rheological model for blood-vessel interaction in endovascular simulation. Prog. Biophys. Mol. Biol. 2010, 103, 252–261. [Google Scholar] [CrossRef]
- Toma, M.; Bloodworth, C.; Einstein, D.; Pierce, E.; Cochran, R.; Yoganathan, A.; Kunzelman, K. High-resolution subject-specific mitral valve imaging and modeling: Experimental and computational methods. Biomech. Model. Mechanobiol. 2016, 15, 1619–1630. [Google Scholar] [CrossRef]
- Toma, M.; Jensen, M.; Einstein, D.; Yoganathan, A.; Cochran, R.; Kunzelman, K. Fluid-Structure Interaction Analysis of Papillary Muscle Forces Using a Comprehensive Mitral Valve Model with 3D Chordal Structure. Ann. Biomed. Eng. 2016, 44, 942–953. [Google Scholar] [CrossRef]
- Mao, W.; Caballero, A.; Kodali, S.; Sun, W. Fully-coupled fluid-structure interaction simulation of the aortic and mitral valves in a realistic 3D left ventricle model. PLoS ONE 2017, 12, e0184729. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Primiano, C.; Hashim, S.; Wei, S. New insights into mitral heart valve prolapse after chordae rupture through fluid—Structure interaction computational modeling. Sci. Rep. 2018, 8, 17306. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Caballero, A.; Hahn, R.; Sun, W. Comparative quantification of primary mitral regurgitation by computer modeling and simulated echocardiography. Am. J. Physiol. Heart Circ. Physiol. 2020, 318, H547–H557. [Google Scholar] [CrossRef]
- Toma, M.; Bloodworth, C.; Pierce, E.; Einstein, D.; Cochran, R.; Yoganathan, A.; Kunzelman, K. Fluid-Structure Interaction Analysis of Ruptured Mitral Chordae Tendineae. Ann. Biomed. Eng. 2017, 45, 619–631. [Google Scholar] [CrossRef]
- Biffi, B.; Gritti, M.; Grasso, A.; Milano, E.; Fontana, M.; Alkareef, H.; Davar, J.; Jeetley, P.; Whelan, C.; Anderson, S.; et al. A workflow for patient-specific fluid–structure interaction analysis of the mitral valve: A proof of concept on a mitral regurgitation case. Med. Eng. Phys. 2019, 74, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Einstein, D.; Kohli, K.; Caroll, S.; Bloodworth, C.; Cochran, R.; Kunzelman, K.; Yoganathan, A. Effect of Edge-to-Edge Mitral Valve Repair on Chordal Strain: Fluid-Structure Interaction Simulations. Biology 2020, 9, 173. [Google Scholar] [CrossRef] [PubMed]
- Toma, M.; Einstein, D.; Bloodworth, C.; Kohli, K.; Cochran, R.; Kunzelman, K.; Yoganathan, A. Fluid-Structure Interaction Analysis of Subject-Specific Mitral Valve Regurgitation Treatment with an Intra-valvular Spacer. Prosthesis 2020, 2, 7. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Hahn, R.; Sun, W. A Comprehensive Engineering Analysis of Left Heart Dynamics After MitraClip in a Functional Mitral Regurgitation Patient. Front. Physiol. 2020, 11, 432. [Google Scholar] [CrossRef] [PubMed]
- Caballero, A.; Mao, W.; McKay, R.; Wei, S. Transapical mitral valve repair with neochordae implantation: FSI analysis of neochordae number and complexity of leaflet prolapse. Int. J. Numer. Methods Biomed. Eng. 2019, 36, e3297. [Google Scholar] [CrossRef] [PubMed]
- Singh-Gryzbon, S.; Sadri, V.; Toma, M.; Pierce, E.; Wei, Z.; Yoganathan, A. Development of a Computational Method for Simulating Tricuspid Valve Dynamics. Ann. Biomed. Eng. 2019, 47, 1422–1434. [Google Scholar] [CrossRef]
- Mao, W.; Li, K.; Sun, W. Fluid—Structure interaction study of transcatheter aortic valve dynamics using smoothed particle hydrodynamics. Cardiovasc. Eng. Technol. 2016, 7, 374–388. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Wei, S. The impact of balloon-expandable transcatheter aortic valve replacement on concomitant mitral regurgitation: A comprehensive computational analysis. J. R. Soc. Interface 2019, 16, 20190355. [Google Scholar] [CrossRef]
- Caballero, A.; Mao, W.; McKay, R.; Sun, W. The Impact of Self-Expandable Transcatheter Aortic Valve Replacement on Concomitant Functional Mitral Regurgitation: A Comprehensive Engineering Analysis. Struct. Heart 2020, 4, 179–191. [Google Scholar] [CrossRef]
- Dabiri, Y.; Yao, Y.; Sack, K.; Kassab, G.; Guccione, J. Tricuspid valve regurgitation decreases after mitraclip implantation: Fluid structure interaction simulation. Mech. Res. Commun. 2019, 97, 96–100. [Google Scholar] [CrossRef]
- Yuan, Q.; Ye, X. A New Way to Simulate the Fluid Structure Interaction between the Bioprosthetic Heart Valve and Blood: FE-SPH Method; Mechanical Science and Engineering IV; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; Volume 472, pp. 125–130. [Google Scholar] [CrossRef]
- Marom, G. Numerical Methods for Fluid–Structure Interaction Models of Aortic Valves. Arch. Comput. Methods Eng. 2015, 22, 595–620. [Google Scholar] [CrossRef]
- Toma, M.; Nguyen, P. Fluid-structure interaction analysis of cerebrospinal fluid with a comprehensive head model subject to a rapid acceleration and deceleration. Brain Inj. 2018, 32, 1576–1584. [Google Scholar] [CrossRef]
- Duckworth, H.; Ghajari, M. Modelling Brain Biomechanics Using a Hybrid Smoothed Particle Hydrodynamics and Finite Element Model; Ohio State University Injury Biomechanics Symposium: Columbus, OH, USA, 2019. [Google Scholar]
- Wilhelm, J.; Ptak, M.; Fernandes, F.; Kubicki, K.; Kwiatkowski, A.; Ratajczak, M.; Sawicki, M.; Szarek, D. Injury Biomechanics of a Child’s Head: Problems, Challenges and Possibilities with a New aHEAD Finite Element Model. Appl. Sci. 2020, 10, 4467. [Google Scholar] [CrossRef]
- Toma, M.; Chan-Akeley, R.; Lipari, C.; Kuo, S.H. Mechanism of Coup and Contrecoup Injuries Induced by a Knock-Out Punch. J. Math. Comput. Appl. 2020, 25, 22. [Google Scholar] [CrossRef]
- Toma, M.; Nguyen, P. Coup-contrecoup brain injury: Fluid-structure interaction simulations. Int. J. Crashworth. 2020, 25, 175–182. [Google Scholar] [CrossRef]
- Toma, M. Predicting Concussion Symptoms Using Computer Simulations. Adv. Intell. Syst. Comput. 2019, 880, 557–568. [Google Scholar] [CrossRef]
- Toma, M.; Kuo, S. Computational Assessment of Risk of Subdural Hematoma Associated with Ventriculoperitoneal Shunt Placement. Lect. Notes Comput. Vis. Biomech. 2020, 36, 36–47. [Google Scholar] [CrossRef]
- Kwon, E.; Singh, M.; Vallabh, R.; Das, R.; Taylor, M.; Fernandez, J. Modelling ballistic cranial injury and backspatter using smoothed particle hydrodynamics. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018. [Google Scholar] [CrossRef]
- Ho, A.; Tsou, L.; Green, S.; Fels, S. A 3D swallowing simulation using smoothed particle hydrodynamics. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2014, 2, 237–244. [Google Scholar] [CrossRef]
- Harrison, S.; Eyres, G.; Cleary, P.; Sinnott, M.; Delahunty, C.; Lundin, L. Computational Modeling of Food Oral Breakdown Using Smoothed Particle Hydrodynamics. J. Texture Stud. 2014, 45, 97–109. [Google Scholar] [CrossRef]
- Brandstaeter, S.; Fuchs, S.; Aydin, R.; Cyron, C. Mechanics of the stomach: A review of an emerging field of biomechanics. GAMM-Mitteilungen 2019, 42, e201900001. [Google Scholar] [CrossRef]
- Sinnott, M.; Cleary, P.; Harrison, S. Peristaltic transport of a particulate suspension in the small intestine. Appl. Math. Model. 2017, 44, 143–159. [Google Scholar] [CrossRef]
- Harrison, S.; Cohen, R.; Cleary, P.; Barris, S.; Rose, G. A coupled biomechanical-Smoothed Particle Hydrodynamics model for predicting the loading on the body during elite platform diving. Appl. Math. Model. 2016, 40, 3812–3831. [Google Scholar] [CrossRef]
- Harrison, S.; Cleary, P.; Cohen, R. Dynamic simulation of flat water kayaking using a coupled biomechanical-smoothed particle hydrodynamics model. Hum. Mov. Sci. 2019, 64, 252–273. [Google Scholar] [CrossRef]
- Stewart, S.; Paterson, E.; Burgreen, G.; Hariharan, P.; Giarra, M.; Reddy, V.; Day, S.; Manning, K.; Deutsch, S.; Berman, M.; et al. Assessment of CFD performance in simulations of an idealized medical device: Results of FDA’s first computational interlaboratory study. Cardiovasc. Eng. Technol. 2012, 3, 139–160. [Google Scholar] [CrossRef]
- Stewart, S.; Hariharan, P.; Paterson, E.; Burgreen, G.; Reddy, V.; Day, S.; Giarra, M.; Manning, K.; Deutsch, S.; Berman, M.; et al. Results of FDA’s first interlaboratory computational study of a nozzle with a sudden contraction and conical diffuser. Cardiovasc. Eng. Technol. 2013, 4, 374–391. [Google Scholar] [CrossRef]
- Toma, M. Computational Fluid Dynamics Simulations Using FDA’s Idealized Medical Device Demonstrating the Importance of Model Validation. Biomed. Res. Rev. 2018, 1, 1. [Google Scholar] [CrossRef]
- Stewart, S.; Day, S.; Burgreen, G.; Paterson, E.; Manning, K.; Hariharan, P.; Deutsch, S.; Giarra, M.; Cheek, C.; Reddy, V.; et al. Preliminary results of FDA’s “Critical Path” project to validate computational fluid dynamic methods used in medical device evaluation. ASAIO J. 2009, 55, 173. [Google Scholar]
- Erdemir, A.; Mulugeta, L.; Ku, J.; Drach, A.; Horner, M.; Morrison, T.; Peng, G.; Vadigepalli, R.; Lytton, W.; Myers, J., Jr. Credible practice of modeling and simulation in healthcare: Ten rules from a multidisciplinary perspective. J. Transl. Med. 2020, 18, 369. [Google Scholar] [CrossRef] [PubMed]
- Bloodworth, C.; Pierce, E.; Easley, T.; Drach, A.; Khalighi, A.; Toma, M.; Jensen, M.; Sacks, M.; Yoganathan, A. Ex Vivo Methods for Informing and Validating Computational Models of the Mitral Valve. Ann. Biomed. Eng. 2017, 45, 496–507. [Google Scholar] [CrossRef]
- Wei, Z.; Sonntag, S.; Toma, M.; Singh-Gryzbon, S.; Sun, W. Computational Fluid Dynamics Assessment Associated with Transcatheter Heart Valve Prostheses: A Position Paper of the ISO Working Group. Cardiovasc. Eng. Technol. 2018, 9, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Vaca, F.; Bordoni, B. Anatomy, Thorax, Mitral Valve. In StatPearls [Internet]; StatPearls Publishing: Treasure Island, FL, USA, 2020. [Google Scholar]
- Schubert, S.; Mehaffey, J.; Charles, E.; Kron, I. Mitral Valve Repair: The French Correction Versus the American Correction. Surg. Clin. N. Am. 2017, 97, 867–888. [Google Scholar] [CrossRef] [PubMed]
- Carpentier, A.; Lessana, A.; Relland, J.; Belli, E.; Mihaileanu, S.; Berrebi, A.; Palsky, E.; Loulmet, D. The “Physio-Ring”: An Advanced Concept in Mitral Valve Annuloplasty. Ann. Thorac. Surg. 1995, 60, 1177–1186. [Google Scholar] [CrossRef]
- Dal-Bianco, J.; Levine, R. Anatomy of the Mitral Valve Apparatus: Role of 2D and 3D Echocardiography. Cardiol. Clin. 2013, 31, 151–164. [Google Scholar] [CrossRef]
- Liu, X.; Wang, R.; Li, Y.; Song, D. Deformation of Soft Tissue and Force Feedback Using the Smoothed Particle Hydrodynamics. Comput. Math. Methods Med. 2015, 2015, 598415. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.J.; Benharash, P.; Dutson, E.; Eldredge, J. Smoothed particle hydrodynamics simulation of biphasic soft tissue and its medical applications. Med. Biol. Eng. Comput. 2020, 59, 227–242. [Google Scholar] [CrossRef] [PubMed]
- Zhu, F.; Qian, Y.; Xu, B.; Gu, Y.; Karunanithi, K.; Zhu, W.; Chen, L.; Mao, Y.; Morgan, M. Quantitative assessment of changes in hemodynamics of the internal carotid artery after bypass surgery for moyamoya disease. J. Neurosurg. 2018, 129, 677–683. [Google Scholar] [CrossRef]
- Toma, M.; Chan-Akeley, R. Biofluid-Biostructure Interaction Analyses Using Comprehensive Patient-Specific Geometries. Adv. Intell. Syst. Comput. 2021, 1290, 1–16. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, Z. Smoothed particle hydrodynamics (SPH) for modeling fluid-structure interactions. Sci. China Phys. Mech. Astron. 2019, 62. [Google Scholar] [CrossRef]
- Winslow, R.; Trayanova, N.; Geman, D.; Miller, M. Computational medicine: Translating models to clinical care. Sci. Transl. Med. 2012, 4, 158rv11. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toma, M.; Chan-Akeley, R.; Arias, J.; Kurgansky, G.D.; Mao, W. Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics. Biology 2021, 10, 185. https://doi.org/10.3390/biology10030185
Toma M, Chan-Akeley R, Arias J, Kurgansky GD, Mao W. Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics. Biology. 2021; 10(3):185. https://doi.org/10.3390/biology10030185
Chicago/Turabian StyleToma, Milan, Rosalyn Chan-Akeley, Jonathan Arias, Gregory D. Kurgansky, and Wenbin Mao. 2021. "Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics" Biology 10, no. 3: 185. https://doi.org/10.3390/biology10030185
APA StyleToma, M., Chan-Akeley, R., Arias, J., Kurgansky, G. D., & Mao, W. (2021). Fluid–Structure Interaction Analyses of Biological Systems Using Smoothed-Particle Hydrodynamics. Biology, 10(3), 185. https://doi.org/10.3390/biology10030185







