1. Introduction
Transarterial chemoembolization (TACE) is used to treat patients with primary liver cancer [
1], which is the third leading cause of cancer deaths in 2018 [
2]. Conventional TACE consists of the intraarterial infusion of anticancer agents mixed with lipiodol followed by occluding particles that reduce blood flow and induce tumor necrosis [
3]. TACE is the standard of care for patients with intermediate hepatocellular carcinoma [
4], although Facciorusso et al. [
5] reported no superiority of TACE over transarterial embolization (TAE).
A novel form of TACE, the balloon-occluded TACE (B-TACE), was recently reported by Irie et al. [
6]. B-TACE is performed with a microballoon catheter that temporarily occludes the feeding arteries. Compared to conventional TACE, it has been reported that B-TACE can improve lipiodol accumulation in tumors, especially when the balloon-occluded arterial stump pressure (BOASP) (i.e., the pressure distal to the catheter tip) is below 64 mmHg [
6,
7,
8].
Once the balloon occludes the feeding arteries, an upstream and a downstream compartment are created, and these remain connected via collateral arterial circulation, which determines the value of BOASP [
9]. These collateral pathways are crucial for the supply of the biliary tract [
10]. Examples of these pathways include the communicating arcade (CA) that connects the right hepatic artery (RHA) and left hepatic artery (LHA) [
11], which are also connected to the 3-o’clock and 9-o’clock arteries that feed the common bile duct [
10], i.e., the pathways of the peribiliary plexus around the intrahepatic bile ducts [
12]. The hilar plexus can also provide connections between the different segments of the liver [
10]. However, it is often difficult to visualize the collateral flow in medical images and, therefore, understand the importance of it.
The liver is an organ with a unique dual blood supply that includes many extra- and intrahepatic collateral vessels [
10,
13]. Extrahepatic collaterals enter the liver parenchyma from nonhiliar entrances; for example, the phrenic artery gives extrahepatic afferences that enter through the nude area. Intrahepatic collaterals deliver blood to the hepatic sinusoids (or hepatocites or tumors) from vessels that may replace this function when the main afferences (i.e., lobar, segmental or subsegmental arteries) are occluded for any reason.
These collateral vessels have been used to allow blood flow redistribution after artery balloon occlusion. Applications ranged from tumor detection [
13,
14] to tumor treatment [
9,
15]. Currently, collateral circulation plays a pivotal role in microballoon-catheter-assisted endovascular procedures [
16,
17]. After balloon occlusion, the upstream and downstream compartments remain connected via the collateral vessels, and the BOASP does not reduce to zero [
9], meaning that collateral pathways that are not always visible under X-ray images exist.
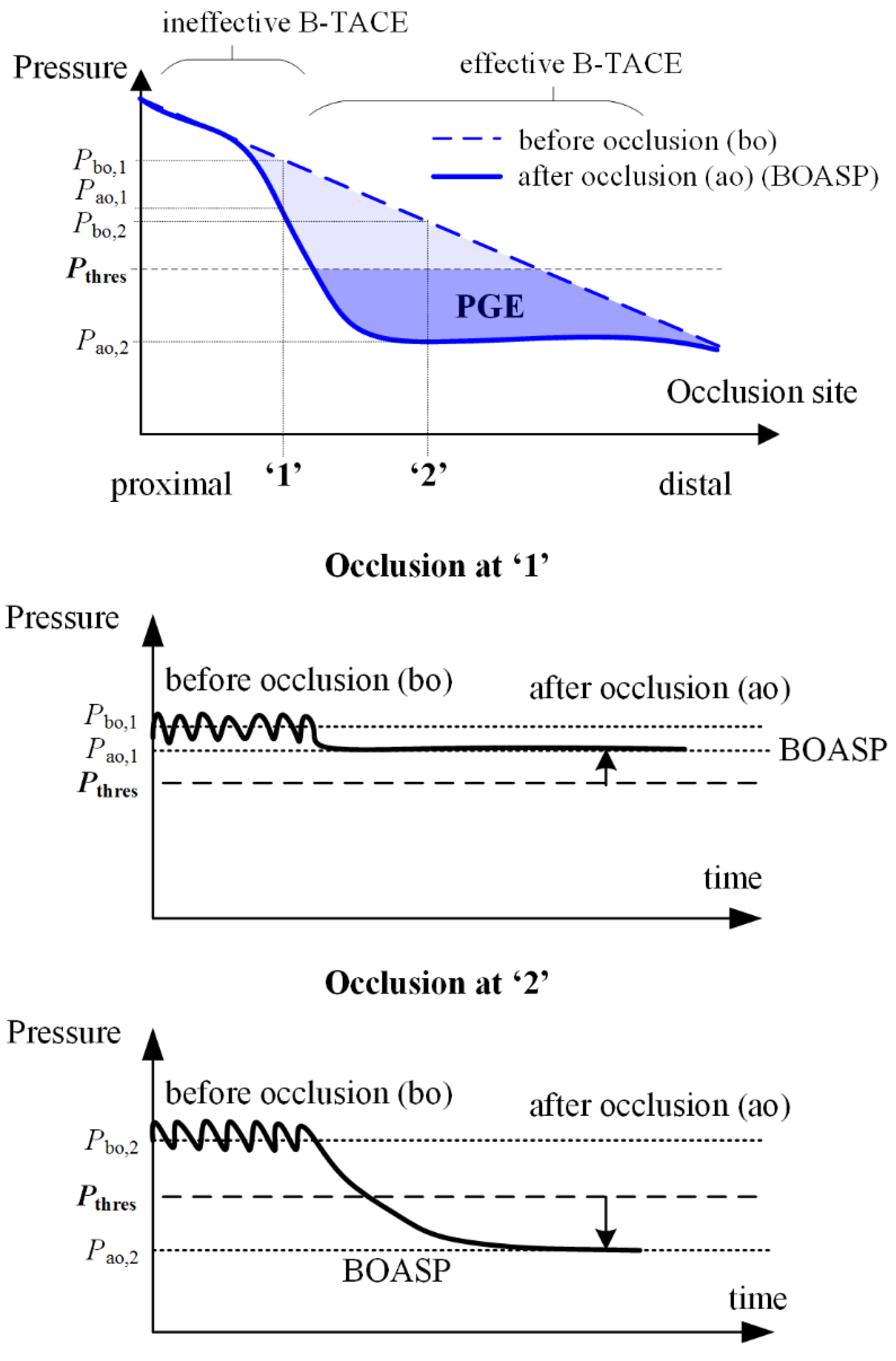
In the case of B-TACE, the blood flow persists after the temporary occlusion of a hepatic artery owing to the existing intrahepatic and extrahepatic collateral pathways. The hepatic artery mean pressure drops from a pressure before occlusion of
Pbo ≈ 90 mmHg to a value known as BOASP (or pressure after occlusion, i.e.,
Pao), which could be used to assess the suitability of a patient for a successful B-TACE: If BOASP is greater than a threshold pressure (i.e.,
Pthres), then collaterality is high and the pressure distal to the occlusion site does not change considerably. Under this setting, the benefits induced by the balloon occlusion (i.e., protection against retrograde lipiodol delivery and preferential targeting of tumors) might be lost [
9].
In contrast, when BOASP goes below
Pthres, the pressure distal to the balloon changes considerably and effectively (
Figure 1). Irie et al. found that
Pthres = 64 mmHg [
6]. Under this second scenario, a pressure gradient between distal normal- and tumor-tissues is promoted, and the pressure-gradient effect (PGE) ensures a preferential tumor-tissue irrigation to redistribute blood flow from normal to tumor tissues through collateral pathways [
6]. PGE during B-TACE enhances lipiodol accumulation in tumor tissues and reduces nontarget embolization in normal tissues. In a later study, Matsumoto et al. [
18] analyzed the influence of the occlusion site, identifying microballoon locations that may result in effective or ineffective B-TACE.
Modeling has shown the potential to analyze the influence of treatment parameters (catheter type, infusion site, infusion velocity, etc.) and even optimize other transcatheter intraarterial treatments, like radioembolization [
19,
20], and modeling could also help to understand the collateral circulation in the liver during B-TACE. Recently, Aramburu et al. [
21,
22] analyzed B-TACE via numerical simulations of hemodynamics and developed a hepatic artery model that includes collateral arteries. The model provides the platform to study hemodynamic changes in various scenarios.
The representative model of hepatic artery studied by Aramburu et al. [
22] was replicated in the in vitro model (IVM) development in this study. Bioengineered IVMs are an invaluable research tool for better understanding of tumor microenvironments and testing anticancer therapies [
23,
24]. To the best of our knowledge, there is no IVM of the hepatic artery hemodynamics available that incorporates collateral circulation or replicates the promotion of collateral flow redistribution when a microballoon catheter is inflated during B-TACE. The aim of this study is to present a simple IVM that replicates a complex phenomenon, i.e., an IVM of the arterial hemodynamics of the liver that includes collateral circulation, to visually study changes in collateral circulation.
2. Materials and Methods
In this study, we first developed the conceptual design of the IVM. Then, we created the mathematical model of the IVM. The purpose of this mathematical model was twofold: it was used to perform a simulation-based sizing of the geometrical characteristics of the IVM (e.g., the height of reservoirs, the length and diameter of tubes, etc.) to ensure that physiologically realistic flowrates flowed through the IVM, and it was also used to perform simulation-based quantitative analyses of pressures and flows in the IVM, which were used to complement the qualitative results observed in the experiments.
Based on the simulation-based sizing, the actual IVM was built. On this IVM, several experiments were carried out, in which qualitative analyses were performed. We examined the influence of the location of the tip and the cancer scenario via a series of experiments. Finally, we compared the results of the experiments with two clinical cases, and we saw that these cases are similar to two of the experiments we conducted, suggesting that the conceptual design was appropriate.
2.1. Conceptual IVM Design
The main objective was to demonstrate PGE during B-TACE in an IVM that permits the visualization of hemodynamic changes due to the collateral circulation in the liver. The hepatic arterial flow is in vitro modeled with a hydraulic system that captures all the important hemodynamic features during B-TACE (e.g., collateral pathways that permit collateral circulation) and is able to replicate PGE (i.e., flow from normal to tumor tissues under appropriate balloon occlusion).
A real-scale in vitro hepatic artery model is included in the IVM to allow for realistic B-TACE in vitro experiments with actual microballoon catheters. For simplicity, steady-state operation of the IVM is adopted, water is used (instead of blood), and dyed-water is injected (instead of chemo-lipiodol emulsion). Therefore, it is difficult to obtain physiologically realistic pulsatile flowrate (mL/min) and pressure (mmHg) values in the hydraulic system. In the IVM, the treatment outcome is regarded as successful when PGE is developed and when the injected agent is directed only to tumor-feeding branches.
The IVM models the whole systemic circulation, which is reduced to a simple hydraulic system.
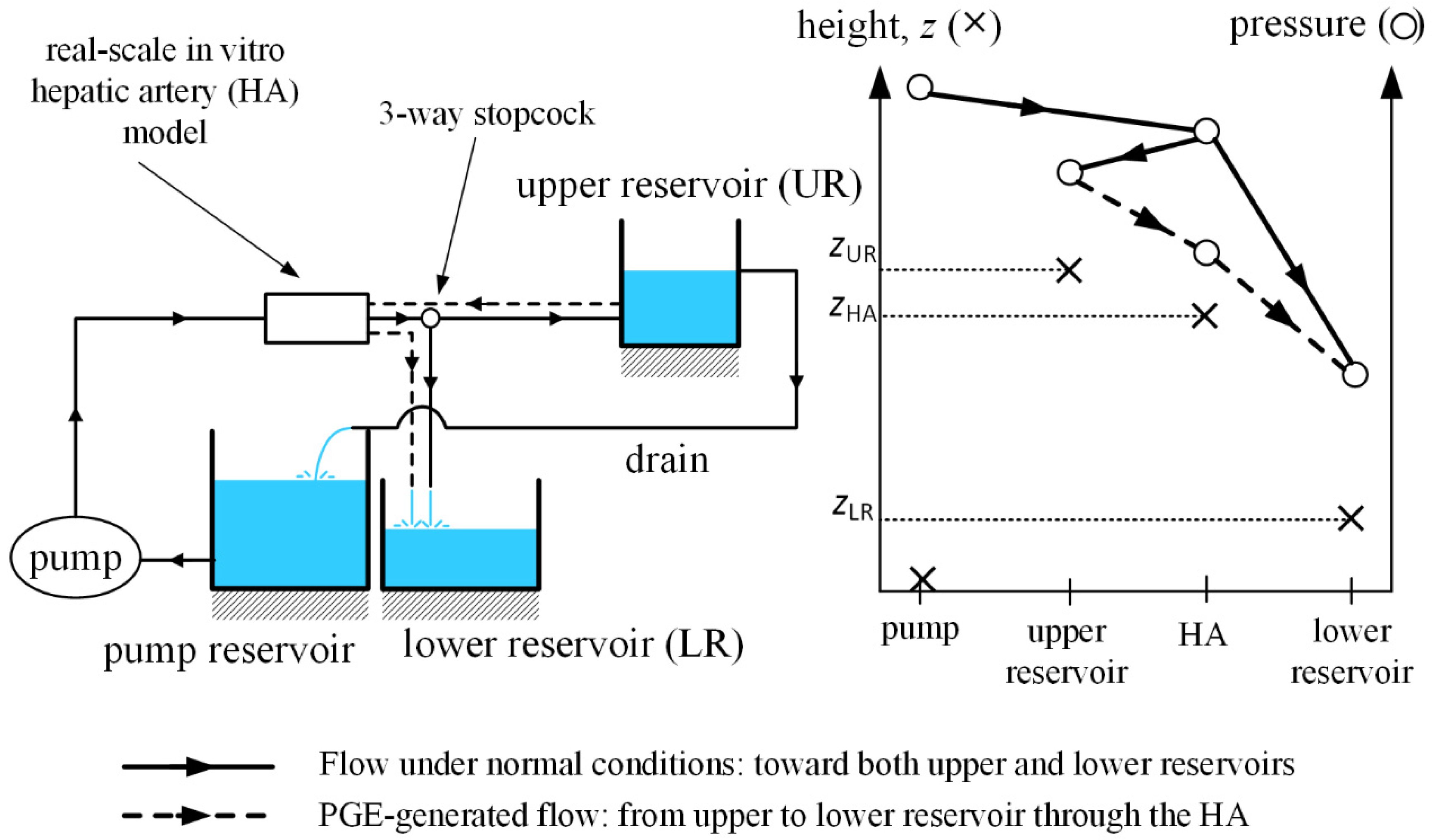
Figure 2 shows the schematics of the system, which consists of three functional reservoirs, a pump, a real-scale in vitro hepatic artery, three-way stopcocks and tubing connecting the parts. Water is irrigated through a pump toward the real-scale in vitro hepatic artery model. The hepatic artery model is horizontally located and consists of a symmetric bifurcating structure with a single inlet and various outlets, with collateral pathways allowing flow between branches at the same level. Each of those outlets is connected to a three-way stopcock, by which the characteristic of the outlet is defined: it feeds either tumor tissue or normal tissue.
If an outlet feeds tumor tissue, the flow is directed toward the lower reservoir, which models tumor-tissue pressure. In contrast, if an outlet feeds normal tissue, the flow is directed toward the upper reservoir, which models normal-tissue pressure. Water in the upper reservoir is drained to the pump reservoir, modeling the venous flow, and the pump pumps the water from venous pressure level to hepatic artery pressure level. Under steady-state operation, the free surface of water in the upper reservoir remains unchanged, and the lower reservoir is filled under the presence of tumors.
The IVM must replicate the hepatic arterial hemodynamics during B-TACE. Under normal conditions, water must flow from the pump toward upper or lower reservoirs through normal-tissue-feeding or tumor-feeding outlets after flowing through the real-scale in vitro hepatic artery model.
To do so, the pressure provided by the pump must be greater than the pressure of water in both the upper and lower reservoirs. When simulating B-TACE by occluding a branch in the hepatic artery, two scenarios can arise. First, when the flow through the pump is interrupted and PGE promotes collateral circulation from upper to lower reservoir through the hepatic artery. In this case, the physiological normal-to-tumor tissue-pressure gradient is replicated with a gravity-driven flow. To do so, the height of the free surface of water in the upper reservoir (
zUR,
Figure 2) must be greater than that of the lower reservoir (
zLR,
Figure 2), and the height of the hepatic artery model (
zHA,
Figure 2) must be between the heights of the water free-surfaces of the reservoirs (i.e.,
zUR <
zHA <
zLR).
Second, when flow through the pump is not interrupted because of a main-flow redirection through collateral arteries and water flows toward upper and lower reservoirs as under normal conditions.
Figure 2 shows the heights and water pressures of the pump, upper reservoir, hepatic artery model, and lower reservoirs. Lines and dashed lines indicate the flow directions.
2.2. Mathematical Modeling and IVM Sizing
In order to size the hydraulic system depicted in
Figure 2, a zero-dimensional (0D) model of fluid dynamics was used. In addition to using the mathematical to size the geometric characteristics of the IVM, this model was used to complement the qualitative results of experiments, by simulating the same experiments numerically and providing quantitative flow and pressure results.
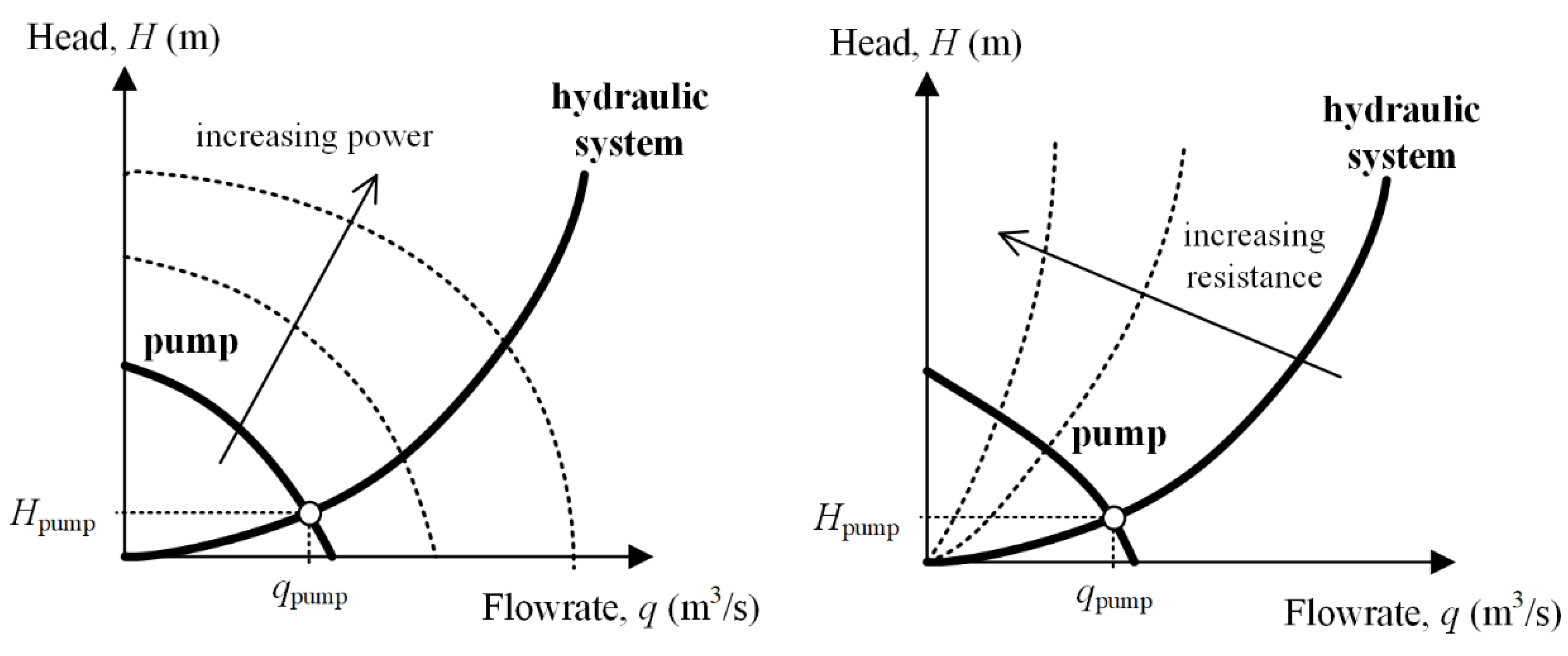
The system consists of a pump, a real-scale hepatic artery model, an upper reservoir, a lower reservoir, a pump reservoir and tubing, and three-way stopcocks that connect the hepatic artery to the reservoirs. The pump must provide the system with sufficient head (i.e., energy per unit weight) to overcome the hydraulic resistance of the system and replicate the flow toward the hepatic artery and upper or lower reservoirs. If the pump is started and its power is gradually increased, the flowrate increases; if the hydraulic resistance of the system increases, the flowrate provided by the pump decreases. For a given hydraulic system and a given pump, the working point corresponds to the intersection of the pump curve and the characteristic curve of the system (
Figure 3).
In a single circular and straight tube where a Newtonian fluid flows in steady state, the following equations apply:
where
(Pa) is the pressure difference between the two ends of the tube,
(Pa·s/m
3) is the hydraulic resistance,
(m
3/s) is the volumetric flowrate,
(Pa·s) is the dynamic viscosity of the fluid, and
(m) and
(m) are the length and the diameter of the tube, respectively.
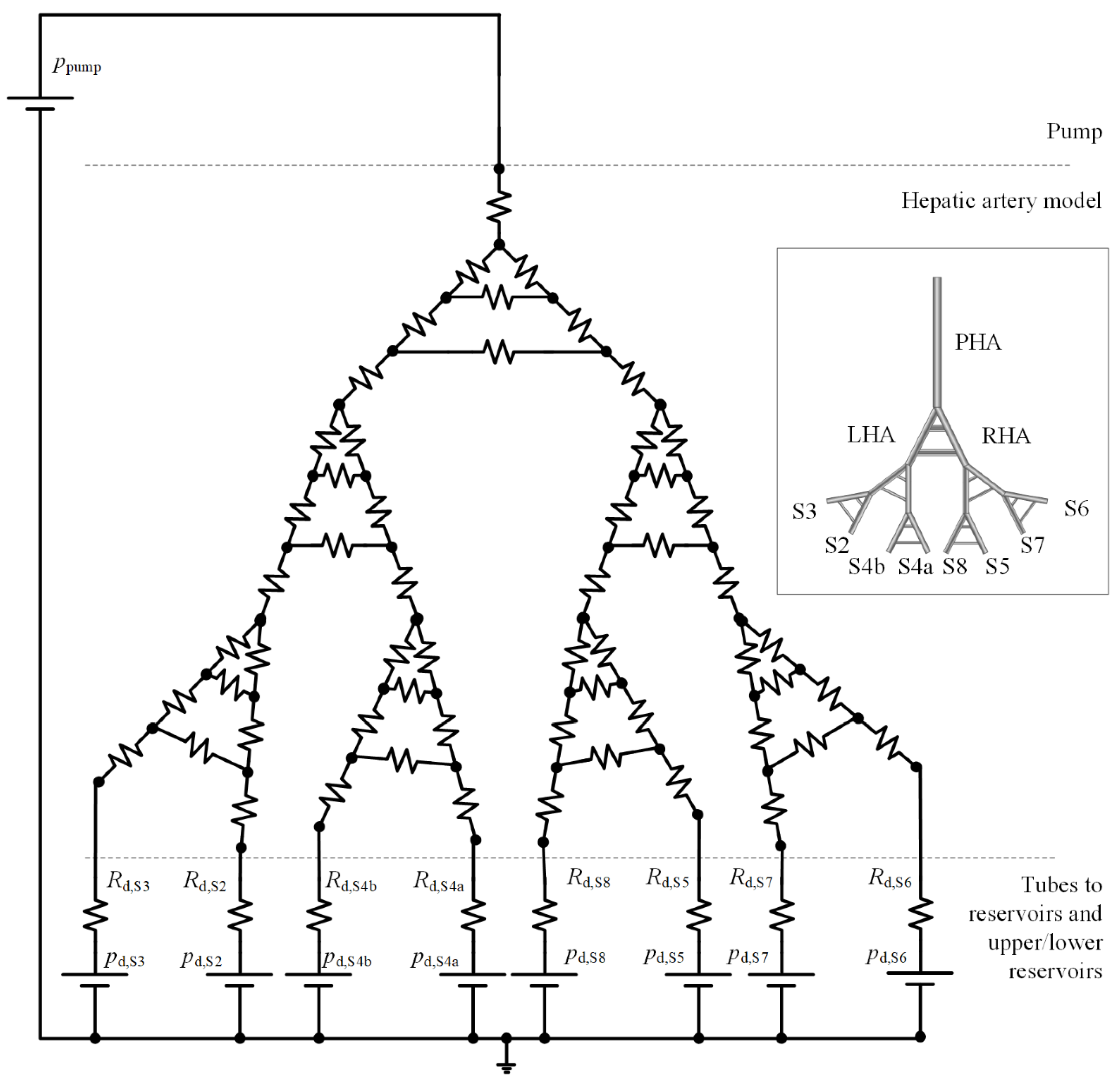
The IVM can be reduced to a 0D model consisting of a set of branches connected by nodes. By using the fluid–electric analogy, the pump is modeled as a constant-voltage source, the hepatic artery and tubes are modeled as resistances, and reservoirs are modeled as constant-voltage sources (
Figure 4).
The hepatic artery resistances are calculated with Equation (2) with the length and diameters of branches known from Aramburu et al. [
22]. To define the remaining parameters of the 0D model, seven parameters must be sized via numerical simulations to meet the specifications in conceptual design and design criteria of easy set-up, transport, and manipulation of the IVM:
Length of tubes connecting outlets of the hepatic artery and lower reservoir, lLR (m).
Diameter of tubes connecting outlets of the hepatic artery and lower reservoir, dLR (m).
Length of tubes connecting outlets of the hepatic artery and upper reservoir, lUR (m).
Diameter of tubes connecting outlets of the hepatic artery and upper reservoir, dUR (m).
Height of the free surface of water in the lower reservoir, zLR (m).
Height of the free surface of water in the upper reservoir, zUR (m).
Head (energy per unit weight) provided by the pump, Hpump (m).
Downstream resistances (
Rd in
Figure 4) are calculated with Equation (2), and downstream constant-pressure sources (
pd in
Figure 4) and pump pressure (
ppump in
Figure 4) are calculated with Equations (3) and (4), respectively, where
ρ is the water density (1000 kg/m
3) and
g = 9.8 m/s
2.
If Kirchhoff’s laws are applied to the system, a system of linear equations with the following form is obtained:
where
is a matrix that contains resistances,
is a vector containing flowrates,
is a vector containing pressure values. Equations (5) was solved as explained in Aramburu et al. [
22].
The cancer scenarios that are defined in
Section 2.4 were used for sizing. For each case, three catheter locations were assumed: conventional TACE (i.e., no balloon occlusion), B-TACE with the microballoon at location 1, and B-TACE with microballoon at location 2. By manually adjusting the sizing parameters, the following values were found to be adequate for a proper demonstration of PGE and appropriate to implement in the IVM:
= 40 mm,
= 1.2 mm,
= 40 mm,
= 1.2 mm,
= 80 mm,
= 110 mm, and
= 200 mm.
Figure 5 shows the results for the two cases (i.e., tumors in S7 and tumors in S5 and S7) and three catheter locations (no balloon occlusion, catheter location 1, and catheter location 2). The results are qualitatively the same for the two cases. Focusing on the case with tumors in S7, the reported combination of sizing values results in physiologically realistic flow distributions. With no occlusion, a greater amount of blood flows toward the tumor-bearing segment S7 compared to the other segments.
Under occlusion at location 1, PGE-driven flow is promoted from S6, S5, and S8 (negative flowrates) toward S7, resulting in a successful treatment. With the occlusion at location 2, flow redirects through a collateral pathway and flow distribution in the right lobe is similar to the distribution during conventional TACE. However, the flowrate values decrease due to the increase in the hydraulic resistance to flow in the collateral pathway. These results suggest a successful sizing of the IVM.
2.3. Actual IVM Design
The design objectives of the IVM are easy set-up, operational stability, educational scenarios, and in vitro PGE performance. The IVM (manufactured by Terumo Corporation, Tokyo, Japan) fulfills the design requirement to enable easy transport in the dedicated carrying case, easy set-up in 20 min with minimal 500 cc of water supply, and stable manipulation of complex tubing, stopcocks and the pump including stable flow distribution in the arterial model. The parts of the IVM are shown and explained in
Figure 6 and
Table 1, respectively. For practical reasons, the length and diameters of the tubes in the IVM differ slightly from those in the preliminary numerical simulation-based sizing shown in the previous section; however, the qualitative results (PGE promotion after a proper balloon occlusion) are the same.
The hepatic artery model follows the model designed by Aramburu et al. [
22] See (2) in
Figure 6 to see the actual IVM and
Figure 7 to see the branching pattern and the outlet nomenclature. This hepatic artery consists of the proper hepatic artery (PHA), which bifurcates into the RHA and LHA, each of which bifurcate until eight segmental arteries are generated, with segments (S2, S3, S4a, S4b, S5, S6, S7, and S8) defined according to Couinaud’s classification [
25]. This morphology is the most common one among the hepatic artery configurations [
26,
27].
It is important to note that the hepatic artery includes the following collateral pathways: connections between the RHA and the LHA modeling the CA [
28], connections between branches of the same level of generation modeling the intersegmental connections via the hilar plexus [
10] or can be seen as the connections when there are watershed tumors that share more than one feeding artery [
29].
Regarding educational scenarios and in vitro PGE performance, variables that users can operate in the IVM are (i) the location of the microballoon catheter and (ii) the location of tumor tissue and healthy tissue, which can be controlled by the state of the three-way stopcock at each outlet. The steps to prepare the IVM and catheters prior to the demonstration of educational scenarios and in vitro PGE performance include the following:
To set-up the IVM by connecting tubing, stopcocks, a pump, and electricity cables.
A camera that transmits live high-resolution video on a screen can be used to simulate the fluoroscopic anterior-posterior projections.
To define the educational scenario to identify the segment with tumors by placing the three-way stopcocks at the desired direction.
To pour water to the pump reservoir and the upper reservoir and start the pump until steady-state flow conditions are obtained.
To introduce the microballoon catheter to the desired location. In this study, the followings are used: a 2.7-F Occlusafe® (Terumo Corporation) for a microballoon catheter, a 4-F Glidacath® (Terumo Corporation) for a guiding catheter, and a 0.016-in Radifocus® GT-wire (Terumo Corporation) for a microwire.
To test the flow distribution by the injection of dyed-water fluid (representing chemo-lipiodol emulsion) and adjust the pump speed.
To demonstrate educational scenarios of combination of the location of the microballoon catheter and the tumor and healthy tissues.
To replace the water in the reservoirs when the transparency is lost due to repeated injections of dyed water fluid.
2.4. IVM Testing
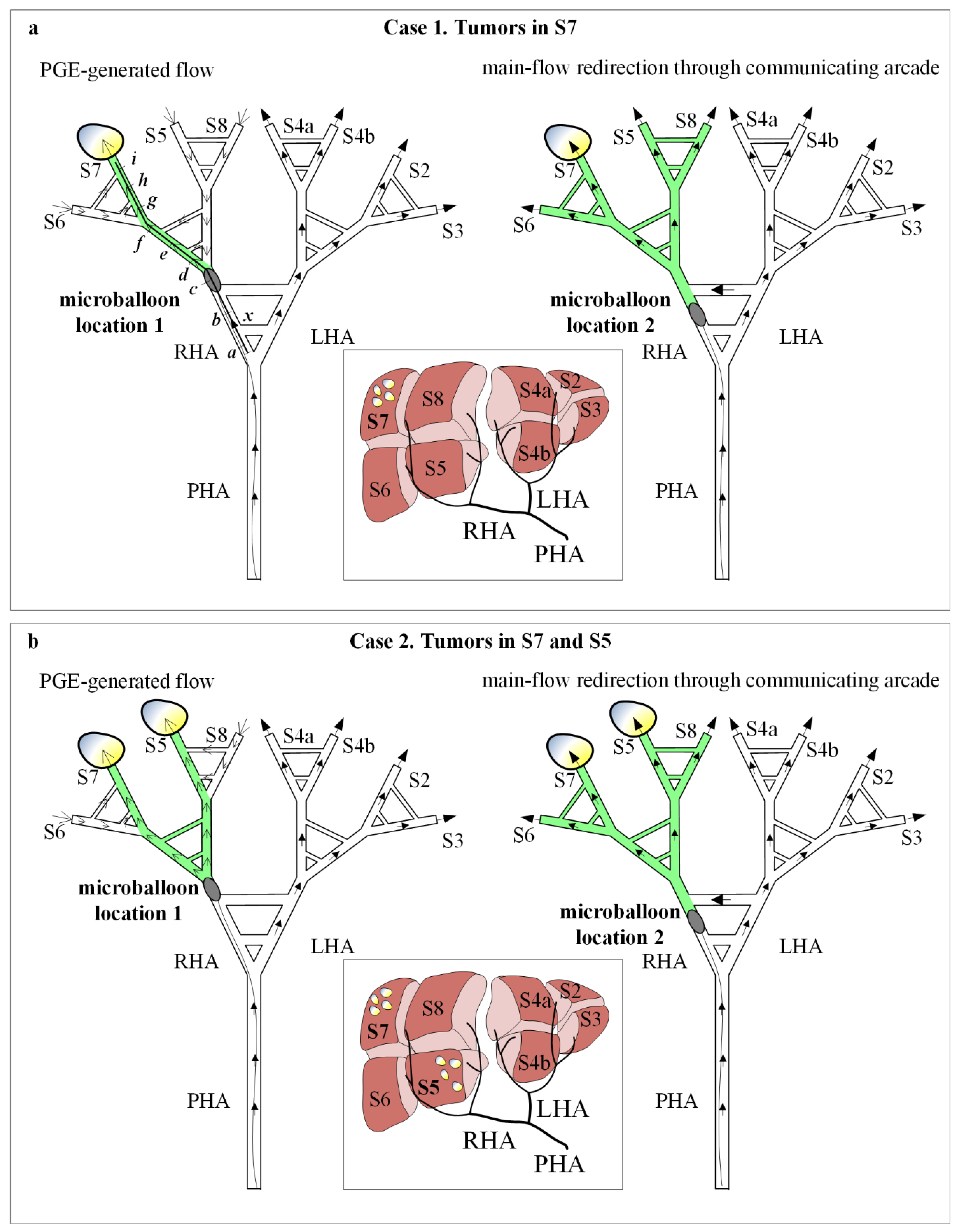
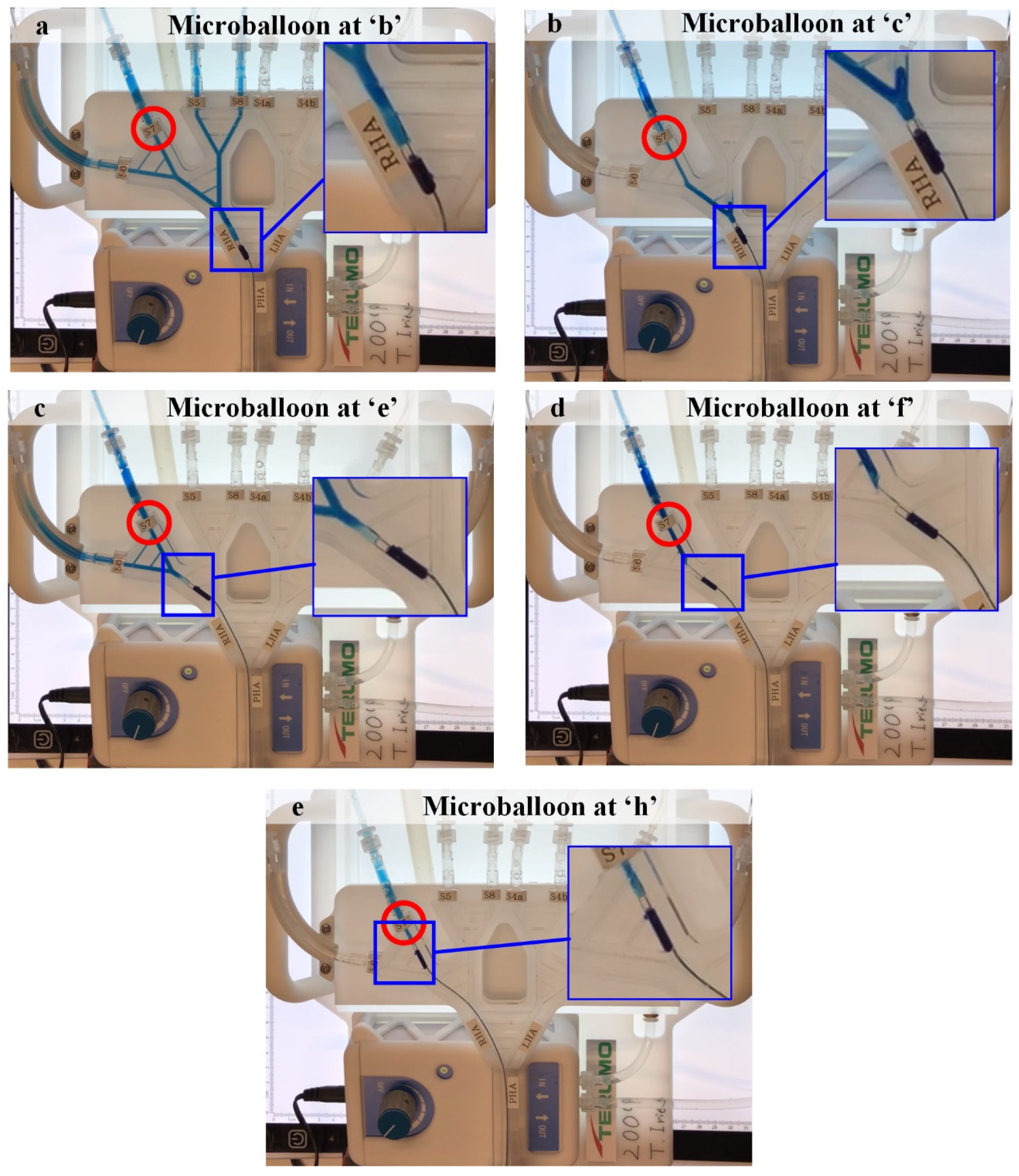
To test the IVM the two user-controllable variables were used: two cancer scenarios and two catheter locations. Case 1 corresponds to tumors in S7 and Case 2 corresponds to tumors in S7 and S5; microballoon location 1 corresponds to the RHA after the pathways that model the CA, and microballoon location 2 corresponds to the RHA between the pathways that model the CA (
Figure 7). Regarding the definition of cancer scenarios, it is important to note that this version of the IVM allows us to consider a liver segment to be either a tumor-bearing segment or a normal segment, by connecting the outlet to the lower reservoir or upper reservoir, respectively.
Therefore, the presence of tumors in a segment is modeled with a segment having a lower pressure compared to that of a normal segment; therefore, the location of the nodules within the segment is not considered. Cases and microballoon locations were combined to define four experiments. In addition, a fifth experiment was defined with one of the cases and multiple proximal-to-distal microballoon locations to analyze when PGE develops and B-TACE is successful. This fifth experiment was also performed numerically, using the mathematical model used during the IVM sizing to support the qualitative results with quantitative results.
Moreover, according to the conceptual IVM design in
Section 2.1, the results of the experiments can be foreseen by analyzing the influence of the microballoon location on the flow in the specific in vitro hepatic artery of the IVM after balloon occlusion.
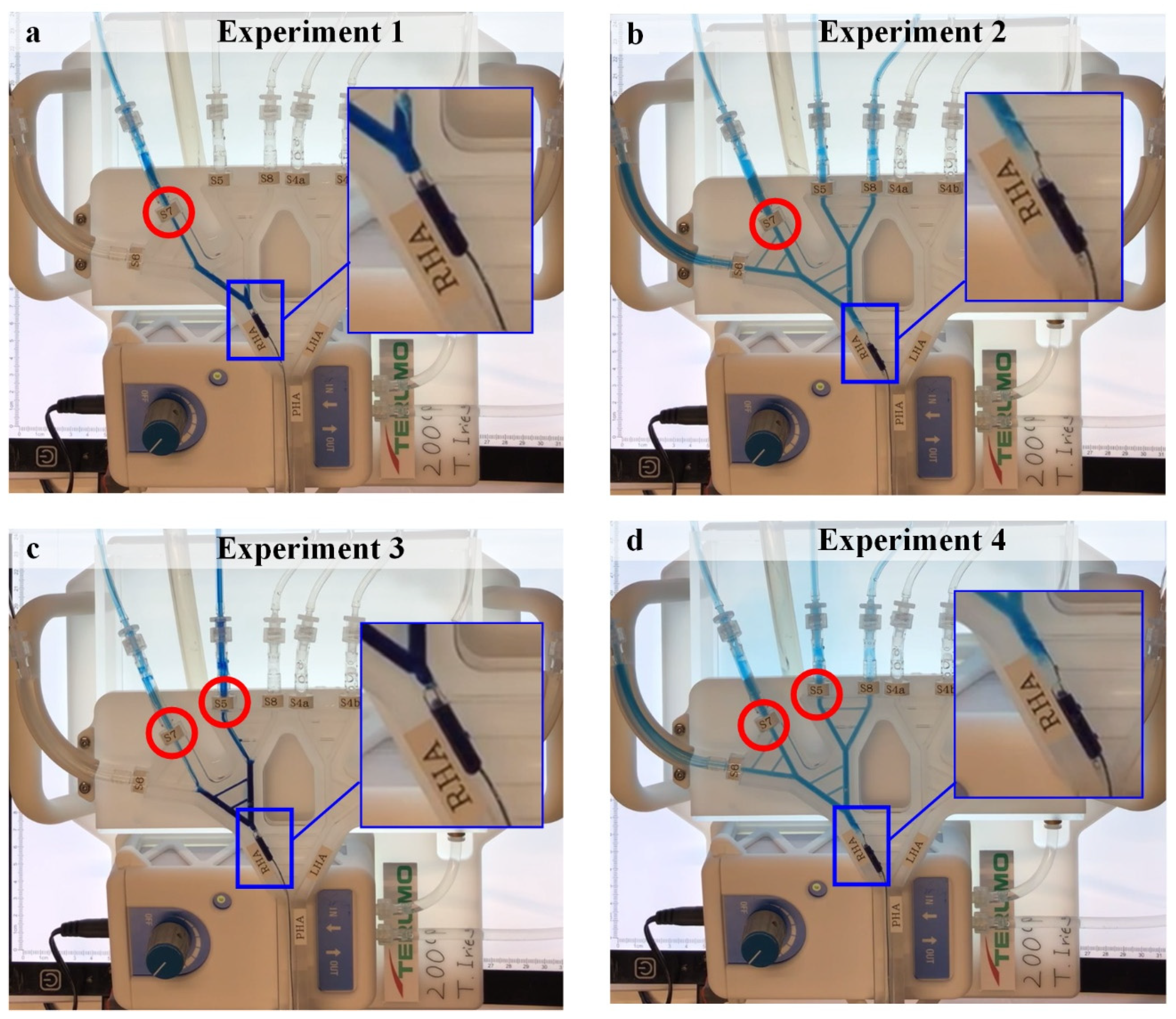
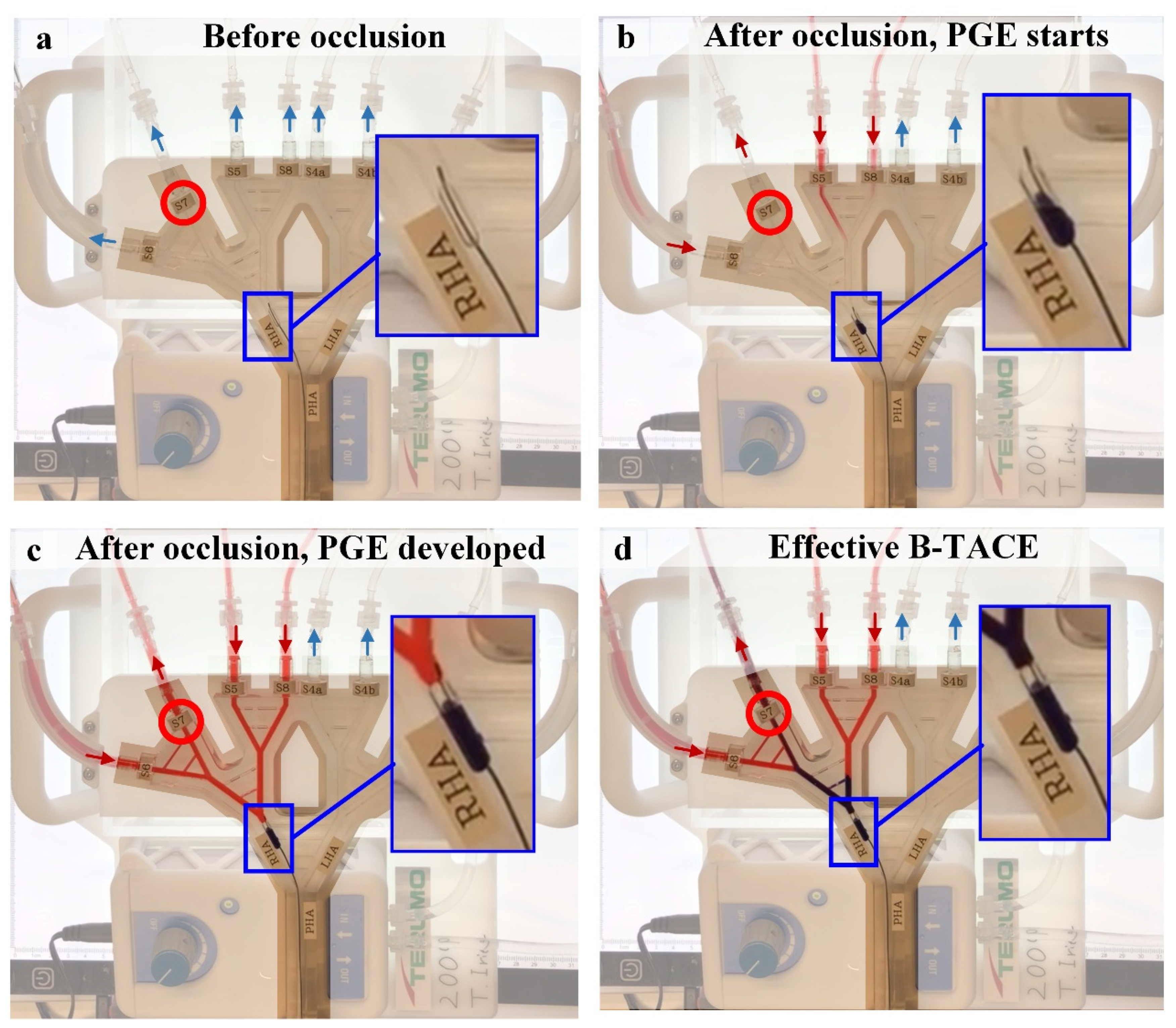
2.4.1. Experiment 1
Experiment 1 consists of the cancer scenario case 1 (i.e., tumors in S7) with microballoon location 1 (
Figure 7a left). Under these conditions, the main arterial flow (filled arrows) toward the right lobe stops and collateral circulation is promoted in the direction of the tumor-bearing S7 (open arrows). The resulting B-TACE treatment is successful in redistributing the treatment agent toward tumors.
2.4.2. Experiment 2
Experiment 2 consists of the cancer scenario case 1 with microballoon location 2 (
Figure 7a right). Under these conditions, main arterial flow (filled arrows) toward the right lobe persists because it redirects through the CA. The resulting B-TACE treatment is unsuccessful because treatment is distributed toward both healthy and tumor tissue.
2.4.3. Experiment 3
Experiment 3 consists of the cancer scenario case 2 with microballoon location 1 (
Figure 7b left). As in Experiment 1, the main arterial flow (filled arrows) toward the right lobe stops and collateral circulation is promoted in the direction of the tumor-bearing S7 and S5 (open arrows). The resulting B-TACE treatment is successful in redistributing the treatment agent toward tumors.
2.4.4. Experiment 4
Experiment 4 consists of the cancer scenario case 2 with microballoon location 2 (
Figure 7b right). As in Experiment 2, the main arterial flow (filled arrows) toward the right lobe persists because it redirects through the CA. The resulting B-TACE treatment is unsuccessful because treatment is distributed toward both healthy and tumor tissue.
2.4.5. Experiment 5
Experiment 5 consists of the cancer scenario 1 with multiple microballoon locations (i.e., ‘
a’ to ‘
i’,
Figure 7a left). Indeed, Experiment 1 and Experiment 2 are part of this experiment, where Experiment 1 is Experiment 5 with the microballoon at ‘
c’, and Experiment 2 is Experiment 5 with the microballoon at ‘
b’. This experiment was conducted to analyze the microballoon locations that promote PGE.
Experiments 1–5 were recorded (see
Supplementary Materials). In addition, Experiments 1 and 2 were recorded with red-colored water in the upper reservoir to visualize how PGE develops.
2.4.6. Numerical Simulations of Experiment 5
In addition to the multiple-location in vitro Experiment 5, numerical simulations of this experiment were carried out using the model explained in
Section 2.2 to support the qualitative experimental results with the quantitative numerical results.
2.5. Clinical Data
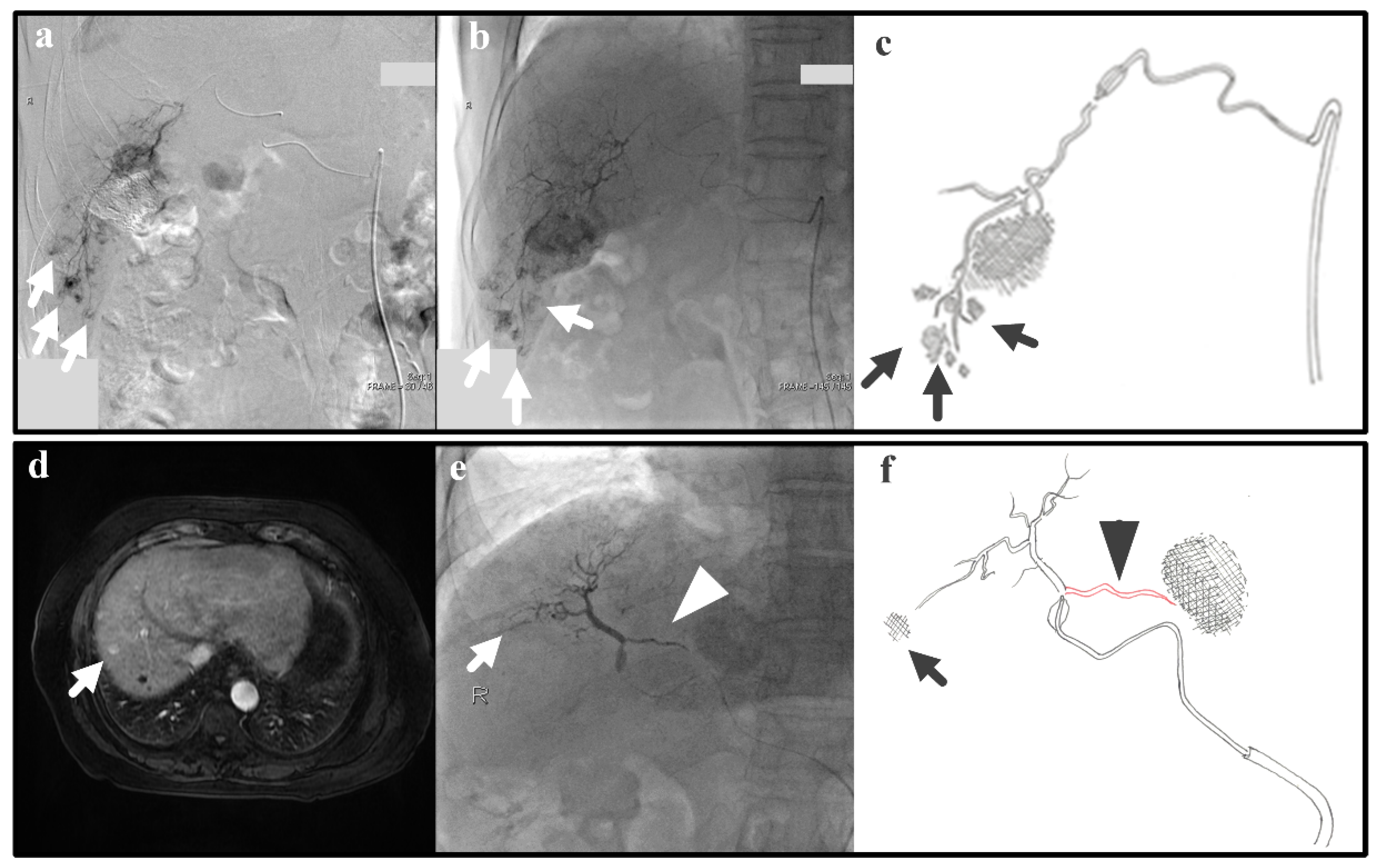
In real clinical cases, arterial hemodynamics is complex due to varied and not-always-visible collateral pathways. Thus, we examine real cases that are relevant to the IVM testing; despite the simplicity of the IVM, the successfulness/unsuccessfulness of clinical cases can also be explained with the IVM. The following two clinical cases represent Experiments 1 and 2, which give as a result efficient and inefficient B-TACE procedures, respectively. Experiment 1 (i.e., a single tumor and successful B-TACE) is similar to the case of a patient (patient 1) with previous embolization of a 3-cm tumor in S6 that underwent B-TACE after multiple early stains were detected in angiogram (arrows in
Figure 8a). Dense accumulation of lipiodol with miriplatin was shown during B-TACE (arrow in
Figure 8b,c).
Experiment 2 (i.e., a single tumor and unsuccessful B-TACE) is similar to the case of a patient (patient 2) that underwent B-TACE after an early 1-cm tumor at S8 (i.e., the therapeutic target) was detected with MRI (
Figure 8d). During embolization of S8, the microballoon tip pressure was above 64 mmHg, suggesting that collateral circulation existed. Indeed, accumulation of lipiodol with miriplatin was not enhanced (arrow in
Figure 8e,f) as a pronounced collateral pathway emerged toward S4 (arrowhead in
Figure 8e,f). These two clinical cases show that the IVM can reproduce clinically realistic scenarios.
4. Discussion
Despite the efficacy of the newly developed therapeutic procedures, it is often difficult to explain the mechanism or to reproduce it in every different clinical scenario. Microballoon catheters have emerged as promising devices to reduce nontarget embolization during various intravascular procedures [
17,
30,
31]. Specifically, in the case of B-TACE, the use of these devices has shown the potential to improve the outcome of conventional TACE [
6,
7,
8,
32]. The use of drug-eluting microspheres injected via a microballoon catheter has also been successfully explored [
33].
When the normal circulation is altered by a temporal balloon occlusion in a main branch of the hepatic artery, collateral circulation is promoted as a result of the arterial connections between the upstream and downstream compartments [
9] through collateral pathways in the liver, such as the interlobar CA [
11,
28], the arteries of the peribiliary plexus [
34], and isolated arteries [
35]. The vascularity of the organ is complex because the collateral circulation is not always visible prior to the treatment; some collateral circulation suddenly emerges during the embolization.
Irie et al. [
6] found PGE and reported a value for the BOASP below 64 mmHg as an indicator for a successful treatment. The conclusion suggested that PGE plays the important role in redistributing the vascular circulation and promotes the accumulation of the lipiodol emulsion in cancer tissues. Microballoon catheters and antireflux catheters were shown to provide safety because they prevent the retrograde treatment agent delivery and an increased efficiency because of the preferential targeting towards tumors [
9]. Thus, microballoon interventions take advantage of the complex vascular circulation of the liver. The present study shows that the IVM, which models the arterial circulation in the liver, is a simple model that is able to replicate PGE.
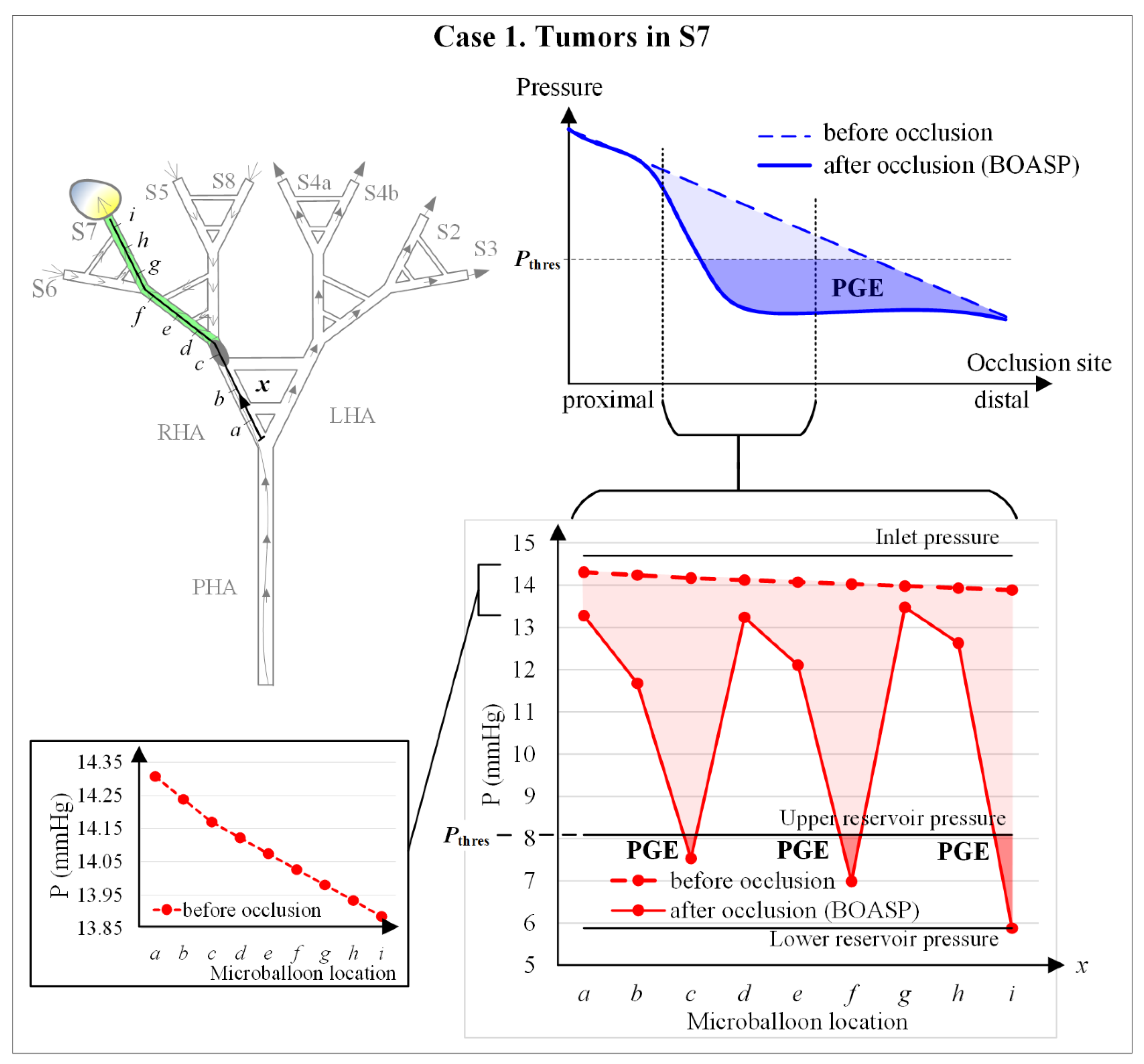
Figure 12 shows the qualitative behavior of the pressure distal to the microballoon. In a physiologically realistic behavior of blood pressure in the hepatic artery, the pressure is expected to decrease linearly from proximal to distal locations with no balloon occlusion. During balloon occlusion, PGE emerges at a certain range of occlusion locations when the BOASP is low enough (top right chart of
Figure 12).
When occluding very proximally, the effect of balloon occluding is unnoticeable because the collaterality is very high. The pressure in the IVM in the numerical simulations of Experiment 5 decreases from proximal to distal locations with no balloon occlusion (the left bottom chart of
Figure 12); and PGE is generated with balloon occlusion near ‘
c’ and ‘
f’, that is, when BOASP is below the URP, the equivalent to the threshold BOASP defined by Irie et al. [
6] as 64 mmHg.
In the in vitro experiments of this study, neither very proximal nor very distal microballoon locations were examined (see the connection between the top right and bottom right charts in
Figure 12). If blood pressures after occlusion in the physiologically realistic behavior and the IVM behavior are compared, PGE is only generated when occluding near ‘
c’ and ‘
f’ in the IVM. This difference is due to the fact that the collaterality in the IVM is represented via the collaterals in the in vitro hepatic artery, while the collateral network existing in the liver is much more complex [
13].
However, although a simple hepatic artery model generates simple, limited scenarios of collateral circulation and flow redistribution triggered by PGE, the IVM allows for the visualization of the seemingly invisible collateral circulation by means of a gravitation-driven hemodynamic phenomenon that represents liver parenchyma at the upper reservoir and tumor tissues at the lower reservoir’s water free surface at different heights.
The IVM allows for the simulation of certain clinically meaningful scenarios by selecting the tumor-bearing or normal segments and the microballoon locations, due to the simplicity of the model. For instance, PGE at the location ‘c’ and ‘f’ represents the scenario of the collateral pathway at hilar plate (RHA to/from LHA). However, the PGE phenomenon can also occur at the micro level in small vascular networks (e.g., in the peribiliary plexus) and this IVM can be used to visualize and understand what occurs at the micro level during B-TACE.
In fact, Experiments 1 and 2 are similar to the clinical cases shown in
Section 2.5 as patients 1 and 2, respectively. Therefore, we could say that, if these experiments represent clinical cases, then the conceptual IVM design was appropriate in the first place. Despite the value of the IVM, the current version of the IVM has three limitations to study in the future.
First, the use of water as the working fluid limits the pressure values in the hepatic artery of the IVM. These pressures are not physiologically realistic because the viscosity of water differs from that of blood. To overcome these limitations, a proper water–glycol mixture resulting in a density of 1050 kg/m3 and a viscosity of 0.0035 Pa·s will be used to better simulate blood.
Second, a representative hepatic artery geometry applied idealized collateral vessels between hepatic artery branches excluding the portal vein system. This also relates to the fact that only two pressure levels are defined in the system: one for the liver parenchyma and the other for tumor tissue. This limits all the hepatic artery branches feeding both liver parenchyma and tumors are at the same pressure level, meaning that the intratumoral vascular resistance is considered equal for all tumor nodules.
Third, the IVM could not replicate tumor tissue accumulation by embolic agents. For future investigation of the model development based on computational fluid dynamics or artificial intelligence-based calculation and simulation of hemodynamics, more challenging hepatic artery geometries will be created together with multiple pressure levels and different types of embolic agents, so that the IVM enables us to simulate patient-specific cases in various treatment options.