Leave or Stay: Simulating Motility and Fitness of Microorganisms in Dynamic Aquatic Ecosystems
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
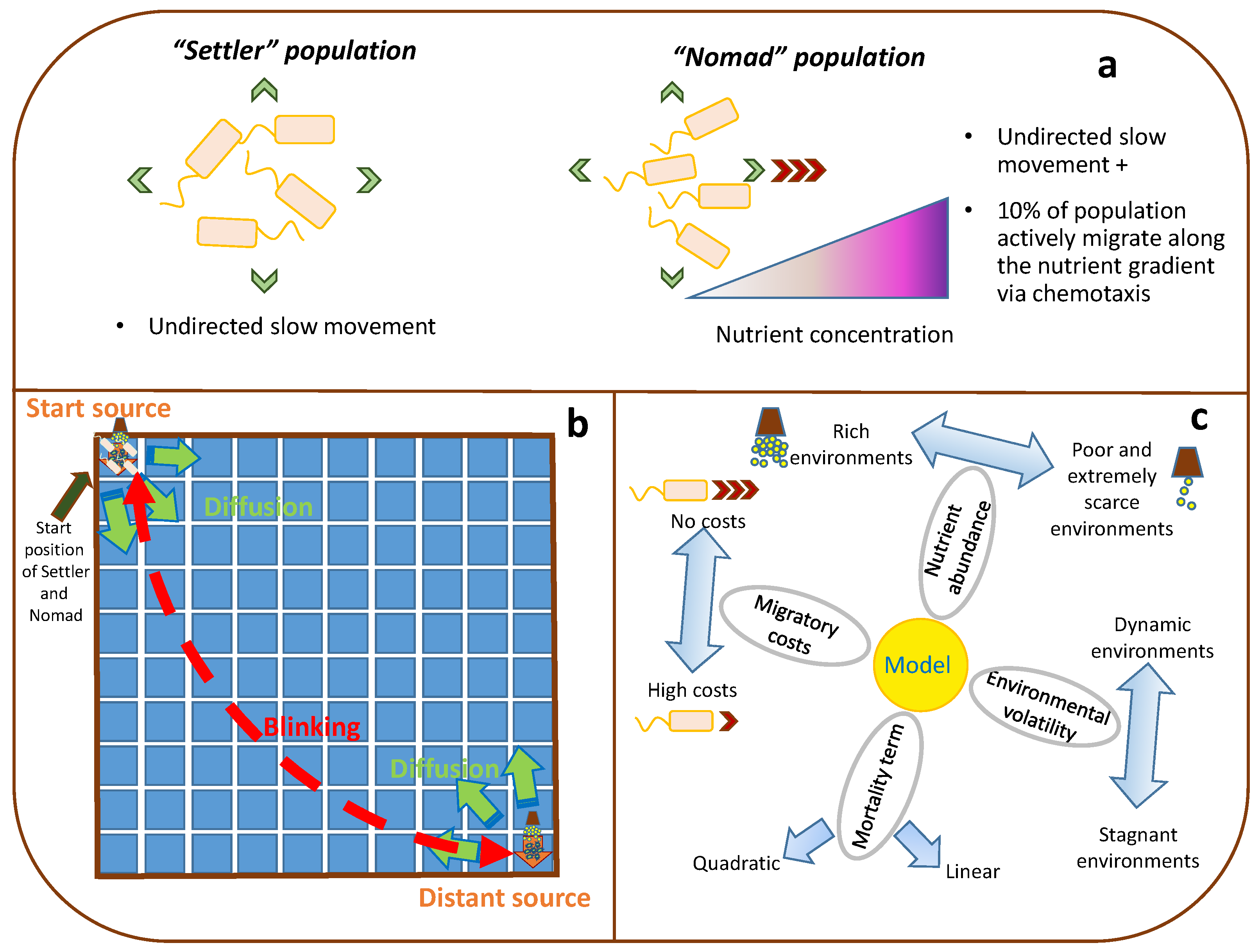
2.1. The Settler–Nomad Model
2.2. Simulation Scenarios
3. Results
- What are the critical migration penalty fee values that Nomad can bear while keeping the dominance in the system?
- How does it depend on other environmental and population factors?
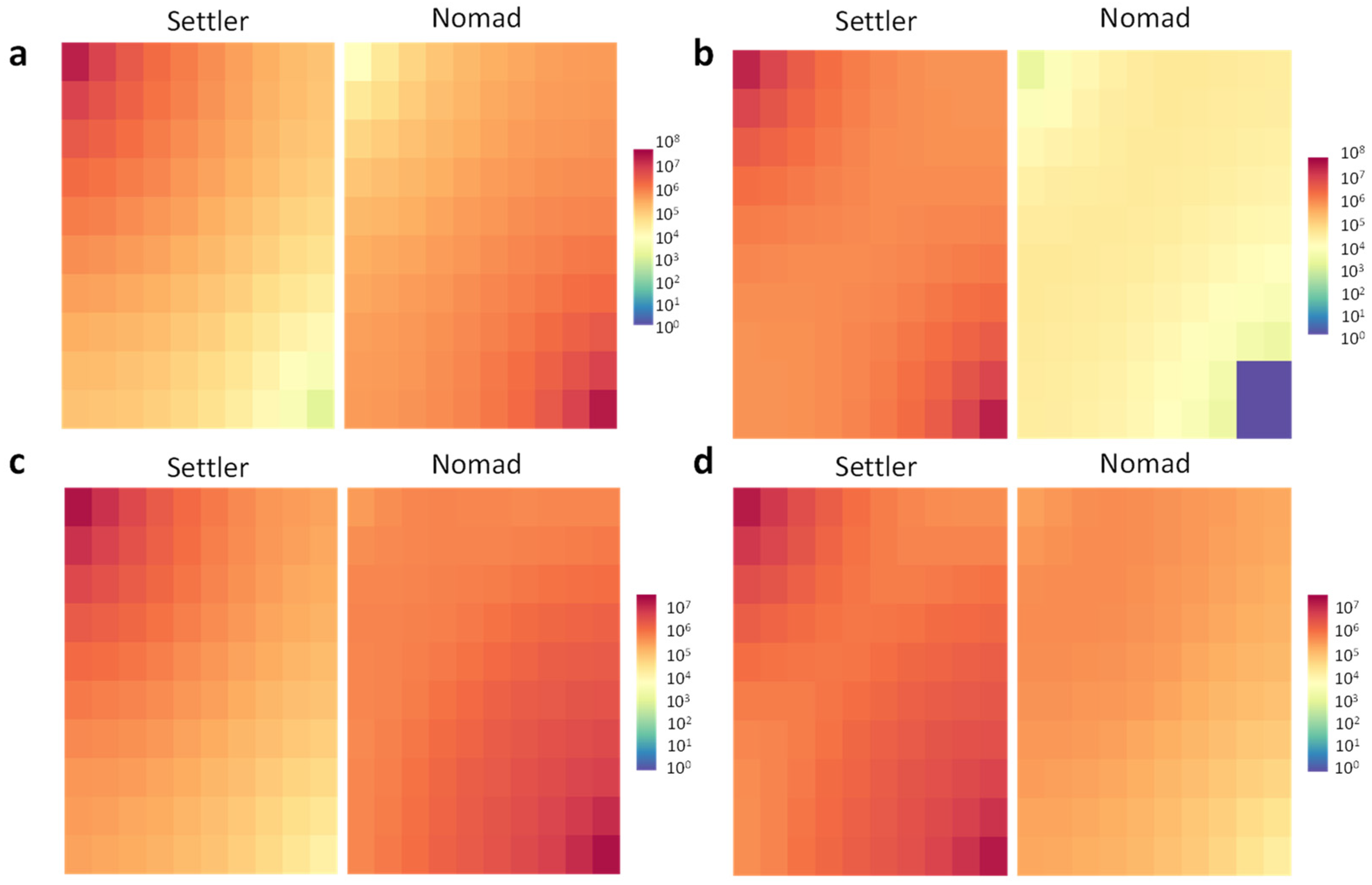
3.1. The Impact of Motility on Fitness
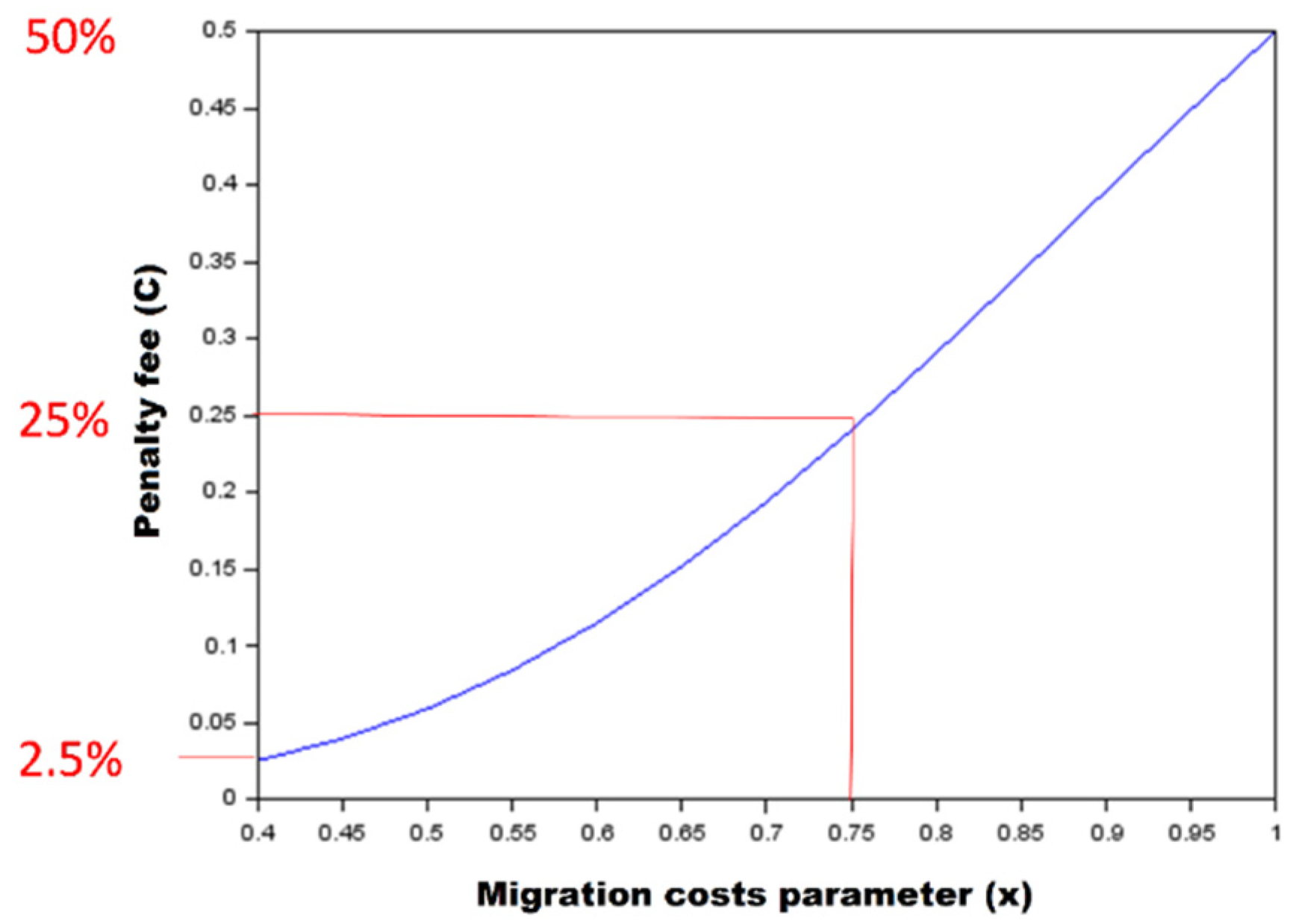
3.2. The Impact of Diversity in Energetic Costs of Migration
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Grossart, H.P.; Riemann, L.; Azam, F. Bacterial Motility in the Sea and Its Ecological Implications. Aquat. Microb. Ecol. 2001, 25, 247–258. [Google Scholar] [CrossRef] [Green Version]
- Wei, Y.; Wang, X.; Liu, J.; Nememan, I.; Singh, A.H.; Weiss, H.; Levin, B.R. The Population Dynamics of Bacteria in Physically Structured Habitats and the Adaptive Virtue of Random Motility. Proc. Natl. Acad. Sci. USA 2011, 108, 4047–4052. [Google Scholar] [CrossRef] [Green Version]
- Adler, J. Chemotaxis in Bacteria. J. Supramol. Struct. 1976, 4, 305–317. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, J.G.; Kogure, K. Bacterial Motility: Links to the Environment and a Driving Force for Microbial Physics. FEMS Microbiol. Ecol. 2006, 55, 3–16. [Google Scholar] [CrossRef] [Green Version]
- Asakura, S.; Honda, H. Two-State Model for Bacterial Chemoreceptor Proteins. The Role of Multiple Methylation. J. Mol. Biol. 1984, 176, 349–367. [Google Scholar] [CrossRef]
- Bren, A.; Eisenbach, M. How Signals Are Heard during Bacterial Chemotaxis: Protein-Protein Interactions in Sensory Signal Propagation. J. Bacteriol. 2000, 182, 6865–6873. [Google Scholar] [CrossRef] [Green Version]
- Falke, J.J.; Bass, R.B.; Butler, S.L.; Chervitz, S.A.; Danielson, M.A. The Two-Component Signaling Pathway Of Bacterial Chemotaxis: A Molecular View of Signal Transduction by Receptors, Kinases, and Adaptation Enzymes. Annu. Rev. Cell Dev. Biol. 1997, 13, 457–512. [Google Scholar] [CrossRef] [Green Version]
- Macnab, R.M.; Koshland, D.E. The Gradient-Sensing Mechanism in Bacterial Chemotaxis. Proc. Natl. Acad. Sci. USA 1972, 69, 2509–2512. [Google Scholar] [CrossRef] [Green Version]
- Tindall, M.J.; Porter, S.L.; Maini, P.K.; Gaglia, G.; Armitage, J.P. Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis I: The Single Cell. Bull. Math. Biol. 2008, 7, 1525–1569. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tindall, M.J.; Maini, P.K.; Porter, S.L.; Armitage, J.P. Overview of Mathematical Approaches Used to Model Bacterial Chemotaxis II: Bacterial Populations. Bull. Math. Biol. 2008, 70, 1570–1607. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wadhams, G.H.; Armitage, J.P. Making Sense of It All: Bacterial Chemotaxis. Nat. Rev. Mol. Cell Biol. 2004, 5, 1024–1037. [Google Scholar] [CrossRef]
- Bridier, A.; Piard, J.-C.; Pandin, C.; Labarthe, S.; Dubois-Brissonnet, F.; Briandet, R. Spatial Organization Plasticity as an Adaptive Driver of Surface Microbial Communities. Front. Microbiol. 2017, 8, 1364. [Google Scholar] [CrossRef] [Green Version]
- Niehus, R.; Mitri, S.; Fletcher, A.G.; Foster, K.R. Migration and Horizontal Gene Transfer Divide Microbial Genomes into Multiple Niches. Nat. Commun. 2015, 6, 8924. [Google Scholar] [CrossRef] [Green Version]
- Callahan, B.J.; Fukami, T.; Fisher, D.S. Rapid Evolution of Adaptive Niche Construction in Experimental Microbial Populations. Evolution 2014, 68, 3307–3316. [Google Scholar] [CrossRef]
- Chew, S.C.; Kundukad, B.; Seviour, T.; van der Maarel, J.R.C.; Yang, L.; Rice, S.A.; Doyle, P.; Kjelleberg, S. Dynamic Remodeling of Microbial Biofilms by Functionally Distinct Exopolysaccharides. MBio 2014, 5, e01536-14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, W.; Røder, H.L.; Madsen, J.S.; Bjarnsholt, T.; Sørensen, S.J.; Burmølle, M. Interspecific Bacterial Interactions Are Reflected in Multispecies Biofilm Spatial Organization. Front. Microbiol. 2016, 7, 1366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yawata, Y.; Cordero, O.X.; Menolascina, F.; Hehemann, J.H.; Polz, M.F.; Stocker, R. Competition-Dispersal Tradeoff Ecologically Differentiates Recently Speciated Marine Bacterioplankton Populations. Proc. Natl. Acad. Sci. USA 2014, 111, 5622–5627. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hein, A.M.; Carrara, F.; Brumley, D.R.; Stocker, R.; Levin, S.A. Natural Search Algorithms as a Bridge between Organisms, Evolution, and Ecology. Proc. Natl. Acad. Sci. USA 2016, 113, 9413–9420. [Google Scholar] [CrossRef] [Green Version]
- Roff, D.A. The Evolution of Migration and Some Life History Parameters in Marine Fishes. Environ. Biol. Fishes 1988, 22, 133–146. [Google Scholar] [CrossRef]
- Waite, A.J.; Frankel, N.W.; Emonet, T. Behavioral Variability and Phenotypic Diversity in Bacterial Chemotaxis. Annu. Rev. Biophys. 2018, 47, 595–616. [Google Scholar] [CrossRef]
- Xu, X.; Wen, X.; Veltman, D.M.; Keizer-Gunnink, I.; Pots, H.; Kortholt, A.; Jin, T. GPCR-Controlled Membrane Recruitment of Negative Regulator C2GAP1 Locally Inhibits Ras Signaling for Adaptation and Long-Range Chemotaxis. Proc. Natl. Acad. Sci. 2017, 114, E10092–E10101. [Google Scholar] [CrossRef] [Green Version]
- Wong-Ng, J.; Melbinger, A.; Celani, A.; Vergassola, M. The Role of Adaptation in Bacterial Speed Races. PLOS Comput. Biol. 2016, 12, e1004974. [Google Scholar] [CrossRef] [Green Version]
- Ni, B.; Colin, R.; Link, H.; Endres, R.G.; Sourjik, V. Growth-Rate Dependent Resource Investment in Bacterial Motile Behavior Quantitatively Follows Potential Benefit of Chemotaxis. Proc. Natl. Acad. Sci. USA 2020, 117, 595–601. [Google Scholar] [CrossRef] [Green Version]
- Micali, G.; Endres, R.G. Bacterial Chemotaxis: Information Processing, Thermodynamics, and Behavior. Curr. Opin. Microbiol. 2016, 30, 8–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kinnison, M.T.; Unwin, M.J.; Hendry, A.P.; Quinn, T.P. Migratory Costs and the Evolution of Egg Size and Number in Introduced and Indigenous Salmon Populations. Evolution 2001, 55, 1656–1667. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M. A Functional Perspective on Phenotypic Heterogeneity in Microorganisms. Nat. Rev. Microbiol. 2015, 497–508. [Google Scholar] [CrossRef] [PubMed]
- Yawata, Y.; Carrara, F.; Menolascina, F.; Stocker, R. Constrained Optimal Foraging by Marine Bacterioplankton on Particulate Organic Matter. Proc. Natl. Acad. Sci. USA 2020, 117, 25571–25579. [Google Scholar] [CrossRef]
- Stocker, R.; Seymour, J.R. Ecology and Physics of Bacterial Chemotaxis in the Ocean. Microbiol. Mol. Biol. Rev. 2012, 76, 792–812. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, J.G.; Pearson, L.; Bonazinga, A.; Dillon, S.; Khouri, H.; Paxinos, R. Long Lag Times and High Velocities in the Motility of Natural Assemblages of Marine Bacteria. Appl. Environ. Microbiol. 1995, 61, 877–882. [Google Scholar] [CrossRef] [Green Version]
- Giovannoni, S.J. Genome Streamlining in a Cosmopolitan Oceanic Bacterium. Science 2005, 309, 1242–1245. [Google Scholar] [CrossRef] [Green Version]
- Giovannoni, S.J. SAR11 Bacteria: The Most Abundant Plankton in the Oceans. Ann. Rev. Mar. Sci. 2017, 9, 231–255. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Nolla, H.A.; Campbell, L. Prochlorococcus Growth Rate and Contribution to Primary Production in the Equatorial and Subtropical North Pacific Ocean. Aquat. Microb. Ecol. 1997, 12, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Macnab, R.M. Flagella and Motility. In Escherichia coli and Salmonella: Cellular and Molecular Biology; Neidhardt, F.C., Ed.; ASM Press: Washington, DC, USA, 1996; pp. 123–143. [Google Scholar]
- Ni, B.; Ghosh, B.; Paldy, F.S.; Colin, R.; Heimerl, T.; Sourjik, V. Evolutionary Remodeling of Bacterial Motility Checkpoint Control. Cell Rep. 2017, 18, 866–877. [Google Scholar] [CrossRef] [PubMed]
- Lashin, S.A.; Matushkin, Y.G. Haploid Evolutionary Constructor: New Features and Further Challenges. In Silico Biol. 2011, 11, 125–135. [Google Scholar] [CrossRef]
- Klimenko, A.I.; Matushkin, Y.G.; Kolchanov, N.A.; Lashin, S.A. Modeling Evolution of Spatially Distributed Bacterial Communities: A Simulation with the Haploid Evolutionary Constructor. BMC Evol. Biol. 2015, 15, S3. [Google Scholar] [CrossRef] [Green Version]
- Klimenko, A.I.; Matushkin, Y.G.; Kolchanov, N.A.; Lashin, S.A. Spatial Heterogeneity Promotes Antagonistic Evolutionary Scenarios in Microbial Community Explained by Ecological Stratification: A Simulation Study. Ecol. Modell. 2019, 399, 66–76. [Google Scholar] [CrossRef]
- Lashin, S.A.; Suslov, V.V.; Kolchanov, N.A.; Matushkin, Y.G. Simulation of Coevolution in Community by Using the Evolutionary Constructor Program. In Silico Biol. 2007, 7, 261–275. [Google Scholar]
- Scheffer, M.; Baveco, J.M.; DeAngelis, D.L.; Rose, K.A.; van Nes, E.H. Super-Individuals a Simple Solution for Modelling Large Populations on an Individual Basis. Ecol. Modell. 1995, 80, 161–170. [Google Scholar] [CrossRef] [Green Version]
- Purcell, E.M. Life At Low Reynolds Number.Pdf. Am. J. Phys. 1977, 45, 3–11. [Google Scholar] [CrossRef] [Green Version]
- Kuo, S.C.; Koshland, D.E. Multiple Kinetic States for the Flagellar Motor Switch. J. Bacteriol. 1989, 171, 6279–6287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Simons, J.E.; Milewski, P.A. The Volcano Effect in Bacterial Chemotaxis. Math. Comput. Model. 2011, 53, 1374–1388. [Google Scholar] [CrossRef] [Green Version]
- Waite, A.J.; Frankel, N.W.; Dufour, Y.S.; Johnston, J.F.; Long, J.; Emonet, T. Non-Genetic Diversity Modulates Population Performance. Mol. Syst. Biol. 2016, 12, 895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frankel, N.W.; Pontius, W.; Dufour, Y.S.; Long, J.; Hernandez-Nunez, L.; Emonet, T. Adaptability of Non-Genetic Diversity in Bacterial Chemotaxis. Elife 2014, 3, e03526. [Google Scholar] [CrossRef] [PubMed]

| Values | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameters | Nutrient concentration in a batch (M) | 1 × 10−1 | 1 × 10−2 | 1 × 10−3 | 1 × 10−4 | 1 × 10−5 | 1 × 10−6 | 1 × 10−7 | 1 × 10−8 | 1 × 10−9 | 1 × 10−10 |
| Migratory costs (%) | 0 | 2 | 5 | 10 | 15 | 20 | 25 | 33.33 | 50 | 99.99 | |
| Period (generations) | 1 | 25 | 50 | 100 | Intermediate values were considered for some cases | 500 | 1000 | ||||
| Mortality term (categorical) | Quadratic mortality | Linear mortality | |||||||||
| Mortality term | Linear | Period 50 | Period 1000 | Period 1 | Period 1000 |
| Nomad | Nomad | Settler (almost parity with Nomad) | Settler | ||
| Quadratic | period 1 | period 1000 | |||
| Nomad | Settler | Settler (Nomad extincts) | Settler (Nomad extincts) | ||
| “Poor” environment (1 × 10−5 M nutrient concentration in a batch) | “Rich” environment (1 × 10−1 M nutrient concentration in a batch) | ||||
| Nutrient abundance | |||||
| Migration Penalty Fee (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Nutrient concentration in a batch (M) | 0% | 2% | 5% | 10% | 15% | 20% | 25% | 33.33% | 50% | 99.99% | |
| 1 × 10−1 | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−2 | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−3 | 66% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−4 | 99% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−5 | 83% | 56% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | |
| 1 × 10−6 | 41% | 67% | 65% | 11% | 11% | 11% | 11% | 11% | 11% | 11% | |
| 1 × 10−7 | 14% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−8 | 61% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−9 | 77% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−10 | 78% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| Migration Penalty Fee (%) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0% | 2% | 5% | 10% | 15% | 20% | 25% | 33.33% | 50% | 99.99% | ||
| Nutrient concentration in a batch (M) | 1 × 10−1 | 49% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% |
| 1 × 10−2 | 49% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−3 | 50% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | 0% | |
| 1 × 10−4 | 52% | 51% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | 1% | |
| 1 × 10−5 | 99% | 65% | 65% | 64% | 6% | 6% | 6% | 6% | 6% | 6% | |
| 1 × 10−6 | 96% | 81% | 80% | 20% | 20% | 20% | 20% | 20% | 20% | 20% | |
| 1 × 10−7 | 61% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−8 | 71% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−9 | 72% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| 1 × 10−10 | 72% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | 50% | |
| Migration Penalty Fee | Fee Value ≤ 0.3% | Period 50 | Period 1000 | Period 1 | Period 1000 |
| Nomad | Nomad | Settler * | Settler | ||
| Fee Value ≥ 0.4% | Period 50 | Period 1000 | Period 1 | Period 1000 | |
| Settler/Nomad (Full Parity). | Settler/Nomad (Full Parity). | Settler | Settler | ||
| “Extremely Scarce” Environment | “Rich” Environment | ||||
| Nutrient Abundance | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimenko, A.; Matushkin, Y.; Kolchanov, N.; Lashin, S. Leave or Stay: Simulating Motility and Fitness of Microorganisms in Dynamic Aquatic Ecosystems. Biology 2021, 10, 1019. https://doi.org/10.3390/biology10101019
Klimenko A, Matushkin Y, Kolchanov N, Lashin S. Leave or Stay: Simulating Motility and Fitness of Microorganisms in Dynamic Aquatic Ecosystems. Biology. 2021; 10(10):1019. https://doi.org/10.3390/biology10101019
Chicago/Turabian StyleKlimenko, Alexandra, Yury Matushkin, Nikolay Kolchanov, and Sergey Lashin. 2021. "Leave or Stay: Simulating Motility and Fitness of Microorganisms in Dynamic Aquatic Ecosystems" Biology 10, no. 10: 1019. https://doi.org/10.3390/biology10101019
APA StyleKlimenko, A., Matushkin, Y., Kolchanov, N., & Lashin, S. (2021). Leave or Stay: Simulating Motility and Fitness of Microorganisms in Dynamic Aquatic Ecosystems. Biology, 10(10), 1019. https://doi.org/10.3390/biology10101019








