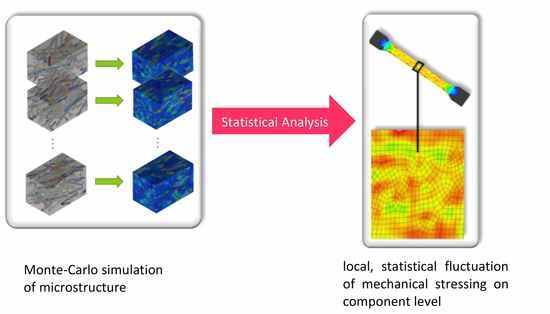
Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements
Abstract
1. Introduction
2. Materials and Methods
3. Results
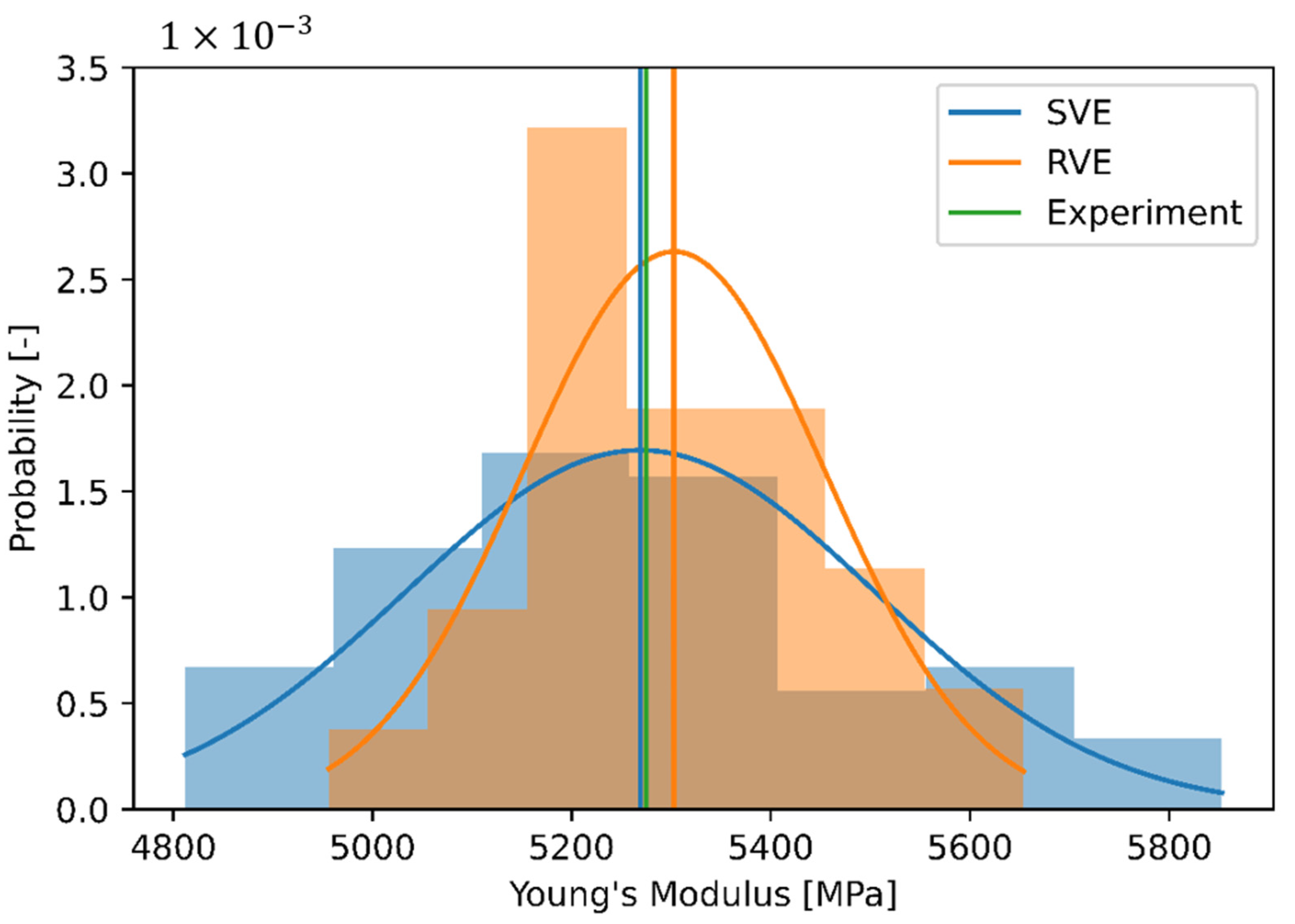
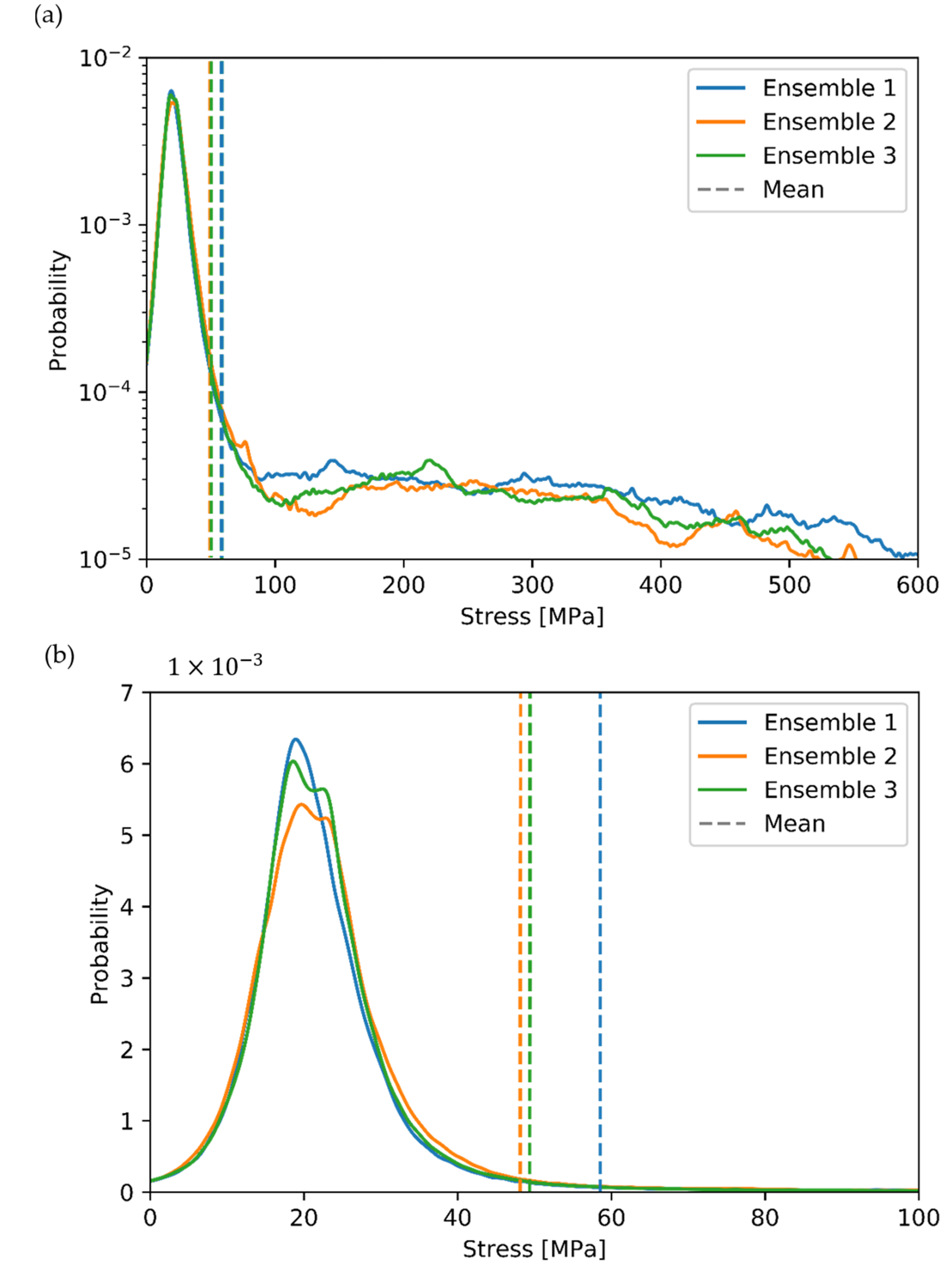
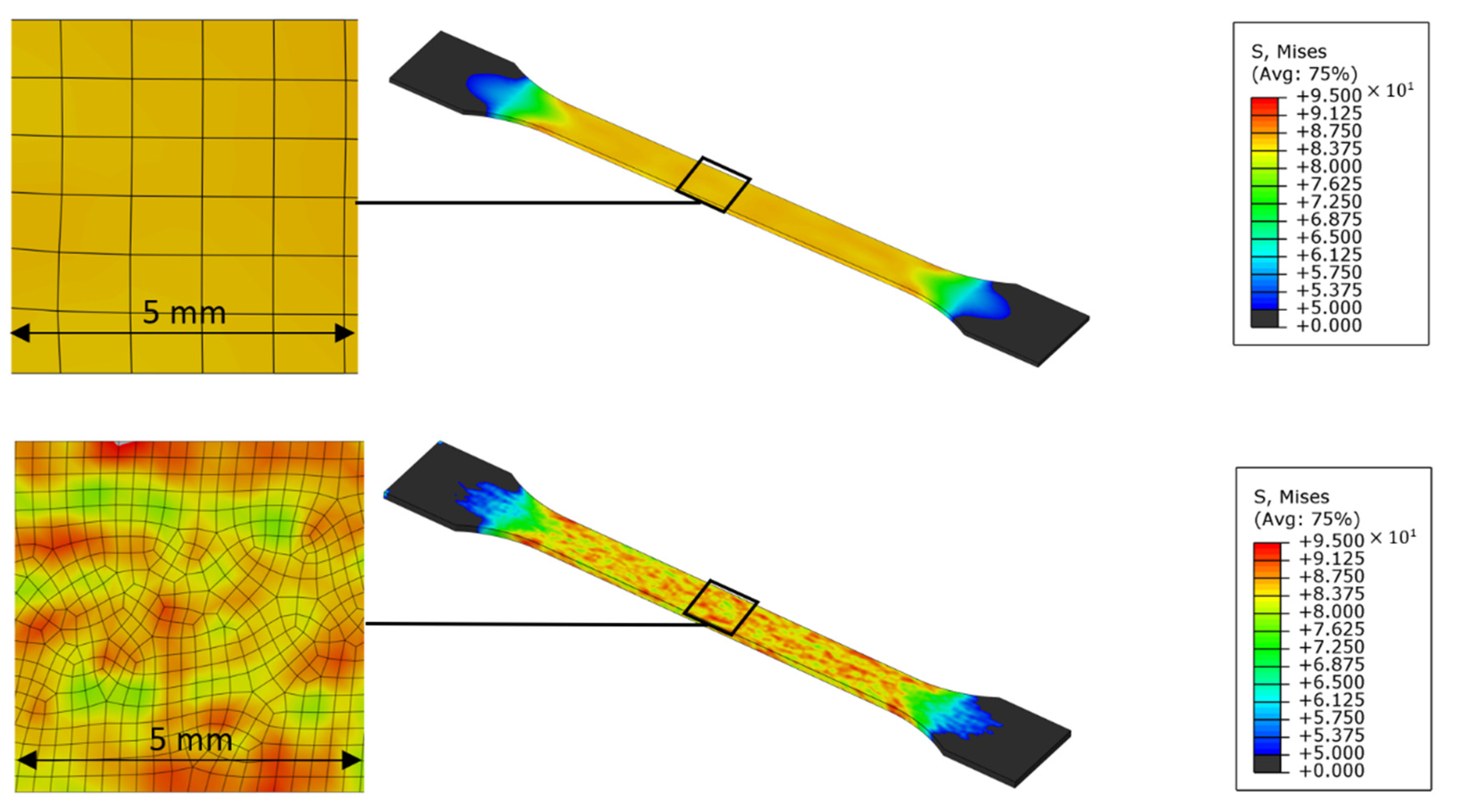
3.1. Influence of Finite Volume Approaches
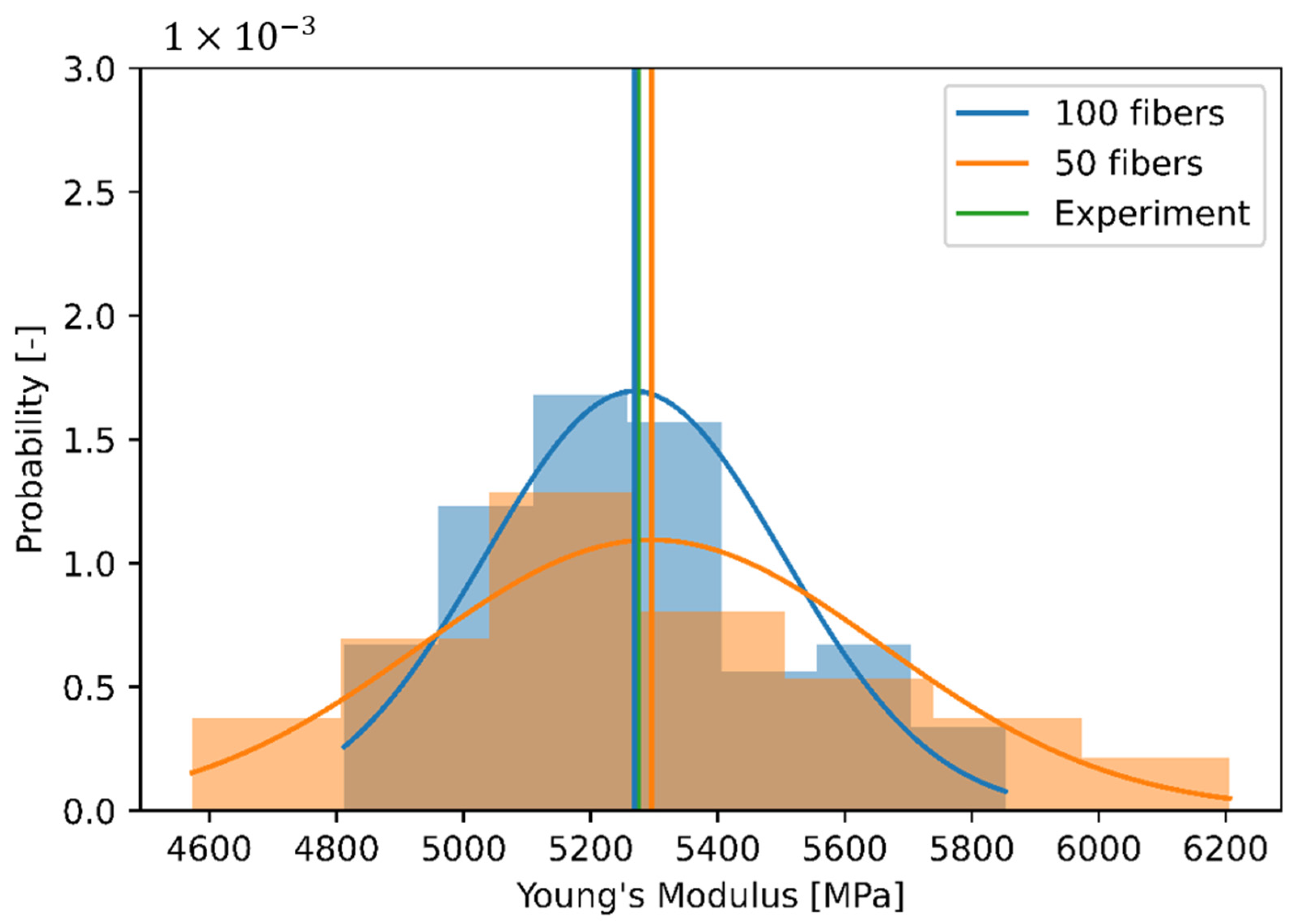
3.2. Influence of Finite Volume Size
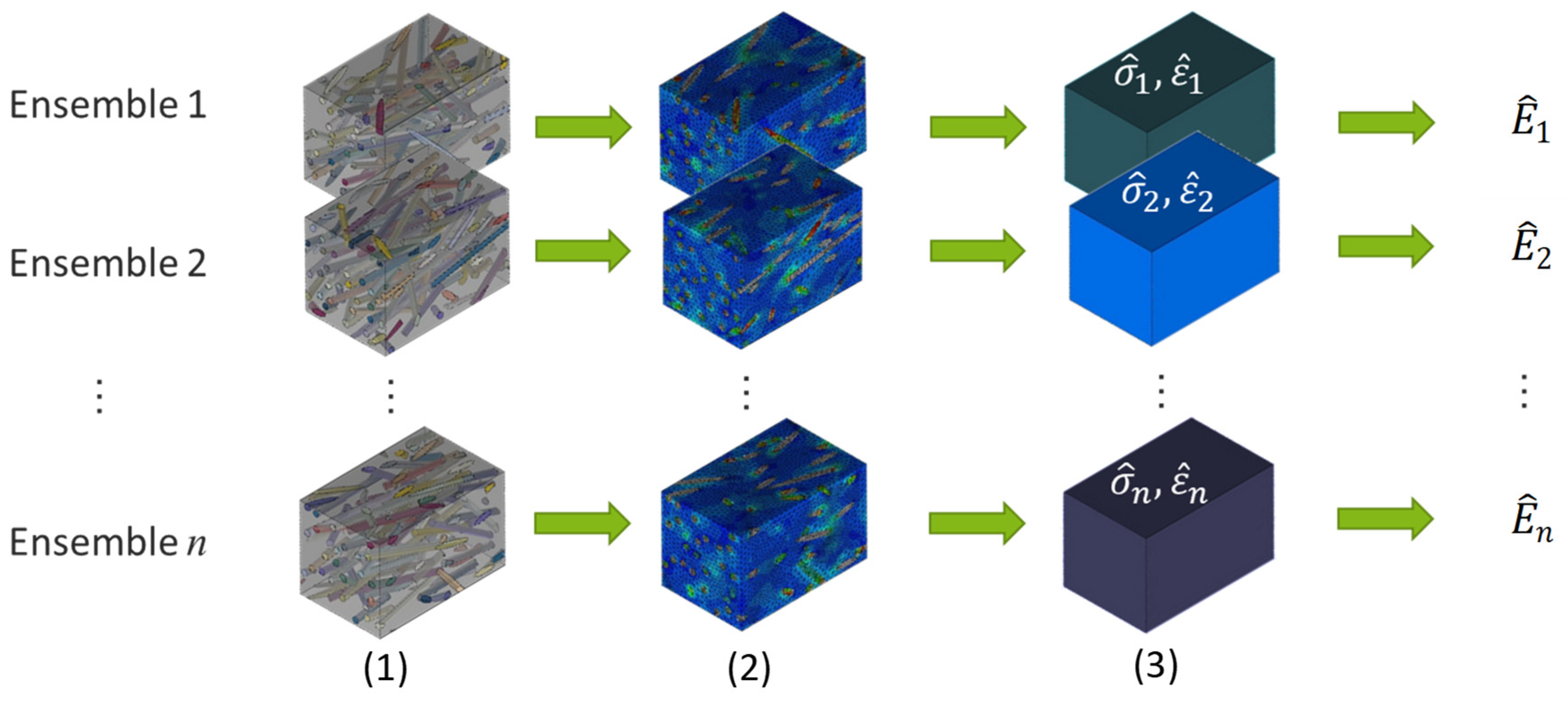
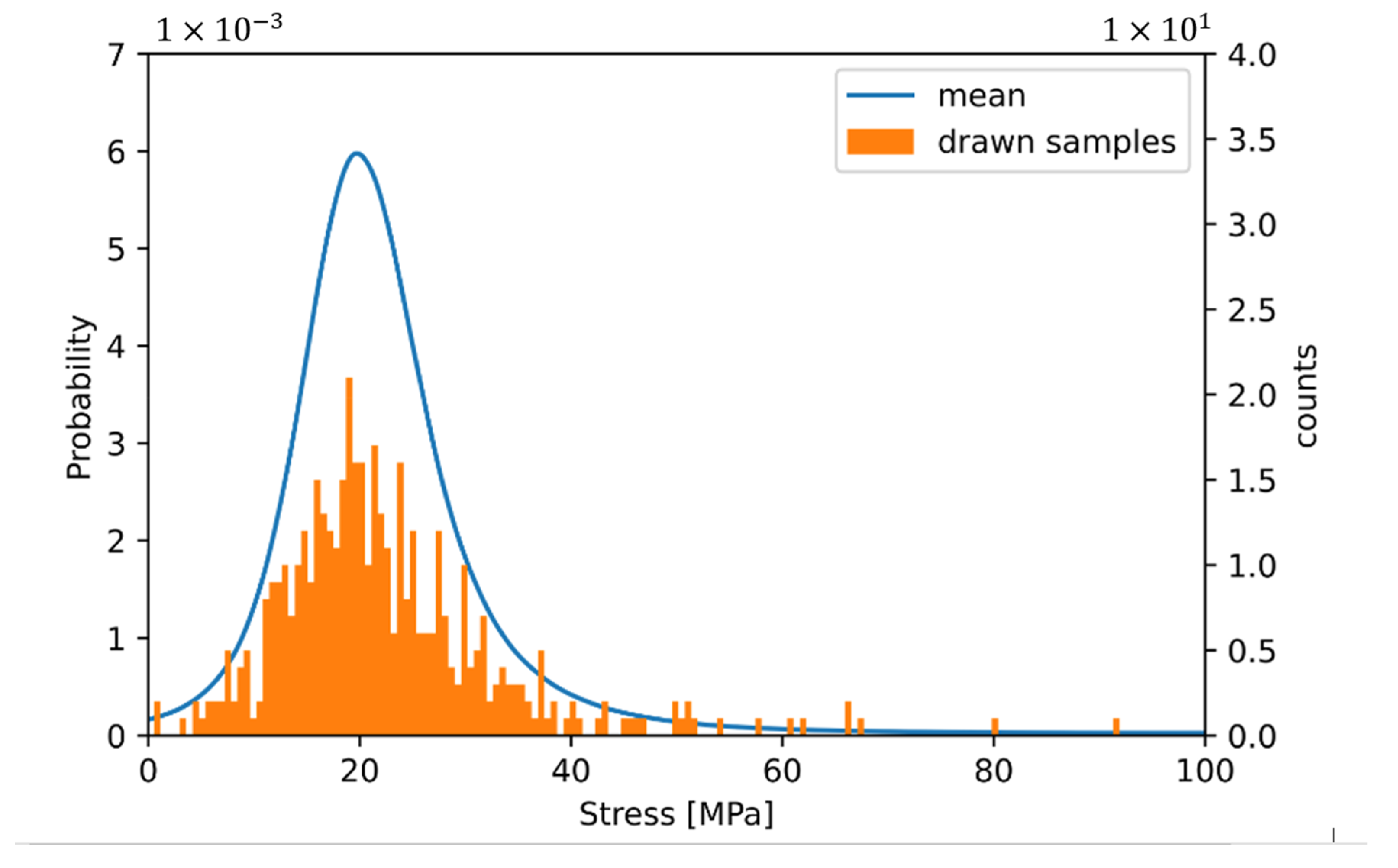
- Sampling stress values from a statistical population;
- Calculating mean value of samples;
- Calculating stiffness out of mean of samples with global strain;
- Repeating steps 1–3 several times to achieve stiffness distribution;
- Repeating steps 1–4 for different volumes.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Duschlbauer, D.; Pettermann, H.E.; Böhm, H.J. Mori–Tanaka based evaluation of inclusion stresses in composites with nonaligned reinforcements. Scr. Mater. 2003, 48, 223–228. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Doghri, I.; Quar, A. Homogenization of two-phase elasto-plastic composite materials and structures: Study of tangent operators, cyclic plasticity and numerical algorithms. Int. J. Solids Struct. 2003, 40, 1681–1712. [Google Scholar] [CrossRef]
- Eshelby, J.D. The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems. Proc. R. Soc. Lon. Ser. A 1957, 241, 376–396. [Google Scholar]
- Sun, C.T.; Vaidya, R.S. Prediction of composite properties from a representative volume element. Compos. Sci. Technol. 1996, 56, 171–179. [Google Scholar] [CrossRef]
- Sab, K. On the homogenization and the simulation of random materials. Eur. J. Mech. A Solids 1992, 11, 585–607. [Google Scholar]
- Akpoyomare, A.I.; Okereke, M.I.; Bingley, M.S. Virtual testing of composites: Imposing periodic boundary conditions on general finite element meshes. Compos. Struct. 2017, 160, 983–994. [Google Scholar] [CrossRef]
- Gusev, A.A. Representative volume element size for elastic composites: A numerical study. J. Mech. Phys. Solids 1997, 45, 1449–1459. [Google Scholar] [CrossRef]
- Okereke, M.I.; Akpoyomare, A.I. A virtual framework for prediction of full-field elastic response of unidirectional composites. Comput. Mater. Sci. 2013, 70, 82–99. [Google Scholar] [CrossRef]
- Schneider, M.; Ospald, F.; Kabel, M. Computational homogenization of elasticity on a staggered grid. Int. J. Numer. Methods Eng. 2016, 105, 693–720. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Drugan, W.J.; Willis, J.R. A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites. J. Mech. Phys. Solids 1996, 44, 497–524. [Google Scholar] [CrossRef]
- Gitman, I.M.; Askes, H.; Sluys, L.J. Representative volume: Existence and size determination. Eng. Fract. Mech. 2007, 74, 2518–2534. [Google Scholar] [CrossRef]
- Brisard, S.; Dormieux, L. FFT-based methods for the mechanics of composites: A general variational framework. Comput. Mater. Sci. 2010, 49, 663–671. [Google Scholar] [CrossRef]
- Wang, Z.; Smith, D.E. Numerical analysis on viscoelastic creep responses of aligned short fiber reinforced composites. Compos. Struct. 2019, 229, 111394. [Google Scholar] [CrossRef]
- Babu, K.P.; Mohite, P.M.; Upadhyay, C.S. Development of an RVE and its stiffness predictions based on mathematical homogenization theory for short fibre composites. Int. J. Solids Struct. 2018, 130–131, 80–104. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Díaz, R. Evaluation of effective material properties of randomly distributed short cylindrical fiber composites using a numerical homogenization technique. J. Mech. Mater. Struct. 2007, 2, 1561–1570. [Google Scholar] [CrossRef]
- Chen, L.; Gu, B.; Tao, J.; Zhou, J. The average response and isotropy of 3D representative volume elements for random distributed short fibers reinforced elastomer. Compos. Struct. 2019, 216, 279–289. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Analysis of 3D random chopped fiber reinforced composites using FEM and random sequential adsorption. Comput. Mater. Sci. 2008, 43, 450–461. [Google Scholar] [CrossRef]
- Chen, L.; Gu, B.; Zhou, J.; Tao, J. Study of the Effectiveness of the RVEs for Random Short Fiber Reinforced Elastomer Composites. Fibers Polym. 2019, 20, 1467–1479. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Numerical generation of a random chopped fiber composite RVE and its elastic properties. Compos. Sci. Technol. 2008, 68, 2792–2798. [Google Scholar] [CrossRef]
- Burgarella, B.; Maurel-Pantel, A.; Lahellec, N.; Bouvard, J.-L.; Billon, N.; Moulinec, H.; Lebon, F. Effective viscoelastic behavior of short fibers composites using virtual DMA experiments. Mech. Time-Depend. Mater. 2019, 23, 337–360. [Google Scholar] [CrossRef]
- Wang, L.; Nygren, G.; Karkkainen, R.L.; Yang, Q. A multiscale approach for virtual testing of highly aligned short carbon fiber composites. Compos. Struct. 2019, 230, 111462. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M. RVE modelling of short fiber reinforced thermoplastics with discrete fiber orientation and fiber length distribution. SN Appl. Sci. 2019, 2, 91. [Google Scholar] [CrossRef]
- Görthofer, J.; Schneider, M.; Ospald, F.; Hrymak, A.; Böhlke, T. Computational homogenization of sheet molding compound composites based on high fidelity representative volume elements. Comput. Mater. Sci. 2020, 174, 109456. [Google Scholar] [CrossRef]
- Greco, A. FEM analysis of the elastic behavior of composites and nanocomposites with arbitrarily oriented reinforcements. Compos. Struct. 2020, 241, 112095. [Google Scholar] [CrossRef]
- Huet, C. Application of variational concepts to size effects in elastic heterogeneous bodies. J. Mech. Phys. Solids 1990, 38, 813–841. [Google Scholar] [CrossRef]
- Hazanov, S.; Huet, C. Order relationships for boundary conditions effect in heterogeneous bodies smaller than the representative volume. J. Mech. Phys. Solids 1994, 42, 1995–2011. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Celanese. Celanex 2300 GV1/20 Datasheet. Available online: http://catalog.ides.com/Datasheet.aspx?I=26793&E=73487 (accessed on 28 April 2021).
- Kaiser, J.-M.; Stommel, M. Modified mean-field formulations for the improved simulation of short fiber reinforced thermoplastics. Compos. Sci. Technol. 2014, 99, 75–81. [Google Scholar] [CrossRef]
- Parra-Venegas, E.J.; Campos-Venegas, K.; Martinez-Sanchez, R.; Herrera-Ramirez, J.M.; Rodriguez-Miranda, A. The Tensile Behavior of E-glass fibers. Microsc. Microanal. 2012, 18, 784–785. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M.; Korte, W. Analysis and Evaluation of Fiber Orientation Reconstruction Methods. J. Compos. Sci. 2019, 3, 67. [Google Scholar] [CrossRef]
- D’Agostino, R.B. An omnibus test of normality for moderate and large sample size. Biometrika 1971, 58, 341–348. [Google Scholar] [CrossRef]
- D’Agostino, R.B.; Pearson, E.S. Tests for departure from normality. Biometrika 1973, 60, 613–622. [Google Scholar]
- Gandhi, U.N.; Goris, S.; Osswald, T.A.; Song, Y.-Y. Discontinuous Fiber-Reinforced Composites, 1st ed.; Hanser: Munich, Germany, 2020. [Google Scholar]

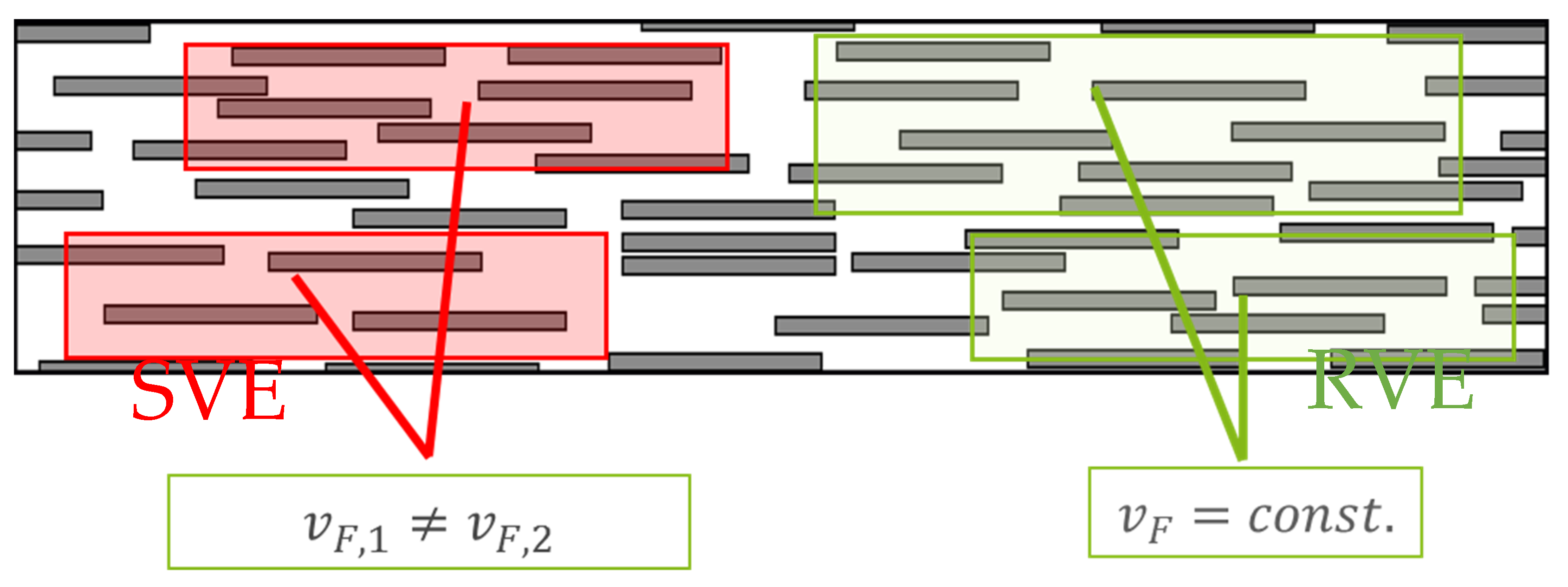



| Parameter | SVE | RVE |
|---|---|---|
| number of fibers | constant | constant |
| fiber geometry | constant | constant |
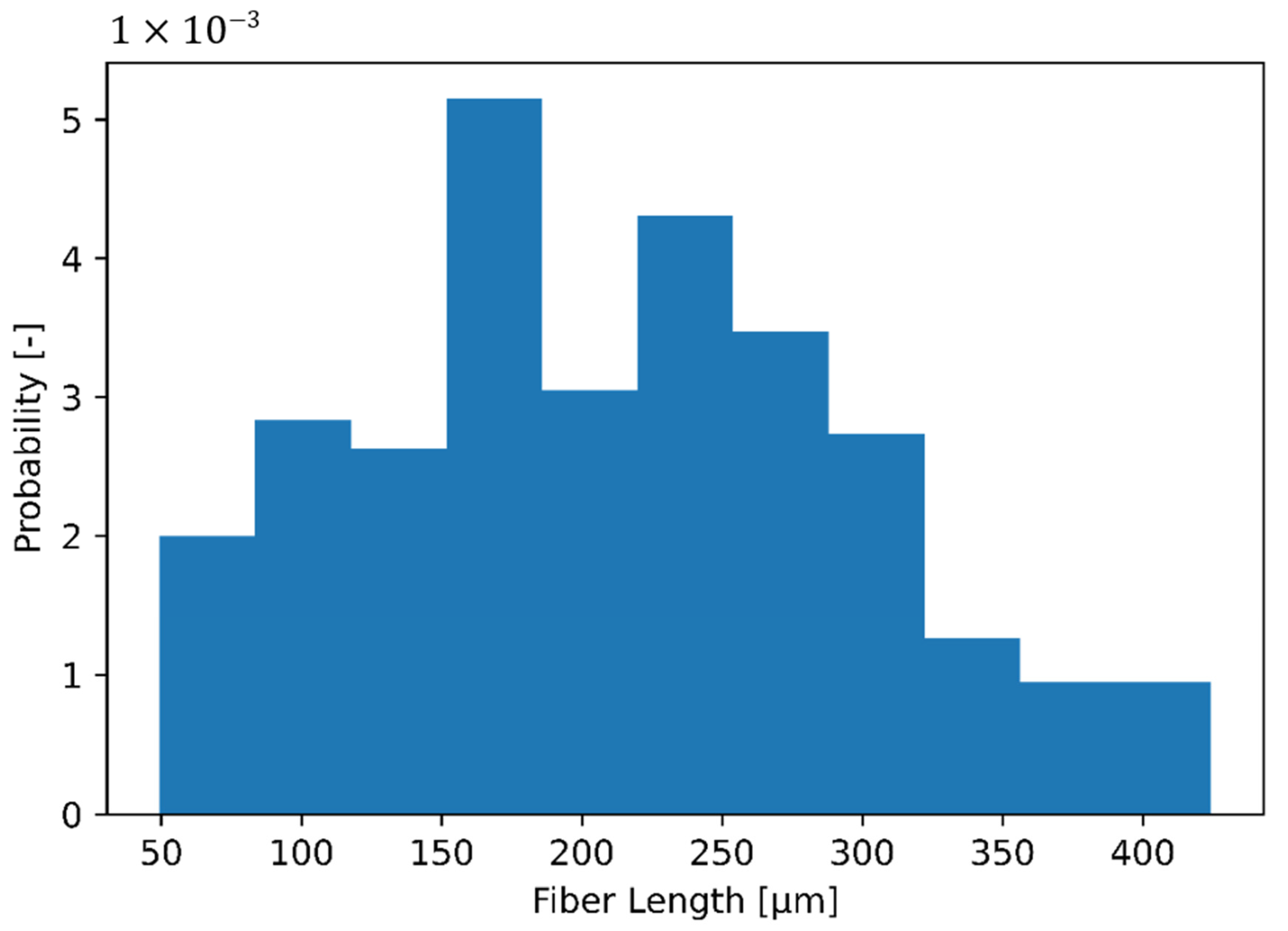
| fiber length | defined by LDF | defined by LDF |
| fiber volume fraction | defined by fibers and total volume | constant |
| total volume | constant | defined by fibers and fiber volume fraction |
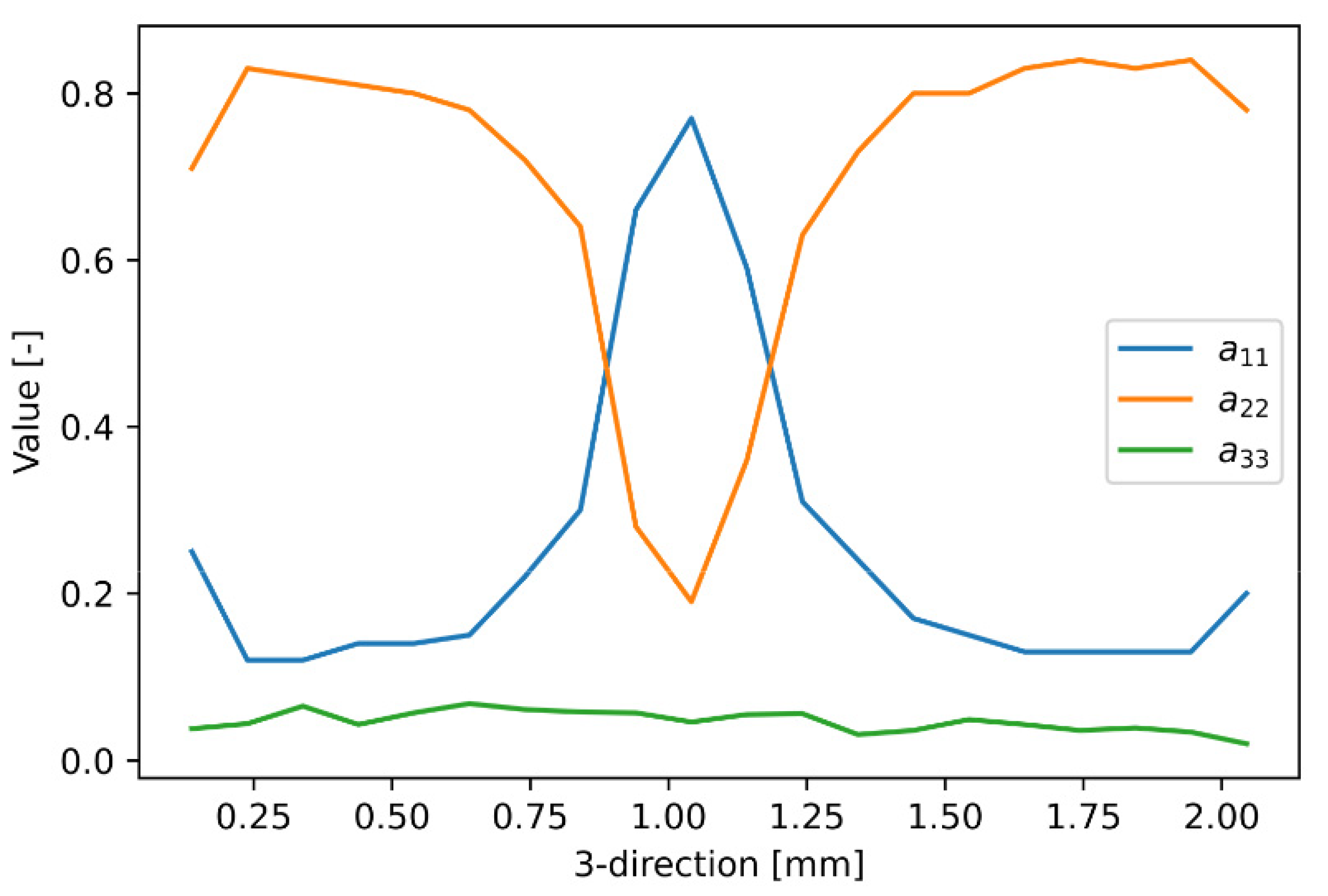
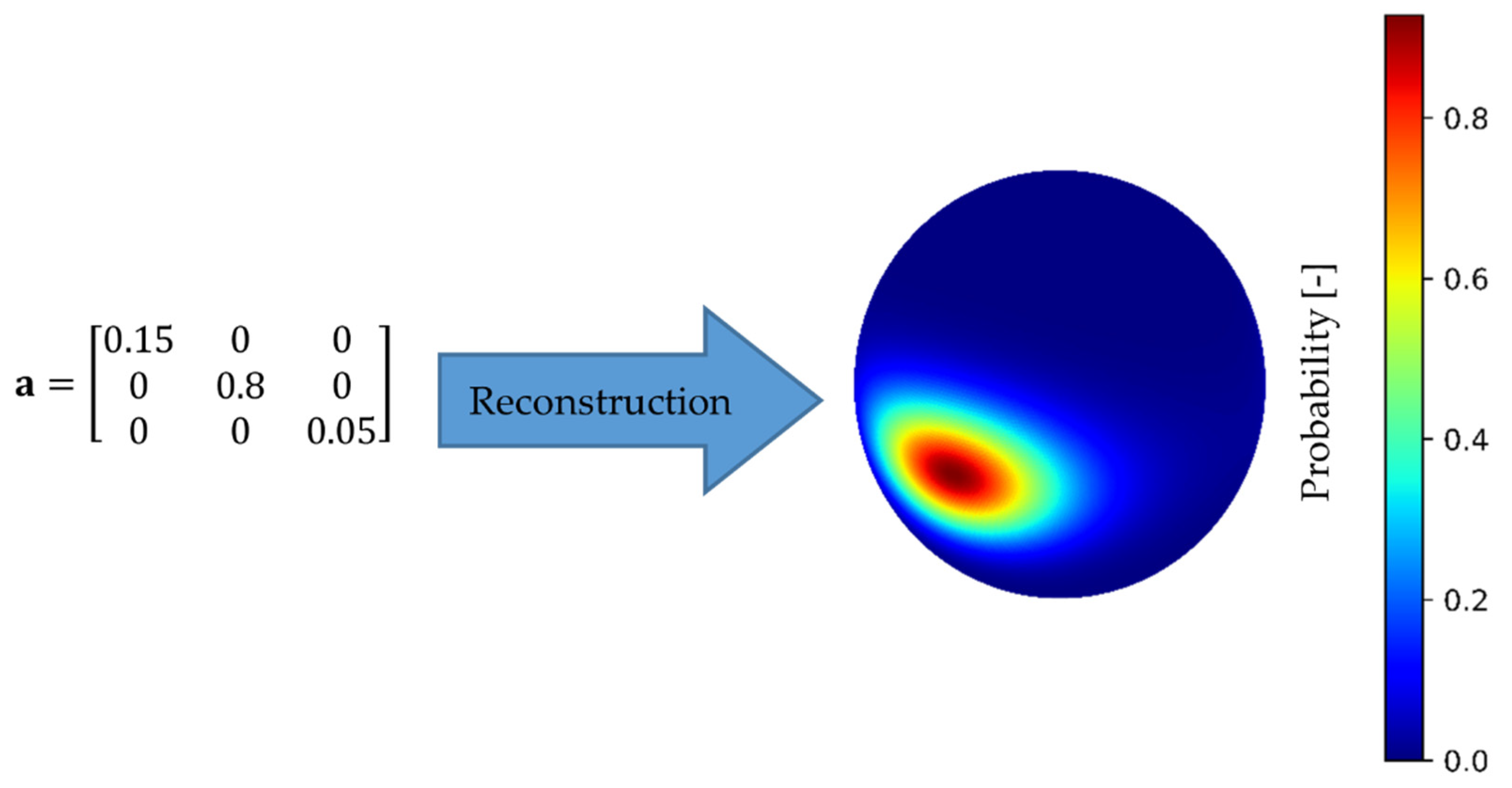
| fiber orientation | defined by ODF | defined by ODF |
| fiber arrangement | random | random |
| phase properties | constant | constant |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Breuer, K.; Spickenheuer, A.; Stommel, M. Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements. Fibers 2021, 9, 32. https://doi.org/10.3390/fib9050032
Breuer K, Spickenheuer A, Stommel M. Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements. Fibers. 2021; 9(5):32. https://doi.org/10.3390/fib9050032
Chicago/Turabian StyleBreuer, Kevin, Axel Spickenheuer, and Markus Stommel. 2021. "Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements" Fibers 9, no. 5: 32. https://doi.org/10.3390/fib9050032
APA StyleBreuer, K., Spickenheuer, A., & Stommel, M. (2021). Statistical Analysis of Mechanical Stressing in Short Fiber Reinforced Composites by Means of Statistical and Representative Volume Elements. Fibers, 9(5), 32. https://doi.org/10.3390/fib9050032