Morphology Development of Polymer Blend Fibers along Spinning Line
Abstract
1. Introduction
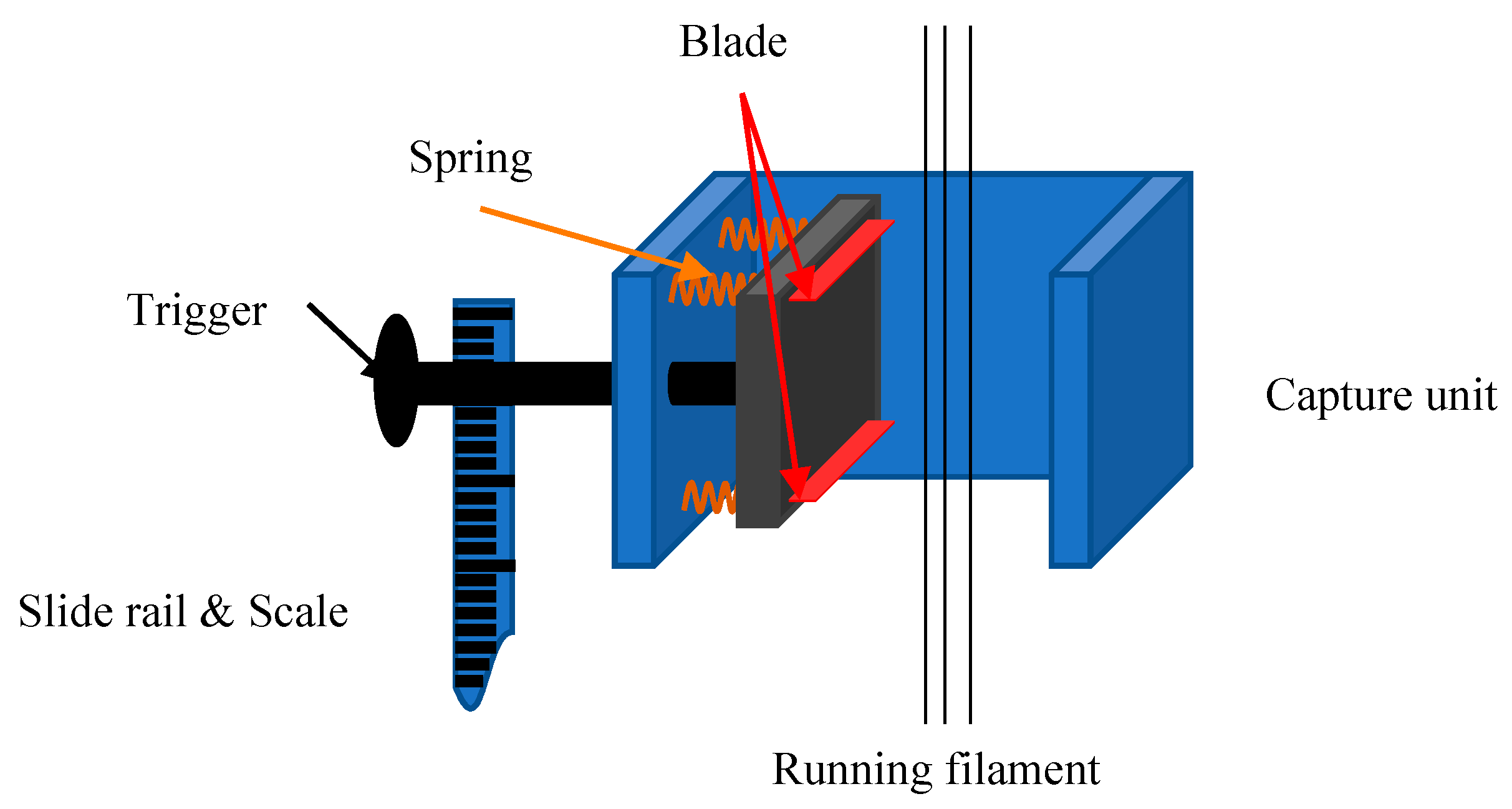
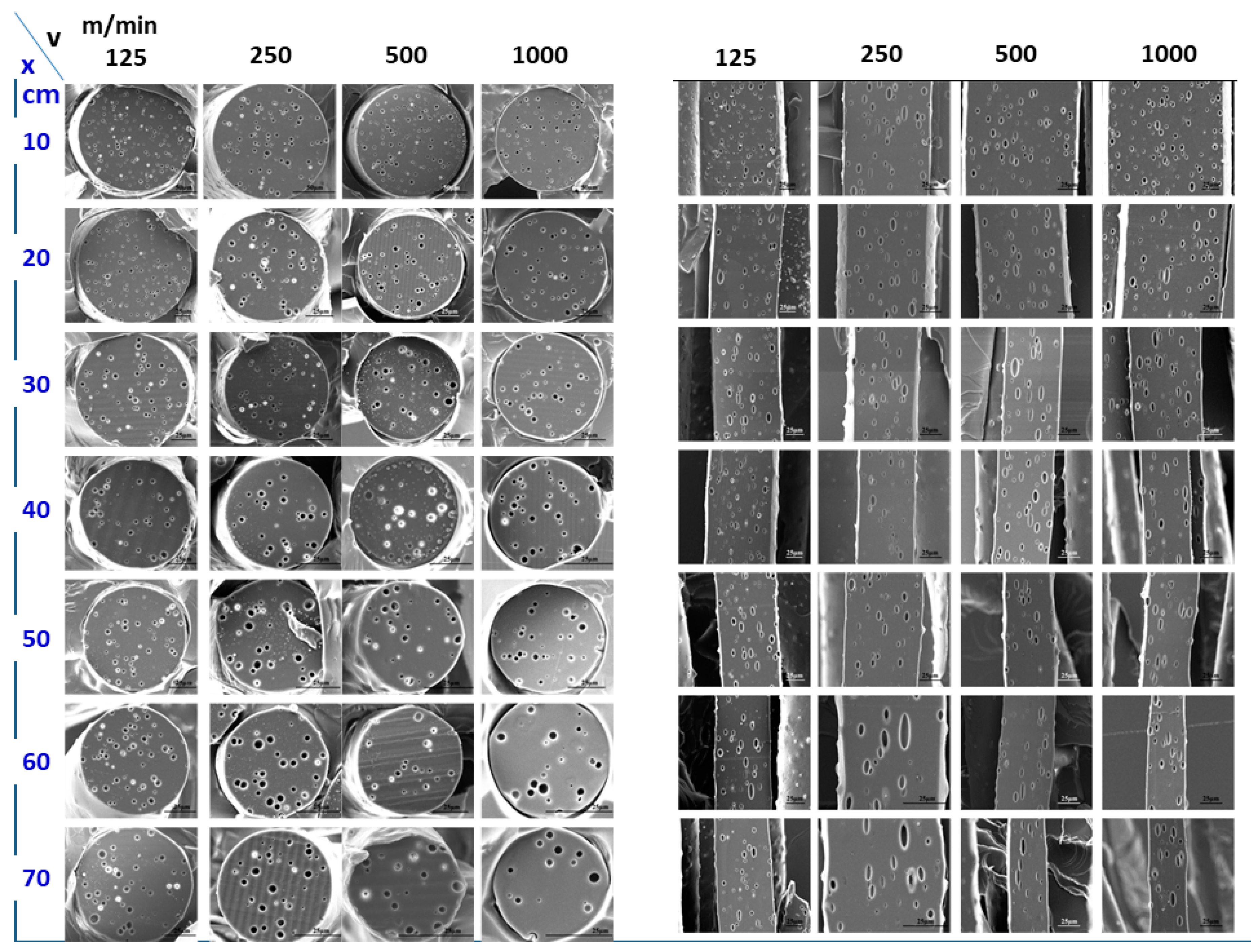
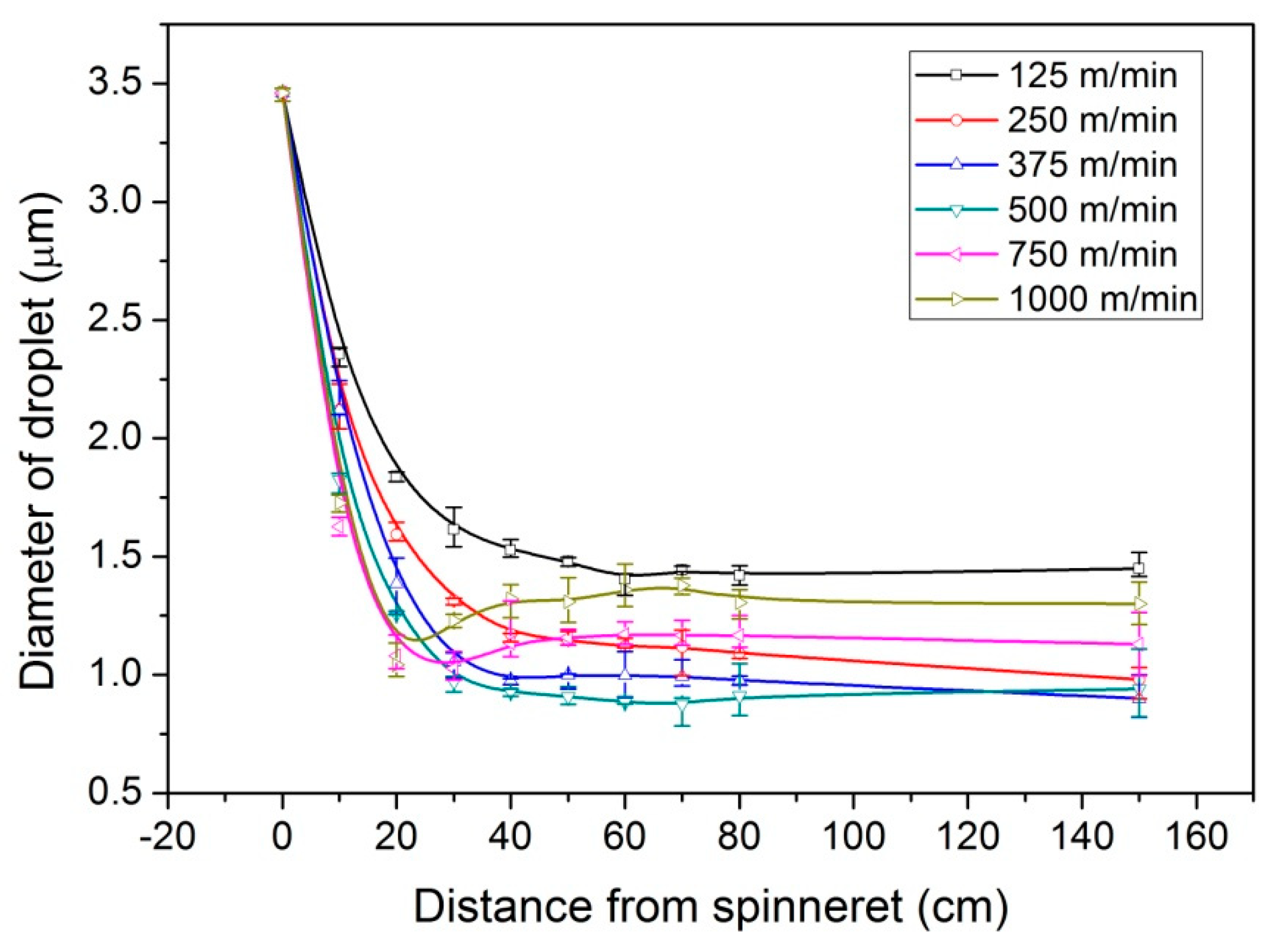
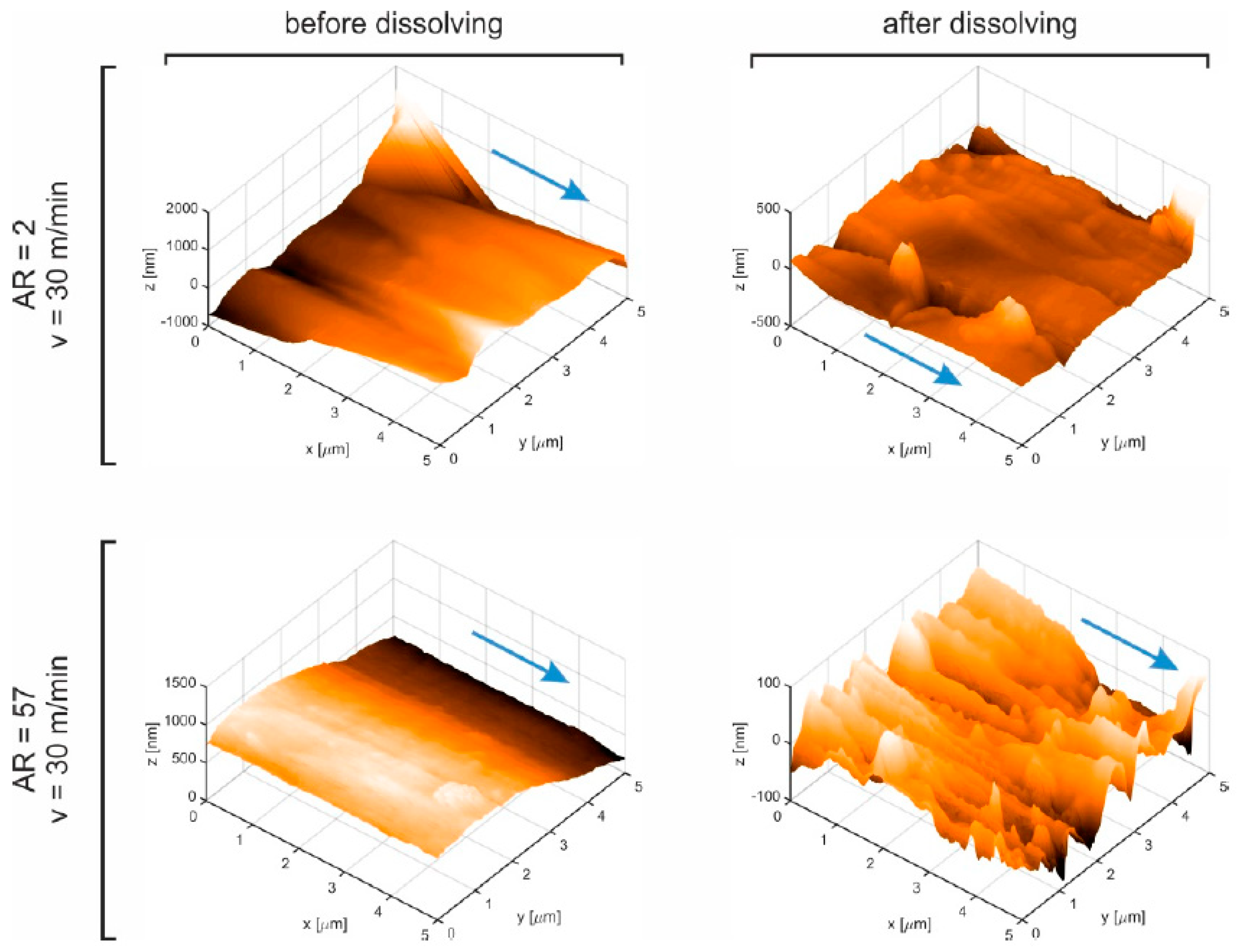
2. Morphology Development along the Spinning Line
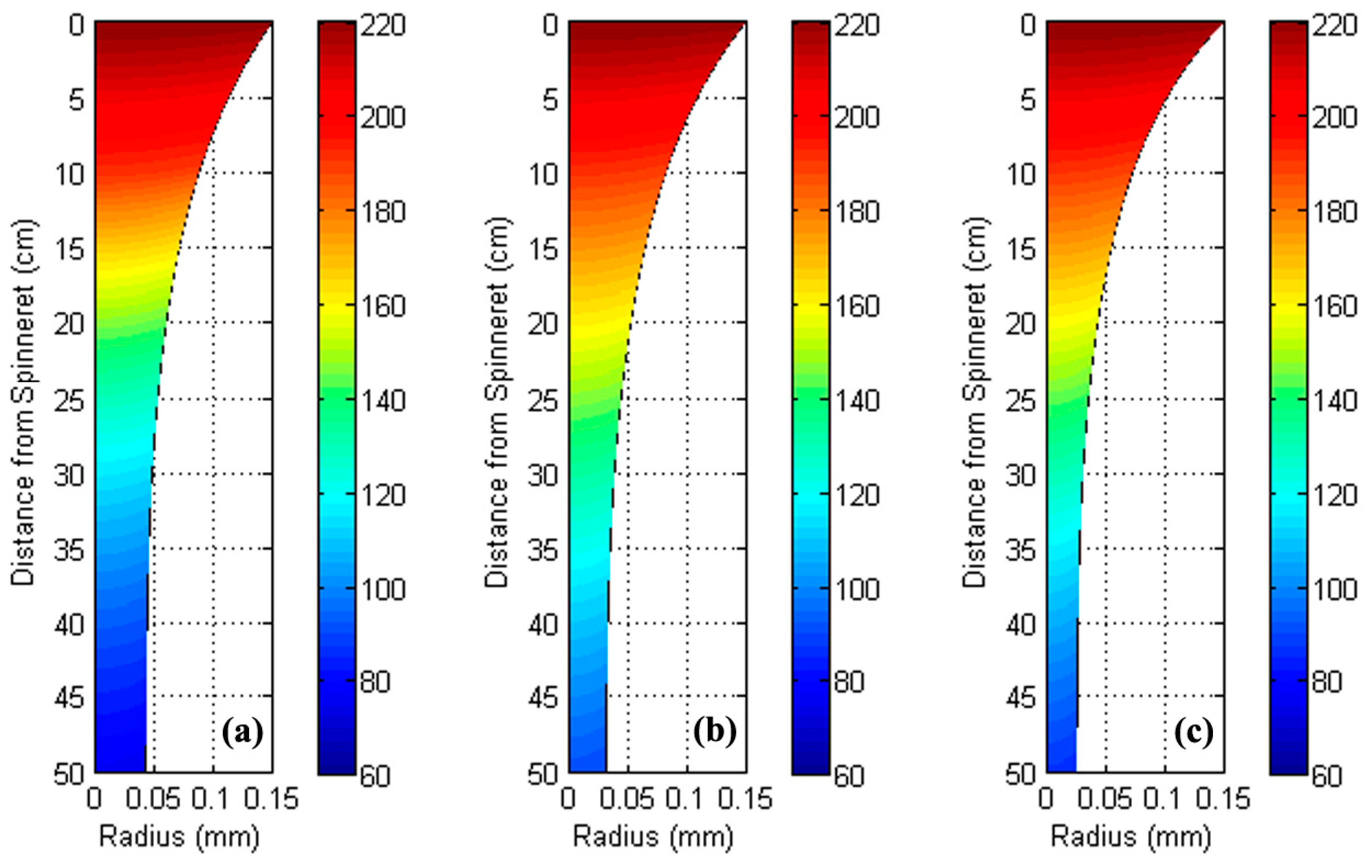
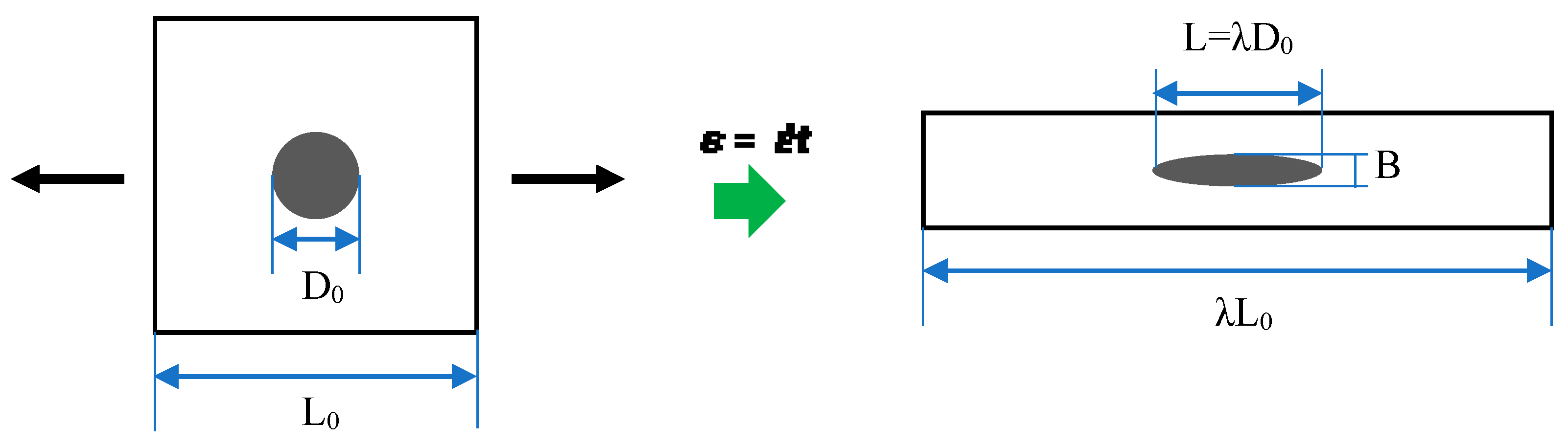
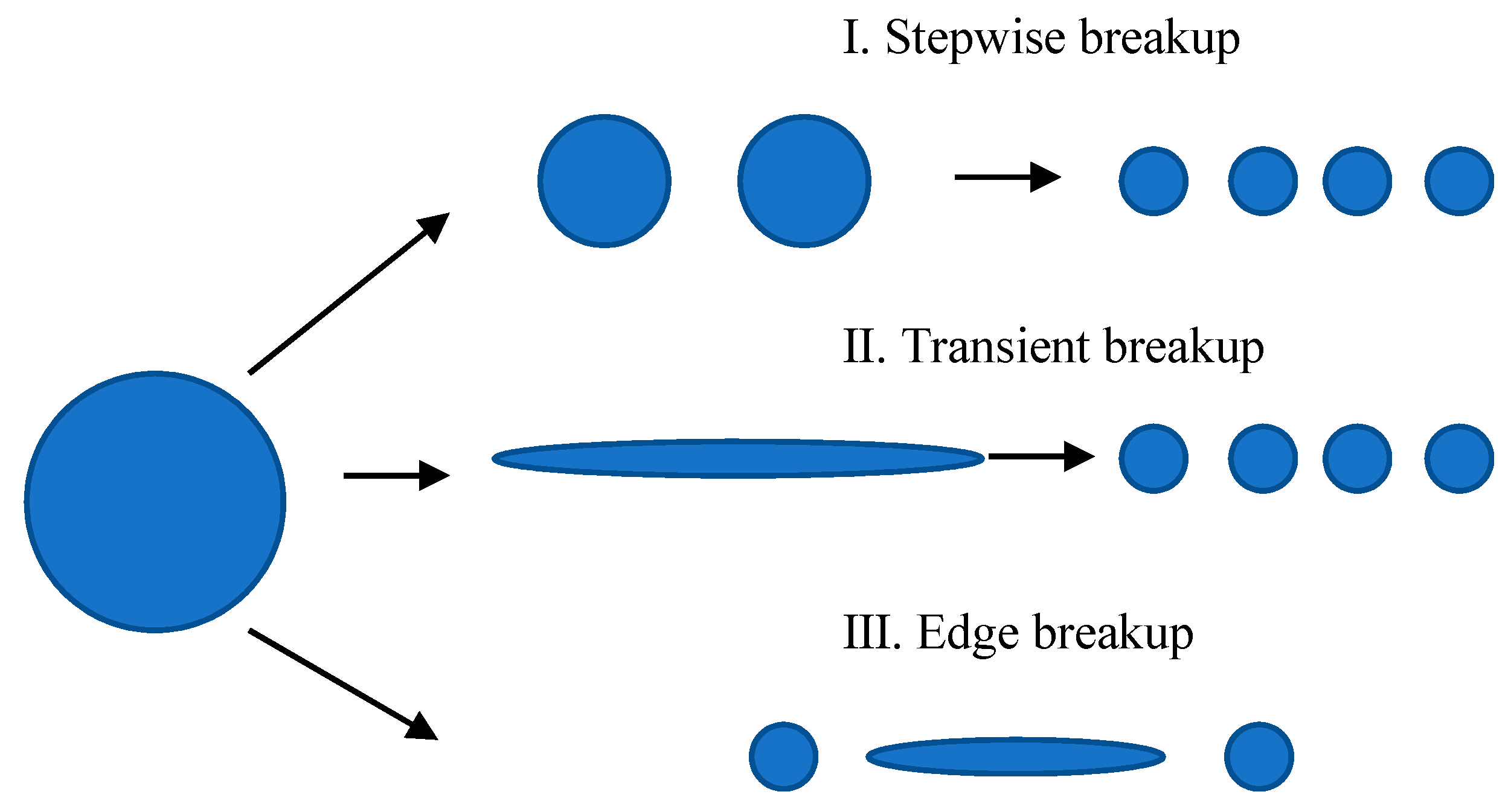
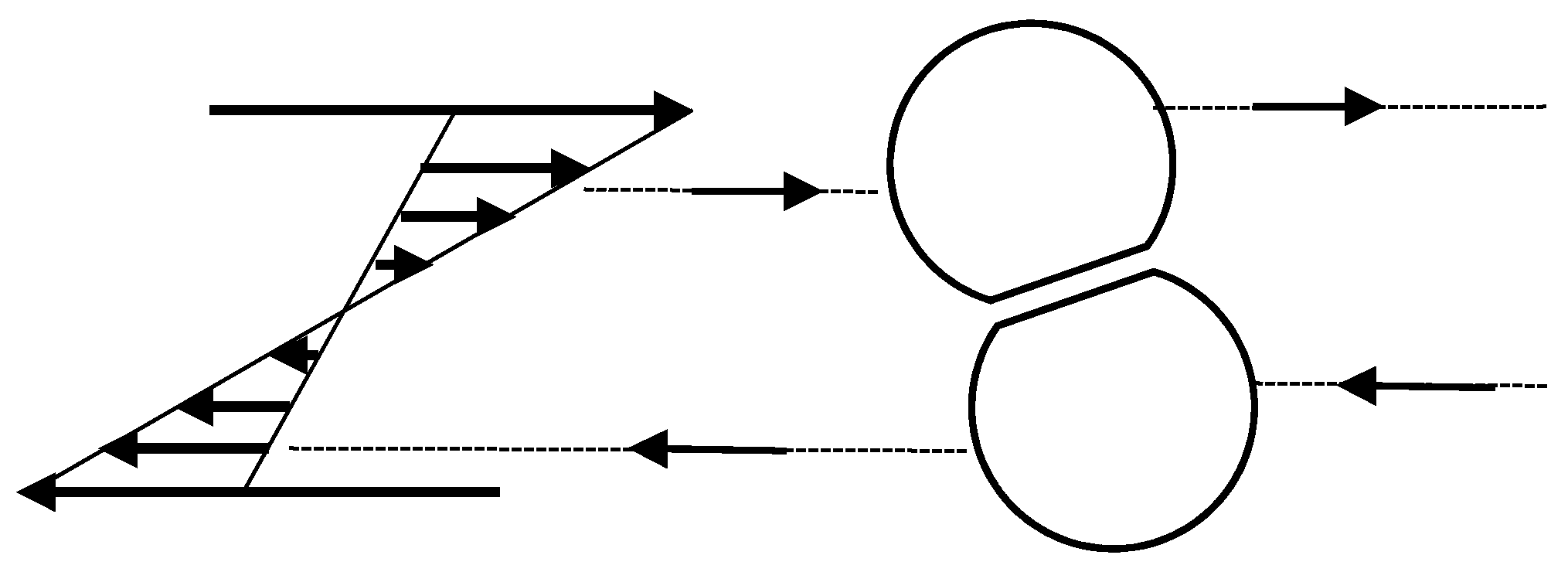
3. Mechanism of Morphology Development
4. Conclusions and Outlooks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Catlow, C.R.A. The structural science of functional materials. IUCrJ 2018, 5, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef] [PubMed]
- Gooneie, A.; Simonetti, P.; Salmeia, K.A.; Gaan, S.; Hufenus, R.; Heuberger, M.P. Enhanced PET processing with organophosphorus additive: Flame retardant products with added-value for recycling. Polym. Degrad. Stab. 2019, 160, 218–228. [Google Scholar] [CrossRef]
- Liang, Y.; Li, L.; Scott, R.A.; Kiick, K.L. Polymeric Biomaterials: Diverse Functions Enabled by Advances in Macromolecular Chemistry. Macromolecules 2017, 50, 483–502. [Google Scholar] [CrossRef] [PubMed]
- Polymeropoulos, G.; Zapsas, G.; Ntetsikas, K.; Bilalis, P.; Gnanou, Y.; Hadjichristidis, N. 50th Anniversary Perspective: Polymers with Complex Architectures. Macromolecules 2017, 50, 1253–1290. [Google Scholar] [CrossRef]
- Pan, D.; Hufenus, R.; Qin, Z.; Chen, L.; Gooneie, A. Tailored Gradient Morphologies and Anisotropic Surface Patterns in Polymer Blends. Macromol. Mater. Eng. 2018, 304, 1800601. [Google Scholar] [CrossRef]
- Janssen, J.M.H. Emulsions: The Dynamics of Liquid–Liquid Mixing; Wiley-VCH Verlag GmbH & Co. KGaA: Eindhoven, UK, 2006. [Google Scholar]
- Chen, D.; Liu, F.; Zhang, Y.; Zhang, Y.; Zhou, H. Simulation of dispersed phase evolution for immiscible polymer blends in injection molding. Eng. Comput. 2017, 34, 2311–2329. [Google Scholar] [CrossRef]
- Fortelny, I. Coalescence in polymer blends: Solved and open problems. Macromol. Symp. 2000, 158, 137–147. [Google Scholar] [CrossRef]
- Cakmak, M.; Teitge, A.; Zachmann, H.G.; White, J.L. On-line small-angle and wide-angle X-ray scattering studies on melt-spinning poly(vinylidene fluoride) tape using synchrotron radiation. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 371–381. [Google Scholar] [CrossRef]
- Dees, J.R.; Spruiell, J.E. Structure development during melt spinning of linear polyethylene fibers. J. Appl. Polym. Sci. 1974, 18, 1053–1078. [Google Scholar] [CrossRef]
- Ellison, M.S.; Lopes, P.E.; Pennington, W.T. In-Situ X-Ray Characterization of Fiber Structure During Melt Spinning. J. Eng. Fiber Fabr. 2008, 3, 10–21. [Google Scholar] [CrossRef]
- Katayama, K.; Nakamura, K.; Amano, T. Structural formation during melt spinning process. Kolloid-Z. Polym. 1968, 226, 125–134. [Google Scholar] [CrossRef]
- Kolb, R.; Seifert, S.; Stribeck, N.; Zachmann, H.G. Investigation of the high speed spinning process of poly(ethylene terephthalate) by means of synchrotron X-ray diffraction. Polymer 2000, 41, 2931–2935. [Google Scholar] [CrossRef]
- Kolb, R.; Seifert, S.; Stribeck, N.; Zachmann, H.G. Simultaneous measurements of small- and wide-angle X-ray scattering during low speed spinning of poly(propylene) using synchrotron radiation. Polymer 2000, 41, 1497–1505. [Google Scholar] [CrossRef]
- Lopes, P.E.; Ellison, M.S.; Pennington, W.T. In situX-ray characterisation of isotactic polypropylene during melt spinning. Plast. Rubber Compos. 2013, 35, 294–300. [Google Scholar] [CrossRef]
- Samon, J.M.; Schultz, J.M.; Hsiao, B.S. Structure development in the early stages of crystallization during melt spinning. Polymer 2002, 43, 1873–1875. [Google Scholar] [CrossRef]
- Samon, J.M.; Schultz, J.M.; Hsiao, B.S.; Khot, S.; Johnson, H.R. Structure development during the melt spinning of poly(oxymethylene) fiber. Polymer 2001, 42, 1547–1559. [Google Scholar] [CrossRef]
- Samon, J.M.; Schultz, J.M.; Wu, J.; Hsiao, B.; Yeh, F.; Kolb, R. Study of the structure development during the melt spinning of nylon 6 fiber by on-line wide-angle synchrotron X-ray scattering techniques. J. Polym. Sci. Pol. Phys. 1999, 37, 1277–1287. [Google Scholar] [CrossRef]
- Schultz, J.M.; Hsiao, B.S.; Samon, J.M. Structural development during the early stages of polymer melt spinning by in-situ synchrotron X-ray techniques. Polymer 2000, 41, 8887–8895. [Google Scholar] [CrossRef]
- Spruiell, J.E.; White, J.L. Structure development during polymer processing: Studies of the melt spinning of polyethylene and polypropylene fibers. Polym. Eng. Sci. 1975, 15, 660–667. [Google Scholar] [CrossRef]
- Ziabicki, A. Fundamentals of Fibre Formation: The Science of Fibre Spinning and Drawing; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Kase, S.; Matsuo, T. Studies on Melt Spinning. I. Fundamental Equations on the Dynamics of Melt Spinning. J. Polym. Sci. Part A Polym. Chem. 2010, 3, 2541–2554. [Google Scholar] [CrossRef]
- Dae Han, C.; Lamonte, R.R. Studies on Melt Spinning. I. Effect of Molecular Structure and Molecular Weight Distribution on Elongational Viscosity. Trans. Soc. Rheol. 1972, 16, 447–472. [Google Scholar] [CrossRef]
- Han, C.D. A theoretical study on fiber spinnability. Rheol. Acta 1970, 9, 355–365. [Google Scholar] [CrossRef]
- Han, C.D.; Lamonte, R.R.; Shah, Y.T. Studies on melt spinning. III. Flow instabilities in melt spinning: Melt fracture and draw resonance. J. Appl. Polym. Sci. 1972, 16, 3307–3323. [Google Scholar] [CrossRef]
- Lamonte, R.R.; Han, C.D. Studies on melt spinning. II. Analysis of the deformation and heat transfer processes. J. Appl. Polym. Sci. 1972, 16, 3285–3306. [Google Scholar] [CrossRef]
- Shimizu, J.; Okui, N.; Imai, Y. High-speed melt spinning of isotactic polypropylene fibers: Crystallization mechanism in the spinline and fiber structure and properties. Sen’i Gakkaishi 1979, 35, T405–T412. [Google Scholar] [CrossRef]
- George, H.H. Model of steady-state melt spinning at intermediate take-up speeds. Polym. Eng. Sci. 1982, 22, 292–299. [Google Scholar] [CrossRef]
- Heuberger, M.; Gottardo, L.; Dressler, M.; Hufenus, R. Biphasic fluid oscillator with coaxial injection and upstream mass and momentum transfer. Microfluid Nanofluid. 2015, 19, 653–663. [Google Scholar] [CrossRef]
- He, H.; Chen, L.; Zhang, Y.; Hong, S.; Zhou, Y.; Zhu, M. Studies on melt spinning of sea-island fibers. I. morphology evolution of polypropylene/polystyrene blend fibers. Fibers Polym. 2014, 15, 1941–1949. [Google Scholar] [CrossRef]
- Tran, N.H.A.; Brünig, H.; Boldt, R.; Heinrich, G. Morphology development from rod-like to nanofibrillar structures of dispersed poly (lactic acid) phase in a binary blend with poly (vinyl alcohol) matrix along the spinline. Polymer 2014, 55, 6354–6363. [Google Scholar] [CrossRef]
- Macosko Christopher, W. Morphology development and control in immiscible polymer blends. Macromol. Symp. 2000, 149, 171–184. [Google Scholar] [CrossRef]
- Liang, B.; Pan, L.; He, X. Structure and properties of blend fibers from poly(ethylene terephthalate) and liquid crystalline polymer. J. Appl. Polym. Sci. 1997, 66, 217–224. [Google Scholar] [CrossRef]
- Grasser, W.; Schmidt, H.W.; Giesa, R. Fibers spun from poly(ethylene terephthalate) blended with a thermotropic liquid crystalline copolyester with non-coplanar biphenylene units. Polymer 2001, 42, 8517–8527. [Google Scholar] [CrossRef]
- Xing, Q.; Zhu, M.; Wang, Y.; Chen, Y.; Zhang, Y.; Pionteck, J.; Adler, H.J. In situ gradient nano-scale fibril formation during polypropylene (PP)/polystyrene (PS) composite fine fiber processing. Polymer 2005, 46, 5406–5416. [Google Scholar] [CrossRef]
- Pan, Z.; Chen, Y.; Zhu, M.; Jiang, C.; Xu, Z.; Lu, W.; Pionteck, J. The non-uniform phase structure in blend fiber. II. The migration phenomenon in melt spinning. Fibers Polym. 2010, 11, 625–631. [Google Scholar] [CrossRef]
- Pan, Z.; Zhu, M.; Chen, Y.; Chen, L.; Wu, W.; Yu, C.; Xu, Z.; Cheng, L. The variation of fibrils’ number in the sea-island fiber -low density polyethylene/polyamide 6. Fibers Polym. 2010, 11, 494–499. [Google Scholar] [CrossRef]
- Tavanaie, M.A.; Shoushtari, A.M.; Goharpey, F. Polypropylene/poly (butylene terephthalate) melt spun alloy fibers dyeable with carrier-free exhaust dyeing as an environmentally friendlier process. J. Clean. Prod. 2010, 18, 1866–1871. [Google Scholar] [CrossRef]
- Yang, J.; White, J.L.; Jiang, Q. Phase morphology development in a low interfacial tension immiscible polyolefin blend during die extrusion and melt spinning. Polym. Eng. Sci. 2010, 50, 1969–1977. [Google Scholar] [CrossRef]
- Li, M.; Xiao, R.; Sun, G. Formation and morphology development of poly(butylene terephthalate) nanofibers from poly(butylene terephthalate)/cellulose acetate butyrate immiscible blends. Polym. Eng. Sci. 2011, 51, 835–842. [Google Scholar] [CrossRef]
- Li, M.F.; Xiao, R.; Sun, G. Morphology development and size control of poly(trimethylene terephthalate) nanofibers prepared from poly(trimethylene terephthalate)/cellulose acetate butyrate in situ fibrillar composites. J. Mater. Sci. 2011, 46, 4524–4531. [Google Scholar] [CrossRef]
- Soroudi, A.; Skrifvars, M. The influence of matrix viscosity on properties of polypropylene/polyaniline composite fibers-Rheological, electrical, and mechanical characteristics. J. Appl. Polym. Sci. 2011, 119, 2800–2807. [Google Scholar] [CrossRef]
- Soroudi, A.; Skrifvars, M.; Liu, H. Polyaniline-polypropylene melt-spun fiber filaments: The collaborative effects of blending conditions and fiber draw ratios on the electrical properties of fiber filaments. J. Appl. Polym. Sci. 2011, 119, 558–564. [Google Scholar] [CrossRef]
- Tavanaie, M.A.; Shoushtari, A.M.; Goharpey, F.; Mojtahedi, M.R. Matrix-fibril morphology development of polypropylene/poly(butylenes terephthalate) blend fibers at different zones of melt spinning process and its relation to mechanical properties. Fibers Polym. 2013, 14, 396–404. [Google Scholar] [CrossRef]
- Dehghan, N.; Tavanaie, M.A.; Payvandy, P. Morphology study of nanofibers produced by extraction from polymer blend fibers using image processing. Korean J. Chem. Eng. 2015, 32, 1928–1937. [Google Scholar] [CrossRef]
- Sugawara, K.; Ikaga, T.; Kim, K.H.; Ohkoshi, Y.; Okada, K.; Masunaga, H.; Kanaya, T.; Masuda, M.; Maeda, Y. Fiber structure development in PS/PET sea-island conjugated fiber during continuous laser drawing. Polymer 2015, 79, 37–46. [Google Scholar] [CrossRef]
- Li, L.; Huang, W.; Wang, B.; Wei, W.; Gu, Q.; Chen, P. Properties and structure of polylactide/poly (3-hydroxybutyrate-co-3-hydroxyvalerate) (PLA/PHBV) blend fibers. Polymer 2015, 68, 183–194. [Google Scholar] [CrossRef]
- Zhang, P.P.; Xu, D.D.; Xiao, R. Morphology development and size control of PA6 nanofibers from PA6/CAB polymer blends. J. Appl. Polym. Sci. 2015, 132, 42184. [Google Scholar] [CrossRef]
- Pan, D.; Chen, L.; He, H.; Deng, K.; Qin, Z. Deformation of dispersed polystyrene droplets in immiscible polypropylene/polystyrene blend fibers under uniaxial elongational flow. Fibers Polym. 2016, 17, 1343–1351. [Google Scholar] [CrossRef]
- Tran Nguyen Hoai, A.; Brünig, H.; Auf der Landwehr, M.; Vogel, R.; Pionteck, J.; Heinrich, G. Controlling micro- and nanofibrillar morphology of polymer blends in low-speed melt spinning process. Part II: Influences of extrusion rate on morphological changes of a PLA/PVA blend through a capillary die. J. Appl. Polym. Sci. 2016, 133, 1–10. [Google Scholar]
- Ayad, E.; Cayla, A.; Rault, F.; Gonthier, A.; Campagne, C.; Devaux, E. Effect of Viscosity Ratio of Two Immiscible Polymers on Morphology in Bicomponent Melt Spinning Fibers. Adv. Polym. Technol. 2018, 37, 1134–1141. [Google Scholar] [CrossRef]
- Chen, L.; He, H.; Zhang, Y.; Chen, Y.; Zhu, M. Studies on melt spinning of sea-island fibers. II. Dynamics of melt spinning of polypropylene/polystyrene blend fibers. Fibers Polym. 2015, 16, 449–462. [Google Scholar] [CrossRef]
- Tran, N.H.A.; Brunig, H.; Heinrich, G. Controlling micro- and nanofibrillar morphology of polymer blends in low-speed melt spinning process. Part I. Profiles of PLA/PVA-filament parameters along the spinline. J. Appl. Polym. Sci. 2016, 133, 47. [Google Scholar] [CrossRef]
- Tran, N.H.A.; Brunig, H.; der Landwehr, M.A.; Heinrich, G. Controlling micro- and nanofibrillar morphology of polymer blends in low-speed melt spinning process. Part III: Fibrillation mechanism of PLA/PVA blends along the spinline. J. Appl. Polym. Sci. 2016, 133, 48. [Google Scholar] [CrossRef]
- Song, C.H.; Isayev, A.I. LCP droplet deformation in fiber spinning of self-reinforced composites. Polymer 2001, 42, 2611–2619. [Google Scholar] [CrossRef]
- Pan, D.; Chen, L.; Qin, Z.; Zhu, M. The Evolution and Formation Mechanism of Gradient Structure During Melt Spinning of Blend Fiber. In Proceedings of the Fiber Society 2017 Spring Conference: Next Generation Fibers for Smart Products, Aachen, Germany, 17–19 May 2017; p. 122. [Google Scholar]
- GonzalezNunez, R.; DeKee, D.; Favis, B.D. The influence of coalescence on the morphology of the minor phase in melt-drawn polyamide-6/HDPE blends. Polymer 1996, 37, 4689–4693. [Google Scholar] [CrossRef]
- Sundararaj, U.; Macosko, C.W. Drop Breakup and Coalescence in Polymer Blends—The Effects of Concentration and Compatibilization. Macromolecules 1995, 28, 2647–2657. [Google Scholar] [CrossRef]
- Chesters, A.K. The Modeling of Coalescence Processes in Fluid Liquid Dispersions—A Review of Current Understanding. Chem. Eng. Res. Des. 1991, 69, 259–270. [Google Scholar]
- Shimizu, J.; Okui, N.; Kikutani, T. High speed melt spinning of poly(ethylene terephthalate) radial variation across fibers. Sen’i Gakkaishi 1981, 37, T135–T142. [Google Scholar] [CrossRef]
- Konda, A.; Toriumi, K.; Nakajima, T. Generation of skin-core structure in poly(ethylene terephthalate) fiber upon drawing hot water. Sen’i Gakkaishi 1985, 41, T530–T538. [Google Scholar] [CrossRef]
- Pan, Z.; Zhu, M.; Chen, Y.; Chen, L.; Sun, B.; Yu, H.; Jiang, C.; Xu, Z. The non-uniform phase structure in blend fiber. I. Non-uniform deformation of the dispersed phase in melt spinning. Fibers Polym. 2010, 11, 249–257. [Google Scholar] [CrossRef]
- He, H.; Chen, L.; Sun, S.; Wang, T.; Zhang, Y.; Zhu, M. Study on the matrix-fibril morphologies of polypropylene/polystyrene blends under non-isothermal uniaxial elongational flow. Fibers Polym. 2014, 15, 744–752. [Google Scholar] [CrossRef]
- Taylor, G.I. The Formation of Emulsions in Definable Fields of Flow. Proc. R. Soc. A Math. Phys. Eng. Sci. 1934, 146, 501–523. [Google Scholar] [CrossRef]
- Taylor, G.I. The Viscosity of a Fluid Containing Small Drops of Another Fluid. Proc. R. Soc. A Math. Phys. Eng. Sci. 1932, 138, 41–48. [Google Scholar] [CrossRef]
- Cox, R.G. The deformation of a drop in a general time-dependent fluid flow. J. Fluid Mech. 1969, 37, 601–623. [Google Scholar] [CrossRef]
- Padsalgikar, A.D.; Ellison, M.S. Modeling droplet deformation in melt spinning of polymer blends. Polym. Eng. Sci. 1997, 37, 994–1002. [Google Scholar] [CrossRef]
- Acrivos, A.; Lo, T.S. Deformation and breakup of a single slender drop in an extensional flow. J. Fluid Mech. 1978, 86, 641–672. [Google Scholar] [CrossRef]
- Grace, H.P. Dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- Janssen, J.M.H.; Meijer, H.E.H. Droplet Breakup Mechanisms—Stepwise Equilibrium Versus Transient Dispersion. J. Rheol. 1993, 37, 597–608. [Google Scholar] [CrossRef]
- Barai, N.; Mandal, N. Breakup modes of fluid drops in confined shear flows. Phys. Fluids. 2016, 28, 073302. [Google Scholar] [CrossRef]
- Huneault, M.A.; Shi, Z.H.; Utracki, L.A. Development of polymer blend morphology during compounding in a twin-screw extruder. Part IV A new computational model with coalescence. Polym. Eng. Sci. 1995, 35, 115–127. [Google Scholar] [CrossRef]
- He, X.; Cox, C.L.; Ellison, M.S. Simulation of TLCP Deformation During Isothermal Melt Spinning of In Situ Composite Fibers. J. Macromol. Sci. Part B 2004, 43, 309–328. [Google Scholar] [CrossRef]
- Delaby, I.; Froelich, D.; Muller, R. Droplet deformation in immiscible polymerblends during transient uniaxial elongational flow. Macromol. Symp. 1995, 100, 131–135. [Google Scholar] [CrossRef]
- Delaby, I.; Ernst, B.; Germain, Y.; Muller, R. Droplet deformation in polymer blends during uniaxial elongational flow: Influence of viscosity ratio for large capillary numbers. J. Rheol. 1994, 38, 1705–1720. [Google Scholar] [CrossRef]
- Delaby, I.; Ernst, B.; Muller, R. Drop deformation during elongational flow in blends of viscoelastic fluids. Small deformation theory and comparison with experimental results. Rheol. Acta 1995, 34, 525–533. [Google Scholar] [CrossRef]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, L.; Pan, D.; He, H. Morphology Development of Polymer Blend Fibers along Spinning Line. Fibers 2019, 7, 35. https://doi.org/10.3390/fib7040035
Chen L, Pan D, He H. Morphology Development of Polymer Blend Fibers along Spinning Line. Fibers. 2019; 7(4):35. https://doi.org/10.3390/fib7040035
Chicago/Turabian StyleChen, Long, Dan Pan, and Houkang He. 2019. "Morphology Development of Polymer Blend Fibers along Spinning Line" Fibers 7, no. 4: 35. https://doi.org/10.3390/fib7040035
APA StyleChen, L., Pan, D., & He, H. (2019). Morphology Development of Polymer Blend Fibers along Spinning Line. Fibers, 7(4), 35. https://doi.org/10.3390/fib7040035





