Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Composite Production
2.3. Thermal and Mechanical Testing
2.4. Composite Fibre Volume Fraction
3. Results
3.1. Composite Fibre Volume Fraction
3.2. Composite and Fibre Modulus
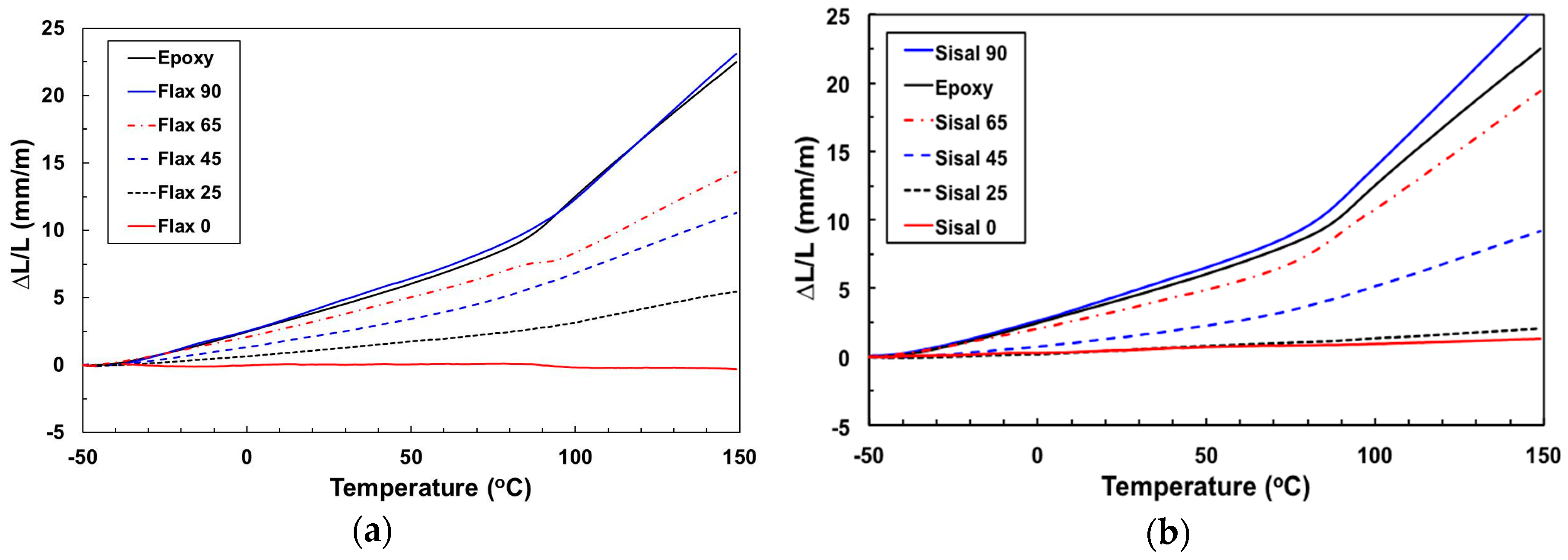
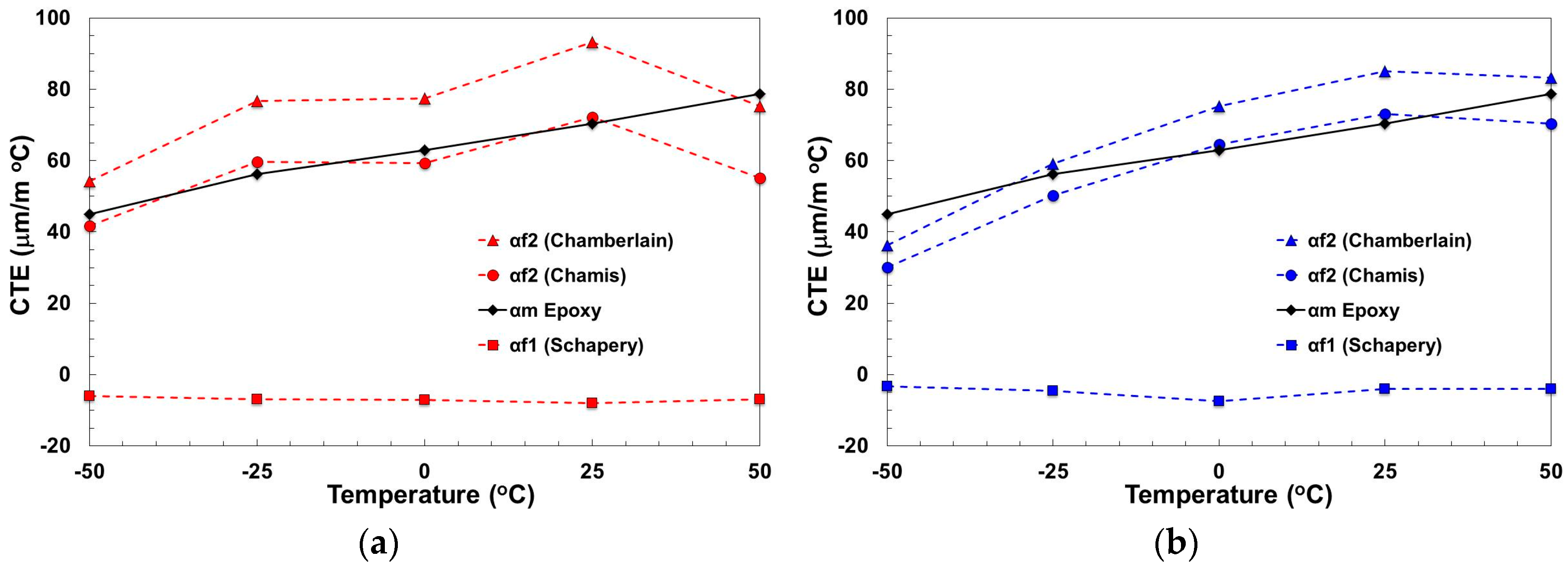
3.3. Composite and Fibre Thermal Expansion
3.4. Implications for Natural Fibre Performance as a Composite Reinforcement
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Thomason, J.L.; Jenkins, P.; Yang, L. Glass fibre strength—A review with relation to composite recycling. Fibers 2016, 4, 18. [Google Scholar] [CrossRef]
- Fortea-Verdejo, M.; Bumbaris, E.; Burgstaller, C.; Bismarck, A.; Lee, K.-Y. Plant fibre-reinforced polymers: Where do we stand in terms of tensile properties? Int. Mater. Rev. 2017, 62, 441–464. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Codispoti, R.; Oliveira, D.V.; Olivito, R.S.; Lourenço, P.B.; Fangueiro, R. Mechanical performance of natural fiber-reinforced composites for the strengthening of masonry. Compos. Part B 2015, 77, 74–83. [Google Scholar] [CrossRef]
- Lu, T.; Jiang, M.; Jiang, Z.; Hui, D.; Wang, Z.; Zhou, Z. Effect of surface modification of bamboo cellulose fibers on mechanical properties of cellulose/epoxy composites. Compos. Part B 2013, 51, 28–34. [Google Scholar] [CrossRef]
- Shahzad, A. Hemp fiber and its composites—A review. J. Compos. Mater. 2011, 46, 973–986. [Google Scholar] [CrossRef]
- Joshi, S.V.; Drzal, L.T.; Mohanty, A.K.; Arora, S. Are natural fiber composites environmentally superior to glass fiber reinforced composites? Compos. Part A 2004, 35, 371–376. [Google Scholar] [CrossRef]
- Wambua, P.; Ivens, J.; Verpoest, I. Natural fibres: Can they replace glass in fibre reinforced plastics? Compos. Sci. Technol. 2003, 63, 1259–1264. [Google Scholar] [CrossRef]
- Li, Y.; Mai, Y.-W.; Ye, L. Sisal fibre and its composites: A review of recent developments. Compos. Sci. Technol. 2000, 60, 2037–2055. [Google Scholar] [CrossRef]
- Saheb, D.N.; Jog, J.P. Natural fiber polymer composites: A review. Adv. Polym. Technol. 1999, 18, 351–363. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J. Composites reinforced with cellulose based fibres. Prog. Polym. Sci. 1999, 24, 221–274. [Google Scholar] [CrossRef]
- Cichocki, F.R., Jr.; Thomason, J.L. Thermoelastic anisotropy of a natural fiber. Compos. Sci. Technol. 2002, 62, 669–678. [Google Scholar] [CrossRef]
- Thomason, J.L. Why are natural fibres failing to deliver on composite performance? In Proceedings of the 17th International Conference on Composite Materials, Edinburgh, UK, 27–31 July 2009. [Google Scholar]
- Virk, A.S.; Hall, W.; Summerscales, J. Tensile properties of jute fibres. Mater. Sci. Technol. 2009, 25, 1289–1295. [Google Scholar] [CrossRef]
- Thomason, J.L. Dependence of interfacial strength on the anisotropic fiber properties of jute reinforced composites. Polym. Compos. 2010, 31, 1525–1534. [Google Scholar] [CrossRef]
- Thomason, J.L.; Carruthers, J.; Kelly, J.; Johnson, G. Fibre cross-section determination and variability in sisal and flax and its effects on fibre performance characterisation. Compos. Sci. Technol. 2011, 71, 1008–1015. [Google Scholar] [CrossRef]
- Thomason, J.L.; Carruthers, J. Natural fibre cross sectional area, its variability and effects on the determination of fibre properties. J. Biobased Mater. Bioenergy 2012, 6, 424–430. [Google Scholar] [CrossRef]
- Ntenga, R.; Béakou, A.; Atangana Atéba, J.; Ayina Ohandja, L. Estimation of the elastic anisotropy of sisal fibres by an inverse method. J. Mater. Sci. 2008, 43, 6206–6213. [Google Scholar] [CrossRef]
- Baley, C.; Perrot, Y.; Busnel, F.; Guezenoc, H.; Davies, P. Transverse tensile behaviour of unidirectional plies reinforced with flax fibres. Mater. Lett. 2006, 60, 2984–2987. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J.; Clifford, M.J.; Licence, P. The tensile behavior of off-axis loaded plant fiber composites: An insight on the nonlinear stress–strain response. Polym. Compos. 2012, 33, 1494–1504. [Google Scholar] [CrossRef]
- Symington, M.C. Vacuum infusion of natural fibre composites. In Proceedings of the 13th European Conference of Composite Materials, Stockholm, Sweden, 2–5 June 2008. [Google Scholar]
- Kawabata, S. Measurement of the transverse mechanical properties of high-performance fibres. J. Text. Inst. 1990, 81, 432–447. [Google Scholar] [CrossRef]
- Schapery, R.A. Thermal expansion coefficients of composite materials based on energy principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Chamberlain, N.J. Derivation of Expansion Coefficients for a Fibre Reinforced Composites; BAC SON(P) Report 33; British Aircraft Corporation: London, UK, 1968. [Google Scholar]
- Chamis, C.C. Simplified Composite Micromechanics Equations for Hygral, Thermal and Mechanical Properties; NASA Report TM-83320; NASA: Washington, DC, USA, 1983.
- Thomason, J.L. Interfacial strength in thermoplastic composites—At last an industry friendly measurement method? Compos. Part A 2002, 33, 1283–1288. [Google Scholar] [CrossRef]
- Thomason, J.L. Micromechanical parameters from macromechanical measurements on glass reinforced polypropylene. Compos. Sci. Technol. 2002, 62, 1455–1468. [Google Scholar] [CrossRef]
- Thomason, J.L.; Yang, L. Temperature dependence of the interfacial shear strength in glass–fibre polypropylene composites. Compos. Sci. Technol. 2011, 71, 1600–1605. [Google Scholar] [CrossRef]
- Thomason, J.L.; Yang, L. Temperature dependence of the interfacial shear strength in glass–fibre epoxy composites. Compos. Sci. Technol. 2014, 96, 7–12. [Google Scholar] [CrossRef]
- Thomason, J.L.; Yang, L.; Bryce, D.; Minty, R. An exploration of the relationship of chemical and physical parameters in the micromechanical characterisation of the apparent interfacial strength in glass fibre epoxy systems. IOP Conf. Ser.: Mater. Sci. Eng. 2016, 139, 012048. [Google Scholar] [CrossRef]
- Charlet, K.; Jernot, J.P.; Eve, S.; Gomina, M.; Bréard, J. Multi-scale morphological characterisation of flax: From the stem to the fibrils. Carbohydr. Polym. 2010, 82, 54–61. [Google Scholar] [CrossRef]

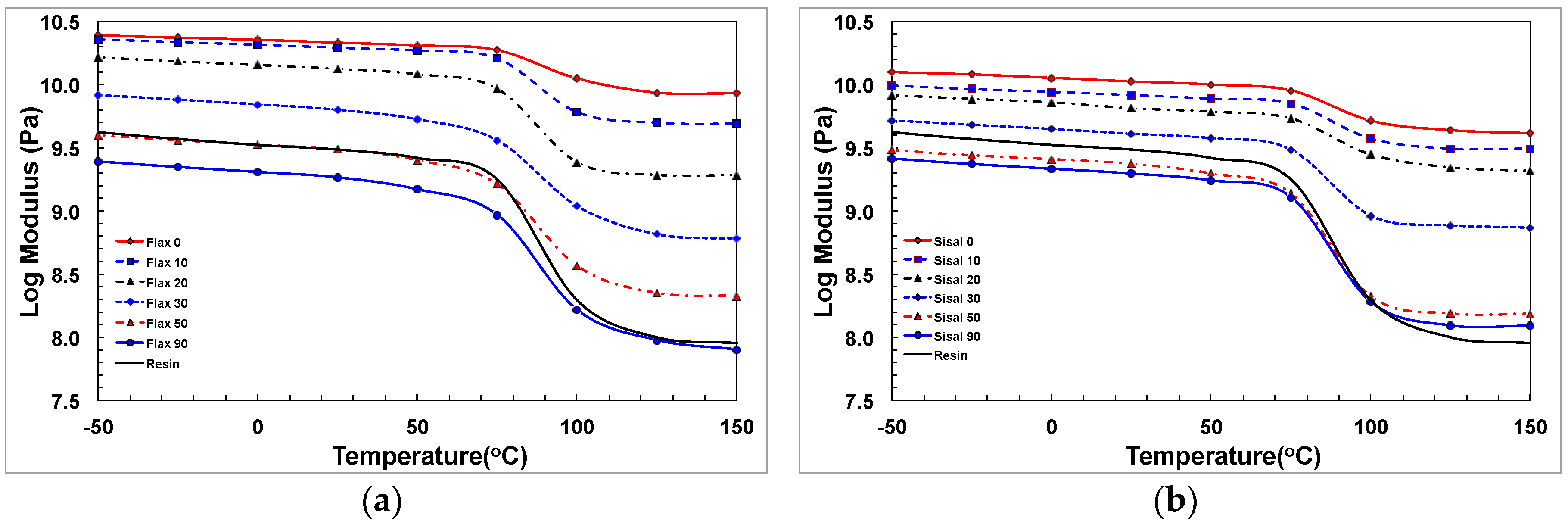

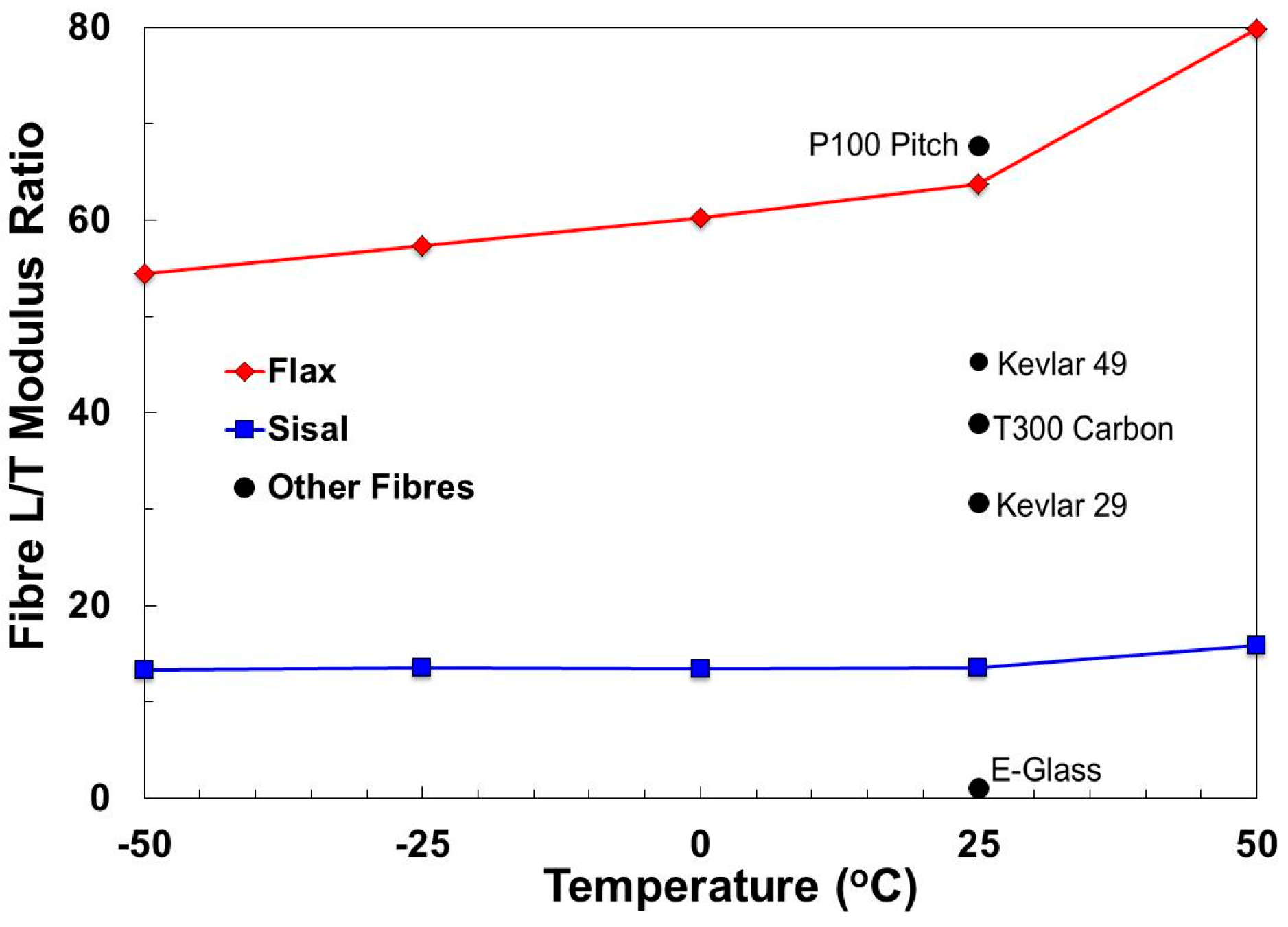
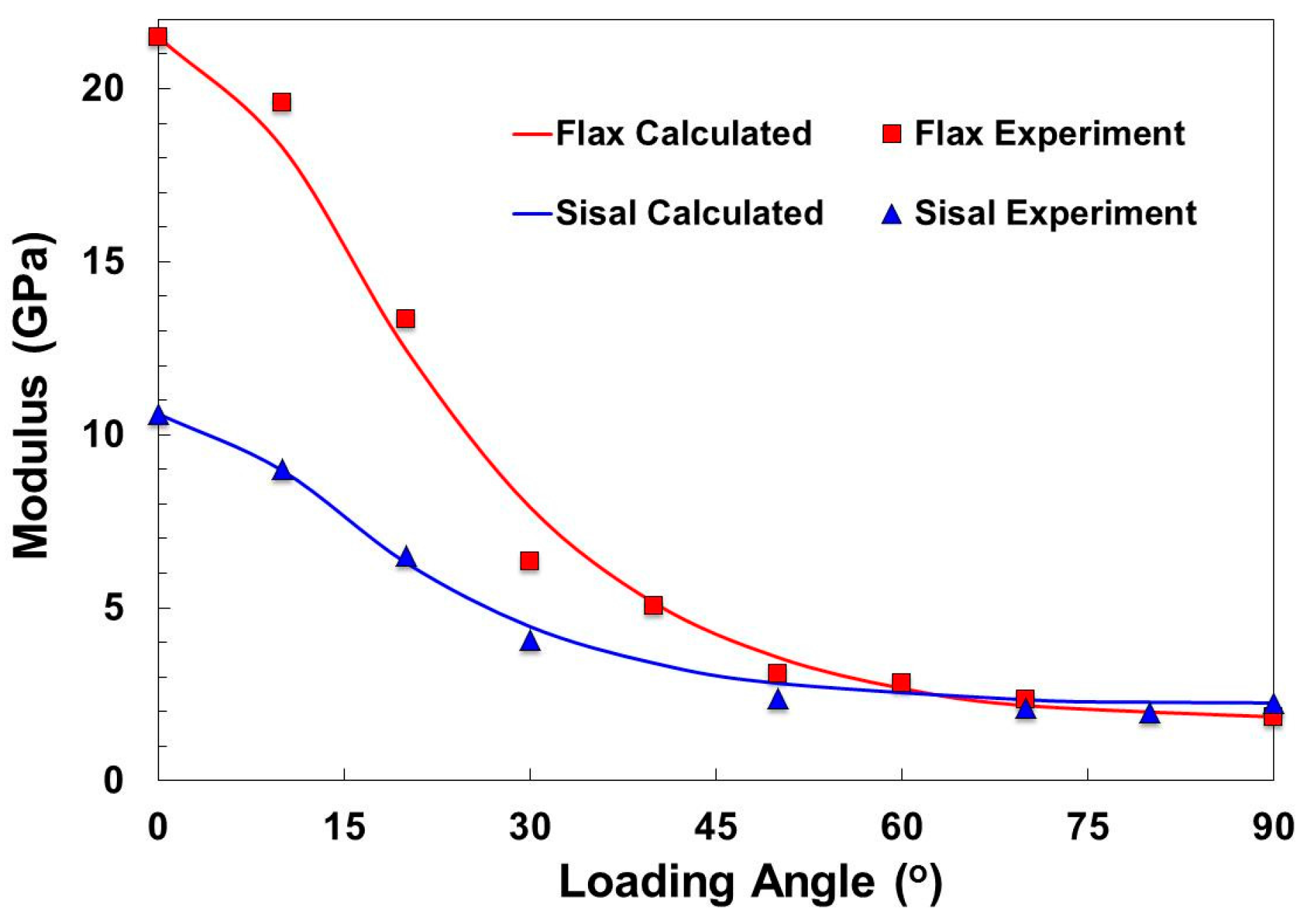
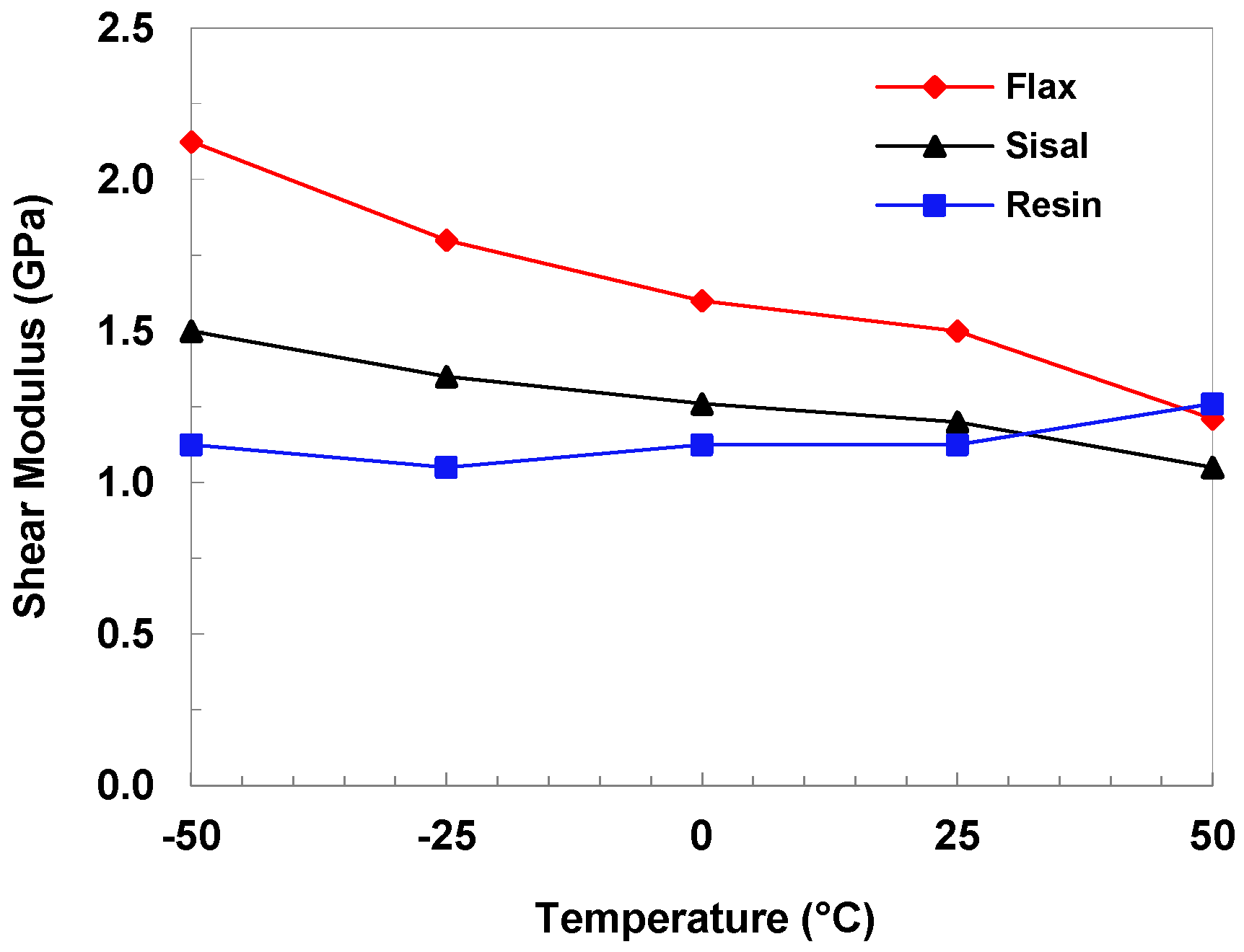
| Flax | Sisal | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| −50 °C | −25 °C | 0 °C | 25 °C | 50 °C | −50 °C | −25 °C | 0 °C | 25 °C | 50 °C | |
| E1f (GPa) | 69.8 | 67.6 | 65.7 | 62.5 | 60.2 | 25.0 | 24.6 | 23.3 | 21.9 | 21.1 |
| E2f (GPa) | 1.3 | 1.2 | 1.1 | 1.0 | 0.75 | 1.9 | 1.8 | 1.7 | 1.6 | 1.3 |
| G12 (GPa) | 2.1 | 1.8 | 1.5 | 1.4 | 1.1 | 1.1 | 1.0 | 1.1 | 1.1 | 1.1 |
| α1f (µm/m °C) | −6.0 | −6.9 | −7.1 | −8.0 | −6.9 | −3.3 | −4.6 | −7.4 | −3.9 | −4.0 |
| α2f (µm/m °C) | 48.0 | 68.1 | 68.4 | 82.7 | 65.2 | 33.2 | 54.7 | 70.0 | 79.1 | 76.8 |
| E-Glass | Carbon | Aramid | Flax | Sisal | |
|---|---|---|---|---|---|
| Ef1 (GPa) | 77 | 220 | 152 | 62.5 | 21.9 |
| Ef2 (GPa) | 68 | 14 | 4.2 | 1.0 | 1.6 |
| Gf12 (GPa) | 30 | 14 | 2.9 | 1.4 | 1.1 |
| αf1 (µm/m °C) | 5 | −0.4 | 3.6 | −8.0 | −3.9 |
| αf2 (µm/m °C) | 5 | 18 | 77 | 83 | 80 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomason, J.; Yang, L.; Gentles, F. Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement. Fibers 2017, 5, 36. https://doi.org/10.3390/fib5040036
Thomason J, Yang L, Gentles F. Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement. Fibers. 2017; 5(4):36. https://doi.org/10.3390/fib5040036
Chicago/Turabian StyleThomason, James, Liu Yang, and Fiona Gentles. 2017. "Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement" Fibers 5, no. 4: 36. https://doi.org/10.3390/fib5040036
APA StyleThomason, J., Yang, L., & Gentles, F. (2017). Characterisation of the Anisotropic Thermoelastic Properties of Natural Fibres for Composite Reinforcement. Fibers, 5(4), 36. https://doi.org/10.3390/fib5040036






