Highlights:
What are the main findings?
- The study demonstrates the viability and effectiveness of using convolutional neural networks (CNNs) for automated quantification of steel microconstituents.
- Among the tested models, VGG19 achieved the best performance, with a mean absolute error (MAE) below 5%, confirming its suitability for this task.
What is the implication of the main finding?
- CNN-based approaches offer a reliable alternative to manual methods, significantly improving speed, consistency, and scalability in microstructural analysis.
- These results suggest that researchers and engineers can adopt deep learning models, such as VGG19, to replace manual quantification in metallurgical quality control processes.
Abstract
The mechanical performance of metallic components is intrinsically linked to their microstructural features. However, the manual quantification of microconstituents in metallographic images remains a time-consuming and subjective task, often requiring over 15 min per image by a trained expert. To address this limitation, this study proposes an automated approach for quantifying the microstructural constituents from low-carbon steel welded zone images using convolutional neural networks (CNNs). A dataset of 210 micrographs was expanded to 720 samples through data augmentation to improve model generalization. Two architectures (AlexNet and VGG16) were trained from scratch, while three pre-trained models (VGG19, InceptionV3, and Xception) were fine-tuned. Among these, VGG19 optimized with stochastic gradient descent (SGD) achieved the best predictive performance, with an of 0.838, MAE of 5.01%, and RMSE of 6.88%. The results confirm the effectiveness of CNNs for reliable and efficient microstructure quantification, offering a significant contribution to computational metallography.
1. Introduction
Microstructures consist of three-dimensional phase distributions that are non-regular and non-random [1,2]. Such distributions influence nearly all aspects of material behavior and are among the most controllable elements in the structural hierarchy of materials [3]. As a result, the material’s mechanical properties are primarily determined by its microstructure [3], which encodes the material’s genesis and dictates its physical and chemical properties [4]. When a material contains multiple phases, the type and distribution of such phases play a crucial role in determining its properties [5]. Thus, accurately identifying and quantifying specific phases are crucial steps to understanding the relationship between the structure and properties of materials [6,7]. The identification of microstructural constituents and their precise quantification are essential components of engineering. These processes are fundamental for assessing the material’s characteristics and overall performance.
An area of industry in which the procedure for counting microconstituents in micrographs is essential is welding, which is present almost everywhere, with important applications in several areas, such as automotive, aerospace, naval, IT, and civil construction [8,9]. Regardless of the type and application of welding, it is always important to analyze the mechanical behavior of the weldment bead obtained, which is achieved by means of microstructural analysis and material quantification [10,11].
The classification of microstructures continues to rely on manual methods performed by experts or through the use of costly and inefficient equipment. The American Society for Testing and Materials (ASTM) has established standards for the human specialist quantification of microstructures. Table 1 provides a compilation of pertinent ASTM standards for the evaluation of microstructure. For instance, the ASTM E562 standard establishes a standard for determining the volumetric fractions of microconstituents via the manual point counting method [12]. However, implementing these standards requires significant effort and presents a risk of mistakes. An experienced specialist implementing these standards takes an average of 15 min per image to adequately identify and quantify microstructures [13,14].

Table 1.
Summary of key ASTM standards for microstructural analysis.
However, convolutional neural network (CNN)-based methods offer effective support for quick, objective, and automated analysis of steel microstructures. Once trained, these models reduce the per-image inference time to seconds and remove human subjectivity from the quantification process. Importantly, CNNs are capable of capturing complex morphological patterns that may be overlooked or inconsistently classified by human observers [17,18,19]. Although DL-based methods require a labeled dataset and significant computational resources for training, their scalability and consistency make them particularly suitable for high-throughput environments aligned with Industry 4.0 initiatives [4,20].
This investigation employs DL architectures, specifically CNNs, to address the aforementioned analytical challenges through automated classification of predominant constituents in welded steel zones. The computational framework distinguishes five distinct morphological variants: Acicular ferrite (AF), characterized by its needle-like structure; intragranular polygonal ferrite (PF(I)), forming within prior austenite grains; primary grain boundary ferrite (PF(G)), nucleating at austenite boundaries; ferrite with non-aligned second phase (FS(NA)); and ferrite with aligned second phase (FS(A)). Each of the aforementioned microstructures exhibits a unique morphology, reflecting a characteristic of the material under consideration, as detailed below [21,22].
- PF(G): Ferrite grains are usually polygonal, located within the previous austenitic grains, and three times larger than the adjacent ferrite grains or sheets. They appear in the form of clear and smooth veins, outlining the columnar grain contour of the austenite, giving it an elongated shape. In general, high amounts of PF(G) are undesirable in welds that must have high resistance to brittle fracture since constituents rich in carbon and impurities can be observed among their grains [21,23].
- PF(I): Presents polygonal grain veins associated with previous austenitic boundaries. It is more common in welds with a low cooling rate and a low content of alloying elements [21].
- FS(A): It appears in the form of coarse grains and is parallel, always growing along a well-defined plane, forming two or more plates of parallel ferrite. Such morphology, precisely with the presence of films of constituents rich in carbon and fragile in their contours, makes FS(A) little desired in the molten zone of welds that must present a certain degree of toughness [23].
- FS(NA): Ferrite involving microphases that appear approximately equiaxed or distributed randomly or isolated AF laminae.
- AF: When seen in two-dimensional cross-sections, AF is commonly described as a complicated microstructure made up of tiny, elongated grains. In particular, these grains have a three-dimensional appearance, taking the form of thin, lenticular plates. Such a chaotic arrangement contributes to AF’s superior mechanical properties, particularly its strength, making it a highly desirable microstructure [3].
Figure 1 presents one of the micrographs analyzed in the present work, and its respective microstructural morphologies are highlighted. The micrograph also presents the grid used for the manual counting of microstructures [23], according to the [24] standard. In manual counting, the operator classifies each cell as the predominant microstructure observed in that cell, and thus performs the frequency count of the image. It can be seen that it is not simple to visually identify the different microstructural regions.
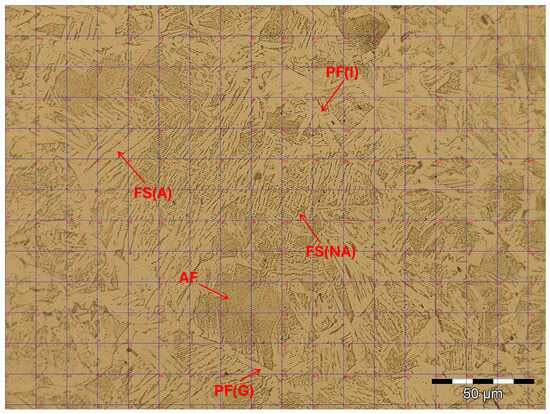
Figure 1.
Melt zone morphology observed in a typical weld bead microphotograph of the dataset analyzed in this work.
The steel industry is currently undergoing a significant transformation, with computational methods being increasingly utilized in product analysis and manufacturing. Such a shift is a key component of Industry 4.0 [25,26]; indeed, several manual and time-consuming tasks could be replaced or enhanced using artificial intelligence (AI) techniques. Despite such progress, certain activities, such as the microstructural quantification of materials, continue to be performed manually. Thus, the latter point motivates the adoption of AI methods to automate the quantification of microconstituents in materials [27].
AI is fundamentally built upon machine learning (ML) and DL techniques, which serve as the core drivers of its ability to learn from data, recognize patterns, and make informed decisions [28,29]. ML focuses on programming algorithms that can learn how to perform a certain task from a set of training data. Moreover, DL, a subset of ML and AI, employs advanced ML algorithms, such as CNNs, which consist of multiple deep layers [30]. Such networks are capable of processing and learning complex tasks from the available training data [31,32]. CNN models can be trained from scratch on the available training dataset, or pre-trained models, which were previously trained on large and diverse datasets, can be leveraged to exploit their existing performance and reduce training time.
Relying on the latest advancements in ML and DL, the primary aims of this study are outlined below:
- To assess the effectiveness of CNNs in the task of quantifying microconstituents in steel micrographs.
- To identify the CNN model that performs best for the considered application.
- To analyze how pre-trained CNN models perform in comparison to models trained entirely from zero on the available dataset.
The structure of the rest of the article is organized as follows: Section 2 reviews related works that focus on the task of automatic quantification of microstructural constituents in low-carbon steel. Section 3 describes the datasets employed to evaluate the proposed CNN-based approaches, along with detailed explanations of the DL methods used and the joint learning and optimization strategies employed. Section 4 presents the results and provides an in-depth analysis. Section 5 summarizes the concluding findings and their implications.
2. Related Works
In order to distinguish between ferrite microstructures, Zaefferer et al. [33] employed index confidence, which is comparable to the image quality approach but makes use of the fit between the diffraction pattern and indexing pattern. With reasonable results, Wu et al. [34] separated several microconstituents using diffraction pattern quality and quantified them using a multi-peak model. Steels with relatively simple microstructures have been subjected to these procedures. One drawback, though, is that more intricate processing settings may affect the quantity of dislocations and skew the outcomes [35]. Grain orientation, sample contamination, and preparation all affect the quality of the diffraction pattern, which further complicates sample comparisons [36].
In recent years, CNNs have emerged as the most effective DL technique for computer vision tasks, owing to their remarkable ability to recognize and classify patterns in images [37,38,39,40]. Their success is largely attributed to the capability to automatically extract and analyze intrinsic features from images, thereby eliminating the need for manually handcrafted feature extraction [37,38]. Specifically, convolution operations enable CNNs to preserve neighborhood information, linking local attributes directly to corresponding labels [41,42].
Despite the above-reported advances, the application of CNNs for quantifying microconstituents remains relatively underexplored [43]. Indeed, traditionally, researchers have relied on conventional ML techniques to classify several microstructures [44,45,46,47,48]. Although the latter methods have yielded satisfactory results, recent investigations have intensified efforts to employ CNNs for microstructural recognition [49]. In particular, early studies by Ling et al. [50] and DeCost et al. [51] showed the potential of CNNs as alternative tools for microstructure classification, primarily by identifying feature representations that maximize classification accuracy for specific datasets. Building on the latter foundation, subsequent methodologies have extended these approaches to offer valuable insights into microstructural trends and their correlations with processing conditions, thereby deepening our understanding of structure–property–process interactions.
Azimi et al. [4] proposed a DL framework for the automatic classification of microstructures in low-carbon steel. The work of the latter authors highlighted the challenges associated with manual microstructural classification, which is often prone to human error and subjectivity. By integrating feature extraction and classification within a fully connected CNN—augmented with pixel-wise segmentation and a max-voting scheme—the proposed method achieved an impressive accuracy of 93.94%, compared to only 48.89% using previous approaches.
Lorena et al. [52] examined the efficacy of CNNs for classifying ultrahigh-carbon steel microstructures. The authors compared four CNN architectures of varying depths to categorize micrographs into seven distinct classes. Their findings revealed that augmenting the LeNet architecture with two additional convolutional layers resulted in improved classification accuracy without a significant increase in training time. This study provides practical guidance for selecting CNN architectures based on factors such as accuracy, computational efficiency, and training duration.
Kim et al. [53] introduced an unsupervised segmentation method for low-carbon steel microstructures that encompassed phases such as ferrite, pearlite, bainite, and martensite. The introduced approach integrated a CNN with the Simple Linear Iterative Clustering (SLIC) superpixel algorithm, thereby obviating the need for labeled image data. In a similar manner, Holm et al. [54] offered a comprehensive review of computer vision techniques—including CNNs—for representing visual data in microstructural images, while Perera et al. [55] developed an advanced ML framework for the automated identification and characterization of features such as pores, particles, grains, and grain boundaries.
Warmuzek et al. [56] explored the use of DL to recognize morphological forms in alloy microstructures. The designed neural network-based approach was capable of classifying features—such as spheres, polyhedra, petals, needles, Chinese script, twigs, and dendrites—from microscope images of cast aluminum and iron alloys. A notable advantage of the introduced method is its adaptability across different image collections, which facilitates classification into predefined categories and overcomes the challenges posed by fuzzy logic in differentiating similar structures.
Baskaran et al. [57] introduced a novel two-stage pipeline for the systematic segmentation of morphological features in microstructures, using a titanium alloy (Ti-6Al-4V) as a case study. The first stage employs a CNN—with three convolutional layers and one fully connected layer developed using the Keras API—to classify microstructures into categories such as “lamellar”, “duplex”, and “acicular”. The developed DL model achieved an average accuracy of over five trials. In the second stage, class-specific image processing techniques are applied: a marker-based watershed method quantifies the area fraction of equiaxed grains in bi-modal microstructures, while a Histogram of Oriented Gradients (HOG) approach measures the area fraction of the dominant -variant in basket-weave structures.
Mishra and Rahul [58] conducted a comparative study of several ML models for microstructure classification, including CNN architectures such as ResNet, VGG, DenseNet, and Inception, alongside non-CNN models like support vector classifiers, tree-based methods, and Multilayer Perceptrons (MLPs). By optimizing CNN architectures—reducing both depth and width—they managed to lower the number of parameters while maintaining high accuracy. The trained optimized DenseNet model achieved testing, validation, and training accuracies of 94.89%, 96.26%, and 97.45%, respectively, and was effectively applied to high-entropy-alloy micrographs. The introduced work underscores the potential of CNNs to accelerate materials development and advance material informatics initiatives.
Arumugam and Kiran [59] developed a CNN framework for identifying critical pixel regions in ferrite–pearlite microstructures, facilitating compact data representation and secure sharing of microstructural images. In parallel, Jung et al. [60] demonstrated the estimation of average grain size from microstructural images using CNNs. Additionally, Zhu et al. [61] compared the performance of the gray-level co-occurrence matrix (GLCM) with that of CNN-based feature extraction in capturing characteristics of various microstructures, including pearlite, martensite, austenite, and bainite. Finally, Tsutsui et al. [62] further explored the application of CNNs for the in situ identification of steel microstructures, particularly addressing class imbalances present in bainite and martensite images.
Motyl and Madej [63] proposed a supervised segmentation method for pearlitic–ferritic steel microstructures by employing a U-Net CNN trained on electron backscattered diffraction (EBSD) data. The developed approach, combined with traditional characterization techniques, significantly improved the classification and quantification of complex microstructures in scanning electron microscope images, demonstrating its robustness and versatility.
Khan et al. [64] introduced a novel ML framework that addresses the challenges posed by irrelevant and redundant features in handcrafted feature vectors for microstructural image classification. The proposed approach incorporates the Uniform variant of the Local Tetra Pattern (ULTrP) for feature extraction and employs a Genetic Algorithm-based feature selection method—DPGA—integrating an ensemble of three filter ranking methods. The proposed method outperformed state-of-the-art techniques on a standard seven-class microstructural image dataset.
Durmaz et al. [20] designed a DL-based approach for the automated classification of hierarchically structured steel microstructures, effectively addressing the limitations of manual inspection. The method introduced by the authors distinguishes between bainite and martensite microstructures and assesses needle morphology according to the ISO 643 grain size standard, achieving accuracies of 96% for microstructure classification and approximately 91% for needle length determination. An interpretability analysis further clarified the model’s decision-making process and generalization capabilities, thus offering a reliable and objective alternative for industrial steel quality control.
Mishra and Rahul [65] further explored CNN applications for microstructure recognition in materials science by evaluating four architectures—VGG, Inception, ResNet, and MobileNet—on high-entropy-alloy micrographs. Through the use of saliency maps to visualize feature importance in eutectic and dendritic structures, the developed analysis provided critical insights into the suitability of each architecture for microstructure classification tasks.
Khurjekar et al. [66] investigated the usage of DL for classifying both textured and untextured microstructures, thus addressing the limitations of traditional methods that depend on time-intensive EBSD or visually observable morphological changes after significant grain growth. By leveraging a CNN to extract high-order morphological features from binary images, their method achieved significantly higher classification accuracy, particularly during the early stages of grain growth, when differences are more subtle.
Table 2 presents a summary of key studies in the field, with references to relevant works, the specific CNN models utilized, and a brief description of the main findings reported in each study.

Table 2.
Summary of CNN-based microstructure classification studies.
3. Materials and Methods
3.1. Experimental Data
The dataset of this work was obtained from [67]. It contains 210 micrographs of 1020 steel in regions of welded fusion zones. The images have a resolution of 2048 × 1532 pixels and were acquired by an Olympus GX5 microscope. Each of these micrographs was manually quantified in [23] following the standards presented in [12]. Thus, we have a supervised ML problem. Table 3 presents the volumetric percentages of some images of the dataset. It is worth noting that the data are compositional since their sum always results in 100% [68].

Table 3.
Manual microstructural quantification of some images from the dataset.
3.2. Data Preprocessing
Since CNNs typically require large datasets to achieve robust performance, data augmentation was applied to artificially increase the amount of training data and reduce the risk of overfitting. The original image set was expanded fourfold by applying mirroring techniques along both the horizontal (x-axis) and vertical (y-axis) directions. This method effectively created variations of the original images while preserving key spatial features, thus enhancing the model’s generalization capabilities without introducing new content. Figure 2 illustrates an example of this quadrupling process.

Figure 2.
Mirroring techniques.
To further diversify the dataset, additional augmentation techniques were explored, including random rotations, Gaussian noise insertion, and brightness adjustments. These methods aimed to simulate real-world variations such as slight misalignments or sensor noise. However, despite their potential, these augmentations led to a substantial increase in computational cost and only marginal improvements in model accuracy, which did not justify their continued use in the training pipeline [69,70].
The original images were of exceptionally high resolution, which significantly strained memory and processing resources during model training. To address this, a resolution reduction strategy was implemented while maintaining sufficient detail for accurate feature extraction. After empirical testing across multiple scales, a reduction factor of 0.15 was identified as the best one. This downsampling resized the images to 307 × 230 pixels, balancing computational efficiency with model performance. The selected resolution preserved critical features needed for classification tasks, as evidenced by consistent accuracy in validation results [71].
3.3. Artificial Neural Network (ANN)
Artificial neural networks (ANNs) are computational models inspired by the nervous connections of the animal nervous system [72]. Similar to biological neurons, these models are made up of interconnected units capable of receiving, processing, and transmitting information. These models are basically composed of three elements: input data, weights, and activation functions. When the model is expanded, bringing together various input data, weights, and activation neurons, a configuration is obtained, known as the MLP [72].
Training an ANN follows the following steps: The loss function () measures how far the network outputs are from the correct outputs. The optimization problem is solved via the gradient descent technique. Then, back-propagation logic is used to propagate the gradient of the loss function to the previous layers [73]. Then, the weights (w) are adapted to reduce the loss function. The step size of this weight update is given by a learning rate, represented by in Equation (1). This parameter has no unit and is defined by the user [73].
3.4. Convolutional Neural Networks (CNNs)
A CNN is a type of neural network that focuses on recognizing visual patterns in images. Currently, CNN models are the most advanced models in the area of computer vision, being present in several complex image recognition, classification, and segmentation applications [41,74,75].
Figure 3 illustrates a standard CNN, which is formed by several repeated types of layers stacked together [4]. Each layer in this network has a name according to the operations it performs. Below is a brief introduction to the main layers and functions that make up a typical CNN.
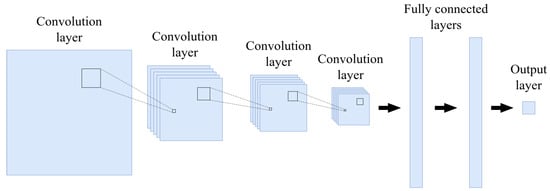
Figure 3.
A typical architecture of a CNN.
The pooling layer gradually reduces the spatial dimensions of the representation, decreasing both the number of parameters and the computational requirements of the network. The two most common types of pooling are max pooling and global average pooling. These methods extract the maximum or average values from each subregion of the input data [52]. In this study, we utilized max pooling for the AlexNet and VGG16 architectures while we applied global average pooling for the other architectures.
The fully connected layer is a fundamental component of neural networks.In this layer, each node is connected to every node in the previous layer. The output of this layer is a linear combination of the attributes from the preceding layer, as demonstrated in Equation (2)
where and are the kth output neuron and the kth weight between and , respectively.
The activation function introduces a nonlinear transformation to an input signal and is typically utilized following a pooling layer or a fully connected layer within a neural network. Various types of activation functions exist, including the sigmoid function and the hyperbolic tangent. Nevertheless, the Rectified Linear Unit (ReLU) function, defined by , was selected due to its capability to facilitate faster training of the neural network without significantly compromising generalization accuracy [4].
The Softmax classification layer represents the final layer of the network and computes the probability associated with each class based on the input data labels. The Softmax function is the most widely employed classification layer in CNNs, making it the most suitable choice for this study. This function implements a categorical probability distribution based on the exponential function, as illustrated in Equation (3), for the kth class and an input X [4].
The loss function quantifies the discrepancy between actual and predicted values and is generally implemented as the final layer of a neural network. Given that this study involves a regression task, the mean squared error (MSE), as defined in Equation (4), was employed. This metric is commonly utilized in regression problems to assess model performance within the loss layer [76].
where n is the number of samples, y is the array of true values, and is the array of predicted values.
The dropout layer serves as a regularization technique designed to mitigate overfitting by randomly disconnecting specific inputs from the preceding layer prior to transitioning to the subsequent layer within the network architecture [76]. This layer was incorporated in each of the architectures employed in this research. The training of the CNNs was executed without delineating the feature extraction and classification phases. The remaining procedures adhere to the methodology outlined in the relevant section. The five CNN architectures applied in this study are elucidated in the following subsections. In all configurations, the ReLU activation function was utilized in the convolutional layers, while the Softmax function was employed in the classification layer.
Table 4 summarizes key characteristics of five widely used CNN architectures. The first column lists the model names, the second column provides reference numbers corresponding to their original publications, and the third column highlights their main architectural features. AlexNet is recognized for its pioneering use of deep architectures with ReLU activations and dropout, while VGG16 and VGG19 are known for their simplicity, utilizing small 3 × 3 filters and deep layers. InceptionV3 introduces the Inception module with multi-level convolutions and batch normalization for efficiency, and Xception uses depthwise separable convolutions to reduce the computational cost, combined with linear residual connections for enhanced feature reuse and optimization.

Table 4.
Brief description and key features of CNN models used in this paper.
The cross-validation (CV) method was used to obtain the results and compare the models. By using this method, it is possible to verify the power of the model in a more reliable way since this approach trains and tests the entire dataset [81]. The K-fold technique is one of the most used CV techniques. This technique divides the available data into K parts and uses some of these parts to train the model and other parts to test it [81]. Five folds were used in the CV testing of the models in this work.
3.5. Assessment Metrics
In this study, three metrics were employed to assess the performance of the algorithms: the mean absolute error (MAE), root mean squared error (RMSE), and coefficient of determination ().
The MAE quantifies the average size of errors in forecasts, ignoring their direction. It is calculated by averaging the absolute differences between predicted values and actual observations, giving equal weight to each difference [76]. The MAE is calculated using the formula in Equation (5) below.
where x is the predicted value, y is the true value, and n is the number of samples.
The RMSE is a metric that quantifies the variation in residuals, or the differences between observed data points and the predicted values generated by a model. It measures the overall accuracy of the model in relation to the data. Lower RMSE values indicate a better fit, making it a reliable indicator of how well the model predicts the response [76].
where N is the number of samples, y is the true value, and is the predicted value.
The is a metric that evaluates the adequacy of the model to the observed data, and its values generally vary between 0 and 1, with an close to 1 generally indicating a good fit of the model to the data [81]. Its mathematical representation is given by Equation (7).
where y is the observed values and f is the values predicted by the network.
3.6. Optimizers
The adaptive moment estimation (ADAM) and stochastic gradient descent (SGD) optimizers were used in this work. For each model, which of these optimizers would be the most appropriate was studied. SGD is a variation of gradient descent (GD) and is one of the most traditional methods in ML problems. These problems are always considered as the problem of minimizing an objective function that has the form of a sum [76]
where the parameter w that minimizes the function has to be estimated. When used to minimize the function , the standard GD method would perform the following iterations [76]:
where is the model learning rate.
Instead of performing computations on the entire set as in GD, which is redundant and inefficient, SGD only performs computations on randomly selected subsets of data. Despite being a considerably older method, SGD, due to its good generalization capacity, is still considered one of the most important algorithms when it comes to training CNNs. However, although SGD is a robust and effective optimizer, it has some imperfections, such as slow convergence in some applications [32]. Extensions to SGD, such as the ADAM optimizer, have been introduced to improve its performance. ADAM is an adaptive learning rate method that adjusts the learning rate for each parameter by using both the first and second gradient moment estimates [82]. Despite the availability of more advanced optimizers like ADAM, SGD remains valuable due to its simplicity and computational efficiency.
After conducting a comprehensive series of tests, the optimal combination of parameters was identified as follows: for the ADAM optimizer, a learning rate of 0.0001 was determined to be most effective. In the case of the SGD optimizer, a momentum of 0.9, a learning rate of 0.01, and a weight decay of yielded the best performance. It is noteworthy that only the VGG19 architecture demonstrated superior results with the SGD optimizer. Conversely, the remaining four models were better suited to the ADAM optimizer.
Figure 4 presents the framework that illustrates the steps taken in this work to analyze steel microstructures from a set of images. The images undergo preprocessing and are then divided into training sets. From these images, the neural network is trained, adjusting the fully connected layers in order to optimize performance. Different CNN architectures are tested: AlexNet, VGG16, VGG19, InceptionV3, and Xception. The performance of the models is measured using metrics such as R2, MAE, and RMSE, which allow for quantification of the accuracy of the predictions and the effectiveness of the models in the context of microstructure analysis.
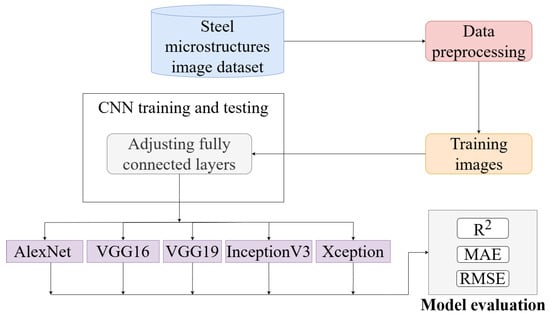
Figure 4.
Framework of the proposed approach.
4. Results and Discussion
The computational experiments were carried out on a computer with the following specifications: NVIDIA Tesla T4 GPU (15079 MiB [83]). The CNN models were built in the Keras [76] library and the data were processed using mainly the numpy [84] and Scikit-Learn [85] libraries. From the dataset, comprising 210 images, 30 were allocated to the test set, while the remaining 180 images were used as the basis for data augmentation. Using the mentioned augmentation techniques, the training set was increased fourfold, producing 720 images in total. Each computational model was executed 10 times over 100 epochs, utilizing 5-fold CV with randomly generated data from various random seeds. Figure 5 shows the MSE (a) and the R2 (b) throughout the training. As can be seen, all models converged and were able to perform the proposed task.
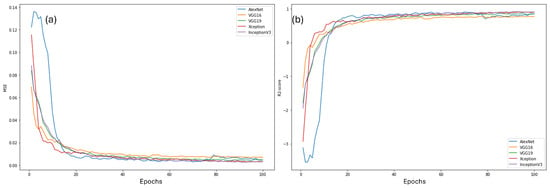
Figure 5.
MSE (a) and R2 (b) throughout model training.
Table 5 contains the results, in terms of execution time and performance, of the five CNN models, with the performance results presented with their respective standard deviations. It can be noted that AlexNet was the fastest model, taking approximately 338 min to obtain the complete solution. This is explained by the fact that this is the least complex model among the five studied. As expected, the VGG16 network took the longest, as this network is computationally intensive to train. It can also be seen that the VGG19 architecture with SGD optimizer achieved the best results in terms of performance.

Table 5.
Performance comparison of DL architectures on training time, R2, MAE, and RMSE metrics. The best results for each metric are shown in bold.
Figure 6 shows the MAE (a) and R2 (b) in each of the 10 iterations for each of the five models. It is possible to observe more clearly the supremacy of the VGG19 model for this application since, in addition to obtaining the best results on average, they did not vary considerably throughout the iterations. It is worth noting that the VGG19 model exhibited a notably smoother curve in both MAE and R2 across iterations when compared to the other architectures. This effect is consistent with its lower prediction variance and more stable convergence behavior during training. The smoothness, therefore, reflects the model’s robustness and is not associated with any computational issue or irregularity in output generation.
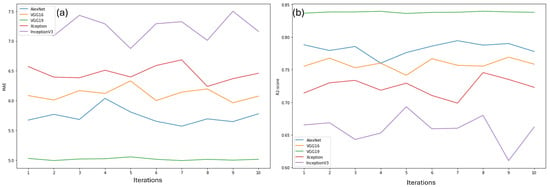
Figure 6.
MAE (a) and R2 (b) in each iteration per model.
Figure 7 displays a boxplot illustrating the mean error of each model across various microconstituents. Notably, the model exhibits higher prediction errors for certain microconstituents compared to others. Specifically, microconstituents with lower data variability, such as PF(I) and FS(A), are predicted more accurately. Conversely, microconstituents like FS(NA) and PF(G), which display significant data variability, pose greater challenges for the model, resulting in reduced prediction accuracy.
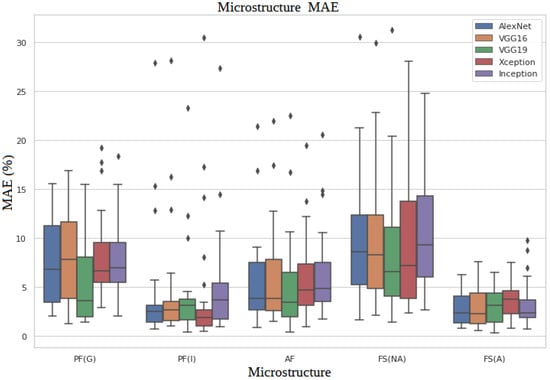
Figure 7.
MAE of each model by microconstituent.
4.1. Quantification vs. Recognition
The performance obtained in the present study, particularly regarding the VGG19 architecture, contrasts significantly with previous findings reported by Warmuzek et al. [56], who evaluated six CNN models for the classification of metallic alloy microstructures based on their morphological characteristics. Among the models analyzed, both VGG19 and Xception were employed—architectures that were also assessed in this work. However, in Warmuzek’s study, VGG19 yielded the lowest accuracy in recognition and classification tasks.
In contrast, within the context of microstructural quantification, the VGG19 architecture exhibited superior performance compared to the other four models examined, achieving the lowest MAE and highest R2 values. These divergent findings suggest that the effectiveness of a given architecture is highly dependent on the specific task—classification or quantification—being addressed. This distinction is further supported by the findings of Kim et al. [53], who applied deep learning techniques for the segmentation of microstructures in low-carbon steels. Although quantification was not the primary objective of their study, the authors reported promising results in predicting the proportion of three microconstituents, with values comparable to manual measurements.
Taken together, these findings indicate that a CNN architecture that performs suboptimally for classification may nonetheless exhibit excellent results for quantification. This suggests that task-specific evaluation of CNNs is essential, and underscores the importance of independently assessing model performance in classification and quantification domains. This insight represents a key contribution of the present study and should be considered in the development of future methodologies for automated microstructural analysis.
4.2. Model Evaluation and Error Behavior
A comparative analysis was conducted using six representative micrographs to evaluate the predictive capabilities of the most effective model, VGG19. Figure 8 illustrates the percentage values of each microconstituent obtained manually and through the model’s predictions, alongside the mean absolute error (MAE) for each image. The microconstituents evaluated include polygonal ferrite at grain boundaries [PF(G)], polygonal ferrite within grains [PF(I)], acicular ferrite [AF], ferrite with a non-aligned second phase [FS(NA)], and ferrite with an aligned second phase [FS(A)].

Figure 8.
Predictions from VGG19 model for six different images [%PF(G), %PF(I), %AF, %FS(NA), %FS(A)]. Sub-figures (a–f) represent distinct samples from the test set, each illustrating the manual and predicted quantification.
It is noteworthy that the VGG19 model was capable of producing predictions with MAEs not exceeding 5% in any of the evaluated images, even for cases with a high degree of uncertainty in manual interpretation, such as the image presented in Figure 8f. This indicates the model’s robustness in handling complex and visually ambiguous microstructures.
To investigate model precision further, the relative errors of each microconstituent were calculated individually for all six test images and are shown in Table 6. The smallest individual relative errors were observed for FS(NA) and PF(G), with absolute values not exceeding 13.8% and 18.2%, respectively. Conversely, the largest relative errors were found for FS(A) and PF(I), reaching values of 300% and 75%. These results reveal that, although the model performs consistently well on average, significant deviations can occur in the quantification of specific microconstituents within individual images.

Table 6.
Predicted and manual quantification with relative error (%) per microconstituent in Figure 8. Format: predicted/manual (error%).
This reinforces the necessity of interpreting CNN-based predictions with caution when applied to single-image evaluations. Instead, it is recommended that predictions be aggregated over multiple observations from the same sample to improve reliability. When the mean values across the six test images are compared to the corresponding manual quantifications, the overall error diminishes considerably, aligning closely with the model’s global MAE. This outcome suggests that machine-based quantification becomes increasingly reliable with larger sample sizes, often surpassing the consistency and speed achievable through manual methods.
Hence, despite isolated deviations, CNN-based approaches—when appropriately validated—hold significant potential for improving both the accuracy and efficiency of microstructural quantification in metallurgical applications.
Although there are limitations, the DL-based method presented in this paper not only accelerates the analysis pipeline compared to ASTM-standard manual methods but also improves consistency and repeatability. As Table 6 shows, once the VGG19 model is trained, the CNN delivers quantification in under one second per image—orders of magnitude faster than manual annotation. Moreover, Figure 8 demonstrates that CNN predictions are robust even in complex cases with visual ambiguity.
While manual methods remain valuable for initial annotation and model training, their limitations in scalability and reproducibility underscore the need for automated approaches. CNNs thus serve as a complementary and ultimately superior solution for microstructure quantification in modern metallurgical workflows.
While this study focused on widely adopted CNN architectures such as VGG16, VGG19, AlexNet, InceptionV3, and Xception, the authors recognize the emergence of other models like EfficientNet [86] and MobileNet [87] that offer state-of-the-art performance with lower computational cost. The current model selection was driven by considerations of dataset size, hardware limitations, and interpretability—critical factors in scientific applications. Nonetheless, incorporating these advanced architectures represents a promising direction for future work, especially as larger annotated datasets and optimized training pipelines become available.
5. Conclusions
In this study, we proposed and validated a convolutional neural network (CNN)-based approach for the automatic quantification of microconstituents in steel microstructures from optical microscopy images. Among the five CNN architectures evaluated, VGG19 demonstrated superior performance, achieving a mean absolute error (MAE) below 5% across the evaluated samples, even in cases where human visual identification was uncertain.
A key finding of this work is the task-dependent behavior of CNN architectures. While previous studies reported VGG19 as one of the least effective architectures for classification tasks involving microstructural images, our results show that VGG19 excels in quantification tasks, providing greater precision and consistency than manual quantification. This reinforces the importance of selecting and validating deep learning models in alignment with the specific objective, be it classification or quantification, when applied to metallurgical image analysis.
The detailed error analysis, both on an individual and averaged basis, demonstrates that CNN-based quantification is especially reliable when applied to ensembles of images, offering high accuracy and reproducibility. These characteristics support its application in scenarios demanding efficiency and standardization, such as quality control in steel production.
Moreover, the methodology presented here has the potential to contribute to the advancement of computational metallurgy and automated image analysis, reducing subjectivity, improving throughput, and paving the way for integrating deep learning tools into routine metallographic workflows.
Future work may explore model generalization across different steel grades and microstructural preparation techniques, as well as the application of attention mechanisms and explainable AI to enhance model interpretability.
Author Contributions
Conceptualization: M.L.L.J. and C.D.d.A.; methodology: M.L.L.J. and C.D.d.A.; software: T.T.F.; validation: M.L.L.J. and C.D.d.A.; formal analysis: L.G., M.B., C.M.S., and C.D.d.A.; investigation: B.d.S.M. and C.D.d.A.; resources: M.L.L.J., C.M.S., M.B., and L.G.; funding: L.G.; data curation: T.T.F., C.D.d.A. and M.L.L.J.; writing—original draft: M.L.L.J., C.D.d.A., and T.T.F.; writing—review and editing: L.G., M.B., C.M.S., and B.d.S.M.; supervision: L.G. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge the financial support provided by the funding agencies CNPq (grants 401796/2021-3, 307688/2022-4, and 409433/2022-5), Fapemig (grants APQ-02513-22, APQ-04458-23 and BPD-00083-22), FINEP (grant SOS Equipamentos 2021 AV02 0062/22), and Capes (Finance Code 001).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- DeHoff, R. Engineering of Microstructures. Mater. Res. 1999, 2, 111–126. [Google Scholar] [CrossRef]
- Li, J.C.M. Microstructure and Properties of Materials; World Scientific: Singapore, 1996; Volume 2. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Honeycombe, R.W.K. Steels: Microstructure and Properties, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 2128. [Google Scholar] [CrossRef] [PubMed]
- Trolier-McKinstry, S.; Newnham, R.E. Materials Engineering: Bonding, Structure, and Structure-Property Relationships, 1st ed.; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Gola, J.; Britz, D.; Staudt, T.; Winter, M.; Schneider, A.S.; Ludovici, M.; Mücklich, F. Advanced microstructure classification by data mining methods. Comput. Mater. Sci. 2018, 148, 324–335. [Google Scholar] [CrossRef]
- Schorr, S.; Weidenthaler, C. (Eds.) Crystallography in Materials Science: From Structure-Property Relationships to Engineering; De Gruyter: Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- Davim, J.P. (Ed.) Welding Technology; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Phillips, D.H. Welding Engineering: An Introduction, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Leng, Y. Materials Characterization: Introduction to Microscopic and Spectroscopic Methods; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar] [CrossRef]
- Abson, D.J. Acicular ferrite and bainite in C–Mn and low-alloy steel arc weld metals. Sci. Technol. Weld. Join. 2018, 23, 635–648. [Google Scholar] [CrossRef]
- ASTM E562-19e1; Standard Test Method for Determining Volume Fraction by Systematic Manual Point Count. Book of Standards Volume: 03.01. ASTM: West Conshohocken, PA, USA, 2019; p. 7. [CrossRef]
- Campbell, A.; Murray, P.; Yakushina, E.; Marshall, S.; Ion, W. New methods for automatic quantification of microstructural features using digital image processing. Mater. Des. 2018, 141, 395–406. [Google Scholar] [CrossRef]
- Ma, W.; Kautz, E.J.; Baskaran, A.; Chowdhury, A.; Joshi, V.; Yener, B.; Lewis, D.J. Image-driven discriminative and generative machine learning algorithms for establishing microstructure–processing relationships. J. Appl. Phys. 2020, 128, 134901. [Google Scholar] [CrossRef]
- ASTM E112-24; Standard Test Methods for Determining Average Grain Size. Book of Standards Volume: 03.01. ASTM: West Conshohocken, PA, USA, 2024; p. 28. [CrossRef]
- ASTM E3-11(2017); Standard Guide for Preparation of Metallographic Specimens. Book of Standards Volume: 03.01. ASTM: West Conshohocken, PA, USA, 2017; p. 12. [CrossRef]
- Franco, V.R.; Hott, M.C.; Andrade, R.G.; Goliatt, L. Hybrid machine learning methods combined with computer vision approaches to estimate biophysical parameters of pastures. Evol. Intell. 2023, 16, 1271–1284. [Google Scholar] [CrossRef]
- Fayer, G.; Lima, L.; Miranda, F.; Santos, J.; Campos, R.; Bignoto, V.; Andrade, M.; Moraes, M.; Ribeiro, C.; Capriles, P.; et al. A temporal fusion transformer deep learning model for long-term streamflow forecasting: A case study in the Funil Reservoir, Southeast Brazil. Knowl.-Based Eng. Sci. 2023, 4, 73–88. [Google Scholar]
- Bodini, M. Daily Streamflow Forecasting Using AutoML and Remote-Sensing-Estimated Rainfall Datasets in the Amazon Biomes. Signals 2024, 5, 659–689. [Google Scholar] [CrossRef]
- Durmaz, A.R.; Potu, S.T.; Romich, D.; Möller, J.J.; Nützel, R. Microstructure quality control of steels using deep learning. Front. Mater. 2023, 10, 1222456. [Google Scholar] [CrossRef]
- Modenesi, P.J. Soldabilidade dos Aços Transformáveis; Universidade Federal de Minas Gerais: Minas Gerais, BZ, USA, 2012. [Google Scholar]
- Singh, R. Applied Welding Engineering: Processes, Codes, and Standards, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2016. [Google Scholar] [CrossRef]
- Silva, G.C.; de Castro, J.A.; Filho, R.M.M.; Caldeira, L.; Lagares, M.L. Comparing two different arc welding processes through the welding energy: A selection analysis based on quality and energy consumption. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 301. [Google Scholar] [CrossRef]
- Abson, D.J. Guide to the Light Microscope Examination of Ferritic Steel Weld Metals; Technical Report IIW Doc. IX-1533-88; International Institute of Welding: Paris, France, 1988. [Google Scholar]
- Devezas, T.; Leitão, J.; Sarygulov, A. (Eds.) Industry 4.0: Entrepreneurship and Structural Change in the New Digital Landscape; Springer: Cham, Switzerland, 2017; p. 431. [Google Scholar] [CrossRef]
- Suleiman, Z.; Shaikholla, S.; Dikhanbayeva, D.; Shehab, E.; Turkyilmaz, A. Industry 4.0: Clustering of concepts and characteristics. Cogent Eng. 2022, 9, 2034264. [Google Scholar] [CrossRef]
- Cheng, Y.; Wang, T.; Zhang, G. Artificial Intelligence for Materials Science; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Winston, P.H. Artificial Intelligence, 3rd ed.; Addison-Wesley: Boston, MA, USA, 1992; p. 737. [Google Scholar]
- Hunt, E.B. Artificial Intelligence; Academic Press: Cambridge, MA, USA, 2014; p. 484. [Google Scholar]
- Bulgarevich, D.S.; Tsukamoto, S.; Kasuya, T.; Demura, M.; Watanabe, M. Automatic steel labeling on certain microstructural constituents with image processing and machine learning tools. Sci. Technol. Adv. Mater. 2019, 20, 532–542. [Google Scholar] [CrossRef] [PubMed]
- Campesato, O. Artificial Intelligence, Machine Learning, and Deep Learning; Mercury Learning and Information: Herndon, VA, USA, 2020; p. 319. [Google Scholar]
- Rosebrock, A. Deep Learning for Computer Vision with Python; PyImageSearch: Philadelphia, PA, USA, 2017. [Google Scholar]
- Zaefferer, S.; Ohlert, J.; Bleck, W. A study of microstructure, transformation mechanisms and correlation between microstructure and mechanical properties of a low alloyed TRIP steel. Acta Mater. 2004, 52, 2765–2778. [Google Scholar] [CrossRef]
- Wu, J.; Wray, P.J.; Garcia, C.I.; Hua, M.; DeArdo, A.J. Image Quality Analysis: A New Method of Characterizing Microstructures. ISIJ Int. 2005, 45, 254–262. [Google Scholar] [CrossRef]
- DeArdo, A.d.; Garcia, C.; Cho, K.; Hua, M. New Method of Characterizing and Quantifying Complex Microstructures in Steels. Mater. Manuf. Process. 2010, 25, 33–40. [Google Scholar] [CrossRef]
- Randle, V. Electron backscatter diffraction: Strategies for reliable data acquisition and processing. Mater. Charact. 2009, 60, 913–922. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Networks Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef]
- Bodini, M. A Review of Facial Landmark Extraction in 2D Images and Videos Using Deep Learning. Big Data Cogn. Comput. 2019, 3, 14. [Google Scholar] [CrossRef]
- Boccignone, G.; Bodini, M.; Cuculo, V.; Grossi, G. Predictive Sampling of Facial Expression Dynamics Driven by a Latent Action Space. In Proceedings of the 2018 14th International Conference on Signal-Image Technology & Internet-Based Systems (SITIS), Las Palmas de Gran Canaria, Spain, 26–29 November 2018; pp. 143–150. [Google Scholar] [CrossRef]
- Bodini, M.; D’Amelio, A.; Grossi, G.; Lanzarotti, R.; Lin, J. Single Sample Face Recognition by Sparse Recovery of Deep-Learned LDA Features. In Proceedings of the Advanced Concepts for Intelligent Vision Systems, Poitiers, France, 24–27 September 2018; Blanc-Talon, J., Helbert, D., Philips, W., Popescu, D., Scheunders, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 297–308. [Google Scholar] [CrossRef]
- Pokuri, B.S.S.; Ghosal, S.; Kokate, A.; Sarkar, S.; Ganapathysubramanian, B. Interpretable deep learning for guided microstructure-property explorations in photovoltaics. Npj Comput. Mater. 2019, 5, 95. [Google Scholar] [CrossRef]
- Lopez Pinaya, W.H.; Vieira, S.; Garcia-Dias, R.; Mechelli, A. Chapter 10—Convolutional Neural Networks; Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 173–191. [Google Scholar] [CrossRef]
- Che, L.; He, Z.; Zheng, K.; Si, T.; Ge, M.; Cheng, H.; Zeng, L. Deep learning in alloy material microstructures: Application and prospects. Mater. Today Commun. 2023, 37, 107531. [Google Scholar] [CrossRef]
- DeCost, B.L.; Holm, E.A. A computer vision approach for automated analysis and classification of microstructural image data. Comput. Mater. Sci. 2015, 110, 126–133. [Google Scholar] [CrossRef]
- Papa, J.P.; Nakamura, R.Y.M.; Albuquerque, V.; Falcão, A.X. Computer techniques towards the automatic characterization of graphite particles in metallographic images of industrial materials. Expert Syst. Appl. 2013, 40, 590–597. [Google Scholar] [CrossRef]
- Souza, A.C.; Silva, G.C.; Caldeira, L.; de Almeida Nogueira, F.M.; Junior, M.L.L.; de Aguiar, E.P. An enhanced method for the identification of ferritic morphologies in welded fusion zones based on gray-level co-occurrence matrix: A computational intelligence approach. Proc. Inst. Mech. Eng. Part C 2021, 235, 1228–1240. [Google Scholar] [CrossRef]
- Nunes, T.M.; de Albuquerque, V.H.C.; Papa, J.P.; Silva, C.C.; Normando, P.G.; Moura, E.P.; Tavares, J.M.R. Automatic microstructural characterization and classification using artificial intelligence techniques on ultrasound signals. Expert Syst. Appl. 2013, 40, 3096–3105. [Google Scholar] [CrossRef]
- Albuquerque, V.H.C.D.; Tavares, J.M.R.; Cortez, P.C. Quantification of the microstructures of hypoeutectic white cast iron using mathematical morphology and an artificial neural network. Int. J. Microstruct. Mater. Prop. 2010, 5, 52–64. [Google Scholar] [CrossRef]
- Chowdhury, A.; Kautz, E.; Yener, B.; Lewis, D. Image driven machine learning methods for microstructure recognition. Comput. Mater. Sci. 2016, 123, 176–187. [Google Scholar] [CrossRef]
- Ling, J.; Hutchinson, M.; Antono, E.; DeCost, B.; Holm, E.A.; Meredig, B. Building data-driven models with microstructural images: Generalization and interpretability. Mater. Discov. 2017, 10, 19–28. [Google Scholar] [CrossRef]
- DeCost, B.L.; Francis, T.; Holm, E.A. Exploring the microstructure manifold: Image texture representations applied to ultrahigh carbon steel microstructures. Acta Mater. 2017, 133, 30–40. [Google Scholar] [CrossRef]
- Lorena, G.; Robinson, G.; Stefania, P.; Pasquale, C.; Fabiano, B.; Franco, M. Automatic Microstructural Classification with Convolutional Neural Network. In Proceedings of the Information and Communication Technologies of Ecuador (TIC.EC): TICEC 2018, Guayaquil, Ecuador, 21–23 November 2018; Advances in Intelligent Systems and, Computing. Botto-Tobar, M., Barba-Maggi, L., González-Huerta, J., Villacrés-Cevallos, P., Gómez, O.S., Uvidia-Fassler, M., Eds.; Springer: Cham, Switzerland, 2019; Volume 884. [Google Scholar] [CrossRef]
- Kim, H.; Inoue, J.; Kasuya, T. Unsupervised microstructure segmentation by mimicking metallurgists’ approach to pattern recognition. Sci. Rep. 2020, 10, 17835. [Google Scholar] [CrossRef]
- Holm, E.A.; Cohn, R.; Gao, N.; Kitahara, A.R.; Matson, T.P.; Lei, B.; Yarasi, S.R. Overview: Computer vision and machine learning for microstructural characterization and analysis. Metall. Mater. Trans. A 2020, 51, 5985–5999. [Google Scholar] [CrossRef]
- Perera, R.; Guzzetti, D.; Agrawal, V. Optimized and autonomous machine learning framework for characterizing pores, particles, grains and grain boundaries in microstructural images. Comput. Mater. Sci. 2021, 196, 110524. [Google Scholar] [CrossRef]
- Warmuzek, M.; Żelawski, M.; Jałocha, T. Application of the convolutional neural network for recognition of the metal alloys microstructure constituents based on their morphological characteristics. Comput. Mater. Sci. 2021, 199, 110722. [Google Scholar] [CrossRef]
- Baskaran, A.; Kane, G.; Biggs, K.; Hull, R.; Lewis, D. Adaptive characterization of microstructure dataset using a two stage machine learning approach. Comput. Mater. Sci. 2020, 177, 109593. [Google Scholar] [CrossRef]
- Mishra, S.P.; Rahul, M. A comparative study and development of a novel deep learning architecture for accelerated identification of microstructure in materials science. Comput. Mater. Sci. 2021, 200, 110815. [Google Scholar] [CrossRef]
- Arumugam, D.; Kiran, R. Compact representation and identification of important regions of metal microstructures using complex-step convolutional autoencoders. Mater. Des. 2022, 223, 111236. [Google Scholar] [CrossRef]
- Jung, J.H.; Lee, S.J.; Kim, H.S. Estimation of Average Grain Size from Microstructure Image Using a Convolutional Neural Network. Materials 2022, 15, 6954. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Z.; Hu, F.; Dai, X.; Wang, L.; Zhang, Y. Feature extraction and microstructural classification of hot stamping ultra-high strength steel by machine learning. JOM 2022, 74, 3466–3477. [Google Scholar] [CrossRef]
- Tsutsui, K.; Matsumoto, K.; Maeda, M.; Takatsu, T.; Moriguchi, K.; Hayashi, K.; Morito, S.; Terasaki, H. Mixing effects of SEM imaging conditions on convolutional neural network-based low-carbon steel classification. Mater. Today Commun. 2022, 32, 104062. [Google Scholar] [CrossRef]
- Motyl, M.; Madej, Ł. Supervised pearlitic–ferritic steel microstructure segmentation by U-Net convolutional neural network. Arch. Civ. Mech. Eng. 2022, 22, 206. [Google Scholar] [CrossRef]
- Khan, A.H.; Sarkar, S.S.; Mali, K.; Sarkar, R. A Genetic Algorithm Based Feature Selection Approach for Microstructural Image Classification. Exp. Tech. 2022, 46, 335–347. [Google Scholar] [CrossRef]
- Mishra, S.P.; Rahul, M. A detailed study of convolutional neural networks for the identification of microstructure. Mater. Chem. Phys. 2023, 308, 128275. [Google Scholar] [CrossRef]
- Khurjekar, I.D.; Conry, B.; Kesler, M.S.; Tonks, M.R.; Krause, A.R.; Harley, J.B. Automated, high-accuracy classification of textured microstructures using a convolutional neural network. Front. Mater. 2023, 10, 1086000. [Google Scholar] [CrossRef]
- Lagares, M.L.; Silva, G.C.; Caldeira, L. Fusion zone microstructure image dataset of the flux-cored and shielded metal arc welding processes. Data Brief 2020, 33, 106353. [Google Scholar] [CrossRef] [PubMed]
- Aitchison, J. Principles of compositional data analysis. In Multivariate Analysis and Its Applications; Institute of Mathematical Statistics: Waite Hill, OH, USA, 1994; pp. 73–81. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Dodge, S.; Karam, L. Understanding how image quality affects deep neural networks. In Proceedings of the 2016 Eighth International Conference on Quality of Multimedia Experience (QoMEX), Lisbon, Portugal, 6–8 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson Education: London, UK, 2009; Volume 3, p. 936. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Zhao, H.; Burkhart, C.; Brinson, L.C.; Chen, W. A Transfer Learning Approach for Microstructure Reconstruction and Structure-property Predictions. Sci. Rep. 2018, 8, 13461. [Google Scholar] [CrossRef]
- Shen, L.; Margolies, L.R.; Rothstein, J.H.; Fluder, E.; McBride, R.; Sieh, W. Deep Learning to Improve Breast Cancer Detection on Screening Mammography. Sci. Rep. 2019, 9, 12495. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media: Sebastopol, CA, USA, 2022. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.E.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2015, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 2nd ed.; Springer: New York, NY, USA, 2021; p. 607. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Bisong, E. Building Machine Learning and Deep Learning Models on Google Cloud Platform: A Comprehensive Guide for Beginners, 1st ed.; Apress: New York, NY, USA, 2019; p. 348. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Tan, M.; Le, Q.V. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 6105–6114. [Google Scholar]
- Sandler, M.; Howard, A.G.; Zhu, M.; Zhmoginov, A.; Chen, L. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).