Machine Learning for Identifying Damage and Predicting Properties in 3D-Printed PLA/Lygeum Spartum Biocomposites
Highlights
- An innovative approach combining acoustic emission (AE) and machine learning (ML) was developed to predict stress levels during mechanical testing of 3D-printed biocomposites.
- AE signal analysis using K-means clustering identified three distinct damage modes: matrix cracking, fiber debonding, and fiber pullout, validated by SEM observations.
- This integrated approach provides a non-destructive monitoring framework for bio-composites, enhancing real-time understanding of damage evolution.
- These findings pave the way for optimizing biocomposite materials by improving fi-ber–matrix bonding to enhance mechanical strength.
Abstract
1. Introduction
- Development of a biodegradable composite based on a PLA matrix reinforced with plant fiber Lygeum Spartum for 3D printing.
- Evaluation of the mechanical properties of the biocomposite in comparison with neat PLA.
- Application of acoustic emission (AE) monitoring during mechanical testing to capture damage evolution, combined with k-means clustering to classify microstructural damage mechanisms.
- Exploration of various techniques for AE data preparation, including noise reduction, normalization, and feature selection.
- Implementation of four ML models for predicting stress levels, with performance evaluated using metrics such as R2 and MSE.
- Investigation of the most influential AE features to guide future input selection.
2. Materials and Methods
2.1. Materials and Feed Filament Production
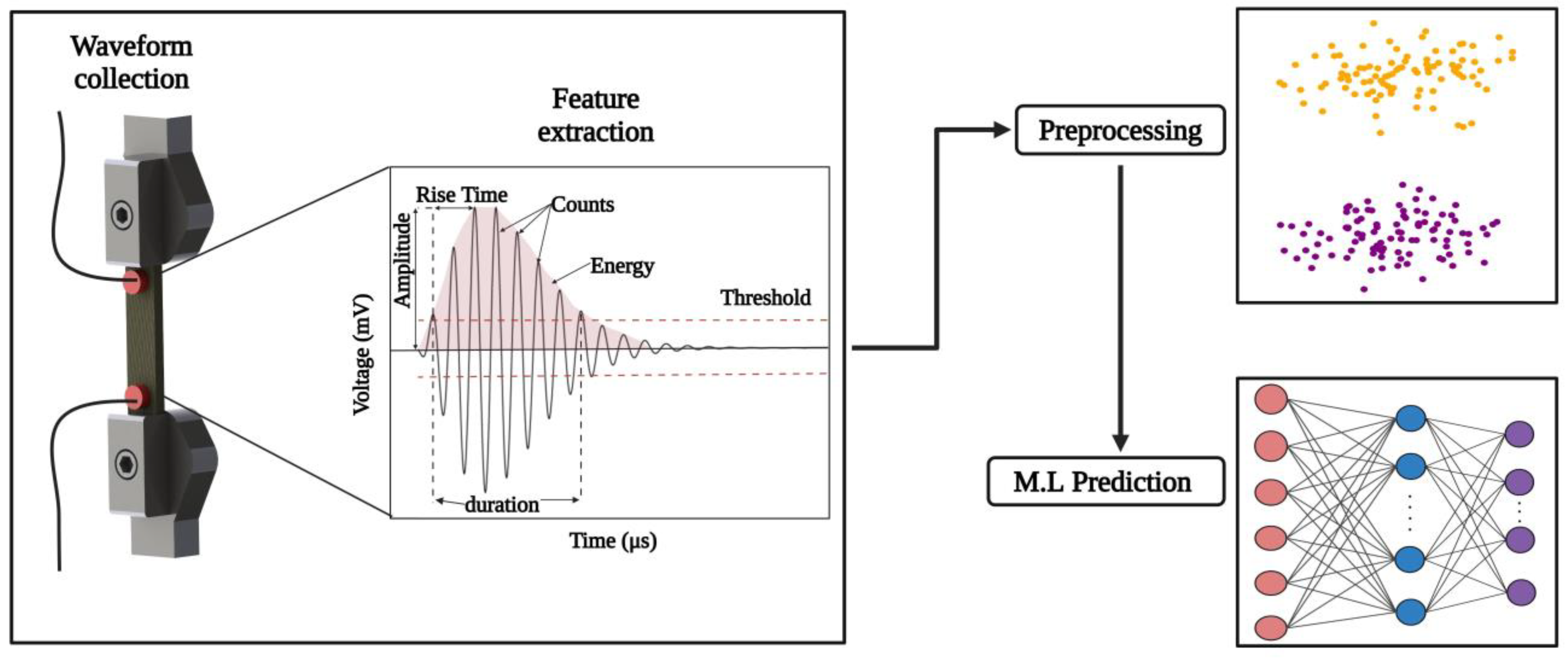
2.2. Mechanical Testing and Acoustic Emission Signal Recording
2.3. Machine Learning Models
2.4. Preparation of Acoustic Emission Data
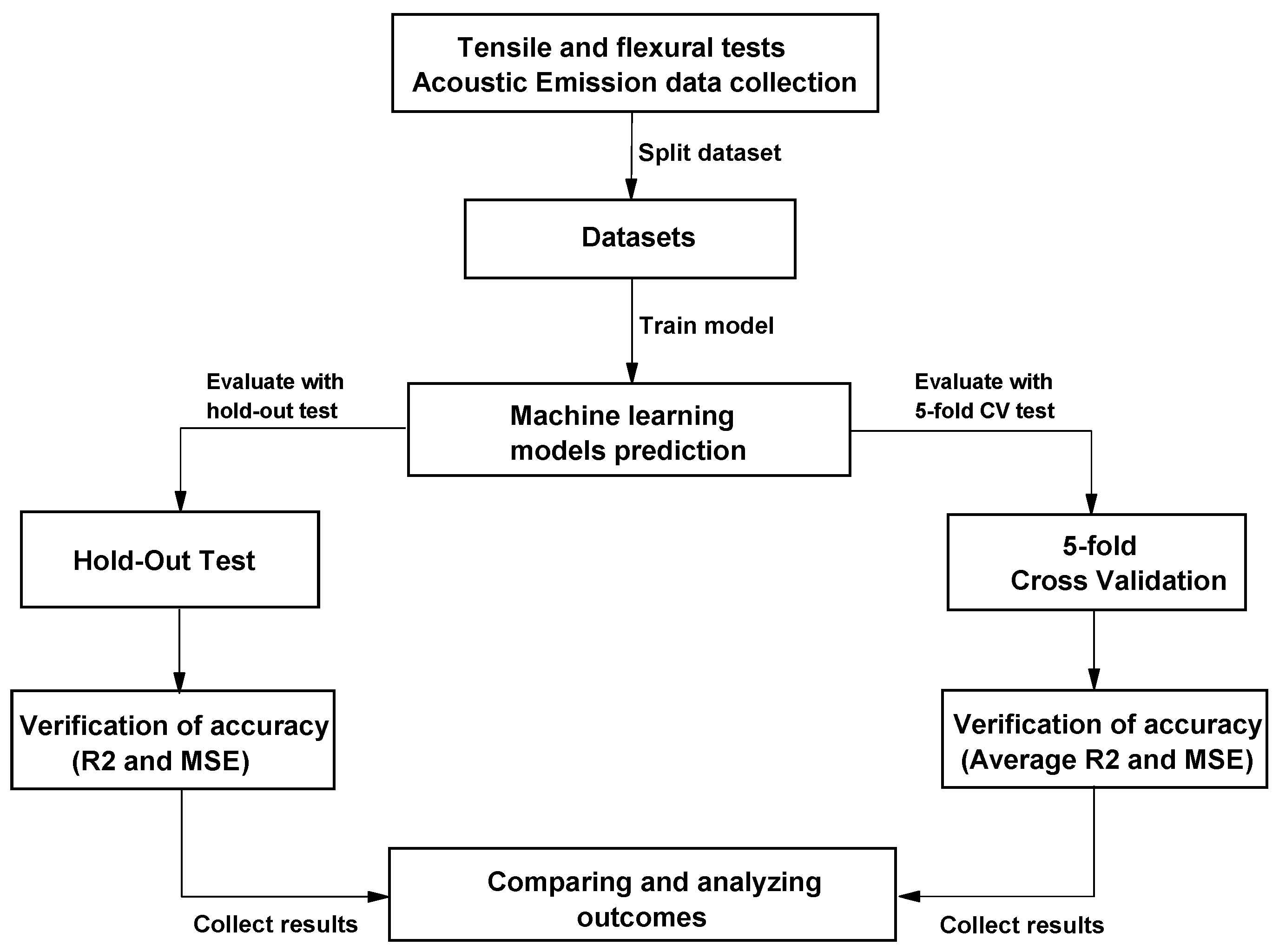
2.5. Cross-Validation and Hold-Out Evaluation
2.6. Verification of Accuracy
2.7. Damage Mode Identification Using k-Means Clustering Algorithm
3. Results and Discussion
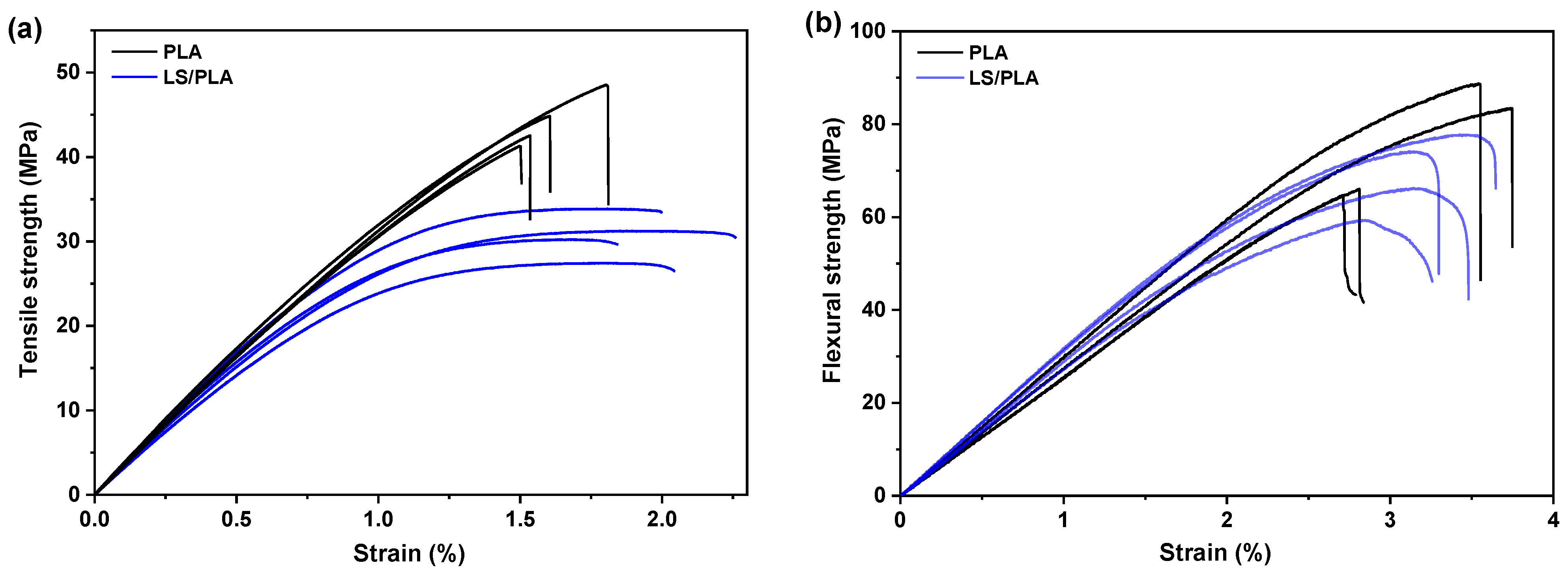
3.1. Mechanical Properties
3.2. Analysis of Damage Using Acoustic Emission
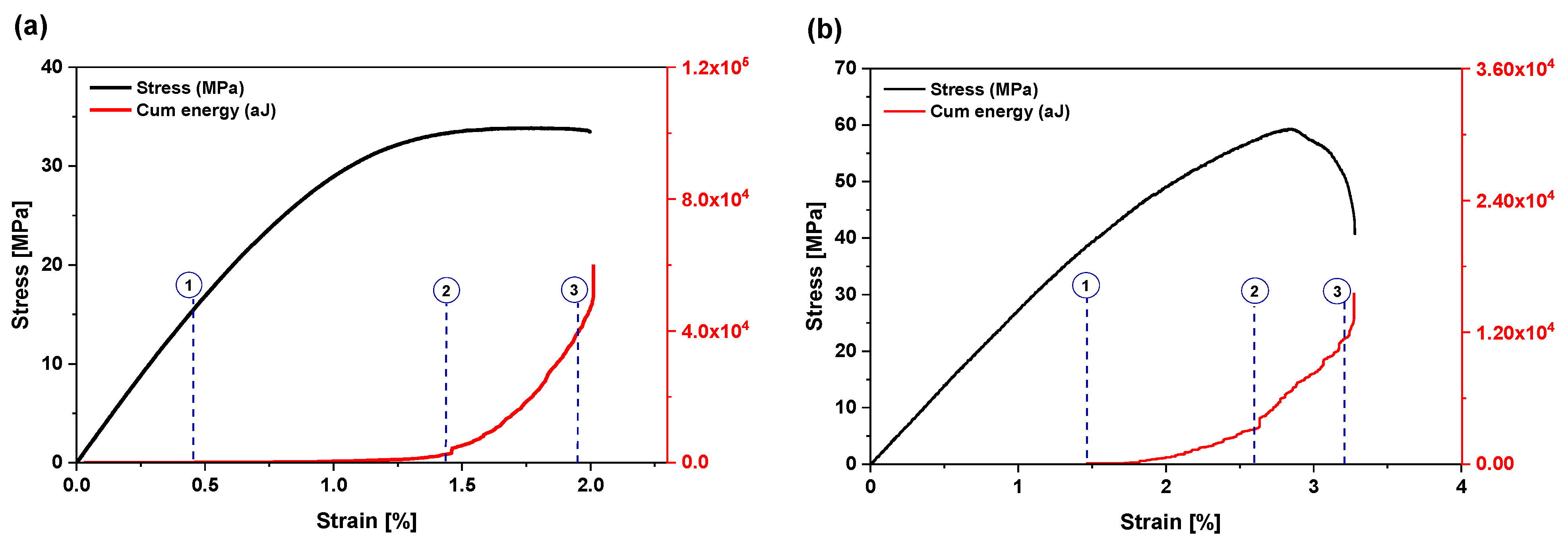
3.2.1. Damage Evolution
3.2.2. Classification of the Damage Modes Using K-Means Clustering
3.3. Prediction of Stress Levels in Tensile and Flexural Tests Using Machine Learning Models
3.3.1. Artificial Neural Network ANN
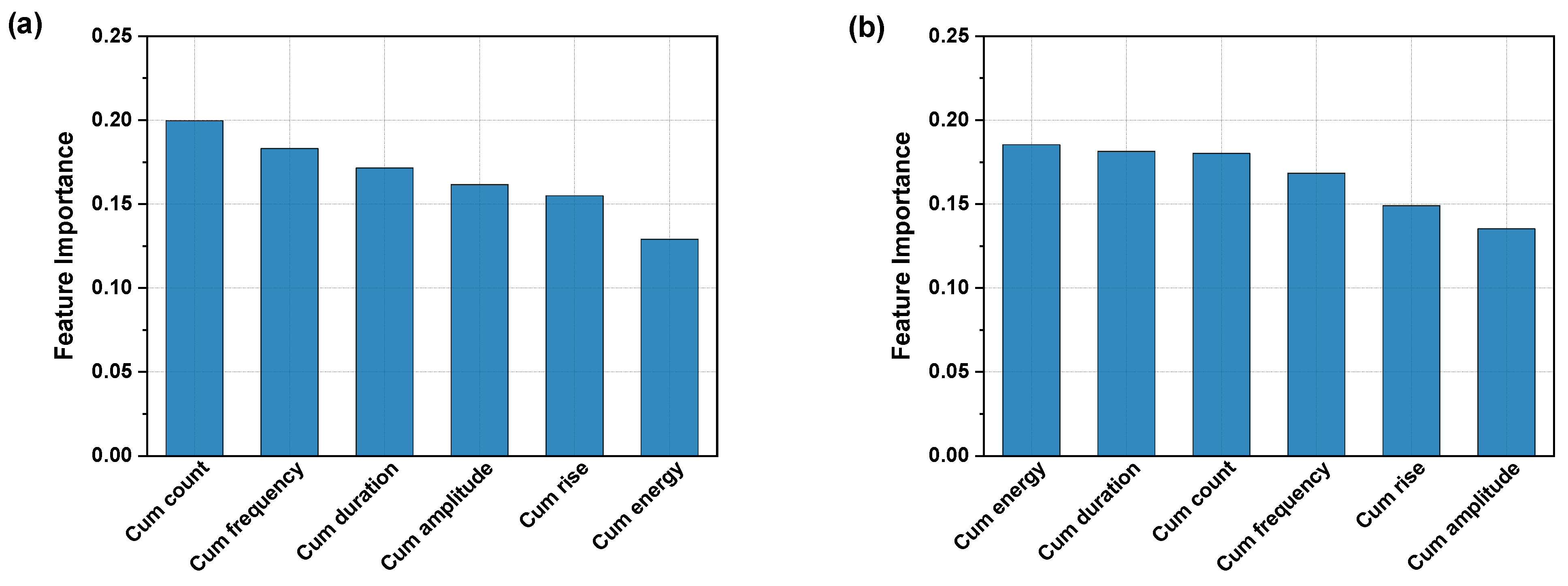
3.3.2. Random Forest Regression RFR
Feature Importance Analysis
Stress Level Prediction Using RFR
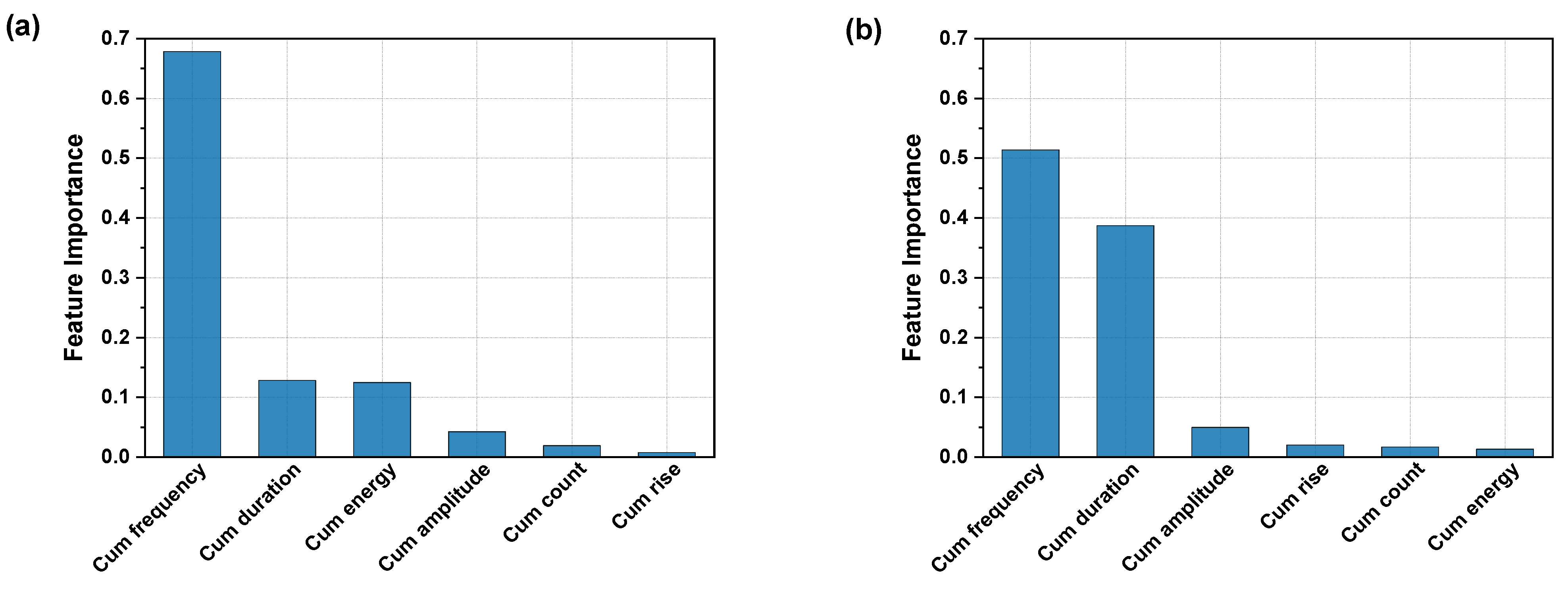
3.3.3. Decision Tree Regression DTR
Feature Importance
Stress Level Prediction Using DTR
3.3.4. Support Vector Regression SVR
3.4. Comparative Performance Analysis of the Employed ML Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ayrilmis, N.; Kariz, M.; Kwon, J.H.; Kuzman, M.K. Effect of printing layer thickness on water absorption and mechanical properties of 3D-printed wood/PLA composite materials. Int. J. Adv. Manuf. Technol. 2019, 102, 2195–2200. [Google Scholar] [CrossRef]
- Bahrami, M.; Abenojar, J.; Martínez, M.Á. Recent progress in hybrid biocomposites: Mechanical properties, water absorption, and flame retardancy. Materials 2020, 13, 5145. [Google Scholar] [CrossRef]
- Trivedi, A.K.; Gupta, M.; Singh, H. PLA based biocomposites for sustainable products: A review. Adv. Ind. Eng. Polym. Res. 2023, 6, 382–395. [Google Scholar] [CrossRef]
- Le Duigou, A.; Castro, M.; Bevan, R.; Martin, N. 3D printing of wood fibre biocomposites: From mechanical to actuation functionality. Mater. Des. 2016, 96, 106–114. [Google Scholar] [CrossRef]
- Bianchi, I.; Forcellese, A.; Gentili, S.; Greco, L.; Simoncini, M. Comparison between the mechanical properties and environmental impacts of 3D printed synthetic and bio-based composites. Procedia CIRP 2022, 105, 380–385. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, H.; Li, Z.; Li, P.; Shi, S.Q. Development and application of wood flour-filled polylactic acid composite filament for 3D printing. Materials 2017, 10, 339. [Google Scholar] [CrossRef]
- Guo, R.; Ren, Z.; Bi, H.; Song, Y.; Xu, M. Effect of toughening agents on the properties of poplar wood flour/poly (lactic acid) composites fabricated with Fused Deposition Modeling. Eur. Polym. J. 2018, 107, 34–45. [Google Scholar] [CrossRef]
- Panasiuk, K.; Dudzik, K. Determining the stages of deformation and destruction of composite materials in a static tensile test by acoustic emission. Materials 2022, 15, 313. [Google Scholar] [CrossRef]
- Barile, C.; Casavola, C.; Pappalettera, G.; Kannan, V.P. Damage monitoring of carbon fibre reinforced polymer composites using acoustic emission technique and deep learning. Compos. Struct. 2022, 292, 115629. [Google Scholar] [CrossRef]
- Huijer, A.; Kassapoglou, C.; Pahlavan, L. Acoustic emission monitoring of carbon fibre reinforced composites with embedded sensors for in-situ damage identification. Sensors 2021, 21, 6926. [Google Scholar] [CrossRef]
- Karami, S.; Khamedi, R.; Azizi, H.; Najafabadi, M.A. Investigation of the effect of nanoparticles on wood-bioplastic composite behavior using the acoustic emission method. J. Compos. Mater. 2022, 57, 23–34. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Jiang, X.; Eckstein, J.; Wang, L. Acoustic emission spectroscopy: Applications in geomaterials and related materials. Appl. Sci. 2021, 11, 8801. [Google Scholar] [CrossRef]
- Hao, W.; Huang, Z.; Xu, Y.; Zhao, G.; Chen, H.; Fang, D. Acoustic emission characterization of tensile damage in 3D braiding composite shafts. Polym. Test. 2020, 81, 106176. [Google Scholar] [CrossRef]
- Ciaburro, G.; Iannace, G. Machine-learning-based methods for acoustic emission testing: A review. Appl. Sci. 2022, 12, 10476. [Google Scholar] [CrossRef]
- Habibi, M.; Laperrière, L.; Lebrun, G.; Toubal, L. Combining short flax fiber mats and unidirectional flax yarns for composite applications: Effect of short flax fibers on biaxial mechanical properties and damage behaviour. Compos. Part B Eng. 2017, 123, 165–178. [Google Scholar] [CrossRef]
- Saidane, E.H.; Scida, D.; Assarar, M.; Ayad, R. Damage mechanisms assessment of hybrid flax-glass fibre composites using acoustic emission. Compos. Struct. 2017, 174, 1–11. [Google Scholar] [CrossRef]
- Sobhani, A.; Saeedifar, M.; Najafabadi, M.A.; Fotouhi, M.; Zarouchas, D. The study of buckling and post-buckling behavior of laminated composites consisting multiple delaminations using acoustic emission. Thin-Walled Struct. 2018, 127, 145–156. [Google Scholar] [CrossRef]
- Malpot, A.; Touchard, F.; Bergamo, S. An investigation of the influence of moisture on fatigue damage mechanisms in a woven glass-fibre-reinforced PA66 composite using acoustic emission and infrared thermography. Compos. Part B Eng. 2017, 130, 11–20. [Google Scholar] [CrossRef]
- Roundi, W.; El Mahi, A.; El Gharad, A.; Rebiere, J.-L. Acoustic emission monitoring of damage progression in Glass/Epoxy composites during static and fatigue tensile tests. Appl. Acoust. 2018, 132, 124–134. [Google Scholar] [CrossRef]
- Saeedifar, M.; Zarouchas, D. Damage characterization of laminated composites using acoustic emission: A review. Compos. Part B Eng. 2020, 195, 108039. [Google Scholar] [CrossRef]
- Xu, D.; Liu, P.; Chen, Z. A deep learning method for damage prognostics of fiber-reinforced composite laminates using acoustic emission. Eng. Fract. Mech. 2022, 259, 108139. [Google Scholar] [CrossRef]
- König, F.; Sous, C.; Chaib, A.O.; Jacobs, G. Machine learning based anomaly detection and classification of acoustic emission events for wear monitoring in sliding bearing systems. Tribol. Int. 2021, 155, 106811. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, Y.; Zhao, W. Tensile Deformation Damage and Clustering Analysis of Acoustic Emission Signals in Three-Dimensional Woven Composites. In Advances in Acoustic Emission Technology: Proceedings of the World Conference on Acoustic Emission-2017; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Almeida, R.S.; Magalhães, M.D.; Karim, N.; Tushtev, K.; Rezwan, K. Identifying damage mechanisms of composites by acoustic emission and supervised machine learning. Mater. Des. 2023, 227, 111745. [Google Scholar] [CrossRef]
- Lu, D.; Yu, W. Predicting the tensile strength of single wool fibers using artificial neural network and multiple linear regression models based on acoustic emission. Text. Res. J. 2020, 91, 533–542. [Google Scholar] [CrossRef]
- Sause, M.G.; Schmitt, S.; Kalafat, S. Failure load prediction for fiber-reinforced composites based on acoustic emission. Compos. Sci. Technol. 2018, 164, 24–33. [Google Scholar] [CrossRef]
- Shimamoto, Y.; Suzuki, T.; Tayfur, S.; Alver, N. Estimation of Concrete Mechanical Properties by Acoustic Emission with Random Forest Algorithm. International Symposium on Non-Destructive Testing in Civil Engineering (NDT-CE 2022), 16–18 August 2022, Zurich, Switzerland. e-J. Nondestruct. Testing 2022, 27. [Google Scholar] [CrossRef]
- Wang, Z.; Chegdani, F.; Yalamarti, N.; Takabi, B.; Tai, B.; El Mansori, M.; Bukkapatnam, S.T. Acoustic emission characterization of natural fiber reinforced plastic composite machining using a random forest machine learning model. J. Manuf. Sci. Eng. 2020, 142, 031003. [Google Scholar] [CrossRef]
- Ai, L.; Flowers, S.; Mesaric, T.; Henderson, B.; Houck, S.; Ziehl, P. Acoustic Emission-Based Detection of Impacts on Thermoplastic Aircraft Control Surfaces: A Preliminary Study. Appl. Sci. 2023, 13, 6573. [Google Scholar] [CrossRef]
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. American Society for Testing and Materials: West Conshohocken, PA, USA, 1998.
- ASTM D790; Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. Annual Book of ASTM Standards: West Conshohocken, PA, USA, 1997.
- Ying, X. An overview of overfitting and its solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Bashir, D.; Montañez, G.D.; Sehra, S.; Segura, P.S.; Lauw, J. An information-theoretic perspective on overfitting and underfitting. In Proceedings of the AI 2020: Advances in Artificial Intelligence: 33rd Australasian Joint Conference, AI 2020, Proceedings 33, Canberra, ACT, Australia, 29–30 November 2020; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Pothuganti, S. Review on over-fitting and under-fitting problems in Machine Learning and solutions. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2018, 7, 3692–3695. [Google Scholar]
- Barsoum, F.F.; Suleman, J.; Korcak, A.; Hill, E.V. Acoustic emission monitoring and fatigue life prediction in axially loaded notched steel specimens. J. Acoust. Emiss. 2009, 27, 40–63. [Google Scholar]
- Benabderazag, K.; Belouadah, Z.; Guebailia, M.; Toubal, L. Characterization of thermomechanical properties and damage mechanisms using acoustic emission of Lygeum spartum PLA 3D-printed biocomposite with fused deposition modelling. Compos. Part A Appl. Sci. Manuf. 2024, 186, 108426. [Google Scholar] [CrossRef]
- Xiong, Z.; Cui, Y.; Liu, Z.; Zhao, Y.; Hu, M.; Hu, J. Evaluating explorative prediction power of machine learning algorithms for materials discovery using k-fold forward cross-validation. Comput. Mater. Sci. 2020, 171, 109203. [Google Scholar]
- Beyeler, M. Machine Learning for OpenCV; Packt Publishing Ltd.: Birmingham, UK, 2017. [Google Scholar]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientists; O’Reilly Media, Inc.: Newton, MA, USA, 2016. [Google Scholar]
- Hadi, A.S.; Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Djabali, A.; Toubal, L.; Zitoune, R.; Rechak, S. Fatigue damage evolution in thick composite laminates: Combination of X-ray tomography, acoustic emission and digital image correlation. Compos. Sci. Technol. 2019, 183, 107815. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating number of hidden layer neurons in multiple hidden layer BPNN architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Li, P.; Zhang, W.; Ye, Z.; Wang, Y.; Yang, S.; Wang, L. Analysis of acoustic emission energy from reinforced concrete sewage pipeline under full-scale loading test. Appl. Sci. 2022, 12, 8624. [Google Scholar] [CrossRef]
- Karthik, M.K.; Kumar, C.S. A comprehensive review on damage characterization in polymer composite laminates using acoustic emission monitoring. Russ. J. Nondestruct. Test. 2022, 58, 705–721. [Google Scholar] [CrossRef]
- Han, S.N.M.F.; Taha, M.M.; Mansor, M.R.; Rahman, M.A.A. Investigation of tensile and flexural properties of kenaf fiber-reinforced acrylonitrile butadiene styrene composites fabricated by fused deposition modeling. J. Eng. Appl. Sci. 2022, 69, 52. [Google Scholar] [CrossRef]
- Lee, H.-L.; Kim, J.-S.; Hong, C.-H.; Cho, D.-K. Ensemble learning approach for the prediction of quantitative rock damage using various acoustic emission parameters. Appl. Sci. 2021, 11, 4008. [Google Scholar] [CrossRef]
- Koya, B.P.; Aneja, S.; Gupta, R.; Valeo, C. Comparative analysis of different machine learning algorithms to predict mechanical properties of concrete. Mech. Adv. Mater. Struct. 2022, 29, 4032–4043. [Google Scholar] [CrossRef]




| Model | Hyperparameter | Optimized Value | Tuning Range Values |
|---|---|---|---|
| ANN | Model activation | tanh | [Relu, tanh] |
| Model optimizer | 0.01 | Adam, learning rate [0.001, 0.01] | |
| Batch_size | 32 | [16, 32] | |
| Epochs | 100 | [50, 100] | |
| RFR | Max depth | 7 | [5, 20] |
| Min samples leaf | 4 | [1, 10] | |
| Min samples split | 4 | [2, 10] | |
| n_estimators | 139 | [50, 200] | |
| Max features | auto | [auto, sqrt, log2] | |
| DTR | Max depth | 7 | [1, 20] |
| Min samples leaf | 5 | [1, 20] | |
| Min samples split | 4 | [2, 20] | |
| Max features | auto | [auto, sqrt, log2] | |
| SVR | kernel | rbf | [linear, rbf] |
| C | 10 | [1, 1000] | |
| gamma | 1 | [0.1, 1, scale] | |
| epsilon | 0.2 | [0.01, 0.1, 0.2] |
| Tensile Test | Flexural Test | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | MSE | RMSE | R2 | Average 5 CV R2 | 5 CV R2 STD | MSE | RMSE | R2 | Average 5 CV R2 | 5 CV R2 STD |
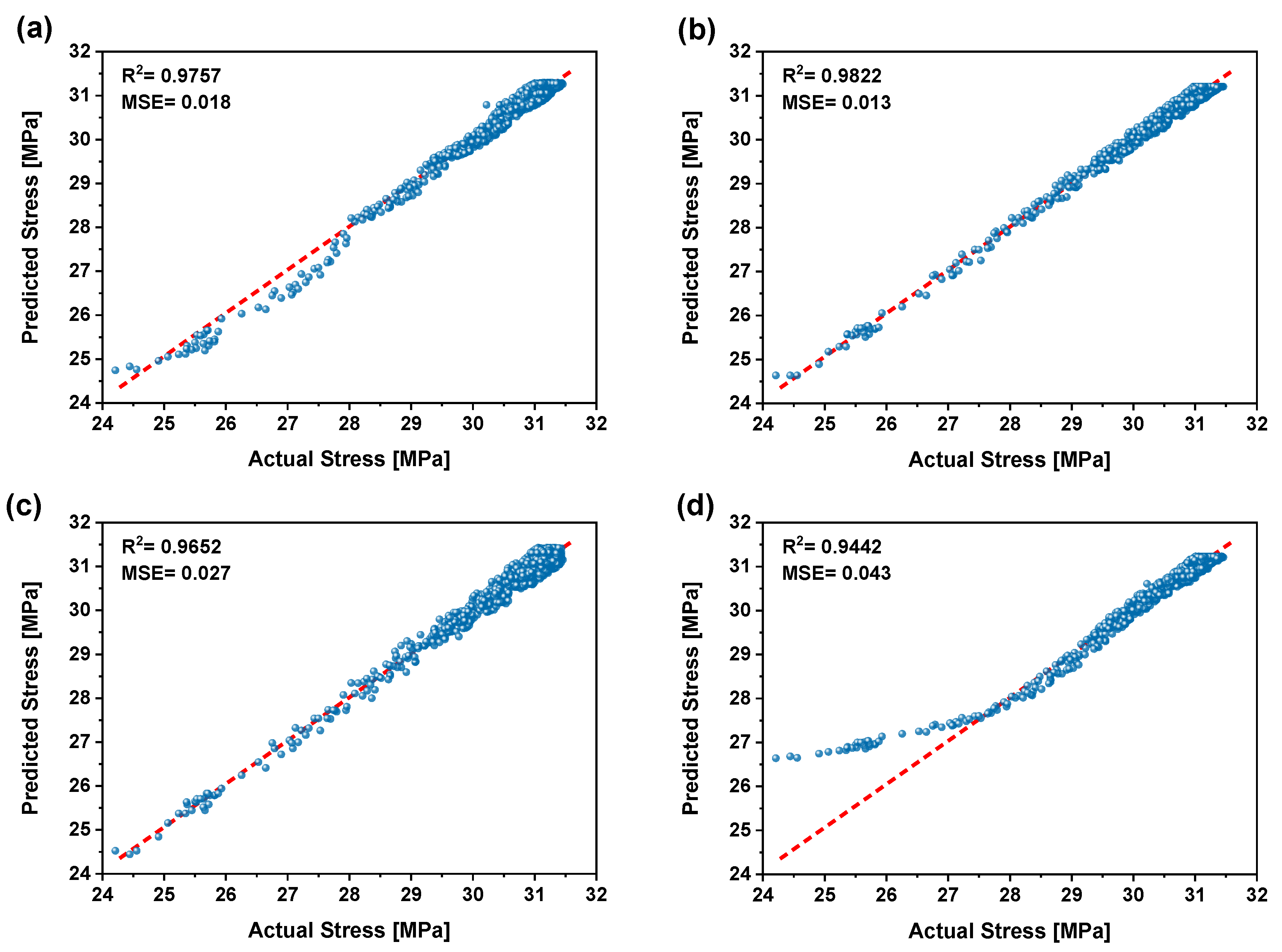
| ANN | 0.0189 | 0.1375 | 0.9757 | 0.9727 | 0.0025 | 0.6490 | 0.8056 | 0.9681 | 0.9575 | 0.012 |
| RFR | 0.0139 | 0.1179 | 0.9822 | 0.9801 | 0.0014 | 0.3792 | 0.6158 | 0.9813 | 0.9806 | 0.0010 |
| DT | 0.0271 | 0.1648 | 0.9652 | 0.9617 | 0.0034 | 0.6480 | 0.8050 | 0.9681 | 0.9659 | 0.0025 |
| SVR | 0.0435 | 0.2087 | 0.9442 | 0.9526 | 0.0063 | 0.4411 | 0.6641 | 0.9683 | 0.9671 | 0.0094 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benabderazag, K.; Guebailia, M.; Belouadah, Z.; Toubal, L.; Tachi, S.E. Machine Learning for Identifying Damage and Predicting Properties in 3D-Printed PLA/Lygeum Spartum Biocomposites. Fibers 2025, 13, 38. https://doi.org/10.3390/fib13040038
Benabderazag K, Guebailia M, Belouadah Z, Toubal L, Tachi SE. Machine Learning for Identifying Damage and Predicting Properties in 3D-Printed PLA/Lygeum Spartum Biocomposites. Fibers. 2025; 13(4):38. https://doi.org/10.3390/fib13040038
Chicago/Turabian StyleBenabderazag, Khalil, Moussa Guebailia, Zouheyr Belouadah, Lotfi Toubal, and Salah Eddine Tachi. 2025. "Machine Learning for Identifying Damage and Predicting Properties in 3D-Printed PLA/Lygeum Spartum Biocomposites" Fibers 13, no. 4: 38. https://doi.org/10.3390/fib13040038
APA StyleBenabderazag, K., Guebailia, M., Belouadah, Z., Toubal, L., & Tachi, S. E. (2025). Machine Learning for Identifying Damage and Predicting Properties in 3D-Printed PLA/Lygeum Spartum Biocomposites. Fibers, 13(4), 38. https://doi.org/10.3390/fib13040038






