The demand to understand the stability mechanism of laminated composite members has increased in the last few decades due to the growth in the use of composites in different industrial applications, such as aerospace, marine, automotive, and civil engineering. Composite materials have many advantages such as a high stiffness-to-weight ratio and high strength-to-weight ratio, as well as fatigue and corrosion resistance. Although a limited amount of research has focused on the buckling of anisotropic laminated composite columns, a significant number of studies have been conducted on the stability of composite shells, plates, and cylinders. Tarjan and Kollar [
1] developed an approximate solution to predict the buckling loads of axially loaded composite plates with elastic springs or stiffeners on all their edges. The buckling behavior of laminated composite rectangular plates with different cutout shapes was studied by Baba [
2], experimentally and numerically. Furthermore, Baba applied in-plane compressive loads to E-glass/Epoxy composite plates, and finite element buckling analysis was conducted using ANSYS software version 8.0 and verified against the experimental results. Based on the Hellinger–Reissner principle, Cortinez and Piovan [
3] developed a theoretical model to study the stability of composite thin-walled beams with shear deformability using a nonlinear displacement field. A finite element with fourteen degrees of freedom was used to solve the governing equations. Based on the results, shear flexibility had a significant effect on the stability of the composite beams. Depending on the unified three-degrees-of-freedom shear deformable beam theory, Aydogdu [
4] studied the buckling of cross-ply laminated beams with general boundary conditions using the Ritz method. The use of the shape functions satisfied the requirements for continuity conditions between symmetric cross-ply layers of the beams. The results were compared with previous works for various length-to-thickness ratios and various layups. Using the Ritz approach, Afsharmanesh et al. [
5] investigated the buckling and vibration of circular laminated composite plates resting on Winkle-type foundations under in-plane edge loading with various boundary conditions. The results were confirmed against finite element analysis and previous existing solutions. Kayat et al. [
6] studied the buckling of laminated composite cylindrical shells using the semi-analytical strip method under deformation-dependent pressure loading. Dong et al. [
7] developed an analytical solution to investigate the local buckling of infinite thin rectangular symmetrically laminated composite plates rested on Winkler foundations and under uniform in-plane shear loading. Their results were verified against finite element analysis yielding a good correspondence. Based on the response surface method and Monte Carlo approach, Schnabl et al. [
8] presented a model to study the buckling of two-layer composite columns with interlayer slip, random material properties, and loading parameters. Using the Rayleigh–Ritz method, Herencia et al. [
9] presented closed-form solutions for the buckling of long plates with flexural anisotropy of their simply supported short edges and various boundary conditions for their longitudinal edges under axial compression. The closed-form solution was expressed with respect to the minimum non-dimensional buckling coefficient and stiffness parameters. The results showed an excellent agreement with previous solutions and finite element analyses. Ovesy et al. [
10] studied the buckling of laminated composite plates with simply supported boundary conditions under uniaxial pure compression using a higher-order semi-analytical finite strip method based on Reddy’s higher-order plate theory. Matsunga [
11] investigated the free vibration and stability of angle-ply laminated composites and sandwich plates under thermal loading. Using two-dimensional global higher-order deformation theory, the following eigenvalue problem was expressed as follows:
where [
K] is the stiffness matrix, which includes the initial thermal stresses term, [
M] is the mass matrix, and {
U} is the generalized displacement vector. The main overarching advantages in all the studies discussed above are their advancements in the area of verified buckling solutions for laminated composite members, while the main shortcomings are the lack of treatments for generally anisotropic laminated layups.
Using the energy method and orthogonal polynomial sequences obtained by a Gram–Schmidt process, Pandey and Sherbourne [
12] presented a general formulation for the buckling of rectangular anisotropic symmetric angle-ply composite plates under linearly varying uniaxial compression loading with clamped and simply supported boundary conditions. Based on the energy approach, Rasheed and Yousif [
13] derived a closed-form buckling solution to investigate the stability of thin laminated orthotropic composite rings/long cylinders under external pressure. Timarci and Aydogdu [
14] studied the buckling of symmetric cross-ply square plates with various boundary conditions under uniaxial compression, biaxial compression, and compression–tension loading based on the unified five-degrees-of-freedom shear deformable plate theory. Their results were verified with existing work for various length-to-thickness ratios. Sun and Harik [
15] investigated the buckling of stiffened antisymmetric laminated composite plates with bending–extension coupling by extending the analytical strip method (ASM) proposed by Harik and Salamoun [
16] to analyze the bending of thin orthotropic and stiffened rectangular plates. Their results showed that plates with free boundary conditions contribute the weakest stiffening effects. Moreover, the number of layers of ply orientations equal to 0° and 90° had no effect on the critical buckling load since the coupling stiffness matrix vanished. The common advantage of the studies cited in this paragraph is their consideration of the effect of stiffness coupling on the buckling behavior of symmetric or antisymmetric laminates. Nevertheless, they all share the same shortcoming of not catering to generally anisotropic layups. In a recent study, Falkowicz [
17] examined the effect of ply orientation on improving post-buckling behavior under axial compression by investigating the extension–bending and extension–twisting coupling effects. Bisheh [
18] analytically computed the natural frequencies for the bending vibration of smart piezoelectric-coupled laminated composite plates reinforced with bamboo fibers.
These authors’ research group investigated a similar problem earlier with different classical boundary conditions [
19,
20,
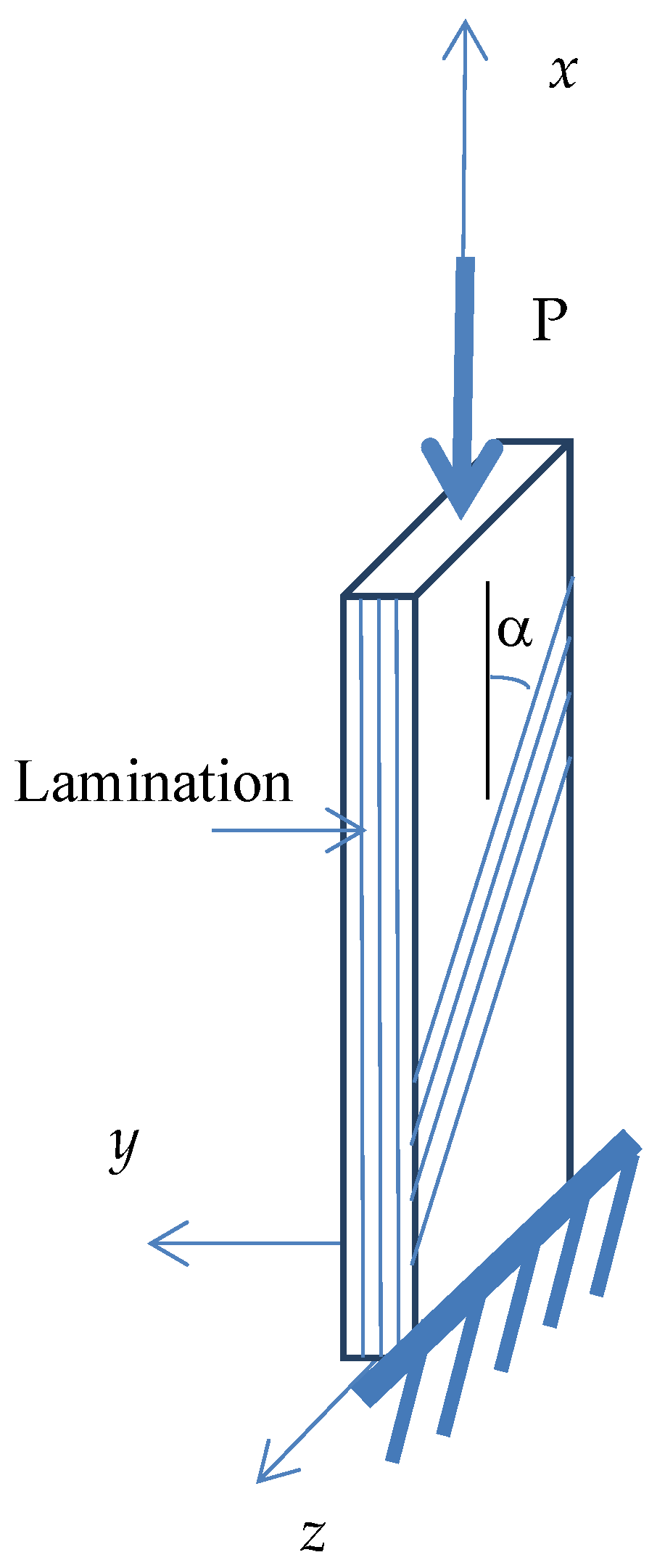
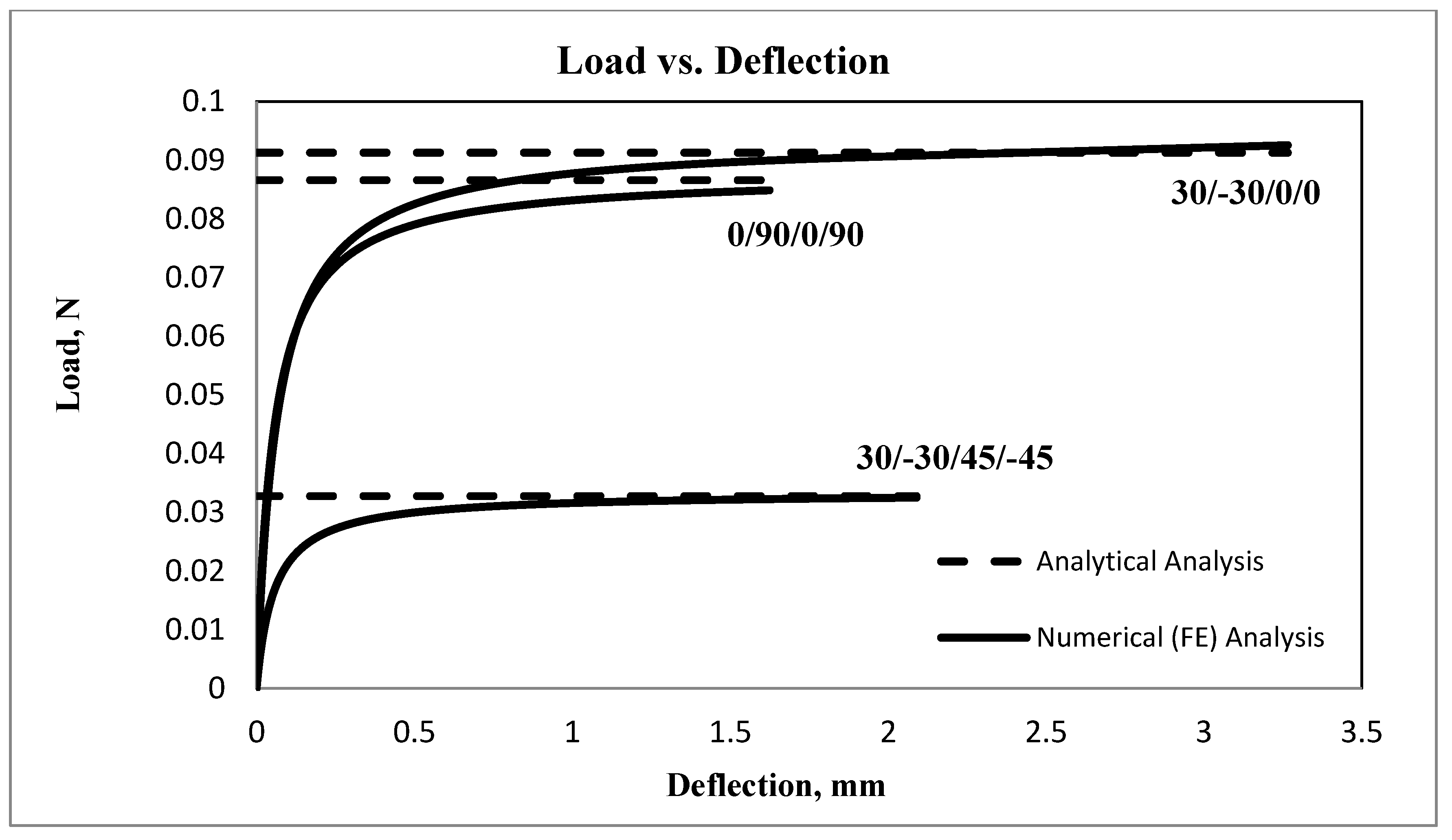
21]. Nevertheless, the fixed–free boundary condition remains to be investigated and reported for anisotropic laminated columns, which is the subject of this study. Accordingly, a closed-form buckling solution is presented for anisotropic laminated composite fixed–free columns under axial compression. The standard Rayleigh–Ritz approximation approach yielded an upper bound solution for the critical buckling load when compared to finite element analysis. A new buckling solution was developed using the critical stability matrix. The three-dimensional 6 × 6 composite stiffness matrix was converted to a one-dimensional 2 × 2 axial, coupling, and flexural rigidity matrix using the static condensation method. Furthermore, the analytical results were verified against finite element analysis using the commercial software Abaqus 2016 yielding a close agreement between the results.