Abstract
This study presents a finite element analysis (FEA)-based numerical homogenization method for evaluating the effective thermo-mechanical properties of a large-area additively manufactured particulate-filled composite using realistic periodic representative volume elements (RVEs) generated from reconstructed X-ray µ-CT image scans of a 3D-printed bead. The numerical results of the predicted effective properties, including the elastic stiffness, coefficient of thermal expansion (CTE) and thermal conductivity, were benchmarked with the Mori–Tanaka–Benveniste analytical estimates, which were found to be comparable. Initial sensitivity analysis using a single region of interest (ROI) extracted from the bead’s volume was performed to determine a suitable RVE size. The impact of inherent micro-porosities on the resulting composite material’s behavior was also quantified in the current investigation and was shown to reduce the composite’s effective properties. Using a suitable RVE size, the effect of anisotropy due to spatial variation in the microstructure across the bead specimen on the computed composite’s effective properties was also assessed. The results show that the regions closer to the exposed surface of the print bead with highly aligned and densely packed fiber particulates have superior properties as compared to inner regions with a more randomly oriented and less densely packed fibrous microstructure.
1. Introduction
Large-scale additive manufacturing is a growing technology with applications ranging from rapid prototyping to the fabrication of load-bearing components. For improved performance of manufactured components, the pelletized polymer feedstock is commonly reinforced with short carbon fiber fillers to improve the mechanical properties of the final part. Studies on the trend and development of AM-manufactured short fiber-reinforced polymer (SFRP) composites can be found in [1,2,3].
The performance of a randomly dispersed SFRP composite depends on its inherent microstructural characteristics, such as the concentration, orientation and length distribution of the fiber reinforcement, the content, distribution and morphology of the inherent micro-voids, the fiber–matrix inter-layer adhesion, etc. [4]. In addition, spatial variation in the heterogenous microstructure results in intrinsic anisotropic macroscopic behavior of the composite material. Material property prediction of randomly dispersed and randomly oriented SFRP composites becomes more complicated with increased non-uniformity and anisotropy across the heterogenous composite microstructure, particularly when micro-voids are present.
Several computational micro-mechanics techniques for estimating the effective thermo-elastic properties of SFRPs have been presented, offering an alternative to experimental characterization; they include analytical mean-field homogenization techniques, numerical modeling methods and statistical continuum mechanics methods [5]. Existing analytical methods involve a two (2)-step homogenization approach for thermo-elastic property prediction of a randomly oriented SFRP composite which includes (a) determination of effective properties for the pseudo-grains of a decomposed representative volume element (RVE) structure based on available analytical mean-field models and (b) averaging the predicted RVE properties over fiber orientation and length distribution using, for example, the Voight or Reuss models [6,7]. Existing definitions of the RVE concept by previous researchers can be found in [8]. Numerous classical analytical micro-mechanics models for predicting material properties of a unidirectional SFRP composite with uniformly distributed fibers currently exist and have varying degrees of accuracy [4,9,10,11,12,13,14,15]. These include models based on variational or energy principles [9,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32], the family of Eshelby’s equivalent inclusion-based models [33,34,35,36,37,38,39,40,41,42,43,44], semi-empirical models [43,45,46,47,48,49,50,51,52,53,54,55], mechanics-based models [4,56], etc. Traditionally, most mean-field theories used in the first homogenization step, such as the Mori–Tanaka–Benveniste formulations, are limited to only two-phase composites. For multiphase heterogenous composites, common homogenization techniques include the direct Voight averaging method and the multi-step and (or) multi-level homogenization schemes [57,58]. Extension of the Mori–Tanaka model for multiphase composites has been shown to seldom violate the Hashin–Shtrikman and Hill–Hashin effective stiffness bounds [59]. While theoretical asymptotic formulations are orders of magnitude faster and less computationally intensive than other computational micro-mechanics techniques, their accuracy is reduced. This has been shown to occur more often when there is interaction between inclusions or when estimating the microscopic stresses associated with the particulates, especially when analyzing composites with sharp phase property contrast or a high inclusion aspect ratio and volume fraction [5,60,61]. Moreover, asymptotic methods lack the capability to accurately model the geometric peculiarities of inclusions such as irregularities in a particle’s morphology and characteristics and spatial variations in the distribution of microstructural features across the RVE, which are typically found in actual SFRP composites [62]. Of the various existing fiber orientation averaging schemes of effective material properties for SFRP composites summarized in various studies [63,64,65], the method of Advani and Tucker [6,66] is perhaps the most widely used.
With growing computational capabilities, numerical boundary value problem (BVP) full-field methods, mainly finite element analysis (FEA)-based homogenization methods, have emerged for computing effective properties of SFRP composites. FEA-based methods provide a high level of accuracy and the ability to model complex microstructural geometric details associated with inclusions including both fibers and micro-voids. Existing studies on numerical homogenization methods for property prediction of random SFRP composites are predominantly based on computer-generated deterministic RVE volumes stochastically filled with particulates [66,67,68,69,70,71,72] and can yield results that are in good agreement with results obtained from analytical-based methods [5,73,74,75]. These studies have shown that numerical-based methods prevail in terms of accuracy over analytical-based methods when predicting properties of composites that have inclusions with a high aspect ratio and high volume fraction [74,76]. Continuum mechanics techniques based on statistical correlation methods have been shown to perform poorly for elastic property prediction of composites with non-spherical-shaped inclusions. In addition, the required number of realizations and the desired precision in predicting properties of heterogenous SFRP composites have been shown to depend on several factors, including the microstructural composition and concentrations, the microconstituents’ phase property contrasts, the morphology, characteristics and dispersion of inclusion phases and the evaluated quantity of interest [66,69,76,77]. More recently, detailed microstructural characterization has become possible with advancements in modern imaging techniques. Reconstruction of 3D-voxelated grayscale radiographs obtained from the X-ray micro-computed tomography (µCT) imaging technique has been used to characterize the microstructure of SFRP composites [44,62,78,79] and to generate realistic RVEs, i.e., RVEs defined directly from a µCT measurement of the internal microstructure, for micro-mechanical analysis. For example, Guven et al. [62] generated realistic or sample-specific RVEs of various sizes from 3D X-ray µ-CT voxelated images to numerically evaluate the effective material properties of a two-phase particulate-filled polymer composite which was shown to be in close agreement with experimentally measured properties. Although their study was based on a two-phase SFRP composite, their approach has been successfully extended to study the influence of micro-porosities and particulate inhomogeneities on predicted effective properties of multiphase particulate composites [57,80]. While extensive studies that numerically assess the influence of porosity on effective properties of SFRP composites using deterministic RVEs have been performed [57,60], to the best of the authors’ knowledge, no known studies that incorporate porosity in the calculation of effective properties of SFRP composites utilizing sample-specific RVEs currently exist. Realistic RVEs were used to evaluate a nickel-reinforced alumina composite with spherical-shaped nickel particle reinforcement [80]; however, this differs from typical AM-manufactured SFRP composite microstructures, which include cylindrical-shaped fibers with a high aspect ratio and often contain micro-voids.
This paper evaluates the effective thermo-mechanical properties of a 13% carbon fiber-filled ABS (13% CF-ABS) SFRP composite manufactured using large-area additive manufacturing (LAAM) technology and assesses the influence of micro-voids on its computed effective properties. A finite element-based numerical homogenization approach is employed using realistic RVEs developed from sample-specific, reconstructed 3D X-Ray µ-CT voxelated grayscale images of the composite print beads. Microstructural characterization of the printed bead specimen based on binary segmentation of the 3D grayscale voxelated data is performed to identify unique phases and microstructural features within the sample. Finite element analysis is performed with models derived from specimen-specific RVEs to compute effective thermo-mechanical properties over the bead cross-section. To ensure domain continuity across RVE boundaries, periodic constraints are imposed on opposing boundary entities, which ensure effective transfer of load across boundary surfaces. The effective elastic stiffness is derived from the resulting homogenized macro-stresses and macro-strains and for different load cases through a least squares linear regression fitting algorithm. In addition, effective CTEs are computed using a procedure similar to that appearing in Wang Z. [81]. Further, effective TCs are computed from homogenized heat flux and temperature gradient obtained from steady-state heat transfer FE analysis based on Fourier’s law. Results of the effective properties obtained from solutions to the numerical based homogenization scheme are compared to results derived from the analytical mean-field homogenization approach based on the Mori–Tanaka–Benveniste formulation. Although studies have shown that effective properties of SFRP composites computed from the analytical MT method may deviate from numerical results, especially with increasing fiber aspect ratios and phase property contrasts [2,60], MT results are presented here to show that our computed numerical values agree reasonably well with what is to be expected. The effects of porosity (i.e., presence of micro-voids) on the effective properties are also quantified. Additionally, a correlation study between the effective thermo-mechanical properties and microstructural properties across regions of the LAAM-printed bead specimen is used to gain an overall understanding of the effect of anisotropy on the resulting effective properties.
2. Materials and Methods
2.1. CF/ABS Composite Bead Specimen and Isotropic Material Properties
In the current study, the effective properties of four (4) regions of interest (ROIs) across the 13% CF/ABS bead specimen shown in Figure 1 are evaluated. These include (a) ROI-I, adjacent to the print bed; (b) ROI-II, near the bead’s center; (c) ROI-III, along the outer edge of the bead; and (d) ROI-IV, adjacent to the top surface of the bead. The dimensions of each ROI are . The CF/ABS bead was printed using a Strangpresse Model 19 single-screw extruder (Strangpresse, Youngstown, OH, USA) on a custom LAAM system at Baylor University. More details on the LAAM printing parameters and operating conditions can be found in [82].

Figure 1.
Regions of interest (ROI, I–IV) of the CF/ABS specimen from a polymer composite bead manufactured using Baylor’s LAAM system. ( and are coordinate directions normal to the print direction , and the red dot dashed line indicates a plane of half-symmetry plane in the direction).
The isotropic properties of the microconstituents of the 13% CF-ABS SFRP composite used in the homogenization analysis appearing in Table 1 are taken from [83], which assumes that the fiber and matrix materials are isotropic. The constituent properties shown are for a Tourayaca® T300 (Touray Industries, Tokyo, Japan) PAN-based carbon fiber and Lustran ® 433 ABS (INEOS Olefins & Polymers, London, UK) for the ABS polymer matrix. In Table 1, E is the elastic modulus, ν is the Poisson’s ratio, κ is the thermal conductivity, is the density and is the specific heat capacity.

Table 1.
Isotropic properties of the microconstituents of the 13% CF-ABS composite material.
2.2. Numerical FE Homogenization Method
FEA models of different RVEs were generated from reconstructed 3D X-ray -CT voxel-based radiographs of each of the ROIs in Figure 1 and Figure 2a. Binary segmentation of each ROI volume into the three (3) microstructural constituents (matrix, fiber and voids) was achieved via grayscale data thresholding, with detailed procedures provided in [82]. Sufficient image resolution to accurately capture the microstructural features was performed using a voxel cube with a side length of 1.4 μm, yielding a total of 250 voxels per length or 15,625,000 voxels per ROI. The FEA models for the elasticity analyses were generated directly using the scripting interface of Abaqus/Standard (Abaqus 2023, Simulia, Dassault Systemes, Waltham, MA, USA), where each voxel within the RVE is represented as a 3D solid 8-node fully integrated iso-parametric continuum brick element (C3D8) where typical morphology normalization methods are not employed. A separate element set is created for each segmented microstructural constituent. For the heat transfer analysis, diffusive-C3D8 elements (i.e., DC3D8) are employed instead based on the same mesh as that for the elasticity analysis. Relevant material property definitions for the individual microstructural phases are also created and assigned to their respective material sections through the section assignment input syntax. Figure 2a,b shows a sample RVE block extracted from ROI-II (cf. Figure 1) which highlights the three microstructural phases, including fibers (gray), micro-voids (red) and the ABS matrix (transparent volume). Figure 2c shows the resulting FEA model created from directly importing the segmented voxelated data which illustrates the three microstructural phases appearing on the outer RVE surfaces. Figure 2d–f show the individual element sets of each of the microstructural phases, including the ABS matrix (cf. Figure 2d), the inherent micro-voids (cf. Figure 2e) and the fiber reinforcements (Figure 2f). Although the stepped-like surface of micro-features within the RVE generated with voxel data is likely to induce stress concentrations, Guven et al. [62] has shown that the impact on the evaluated effective properties for small displacement analysis is only minimal.
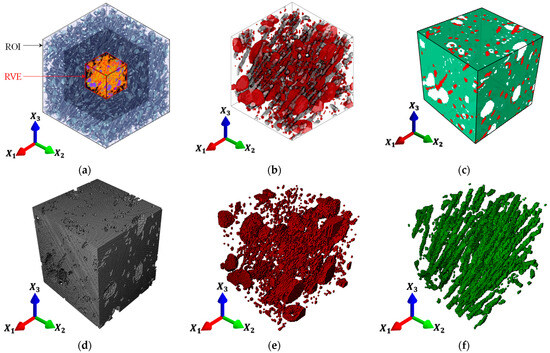
Figure 2.
(a) Reconstructed 3D scans of ROI-II highlighting mid-block RVE volume; (b) magnified view of mid-block RVE showing segmented micro-constituents; (c) FEA model imported from voxel data of the RVE; (d) ABS matrix FEA elements; (e) micro-void FEA elements; and (f) fiber reinforcement FEA elements.
This study compares results for three RVE sizes, using ROI-II as a case study. The smallest sized RVE (RVE-I) has a cube side length of 70 µm, with 125,000 elements and 125 RVE realizations (cf. Figure 3a) within ROI-II, while the mid-sized RVE (RVE-II) has a side length of 116.2 µm, with 571,787 elements and 27 RVE realizations (cf. Figure 3b) within ROI-II. The largest RVE (RVE-III) has a side length of 175 µm, with a total of 1,953,125 elements and 8 RVE realizations within ROI-II (cf. Figure 3c). With the foregoing RVE classification, a numbering scheme for identifying a particular realization Z, belonging to RVE type Y within ROI volume X, is defined as ROI-X, RVE-Y, #Z. Complete adhesion between the filler and matrix constituents is assumed. In all cases, the element side length equals a voxel cube length of , which is one-fifth the average fiber diameter of .
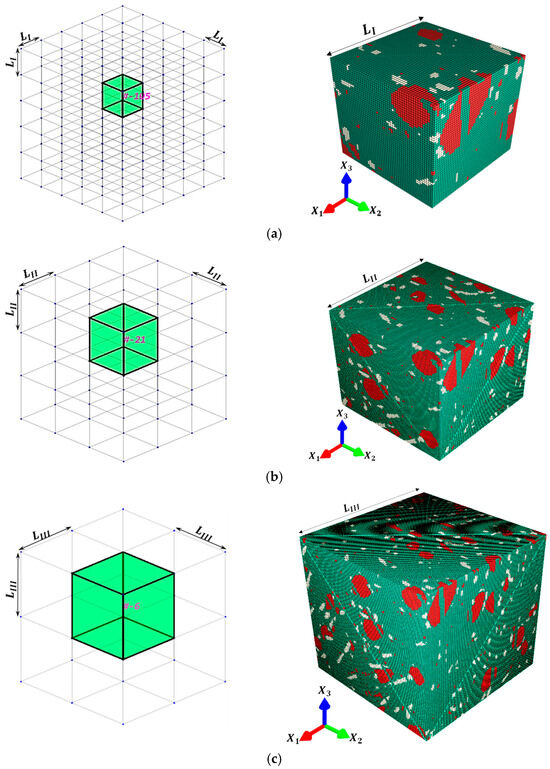
Figure 3.
ROI-II partitioning into (a) RVE—I: 125 realizations with 125,000 elements per realization with ; (b) RVE—II: 27 realizations with 571,787 elements per realization with ; (c) RVE—III: 8 realizations with 1,953,125 elements per realization with .
Periodic boundary conditions (PBCs) on the cubic RVE’s outer surfaces are defined according to the formulations in [84,85,86] for stress and thermal RVE simulations as
where is the component of displacement and is the temperature, both applied on the directional identifier on opposing entities of the periodic structure including faces , edges and vertices . is the Kronecker delta and is the Levi-Civita permutation tensor. Quantity is the average macro-strain tensor over the periodic RVE. is the projection of the dimension of the RVE along the direction, and for our orthogonal shaped RVE, (cf. Figure 4). Indices identify the Cartesian degrees of freedom and in Equation (2). The PBC multi-point constraints (MPCs) on opposing entities are defined in the model via the Abaqus equation input syntax. To avoid redundancy, edges and vertices are excluded from the facet node set definitions, and vertices are excluded from the edge node set definitions. The prescribed macro-strains or temperature gradient are imposed through an extra set of dummy nodes that are coupled to degree-of-freedom-MPC nodes on opposing PBC entities with a respective displacement or temperature magnitude equal to the RHS value of the constraint equation.
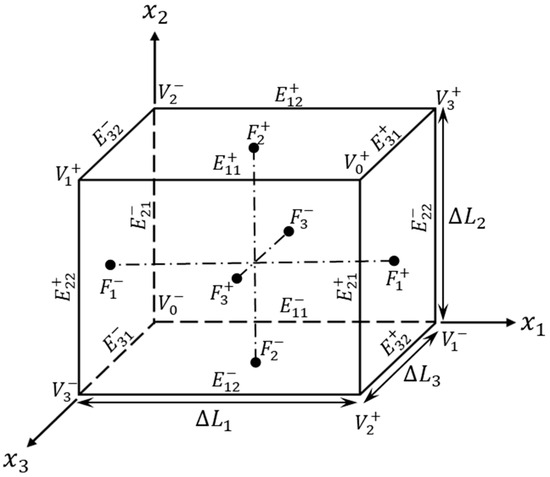
Figure 4.
Single periodic RVE structure showing definitions of entities and coordinate directions used in the PBC formulations (Equations (1)–(3)).
Although we have enforced periodic constraints on an RVE structure that is strictly non-geometrically periodic, similar studies from the literature [43,62,66,80] have shown that utilization of PBCs for effective property prediction for this type of analysis yields the most accurate results compared to other boundary conditions like static and kinematic uniform boundary conditions (SUBCs and KUBCs).
2.2.1. Effective Elastic Engineering Constants—A Numerical Approach
For the stress analysis, six load cases are employed, with permutation indices , which are applied through the displacement PBC equations (cf. Equations (1)–(3)). For load case , the applied strain may be written as
where is the magnitude of the imposed strain and repeated indices do not imply summation. A value of is assumed in all elasticity analyses. The homogenized equivalent macro-stresses and macro-strains of the heterogenous RVE volume are evaluated through volume averaging, satisfying the Hill–Mandel condition of equivalent strain energy [87,88] between the idealized homogenized volume with macro-stress and macro-strain and heterogenous volume with stress and strain (both a function of material point within the domain of the RVE), given as
where the equivalent macro-stresses and macro-strains in Equation (5) are given as
The effective elastic constant tensor is obtained from the homogenized quantities according to the constitutive relation
which is conveniently written in contracted notation as
where is a linear indices transformation functions given as
The material constant is computed from a least squares linear regression fitting algorithm that minimizes the relative error in the components of the stress tensor of Equation (8). Let the th component of the stress and strain tensors for the th load case be denoted as and , respectively; A tensor is defined such that and the block diagonal matrices and , respectively, as
The material constant is then computed from the linear algebraic expression given as
For simplicity, the expression of Equation (11) can represented in the reduced order form as
The linear index transformation functions that appear in Equation (12) are given as
The reduced order tensor is a 36 × 36 matrix and the tensors and are 36 × 1 vectors. Depending on the requirements of material property behavior desired from the least squares fitting of the elastic constant , such as matrix and material symmetry, orthogonality, isotropy, etc., constraints that define linear relationships between components are imposed with the constraint matrix through the linear relation
In the current study, only two material requirements are needed for a complete definition of the constraint matrix , which include the condition of matrix symmetry and material orthogonality defined through sets of linear equation constraint submatrices and , respectively, such that
The necessary condition of matrix symmetry requires 15 essential constraints, and thus, is a 15 × 36 sized submatrix such that
where the linear indices transformation functions are given as
Further conditions for material orthotropy with three orthogonal planes of symmetry require the definition of 12 additional constraints that set the shear–extension (9) and biplanar shear–shear (3) coupling terms of the elastic constants to zero, i.e.,
The constraint submatrix is thus a 12 × 36 matrix given as
The linear indices transformation functions that appear in Equation (19) are given as
A Lagrange multiplier method is used to combine the constitutive relation of Equation (12) and the constraint equations in Equation (14) to obtain the linear algebraic systems of the equation, given as [81]
where is the vector of the Lagrange multipliers with one component for each imposed constraint. The accuracy of the regression fit is assessed by the coefficient of determination for each load case given as,
where
The computed solution of transformed to the 6 × 6 matrix from and inverted yields the effective compliance matrix , from which the 9 independent engineering constants are derived according to
2.2.2. Effective Coefficient of Thermal Expansion—A Numerical Approach
The evaluation of the effective CTE in our approach is based on the Duhamel–Neumann law [89,90], where the fundamental constitutive expression that relates the effective stress to the effective total strain for a structure subjected to temperature change is given as
where is the effective elastic stiffness tensor of the homogenized material and is the effective CTE tensor. In contracted notation, Equation (25) becomes
A temperature change of °C is assumed for the thermal expansion analysis. In evaluating the effective CTE, the total strain in the sets of defined PBC constraints in Equations (1)–(3) above is set to zero, giving . Equation (26) reduces to
From the results of the homogenized equivalent macro-stresses derived from the thermal expansion analysis based on an applied temperature difference over the entire RVE volume, the effective CTE can be computed by rearranging Equation (27) above as
2.2.3. Effective Thermal Conductivity—A Numerical Approach
A heat transfer analysis is performed on the RVE to compute the effective thermal conductivity using three thermal load cases with permutation indices ( applied through the temperature PBC constraints in Equations (1)–(3). These thermal loads are defined to produce orthogonal temperature gradients, such that for case
where is the magnitude of the imposed temperature difference across the RVE in the direction. A value of °C is assumed for the heat transfer analyses. The general heat conduction energy conservation equation, assuming a steady state with no internal heat generation at an arbitrary material point within the RVE volume, is given as
where is the gradient operator vector, is the thermal conductivity of the material and is the temperature, with all quantities being evaluated at specified material point within the RVE volume. From Fourier’s law of steady-state heat conduction, the heat flux at any material point within the conducting medium is
Integrating Equation (30) over domain , applying the Gauss divergence theorem and making appropriate substitution for the heat flux from Equation (31) yields
The Hill–Mandel condition of equivalent thermal dissipation between the assumed homogenous and heterogenous regions yields [60]
Applying the same macrohomogeneity principle as with the elasticity solution in Section 2.2.1, the spatial averages of local heat flux and temperature gradient are obtained and given as [43,77,91]
The effective TC tensor of the RVE volume is obtained from Fourier’s law of steady heat conduction, given as
For simplicity, let the th component of the equivalent homogenized heat flux vector and temperature gradient for the th load case be denoted as and , respectively, such that Equation (35) can be rewritten as
Rearranging Equation (36) yields the effective ETC tensor , given as
2.3. Analytical Mean-Field Homogenization Method
Analytical methods for computing the thermal–elastic properties of discontinuous fiber-reinforced composites with suspended fibers of random orientation first appeared in Advani and Tucker’s [6,66] two-step micro-mechanics homogenization evaluations. In their approach, the first step computes the average properties of decomposed pseudo-grains with unidirectional, uniform-length fibers using mean-field theory (see, e.g., [9]) or numerical FE analysis, and the second step performs an orientation and/or a fiber length averaging of the aggregates using either Voight’s or Reuss’ assumption. This widely accepted approach for computing elastic material properties from orientation tensor data accounts for randomly dispersed, spatially varying fiber orientation and length distributions in the heterogenous macro-scale volume of fiber-filled polymer composites. The following section presents the Mori–Tanaka–Benveniste analytical mean field homogenization approach to computing effective material properties, i.e., components of the 4th-order elastic stiffness tensor , the 2nd-order coefficient of thermal expansion (CTE) and the 2nd-order thermal conductivity tensor .
2.3.1. Effective Elastic Engineering Constants—An Analytical Approach
Various empirical micro-mechanics models have been developed to predict the elastic properties of unidirectionally aligned discontinuous short fiber-reinforced polymer composite such as those briefly discussed above and summarized in [9]. One such model which is used to validate results from our numerical calculations are Eshelby-based Mori–Tanaka formulations for calculating the effective composite moduli. The general equation for the mean-field homogenized composite stiffness is given as
where and are the isotropic matrix and particulate (either fiber or void) stiffness tensors, respectively. The particle’s strain concentration tensor , according to the Mori–Tanaka model, corresponds to the Hashin–Shtrikman–Willis lower bounds solution for the stiffness tensor, computed as
where is the Eshelby elasticity tensor appearing in Appendix A. The micro-void inclusions are assumed to be spherical-shaped, with unity aspect ratio. Length averaging of the stiffness tensor is first performed using the length distribution of the inclusions within the composite as
where is the weight fraction of the pseudo-grain of an inclusion phase with average aspect ratio . Subsequently, the orientation average of the fourth-order transversely isotropic elastic stiffness tensor is computed using the fourth-order fiber orientation averaging scheme [6]:
where is the 4th-order orientation tensor of an inclusion phase computed using any of the suitable closure approximations detailed in [6,66,92], and , are invariants of the unidirectional transversely isotropic elasticity tensor (written in contracted notation):
The elastic engineering constants are computed from the orthotropic stiffness matrix of the contracted form of Equation (41) based on Equation (24).
2.3.2. Effective Coefficient of Thermal Expansion—An Analytical Approach
Similar to the approach presented above for the analytical elastic stiffness prediction, a two-step homogenization approach is employed to analytically evaluate the effective CTE tensor for the discontinuous fiber-reinforced polymer composite with voids considered in this work. The analytical orientation-averaged effective CTE tensor for a discontinuous fiber-reinforced composite with randomly oriented cylindrical fiber inclusions may be computed from [6,85,86]
and is given in Equation (42). The orientation average for tensor product may be calculated using the second-order orientation averaging scheme from Advani & Tucker [6,66], given as
where and are, respectively, the invariants of the tensor product obtained from the double contraction of the transversely isotropic elasticity tensor and CTE tensor for a unidirectional discontinuous fiber composite given as
For consistency, the Mori–Tanaka–Benveniste equation is used for estimating the tensor product of the unidirectional short fiber-reinforced polymer composite with isotropic constituents, given as [37,38,39,40,41]
Terms given here appear in Section 2.3.1. Length averaging of the tensor product is performed prior to orientation averaging on the right-hand side of Equation (44) according to
2.3.3. Effective Thermal Conductivity—An Analytical Approach
The Mori–Tanaka model presented above for predicting the homogenized 4th-order elasticity tensor for the unidirectional particulate composite has been extended [42,43,44] to estimate other 2nd-order tensor properties of the composite material, including the thermal conductivity tensor. The resulting expression for evaluating the composite’s thermal conductivity tensor is as
where and are the isotropic matrix and particulate (either fiber or void) thermal conductivity tensors. The intensity–concentration tensor that couples the mean temperature gradients between the particulate inclusions and the isotropic matrix corresponds to the lower bound solution based on Hashin–Shtrikman–Willis single variational principle and is computed as
In Equations (48) and (49) above, is Eshelby’s thermal conductance tensor with only non-zero diagonal components, which for spheroidal inclusions is given as
In our calculations, the void particles are assumed to be spherical-shaped for simplicity. In this case, Eshelby’s tensor is simply one-third the identity tensor, i.e., . Similar to the procedure adopted in elasticity stiffness tensor homogenization, length averaging of the computed transversely isotropic thermal conductivity tensor using the length distribution of the fiber inclusion phase within the SFRP composite is performed on a weight-based averaging scheme according to
The invariants of , i.e., , are computed in the usual manner as
Subsequently, the second-order orientation-averaged thermal conductivity tensor for the misaligned fiber-reinforced composite is calculated as [6,44]
2.3.4. Density and Specific Heat Estimation
The average density and specific heat capacity for the composite material are also computed here using the basic rule of mixture equation, since these scalar quantities do not depend on the distribution of fiber orientation or fiber length within the RVE. The average density for p particulate phases is given as
where and are the matrix and particulate (either fiber or void) isotropic density. Likewise, the average specific heat capacity for p particulate phases is given as
where and are the matrix and particulate (fiber and void) isotropic specific heat capacity values.
2.4. Magnitude of the Effective Quantities
The magnitude of the effective quantities is used here to define equivalent isotropic properties of the RVE for the elastic modulus, the CTE and the TC. This provides a convenient means for quantifying the dispersion in the effective quantity and for comparing the numerical FE results with the analytical MT estimates. The effective elastic modulus magnitude and effective Poisson ratio magnitude are given as [93]
where is the apparent effective bulk modulus, defined as the average between the Voight upper and Reuss lower first-order bounds on the bulk modulus and is given as
The effective shear modulus magnitude is obtained from the average of the Voight upper and Reuss lower first-order bounds on the shear modulus and is given as
Likewise, the apparent effective CTE magnitude is computed from Hill’s average of the Voight lower bound and Reuss upper bound values of the CTE tensor [94]. i.e.,
where summation convention is implied. The apparent effective TC magnitude is given as [60,66]
3. Results and Discussion
The results of the thermo-mechanical properties, including the engineering constants, effective CTE and TC obtained from both numerical and analytical homogenization approaches, are presented in this section. The influence of the inherent microstructural porosity on the resulting thermo-mechanical properties is also evaluated, and a quantitative assessment of the macroscale property anisotropy due to spatial variation in microstructural configurations across various ROIs is presented. The measure of dispersion in the computed effective properties for each ROI is quantified using the coefficient of variation statistical parameter, given as
where assesses the ability of selected RVE size in representing the ROI volume. The parameters and are, respectively, the standard deviation and mean value of the reported effective quantity from the different RVEs of the ROI volume. Minimization of the value is desirable when determining a suitable RVE size in accurately predicting a composite property . From this point onward, the effective composite properties are reported in their normalized form with respect to the equivalent properties of the isotropic matrix phase and are distinguished from actual dimensional quantities by an overbar accent, i.e., .
3.1. Thermo-Mechanical Property Estimates for ROI-II
The first set of results presented here are solutions obtained for the three RVE sizes within ROI-II appearing in Figure 3, based on the numerical FE homogenization method presented in Section 2.2. Numerically computed quantities are compared to the results obtained from corresponding analytical solutions from Section 2.3. The effect of the inherent micro-voids on the resulting effective thermo-mechanical properties is also quantified. Average microstructural properties of ROI–II follow from results provided in [82] and include the fiber volume fraction , the void volume fraction and the region-averaged second-order fiber orientation tensor , given as [82]
From the region averaged orientation , higher fiber alignment was observed in the print direction (-direction), with less fiber alignment in the -direction parallel to the build surface. The distribution of the fiber aspect ratio for the ROI-II region appears in Figure 5, where it is fitted to a Weibull function with a shape parameter and a scale parameter . The weighted average aspect ratio for this region is . The average fiber aspect ratio is limited by the ROI envelope, which may under-represent the specimen’s true mean aspect ratio. Partitioning of the ROI into several RVE realizations further limits the average fiber aspect ratio. The mean fiber aspect ratio and fiber aspect ratio coefficient of variation from all realizations (cf. Section 2.2) of each RVE size (RVE-I, RVE-II and RVE-III) from ROI-II are presented in Table 2. These microstructural characteristics for ROI-II are used to compute the thermo-mechanical properties of the region.
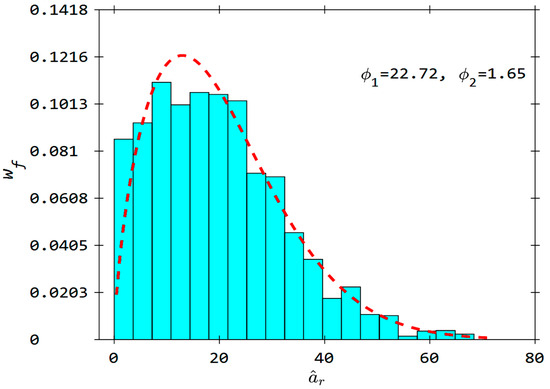
Figure 5.
Fiber aspect ratio distribution extracted for ROI-II. (red dashed line represents the fitted Weibull distribution function curve).

Table 2.
Mean fiber aspect ratio and fiber length coefficient of variation from all realizations of RVE-I, RVE-II and RVE-III from ROI-II.
3.2. Effective Elastic Stiffness and Engineering Constants for ROI-II
Typical displacement contours of the single RVE-II, instance #14 extracted from partitioning of ROI-II, as shown in Figure 3, appear in Figure 6a–c. In this example, the RVE is subjected to tensile and shear loading corresponding to a total of six load cases, as described in Section 2.2.1. The loads are prescribed on the bounding entities of the RVE through periodic boundary conditions, as described in Section 2.2. The single-step static stress analysis considers the effect of all three microstructural constituents, including the ABS matrix, fiber and micro-void inclusion (cf. Figure 2), on the stiffness behavior of the RVE using the micro-constituents’ material properties presented in Table 1. The homogenized stresses and strains obtained from the six different load cases are used to compute the effective stiffness using procedures detailed in Section 2.2.1. Figure 6a,b show the uneven displacement on opposing faces of the RVE in response to the tensile loading, which is due to the anisotropy introduced by the non-uniform spatial and orientation distribution of the fiber and void inclusions within the RVE. Additionally, the distinct features of the inherent microstructure are reflected by the local deformations (undulations) on the boundaries of the RVE (cf. Figure 6).
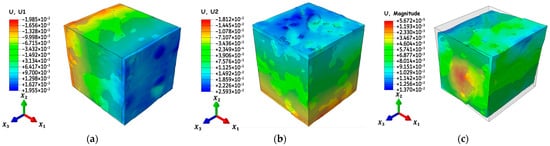
Figure 6.
Isometric view of the deformation contours of RVE-II, #14 from ROI-II, overlayed over the undeformed volume under different loading values: (a) tensile response in -direction; (b) tensile response in -direction; (c) shear response in -plane.
Figure 7a–c presents contours of displacement magnitude on opposing bounding faces of the RVE in the direction of the applied load for the and tensile deformations and the – shear deformation load cases, which verifies the correct implementation of the periodic constraints on the boundaries of the RVE. This is evident from similar topographical features on opposing bounding faces of the RVE, as shown in Figure 7. The periodic constraints enforce domain continuity without overlapping or separation among neighboring RVE boundaries, which ensures the effective transfer of loads between adjacent RVE boundaries.
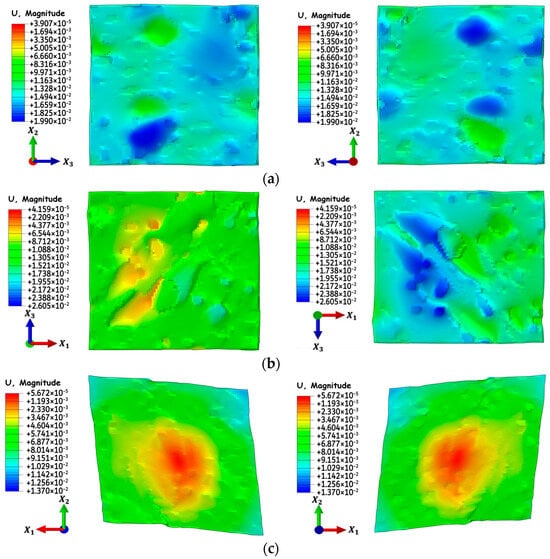
Figure 7.
Deformation contours of RVE-II, #14 from ROI-II, showing the topography of opposing bounding face pairs to validate the implementation of PBC for loading in the (a) -direction, (b) -direction and (c) -plane. The images show RVE bounding faces in the negative (left column) and positive (right column) direction (or normal in case of shear) to the direction of the applied loading.
The homogenized stresses and strains from the six (6) different load cases are used to compute the effective stiffness and compliance of the RVE volume, as described in Section 2.2.1, which appear in Table 3 and Table 4. The results are presented for both (a) a non-porous microstructure without considering micro-void inclusions (i.e., the micro-void constituent properties are replaced by ABS properties) and (b) a porous microstructure considering the micro-void inclusions. Table 3 below provides the computed mean elastic stiffness derived from the orthotropic regression fitting procedure in Section 2.2.1 for the complete sets of 27 RVE-II realizations of ROI-II (cf. Figure 3b), which are compared to the Mori–Tanaka mean-field estimate using the length distribution in Figure 5 and the region-averaged orientation tensor of ROI-II appearing in Equation (62). The values in Table 3 show a good agreement between the results obtained from our computational approach and those from the related analytical method. The results of the stiffness tensor in Table 3 and elastic moduli in Table 4 show that the 13% CF/ABS bead RVE specimen exhibits a somewhat transversely isotropic behavior along the -plane. These results show that the largest component of the stiffness tensor (cf. Table 3) and the largest elastic moduli (cf. Table 4) both coincide with the largest average fiber orientation tensor component , showing that material stiffness increases with an increasing degree of fiber alignment, as expected. Further, the results in Table 3 and Table 4 confirm that there is a clear reduction in elastic stiffness when micro-void inclusions are considered [42,57,80]. In addition, regression coefficients from the computational homogenization least squares approach given in Section 2.2.1 for ROI-II data indicate a moderately high accuracy of the regression fitting procedure (i.e., from the set of realizations of the various RVE sizes reported in Table 5. This, along with the relatively low standard deviations , also appearing in Table 5, shows that the computed homogenized elastic constants provide a good fit to the data with minor variation. Although Table 4 shows that the effective moduli increase with increasing RVE size, the rate of increase between consecutive RVEs is seen to decrease by an average of −22.8% and −44.3% for the elastic and shear moduli, respectively, of the non-porous microstructure and by an average of −42.7% and −42.9% for the elastic and shear moduli, respectively, of the porous microstructure. Additionally, Table 5 shows that the average regression fitting coefficients are seen to decrease with increasing RVE size.

Table 3.
Computed values of average elastic stiffness for ROI-II region obtained from the numerical (FE) homogenization approach based on RVE-II and the orientation-averaged Mori–Tanaka (MT) method for the 13% CF/ABS SFRP composite (components not shown indicate a zero value).

Table 4.
Mean values of engineering elastic constants for ROI-II computed from the numerical FE homogenization schemes for all RVE cases (i.e., RVE-I, II and III, with 125, 27 and 8 realizations, respectively) with non-porous and porous microstructures.

Table 5.
Mean values and standard deviation of the coefficient of determination for ROI-II computed from the least squares regression fitting procedure for all RVE cases (i.e., RVE-I, II and III).
Figure 8 presents box plots showing the mean value (‘x’ marker), the interquartile range (box), consisting of the lower quartile, median line and upper quartile, the extremums of the data range (whiskers) and outliers (isolated dots) for the predicted engineering constants for each set of realizations RVE-I, RVE-II and RVE-III of ROI-II appearing in Figure 3. The results show an overall reduction in the variability of computed properties with increasing RVE size. Mean values tend to converge as the RVE size is increased for all engineering constants, which agrees with the work of Kanit et al. [66]. Their work showed that small but reasonable-sized RVEs with a sufficient number of realizations can accurately predict effective properties, as would larger-sized RVE with a smaller number of realizations. However, there were some deviations in computed engineering constants observed for the smallest RVE (i.e., RVE-I). Although micro-voids appear to reduce the elastic moduli for all RVE cases (i.e., up to 24% reduction observed), the mean Poisson ratios computed from RVE-II and III are unaffected by micro-void inclusions (cf. Figure 8b and Figure 8c, respectively), contrary to what is shown in the RVE-I results (cf. Figure 8a), which show a significant effect of voids on the Poisson ratio, with deviations as high as 11.6%. This suggests that RVE-I is insufficient in accurately predicting the elastic modulus of the CF/ABS composite. Partitioning of the ROI into smaller RVE volumes results in increased variability in average microstructural characteristics across the RVE realizations, which potentially leads to increased dispersion in the predicted effective properties of the ROI volume, as observed from the box plots of Figure 8.
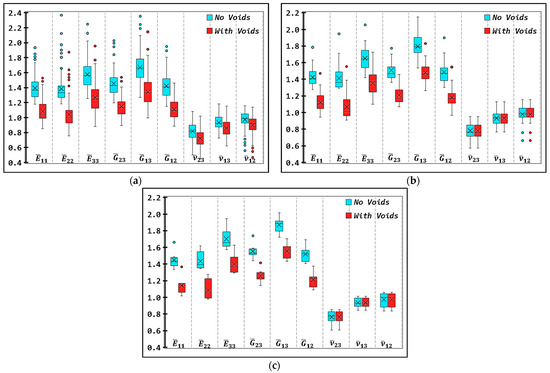
Figure 8.
Box plot showing the mean values (‘x’ markers), median values (horizontal lines), interquartile intervals (box limits), extremums (whiskers) and outliers (isolated points) of the computed normalized engineering constants from RVE realization datasets for (a) RVE-I, (b) RVE-II and (c) RVE-III. Results are shown for analysis cases with micro-voids (red) and without micro-voids (blue) present within the bead’s microstructure.
The microstructural features measured within ROI-II, including fiber length distribution, fiber orientation tensor values, fiber volume fraction and micro-voids, are used to compute and compare the mean effective elastic modulus obtained from both the Mori–Tanaka mean-field and the numerical FE-based homogenization approaches using the method of Hills [93] according to Equation (56). The relative error in predicted values between both methods presented in Table 6 shows that the Mori–Tanaka estimates are reasonably comparable to the numerical predictions, with errors that are mostly below 10% for the elastic moduli. Further, these results indicate a good degree of accuracy, which improves with increasing RVE size. Likewise, the predicted effective elastic modulus for the porous case (~1.235) is comparable to the mean values obtained from the tensile test experiment by Russell T. [95] for the same 13% CF/ABS test sample (~1.221), and the predicted effective shear modulus (~1.286) aligns closely with the flexural test experimental mean values (~1.295) for the same test sample [95].The higher errors may stem from the original Mori–Tanaka–Benveniste model, which was formulated for two-phase composites with ellipsoidal inclusions, as Norris A. N [59] has shown that the model’s extension to multiphase inclusions may perform poorly and may violate the Hashin–Shtrikman stiffness bounds. Moreover, Mori–Tanaka predictions have been reported by Mortazavi et al. [5] and Breuer et al. [61] to deviate significantly from numerical estimates with increasing aspect ratio and volume fraction of fiber inclusions.

Table 6.
Relative error [%] in the magnitude of the predicted effective elastic modulus, , of ROI-II between the Mori–Tanaka analytical model and numerical FE homogenization schemes for all RVE cases (I, II and III).
The coefficient of variation computed with Equation (61) for each RVE computation of ROI-II appears in Table 7. These results show that the value decreases with increasing RVE size by roughly −45% from RVE-I to RVE-II and −40% from RVE-II to RVE-III for the numerical FE calculation. Additionally, the values are relatively higher for the porous RVE structures compared to the corresponding non-porous RVE due to the increased variability introduced by the non-uniform distribution of the inherent micro-voids. The values computed from the analytical MT approach are relatively lower than the numerical FE counterparts for all RVE sizes. The value of RVE-II in both cases is less than 5%. Although RVE-III yields slightly more accurate results than the others considered, the computational requirements are excessive, and the gains of higher accuracy do not justify the higher computational cost.

Table 7.
Coefficient of variation [%] for the magnitude of the effective elastic modulus, , for all RVE cases (I, II and III) of ROI-II and for both the Mori–Tanaka analytical model and the numerical FE homogenization scheme.
3.3. Effective Coefficient of Thermal Expansion for ROI-II
Effective CTEs are presented here, where results from the numerical FE homogenization approach (cf. Section 2.2.2) are compared to those computed using the Mori–Tanaka mean-field method in Section 2.3.2. Typical displacement contours from the numerical FE simulation are plotted in Figure 9 for RVE-II, realization #14, subjected to a uniform thermal load of °C. As stated earlier, PBC constraints are imposed on the bounding entities of the RVE with zero applied strain (cf. Section 2.2.2). The displacement contour of Figure 9 shows the thermal response of the porous RVE microstructure consisting of the ABS matrix, fiber and micro-void inclusion (cf. Figure 2) based on the micro-constituents’ material properties presented in Table 1. The stresses computed from the single-step static stress analysis are used to obtain the effective CTE from Equation (28) using the stiffness tensor for the corresponding RVE instances computed in the preceding section (i.e., Section 3.2). Figure 9 shows the non-uniform deformation of the RVE in all directions due to the anisotropic nature of the inherent microstructure. Additionally, there are distinct local deformations at the RVE boundaries, which are likely introduced by the property contrast of the various micro-constituents at the RVE boundaries.
Figure 9.
Deformation contour of RVE-II, #14 from ROI-II region, overlayed on the undeformed mesh geometry and showing the bulk response of the volume under thermal load of °C.
The mean values of the diagonal components of the effective CTE tensor for the three RVE sizes shown in Figure 3, including both non-porous and porous microstructure of the CF/ABS SFRP bead, are presented in Table 8. The maximum observed discrepancy in the effective CTE component values between RVE sizes is seen to drop from 6.3% between RVE-I and II to 3.3% between RVE-II and III. The CTE component values in Table 8 are observed to be consistently lower for the component with the highest degree of fiber alignment (, and the CTE is highest for the component with the lowest degree of fiber alignment, i.e., (cf. Equation (62)), for all RVE cases considered. Additionally, the inherent micro-voids are seen to only slightly reduce the CTE component values.

Table 8.
Mean values of the diagonal components of the effective CTE tensor for all RVE cases (I, II and III) of ROI-II computed using numerical FE homogenization.
Box plots appearing in Figure 10 indicate that the degree of variation in effective CTE decreases with increasing RVE size. Higher variance was observed in the predicted quantities, with the smallest RVE (RVE-I) having more outliers outside the interquartile range (cf. Figure 10a) compared to the largest RVE (RVE-III), with shorter error bars and minimal variation in predicted effective CTE values. From these results, the presence of micro-voids within the bead microstructure only slightly reduces the predicted effective CTE values in all RVE cases (i.e., less than 5%). The estimated effects of micro-voids on the volumetric effective CTE values are much lower (i.e., less than 3.25%). These trends agree well with results provided by others (see, e.g., [40,80,96]). The Mori–Tanaka (MT) mean-field estimates of the effective CTE magnitude, (cf. Equations (57)–(59)), agree well with the numerical FE predictions, with a maximum observed discrepancy of about 5.5% for the non-porous composite and 7.0% for the porous composite (cf. Table 9).
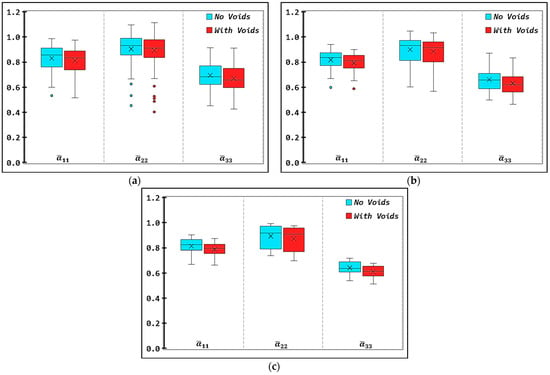
Figure 10.
Box plot showing the mean values (‘x’ markers), median values (horizontal lines), interquartile intervals (box limits), extremums (whiskers) and outliers (isolated points) of the computed components of the normalized effective CTE tensor from the RVE realization datasets for (a) RVE-I, (b) RVE-II and (c) RVE-III. Results are shown for analyzed cases with micro-voids (red) and without micro-voids (blue) present within the bead’s microstructure.

Table 9.
Computed normalized and the associated relative error [%] in the computed effective CTE magnitude of ROI-II between the numerical FE homogenized results and the Mori–Tanaka (MT) analytical results for all RVE sizes (RVE-I, II and III).
Note that the analytical MT-calculated CTE values depend on the accuracy of the calculated stiffness tensor in Table 3, and they appear to improve with increasing RVE size, dropping to about 2.0% for the non-porous composite and 4.6% for the porous composite. Similar to the numerical FE results, porosity appears to have the same effect on the analytical MT results as that seen with the numerical FE data, where effective CTEs are reduced less to than 1% when micro-voids are considered.
Based on the results of the calculated coefficient of variation for the effective CTE magnitude computed from the different realizations of the various RVEs of ROI-II presented in Table 10, the values are much lower compared to corresponding values computed for the effective modulus (cf. Table 7), with for the non-porous RVE and for the porous RVE. Like the effective modulus, the values for the effective CTE are relatively higher for the porous RVE compared to the non-porous RVE. Additionally, the values from the numerical FE approach are relatively higher than the analytical MT values for RVE-I and RVE-II but relatively lower for RVE-III.

Table 10.
Coefficient of variation [%] for the normalized effective CTE magnitude ( for all RVE cases (I, II and III) of ROI-II and for the Mori–Tanaka analytical model and the numerical FE homogenization schemes.
The influence of micro-voids on the effective CTE is shown to be minimal in these results. The impact studies may thus be more relevant to the effective composite stiffness and thermal conductivity.
3.4. Effective Thermal Conductivity for ROI-II
The results of the effective TC of the 13% CF/ABS composite based on the numerical and analytical FE homogenization evaluation procedures described in Section 2.2.3 and Section 2.3.3, respectively, are reported here. First, this section presents the analysis results for the non-porous structure of RVE-II, realization #14 from ROI-II, subjected to a thermal gradient along each of the three principal reference axes. The thermal gradients are prescribed on the bounding entities of the RVE through the set of PBC equations given in Equations (1)–(3). The material properties of the micro-constituents used for the analysis are also provided in Table 1. Single-step steady-state heat transfer analysis is carried out and the output of the homogenized heat fluxes and temperature gradients computed from the FE analysis for the three different load cases are used to compute the effective thermal conductivity tensor using the numerical FE homogenization procedures detailed in Section 2.2.3.
The temperature contours of three separate simulations appear in Figure 11. The plots show a non-uniform distribution of the temperature gradients along the principal coordinate axes due to microstructural heterogeneity across the composite sample, coupled with the relatively high contrast in the isotropic thermal conductivity between the fiber and matrix phases (~17.5).

Figure 11.
Temperature contours of RVE-II, realization #14 from ROI-II, for three thermal load conditions: (a) thermal gradient in -direction, (b) thermal gradient in -direction and (c) thermal gradient in -direction. Units of in [°C].
Table 11 shows the principal components of the predicted effective TC tensor for all three RVE sizes appearing in Figure 3 for both non-porous and porous composite microstructures. The effective mean component values of TC from all RVEs considered are seen to be within close range of each other (ranging from 0% to a maximum of 1.5% discrepancy between consecutive RVE values). The micro-voids are seen to reduce the computed effective TC values by 10–12%. The maximum component of the conductivity tensor (i.e., ) is observed to coincide with the component of maximum average fiber orientation (i.e., .

Table 11.
Mean values of effective TCs for all RVE cases (RVE-I, I and III) for ROI-II computed with the numerical FE homogenization scheme.
As seen in the error bar plots in Figure 12, there is a clear reduction in the dispersion of quantities as the RVE size increases from RVE-I (cf. Figure 12a) to RVE-III (cf. Figure 12c). The error bar shrinks considerably for the largest RVE case, i.e., RVE-III, although the mean values for all three RVE cases are within close range to each other, with the maximum discrepancy in all quantities observed between consecutive RVE sizes for both porous and non-porous microstructural considerations, dropping from about 1.8% between RVE-I and II to a value of only 0.8% between RVE II and III.
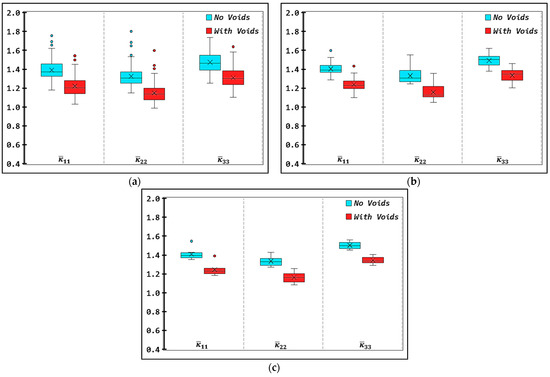
Figure 12.
Box plot showing the mean values (‘x’ markers), median values (horizontal lines), interquartile intervals (box limits), extremums (whiskers) and outliers (isolated points) of the diagonal components of the normalized effective TC tensor from the RVE realizations for (a) RVE–I, (b) RVE-II and (c) RVE-III. Results are shown for the analyzed cases with micro-voids (red) and without micro-voids (blue) present within the bead’s microstructure.
The results of the effective TC magnitude presented in Table 12 below show very good agreement between the values obtained from both numerical (FE) homogenization and the Mori–Tanaka (MT) analytical methods, with a maximum discrepancy of only 3.5% recorded for the smallest sized RVE (RVE-I), which reduces with increasing RVE size to about 1% for RVE-III.

Table 12.
Relative error [%] in the predicted effective TC magnitude ( for ROI-II between the numerical FE homogenization scheme and the Mori–Tanaka (MT) analytical results for all RVE sizes (RVE-I, II and III).
Although there are minimal differences in computed effective TC values among the various RVE sizes in Table 11, the results of the dispersion in the measured effective TC appearing in Table 13 show that the coefficient of variation decreases with increasing RVE size, as observed with other effective quantities, and falls below for both the porous and non-porous RVE-II micro-structures, computed from both numerical FE and analytical MT methods. The values for the effective TC are seen to be relatively lower than the values computed for the effective moduli, and in some cases, they are slightly higher than those computed for the effective ETC. This is because the determination of sufficient RVE size is known to be dependent on the property being evaluated [66]. Although there is less dispersion in the computed effective TC quantities observed for RVE-III (, the gain in accuracy does not measure up to the added cost of computation (i.e., in terms of analysis time with same computing configuration) due to the increased RVE size and associated mesh points.

Table 13.
Coefficient of variation [%] for the predicted normalized apparent ETC ( of ROI-II for both the Mori–Tanaka analytical model and the numerical FE homogenization schemes and for all RVE cases (I, II and III).
3.5. Effective Properties over the LAAM Bead Specimen
To better understand the variation in the effective properties across the 13% CF/ABS bead appearing in Figure 1, the numerical FE homogenization procedure in Section 2.2 is used to compute the outputs of the reference quantities for all RVE-II realizations over all four ROIs. Renderings of these realizations appear for the various ROI volumes in Figure 13. Correlations between computed quantities across the bead cross-section for each ROI volume are presented here. Moreover, with knowledge of the overall average bead microstructural properties, these relationships provide insight into the average effective properties of the overall bead microstructure.
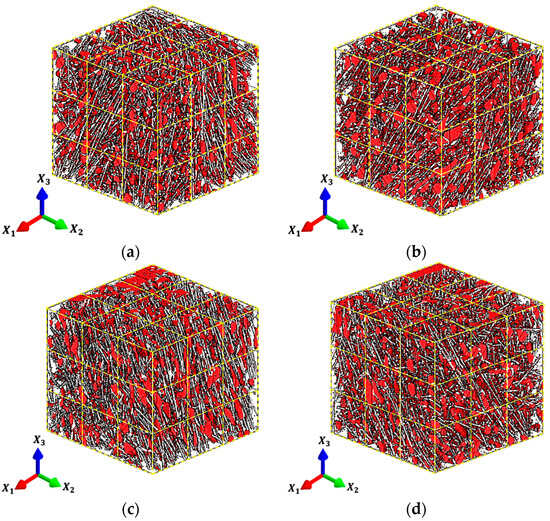
Figure 13.
Three-dimensional µCT volume view showing internal microstructure (fiber—gray; voids—red) of the various ROI volumes and the RVE-II instances for each: (a) ROI-I, (b) ROI-II, (c) ROI-III and (d) ROI-IV.
Figure 14 presents the least squares linear fitted curve effective elastic modulus (cf. Equation (63)) as a function of average fiber volume fraction over all ROIs. The volume fraction is shown to vary between 5% and 9%, which is reasonable for our CF/ABS samples that have an average of about 8.4% by volume (or 13% by weight). Similarly, Figure 14b shows the correlation between the elastic modulus (cf. Equation (64)) and average fiber orientation tensor component in the print direction obtained from datasets for the non-porous RVE-II realizations for the various ROIs.
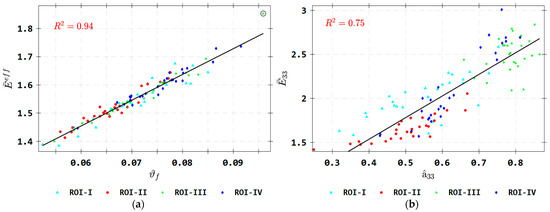
Figure 14.
Linear correlation plots between (a) the effective elastic modulus and the fiber volume fraction and between (b) the elastic modulus component and the average fiber orientation tensor component for non-porous RVE-II instances of the various ROIs. (circled markers indicate outlier datapoints).
The results in Figure 14 indicate a good correlation exists between the fiber volume fraction and effective elastic modulus, with a correlation coefficient , which implies that the fiber volume fraction is an important microstructural parameter for predicting the modulus of SFRP composites, as expected. Similarly, there is a reasonable correlation between the elastic modulus and average fiber orientation tensor component, with a correlation coefficient , which suggests that the degree of fiber alignment with the print direction is a key indicator of this effective elastic property for our SFRP composite.
Linear correlations between effective CTE and the average fiber volume fraction (cf. Equation (65)) for the non-porous RVE-II realizations for the various ROIs appear in Figure 15a, which reveals an inverse relationship, where a higher-volume fraction of particles yields a lower effective CTE. This is also expected given the relatively low CTE of the carbon fiber material (see, e.g., [40,80,96]).

Figure 15.
Linear correlation plots between (a) the apparent ECTE magnitude with the fiber volume fraction and between (b) the ECTE tensor component and the average fiber orientation tensor component for non-porous RVE-II instances of the various ROIs.
These results show a good correlation between and , with a correlation coefficient . Similarly, a good correlation is seen between the average fiber orientation component in the print direction and the component (cf. Equation (66), Figure 15b) of the effective CTE tensor . The degree of fiber alignment in the print direction is observed to vary inversely with the component of the effective CTE tensor along the same direction. Higher fiber alignment tends to allow for a higher packing density, giving more weight to the suspended carbon fiber properties.
A near-perfect correlation is seen between the fiber volume fraction and the apparent effective TC magnitude (cf. Equation (67), Figure 16a) for the non-porous RVE-II realizations for various ROIs. Conversely, a very weak correlation is seen to occur between the average fiber orientation component in the print direction and the component (cf. Equation (68), Figure 16b) of the effective TC tensor.
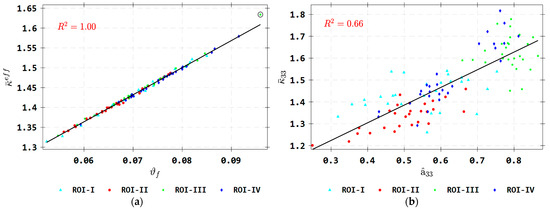
Figure 16.
Linear correlation plots between (a) the apparent ETC magnitude and the fiber volume fraction and between (b) the ETC tensor component and the average fiber orientation tensor component for non-porous RVE-II instances of the various ROIs. (circled markers indicate outlier datapoints).
This implies that for the two-phase SFRP composite, the apparent effective TC has a strong linear dependence on the volume fraction of the fiber reinforcement, as was also identified in Tian et al. [91].
While the above numerical studies carried out to estimate the effective properties of a given ROI requires computation of all its associated RVE realizations which may be computationally expensive and time consuming, a more efficient method for quickly extrapolating a ROI effective properties based on a minimization approach using a single characteristic RVE instance from the realization set of the parent ROI is presented in the Supplementary Materials.
4. Conclusions
A numerical FE homogenization method was developed and applied to evaluate the effective thermo-mechanical properties of a 13% CF-ABS SFRP composite. The material’s microstructure was obtained using X-ray µ-CT characterization techniques, which provided realistic, 3D voxel-based RVEs. Sensitivity analysis was performed to determine a suitable computationally efficient RVE based on three RVE sizes and realization sets, which yielded effective properties with minimum dispersion in predicted quantities. Our results show that dispersion in the predicted effective quantities decreases with increasing RVE size to less than 2.5% for the largest sized RVE. On average, the dispersion in predicted quantities decreased by about 68% for a 1.5 times increase in RVE side length. The predicted effective properties obtained from our numerical FE approach were shown to agree well with the estimated properties based on the Mori–Tanaka mean-field homogenization technique. Discrepancies of less than 10.2%, 7% and 3.5% were observed between both techniques for the predicted effective modulus, CTE and TC, respectively, for all RVE cases, and the degree of alignment increased significantly with increasing RVE size. Assessment of the influence of micro-voids on the material behavior of the SFRP composite indicated an overall reduction in the equivalent properties of the composite by about 21% and 12% for the predicted effective modulus and TC, respectively, while the effect of porosity on the effective CTE was minimal, and only about a 4% reduction was observed. Parameter-dependent studies showed that the computed effective properties had a linear correlation with the fiber volume fraction and the average fiber orientation within the bead specimen, consistent with the literature [61,75,76]. Depending on the computed effective quantity, a correlation coefficient between 0.81 and 1.00 was observed with the fiber volume fraction, while a coefficient between 0.66 and 0.85 was observed with the average fiber orientation. The effective modulus and thermal conductivity were observed to vary proportionally with the fiber volume fraction and degree of fiber alignment with the print direction. Conversely, the effective thermal expansion coefficient was observed to vary inversely with fiber volume fraction and degree of fiber alignment in the print direction. Overall, the effective modulus and thermal conductivity were predicted to be higher at the edges and top surface of the print bead, where the volume fraction and degree of fiber alignment in the print direction are seen to be highest, and the properties were lower in regions closer to the bead center, with a less densely packed and more randomly oriented fibrous microstructure. The opposite behavior was observed for the thermal expansion coefficient across the bead sections.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/fib13110147/s1. Figure S1. Three-dimensional correlation plot between the distribution of the deviation in fiber fraction and orientation vector versus the deviation in the (a) apparent effective modulus, ; (b) apparent ECTE, ; and (c) apparent ETC, for the various RVE-II instances of ROI-II. Figure S2. Deviation in the fiber volume fraction and average fiber orientation for the RVE-II realizations of each ROI, (a) ROI-I, (b) ROI-II, (c) ROI-III and (d) ROI-IV for the non-porous RVE microstructure. Figure S3. Three-dimensional µCT volumes showing the microstructure (fiber—gray; voids—red) of select RVE-II realizations of each ROI volume: (a) ROI-I, RVE-II, realization #14; (b) ROI- II, RVE-II, realization #24; (c) ROI- III, RVE-II, realization #23; and (d) ROI- IV, RVE-II, realization #3. Figure S4. Correlation between the deviation in the (a) net effective modulus; (b) net product of the effective modulus and thermal expansion coefficient; and (c) net thermal conductivity versus the deviation in the void fraction for the various RVE-II instances of ROI-II volume. Table S1. Deviation in microstructural parameter values for the non-porous RVEs of each ROI: (a) ROI-I, RVE-II, realization #14; (b) ROI-II, RVE-II, realization #24; (c) ROI- III, RVE-II, realization #23; and (d) ROI- IV, RVE-II, realization #3. Table S2. Average values of the fiber volume fraction and orientation tensor components for the select RVE-II realizations: (a) ROI-I, RVE-II, realization #14; (b) ROI- II, RVE-II, realization #24; (c) ROI- III, RVE-II, realization #23; and (d) ROI- IV, RVE-II, realization #3. Table S3. (a) Computed values of effective thermo-mechanical properties for selected non-porous RVE-II realizations: (a) ROI-I, RVE-II, realization #14; (b) ROI-II, RVE-II, realization #24; (c) ROI- III, RVE-II, realization #23; and (d) ROI- IV, RVE-II, realization #3. Table S4. (a) Estimated values of differences in effective thermo-mechanical properties (ΔZ_ ^RVE) between the porous and non-porous microstructures for selected RVE-II instances of the various ROI volumes: (a) ROI-I, RVE-II, #14; (b) ROI-II, RVE-II, #24; (c) ROI- III, RVE-II, #23; and (d) ROI- IV, RVE-II, #3. Table S5. (a) Approximate values of effective thermo-mechanical properties of the porous microstructures for the various ROI volumes: (a) ROI-I, RVE-II, #14; (b) ROI- II, RVE-II, #24; (c) ROI- III, RVE-II, #23; and (d) ROI- IV, RVE-II, #3.
Author Contributions
Conceptualization, A.E.A. and D.E.S.; methodology, A.E.A. and D.E.S.; software, D.E.S.; validation, A.E.A. and D.E.S.; formal analysis, A.E.A.; investigation, A.E.A.; resources, D.E.S.; data curation, A.E.A.; writing—original draft preparation, A.E.A.; writing—review and editing, D.E.S.; visualization, A.E.A.; supervision, D.E.S.; project administration, D.E.S.; funding acquisition, D.E.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation (NSF), grant number 2055628.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy restrictions.
Acknowledgments
The authors wish to acknowledge the National Science Foundation for providing the necessary grants that made this publication possible. We would also like to thank Strangpresse for donating the Model 19 single-screw extruder that enabled us to study LAAM extrusion deposition of polymer composite materials in Baylor’s Laboratory.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1
The strain concentration tensor, or Eshelby’s tensor ( that appears in the Mori–Tanaka model for predicting the homogenized elasticity tensor of a short fiber-reinforced composite material is presented in this section. Given
then, for spheroidal inclusions, the non-zero components of are given as
For spherical-shaped inclusions, the non-zero components of the Eshelby tensor are given as
References
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Van de Werken, N.; Tekinalp, H.; Khanbolouki, P.; Ozcan, S.; Williams, A.; Tehrani, M. Additively manufactured carbon fiber-reinforced composites: State of the art and perspective. Addit. Manuf. 2020, 31, 100962. [Google Scholar] [CrossRef]
- Brenken, B.; Barocio, E.; Favaloro, A.; Kunc, V.; Pipes, R.B. Fused filament fabrication of fiber-reinforced polymers: A review. Addit. Manuf. 2018, 21, 1–16. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B.; Mai, Y.W. Science and engineering of short fibre-reinforced polymer composites. In Woodhead Publishing; Elsevier: Oxford, UK, 2019. [Google Scholar]
- Mortazavi, B.; Baniassadi, M.; Bardon, J.; Ahzi, S. Modeling of two-phase random composite materials by finite element, Mori–Tanaka and strong contrast methods. Compos. Part B Eng. 2013, 45, 1117–1125. [Google Scholar]
- Tucker, C.L., III. Fundamentals of Fiber Orientation: Description, Measurement, and Prediction; Carl Hanser Verlag GmbH Co. KG: Munich, Germany, 2022. [Google Scholar]
- Kaiser, J.M.; Stommel, M. Micromechanical modeling and strength prediction of short fiber reinforced polymers. J. Polym. Eng. 2012, 32, 43–52. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A. Numerical evaluation of the representative volume element for random composites. Eur. J. Mech. A/Solids 2021, 86, 104181. [Google Scholar]
- Tucker, C.L., III; Liang, E. Stiffness predictions for unidirectional short-fiber composites: Review and evaluation. Compos. Sci. Technol. 1999, 59, 655–671. [Google Scholar] [CrossRef]
- Kim, H.G.; Kwac, L.K. Evaluation of elastic modulus for unidirectionally aligned short fiber composites. J. Mech. Sci. Technol. 2009, 23, 54–63. [Google Scholar] [CrossRef]
- Abrate, S. The mechanics of short fiber-reinforced composites: A review. Rubber Chem. Technol. 1986, 59, 384–404. [Google Scholar] [CrossRef]
- Huang, H.B.; Huang, Z.M.; Wan, Y.-P. Micromechanical predictions on elastic moduli of a short fiber composite with arbitrary geometric combination. Compos. Part A Appl. Sci. Manuf. 2023, 168, 107477. [Google Scholar] [CrossRef]
- Sideridis, E. Thermal expansion coefficients of fiber composites defined by the concept of the interphase. Compos. Sci. Technol. 1994, 51, 301–317. [Google Scholar] [CrossRef]
- Karch, C. Micromechanical analysis of thermal expansion coefficients. Model. Numer. Simul. Mater. Sci. 2014, 4, 104–118. [Google Scholar] [CrossRef][Green Version]
- Sevostianov, I. On the thermal expansion of composite materials and cross-property connection between thermal expansion and thermal conductivity. Mech. Mater. 2012, 45, 20–33. [Google Scholar] [CrossRef]
- Wu, C.-T.D.; McCullough, R.L. Constitutive relationships for heterogeneous materials. In Developments in Composites Materials–1, Applied Science; Holister, G.S., Ed.; Applied Science Publishers: London, UK, 1977; pp. 118–186. [Google Scholar]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behavior of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Walpole, L.J. On bounds for the overall elastic moduli for inhomogeneous, systems.—I. J. Mech. Phys. Solids 1966, 14, 151–162. [Google Scholar] [CrossRef]
- Walpole, L.J. On bounds for the overall elastic moduli for inhomogeneous, systems.—II. J. Mech. Phys. Solids 1966, 14, 289–301. [Google Scholar] [CrossRef]
- Walpole, L.J. On the overall elastic moduli of composite materials. J. Mech. Phys. Solids 1969, 17, 235–251. [Google Scholar] [CrossRef]
- Willis, J.R. Bounds self-consistent estimates for the overall properties of anisotropic composites. J. Mech. Phys. Solids 1977, 25, 185–202. [Google Scholar] [CrossRef]
- Miller, M. Bounds for the effective electrical thermal magnetic properties of heterogeneous materials. J. Math. Phys. 1969, 10, 1988–2004. [Google Scholar] [CrossRef]
- Milton, G. Bounds on the elastic and transport properties of two component composites. J. Mech. Phys. Solids 1982, 30, 177–191. [Google Scholar] [CrossRef]
- Beran, M.; Molyneux, J. Use of classical variational principles to determine bounds for the effective bulk modulus in heterogeneous media. Q. Appl. Math. 1966, 24, 107–118. [Google Scholar] [CrossRef]
- Voigt, W. Theoretische studien über die elasticitätsverhältnisse der krystalle. Königliche Gesellschaft der Wissenschaften zu Göttingen. of thermal expansion coefficients. Model. Numer. Simul. Mater. Sci. 1887, 34, 3–52. [Google Scholar]
- Kerner, E.H. The elastic and thermo-elastic properties of composite media. Proc. Phys. Soc. Sect. B 1956, 69, 808. [Google Scholar] [CrossRef]
- Reuss, A. Calculation of the yield strength of mixed crystals on the basis of the plasticity condition for single crystals. ZAMM-J. Appl. Math. Mech./Z. Für Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Turner, P.S. Thermal Expansion Stresses in Reinforces Plastics. J. Res. Natl. Bur. Stand. 1946, 37, 239–250. [Google Scholar] [CrossRef]
- Fo-Fê, G.A. Elastic Constants and Thermal Expansion of Certain Bodies with Inhomogeneous Regular Structure. Sov. Phys. Dokl. 1966, 11, 176. [Google Scholar]
- Schapery, R.A. Thermal expansion coefficients of composite materials based on energy principles. J. Compos. Mater. 1968, 2, 380–404. [Google Scholar] [CrossRef]
- Chamberlain, N.J. Derivation of expansion coefficients for a fibre reinforced composite. BAC Rep. SON (P) 1968, 33, 23. [Google Scholar]
- Nomura, S.; Chou, T.W. Bounds of effective thermal conductivity of short-fiber composites. J. Compos. Mater. 1980, 14, 120–129. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Tandon, G.P.; Weng, G.J. The effect of aspect ratio of inclusions on the elastic properties of unidirectionally aligned composites. Polym. Compos. 1984, 5, 327–333. [Google Scholar] [CrossRef]
- Lielens, G.; Pirotte, P.; Couniot, A.; Dupret, F.; Keunings, R. Prediction of thermo-mechanical properties for compression-moulded composites. Compos. A 1997, 29, 63–67. [Google Scholar] [CrossRef]
- Chou, T.W.; Nomura, S.; Taya, M. A self-consistent approach to the elastic stiffness of short-fiber composites. J. Compos. Mater. 1980, 14, 178–188. [Google Scholar] [CrossRef]
- Takahashi, K.; Harakawa, K.; Sakai, T. Analysis of the thermal expansion coefficients of particle-filled polymers. J. Compos. Mater. 1980, 14, 144–159. [Google Scholar] [CrossRef]
- Takao, Y.; Taya, M. Thermal expansion coefficients and thermal stresses in an aligned short fiber composite with application to a short carbon fiber/aluminum. J. Appl. Mech. 1985, 52, 806–810. [Google Scholar] [CrossRef]
- Hatta, H.; Takei, T.; Taya, M. Effects of dispersed microvoids on thermal expansion behavior of composite materials. Mater. Sci. Eng. A 2000, 285, 99–110. [Google Scholar] [CrossRef]
- Takei, T.; Hatta, H.; Taya, M. Thermal expansion behavior of particulate-filled composites I: Single reinforcing phase. Mater. Sci. Eng. A 1991, 131, 133–143. [Google Scholar] [CrossRef]
- Benveniste, Y.; Dvorak, G.J. On a correspondence between mechanical and thermal effects in two-phase composites. In Micromechanics and Inhomogeneity: The Toshio Mura 65th Anniversary Volume; Springer: New York, NY, USA, 1990; pp. 65–81. [Google Scholar]
- Guo, W.; Han, F.; Jiang, J.; Xu, W. A micromechanical framework for thermo-elastic properties of multiphase cementitious composites with different saturation. Int. J. Mech. Sci. 2022, 224, 107313. [Google Scholar] [CrossRef]
- Tian, W.; Fu, M.W.; Qi, L.; Ruan, H. Micro-mechanical model for the effective thermal conductivity of the multi-oriented inclusions reinforced composites with imperfect interfaces. Int. J. Heat Mass Transf. 2020, 148, 119167. [Google Scholar] [CrossRef]
- Mokarizadehhaghighishirazi, M.; Buffel, B.; Lomov, S.V.; Desplentere, F. Homogenisation of the Local Thermal Conductivity in Injection-Moulded Short Fibre Reinforced Composites. Polymers 2022, 14, 3360. [Google Scholar] [CrossRef]
- Halpin, J.C. Stiffness and expansion estimates for oriented short fiber composites. J. Compos. Mater. 1969, 3, 732–734. [Google Scholar] [CrossRef]
- Halpin, J.C.; Kardos, J.L. The Halpin-Tsai equations: A review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar]
- Chamis, C.C.; Sendeckyj, G.P. Critique on theories predicting thermoelastic properties of fibrous composites. J. Compos. Mater. 1968, 2, 332–358. [Google Scholar] [CrossRef]
- Thomas, J.P. Effect of inorganic fillers on coefficient of thermal expansion of polymeric materials. Fort Worth, TX: General Dynamics Corporation. 1960. Available online: https://apps.dtic.mil/sti/trecms/pdf/AD0287826.pdf (accessed on 23 June 2024).
- Cribb, J.L. Shrinkage and thermal expansion of a two-phase material. Nature 1968, 220, 576–577. [Google Scholar] [CrossRef]
- Halpin, J. Primer on Composite Materials Analysis; Technomic Publishing Co., Inc.: Lancaster, PA, USA, 1984; p. 192. [Google Scholar]
- Nielsen, L.E. Thermal conductivity of particulate—Filled polymers. J. Appl. Polym. Sci. 1973, 17, 3819–3820. [Google Scholar] [CrossRef]
- Nielsen, L.E. The thermal and electrical conductivity of two-phase systems. Ind. Eng. Chem. Fundam. 1974, 13, 17–20. [Google Scholar] [CrossRef]
- Bigg, D.M. Thermally conductive polymer composites. Polym. Compos. 1986, 7, 125–140. [Google Scholar] [CrossRef]
- Thornburgh, J.D.; Pears, C.D. Prediction of the thermal conductivity of filled and reinforced plastics. In ASME Paper No. 65-WA/HT-4; American Society of Mechanical Engineers: New York, NY, USA, 1965. [Google Scholar]
- Springer, G.S.; Tsai, S.W. Thermal conductivities of unidirectional materials. J. Compos. Mater. 1967, 1, 166–173. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72. [Google Scholar] [CrossRef]
- Naili, C.; Doghri, I.; Demey, J. Porous materials reinforced with short fibers: Unbiased full-field assessment of several homogenization strategies in elasticity. Mech. Adv. Mater. Struct. 2022, 29, 2857–2872. [Google Scholar] [CrossRef]
- Abaimov, S.G.; Trofimov, A.; Sergeichev, I.V.; Akhatov, I.S. Multi-step homogenization in the Mori-Tanaka-Benveniste theory. Compos. Struct. 2019, 223, 110801. [Google Scholar] [CrossRef]
- Norris, A.N. An examination of the Mori-Tanaka effective medium approximation for multiphase composites. J. Appl. Mech. 1989, 56, 83–88. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A.; El Minor, H. Computational thermal conductivity in porous materials using homogenization techniques: Numerical and statistical approaches. Comput. Mater. Sci. 2015, 97, 148–158. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M. RVE modelling of short fiber reinforced thermoplastics with discrete fiber orientation and fiber length distribution. SN Appl. Sci. 2020, 2, 91. [Google Scholar] [CrossRef]
- Guven, I.; Cinar, K. Micromechanical modeling of particulate-filled composites using micro-CT to create representative volume elements. Int. J. Mech. Mater. Des. 2019, 15, 695–714. [Google Scholar] [CrossRef]
- Eduljee, R.F.; McCullough, R.L.; Gillespie, J.W., Jr. The influence of aggregated and dispersed textures on the elastic properties of discontinuous-fiber composites. Compos. Sci. Technol. 1994, 50, 381–391. [Google Scholar] [CrossRef]
- Christensen, R.M.; Waals, F.M. Effective stiffness of randomly oriented fibre composites. J. Compos. Mater. 1972, 6, 518–532. [Google Scholar] [CrossRef]
- Camacho, C.W.; Tucker, C.L., III; Yalvaç, S.; McGee, R.L. Stiffness and thermal expansion predictions for hybrid short fiber composites. Polym. Compos. 1990, 11, 229–239. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker III, C.L. The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Hbaieb, K.; Wang, Q.X.; Chia, Y.H.J.; Cotterell, B. Modelling stiffness of polymer/clay nanocomposites. Polymer 2007, 48, 901–909. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A.; El Minor, H. Effect of reinforcement shape on physical properties and representative volume element of particles-reinforced composites: Statistical and numerical approaches. Mech. Mater. 2015, 83, 1–16. [Google Scholar] [CrossRef]
- Drach, B.; Tsukrov, I.; Trofimov, A. Comparison of full field and single pore approaches to homogenization of linearly elastic materials with pores of regular and irregular shapes. Int. J. Solids Struct. 2016, 96, 48–63. [Google Scholar] [CrossRef]
- Djebara, Y.; El Moumen, A.; Kanit, T.; Madani, S.; Imad, A. Modeling of the effect of particles size, particles distribution and particles number on mechanical properties of polymer-clay nanocomposites: Numerical homogenization versus experimental results. Compos. Part B Eng. 2016, 86, 135–142. [Google Scholar] [CrossRef]
- Zhang, P.; Abedi, R.; Soghrati, S. A finite element homogenization-based approach to analyze anisotropic mechanical properties of chopped fiber composites using realistic microstructural models. Finite Elem. Anal. Des. 2024, 235, 104140. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodriguez Ramos, R.; Bravo Castillero, J.; Guinovart Diaz, R. Evaluation of effective material properties of randomly distributed short cylindrical fiber composites using a numerical homogenization technique. J. Mech. Mater. Struct. 2007, 2, 1561–1570. [Google Scholar] [CrossRef]
- Moussaddy, H.; Therriault, D.; Lévesque, M. Modeling elastic properties of randomly oriented fiber composites. In Proceedings of the 19th International Conference on Composite Materials (ICCM19), Montréal, QC, Canada, 28 July–2 August 2013. [Google Scholar]
- Qi, L.; Tian, W.; Zhou, J. Numerical evaluation of effective elastic properties of composites reinforced by spatially randomly distributed short fibers with certain aspect ratio. Compos. Struct. 2015, 131, 843–851. [Google Scholar] [CrossRef]
- Kari, S.; Berger, H.; Gabbert, U. Numerical evaluation of effective material properties of randomly distributed short cylindrical fibre composites. Comput. Mater. Sci. 2007, 39, 198–204. [Google Scholar] [CrossRef]
- Sukiman, M.S.; Kanit, T.; N’Guyen, F.; Imad, A.; El Moumen, A.; Erchiqui, F. Effective thermal and mechanical properties of randomly oriented short and long fiber composites. Mech. Mater. 2017, 107, 56–70. [Google Scholar] [CrossRef]
- Hanhan, I.; Agyei, R.F.; Xiao, X.; Sangid, M.D. Predicting microstructural void nucleation in discontinuous fiber composites through coupled in-situ X-Ray tomography experiments and simulations. Sci. Rep. 2020, 10, 3564. [Google Scholar] [CrossRef]
- Pei, S.; Wang, K.; Li, J.; Li, Y.; Zeng, D.; Su, X.; Xiao, X.; Yang, H. Mechanical properties prediction of injection molded short/long carbon fiber reinforced polymer composites using micro-X-Ray computed tomography. Compos. Part A Appl. Sci. Manuf. 2020, 130, 105732. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Akhtar, S.S.; Arif, A.F.M.; Basirun, W.J.; Al-Athel, K.S.; Schneider, M.; Shakelly, N.; Hakeem, A.S.; Abubakar, A.A.; Wu, P.D. Thermo-mechanical properties prediction of Ni-reinforced Al2O3 composites using micro-mechanics based representative volume elements. Sci. Rep. 2022, 12, 11076. [Google Scholar] [CrossRef]
- Wang, Z. Numerical Determination of Elastic and Viscoelastic Properties of Aligned Continuous and Discontinuous Fiber Reinforced Composites. Master’s Thesis, Baylor University, Waco, TX, USA, 2016. [Google Scholar]
- Awenlimobor, A.; Sayah, N.; Smith, D.E. Micro-void nucleation at fiber-tips within the microstructure of additively manufactured polymer composites bead. Compos. Part A Appl. Sci. Manuf. 2025, 190, 108629. [Google Scholar] [CrossRef]
- Heller, B.P. Non-Isothermal Non-Newtonian Flow and Interlayer Adhesion in Large Area Additive Manufacturing Polymer Composite Deposition. Ph.D. Thesis, Baylor University, Waco, TX, USA, 2019. [Google Scholar]
- Xia, Z.; Zhang, Y.; Ellyin, F. A unified periodical boundary conditions for representative volume elements of composites and applications. Int. J. Solids Struct. 2003, 40, 1907–1921. [Google Scholar] [CrossRef]
- Omairey, S.L.; Dunning, P.D.; Sriramula, S. Development of an ABAQUS plugin tool for periodic RVE homogenization. Eng. Comput. 2019, 35, 567–577. [Google Scholar] [CrossRef]
- Ye, F.; Wang, H. A simple Python code for computing effective properties of 2D and 3D representative volume element under periodic boundary conditions. arXiv 2017, arXiv:1703.03930. [Google Scholar] [CrossRef]
- Hill, R. Elastic properties of reinforced solids: Some theoretical principles. J. Mech. Phys. Solids 1963, 11, 357–372. [Google Scholar] [CrossRef]
- Suquet, P.M. Plasticity Today: Modelling, Methods and Applications; Sawczuk, A., Bianchi, G., Eds.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Duhamel, J.M. Second memoire sur les phenomenes thermo-mecaniques. J. L’école Polytech. 1837, 15, 1–57. [Google Scholar]
- Neumann, F.E. Die Gesetze der Doppelbrechung des Lichts in Comprimirten oder Ungleichförmig Erwärmten Unkrystallinischen Körpern; Gedruckt in der Druckerei der Königlichen Akademie der Wissenschaften: Berlin, Germany, 1843; Volume 2. [Google Scholar]
- Tian, W.; Qi, L.; Chao, X.; Liang, J.; Fu, M.W. Numerical evaluation on the effective thermal conductivity of the composites with discontinuous inclusions: Periodic boundary condition and its numerical algorithm. Int. J. Heat Mass Transf. 2019, 134, 735–751. [Google Scholar] [CrossRef]
- Kuzmin, D. Planar and orthotropic closures for orientation tensors in fiber suspension flow models. SIAM J. Appl. Math. 2018, 78, 3040–3059. [Google Scholar] [CrossRef]
- Hill, R. The elastic behavior of a crystalline aggregate. Proc. Phys. Society. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- deWit, R. Elastic constants and thermal expansion averages of a nontextured polycrystal. J. Mech. Mater. Struct. 2008, 3, 195–212. [Google Scholar] [CrossRef]
- Russell, T.; Jack, D.A. Mechanical and Thermal Property Prediction in Single Beads of Large Area Additive Manufactured Short-Fiber Polymer Composites. Ph.D. Thesis, Baylor University, Waco, TX, USA, 2021. [Google Scholar]
- Wei, K.; Li, J.; Shi, H.B.; Tang, M. Numerical evaluation on the influence of void defects and interphase on the thermal expansion coefficients of three-dimensional woven carbon/carbon composites. Compos. Interfaces 2020, 27, 873–892. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).