Next Article in Journal
Antimicrobial Properties of AgNP/TEMPO-Oxidized Cellulose Nanofiber/Chitosan Composite Fibers
Previous Article in Journal
Analytical Methods for the Identification and Quantitative Determination of Wool and Fine Animal Fibers: A Review
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Fibers
Volume 11
Issue 8
10.3390/fib11080068
fibers-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Sensitivity of Offline and Inline Indicators for Fiber Stretching in Continuous Polyacrylonitrile Stabilization

by
Mohsen Sadeghi Bogar
1,2,*,
Jan Wolf
1,2,
Daniel Sebastian Jens Wolz
1,2,*,
Robert Seidel-Greiff
1,2,
Evgenia Dmitrieva
3,
Noel Israel
3,
Marco Rosenkranz
3,
Thomas Behnisch
1,2,
Michael Thomas Müller
4 and
Maik Gude
1,2
1
Institute of Lightweight Engineering and Polymer Technology (ILK), Technical University of Dresden, 01307 Dresden, Germany
2
Research Center Carbon Fibers Saxony (RCCF), Technical University of Dresden, 01069 Dresden, Germany
3
Leibniz Institute for Solid State and Materials Research Dresden (IFW), 01069 Dresden, Germany
4
Leibniz Institute for Polymer Research Dresden (IPF), 01069 Dresden, Germany
*
Authors to whom correspondence should be addressed.
Fibers 2023, 11(8), 68; https://doi.org/10.3390/fib11080068
Submission received: 25 May 2023 / Revised: 21 July 2023 / Accepted: 25 July 2023 / Published: 4 August 2023
Browse Figures
Versions Notes

Abstract

:
In carbon fiber (CF) production, the stabilization process step is the most energy- and time-consuming step in comparison with carbonization and graphitization. To develop optimization routes for energy and productivity, the stabilization needs to be monitored continuously via inline analysis methods. To prognose the evolution of high-performance CF, the density of stabilized fibers has been identified as a robust pre-indicator. As the offline analysis of density is not feasible for inline analysis, a density-soft sensor based on the stabilization indices of Fourier Transform Infrared spectrum (FTIR)-analysis and Electron Paramagnetic Resonance (EPR) Spectroscopy could potentially be used for inline monitoring. In this study, a Polyacrylonitrile-based precursor fiber (PF) stabilized in a continuous thermomechanical stabilization line with varying stretching profiles was incrementally analyzed using density, FTIR-based relative cyclization index (RCI), and EPR-based free radical concentration (FRC). Our findings show RCI and EPR dependencies for density, correlated for RCI with sensitivity by stretching to cubic model parameters, while FRC exhibits linear relationships. Therefore, this study identifies two possible soft sensors for inline density measurement, enabling autonomous energy optimization within industry 4.0-based process systems.

1. Introduction

Carbon fiber’s excellent intrinsic properties, such as high strength, high modulus, thermal and electrical conductivity, excellent chemical resistivity, and low density, have expanded its appeal in a variety of fields, including lightweight engineering, turbine, energy storage battery, automotive, and health [1,2,3,4,5,6,7]. The basic process steps in the production of polyacrylonitrile (PAN)-based CF are polymerization, fiber wet spinning, and thermal conversion, consisting of the stabilization, carbonization, and optional graphitization steps. Stabilization is a crucial process step as it converts the thermodegradative polymeric PF to a thermostable stabilized fiber (SF), which is able to endure the subsequent high-temperature conversion process. This involves numerous simultaneous complex chemical reactions within the stabilization process and uses up to 56% of the energy needed to produce CF [4,8,9,10]. This process, which affects the chemical structure of PF, can take up to two hours depending on the quality and type of PF used, as well as the applied process variables (e.g., oven temperature or heating rate) [11]. Most of the research in this field is aimed at introducing indicators, which have the potential to show changes in the chemical structure of the fiber during thermal treatment [12,13,14,15,16]. If CF are to behave as expected, the online monitoring of the stabilization process is an essential phase in the manufacturing process. Using inline indexes along with the classical ones during the stabilization process can enable the production of a structure with fewer defects and voids, and subsequently high tensile strength, and to minimize energy consumption.
Fiber density is a common indicator in CF research [10,17,18] to ensure that, during stabilization, the fibers concurrently transition from a linear structure to a thermostable ladder structure in the presence of oxygen. Density has been employed as an indicator for the relationship with CF tensile characteristics and the extent of SF [19]. According to this, the best tensile properties are obtained in the density range of 1.34–1.39 g/cm3 and, in terms of energy usage, an SF with a lower density was favored [19]. There exists a considerable amount of literature on the impact of different processing parameters such as the residence time [20,21,22], temperature profile [17,22,23,24], and steam ratio of the pretreatment step [25] on SF density. Qin et al. [25] investigated the effect of stretching the PF on the preferred orientation and ladder molecules. The orientation of the final CF increased with the increasing stretching of the SF. It has also been attempted in recent years to offer a numerical relationship between fiber physical attributes and chemical structure based on density and FTIR spectra acquired from SF [12,15]. Although density is an applicable indicator to control the trend of physical and chemical change, it is a destructive and offline, time- and resource-consuming measurement method, which should be replaced with an inline indicator for fast and reliable process feedback.
The research on structure change and simultaneous complex chemical reactions such as oxidation, cross-linking, dehydrogenation, and cyclization, occurring within the stabilization typical temperature range of 180 to 300 °C, has a long tradition [10,13,23,26,27,28,29,30,31]. Among them, the degree of the cyclization reaction acquired from the FTIR spectrum device is an important criterion for analyzing the evolution of the chemical transformation of PAN fiber and the subsequent physical and mechanical properties. In 2012, Liu et al. [27] investigated the effect of pretreatment hot stretching at 180 °C by various ratios ranging from 0 to 16% on the conversion of PF to CF. They exhibited a perfect linear relationship between RCI and the orientation of PAN chains for stretching ratios under 6%. When the stretching ratio is less than 6%, an obvious reduction in the onset temperature and an increase in the activation energy of the cyclization reaction was reported. The chemical shrinkage as a subsequent effect of the transformation of linear chains to ladder polymer during stabilization was studied by many researchers [13,22]. It is confirmed that the nitrile cyclization reaction causes the chemical shrinkage that has an exponential relation with cyclization time. Despite the demonstration of the impact of shrinkage, particularly free shrinkage, on fiber morphology and attributes in the batch process [32,33], no research has been done on the effects of negative stretching or shrinkage on the structural changes of stabilized fibers and associated indices in the chemical shrinkage temperature range or higher.
To address this issue, we produced PAN-SF with three different stretching profiles. The first trial encountered a negative stretch ratio in heating zone (HZ) 1. The second one experienced constant fiber length, while the third trial began its stretching profile with a positive stretch ratio in the first oven. Additionally, in order to facilitate the monitoring of the change in the structure of PAN fibers during the stabilization process, a quantitative relationship of the density index as a function of inline indices such as RCI and FRC was extracted in this study. It should be mentioned that using the concentration of free radicals generated by thermal treatment as an inline indicator and its relationship with the density of the SF was a novel notion adopted in the present research. Although the radical concentration acquired from the EPR test has been widely reported in recent years to detect the influence of electron beam treatment (rather than thermal treatment) on PAN fibers for pre-oxidation processes [34,35,36,37,38,39]. FRC is studied here for the first time, for its possible implementation as an inline analyzing standard for thermal processes such as a continuous stabilization line. Therefore, in general, it can be mentioned that by using inline indicators and the resulting smart equipment in the future, process engineers will be enabled to monitor the performance of the CF manufacturing line in real time. They can speed up the adaptation of process parameters based on the instantaneous properties of the production materials and thereby prevent poor-quality products or enhance energy efficiency. Hence, inline monitoring shortens decision-making time and increases efficiency throughout the CF manufacturing supply chain.

2. Materials and Methods

2.1. Materials

A total of 23 wt.-% of PAN copolymer powder (Mw = 200,000 g/mol) in dimethyl formamide was used to prepare the spinning dope solution. PAN powder, produced by DOLAN GmbH in Germany, consisted of 99.5% of acrylonitrile and less than 0.5% methyl acrylate [40,41]. A fiber bundle containing 1000 single filaments was produced during a wet spinning pilot plant by Fourne Polymertechnik GmbH, Germany [42]. The physical properties of PAN-PF used in this research are presented in Table 1. Also, the light microscope image of the surface of the filaments in the fiber bundle and the box plot of the average diameter of the filament for trials 1, 2, and 3 are presented in Figure A1 as Supplemental Information.

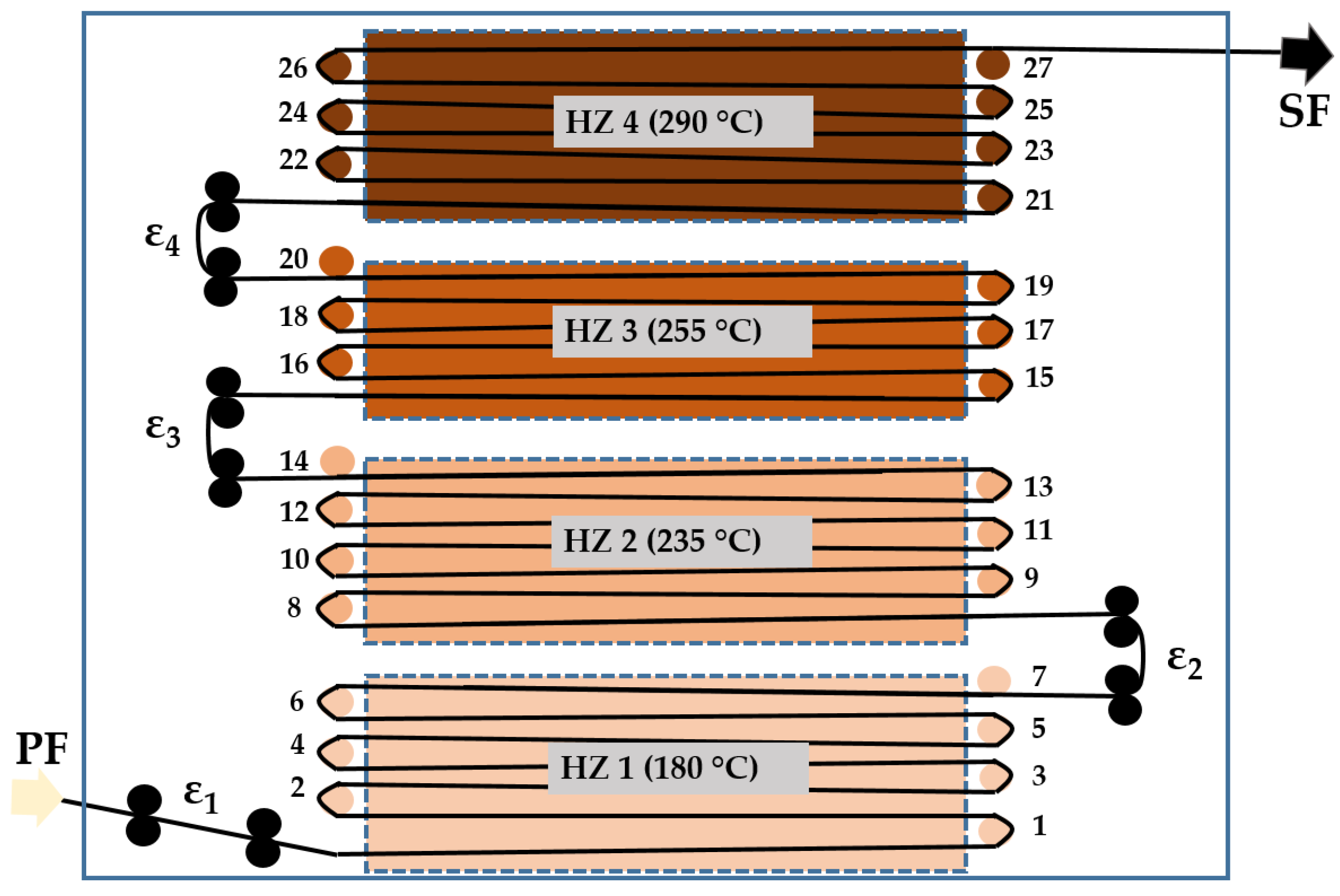
2.2. Thermal Treatment—Stabilization

The stabilization procedure for PAN-PF was carried out using a continuous oxidation line that has four oxidizing furnaces, as shown in Figure 1. The temperature of the four stabilizing furnaces was set to 180–235–255–290 °C. It is noteworthy that for identification of the stretching impact on the ladder-like structure of the SF, stabilization processes were stopped and 27 samples were extracted at different measurement points during the continuous heat treatment process as shown in Figure 1. Figure 1’s numbers 1 through 27 represent various measurement points. Table A1 , Table A2 and Table A3 contain further information on the process parameters for each of the 27 measured points. The total heat treatment time was equal for the three trials (tstabilitation ~ 120 min). On average, the time interval between two measurement points was 4.5 min. Furthermore, four points (ε1 to ε4) were designed to apply the required stretching profile during the process. Two sets of rollers applied the appropriate stretch before each HZ, as shown in Figure 1. Table 2 displays the specifics of three designed stretching profiles at various stabilization phases. As seen, trials 1, 2, and 3 began with negative, zero, and positive stretch ratios in HZ 1, respectively. It should be noted that the total fiber stretching increases after passing the fibers through each stabilizing oven. A negative stretch exists when the front roller’s speed is slower than the rear roller’s speed.

2.3. Characterization

A density gradient column filled with a mixture of two liquids (Acetone, ρA = 0.79 g/cm³; Dibromomethane, ρd = 2.49 g/cm³) was applied for a uniform and reproducible density measurement of PF and SF based on DIN 65569. Fiber samples of about 10 mm in the form of a loop were floated within the gradient column and measured for at least three specimen samples. In this study, there are a total of 81 measured points for 3 different stretching trials (3 trials ∗ 27 measured points = 81 measured points). For all 81 points, the density was determined as an offline index over 3 repetitions.
For FTIR spectrum analysis, the Nicolet iS-50 instrument was used to detect the absorbance spectra of fiber samples at room temperature (BRUKER TENSOR-37, BRUKER OPTICS., Billerica, MA, USA). Each acquired spectrum resulted from an average of 64 scans with a resolution of 4 cm−1 in the wave range of 4000–650 cm−1. Moreover, at least five FTIR spectra were taken from different measured points for the same sample. That is, all 81 noticed points were measured using FTIR spectrum analysis with five repetitions. The function ‘‘msbackadj’’ in MATLAB software (MathWorks, version R2022a, Natick, MA, USA) was applied to adjust a multi-point baseline of raw signal with peaks. In addition, the “findpeaks” function was used to calculate the relative cyclization index (RCI) using Equation (1) [43,44]:
RCI = 0.29 × Abs   ( 1590 ) Abs   ( 2242 ) + 0.29 × Abs   ( 1590 )
where Abs (1590) denotes the absorbance intensity of imine groups (1590 cm−1, C=N functional groups), and Abs (2242) represents the absorbance intensity of nitrile groups (2242 cm−1, C≡N groups). The constant value of 0.29 indicates the absorption ratio between nitrile and imine functional groups.
The EPR spectrometer EMXplus with software package Xenon (BRUKER, Billerica, USA) at the Leibniz Institute for Solid State and Materials Research Dresden was used for all EPR measurements. The X-band spectrometer with a field modulation of 100 kHz and an ER4119 HS cylindrical cavity (active length: 40 mm) was used. The calibration of spin concentration was verified using alanine sample (ER 213ASC, BRUKER, Billerica, USA). The determination of the absolute spin concentration (FRC) was undertaken using spin counting procedures in the Xenon software package (BRUKER, version 1.1b60, Billerica, USA). The PF and SF were filled in a glass tube (ID: 2.36 mm). The values of the FRC were normalized to the sample mass. The operating conditions of the EPR spectrometer were 0.2 mT microwave modulation and 2 mW microwave power. The sweep time, center field, and field sweep amounted to 60 s, 352.24 mT, and 15 mT, respectively. Each sample was measured in ten scans. The FRC was evaluated using EPR at 6 different points in each trial, with measured point numbers 7, 14, 15, 20, 21, and 27, respectively (18 measurements for 3 trials).

3. Results and Discussion

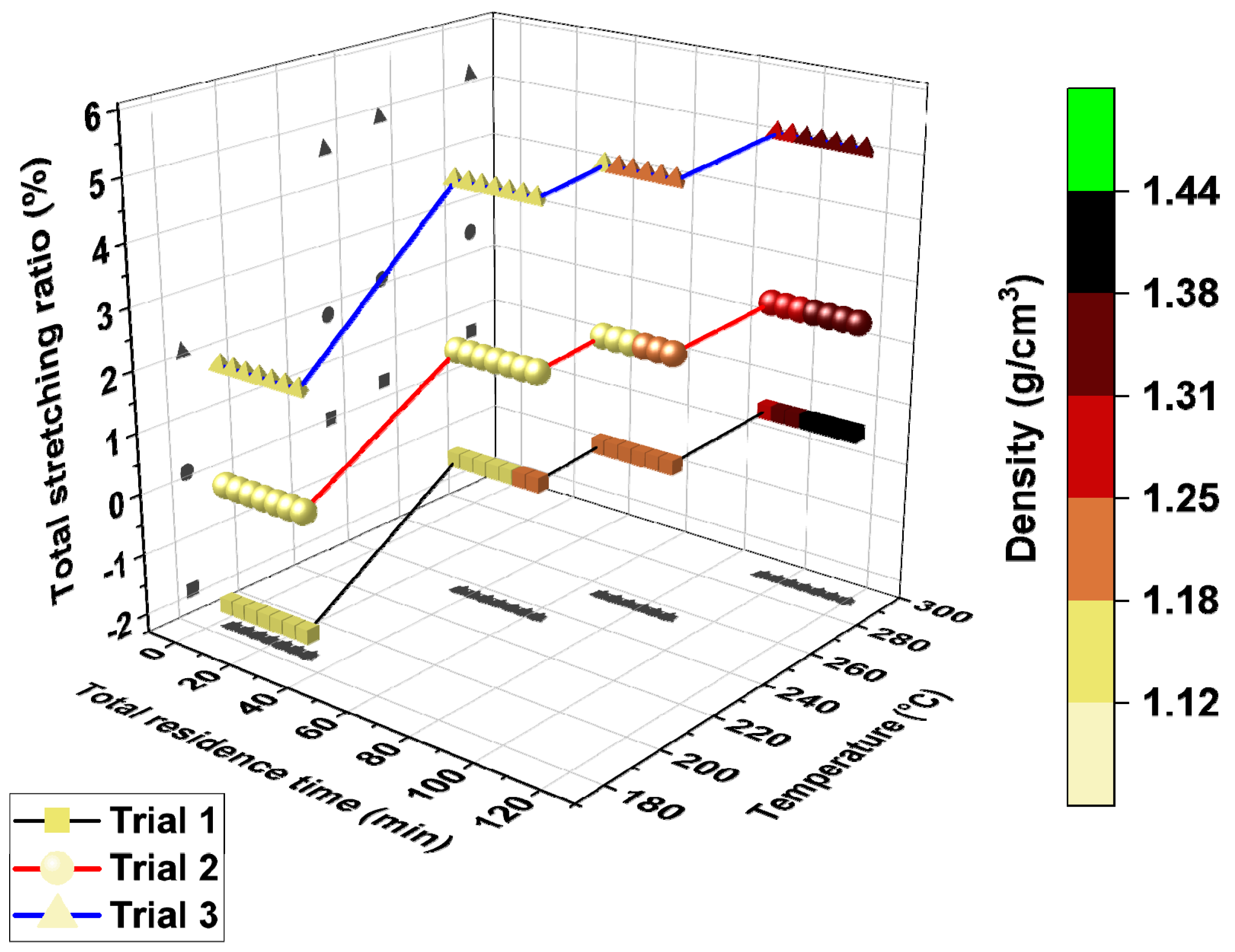
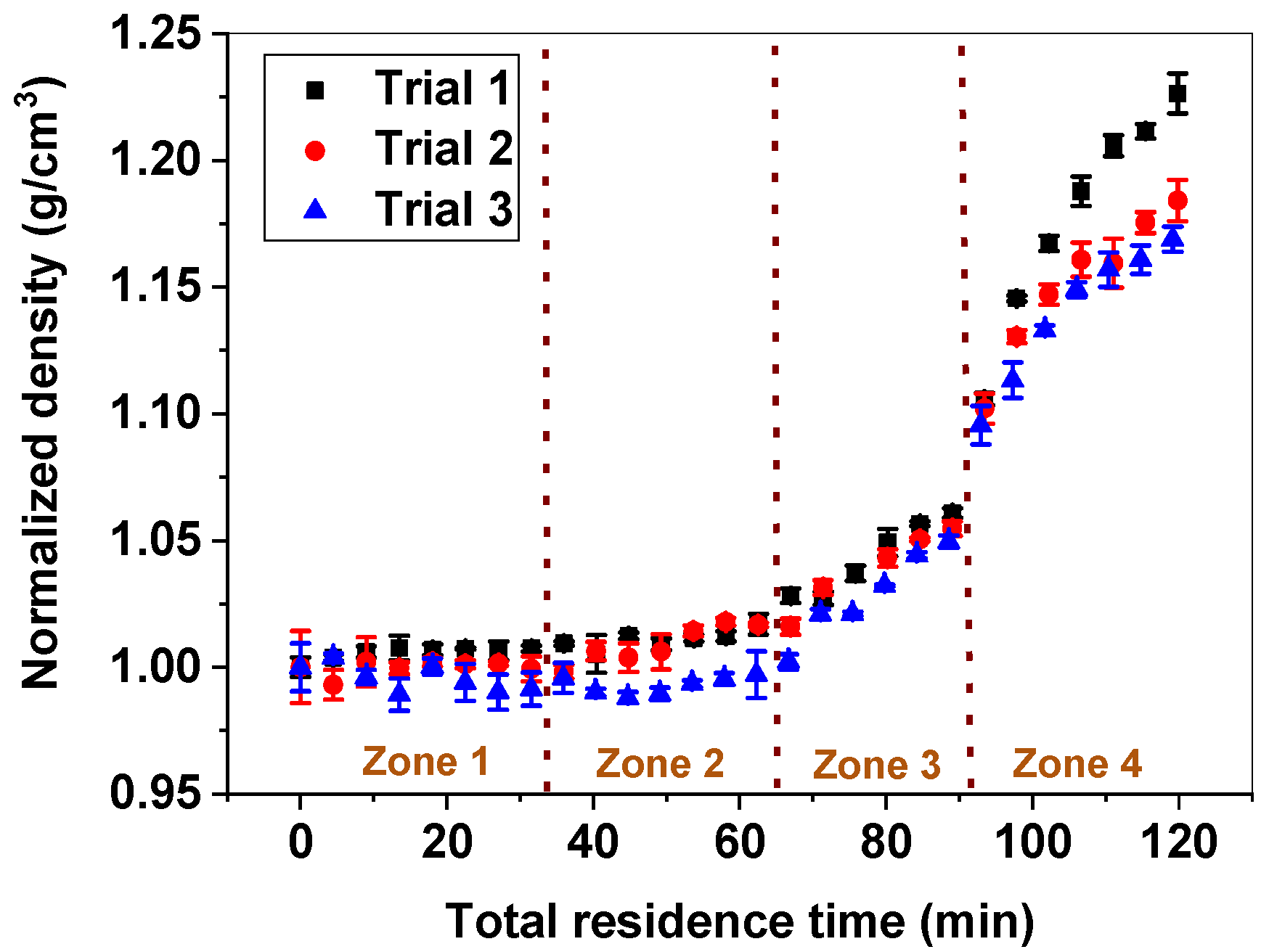
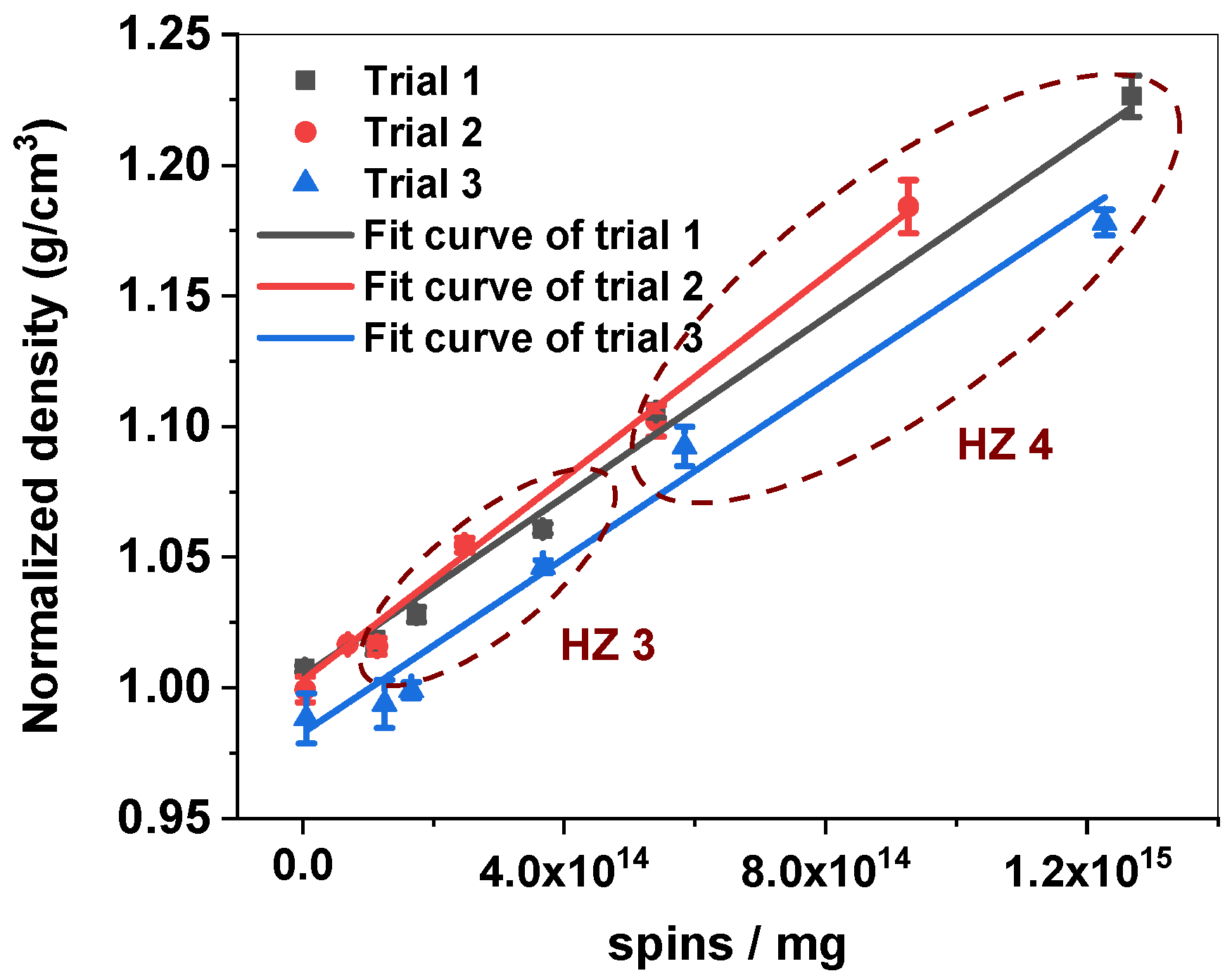
3.1. Effect of Stretching on Stabilized Fiber Density (Offline Indicator)

As linear chains of PAN-PF gradually evolve into ladder structures, macroscopic physical properties alter because of molecular changes. Among other physical properties, the density of PAN-SF is one of the most typical indicators for estimating the chemical structural alterations of PAN-PF through cyclization, dehydrogenation, and oxidation [15]. As a result, it can indicate process optimization pathways for the stabiliziation process. Figure 2 depicts the effect of three process variables on SF density: heat treatment time, temperature, and stretch ratio.
In contrast to the stretching profile, the density appears to increase with time and temperature profiles at first glance. The highest final density of 1.43 g/cm³ was attained in trial 1 (−1.92 to 0.58% stretch ratio), while trials 2 and 3 (0.07 to 2.38% stretch ratio and 2.01 to 5.11% stretch ratio) reached 1.35 and 1.37 g/cm³, respectively. Earlier investigations have shown that SF with densities between 1.34 and 1.39 g/cm³ are preferable for processing and frequently have outstanding and better tensile properties [19,45,46]. Hence, the produced SF perfectly meets the density requirements.
It is worth noting that, as shown in Figure 2, trial 1, with a stretching profile that starts with a negative value, results in the highest final density and also has the earliest change in density. This is in regard to chemical shrinkage in PAN fiber in the range of 175–250 °C, which is brought on by intramolecular and intermolecular reactions (cyclization and dehydrogenation) [47]. Within this temperature range, stretched fibers undergo intramolecular conversion, whereas negatively stretched fibers (trial 1) are hypothesized to initiate intermolecular reactions at sites of changing tacticity. The intermolecular cyclization network somehow holds the stabilized chains together, resulting in more voids in the SF [33] and possibly higher oxygen permeability, both of which are critical for the oxidation reaction and density rise [32]. Instead, the positive stretching ratio in trials 2 and 3 restrict the oxygen availability to the fibers, and therefore the oxidation reaction, as well as result in enhanced fiber orientation [27], and consequently higher crystallinity [31], and intramolecular conversion [33,47], which all leads to lower density.
Figure 3 displays the change in density as a function of treatment duration for trials 1-3, normalized to the density of the PF. In this study, the densities of PAN-PF in trials 1, 2, and 3 are 1.17 ± 0.01, 1.14 ± 0.02, and 1.17 ± 0.01 g/cm3, respectively. Therefore, the normalized density values (ND) are employed due to the discrepancies in PF densities. It should be noted that Figure 3 demonstrates the same variation pattern for the density index with time in the stabilization line throughout all three trials. Until the heat treatment implementation time exceeds 64 min, which corresponds to the first two HZs, the density does not change significantly. The results of HZ 3 and 4 are consistent with previous studies in that it is clear that chemical structural changes in the polymer backbone significantly improve the structure’s growing compactness as a function of processing parameters, resulting in denser SF [17,21,26]. All three trials show that the rate of density growth in HZ 4 deviates from linearity, which is consistent with observations of the non-linear rate of oxygen content growth at temperatures greater than 260 °C [26]. Both cyclic and oxidative dehydrogenation reduce the hydrogen element. In contrast, the oxygen element in the air atmosphere participated in the oxygen absorption reaction and increased the oxygen-containing groups [17,44]. In other words, the non-linear enhancement in density at 290 °C, as shown for all trials in Figure 3, results from heavy oxygen molecule absorption and light hydrogen molecule repulsion [17].
In order to analyze density variations versus residence time in HZ 4, the normalized density data were fitted with a non-linear exponential predictive model (Equation (2)) [13] in order to continuously monitor chemical shrinkage as a function of stabilization time (Figure 4). It was found, notably, that curves represented by an exponential growth to their maximum with constant parameters a, b, and tR could fit the change in density with consideration of dwell duration quite well:
ND = a   ( 1 − e − b   ( t − t R ) )
where ND represents normalized density values, a (pre-exponential), b (exponential), and tR are constant parameters, and t is residence time at 290 °C. The fit results of Figure 4 are detailed in Table 3.
The parameter (a) in Table 3 reflects a proportionality constant between chemical shrinkage and nitrile group concentration, which can be influenced by the inter- and intramolecular cyclization ratio caused by different stretching profiles [13]. As a consequence, trial 1 with a negative start in the stretching profile results in a higher degree of intermolecular cyclization, which is reflected in the higher value of a. Moreover, the kinetic parameters of the chemical cyclization (inter- and intramolecular cyclization) can be computed using the values of b as a constant parameter. Namely, the activation energy Ea is specifically obtained from Equation (3) as follows:
E a = R ( T ln c b )
where R, T, and c are the gas constant (8.314 J K−1 mol−1), the absolute temperature, and the constant parameter, respectively. The absolute temperature for HZ 4 is 563 K. In an isothermal condition, such as HZ 4, the activation energy is inversely related to the constant b, as shown in Equation (3). As the stretch ratio rises from trials 1 to 3, the value of the constant b in Table 3 falls. To put it another way, a higher stretch ratio (trial 3) causes a higher activation energy and a slower reaction rate [32]. Therefore, increased activation energy, intra- and intermolecular cyclization ratios, and crystallinity [31] can all be affected by increased stretch. Higher crystallinity and intramolecular cyclization can limit oxygen penetration and hence the extent of the oxidation reaction, resulting in a lower density of the stabilized fiber.

3.2. FTIR Results and Corresponding Relative Cyclization Index (Inline Soft Sensor)

To accomplish the establishment of FTIR as non-destructive tool with inline capability, it is critical to understand the dependency of FTIR spectra with regard to structural transformations for the optimization of the stabilization. The variation trend of the chemical reactions during the thermal stabilization process can be revealed by examining the changes in the peaks in the FTIR spectrum. Figure 5a depicts an overall view of the thermal treatment-related variation of functional groups in the PAN fiber structure at different stabilization times for trial 1. Samples with stabilization times of 31.5 min, 62.5 min, 89 min, and 119.8 min are the last measured points from HZs 1, 2, 3, and 4, respectively. As shown in Figure 5a, as PAN fibers pass from HZ 1 to HZ 4, the intensity of the C≡N peak (wavenumber 2242 cm−1) decreases while the intensity of the C=N peak (wavenumber 1590 cm−1) increases, indicating the formation of a heterocyclic structure [21]. Cyclization, which occurs as a result of the conversion of CN to C=N, was calculated using Equation (1) and plotted against residence time in Figure 5b. Figure 5b shows that the change pattern of the relative cyclization index versus residence time has the same sigmoid form for all three different trials. These findings are consistent with [43]. The two plateaus in HZ 1 (<22 min) and HZ 4 (>106 min) show that the lowest stabilization temperature requires a long stabilization time to create structural changes in PAN fiber and that, at the highest stabilization temperature, the conversion process is completed. Furthermore, in HZ 2, it is obviously demonstrated that trial 1 with an overall stretch ratio of 0% has a lower RCI% than trials 2 and 3. This could be caused by an increased orientation due to a higher stretch ratio, which leads to more cyclization in the amorphous area [31].
For further investigation of the relationship between the chemical and physical changes in the PAN-SF structure and to find quantitative relationships between the inline and offline indicators, normalized density-RCI plots are presented in Figure 6. In Figure 6a, which plots the normalized density versus the cyclization index, it is revealed that within HZs 1 to 3, the SF significantly undergoes changes in chemical structure with increasing heat treatment time, while HZ 4 increases in density with increasing time [17]. To take it a step further, it can be said that the RCI indicator in the chemical shrinkage range is a potent index for observing how process variables affect microstructural alterations during stabilization trials utilizing various stretching profiles. At elevated temperatures (>255 °C), the normalized density is a more excellent tool for monitoring structural changes. It has been proved that the RCI data using a cubic model clearly represents the fiber density during thermal stabilization [12] and that both measurement techniques are excellent predictors of the stability level of the PAN precursor Figure 6b depicts several cubic polynomial fitting curves for normalized density as a function of RCI and the cubic polynomial reported by Wilde et al. [12]. As can be seen, the fitting curve reported by Wilde et al. shows a significant deviation from the original data of ND versus RCI, especially in HZs 2 and 3. Therefore, three cubic functions were fitted to get the exact constants of the polynomial functions corresponding to the stretching profiles described in this work. The fitting parameters of these statistical models are summarized in Table 4.
It is interesting to note that for trial 2 starting at 0% stretch, the parameter (B3), which affects the sharpness of the cubic function, has the highest value. This indicates that trial 2 has the highest growth rate. Compared with trial 1, trial 2 achieves reduced ND and RCI values within our experimental time and temperature window. As an intriguing finding, it demonstrates that stretching profiles that begin with a negative stretch ratio at the chemical shrinkage area, while not having a larger growth rate (B3), do result in a higher value of ND. The R-squared data presented in Table 4 show the high accuracy of the fitting function for experiments 1 to 3.
Since the patterns of density changes with RCI for all three stretching profiles are similar, an independent model of the stretch profile can be presented. Although using an overall cubic polynomial function diminishes the fit’s accuracy, it can be used to anticipate density change in a continuous PAN fiber stabilization procedure with a stretching range of about −2% to 6%. In Figure 7, the overall cubic polynomial model is verified against data points from all trials 1, 2, and 3 for the continuous stabilization process. With the exception of one measured point from trial 3, the fitted model with a 2.5% error bar in Figure 7 shows that all values are within the predictable range. Table 5 displays the cubic polynomial constants and goodness of fit. According to the R-squared value, the cubic model explains 94.5% of the variability observed in the normalized density as a response attribute.

3.3. EPR Results and Corresponding Free Radical Concentration Index (Inline Soft Sensor)

PAN fibers are thermally treated in air to generate free radicals during the stabilization process. These free radicals then start the cyclization reaction of the nitrile groups, forming the ladder from the linear construction [48]. In order to expose the structural changes and the degree of stabilized PAN fibers, it will be useful to investigate the relationship between the FRC and the output fiber density in each HZ of the stabilization line. So far, there has been no cost-effective FRC analysis method that might potentially be applied inline. Therefore, FRC was only measured for a limited number of measurement sites, with sample numbers 7, 14, 15, 20, 21, and 27 corresponding to, respectively, the last measured point of HZ 1, the last measured point of HZ 2, the first measured point of HZ 3, the last measured point of HZ 3, the first measured point of HZ 4, and the last measured point of HZ 4 (as shown in Figure 1). Figure 8 illustrates the normalized density as a function of FRC for trials 1 to 3, and their corresponding linear fitting models. Table 6 presents the linear fitting parameters for different ND-FRC curves. As shown, there is a linear relationship between FRC and density with R2 of 0.98 for all trials. This makes FRC an appropriate index with inline usability for tracking structural and physical changes. It should be noted that, in accordance with [35], the changes in FRC, as depicted in Figure 8 with dotted lines, start to rapidly grow at temperatures higher than 235 °C (HZ 3 and 4). This means that the dehydrogenation reaction intensifies as the fiber moves from the low temperature to the higher temperature, which can result in free radicals that are able to react with oxygen and raise the fiber’s density. The higher FRC and lower density in trial 3 indicate that the reaction rate with oxygen is slower, which could be due to an increase in crystallinity caused by a higher stretching ratio. The accessibility of polymer chains to oxygen is reduced as crystallinity increases.
Interestingly, trial 2 has the highest parameter (f), which influences the slope of the linear fitting function, as shown in Table 6. This suggests that the ND grows higher with increasing FRC in experiment 2 than in trials 1 and 3, which is consistent with the data in B3 of Table 4.

4. Conclusions

The effect of a wide range of stretch ratios (−1.92% to 5.11%) on density as an offline index was investigated in a continuous stabilization line with four HZs—180 °C, 235 °C, 255 °C, and 290 °C—respectively. It is visible that negative stretching results in higher densities, while higher stretching leads to lower densities, caused by the induced orientation that reduces polymer chain accessibility to oxygen, resulting in a reduced oxidation reaction. The relative cycle index derived by the FTIR instrument identifies the chemical transformation well in the temperature ranges of HZs 2 and 3, while the free radical concentration index would be a useful inline tool to predict the structural change to the KGB of HZs 3 and 4. A cubic polynomial model vividly depicts the link between density and the cyclization index. Furthermore, the use of powerful quantitative EPR spectroscopy aids us in developing a linear model to forecast density variations. Therefore, the findings in this study open up the way for inline monitoring for density soft sensors for continuous stabilization. This will enable future industry 4.0-based automated energy optimization, efficiency process routes, and quality assurance for CF production.

Author Contributions

Conceptualization, M.S.B., D.S.J.W. and E.D.; methodology, M.S.B., J.W., D.S.J.W. and R.S.-G.; software, M.S.B.; validation, J.W., D.S.J.W. and E.D.; formal analysis, M.S.B., J.W., D.S.J.W., R.S.-G., N.I. and M.R.; investigation, M.S.B., J.W., D.S.J.W. and T.B.; resources, D.S.J.W., E.D. and M.G.; data curation, R.S.-G., N.I. and M.R.; writing—original draft preparation, M.S.B. and D.S.J.W.; writing—review and editing, M.S.B., J.W., D.S.J.W., R.S.-G., E.D., N.I., M.R., T.B., M.T.M. and M.G.; visualization, M.S.B., J.W., N.I. and M.R.; supervision, D.S.J.W., E.D., T.B., M.T.M. and M.G.; project administration, D.S.J.W. and T.B.; funding acquisition, T.B. and M.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the German Federal Ministry of Education and Research, grant number 20E2118A.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgments

The Article Processing Charge (APC) was funded by the joint publication funds of the TU Dresden, including Carl Gustav Carus Faculty of Medicine and the SLUB Dresden, as well as the Open Access Publication Funding of the DFG. The authors also wish to thank Uwe Gohs for the fruitful discussion.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Table A1. Experiment design and stabilization line parameters for trial 1 with a total stretch of 0.58%.
Table A1. Experiment design and stabilization line parameters for trial 1 with a total stretch of 0.58%.
Measured Point NumberResidence Time Per Zone (mins)Total Residence Time (mins)Stretching Ratio Per Zone (%)Total Stretching Ratio (%)
HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)
14.5---4.5−1.92---−1.92
29.0---9.0−1.92---−1.92
313.5---13.5−1.92---−1.92
418.0---18.0−1.92---−1.92
522.5---22.5−1.92---−1.92
627.0---27.0−1.92---−1.92
731.5---31.5−1.92---−1.92
831.54.4--36.0−1.921.92--0.00
931.58.8--40.4−1.921.92--0.00
1031.513.3--44.8−1.921.92--0.00
1131.517.7--49.3−1.921.92--0.00
1231.522.1--53.7−1.921.92--0.00
1331.526.5--58.1−1.921.92--0.00
1431.531.0--62.5−1.921.92--0.00
1531.531.04.4-67.0−1.921.920.29-0.29
1631.531.08.8-71.4−1.921.920.29-0.29
1731.531.013.3-75.8−1.921.920.29-0.29
1831.531.017.7-80.2−1.921.920.29-0.29
1931.531.022.1-84.6−1.921.920.29-0.29
2031.531.026.5-89.0−1.921.920.29-0.29
2131.531.026.54.493.4−1.921.920.290.290.58
2231.531.026.58.897.8−1.921.920.290.290.58
2331.531.026.513.3102.2−1.921.920.290.290.58
2431.531.026.517.7106.6−1.921.920.290.290.58
2531.531.026.522.1111.0−1.921.920.290.290.58
2631.531.026.526.5115.4−1.921.920.290.290.58
2731.531.026.531.0119.8−1.921.920290.290.58
Table A2. Experiment design and stabilization line parameters for trial 2 with a total stretch of 2.38%.
Table A2. Experiment design and stabilization line parameters for trial 2 with a total stretch of 2.38%.
Measured Point NumberResidence Time Per Zone (mins)Total Residence Time (mins)Stretching Ratio Per Zone (%)Total Stretching Ratio (%)
HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)
14.5---4.50.07---0.07
29.0---9.00.07---0.07
313.5---13.50.07---0.07
418.0---18.00.07---0.07
522.5---22.50.07---0.07
627.0---27.00.07---0.07
731.5---31.50.07---0.07
831.54.4--36.00.071.73--1.80
931.58.8--40.40.071.73--1.80
1031.513.3--44.80.071.73--1.80
1131.517.7--49.30.071.73--1.80
1231.522.1--53.70.071.73--1.80
1331.526.5--58.10.071.73--1.80
1431.531.0--62.50.071.73--1.80
1531.531.04.4-67.00.071.730.29-2.09
1631.531.08.8-71.40.071.730.29-2.09
1731.531.013.3-75.80.071.730.29-2.09
1831.531.017.7-80.20.071.730.29-2.09
1931.531.022.1-84.60.071.730.29-2.09
2031.531.026.5-89.00.071.730.29-2.09
2131.531.026.54.493.40.071.730.290.292.38
2231.531.026.58.897.80.071.730.290.292.38
2331.531.026.513.3102.20.071.730.290.292.38
2431.531.026.517.7106.60.071.730.290.292.38
2531.531.026.522.1111.00.071.730.290.292.38
2631.531.026.526.5115.40.071.730.290.292.38
2731.531.026.531.0119.80.071.730290.292.38
Table A3. Experiment design and stabilization line parameters for trial 3 with a total stretch of 5.11%.
Table A3. Experiment design and stabilization line parameters for trial 3 with a total stretch of 5.11%.
Measured Point NumberResidence Time Per Zone (mins)Total Residence Time (mins)Stretching Ratio Per Zone (%)Total Stretching Ratio (%)
HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)HZ 1 (180 °C)HZ 2 (235 °C)HZ 3 (255 °C)HZ 4 (290 °C)
1----0.0----0.00
14.5---4.52.01---2.01
29.0---9.02.01---2.01
313.5---13.52.01---2.01
418.0---18.02.01---2.01
522.5---22.52.01---2.01
627.0---27.02.01---2.01
731.5---31.52.01---2.01
831.54.4--36.02.012.52--4.53
931.58.8--40.42.012.52--4.53
1031.513.3--44.82.012.52--4.53
1131.517.7--49.32.012.52--4.53
1231.522.1--53.72.012.52--4.53
1331.526.5--58.12.012.52--4.53
1431.531.0--62.52.012.52--4.53
1531.531.04.4-67.02.012.520.29-4.82
1631.531.08.8-71.42.012.520.29-4.82
1731.531.013.3-75.82.012.520.29-4.82
1831.531.017.7-80.22.012.520.29-4.82
1931.531.022.1-84.62.012.520.29-4.82
2031.531.026.5-89.02.012.520.29-4.82
2131.531.026.54.493.42.012.520.290.295.11
2231.531.026.58.897.82.012.520.290.295.11
2331.531.026.513.3102.22.012.520.290.295.11
2431.531.026.517.7106.62.012.520.290.295.11
2531.531.026.522.1111.02.012.520.290.295.11
2631.531.026.526.5115.42.012.520.290.295.11
2731.531.026.531.0119.82.012.520290.295.11
Fibers 11 00068 g0a1
Figure A1. Light microscope image of the surface of the filaments in the fiber bundle: (a) trial 1, (b) trial 2, (c) trial 3, (d) the average filament diameter for trials 1, 2, and 3.
Figure A1. Light microscope image of the surface of the filaments in the fiber bundle: (a) trial 1, (b) trial 2, (c) trial 3, (d) the average filament diameter for trials 1, 2, and 3.
Fibers 11 00068 g0a1

References

  1. Chua, C.Y.X.; Liu, H.C.; Trani, N.D.; Susnjar, A.; Ho, J.; Scorrano, G.; Rhudy, J.; Sizovs, A.; Lolli, G.; Hernandez, N.; et al. Carbon fiber reinforced polymers for implantable medical devices. Biomaterials 2021, 271, 120719. [Google Scholar] [CrossRef] [PubMed]
  2. Fitzer, E. Pan-based carbon fibers—Present state and trend of the technology from the viewpoint of possibilities and limits to influence and to control the fiber properties by the process parameters. Carbon 1989, 27, 621–645. [Google Scholar] [CrossRef]
  3. Liu, C.; Li, Q.; Kang, W.; Lei, W.; Wang, X.; Lu, C.; Naebe, M. Structural design and mechanism analysis of hierarchical porous carbon fibers for advanced energy and environmental applications. J. Mater. Chem. A 2021, 10, 10–49. [Google Scholar] [CrossRef]
  4. Wang, G.; Lu, C.; Sun, T.; Li, Y. Accelerating the stabilization of polyacrylonitrile fibers by nitrogen pretreatment. J. Appl. Polym. Sci 2022, 139, 52129. [Google Scholar] [CrossRef]
  5. Zhang, J.; Lin, G.; Vaidya, U.; Wang, H. Past, present and future prospective of global carbon fibre composite developments and applications. Compos. Part B Eng. 2023, 250, 110463. [Google Scholar] [CrossRef]
  6. Böhm, R.; Thieme, M.; Wohlfahrt, D.; Wolz, D.S.; Richter, B.; Jäger, H. Reinforcement Systems for Carbon Concrete Composites Based on Low-Cost Carbon Fibers. Fibers 2018, 6, 56. [Google Scholar] [CrossRef] [Green Version]
  7. Kraft, R.; Kahnt, A.; Grauer, O.; Thieme, M.; Wolz, D.S.; Schlüter, D.; Tietze, M.; Curbach, M.; Holschemacher, K.; Jäger, H.; et al. Advanced Carbon Reinforced Concrete Technologies for Façade Elements of Nearly Zero-Energy Buildings. Materials 2022, 15, 1619. [Google Scholar] [CrossRef]
  8. Khayyam, H.; Jazar, R.N.; Nunna, S.; Golkarnarenji, G.; Badii, K.H.; Fakhrhoseini, S.M.; Kumar, S.; Naebe, M. PAN precursor fabrication, applications and thermal stabilization process in carbon fiber production: Experimental and mathematical modelling. Prog. Mater. Sci. 2020, 107, 100575. [Google Scholar] [CrossRef]
  9. Khayyam, H.; Naebe, M.; Milani, A.S.; Fakhrhoseini, S.M.; Date, A.; Shabani, B.; Atkiss, S.; Ramakrishna, S.; Fox, B.; Jazar, R.N. Improving energy efficiency of carbon fiber manufacturing through waste heat recovery: A circular economy approach with machine learning. Energy 2021, 225, 120113. [Google Scholar] [CrossRef]
  10. Bajaj, P.; Roopanwal, A.K. Thermal Stabilization of Acrylic Precursors for the Production of Carbon Fibers: An Overview. J. Macromol. Sci. Part C Polym. Rev. 1997, 37, 97–147. [Google Scholar] [CrossRef]
  11. Dunham, M.G.; Edie, D.D. Model of stabilization for pan-based carbon fiber precursor bundles. Carbon 1992, 30, 435–450. [Google Scholar] [CrossRef]
  12. Wilde, A.L.; Alexander, D.L.J.; Pierlot, A.P.; Denning, R.; Miao, M. Predicting the Cyclization Index and Density of Stabilized Polyacrylonitrile Tow from Processing Conditions. Fibers Polym. 2021, 22, 3241–3250. [Google Scholar] [CrossRef]
  13. Simitzis, J.; Soulis, S. Correlation of chemical shrinkage of polyacrylonitrile fibres with kinetics of cyclization. Polym. Int. 2008, 57, 99–105. [Google Scholar] [CrossRef]
  14. Shin, H.K.; Park, M.; Kim, H.-Y.; Park, S.-J. An overview of new oxidation methods for polyacrylonitrile-based carbon fibers. Carbon Lett. 2015, 16, 11–18. [Google Scholar] [CrossRef] [Green Version]
  15. Badii, K.; Church, J.S.; Golkarnarenji, G.; Naebe, M.; Khayyam, H. Chemical structure based prediction of PAN and oxidized PAN fiber density through a non-linear mathematical model. Polym. Degrad. Stab. 2016, 131, 53–61. [Google Scholar] [CrossRef]
  16. Mädler, J.; Richter, B.; Wolz, D.S.J.; Behnisch, T.; Böhm, R.; Jäger, H.; Gude, M.; Urbas, L. Hybride semi-parametrische Modellierung der thermooxidativen Stabilisierung von PAN-Precursorfasern. Chem. Ing. Tech. 2022, 94, 889–896. [Google Scholar] [CrossRef]
  17. Choi, J.; Kim, S.-S.; Chung, Y.-S.; Lee, S. Evolution of structural inhomogeneity in polyacrylonitrile fibers by oxidative stabilization. Carbon 2020, 165, 225–237. [Google Scholar] [CrossRef]
  18. Yang, J.; Liu, Y.; Liu, J.; Shen, Z.; Liang, J.; Wang, X. Rapid and Continuous Preparation of Polyacrylonitrile-Based Carbon Fibers with Electron-sBeam Irradiation Pretreatment. Materials 2018, 11, 1270. [Google Scholar] [CrossRef] [Green Version]
  19. Takaku, A.; Hashimoto, T.; Miyoshi, T. Tensile properties of carbon fibers from acrylic fibers stabilized under isothermal conditions. J. Appl. Polym. Sci. 1985, 30, 1565–1571. [Google Scholar] [CrossRef]
  20. Yu, M.; Wang, C.; Bai, Y.; Wang, Y.; Zhu, B. Evolution of tension during the thermal stabilization of polyacrylonitrile fibers under different parameters. J. Appl. Polym. Sci. 2006, 102, 5500–5506. [Google Scholar] [CrossRef]
  21. Nunna, S.; Maghe, M.; Rana, R.; Varley, R.J.; Knorr, D.B.; Sands, J.M.; Creighton, C.; Henderson, L.C.; Naebe, M. Time Dependent Structure and Property Evolution in Fibres during Continuous Carbon Fibre Manufacturing. Materials 2019, 12, 1069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Heine, M. Optimisation of the Reaction Conditions of Thermoplastic Polymer Fibers Like Polyacrylonitrile for Carbon Fiber Production. Ph.D. Dissertation, Technical University of Karlsruhe, Karlsruhe, Germany, 1989. [Google Scholar] [CrossRef]
  23. Jing, M.; Wang, C.; Bai, Y.; Zhu, B.; Wang, Y. Effect of temperatures in the rearmost stabilization zone on structure and properties of PAN-based oxidized fibers. Polym. Bull. 2007, 58, 541–551. [Google Scholar] [CrossRef]
  24. Leopold, A.-K.; Müller, M.T.; Zimmerer, C.; Bogar, M.S.; Richter, M.; Wolz, D.S.; Stommel, M. Influence of Temperature and Dose Rate of E-Beam Modification on Electron-Induced Changes in Polyacrylonitrile Fibers. Macro Chem. Phys. 2023, 224, 2200265. [Google Scholar] [CrossRef]
  25. Qin, X.; Lu, Y.; Xiao, H.; Zhao, W. Effect of heating and stretching polyacrylonitrile precursor fibers in steam on the properties of stabilized fibers and carbon fibers. Polym. Eng. Sci. 2013, 53, 827–832. [Google Scholar] [CrossRef]
  26. Yu, M.; Wang, C.; Bai, Y.; Wang, Y.; Wang, Q.; Liu, H. Combined Effect of Processing Parameters on Thermal Stabilization of PAN Fibers. Polym. Bull. 2006, 57, 525–533. [Google Scholar] [CrossRef]
  27. Liu, J.; Lian, F.; Ma, Z.; Liang, J. Effects of deformation-induced orientation on cyclization and oxidation of polyacrylonitrile fibers during stabilization process. Chin. J. Polym. Sci. 2012, 30, 786–795. [Google Scholar] [CrossRef]
  28. Wang, Y.; Wang, C.; Gao, Q.; Wang, Y.; Zhao, S.; Cui, B.; Yue, Y. Study on the relationship between chemical structure transformation and morphological change of polyacrylonitrile based preoxidized fibers. Eur. Polym. J. 2021, 159, 110742. [Google Scholar] [CrossRef]
  29. Wang, B.; Li, C.; Cao, W. Effect of stretching on the orientation structure and reaction behavior of PAN fiber during the thermal stabilization. Mater. Res. Express 2021, 8, 85603. [Google Scholar] [CrossRef]
  30. Wang, B.; Xiao, S.; Cao, W.; Shi, X.; Xu, L. Evolution of aggregation structure of polyacrylonitrile fibers in the cyclization reaction. J. Appl. Polym. Sci. 2012, 124, 3413–3418. [Google Scholar] [CrossRef]
  31. Wang, B.; Li, C.; Cao, W. Effect of Polyacrylonitrile Precursor Orientation on the Structures and Properties of Thermally Stabilized Carbon Fiber. Materials 2021, 14, 3237. [Google Scholar] [CrossRef]
  32. Gupta, A.; Harrison, I.R. New aspects in the oxidative stabilization of PAN-based carbon fibers: II. Carbon 1997, 35, 809–818. [Google Scholar] [CrossRef]
  33. Tsai, J.-S. Tension effects on the properties of oxidized polyacrylonitrile and carbon fibers during continuous oxidation. Polym. Eng. Sci. 1995, 35, 1313–1316. [Google Scholar] [CrossRef]
  34. Liu, W.; Wang, M.; Xing, Z.; Wu, G. The free radical species in polyacrylonitrile fibers induced by γ-radiation and their decay behaviors. Radiat. Phys. Chem. 2012, 81, 835–839. [Google Scholar] [CrossRef]
  35. Gohs, U.; Böhm, R.; Brünig, H.; Fischer, D.; Leopold, A.-K.; Malanin, M.; Müller, M.-T.; Cherif, C.; Richter, M.; Wolz, D.S.J.; et al. Influence of gas atmosphere on electron-induced reactions of polyacrylonitrile homopolymer powder at elevated temperature. Radiat. Phys. Chem. 2019, 158, 94–102. [Google Scholar] [CrossRef]
  36. Liu, W.; Shen, R.; Liu, S.; Tian, F.; Zhang, X.; Li, X.; Wang, M.; Tang, Z. Free radical evolution and decay of PAN nano-fibers formed by irradiation and thermal stabilization. Polym. Degrad. Stab. 2021, 188, 109570. [Google Scholar] [CrossRef]
  37. Park, S.; Yoo, S.H.; Kang, H.R.; Jo, S.M.; Joh, H.-I.; Lee, S. Comprehensive stabilization mechanism of electron-beam irradiated polyacrylonitrile fibers to shorten the conventional thermal treatment. Sci. Rep. 2016, 6, 27330. [Google Scholar] [CrossRef] [Green Version]
  38. Zhang, W.; Wang, M.; Zhang, W.; Liu, W.; Yang, C.; Shen, R.; Wu, G. Significantly reduced pre-oxidation period of PAN fibers by continuous electron beam irradiation: Optimization by monitoring radical variation. Polym. Degrad. Stab. 2018, 158, 72–82. [Google Scholar] [CrossRef]
  39. Zhang, W.; Wang, M.; Liu, W.; Yang, C.; Wu, G. Higher dose rate effect of 500-keV EB irradiation favoring free radical annealing and pre-oxidation of polyacrylonitrile fibers. Polym. Degrad. Stab. 2019, 167, 201–209. [Google Scholar] [CrossRef]
  40. Kirsten, M.; Meinl, J.; Schönfeld, K.; Michaelis, A.; Cherif, C. Characteristics of wet-spun and thermally treated poly acrylonitrile fibers. J. Appl. Polym. Sci. 2016, 133, 43698. [Google Scholar] [CrossRef]
  41. Nunna, S.; Blanchard, P.; Buckmaster, D.; Davis, S.; Naebe, M. Development of a cost model for the production of carbon fibres. Heliyon 2019, 5, e02698. [Google Scholar] [CrossRef] [Green Version]
  42. Kirsten, M.; Freudenberg, C.; Cherif, C. Carbonfasern, der Werkstoff des 21. Jahrhunderts. Beton-Und Stahlbetonbau 2015, 110, 8–15. [Google Scholar] [CrossRef]
  43. Collins, G.L.; Thomas, N.W.; Williams, G.E. Kinetic relationships between heat generation and nitrile consumption in the reaction of poly(acrylonitrile) in air at 265 °C. Carbon 1988, 26, 671–679. [Google Scholar] [CrossRef]
  44. Ge, Y.; Fu, Z.; Zhang, M.; Zhang, H. The role of structural evolution of polyacrylonitrile fibers during thermal oxidative stabilization on mechanical properties. J. Appl. Polym. Sci. 2021, 138, 49603. [Google Scholar] [CrossRef]
  45. Maghe, M.; Creighton, C.; Henderson, L.C.; Huson, M.G.; Nunna, S.; Atkiss, S.; Byrne, N.; Fox, B.L. Using ionic liquids to reduce energy consumption for carbon fibre production. J. Mater. Chem. A 2016, 4, 16619–16626. [Google Scholar] [CrossRef]
  46. Li, X.; Ji, X.; He, C. Evolution of the morphological and structural properties of plasticized spinning polyacrylonitrile fibers during the stabilization process. RSC Adv. 2015, 5, 81399–81406. [Google Scholar] [CrossRef]
  47. Fitzer, E.; Frohs, W.; Heine, M. Optimization of stabilization and carbonization treatment of PAN fibres and structural characterization of the resulting carbon fibres. Carbon 1986, 24, 387–395. [Google Scholar] [CrossRef]
  48. Barua, B.; Saha, M.C. Studies of reaction mechanisms during stabilization of electrospun polyacrylonitrile carbon nanofibers. Polym. Eng. Sci. 2018, 58, 1315–1321. [Google Scholar] [CrossRef]
Fibers 11 00068 g001
Figure 1. Schematics of the continuous thermal stabilization line used in this study: [(1)–(27)] represent various measurement points, [ε1 to ε4] applied stretch points.
Figure 1. Schematics of the continuous thermal stabilization line used in this study: [(1)–(27)] represent various measurement points, [ε1 to ε4] applied stretch points.
Fibers 11 00068 g001
Fibers 11 00068 g002
Figure 2. Changes of bulk density as a function of treatment time, temperature, and the stretching ratio.
Figure 2. Changes of bulk density as a function of treatment time, temperature, and the stretching ratio.
Fibers 11 00068 g002
Fibers 11 00068 g003
Figure 3. Normalized densities versus the total residence time of PAN fibers stabilized in air with different stretching profiles during a continuous stabilization line.
Figure 3. Normalized densities versus the total residence time of PAN fibers stabilized in air with different stretching profiles during a continuous stabilization line.
Fibers 11 00068 g003
Fibers 11 00068 g004
Figure 4. Fitted and normalized densities versus residence time for PAN-SF with various stretching ratios in HZ 4 from all three trials (absolute density normalized to the density of the least measured point in HZ 3).
Figure 4. Fitted and normalized densities versus residence time for PAN-SF with various stretching ratios in HZ 4 from all three trials (absolute density normalized to the density of the least measured point in HZ 3).
Fibers 11 00068 g004
Fibers 11 00068 g005
Figure 5. (a) Different FTIR spectra of PAN-PF and -SF spectra with different heat treatment times of 31.5 min, 62.5 min, 89 min, and 119.8 min for trial 1; (b) Relative cyclization index (RCI) versus the total residence time of PAN-SF stabilized in air with different stretching profiles during a continuous stabilization line.
Figure 5. (a) Different FTIR spectra of PAN-PF and -SF spectra with different heat treatment times of 31.5 min, 62.5 min, 89 min, and 119.8 min for trial 1; (b) Relative cyclization index (RCI) versus the total residence time of PAN-SF stabilized in air with different stretching profiles during a continuous stabilization line.
Fibers 11 00068 g005
Fibers 11 00068 g006
Figure 6. The normalized density versus RCI for trials 1, 2, and 3 with (a) the determined HZs and (b) the different fitted cubic polynomial functions, including the cubic function reported by Wilde et al. [12].
Figure 6. The normalized density versus RCI for trials 1, 2, and 3 with (a) the determined HZs and (b) the different fitted cubic polynomial functions, including the cubic function reported by Wilde et al. [12].
Fibers 11 00068 g006
Fibers 11 00068 g007
Figure 7. Experimental data of the normalized density versus RCI, as well as the overall fitted cubic polynomial curve with a 2.5% error bar.
Figure 7. Experimental data of the normalized density versus RCI, as well as the overall fitted cubic polynomial curve with a 2.5% error bar.
Fibers 11 00068 g007
Fibers 11 00068 g008
Figure 8. Fitted and experimental normalized densities against the free radical concentration (FRC) generated by thermal treatment in PAN fiber stabilization.
Figure 8. Fitted and experimental normalized densities against the free radical concentration (FRC) generated by thermal treatment in PAN fiber stabilization.
Fibers 11 00068 g008
Table 1. Characteristics of polyacrylontrile precursor fibers.
Table 1. Characteristics of polyacrylontrile precursor fibers.
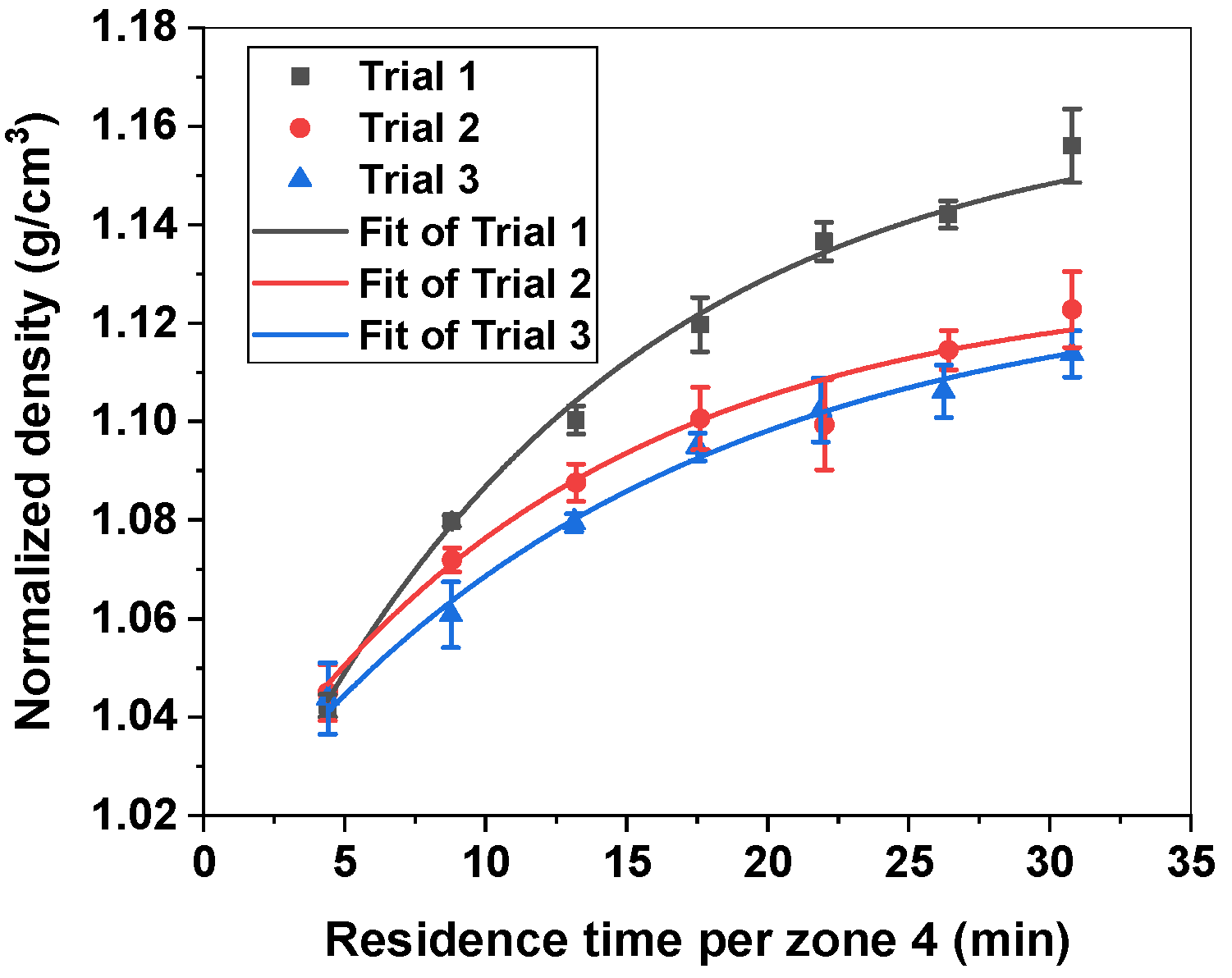
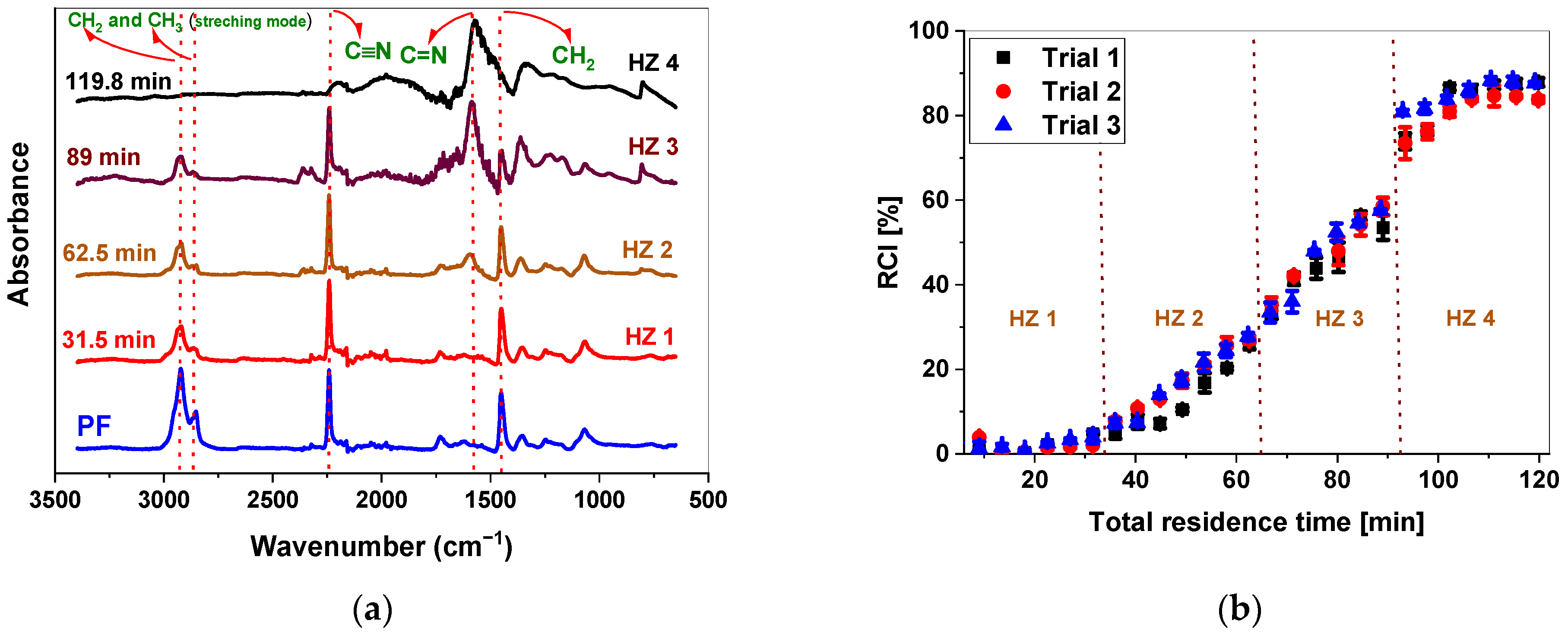
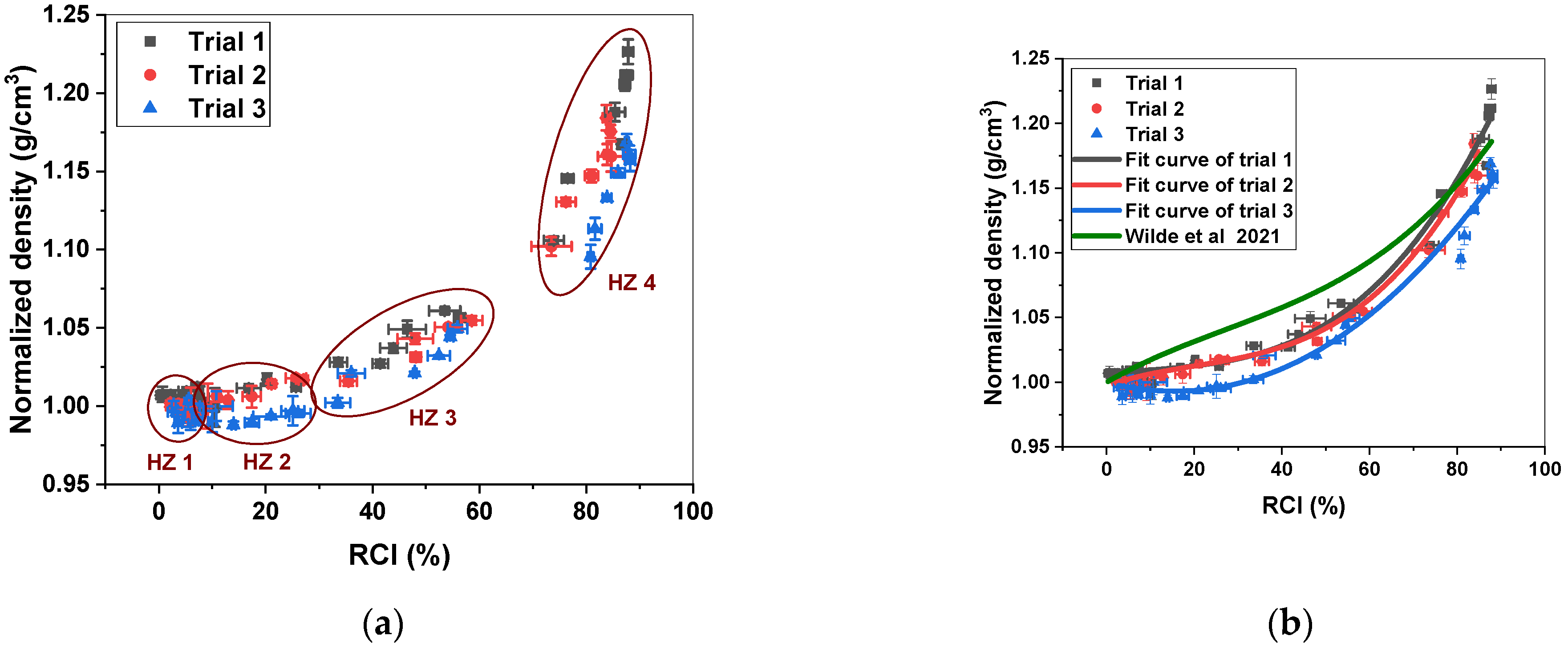
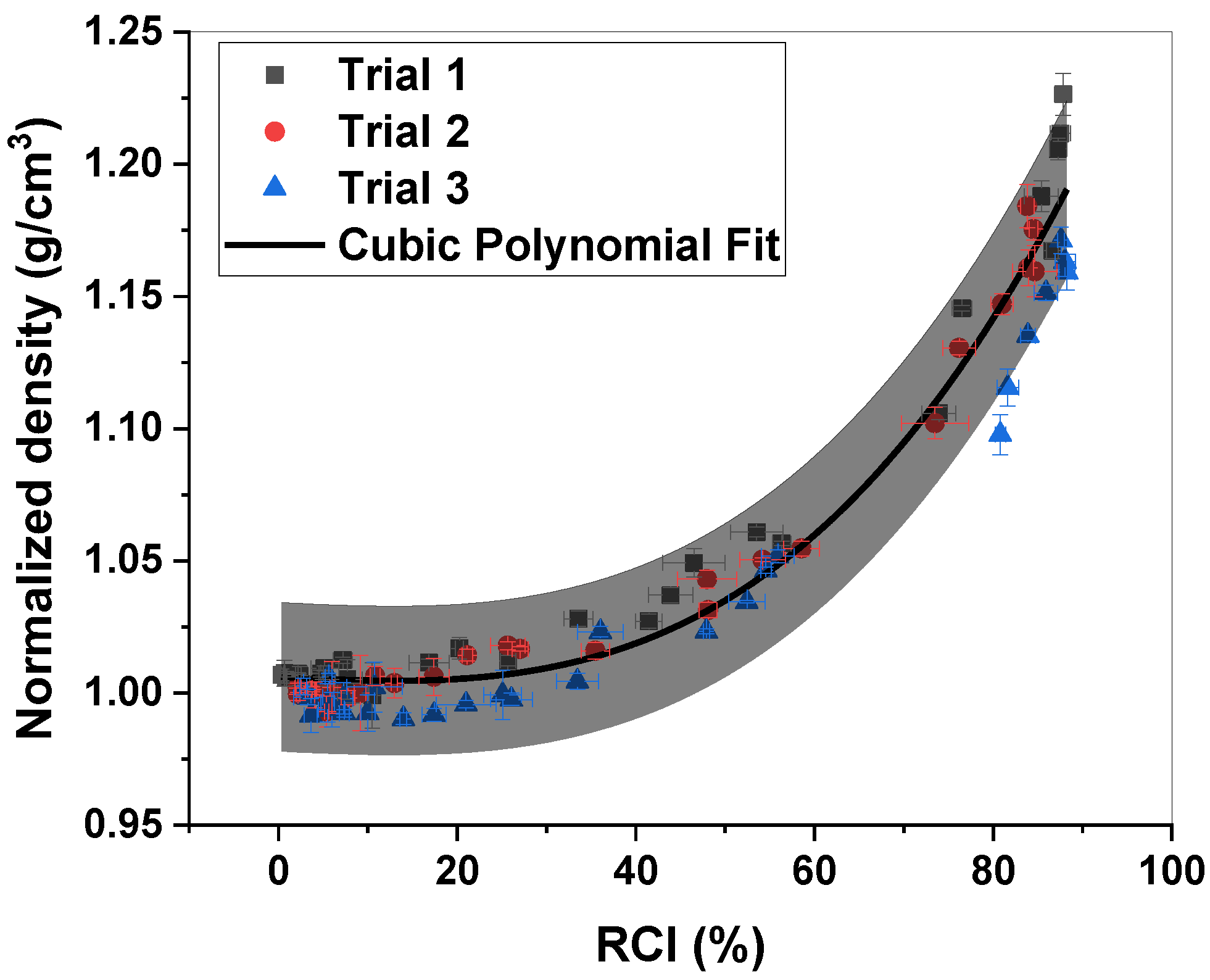
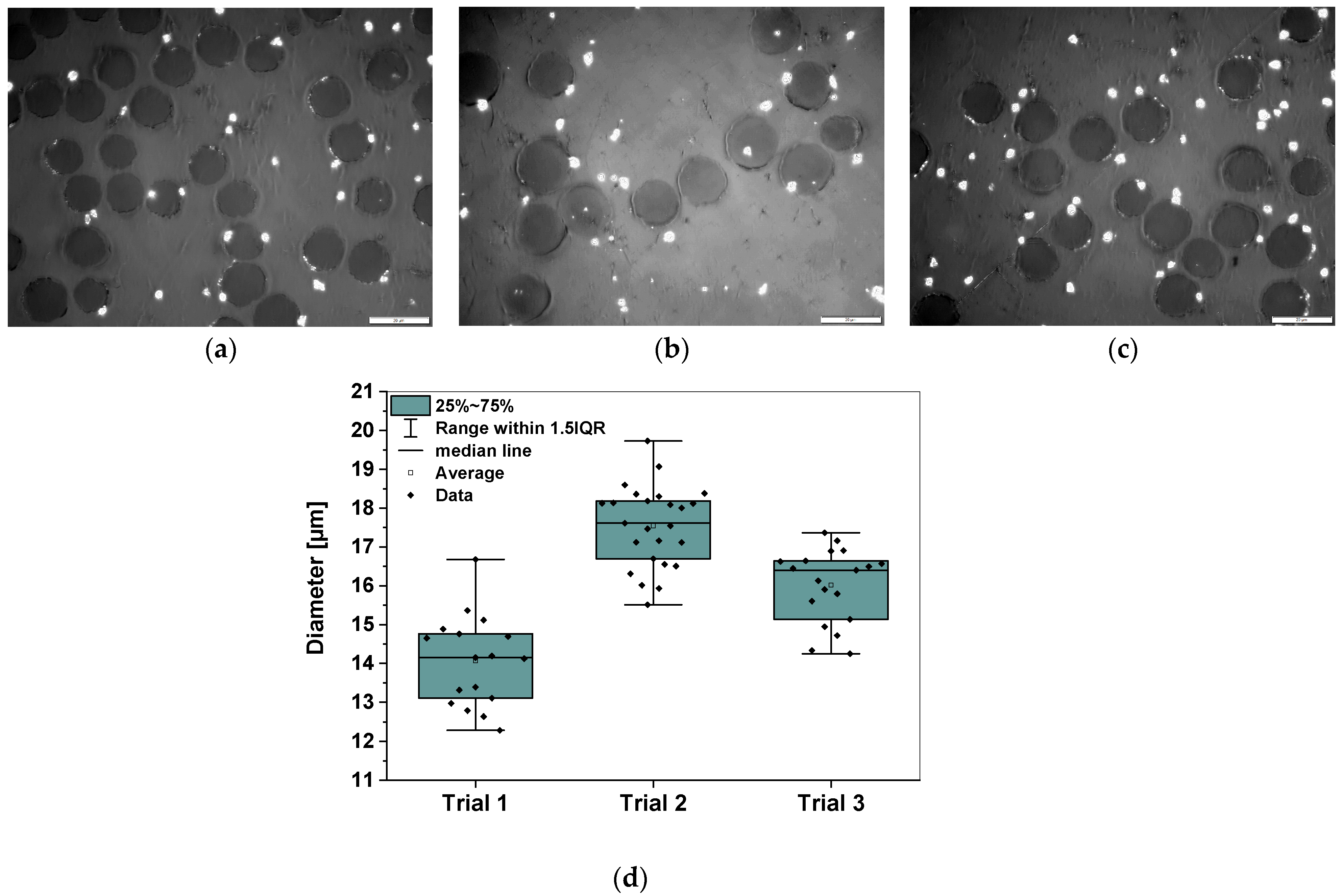
Precursor Fiber
(PAN Fiber)		Glass Transition
Temperature (°C)		Diameter
(µm)		Density
(g/cm3)
Trial 1100.414.06 ± 1.161.17 ± 0.01
Trial 2100.517.55 ± 0.991.14 ± 0.02
Trial 3100.515.93 ± 1.011.17 ± 0.01
Table 2. Applied stretching ratio for three different trials before each HZ.
Table 2. Applied stretching ratio for three different trials before each HZ.
Stretching Ratio (%)
ε1ε2ε3ε4εtotal *
Trial 1−1.921.920.290.290.58
Trial 20.071.730.290.292.38
Trial 32.012.520.290.295.11
* εtotal is the sum of all the stretching ratios applied to the fiber during the stabilization process.
Table 3. Corresponding fitting parameters of non-linear fit model from HZ 4 for all three trials with the different stretching profiles.
Table 3. Corresponding fitting parameters of non-linear fit model from HZ 4 for all three trials with the different stretching profiles.
ModelNon-Linear Fit
Equationy = a(1 − exp(−b(t − tonset)))
ExperimentsTrial 1Trial 2Trial 3
a1.16387 ± 0.006481.12834 ± 0.006431.12856 ± 0.00692
tR−23.97247 ± 2.77552−28.0991 ± 5.55655−33.29719 ± 5.89252
b0.07994 ± 0.008880.0808 ± 0.014960.06781 ± 0.01148
R-Squared (R2)0.996520.990860.98934
Table 4. Fitting parameters of cubic polynomial functions of the normalized density-RCI plot for trials 1, 2, and 3.
Table 4. Fitting parameters of cubic polynomial functions of the normalized density-RCI plot for trials 1, 2, and 3.
ModelCubic Polynomial Function
EquationND = A + B1 RCI + B2 RCI2 + B3 RCI3
ExperimentsTrial 1Trial 2Trial 3
Y-intercept (A)1.007 ± 0.0020.997 ± 0.0011.000 ± 0.005
B13.464 × 10−4 ± 4.143 × 10−40.001 ± 1.726 × 10−4−8.450 × 10−4 ± 5.253 × 10−4
B2−9.445 × 10−6 ± 1.237 × 10−5−2.870 × 10−5 ± 5.338 × 10−62.633 × 10−5 ± 1.374 × 10−5
B33.564 × 10−7 ± 9.556 × 10−84.705 × 10−7 ± 4.462 × 10−83.775 × 10−8 ± 9.760 × 10−8
R-squared (R2)0.9890.9940.981
Table 5. Overall fitting parameters for the three trials (trials 1, 2, and 3).
Table 5. Overall fitting parameters for the three trials (trials 1, 2, and 3).
ModelCubic Polynomial Fnction
EquationND = A + B1 RCI + B2 RCI2 + B3 RCI3
Y-intercept (A)1.006 ± 0.002
B1−1.688 × 10−4 ± 3.759 × 10−4
B21.039 × 10−6 ± 1.114 × 10−5
B32.784 × 10−7 ± 8.609 × 10−8
R-Squared (R2)0.946
Table 6. Fitting parameters of the linear function of the normalized density-FRC plot for trials 1, 2, and 3.
Table 6. Fitting parameters of the linear function of the normalized density-FRC plot for trials 1, 2, and 3.
ModelLinear Function
EquationND = d + f FRC
ExperimentsTrial 1Trial 2Trial 3
Y-intercept (d)1.004 ± 0.0031.003 ± 0.0020.983 ± 0.006
Slope (f)1.72 × 10−16 ± 1.12 × 10−171.94 × 10−16 ± 1.33 × 10−171.67 × 10−16 ± 1.14 × 10−17
R-Squared (R2)0.9830.9810.981
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sadeghi Bogar, M.; Wolf, J.; Wolz, D.S.J.; Seidel-Greiff, R.; Dmitrieva, E.; Israel, N.; Rosenkranz, M.; Behnisch, T.; Müller, M.T.; Gude, M. Sensitivity of Offline and Inline Indicators for Fiber Stretching in Continuous Polyacrylonitrile Stabilization. Fibers 2023, 11, 68. https://doi.org/10.3390/fib11080068

AMA Style

Sadeghi Bogar M, Wolf J, Wolz DSJ, Seidel-Greiff R, Dmitrieva E, Israel N, Rosenkranz M, Behnisch T, Müller MT, Gude M. Sensitivity of Offline and Inline Indicators for Fiber Stretching in Continuous Polyacrylonitrile Stabilization. Fibers. 2023; 11(8):68. https://doi.org/10.3390/fib11080068

Chicago/Turabian Style

Sadeghi Bogar, Mohsen, Jan Wolf, Daniel Sebastian Jens Wolz, Robert Seidel-Greiff, Evgenia Dmitrieva, Noel Israel, Marco Rosenkranz, Thomas Behnisch, Michael Thomas Müller, and Maik Gude. 2023. "Sensitivity of Offline and Inline Indicators for Fiber Stretching in Continuous Polyacrylonitrile Stabilization" Fibers 11, no. 8: 68. https://doi.org/10.3390/fib11080068

APA Style

Sadeghi Bogar, M., Wolf, J., Wolz, D. S. J., Seidel-Greiff, R., Dmitrieva, E., Israel, N., Rosenkranz, M., Behnisch, T., Müller, M. T., & Gude, M. (2023). Sensitivity of Offline and Inline Indicators for Fiber Stretching in Continuous Polyacrylonitrile Stabilization. Fibers, 11(8), 68. https://doi.org/10.3390/fib11080068

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop