Dispersive Propagation of Terahertz Pulses in a Plasmonic Fiber
Abstract
1. Introduction
2. Problem Formulation
3. Pulse Velocity and Dispersion
3.1. Propagation along a Bare Wire
3.2. Effect of a Dielectric Coating
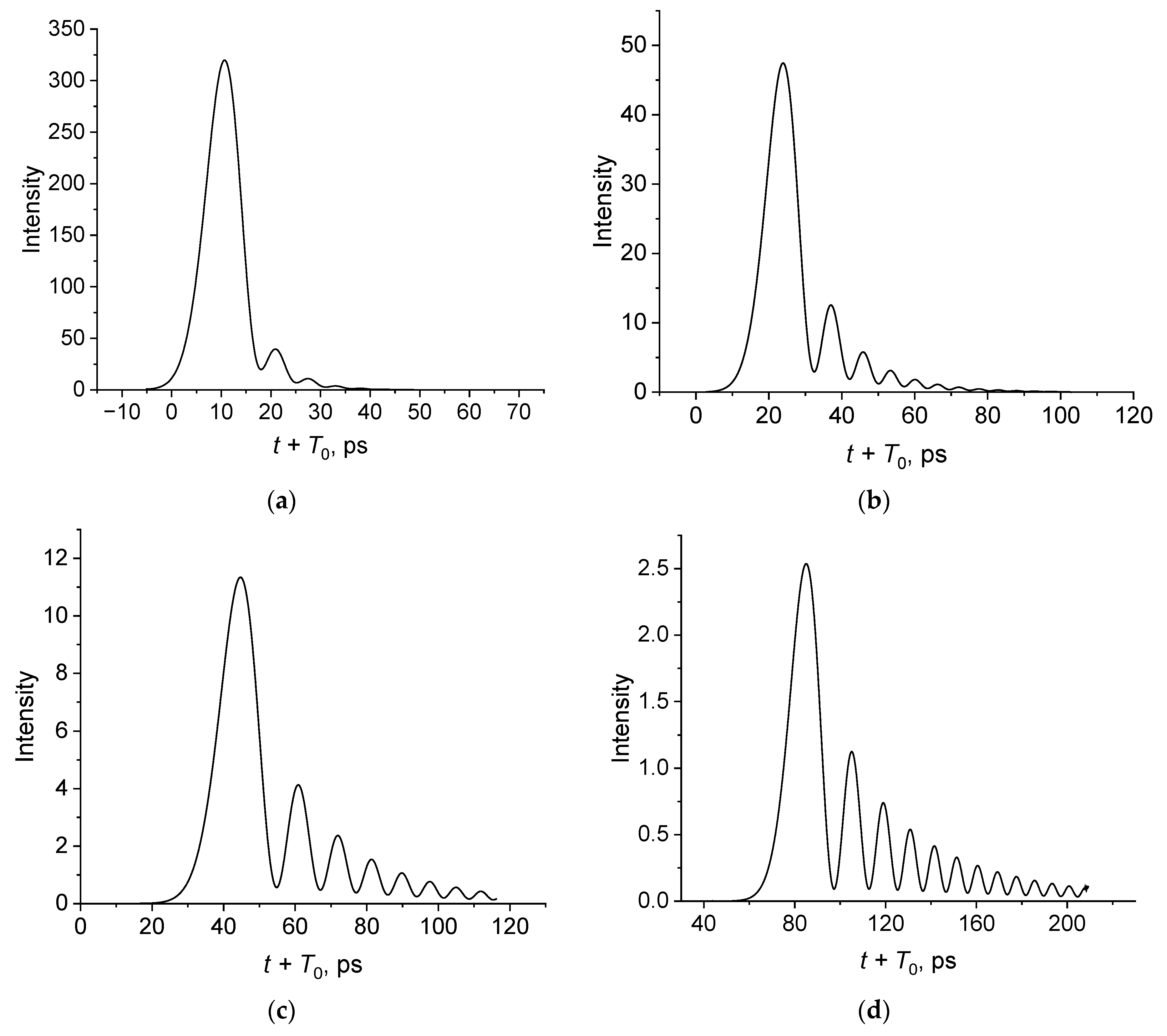
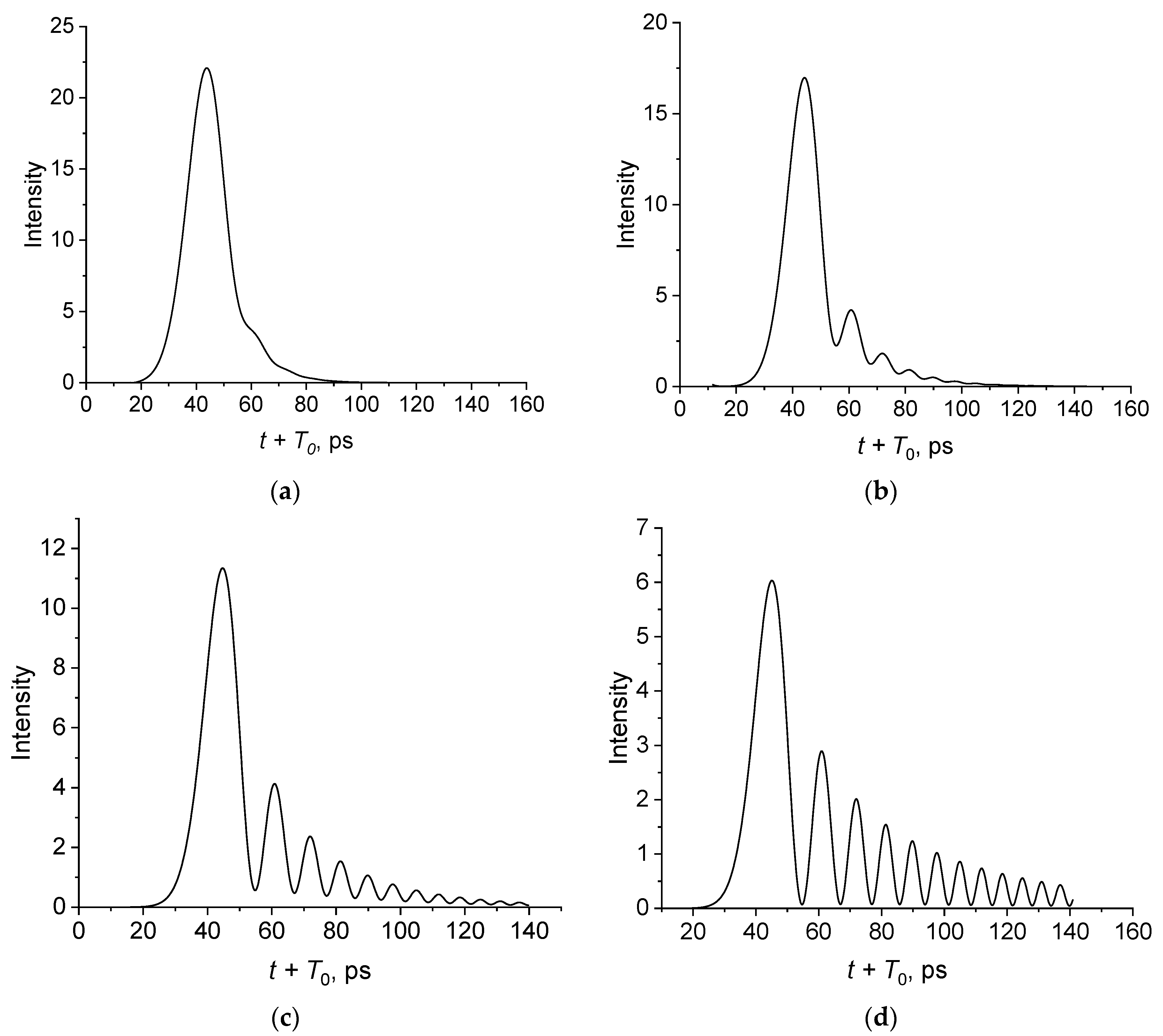
3.3. Effect of a Pulse Duration
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Mittleman, D.M. Metal wires for terahertz wave guiding. Nature 2004, 432, 376–379. [Google Scholar] [CrossRef]
- Wang, K.; Mittleman, D.M. Dispersion of surface plasmon polaritons on metal wires in the terahertz frequency range. Phys. Rev. Lett. 2006, 96, 157401. [Google Scholar] [CrossRef] [PubMed]
- Saxler, J.; Rivas, J.G.; Janke, C.; Pellemans, H.P.M.; Bolivar, P.H.; Kurz, H. Time-domain measurements of surface plasmon polaritons in the terahertz frequency range. Phys. Rev. B 2004, 69, 155427. [Google Scholar] [CrossRef]
- Van der Valk, N.C.J.; Planken, P.C.M. Effect of a dielectric coating on terahertz surface plasmon polaritons on metal wires. Appl. Phys. Lett. 2005, 87, 071106. [Google Scholar] [CrossRef]
- Bessel, P.; Niebur, A.; Kranz, D.; Lauth, J.; Dorfs, D. Probing Bidirectional Plasmon-Plasmon Coupling-Induced Hot Charge Carriers in Dual Plasmonic Au/CuS Nanocrystals. Small 2023, 19, 2206379. [Google Scholar] [CrossRef]
- Yi, R.; Wu, W.; Zhang, X. Femtosecond Autocorrelation of Localized Surface Plasmons. Nanomaterials 2023, 13, 1513. [Google Scholar] [CrossRef]
- Beiranvand, B.; Sobolev, A.S. A proposal for a multi-functional tunable dual-band plasmonic absorber consisting of a periodic array of elliptical grooves. J. Opt. 2020, 22, 105005. [Google Scholar] [CrossRef]
- Ntemogiannis, D.; Floropoulos, P.; Karoutsos, V.; Grammatikopoulos, S.; Poulopoulos, P.; Alexandropoulos, D. Plasmonic Nanostructuring by Means of Industrial-Friendly Laser Techniques. Photonics 2023, 10, 384. [Google Scholar] [CrossRef]
- Mitrofanov, O.; Harrington, J.A. Dielectric-lined cylindrical metallic THz waveguides: Mode structure and dispersion. Opt. Express 2010, 18, 1898–1903. [Google Scholar] [CrossRef]
- Chen, Y.; Song, Z.; Li, Y.; Hu, M.; Xing, Q.; Zhang, Z.; Chai, L.; Wang, C.Y. Effective surface plasmon polaritons on the metal wire with arrays of subwavelength grooves. Opt. Express 2006, 14, 13021–13029. [Google Scholar] [CrossRef]
- Williams, C.R.; Andrews, S.R.; Maier, S.; Fernandez-Dominguez, A.I.; Martín-Moreno, L.; Garcia-Vidal, F. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat. Photonics 2008, 2, 175–179. [Google Scholar] [CrossRef]
- Rivas, J.G.; Kuttge, M.; Bolivar, P.H.; Kurz, H.; Sánchez-Gil, J.A. Propagation of surface plasmon polaritons on semiconductor gratings. Phys. Rev. Lett. 2004, 93, 256804. [Google Scholar] [CrossRef] [PubMed]
- Gan, C.H.; Chu, H.S.; Li, E.P. Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 2012, 85, 125431. [Google Scholar] [CrossRef]
- Bulgakova, V.V.; Gerasimov, V.V.; Goldenberg, B.G.; Lemzyakov, A.G.; Malkin, A.M. Study of terahertz spoof surface plasmons on subwavelength gratings with dielectric substance in grooves. Phys. Procedia 2017, 201, 14–23. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Kong, L.B.; Du, C.H.; Liu, P.K. Spoof surface plasmon modes on doubly corrugated metal surfaces at terahertz frequencies. J. Phys. D Appl. Phys. 2016, 49, 235501. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Sun, J.; Li, L.; Yin, H. Asymmetric propagation of spoof surface plasmons along doubly corrugated metal surfaces. AIP Adv. 2020, 10, 045005. [Google Scholar] [CrossRef]
- Liu, Y.Q.; Li, L.; Yin, H. Surface plasmon dispersion and modes on the graphene metasurface with periodical ribbon arrays. Mater. Res. Express 2020, 7, 075801. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Li, L.; Yin, H. Long-range spoof surface plasmons (LRSSP) on the asymmetric double metal gratings. IEEE Photon. J. 2021, 13, 4800209. [Google Scholar] [CrossRef]
- Liu, Y.-Q.; Ren, Z.; Yin, H.; Sun, J.; Li, L. Dispersion Theory of Surface Plasmon Polaritons on Bilayer Graphene Metasurfaces. Nanomaterials 2022, 12, 1804. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.; Hoffmann, M.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Chen, S.H.; Chen, K.W.; Chu, K.R. A comparative study of single-wire and hollow metallic waveguides for terahertz waves. AIP Adv. 2018, 8, 115028. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Xia, L.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Han, J.; Zhang, W. Terahertz surface plasmonic waves: A review. Adv. Photonics 2020, 2, 014001. [Google Scholar] [CrossRef]
- Atakaramians, A.; Afshar, S.V.; Monro, T.M.; Abbott, D. Terahertz dielectric waveguides. Adv. Opt. Photon. 2013, 5, 169–215. [Google Scholar] [CrossRef]
- Islam, M.S.; Cordeiro, C.M.B.; Franco, M.A.R.; Sultana, J.; Cruz, A.L.S.; Abbott, D. Terahertz optical fibers [Invited]. Opt. Express 2020, 28, 16089–16117. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core. Fibers 2022, 10, 89. [Google Scholar] [CrossRef]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Snyder, A.W.; Love, J. Optical Waveguide Theory; Chapman and Hall: New York, NY, USA, 1983. [Google Scholar]
- Sommerfeld, A. Ueber die Fortpflanzung elektrodynamischer Wellen längs eines Drahtes. Ann. Phys. 1899, 303, 233–290. [Google Scholar] [CrossRef]
- Petrov, N.I. Synchrotron mechanism of X-ray and gamma-ray emissions in lightning and spark discharges. Sci. Rep. 2021, 11, 19824. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Knyazev, B.A.; Lemzyakov, A.G.; Nikitin, A.K.; Zhizhin, G.N. Growth of terahertz surface plasmon propagation length due to thin-layer dielectric coating. J. Opt. Soc. Am. B 2016, 33, 2196–2203. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.S.; Kim, G.J.; Jeon, S.G. Terahertz Dielectric Properties of Polymers. J. Korean Phys. Soc. 2006, 49, 513–517. [Google Scholar]
- Stefani, A.; Fleming, S.C.; Kuhlmey, B.T. Terahertz orbital angular momentum modes with flexible twisted hollow core antiresonant fiber. APL Photonics 2018, 3, 051708. [Google Scholar] [CrossRef]
- Hassani, A.; Dupuis, A.; Skorobogatiy, M. Porous polymer fibers for low-loss Terahertz guiding. Opt. Express 2008, 16, 6340–6351. [Google Scholar] [CrossRef] [PubMed]
- Paul, B.K.; Bhuiyan, T.; Abdulrazak, L.F.; Sarker, K.; Hassan, M.M.; Shariful, S.; Ahmed, K. Extremely low loss optical waveguide for terahertz pulse guidance. Results Phys. 2019, 15, 102666. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Gong, C.; Tian, H.; Sun, L.; Chen, P.; Lin, L.; Liu, W. 3D printed low-loss THz waveguide based on Kagome photonic crystal structure. Opt. Express 2016, 24, 22454–22460. [Google Scholar] [CrossRef]
- Stefani, A.; Skelton, J.H.; Tuniz, A. Bend losses in flexible polyurethane antiresonant terahertz waveguides. Opt. Exp. 2021, 29, 28692–28703. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef]
- Petrov, N.I. Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines 2023, 14, 38. [Google Scholar] [CrossRef]
- Farmani, A.; Miri, M.; Sheikhi, M.H. Tunable resonant Goos–Hänchen and Imbert–Fedorov shifts in total reflection of terahertz beams from graphene plasmonic metasurfaces. J. Opt. Soc. Am. B 2017, 34, 1097–1106. [Google Scholar] [CrossRef]
- Petrov, N.I.; Sokolov, Y.M.; Stoiakin, V.V.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Observation of Giant Angular Goos-Hanchen Shifts Enhanced by Surface Plasmon Resonance in Subwavelength Grating. Photonics 2023, 10, 180. [Google Scholar] [CrossRef]
- Kan, X.F.; Zou, Z.X.; Yin, C.; Xu, H.P.; Wang, X.P.; Han, Q.B.; Cao, Z.Q. Continuous Goos-Hänchen Shift of Vortex Beam via Symmetric Metal-Cladding Waveguide. Materials 2022, 15, 4267. [Google Scholar] [CrossRef] [PubMed]

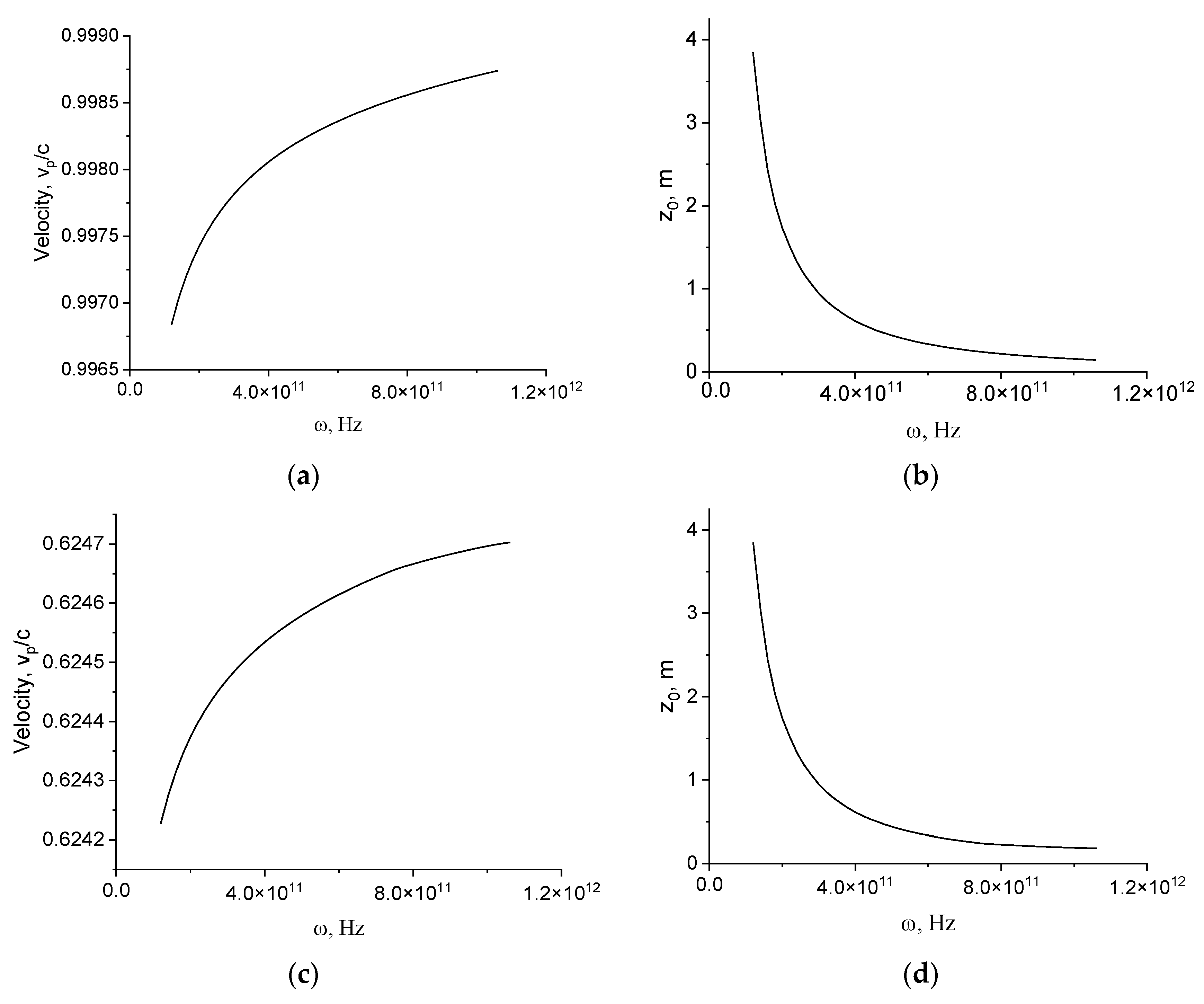
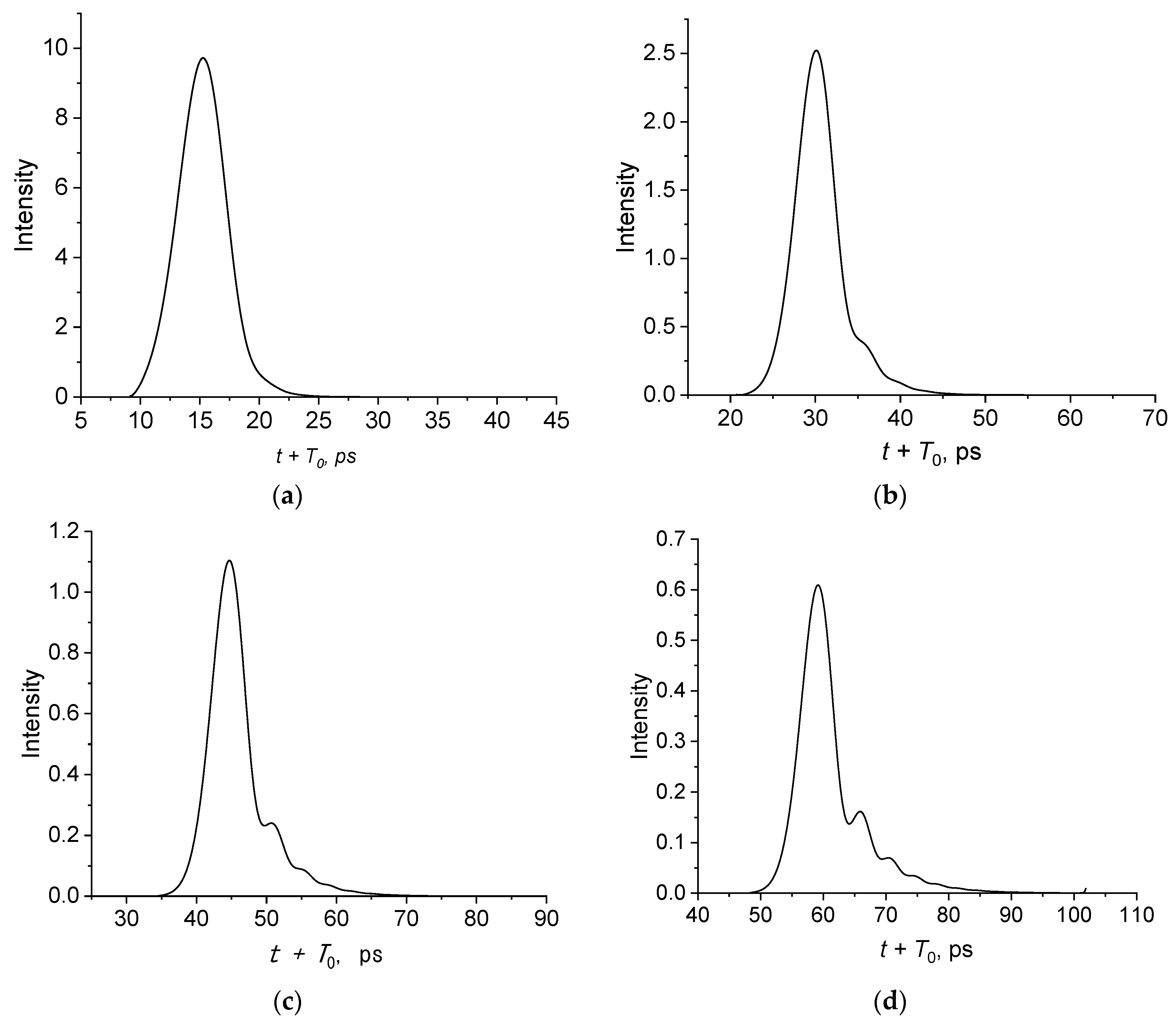
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, N.I. Dispersive Propagation of Terahertz Pulses in a Plasmonic Fiber. Fibers 2023, 11, 62. https://doi.org/10.3390/fib11070062
Petrov NI. Dispersive Propagation of Terahertz Pulses in a Plasmonic Fiber. Fibers. 2023; 11(7):62. https://doi.org/10.3390/fib11070062
Chicago/Turabian StylePetrov, Nikolai I. 2023. "Dispersive Propagation of Terahertz Pulses in a Plasmonic Fiber" Fibers 11, no. 7: 62. https://doi.org/10.3390/fib11070062
APA StylePetrov, N. I. (2023). Dispersive Propagation of Terahertz Pulses in a Plasmonic Fiber. Fibers, 11(7), 62. https://doi.org/10.3390/fib11070062





