Abstract
The numerical modeling of transverse laminar flow past a new type of hollow-fiber membranes with external profiling has been performed. A model system of parallel fibers with symmetrical parallel protrusion obstacles or grooves is considered. The absorption of point particles (solute or gas molecules) from a laminar transverse flow of a viscous incompressible liquid (gas) is calculated for a row of fibers, and the dependences of the efficiency of retention of particles by fibers on the Peclet (Pe), Reynolds (Re), and Schmidt (Sc) numbers and on the distance between neighbor fibers in a row are determined. The flow velocity and concentration fields are calculated by numerical solution of the Navier–Stokes equations and the convective diffusion equation in a wide range of Peclet numbers Pe = 0.1 − 105 for Sc = 1, 10, 1000 and Re ≤ 100.
1. Introduction
One of the promising directions for intensifying the processes of membrane separation, catalysis, and filtration is to increase the surface area of the streamlined selective membrane layer or the surface of the filter collector (fibers or granules) [1,2,3,4,5,6,7]. Hollow-fiber [2] and flat [3] profiled membranes with protrusions and grooves both on the outer and inner surfaces are used in various applications. Hollow-fiber membranes with external and internal profiling were considered in [2,3,4,5,6]. For inertial flows the greatest effect from profiling is achieved with an increase in the Reynolds number, when the surface protrusions serve as the so-called turbulence promoters (spacers) that reduce the effect of concentration (temperature) polarization due to the destruction of the boundary layers. This effect has long been used in convective heat and mass transfer [7].
In high-efficient aerosol filtration, a related direction of investigation is under development, which is associated with the coating of filter fibers with highly porous permeable layers (for example, from radial nanowhiskers) [8]. Coaxial porous layers or “furs” act as extra filters and provide a noticeable increase in the efficiency of capture of suspended particles on the modified fibers with little additional flow resistance. The theory of deposition of aerosol nano and sub-micron particles on fibers with such porous shells was developed in [9,10].
In this communication, the problem of the absorption of point-like particles (solute or gas molecules or suspended tiny macro-particles) in a model system of profiled fibers in a transverse laminar flow at Reynolds numbers is solved. This range of the Re values corresponds to typical operating conditions of a membrane contactor employed for the separation of gases and liquids. However, in a number of processes, for example, in membrane distillation or heat exchangers, the Reynolds numbers can be several times higher. We assume that the particle size is much smaller than the fiber radius and that particles are completely absorbed (retained) upon contact with the surface. We assume that the particles do not interact with each other in the flow.
The solute transport towards the streamlined fiber is strongly influenced by the velocity distribution in the vicinity of the fiber. For very slow “creeping” flows at low Reynolds numbers of Re < 1 the flow field within fibrous media depends on the single parameter—the fiber packing density α, whereas at higher velocities at Re ≥ 1 it is governed by the two parameters, α and Re. In studying hydrodynamic and transport processes in real porous media, the models with prescribed well-defined structure and with known flow fields are used in order to eliminate the influence of the structural uncertainty. The ordered systems of parallel cylinders with circular cross-sections, arranged normally to the laminar flow, with square or hexagonal packing, or a single row of parallel fibers are usually used as models [11]. These models account for the constrained flow between the fibers, and are applicable for studies of membrane contactors, fibrous filters, and other fibrous media. The so-called cell models with axially symmetric flow past a fiber in a cell are commonly used at low Reynolds numbers [12,13,14,15]. These models are highly popular since they provide simple exact analytical expressions for the flow velocities and for the fiber drag force. The Kuwabara cell model was found experimentally and theoretically to describe the flow within a lattice of fibers with hexagonal packing [11]. This model helped to clarify the mass transfer of Brownian and Langevin (inertial) particles in symmetric flows past fibers [11]. One should remember that the Kuwabara cell solution is derived in the low packing density limit from a more general analytical solution for the transverse Stokes flow past a hexagonal lattice of parallel fibers, which was first derived by Golovin and Lopatin in [16].
It should be noted the cell models have their limits of applicability. They are not quite applicable for the case of non-symmetrical inertial transverse flows at non-zero Reynolds numbers, Re > 1, and for dense systems of fibers, such as hollow-fiber membrane contactors, which are characterized by a high packing density with > 0.3 ( > 0.5, where is the fiber radius, is the distance between the axes of neighboring fibers). It is still little recognized, judging by the appearing articles, that the cell models give incorrect results for the efficiency of diffusion deposition of the point particles at low Peclet numbers, as was first shown in [17]. Additionally, the cell models cannot be used for modeling the process deposition of inertial particles at high Stokes numbers, since the particle inlet distance is limited by the cell radius. In all of the mentioned “negative” cases, models of a single row of parallel fibers or multi-fiber lattices come to help [18,19,20,21,22].
As a simple model, we use a row of parallel fibers. We consider fibers of radius with rectangular protrusions of various heights on the surface, as shown in Figure 1. Note that we do not consider turbulence. The main attention is paid to the study of the contribution of the profiled surface to mass transport in the laminar regime, which is typical for a large number of membrane and filtration processes. In the solution, we use the approach developed for calculating the convective-diffusion transport in a laminar flow past a row of circular fibers with a smooth surface [17,23,24,25].
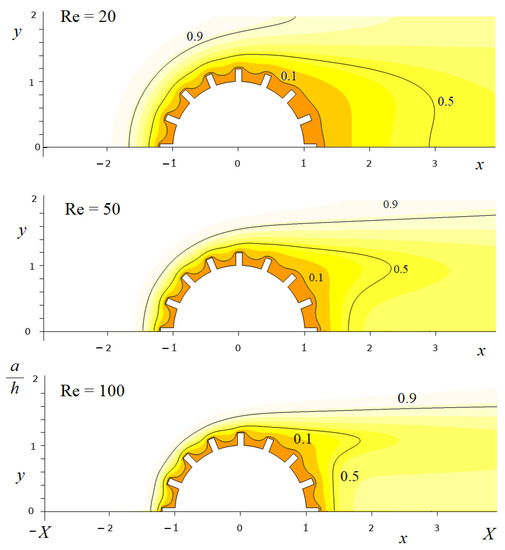
Figure 1.
Distribution of the dimensionless concentration of the point particles in the transverse flow past a row of parallel profiled fibers with protrusions for different Reynolds numbers; the concentration values are marked on the curves; Sc = 1; a/h = 0.5; flow direction from left to right.
2. Governing Equations and Simulation Methods
The fields of flow of a viscous incompressible liquid (gas) and the field of the particle concentration past a row of parallel fibers are found by numerical simulation. The computational cell with dimensionless length 2 and height is shown in Figure 1. Here is the distance between the axes of parallel fibers. Based on the calculated concentration fields, the multi-parametric dependences of the efficiency of particle deposition on the fiber are determined. To calculate the flow field of a viscous incompressible liquid (gas) and the concentration field of the dissolved component, we numerically solve the Navier–Stokes equations
and the equation of convective diffusion in the stationary approximation
where is pressure, is the concentration of the dissolved component in the flow, is the flow velocity vector, and are the x- and y-direction components, respectively (the axis direction is shown in Figure 1); is the Reynolds number, is the Peclet number, is the Schmidt number, is the kinematic viscosity, is the diffusion coefficient of the point particles, is the Laplace operator, is the nabla operator. Here, all quantities are reduced to a dimensionless form by normalization to the fiber radius , the unperturbed inlet velocity and concentration . We set the following conditions on a streamlined solid surface: a no-slip condition for the velocity components, , and the condition of a constant concentration, . On the side faces of the computational cells, we use the symmetry conditions for the velocity and concentration; the conditions of the homogeneous undisturbed flow, = 1, = 1, are set at the inlet, and the conditions of zero velocity gradients and zero concentration gradient are imposed at the outlet.
Numerical solution of the convective diffusion processes is a nontrivial task. The current state of this branch of computational mathematics and physics is described in [26,27,28,29,30,31,32,33,34,35,36]. We used a finite-difference approach for solving the governing equations on a composite grid, defined in Cartesian and polar co-ordinates. The “polar” grid was placed along the fiber surface, while the Cartesian grid was placed in the elongated channel-type region of the simulation cell (inlet and outlet regions, bounded with symmetry lines, Figure 1). The two overlapping grids were matched with interpolation conditions. We have used the ideas of the work [26]. The Navier–Stokes equations were solved in the stream function-vorticity formulation [27]. The convection diffusion and vorticity transport equations were solved with the help of the “boundary layer type” scheme. It is known that the conventional schemes with central differences show instability in the convective diffusion regime at high Peclet numbers. Thus, we used the second-order monotone conservative scheme proposed by Berkovskii and Polevikov [28], which is defined on a five-point stencil (on a nine-point stencil, if half-integer indices are taken into account). In this scheme, to stabilize the oscillating solution, the convective terms of the convective diffusion equation were approximated by asymmetric upstream differences, while a regularization term was introduced into the diffusion terms in order to increase the order of approximation. This absolutely stable monotone scheme is an extension of the Allen-Southwell scheme [29]. The resulting five-diagonal system of algebraic equations for this scheme is equivalent to the block three-diagonal system, which was solved by the matrix sweep method [30]. The computations were performed on the 2-processor 128 Gb RAM server.
The knowledge of the velocity field around a fiber enables one to calculate the distribution of concentration via Equation (2) and to estimate the fiber row resistance to flow. The dimensionless pressure drop across the single fiber row is related with the fiber drag force as [22]. The dimensionless drag force per unit length of a fiber is found as the surface integral of the projection of the local total stress on the flow direction
where is the local total stress, —the viscous stress tensor, I—the unit tensor, n—the outer normal vector to the surface, —the surface element, —the fiber surface area.
The knowledge of the concentration field around a fiber enables one to calculate the dimensionless fiber retention efficiency [37]
where is the normal to the fiber surface, is an element of the surface. This quantity can be expressed via commonly used Sherwood number , [38]. The value of can be found also from the simulated concentration behind the row of fibers at the outlet of the computational cell at
Retention efficiency of a row of fibers is related to the output concentration as . The retention efficiency for a fibrous bed—a system of many rows of fibers, is found by the formula
where is the number of rows of fibers. Formula (6) is applicable provided that = , >> 1.
3. Simulation Results and Discussion
The calculations were performed for a row of fibers with different profiling heights (Figure 1). Figure 1 shows the concentration profiles for a transverse flow around a fiber in a row at for different Reynolds numbers (given in the Figure 1), calculated for an example of a dense row of fibers with = 0.5. Note that small Schmidt numbers correspond to convective diffusion in a gas, and large ones for a liquid. Let us show what the increase in the height of protrusions on a fiber of a given radius leads to. It follows from the calculations that the creation of small protrusions on the fiber leads to a noticeable increase in its resistance (Figure 2) and only a slight increase in the efficiency of retention of the particles from the external flow (Figure 3). An increase in the height of the protrusions (while maintaining the distance between the axes of the fibers ) leads to a noticeable increase in efficiency and a sharp increase in resistance. In the examples shown in Figure 2 and Figure 3, the number of rectangular protrusions was = 16 with a protrusion thickness of 0.1 (in units of ). The next, Figure 4, shows which part of point particles is absorbed on the protrusions, and which part is absorbed on the fiber with radius . It follows from these figures that, as the protrusion height increases, the fraction of particles reaching the fiber decreases. Absorption occurs mainly on the outer radius, on the protrusions. This effect is stronger for the absorption of molecules from a gas at small Sc values (Figure 4a) than from a liquid, which is characterized by higher Sc values. Further, a fiber of a given outer radius was considered not with protrusions, but with symmetrical parallel grooves. Calculations have shown that the deepening of the grooves does not lead to a noticeable decrease in the resistance force of the fiber to the flow (Figure 2, curve 6), and does not contribute to a noticeable increase in the retention efficiency of the substance supplied from the convective flow. However, these conclusions are valid when the condition of a zero concentration on the outer surface is imposed.
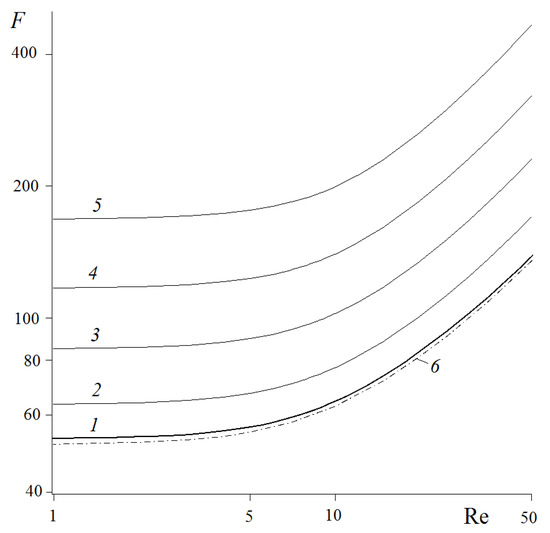
Figure 2.
Dimensionless drag forces per unit length of profiled fibers with parallel rectangular protrusion obstacles (curves 2–5) with a protrusion thickness of 0.1 and a protrusion height of 0.1 (2), 0.2 (3), 0.3 (4), 0.4 (5), solid curve 1—smooth fiber; dashed-dotted curve 6—a fiber with parallel grooves with width and depth equal to 0.1 and 0.4; a/h = 0.5.
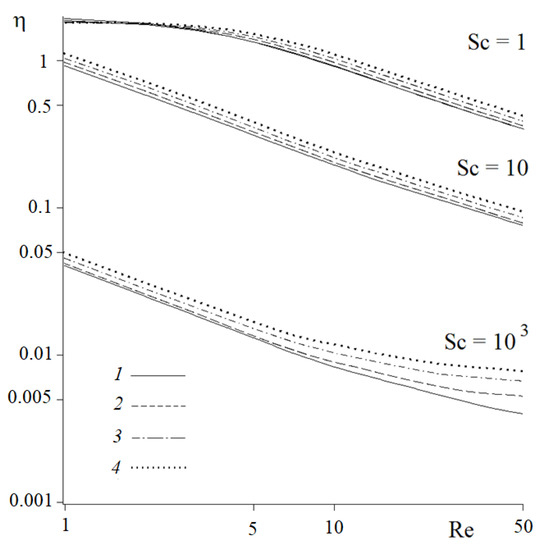
Figure 3.
Retention efficiencies for a profiled fiber with protrusion obstacles vs. Reynolds number at different values of the Schmidt number (given in the Figure); the thickness of the protrusion is 0.1 and the heights of the protrusions are 0.1 (1), 0.2 (2), 0.3 (3), 0.4 (4); a/h = 0.5.
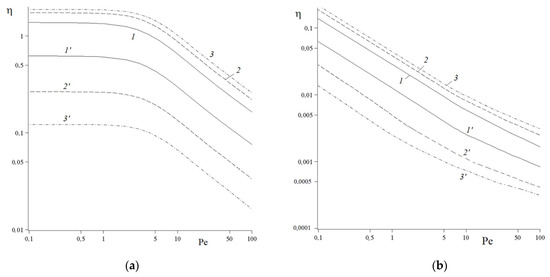
Figure 4.
Retention efficiencies for fibers with profiling (with protrusions of rectangular cross section) vs. Peclet number at = 1 (a), 1000 (b): (curves 1–3)—deposition on external protrusions, (1’–3’)—deposition on the part of the fiber surface of radius . Calculations for different protrusion heights 0.1 (1, 1’), 0.2 (2, 2’), 0.3 (3, 3’).
Grooves or dimples should enhance trans-membrane diffusion transport by reducing the membrane thickness. As an example, the problem of the convective-diffusion supply of a substance to a profiled fiber was solved, with account for the diffusion flux inside the impermeable membrane. Figure 5 compares the calculated dependences for the retention efficiency on the Reynolds number for a grooved fiber and a smooth fiber with the same outer radius. Here, the ratio of the outer to the inner radii of the hollow-fiber membrane is 2, the ratio of the diffusion coefficients of molecules (point particles) in the membrane and in the outer region is = 0.0001, and the dimensionless distance between the axes of adjacent fibers is 4. We normalize the radial coordinate to the outer radius and set the condition of a zero concentration on the inner radius of the hollow-fiber membrane. On the outer streamlined surface, we match the concentrations within the impermeable membrane and in the external flow region:
where is the dimensionless partition coefficient. From the results obtained (with account for the trans-membrane transport), it follows that profiling increases absorption from the external cross flow. The obvious conclusion also follows that the external flow has little effect on the concentration distribution inside the membrane if its own resistance is high.
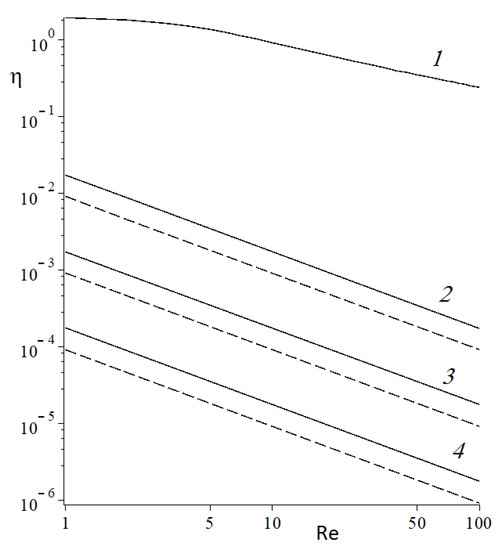
Figure 5.
Retention efficiencies of profiled hollow fibers with parallel grooves (solid lines) and smooth circular hollow fibers with the same outer radius (dotted lines) on the Reynolds number: pairs of curves 1—K = 0 (solid and dotted curves merge), 2—K = 0.1, 3—K = 1, 4—K = 10; Sc = 1.
4. Conclusions
The intensification of mass transfer from a convective flow to hollow-fiber profiled membranes is theoretically substantiated. The absorption of molecules (suspended point-like particles) by profiled fibers in a transverse laminar flow of a viscous incompressible liquid (gas) is calculated in the stationary approximation. Modified fibers with alternating symmetrical protrusion obstacles or grooves parallel to the fiber axis are considered. Gas or solute molecules are represented as point particles suspended in the convective flow. It is also assumed that upon contact with the surface, the molecules are completely absorbed. The fields of flow and concentration of the particles are determined by the joint numerical solution of the Navier–Stokes and convective diffusion equations. The computations were performed in a wide range of Peclet numbers = 0.1–105 for Schmidt numbers = 1, 10, 1000, and Reynolds numbers . The effect of the protrusion/groove on the flow and convective diffusion has been investigated. The efficiency of supplying a substance from an external flow to the absorbing fibers is determined, and it is shown that the profiling of the fibers improves the fiber retention (absorption, collection) efficiency. The effect of external protrusions for a fiber of a given radius is greater than that from the grooves (dimples). The depth of the groove has little impact, while the altering the width of the groove has a bigger impact. However, grooves or dimples made on the surface of the fiber might enhance trans-membrane diffusion transport, since the membrane thickness becomes locally smaller, while the rest of the material serves as a stiffener. Overall, the design of novel sorption (filtration) materials composed from profiled fibers is a promising direction of investigations. The results obtained may be of interest in solving practical problems of liquid (gas) filtration, sorption, catalysis, membrane separation, electrochemistry, and convective heat transfer (heat exchangers). The future investigations should involve not only 2D transverse flow case, but also parallel flow, including inner flow in a hollow-fiber membrane with the internal surface profiling.
Funding
This work was carried out in the A.V. Topchiev Institute of Petrochemical Synthesis (Russian Academy of Sciences) and was funded by the Russian Science Foundation, grant number 19-19-00647, https://rscf.ru/project/19-19-00647/.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author acknowledge the financial support of the Russian Science Foundation.
Conflicts of Interest
The author declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- van der Waal, M.J.; Racz, L.G. Mass transfer in corrugated-plate membrane modules. I. Hyperfiltration experiments. J. Membr. Sci. 1989, 40, 243–260. [Google Scholar] [CrossRef]
- Nijdam, W.; de Jong, J.; van Rijn, C.J.M.; Visser, T.; Versteeg, L.; Kapantaidakis, G.; Koops, G.-H.; Wessling, M. High performance micro-engineered hollow fiber membranes by smart spinneret design. J. Membr. Sci. 2005, 256, 209–215. [Google Scholar] [CrossRef]
- Heinz, O.; Aghajani, M.; Greenberg, A.R.; Ding, Y. Surface-patterning of polymeric membranes: Fabrication and performance. Curr. Opin. Chem. Eng. 2018, 20, 1–12. [Google Scholar] [CrossRef]
- Culfaz, P.Z.; Wessling, M.; Lammertink, R.G.H. Hollow Fiber Ultrafiltration Membranes With Microstructured Inner Skin. J. Membr. Sci. 2011, 369, 221–227. [Google Scholar] [CrossRef]
- García-Fernández, L.; García-Payo, C.; Khayet, M. Hollow fiber membranes with different external corrugated surfaces for desalination by membrane distillation. Appl. Surf. Sci. 2017, 416, 932–946. [Google Scholar] [CrossRef]
- Chwojnowski, A.; Wojciechowski, C.; Dudzinski, K.; Lukowska, E. Polysulphone and Polyethersulphone Hollow Fiber Membranes with Developed Inner Surface as Material for Bio-medical Applications. Biocybern. Biomed. Eng. 2009, 29, 47–59. Available online: http://www.pup.prudnik.ibib.pl/images/ibib/grupy/Wydawnictwa-Tomy/dokumenty/2009/BBE_29_3_047_FT.pdf (accessed on 1 September 2022).
- Culfaz, P.Z.; Rolevink, E.; van Rijn, C.J.M.; Lammertink, R.G.H.; Wessling, M. Microstructured Hollow Fibers for Ultrafiltration. J. Membr. Sci. 2010, 347, 32–41. [Google Scholar] [CrossRef]
- Brewers, J.M.; Goren, S.L. Evaluation of metal oxide whiskers grown on screens for use as aerosol filtration medium. Aerosol. Sci. Techn. 1984, 3, 411–429. [Google Scholar] [CrossRef]
- Kirsh, V.A. Aerosol filters made of porous fibers. Colloid. J. 1996, 58, 786–790. [Google Scholar]
- Kirsh, V.A. Deposition of aerosol nanoparticles in filters composed of fibers with porous shells. Colloid J. 2007, 69, 615–619. [Google Scholar] [CrossRef]
- Kirsch, A.A.; Stechkina, I.B. The theory of aerosol filtration with fibrous filters. In Fundamentals of Aerosol Science; Shaw, D.T., Ed.; John Wiley & Sons: New York, NY, USA, 1978; Chapter 4, pp. 165–256; ISBN 0471029491. [Google Scholar]
- Slezkin, N.A. Dynamics of Viscous Incompressible Fluids; Gostekhizdat: Moscow, Russia, 1955. (In Russian) [Google Scholar]
- Happel, J. Viscous flow relative to arrays of cylinders. J. Amer. Inst. Chem. Eng. 1959, 5, 174–177. [Google Scholar] [CrossRef]
- Kuwabara, S. The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds number. J. Phys. Soc. Jpn. 1959, 14, 527–532. [Google Scholar] [CrossRef]
- Kvashnin, A.G. Cell model of suspension of spherical particles. Fluid Dyn. 1979, 14, 598–602. [Google Scholar] [CrossRef]
- Golovin, A.M.; Lopatin, V.A. The flow of a viscous fluid through a doubly periodic rows of cylinders (English transl.). J. Appl. Mech. Tech. Phys. 1968, 9, 198–201. [Google Scholar] [CrossRef]
- Kirsh, V.A. Deposition of aerosol nanoparticles in fibrous filters. Colloid J. 2003, 65, 726–732. [Google Scholar] [CrossRef]
- Tamada, K.; Fujikawa, H. The steady two-dimensional flow of viscous fluid at low Re numbers passing through an infinite row of equal parallel circular cylinders. Quart. J. Mech. Appl. Math. 1957, 10, 425–432. [Google Scholar] [CrossRef]
- Miyagi, T. Viscous flow at low Reynolds numbers past an infinite row of equal circular cylinders. J. Phys. Soc. Jpn. 1958, 13, 493–496. [Google Scholar] [CrossRef]
- Sangani, A.; Acrivos, A. Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiph. Flow 1982, 8, 193–206. [Google Scholar] [CrossRef]
- Wang, W.; Sangani, A.S. Nusselt number for flow perpendicular to arrays of cylinders in the limit of small Reynolds and large Peclet numbers. Phys. Fluids 1997, 9, 1529–1539. [Google Scholar] [CrossRef]
- Wang, C.Y. Stokes flow through a rectangular array of circular cylinders. Fluid Dyn. Res. 2001, 29, 65–80. [Google Scholar] [CrossRef]
- Kirsch, V.A.; Roldugin, V.I.; Bildyukevich, A.V.; Volkov, V.V. Simulation of convective-diffusional processes in hollow fiber membrane contactors. Sep. Purif. Technol. 2016, 167, 63–69. [Google Scholar] [CrossRef]
- Kirsch, V.A.; Bildyukevich, A.V.; Bazhenov, S.D. Simulation of convection-diffusion transport in a laminar flow past a row of parallel absorbing fibers. Fibers 2018, 6, 90–100. [Google Scholar] [CrossRef] [Green Version]
- Kirsch, V.A.; Bazhenov, S.D. Numerical simulation of solute removal from a cross-flow past a row of parallel hollow-fiber membranes. Sep. Purif. Technol. 2020, 242, 116834. [Google Scholar] [CrossRef]
- Launder, B.E.; Massey, T.H. The Numerical Prediction of Viscous Flow and Heat Transfer in Tube Banks. ASME J. Heat Transfer. 1978, 100, 565–571. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Vabishchevich, P.N. Computational Heat Transfer, Volume 2: The Finite Difference Methodology, 2nd ed.; John Wiley & Sons: Chichester, UK, 1995; ISBN 0471956600/9780471956600. [Google Scholar]
- Berkovskii, B.M.; Polevikov, V.K. Effect of the Prandtl number on the convection field and the heat transfer during natural convection (English translation). J. Eng. Phys. 1973, 24, 598–603. [Google Scholar] [CrossRef]
- Allen, D.N.; Southwell, R.V. Relaxation methods applied to determine the motion, in two dimensions of a viscous fluid past a fixed cylinder. Quart. J. Mech. Appl. Math. 1955, 8, 129–143. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics 2, Specific Techniques for Different Flow Categorie; Springer: Berlin/Heidelberg, Germany, 1991; ISBN 1434-8322. [Google Scholar] [CrossRef]
- Berkovskii, B.M.; Nogotov, E.F. Difference Methods for Investigating Heat Exchange Problems; Nauka i Tekhnika: Minsk, Belarus, 1976. (In Russian) [Google Scholar]
- Roos, H.-G.; Stynes, M.; Tobiska, L. Numerical Methods for Singularly Perturbed Differential Equations. In Convection-Diffusion and Flow Problems; Springer: Berlin/Heidelberg, Germany, 1996; ISBN 3-540-60718-8. [Google Scholar]
- Miller, J.J.H.; O’Riordan, E.; Shishkin, G.I. Fitted Numerical Methods for Singular Perturbation Problems, Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions, Revised Edition; World Scientific Publishing Company: Singapore, 2012; ISBN 9814390739. [Google Scholar] [CrossRef]
- Yu, Y.; Luo, X.; Zhang, H.Y.; Zhang, Q. The Solution of Backward Heat Conduction Problem with Piecewise Linear Heat Transfer Coefficient. Mathematics 2019, 7, 388–404. [Google Scholar] [CrossRef]
- Savović, S.; Drljača, B.; Djordjevich, A. A comparative study of two different finite difference methods for solving advection–diffusion reaction equation for modeling exponential traveling wave. Ric. Di Mat. 2022, 71, 245–252. [Google Scholar] [CrossRef]
- Ivanovic, M.; Svicevic, M.; Savovic, S. Numerical solution of Stefan problem with variable space grid method based on mixed finite element/finite difference approach. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2682–2695. [Google Scholar] [CrossRef]
- Natanson, G.L. Diffusional precipitation of aerosols on a streamlined cylinder with a small capture coefficient (English translation, Dokl. Akad. Nauk SSSR). Proc. Acad. Sci. USSR Phys. Chem. Sect. 1957, 112, 21–25. Available online: http://mi.mathnet.ru/eng/dan21504 (accessed on 1 September 2022).
- Polyanin, A.D.; Kutepov, A.M.; Kazenin, D.A.; Vyazmin, A.V. Hydrodynamics, Mass and Heat Transfer in Chemical Engineering. Series: Topics in Chemical Engineering (Book 14), 1st ed.; CRC Press: Boca Raton, FL, USA, 2001; ISBN 0415272378. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).