Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core
Abstract
1. Introduction
2. Problem Formulation
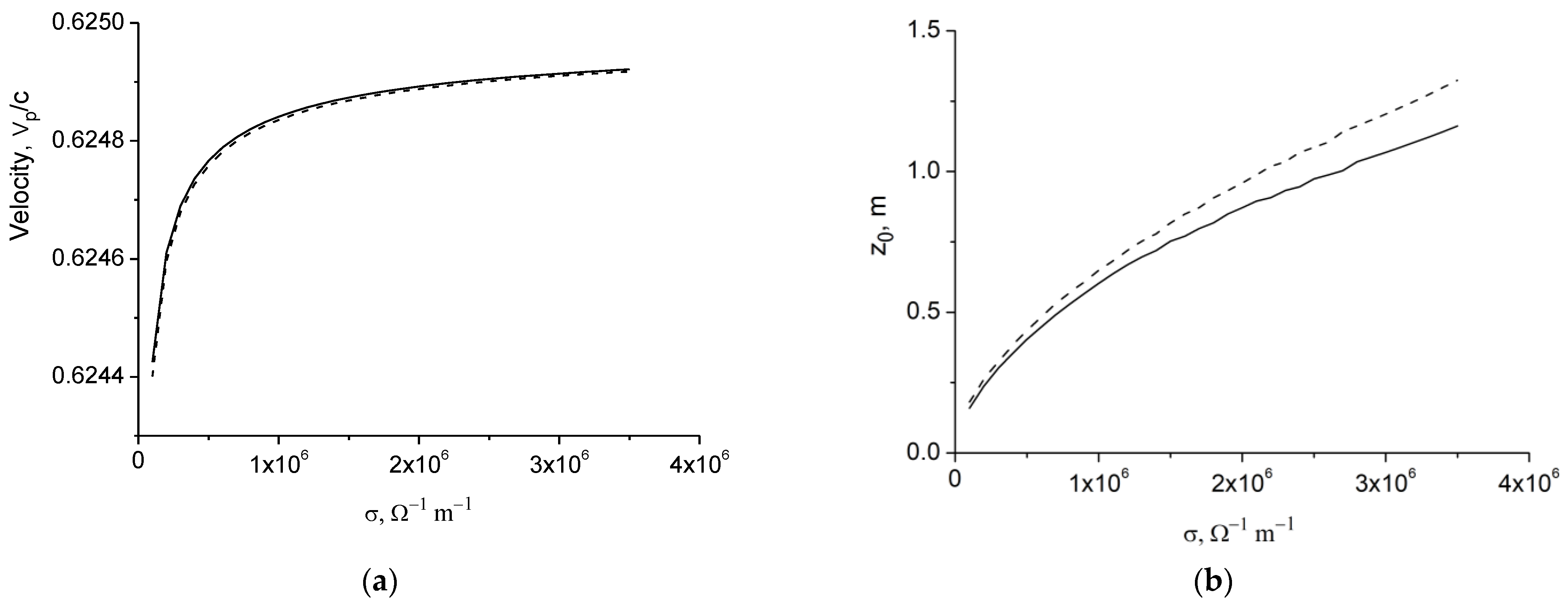
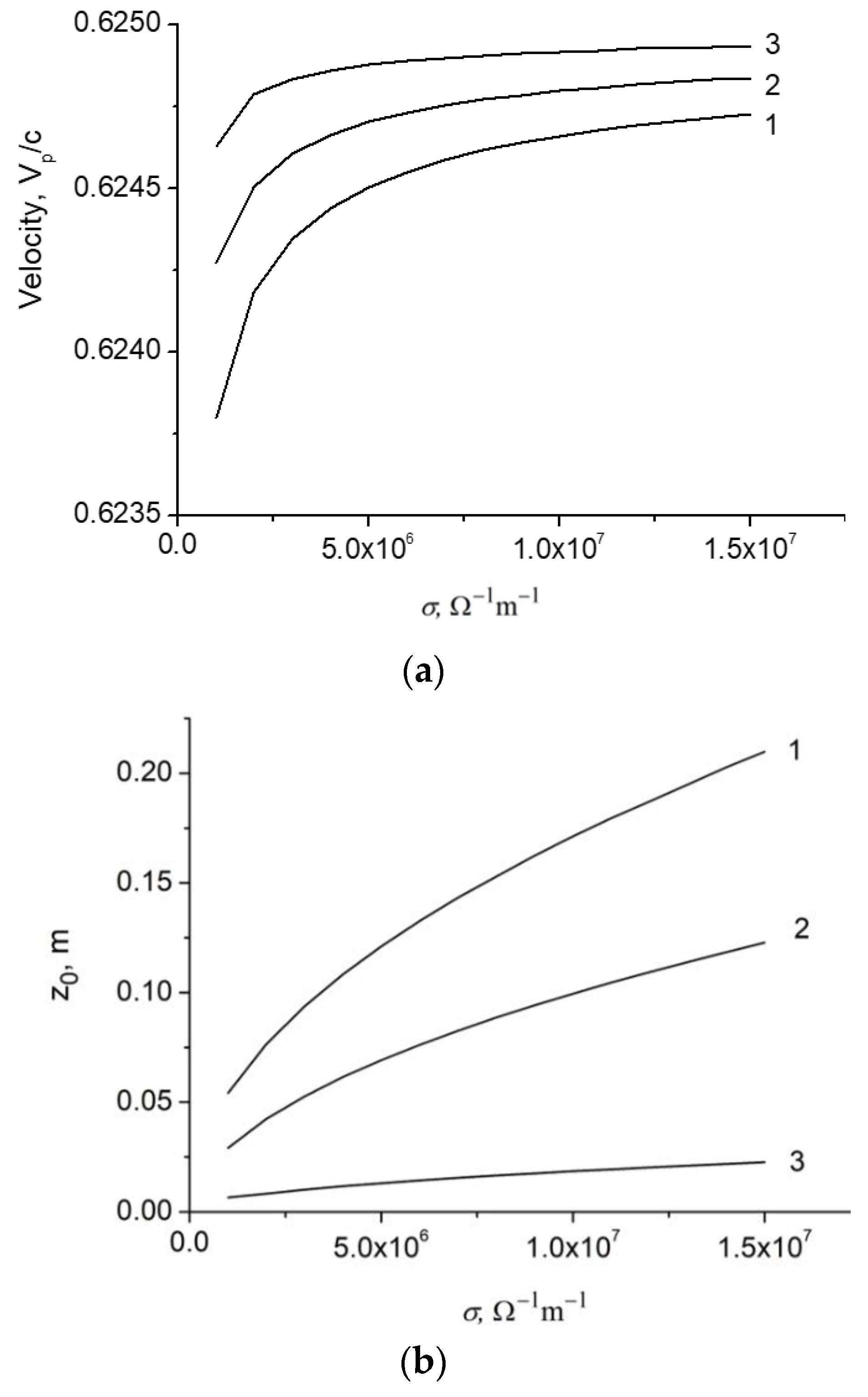
3. Velocity and Propagation Distance of Surface Wave as Function of Wire Conductivity
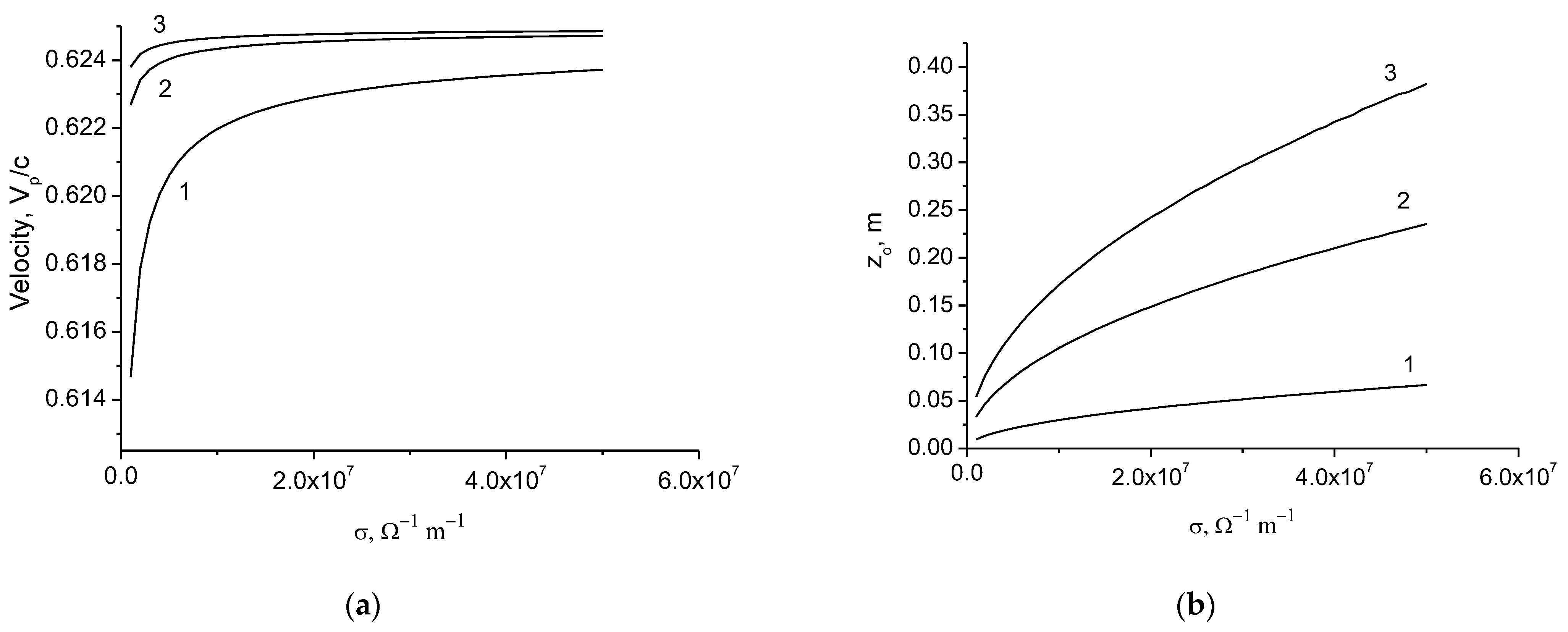
Effect of a Dielectric Coating
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, K.; Mittleman, D.M. Metal wires for terahertz wave guiding. Nature 2004, 432, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Mittleman, D.M. Dispersion of surface plasmon polaritons on metal wires in the terahertz frequency range. Phys. Rev. Lett. 2006, 96, 157401. [Google Scholar] [CrossRef] [PubMed]
- Saxler, J.; Rivas, J.G.; Janke, C.; Pellemans, H.P.M.; Bolívar, P.H.; Kurz, H. Time-domain measurements of surface plasmon polaritons in the terahertz frequency range. Phys. Rev. B 2004, 69, 155427. [Google Scholar] [CrossRef]
- Van der Valk, N.C.J.; Planken, P.C.M. Effect of a dielectric coating on terahertz surface plasmon polaritons on metal wires. Appl. Phys. Lett. 2005, 87, 071106. [Google Scholar] [CrossRef]
- Cao, Q.; Jahns, J. Azimuthally polarized surface plasmons as effective terahertz waveguides. Opt. Express 2005, 13, 511–518. [Google Scholar] [CrossRef]
- Mitrofanov, O.; Harrington, J.A. Dielectric-lined cylindrical metallic THz waveguides: Mode structure and dispersion. Opt. Express 2010, 18, 1898–1903. [Google Scholar] [CrossRef]
- Chen, Y.; Song, Z.; Li, Y.; Hu, M.; Xing, Q.; Zhang, Z.; Chai, L.; Wang, C.Y. Effective surface plasmon polaritons on the metal wire with arrays of subwavelength grooves. Opt. Express 2006, 14, 13021–13029. [Google Scholar] [CrossRef]
- Akalin, T.; Treizebre, A.; Bocquet, B. Single-wire transmission lines at terahertz frequencies. IEEE Trans. Microw. Theory Tech. 2006, 54, 2762–2767. [Google Scholar] [CrossRef]
- Williams, C.R.; Andrews, S.R.; Maier, S.; Fernandez-Dominguez, A.I.; Martín-Moreno, L.; Garcia-Vidal, F. Highly confined guiding of terahertz surface plasmon polaritons on structured metal surfaces. Nat. Photonics 2008, 2, 175–179. [Google Scholar] [CrossRef]
- Rivas, J.G.; Kuttge, M.; Bolivar, P.H.; Kurz, H.; Sánchez-Gil, J.A. Propagation of surface plasmon polaritons on semiconductor gratings. Phys. Rev. Lett. 2004, 93, 256804. [Google Scholar] [CrossRef]
- Gan, C.H.; Chu, H.S.; Li, E.P. Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 2012, 85, 125431. [Google Scholar] [CrossRef]
- Bulgakova, V.V.; Gerasimov, V.V.; Goldenberg, B.G.; Lemzyakov, A.G.; Malkin, A.M. Study of terahertz spoof surface plasmons on subwavelength gratings with dielectric substance in grooves. Phys. Procedia 2017, 201, 14–23. [Google Scholar] [CrossRef]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.; Hoffmann, M.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Chen, S.H.; Chen, K.W.; Chu, K.R. A comparative study of single-wire and hollow metallic waveguides for terahertz waves. AIP Adv. 2018, 8, 115028. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Q.; Xia, L.; Li, Y.; Gu, J.; Tian, Z.; Ouyang, C.; Han, J.; Zhang, W. Terahertz surface plasmonic waves: A review. Adv. Photonics 2020, 2, 014001. [Google Scholar] [CrossRef]
- Atakaramians, A.; Afshar, S.V.; Monro, T.M.; Abbott, D. Terahertz dielectric waveguides. Adv. Opt. Photon. 2013, 5, 169–215. [Google Scholar] [CrossRef]
- Islam, M.S.; Cordeiro, C.M.B.; Franco, M.A.R.; Sultana, J.; Cruz, A.L.S.; Abbott, D. Terahertz optical fibers [Invited]. Opt. Express 2020, 28, 16089–16117. [Google Scholar] [CrossRef]
- Arnaud, J.A. Beam and Fiber Optics; Academic Press: New York, NY, USA, 1976. [Google Scholar]
- Marcuse, D. Light Transmission Optics; Van Nostrand Reinhold: New York, NY, USA, 1982. [Google Scholar]
- Snyder, A.W.; Love, J. Optical Waveguide Theory; Chapman and Hall: New York, NY, USA, 1983. [Google Scholar]
- Petrov, N.I. Evolution of polarization in an inhomogeneous isotropic medium. J. Exp. Theor. Phys. 1997, 85, 1085–1093. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of light in a graded-index isotropic medium. J. Mod. Opt. 1996, 43, 2239–2249. [Google Scholar] [CrossRef]
- Petrov, N.I. Evanescent and propagating fields of a strongly focused beam. J. Opt. Soc. Am. A 2003, 20, 2385–2389. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of vector light beams on propagation in free space. Photonics 2022, 9, 162. [Google Scholar] [CrossRef]
- Pfeiffer, C.A.; Economou, E.N.; Ngai, K.L. Surface polaritons in a circularly cylindrical interface: Surface plasmons. Phys. Rev. B 1974, 10, 3038–3051. [Google Scholar] [CrossRef]
- Novotny, L.; Hafner, C. Light propagation in a cylindrical waveguide with a complex, metallic, dielectric function. Phys. Rev. E 1994, 50, 4094–4106. [Google Scholar] [CrossRef] [PubMed]
- Khosvari, H.; Tilley, D.R.; Loudon, R. Surface polaritons in cylindrical optical fibers. J. Opt. Soc. Am. A 1991, 8, 112–122. [Google Scholar]
- Al-Bader, S.J.; Imtaar, M. Optical fiber hybrid-surface plasmon polaritons. J. Opt. Soc. Am. B 1993, 10, 83–88. [Google Scholar] [CrossRef]
- Sommerfeld, A. Ueber die Fortpflanzung elektrodynamischer Wellen längs eines Drahtes. Ann. Phys. 1899, 303, 233–290. [Google Scholar] [CrossRef]
- Petrov, N.I. Synchrotron mechanism of X-ray and gamma-ray emissions in lightning and spark discharges. Sci. Rep. 2021, 11, 19824. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.S.; Kim, G.J.; Jeon, S.G. Terahertz Dielectric Properties of Polymers. J. Korean Phys. Soc. 2006, 49, 513–517. [Google Scholar]
- Stefani, A.; Skelton, J.H.; Tuniz, A. Bend losses in flexible polyurethane antiresonant terahertz waveguides. Opt. Express 2021, 29, 28692–28703. [Google Scholar] [CrossRef]
- Gerasimov, V.V.; Knyazev, B.A.; Lemzyakov, A.G.; Nikitin, A.K.; Zhizhin, G.N. Growth of terahertz surface plasmon propagation length due to thin-layer dielectric coating. J. Opt. Soc. Am. B 2016, 33, 2196–2203. [Google Scholar] [CrossRef]
- Paul, B.K.; Bhuiyan, T.; Abdulrazak, L.F.; Sarker, K.; Hassan, M.M.; Shariful, S.; Ahmed, K. Extremely low loss optical waveguide for terahertz pulse guidance. Results Phys. 2019, 15, 102666. [Google Scholar] [CrossRef]
- Yudasari, N.; Anthony, J.; Leonhardt, R. Terahertz pulse propagation in 3D-printed waveguide with metal wires component. Opt. Express 2014, 22, 26042–26054. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, J.; Gong, C.; Tian, H.; Sun, L.; Chen, P.; Lin, L.; Liu, W. 3D printed low-loss THz waveguide based on Kagome photonic crystal structure. Opt. Express 2016, 24, 22454–22460. [Google Scholar] [CrossRef] [PubMed]
- Stefani, A.; Fleming, S.C.; Kuhlmey, B.T. Terahertz orbital angular momentum modes with flexible twisted hollow core antiresonant fiber. APL Photonics 2018, 3, 051708. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector and tensor polarizations of light beams. Laser Phys. 2008, 18, 522–525. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-orbit and tensor interactions of light in inhomogeneous isotropic media. Phys. Rev. A 2013, 88, 023815. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-dependent transverse force on a vortex light beam in an inhomogeneous medium. JETP Lett. 2016, 103, 443–448. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef] [PubMed]
- Petrov, N.I. Depolarization of Light in Optical Fibers: Effects of Diffraction and Spin-Orbit Interaction. Fibers 2021, 9, 34. [Google Scholar] [CrossRef]
- Farmani, A.; Miri, M.; Sheikhi, M.H. Tunable resonant Goos–Hänchen and Imbert–Fedorov shifts in total reflection of terahertz beams from graphene plasmonic metasurfaces. J. Opt. Soc. Am. B 2017, 34, 1097–1106. [Google Scholar] [CrossRef]
- Petrov, N.I.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Express 2020, 28, 7552–7564. [Google Scholar] [CrossRef] [PubMed]
- Kan, X.F.; Zou, Z.X.; Yin, C.; Xu, H.P.; Wang, X.P.; Han, Q.B.; Cao, Z.Q. Continuous Goos-Hänchen Shift of Vortex Beam via Symmetric Metal-Cladding Waveguide. Materials 2022, 15, 4267. [Google Scholar] [CrossRef]
- Moradi, A. Surface and bulk plasmons in cylindrical electric-gyrotropic wires. J. Opt. Soc. Am. B 2020, 37, 2947–2955. [Google Scholar] [CrossRef]
- Petrov, N.I.; Pustovoit, V.I. Small-sized interferometer with Fabry-Perot resonators for gravitational wave detection. Sensors 2021, 21, 1877. [Google Scholar] [CrossRef]


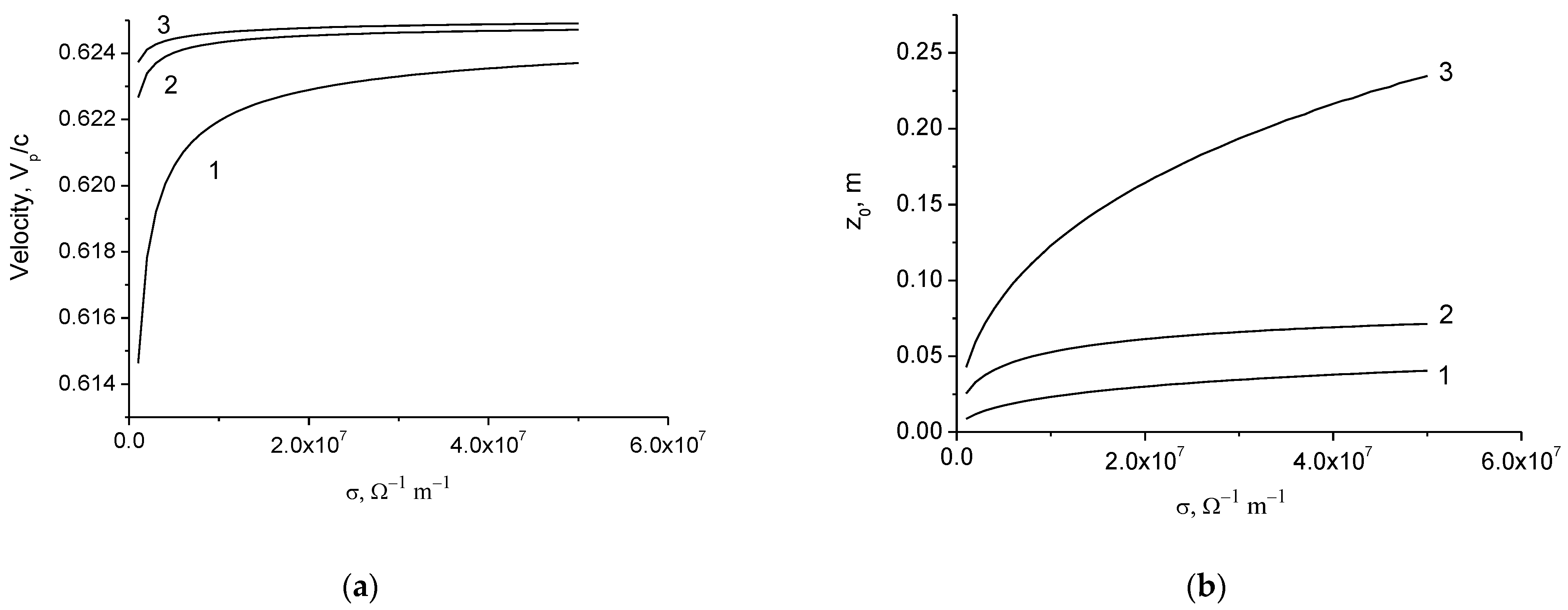
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, N.I. Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core. Fibers 2022, 10, 89. https://doi.org/10.3390/fib10100089
Petrov NI. Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core. Fibers. 2022; 10(10):89. https://doi.org/10.3390/fib10100089
Chicago/Turabian StylePetrov, Nikolai I. 2022. "Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core" Fibers 10, no. 10: 89. https://doi.org/10.3390/fib10100089
APA StylePetrov, N. I. (2022). Propagation of Terahertz Surface Plasmon Polaritons in a Dielectric Fiber with a Metal Wire Core. Fibers, 10(10), 89. https://doi.org/10.3390/fib10100089





