Numerical Investigation of Multiple Solutions for Caputo Fractional-Order-Two Dimensional Magnetohydrodynamic Unsteady Flow of Generalized Viscous Fluid over a Shrinking Sheet Using the Adams-Type Predictor-Corrector Method
Abstract
:1. Introduction
2. Problem Formulation
2.1. Boundary Layer Governing Equations
2.2. Preliminaries on the Caputo Fractional Derivatives
2.3. Solution Methodology
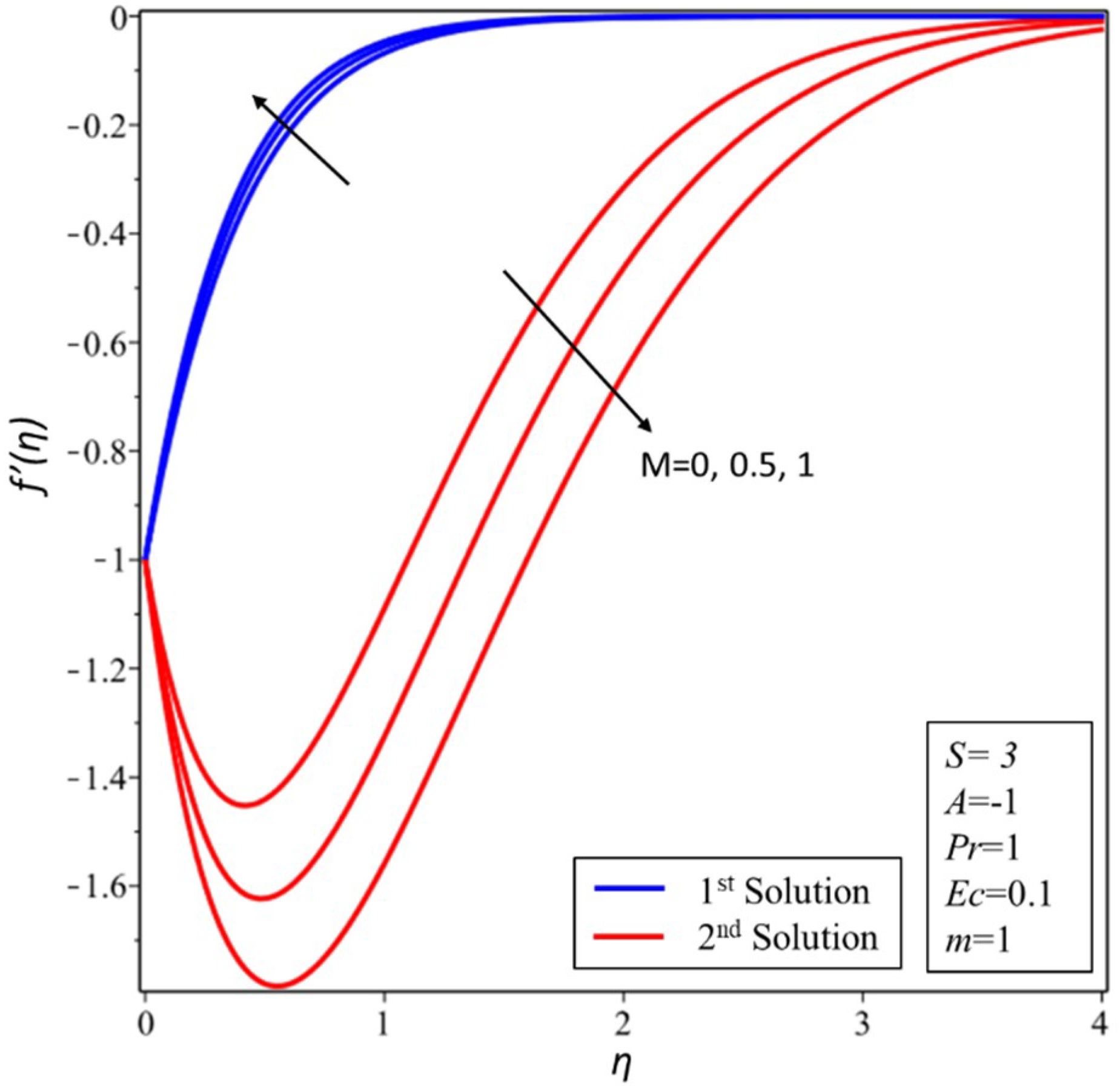
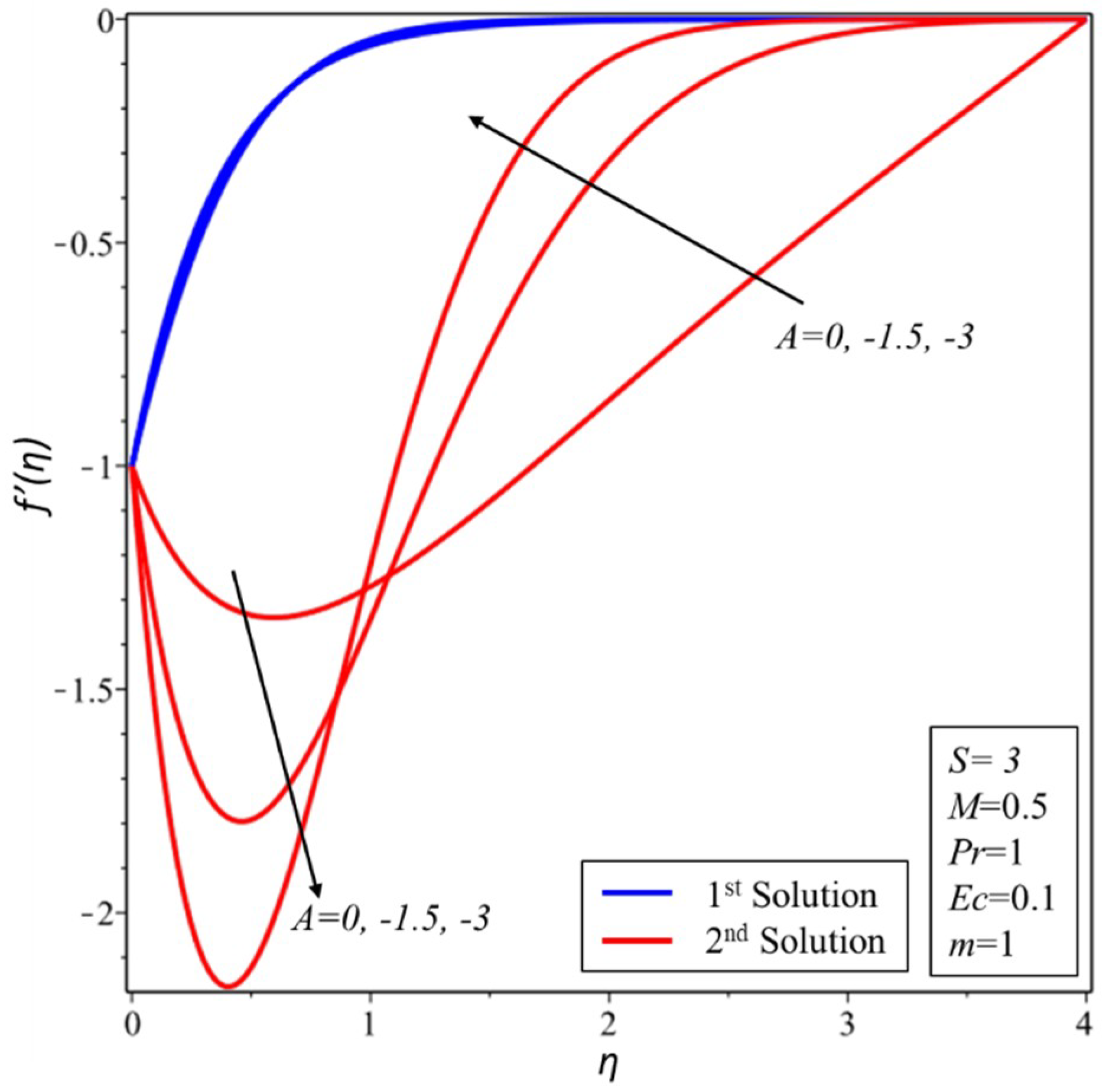
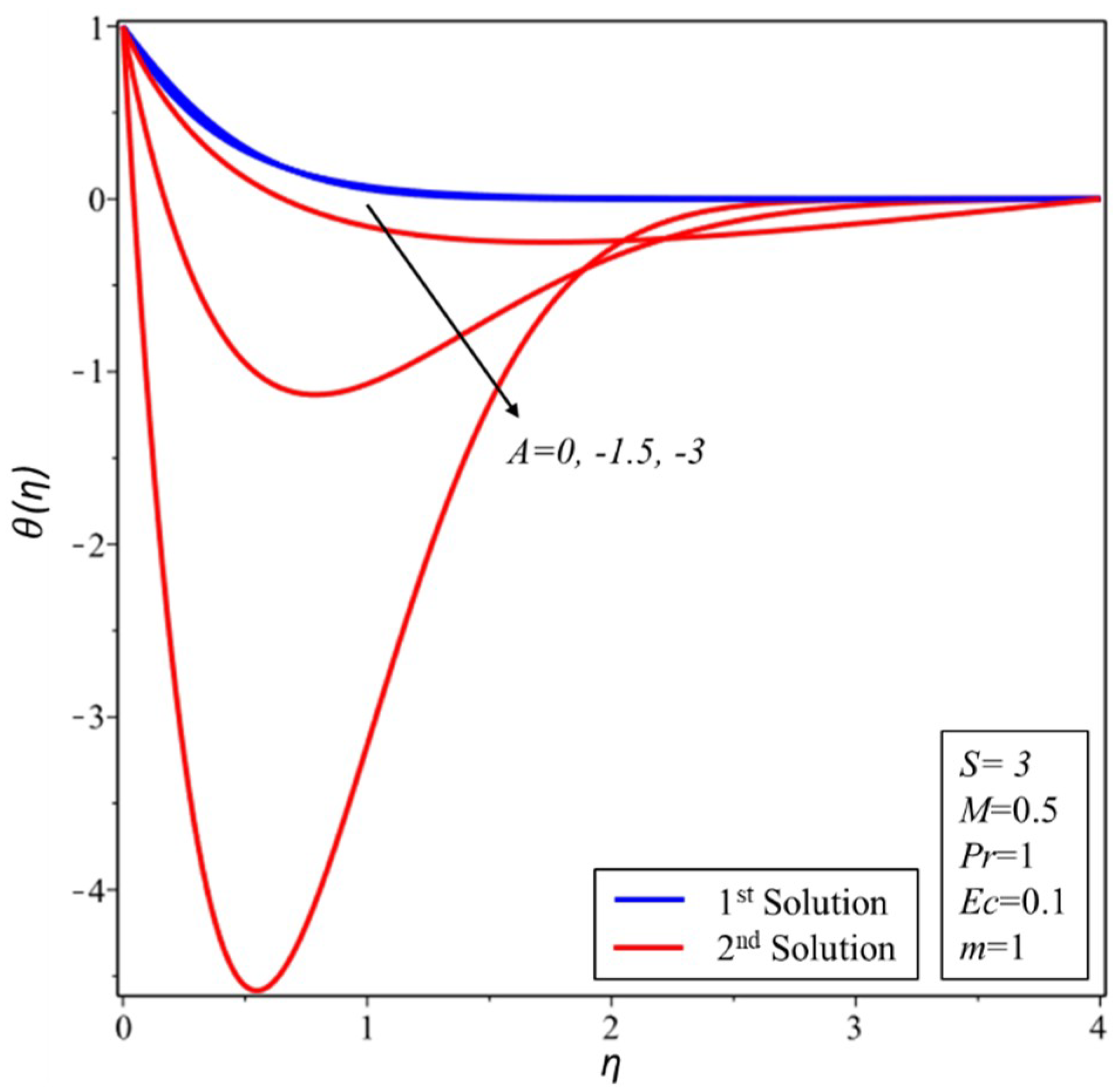
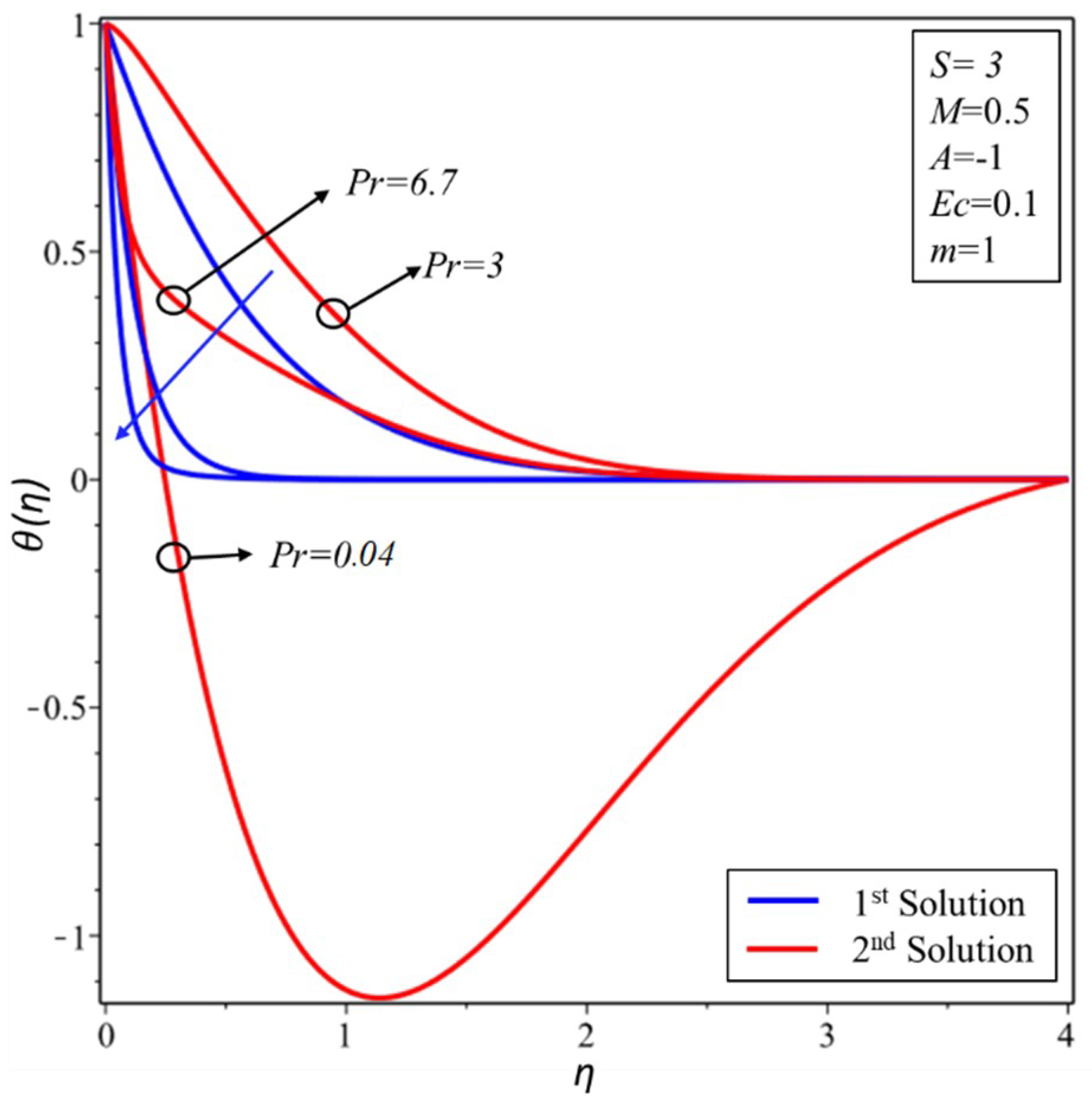
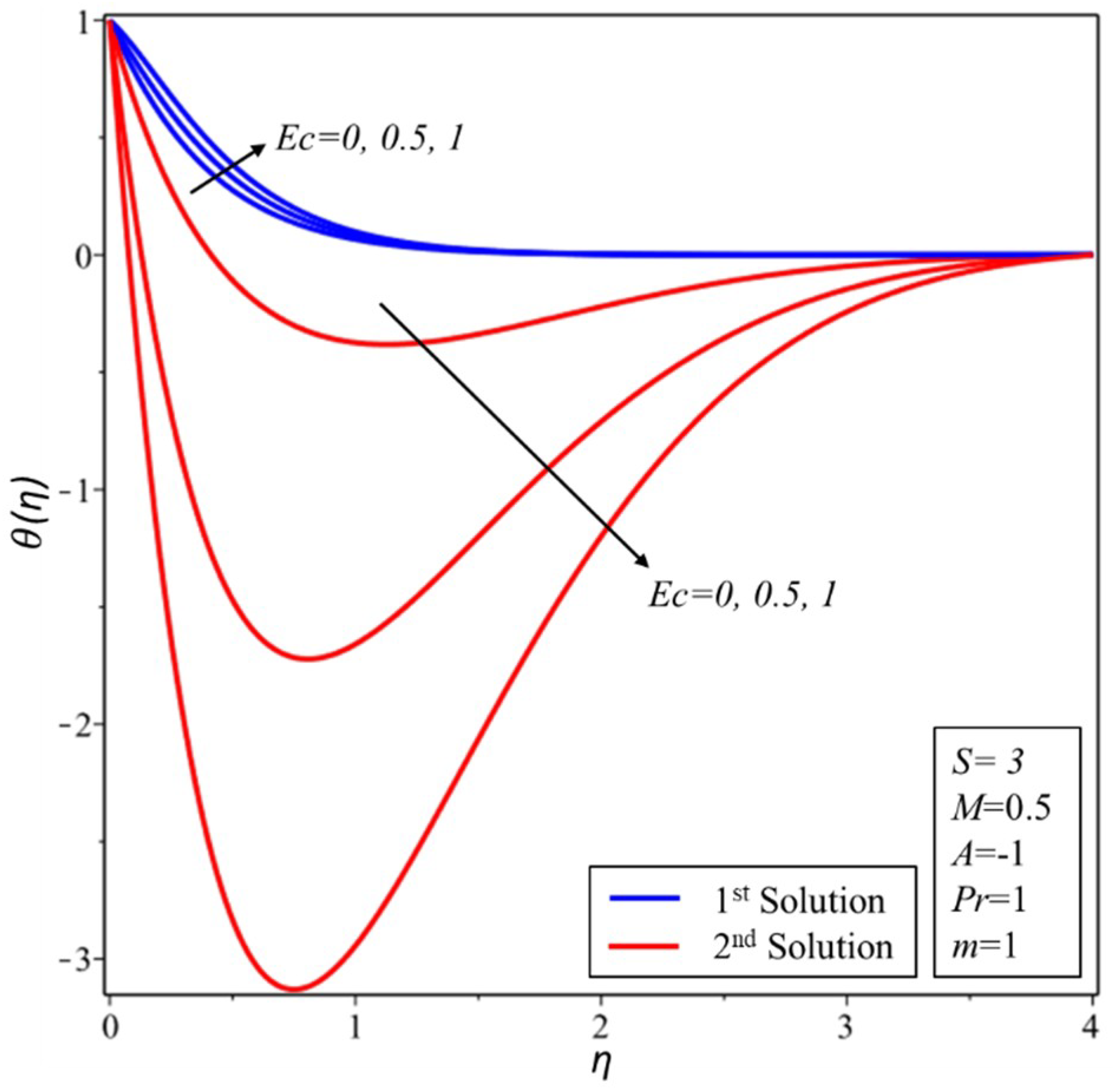
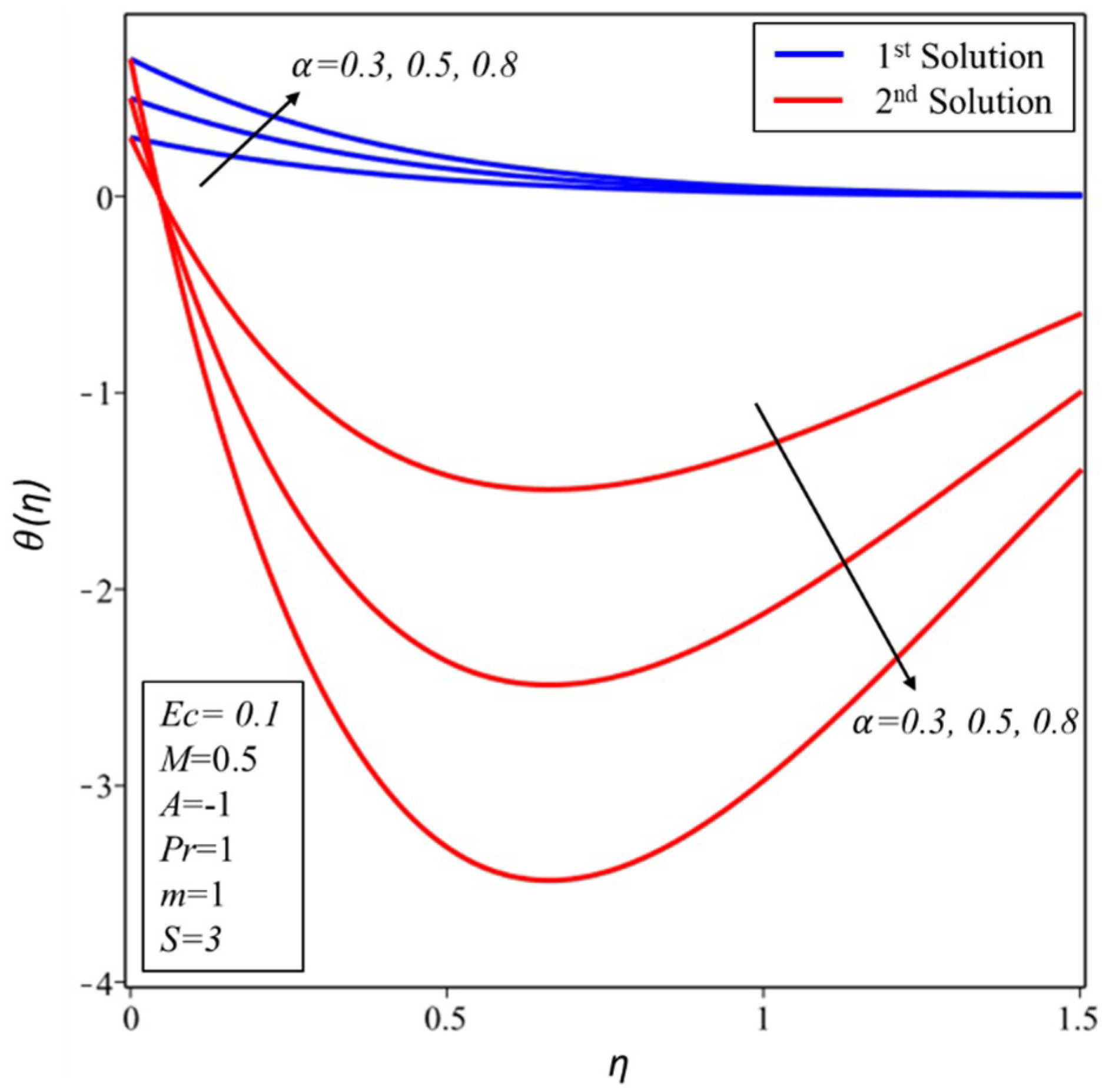
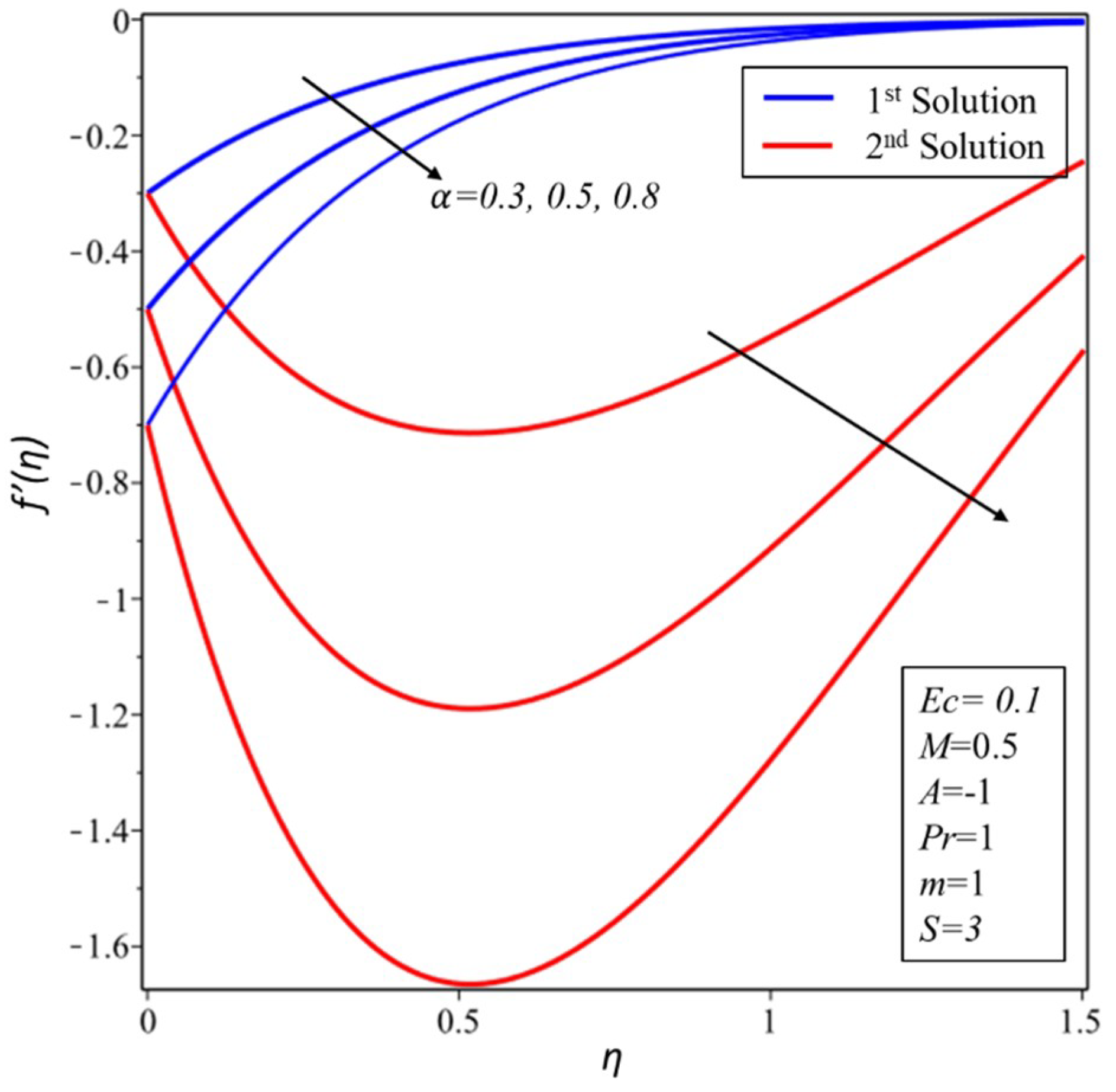
3. Results and Discussion
4. Conclusion Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rohni, A.M.; Ahmad, S.; Pop, I. Flow and heat transfer at a stagnation-point over an exponentially shrinking vertical sheet with suction. Int. J. Therm. Sci. 2014, 75, 164–170. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Chen, H.; Cai, H.; Deng, L. A novel fractal model for relative permeability of gas diffusion layer in proton exchange membrane fuel cell with capillary pressure effect. Fractals 2019, 27, 1950012. [Google Scholar] [CrossRef]
- Liang, M.; Liu, Y.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Long, G.; Liu, S.; Xu, G.; Wong, S.W.; Chen, H.; Xiao, B. A perforation-erosion model for hydraulic-fracturing applications. SPE Prod. Oper. 2018, 33, 770–783. [Google Scholar] [CrossRef]
- Long, G.; Xu, G. The effects of perforation erosion on practical hydraulic-fracturing applications. SPE J. 2017, 22, 645–659. [Google Scholar] [CrossRef]
- Miklavčič, M.; Wang, C.Y. Viscous flow due to a shrinking sheet. Q. Appl. Math. 2006, 14, 283–290. [Google Scholar] [CrossRef]
- Gupta, D.; Kumar, L.; Bég, O.A.; Singh, B. Finite Element Analysis of MHD Flow of Micropolar Fluid over a Shrinking Sheet with a Convective Surface Boundary Condition. J. Eng. Thermophys. 2018, 27, 202–220. [Google Scholar] [CrossRef]
- Naveed, M.; Abbas, Z.; Sajid, M.; Hasnain, J. Dual solutions in hydromagnetic viscous fluid flow past a shrinking curved surface. Arab. J. Sci. Eng. 2018, 43, 1189–1194. [Google Scholar] [CrossRef]
- Khan, U.; Ahmed, N.; Mohyud-Din, S.T.; Bin-Mohsin, B. Nonlinear radiation effects on MHD flow of nanofluid over a nonlinearly stretching/shrinking wedge. Neural Comput. Appl. 2017, 28, 2041–2050. [Google Scholar] [CrossRef]
- Soid, S.K.; Ishak, A.; Pop, I. Unsteady MHD flow and heat transfer over a shrinking sheet with ohmic heating. Chin. J. Phys. 2017, 55, 1626–1636. [Google Scholar] [CrossRef]
- Zaib, A.; Haq, R.U.; Chamkha, A.J.; Rashidi, M.M. Impact of nonlinear radiative nanoparticles on an unsteady flow of a Williamson fluid towards a permeable convectively-heated shrinking sheet. World J. Eng. 2018, 15, 731–742. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability analysis of Darcy-Forchheimer flow of Casson type nanofluid over an exponential sheet: Investigation of critical points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Dero, S.; Uddin, M.J.; Rohni, A.M. Stefan blowing and slip effects on unsteady nanofluid transport past a shrinking sheet: Multiple solutions. Heat Transf.—Asian Res. 2019, 48, 1149–1544. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Dero, S.; Rohni, A.M.; Saaban, A. MHD micropolar nanofluid flow over an exponentially stretching/shrinking surface: Triple solutions. J. Adv. Res. Fluid Mech. Therm. Sci. 2019, 56, 165–174. [Google Scholar]
- Lund, L.A.; Omar, Z.; Khan, I. Analysis of dual solution for MHD flow of Williamson fluid with slippage. Heliyon 2019, 5, e01345. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, K.; Banerjee, A.; Zaib, A.; Mahato, S.K. MHD mixed convection flow of a non-Newtonian Powell-Erying fluid over a permeable exponentially shrinking sheet. FHMT 2018, 10, 30. [Google Scholar] [CrossRef]
- Mishra, S.; DebRoy, T. A computational procedure for finding multiple solutions of convective heat transfer equations. J Phys. D Appl. Phys. 2005, 38, 2977. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary-Layer Theory; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Rahman, M.M.; Rosca, A.V.; Pop, I. Boundary layer flow of a nanofluid past a permeable exponentially shrinking surface with convective boundary condition using Buongiorno’s model. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 299–319. [Google Scholar] [CrossRef]
- Fang, T.; Zhang, J. Closed-form exact solutions of MHD viscous flow over a shrinking sheet. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2853–2857. [Google Scholar] [CrossRef]
- Rana, P.; Shukla, N.; Gupta, Y.; Pop, I. Homotopy analysis method for predicting multiple solutions in the channel flow with stability analysis. Commun. Nonlinear Sci. Numer. Simul. 2018, 66, 183–193. [Google Scholar] [CrossRef]
- Rohni, A.M.; Ahmad, S.; Pop, I. Boundary layer flow over a moving surface in a nanofluid beneath a uniform free stream. Int. J. Numer. Methods Heat Fluid Flow 2011, 21, 828–846. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Mixed convection boundary layer flow adjacent to a vertical surface embedded in a stable stratified medium. Int. J. Heat Mass Transf. 2008, 51, 3693–3695. [Google Scholar] [CrossRef]
- Fang, T.; Yao, S.; Zhang, J.; Aziz, A. Viscous flow over a shrinking sheet with a second order slip flow model. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1831–1842. [Google Scholar] [CrossRef]
- Raza, J.; Rohni, A.M.; Omar, Z. Rheology of micropolar fluid in a channel with changing walls: Investigation of multiple solutions. J. Mol. Liq. 2016, 223, 890–902. [Google Scholar] [CrossRef]
- Mutuku-Njane, W.N. Analysis of Hydromagnetic Boundary Layer Flow and Heat Transfer of Nanofluids. Ph.D. Thesis, Cape Peninsula University of Technology, Cape Town, South Africa, 2014. [Google Scholar]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ellahi, R. Simulation of ferrofluid flow for magnetic drug targeting using the lattice Boltzmann method. Z. Für Naturforschung A 2015, 70, 115–124. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of Titanium dioxide—Water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Two-phase Couette flow of couple stress fluid with temperature dependent viscosity thermally affected by magnetized moving surface. Symmetry 2019, 11, 647. [Google Scholar] [CrossRef]
- Makinde, O.D.; Mabood, F.; Khan, W.A.; Tshehla, M.S. MHD flow of a variable viscosity nanofluid over a radially stretching convective surface with radiative heat. J. Mol. Liq. 2016, 219, 624–630. [Google Scholar] [CrossRef]
- Tie-Gang, F.; Ji, Z.; Shan-Shan, Y. Viscous flow over an unsteady shrinking sheet with mass transfer. Chin. Phys. Lett. 2009, 26, 014703. [Google Scholar] [CrossRef]
- Rohni, A.M.; Ahmad, S.; Pop, I. Flow and heat transfer over an unsteady shrinking sheet with suction in nanofluids. Int. J. Heat Mass Transf. 2012, 55, 1888–1895. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. J. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Baleanu, D.; Mousalou, A.; Rezapour, S. On the existence of solutions for some infinite coefficient-symmetric Caputo-Fabrizio fractional integro-differential equations. Bound. Value Probl. 2017, 2017, 145. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Chamkha, A.J. Influence of Lorentz forces on nanofluid forced convection considering Marangoni convection. J. Mol. Liq. 2017, 225, 750–757. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu–C6H9NaO7 and Ag–C6H9NaO7 nanofluids flow over nonlinear shrinking surface. J. Cent. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lund, L.A.; Omar, Z.; Alharbi, S.O.; Khan, I.; Nisar, K.S. Numerical Investigation of Multiple Solutions for Caputo Fractional-Order-Two Dimensional Magnetohydrodynamic Unsteady Flow of Generalized Viscous Fluid over a Shrinking Sheet Using the Adams-Type Predictor-Corrector Method. Coatings 2019, 9, 548. https://doi.org/10.3390/coatings9090548
Lund LA, Omar Z, Alharbi SO, Khan I, Nisar KS. Numerical Investigation of Multiple Solutions for Caputo Fractional-Order-Two Dimensional Magnetohydrodynamic Unsteady Flow of Generalized Viscous Fluid over a Shrinking Sheet Using the Adams-Type Predictor-Corrector Method. Coatings. 2019; 9(9):548. https://doi.org/10.3390/coatings9090548
Chicago/Turabian StyleLund, Liaquat Ali, Zurni Omar, Sayer O. Alharbi, Ilyas Khan, and Kottakkaran Sooppy Nisar. 2019. "Numerical Investigation of Multiple Solutions for Caputo Fractional-Order-Two Dimensional Magnetohydrodynamic Unsteady Flow of Generalized Viscous Fluid over a Shrinking Sheet Using the Adams-Type Predictor-Corrector Method" Coatings 9, no. 9: 548. https://doi.org/10.3390/coatings9090548
APA StyleLund, L. A., Omar, Z., Alharbi, S. O., Khan, I., & Nisar, K. S. (2019). Numerical Investigation of Multiple Solutions for Caputo Fractional-Order-Two Dimensional Magnetohydrodynamic Unsteady Flow of Generalized Viscous Fluid over a Shrinking Sheet Using the Adams-Type Predictor-Corrector Method. Coatings, 9(9), 548. https://doi.org/10.3390/coatings9090548







