Irradiance in Mixed Coherent/Incoherent Structures: An Analytical Approach
Abstract
:1. Introduction
2. Transfer Matrices
2.1. Coherent Structure
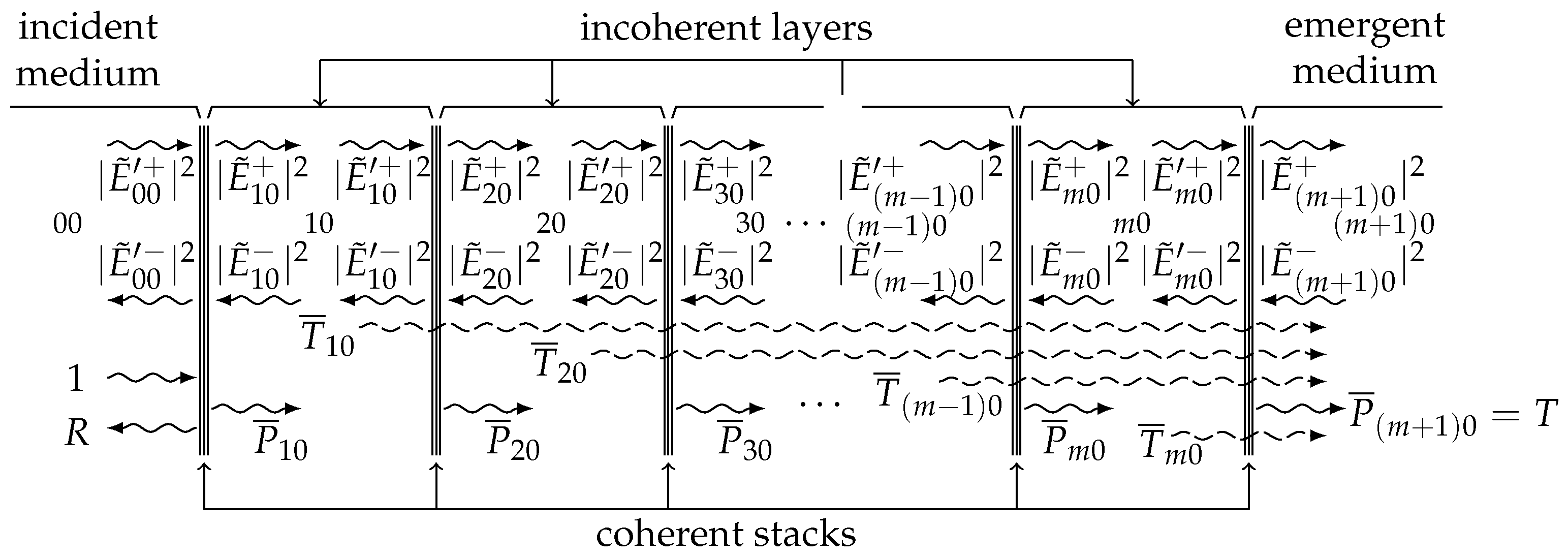
2.2. Mixed Coherent/Incoherent Structure
3. Phase-Shift Integration
3.1. Theory
3.2. PIM Algorithm
| Algorithm 1 PIM algorithm |
|
4. Verification Cases
4.1. Encapsulated Bifacial Heterojunction Silicon Solar Cell
4.2. Perovskite Solar Cell
4.3. Perovskite/Silicon Tandem Solar Cell
5. Potential Use of PIM in Gradient Optimization Procedures
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| TMM | Transfer-Matrix Method |
| TLM | Transmission Line Method |
| GTMM | General Transfer-Matrix Method |
| GTLM | Generalized Transmission Line Method |
| EMM | Equivalent Matrix Method |
| SAM | Spectral Averaging Method |
| SCM | Spectral Convolution Method |
| RTM | Random Thickness Method |
| RPM | Random Phase Method |
| ETAM | Equispaced Thickness Averaging Method |
| EPAM | Equispaced Phase Averaging Method |
| PEM | Phase Elimination Method |
| FEM | Finite Element Method |
| FDTD | Finite Difference Time Domain |
| RCWA | Rigorous Coupled Wave Analysis |
| PIM | Phase Integration Method |
| CROWM | combined ray optics/wave optics model |
| HJ Si | heterojunction silicon solar cell |
| EVA | ethylene-vinyl acetate |
| ITO | indium tin oxide |
| n-a-Si:H | n-type hydrogenated amorphous silicon |
| i-a-Si:H | intrinsic hydrogenated amorphous silicon |
| p-a-Si:H | p-type hydrogenated amorphous silicon |
| c-Si | n-type crystalline silicon |
| PTAA | polytriaryl amine |
| PCBM | phenyl-C61-butyric acid methyl ester |
| LiF | lithium fluoride |
| Ag | silver |
| SHJ | silicon-heterojunction |
| IZO | indium zinc oxide |
| tin oxide | |
| nc-:H | n-doped nanocrystalline silicon oxide |
Appendix A
References
- Knittl, Z. Optics of dielectric layers. In Optics of Thin Films (An Optical Multilayer Theory); Ballard, S.S., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 1976; pp. 35–68. [Google Scholar]
- Born, M.; Wolf, E. Basic properties of the electromagnetic field. In Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Cambridge University Press: Cambridge, UK, 2002; pp. 1–74. [Google Scholar]
- Macleod, H.A. Basic theory. In Thin-Film Optical Filters; Pike, E.R., Brown, R.G.W., Eds.; CRC Press: Boca Raton, FL, USA, 2010; pp. 13–71. [Google Scholar]
- Stathopoulos, N.A.; Palilis, L.C.; Savaidis, S.P.; Yesayan, S.R.; Vasilopoulou, M.; Papadimitropoulos, G.; Davazoglou, D.; Argitis, P. Optical Modeling of Hybrid Polymer Solar Cells Using a Transmission-Line Model and Comparison with Experimental Results. IEEE J. Sel. Top. Quantum Electron. 2010, 16, 1784–1791. [Google Scholar] [CrossRef]
- Stathopoulos, N.A.; Palilis, L.C.; Yesayan, S.R.; Savaidis, S.P.; Vasilopoulou, M.; Argitis, P. A transmission line model for the optical simulation of multilayer structures and its application for oblique illumination of an organic solar cell with anisotropic extinction coefficient. J. Appl. Phys. 2011, 110, 114506. [Google Scholar] [CrossRef]
- Donges, A. The coherence length of black-body radiation. Eur. J. Phys. 1998, 19, 245–249. [Google Scholar] [CrossRef]
- Lee, W.; Lee, S.Y.; Kim, J.; Kim, S.C.; Lee, B. A numerical analysis of the effect of partially-coherent light in photovoltaic devices considering coherence length. Opt. Express 2012, 20, A941–A953. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, L.A.A.; Roman, L.S.; Iganäs, O. Modeling photocurrent action spectra of photovoltaic devices based on organic thin films. J. Appl. Phys. 1999, 86, 487–496. [Google Scholar] [CrossRef]
- Peumans, P.; Yakimov, A.; Forrest, S.R. Small molecular weight organic thin-film photodetectors and solar cells. J. Appl. Phys. 2003, 93, 3693–3723. [Google Scholar] [CrossRef]
- Kim, J.; Jung, S.; Jeong, I. Optical Modeling for Polarization-dependent Optical Power Dissipation of Thin-film Organic Solar Cells at Oblique Incidence. J. Opt. Soc. Korea 2012, 16, 6–12. [Google Scholar] [CrossRef] [Green Version]
- Larouche, S.; Martinu, L. Openfilters: Open-source software for the design, optimization, and synthesis of optical filters. Appl. Opt. 2008, 47, C219–C230. [Google Scholar] [CrossRef]
- Kang, K.; Lee, S.; Kim, J. Effect of an Incoherent Glass Substrate on the Absorption Efficiency of Organic Solar Cells at Oblique Incidence Analyzed by the Transfer Matrix Method with a Glass Factor. Jpn. J. Appl. Phys. 2013, 52, 052301. [Google Scholar] [CrossRef]
- Mitsas, C.L.; Siapkas, D.I. Generalized matrix method for analysis of coherent and incoherent reflectance and transmittance of multilayer structures with rough surfaces, interfaces, and finite substrates. Appl. Opt. 1995, 34, 1678–1683. [Google Scholar] [CrossRef]
- Katsidis, C.C.; Siapkas, D.I. General transfer-matrix method for optical multilayer systems with coherent, partially coherent, and incoherent interference. Appl. Opt. 2002, 41, 3978–3987. [Google Scholar] [CrossRef]
- Stathopoulos, N.A.; Savaidis, S.P.; Botsialas, A.; Ioannidis, Z.C.; Georgiadou, D.G.; Vasilopoulou, M.; Pagiatakis, G. Reflection and transmission calculations in a multilayer structure with coherent, incoherent, and partially coherent interference, using the transmission line method. Appl. Opt. 2015, 54, 1492–1504. [Google Scholar] [CrossRef] [PubMed]
- Centurioni, E. Generalized matrix method for calculation of internal light energy flux in mixed coherent and incoherent multilayers. Appl. Opt. 2005, 44, 7532–7539. [Google Scholar] [CrossRef]
- Puhan, J.; Lipovšek, B.; Bűrmen, A.; Fajfar, I. An Accurate Representation of Incoherent Layers Within One-Dimensional Thin-Film Multilayer Structures With Equivalent Propagation Matrices. IEEE Photonics J. 2017, 9, 6501112. [Google Scholar] [CrossRef]
- Sarrazin, M.; Herman, A.; Deparis, O. First-principle calculation of solar cell efficiency under incoherent illumination. Opt. Express 2013, 21, A616–A630. [Google Scholar] [CrossRef] [PubMed]
- Prentice, J.S.C. Coherent, partially coherent and incoherent light absorption in thin-film multilayer structures. J. Phys. D Appl. Phys. 2000, 33, 3139–3145. [Google Scholar] [CrossRef]
- Troparevsky, M.C.; Sabau, A.S.; Lupini, A.R.; Zhang, Z.Y. Transfer-matrix formalism for the calculation of optical response in multilayer systems: From coherent to incoherent interference. Opt. Express 2010, 18, 24715–24721. [Google Scholar] [CrossRef]
- Kang, K.; Lee, S.; Kim, J.; Kim, S.; Han, Y.; Baek, S. A Simple Numerical Modeling of the Effect of the Incoherent Thick Substrate in Thin-Film Solar Cells Based on the Equispaced Thickness Method. IEEE Photonics J. 2016, 8, 8400312. [Google Scholar] [CrossRef]
- Kang, K.; Kim, S.; Kim, J. Numerical modeling of the effect of multiple incoherent layers in Cu(In,Ga)Se-2 solar cells based on the equispaced thickness averaging method. Appl. Opt. 2018, 57, 2758–2765. [Google Scholar] [CrossRef]
- Santbergen, R.; Smets, A.H.M.; Zeman, M. Optical model for multilayer structures with coherent, partly coherent and incoherent layers. Opt. Express 2013, 21, A262–A267. [Google Scholar] [CrossRef] [Green Version]
- Čampa, A.; Krč, J.; Topič, M. Two Approaches for Incoherent Propagation of Light in Rigorous Numerical Simulations. Prog. Electromagn. Res. 2013, 137, 187–202. [Google Scholar] [CrossRef]
- Lipovšek, B.; Čampa, A.; Guo, F.; Brabec, C.J.; Forberich, K.; Krč, J.; Topič, M. Detailed optical modelling and light-management of thin-film organic solar cells with consideration of small-area effects. Opt. Express 2017, 25, A176–A190. [Google Scholar] [CrossRef] [PubMed]
- Lokar, Ž.; Lipovšek, B.; Razzaq, A.; Depauw, V.; Gordon, I.; Poortmans, J.; Krč, J.; Topič, M. Coupled modelling approach for optimization of bifacial silicon heterojunction solar cells with multi-scale interface textures. Opt. Express 2019, 27, A1554–A1568. [Google Scholar]
- Lokar, Ž.; Lipovšek, B.; Topič, M.; Krč, J. Performance analysis of rigorous coupled-wave analysis and its integration in a coupled modeling approach for optical simulation of complete heterojunction silicon solar cells. Beilstein J. Nanotechnol. 2018, 9, 2315–2329. [Google Scholar] [CrossRef] [PubMed]
- PhotoVoltaic Lighthouse Refractive Index Library. Available online: https://www.pvlighthouse.com.au/refractive-index-library (accessed on 18 June 2019).
- Lipovšek, B.; Krč, J.; Topič, M. Microtextured Light-Management Foils and Their Optimization for Planar Organic and Perovskite Solar Cells. IEEE J. Photovolt. 2018, 8, 783–792. [Google Scholar] [CrossRef]
- Bush, K.A.; Palmstrom, A.F.; Yu, Z.J.; Boccard, M.; Cheacharoen, R.; Mailoa, J.P.; McMeekin, D.P.; Hoye, R.L.Z.; Bailie, C.D.; Leijtens, T.; et al. 23.6%-efficient monolithic perovskite/silicon tandem solar cells with improved stability. Nat. Energy 2017, 2, 17009. [Google Scholar] [CrossRef]
- Jošt, M.; Köhnen, E.; Morales-Vilches, A.B.; Lipovšek, B.; Jäger, K.; Macco, B.; Al-Ashouri, A.; Krč, J.; Korte, L.; Rech, B.; et al. Textured interfaces in monolithic perovskite/silicon tandem solar cells: advanced light management for improved efficiency and energy yield. Energy Environ. Sci. 2018, 11, 3511–3523. [Google Scholar] [CrossRef] [Green Version]
- Tikhonravov, A.V.; Trubetskov, M.K.; DeBell, G.W. Optical coating design approaches based on the needle optimization technique. Appl. Opt. 2007, 46, 704–710. [Google Scholar] [CrossRef]










© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puhan, J.; Bűrmen, Á.; Tuma, T.; Fajfar, I. Irradiance in Mixed Coherent/Incoherent Structures: An Analytical Approach. Coatings 2019, 9, 536. https://doi.org/10.3390/coatings9090536
Puhan J, Bűrmen Á, Tuma T, Fajfar I. Irradiance in Mixed Coherent/Incoherent Structures: An Analytical Approach. Coatings. 2019; 9(9):536. https://doi.org/10.3390/coatings9090536
Chicago/Turabian StylePuhan, Janez, Árpád Bűrmen, Tadej Tuma, and Iztok Fajfar. 2019. "Irradiance in Mixed Coherent/Incoherent Structures: An Analytical Approach" Coatings 9, no. 9: 536. https://doi.org/10.3390/coatings9090536
APA StylePuhan, J., Bűrmen, Á., Tuma, T., & Fajfar, I. (2019). Irradiance in Mixed Coherent/Incoherent Structures: An Analytical Approach. Coatings, 9(9), 536. https://doi.org/10.3390/coatings9090536




