Oscillating Magnetic Drop: How to Grade Water-Repellent Surfaces
Abstract
1. Introduction
2. Materials and Methods
2.1. Fabrication of Superhydrophobic Glass Samples
2.2. Ferrofluid Preparation
2.3. Contact Angle Measurements
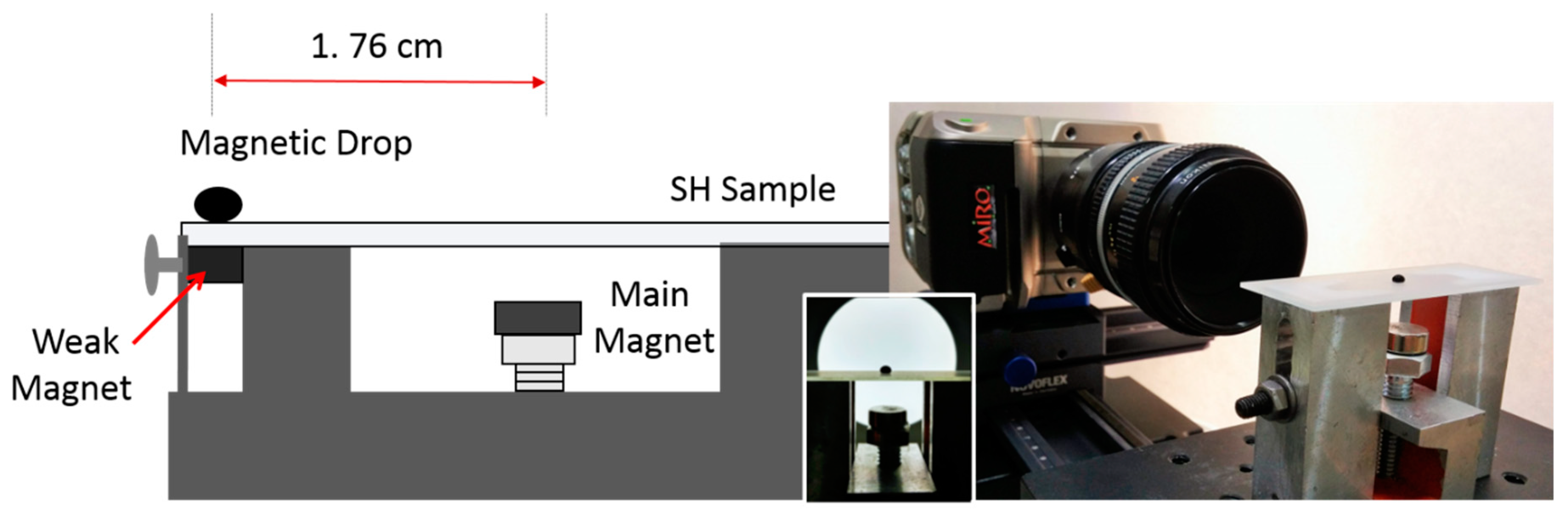
2.4. Oscillating Magnetic Drop Set-up
3. Results
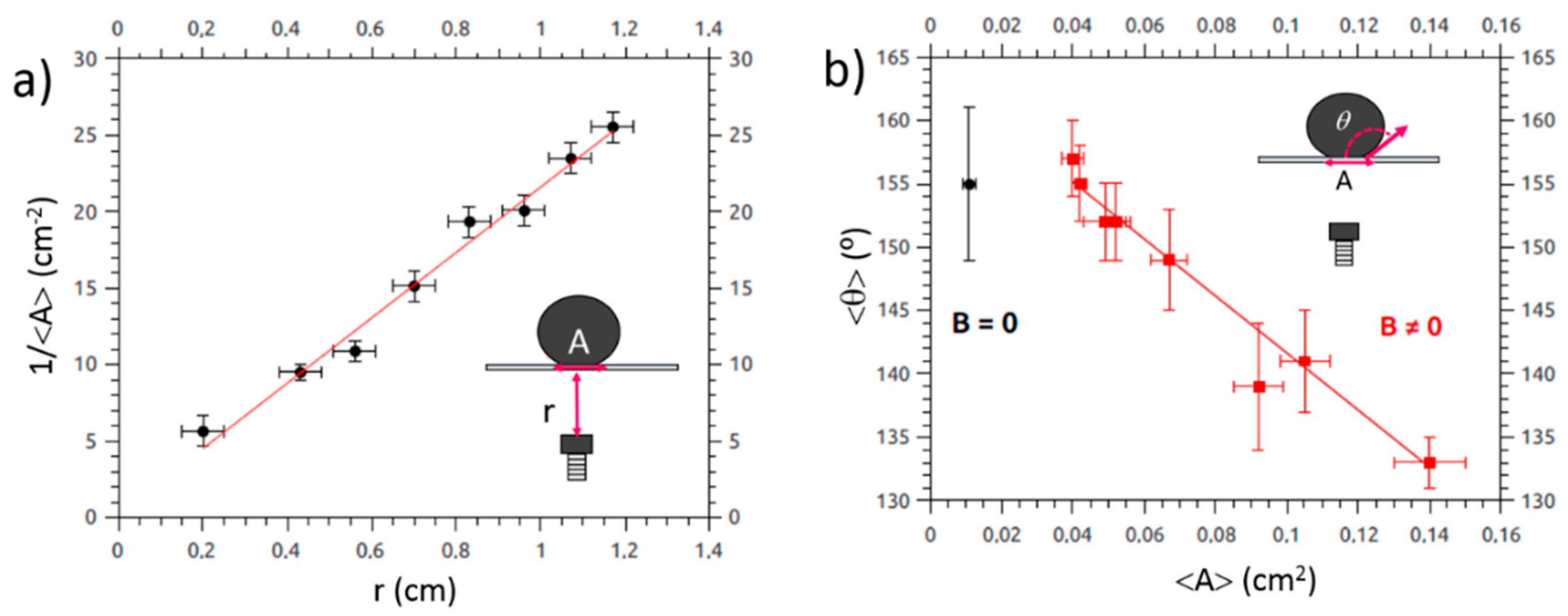
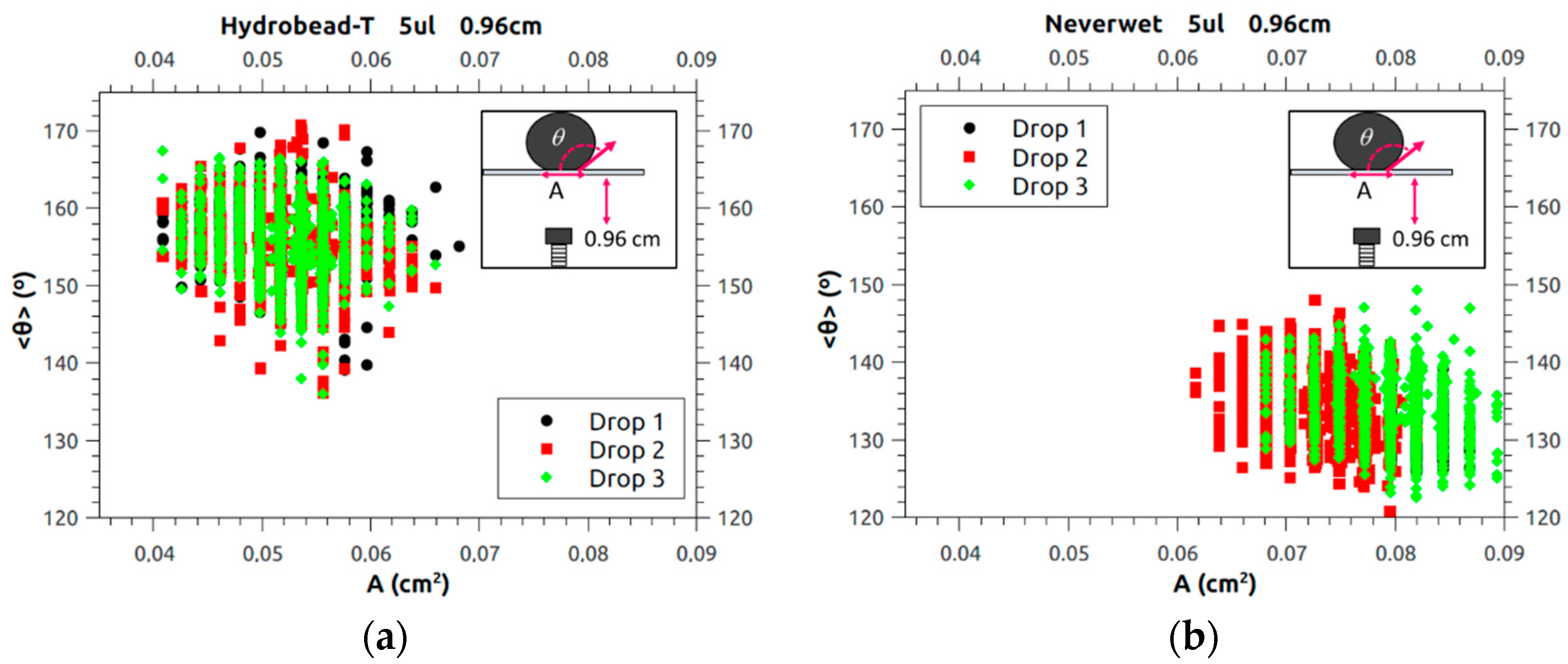
3.1. Contact Angle Measurements
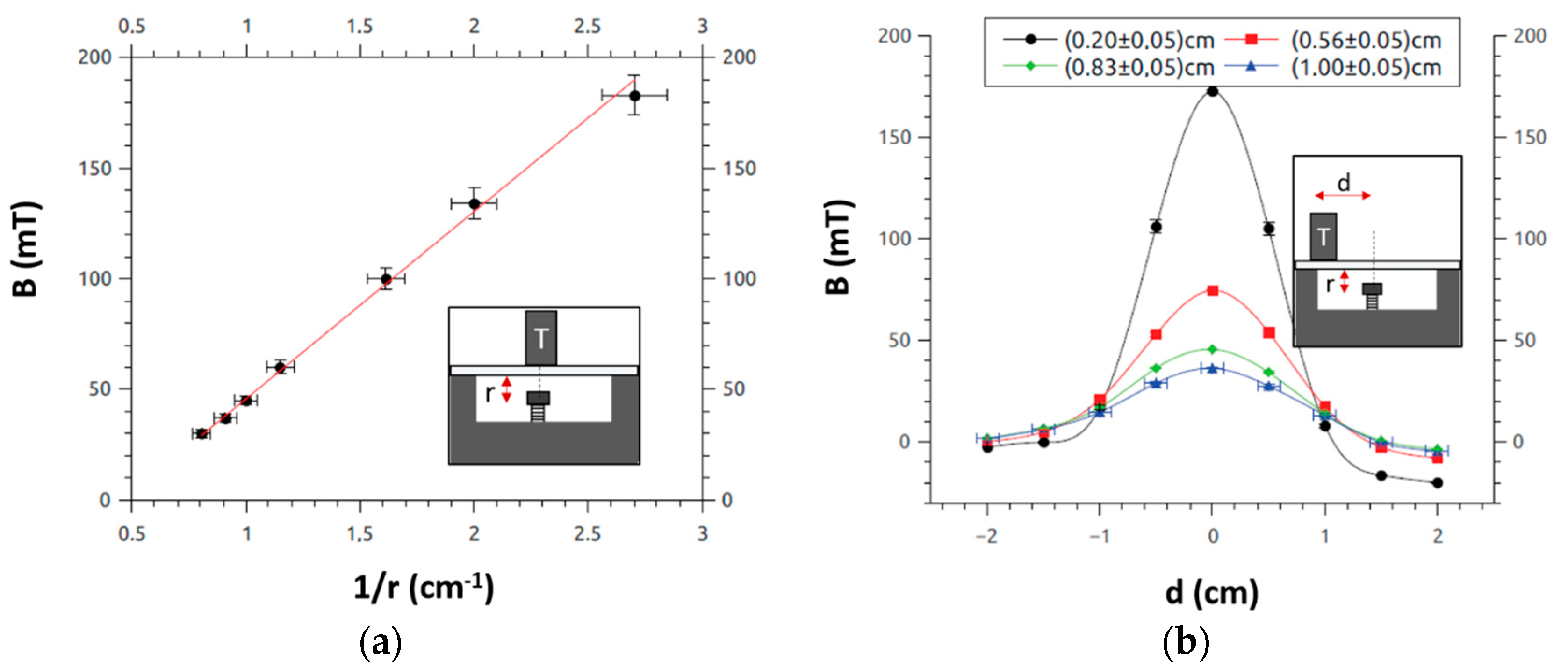
3.2. Magnetic Field Strength
3.3. Drop Shape Distortion Induced by the Magnetic Field
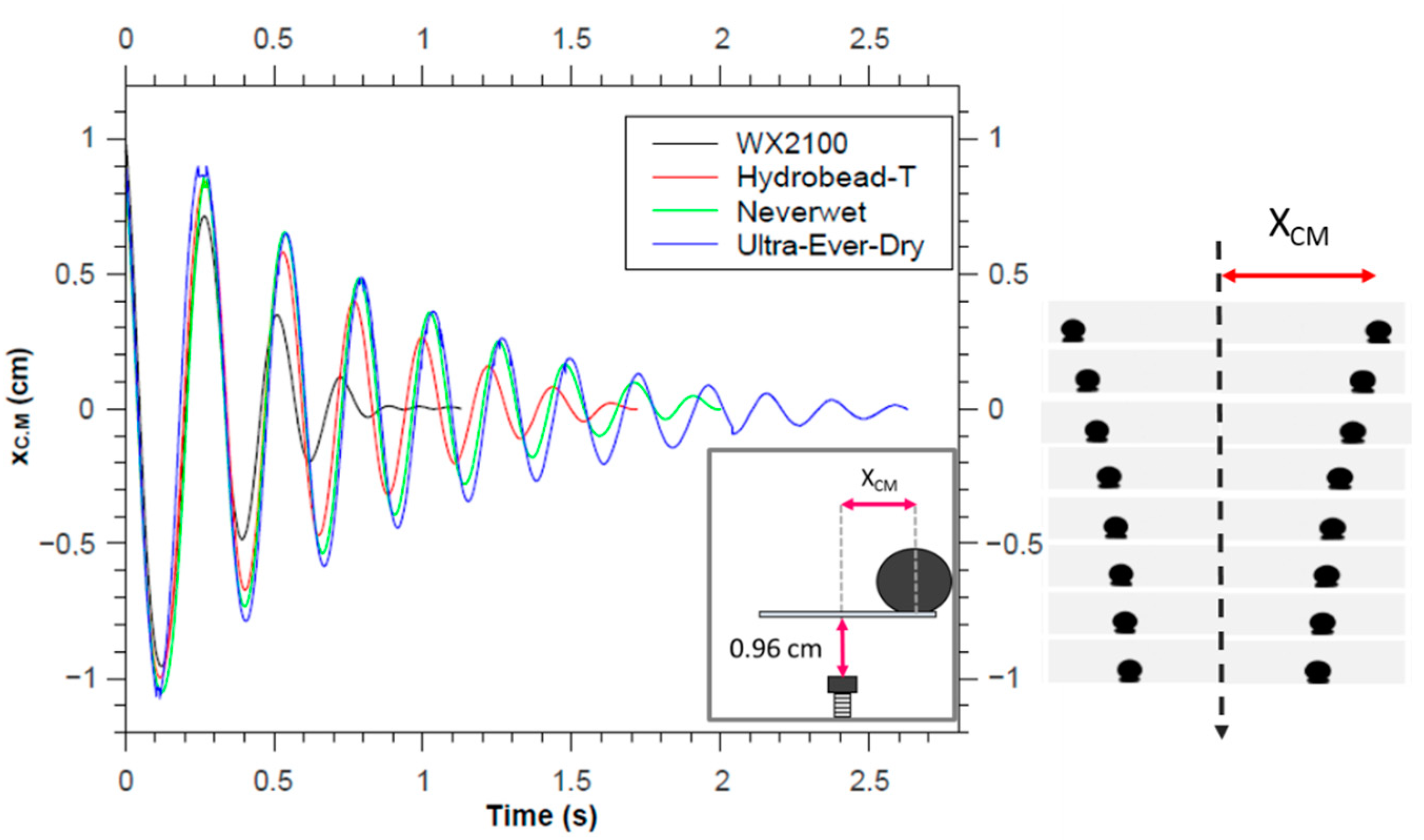
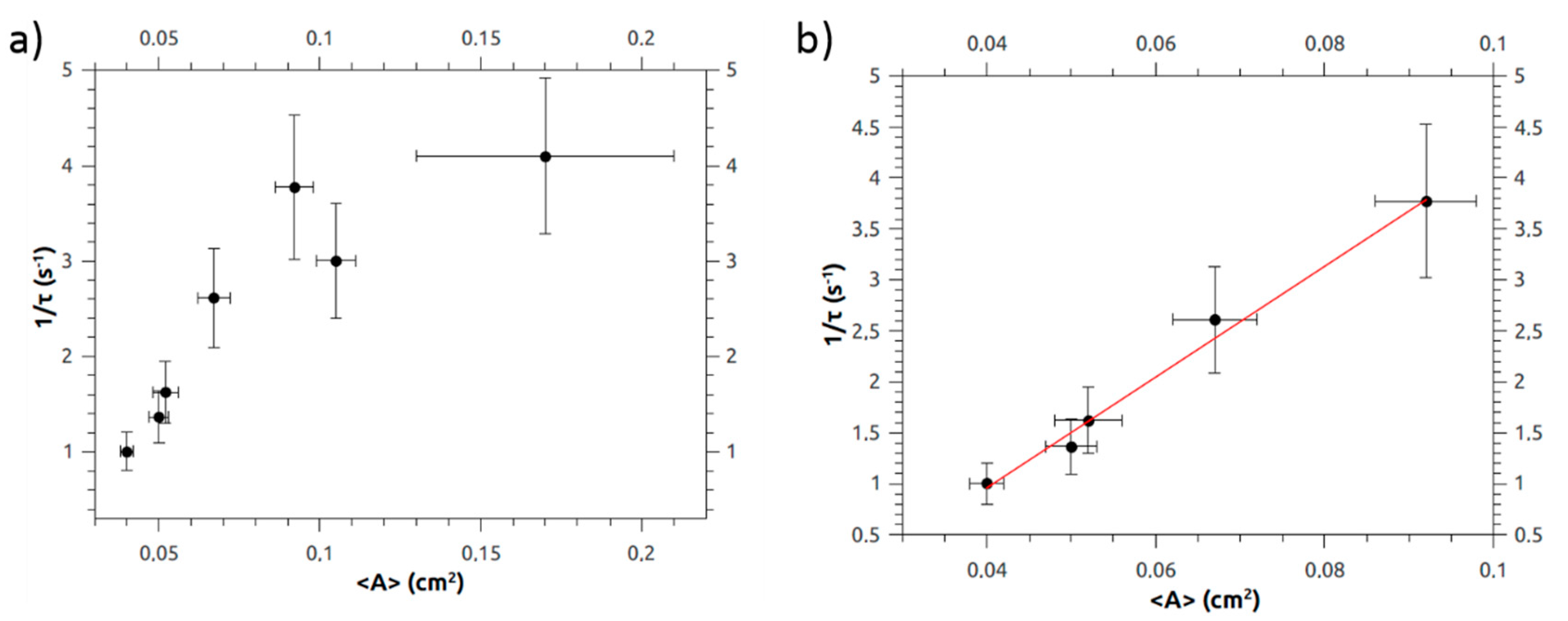
3.4. Dynamics of Oscillating Magnetic Drops
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lv, X.; Tian, D.; Peng, Y.; Li, J.; Jiang, G. Superhydrophobic magnetic reduced graphene oxide-decorated foam for efficient and repeatable oil-water separation. Appl. Surf. Sci. 2019, 466, 937–945. [Google Scholar] [CrossRef]
- Ruiz-Cabello, F.J.M.; Rodriguez-Valverde, M.A.; Cabrerizo-Vilchez, M. A new method for evaluating the most stable contact angle using tilting plate experiments. Soft Matter 2011, 7, 10457–10461. [Google Scholar] [CrossRef]
- Srinivasan, S.; McKinley, G.H.; Cohen, R.E. Assessing the accuracy of contact angle measurements for sessile drops on liquid-repellent surfaces. Langmuir 2011, 27, 13582–13589. [Google Scholar] [CrossRef] [PubMed]
- Tian, X.; Verho, T.; Ras, R.H.A. Moving superhydrophobic surfaces toward real-world applications. Science 2016, 352, 142–143. [Google Scholar] [CrossRef] [PubMed]
- Bormashenko, E.; Pogreb, R.; Bormashenko, Y.; Musin, A.; Stein, T. New investigations on ferrofluidics: Ferrofluidic marbles and magnetic-field-driven drops on superhydrophobic surfaces. Langmuir 2008, 24, 12119–12122. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Zhu, G.; Chua, Y.-C.; Phan, V.-N.; Tan, S.-H. Magnetowetting and sliding motion of a sessile ferrofluid droplet in the presence of a permanent magnet. Langmuir 2010, 26, 12553–12559. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Ristenpart, W.D.; Stroeve, P. Magnetically induced decrease in droplet contact angle on nanostructured surfaces. Langmuir 2011, 27, 11747–11751. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.-P.; Nguyen, N.-T.; Ramanujan, R.V.; Huang, X.-Y. Nonlinear deformation of a ferrofluid droplet in a uniform magnetic field. Langmuir 2011, 27, 14834–14841. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Lai, H.; Zhang, N.; Sun, K.; Jiang, L. Magnetically induced reversible transition between cassie and wenzel states of superparamagnetic microdroplets on highly hydrophobic silicon surface. J. Phys. Chem. C 2012, 116, 18796–18802. [Google Scholar] [CrossRef]
- Nguyen, N.-T. Deformation of ferrofluid marbles in the presence of a permanent magnet. Langmuir 2013, 29, 13982–13989. [Google Scholar] [CrossRef] [PubMed]
- Manukyan, S.; Schneider, M. Experimental investigation of wetting with magnetic fluids. Langmuir 2016, 32, 5135–5140. [Google Scholar] [CrossRef] [PubMed]
- Timonen, J.V.I.; Latikka, M.; Ikkala, O.; Ras, R.H.A. Free-decay and resonant methods for investigating the fundamental limit of superhydrophobicity. Nat. Commun. 2013, 4, 2398. [Google Scholar] [CrossRef] [PubMed]
- Schellenberger, F.; Encinas, N.; Vollmer, D.; Butt, H.-J. How water advances on superhydrophobic surfaces. Phys. Rev. Lett. 2016, 116, 096101. [Google Scholar] [CrossRef] [PubMed]
- Mahadevan, L.; Pomeau, Y. Rolling droplets. Phys. Fluids 1999, 11, 2449–2453. [Google Scholar] [CrossRef]
- Ménager, C.; Sandre, O.; Mangili, J.; Cabuil, V. Preparation and swelling of hydrophilic magnetic microgels. Polymer 2004, 45, 2475–2481. [Google Scholar] [CrossRef]
- Aldana, S.; Vereda, F.; Hidalgo-Alvarez, R.; de Vicente, J. Facile synthesis of magnetic agarose microfibers by directed self-assembly in W/O emulsions. Polymer 2016, 93, 61–64. [Google Scholar] [CrossRef]
- Nosonovsky, M. Model for solid-liquid and solid-solid friction of rough surfaces with adhesion hysteresis. J. Chem. Phys. 2007, 126, 224701. [Google Scholar] [CrossRef] [PubMed]
| Coating | ACA (°) | RCA (°) | CAH (°) |
|---|---|---|---|
| WX-2100 | 149 ± 2 | 147 ± 4 | 2 ± 6 |
| Hydrobead | 152 ± 1 | 146 ± 3 | 6 ± 4 |
| Ultra-Ever-Dry | 148 ± 2 | 146 ± 2 | 2 ± 4 |
| Neverwet | 151 ± 3 | 148 ± 3 | 3 ± 6 |
| Coating | <A> (mm2) |
|---|---|
| WX-2100 | 5.7 ± 0.4 |
| Hydrobead | 5.2 ± 0.4 |
| Ultra-Ever-Dry | 5.1 ± 0.4 |
| Neverwet | 7.8 ± 0.4 |
| Coating | τ (s)-5 µL | τ (s)-10 µL |
|---|---|---|
| WX-2100 | 0.25 ± 0.04 | 0.40 ± 0.03 |
| Hydrobead | 0.61 ± 0.05 | 0.61 ± 0.06 |
| Ultra-Ever-Dry | 0.70 ± 0.10 | 0.84 ± 0.10 |
| Neverwet | 0.66 ± 0.04 | 0.52 ± 0.09 |
| Coating | 1/(τ<A>) (cm−2 s−1)-5 µL | 1/(τ<A>) (cm−2 s−1)-10 µL |
|---|---|---|
| WX-2100 | 70 ± 16 | 33 ± 7 |
| Hydrobead | 32 ± 5 | 23 ± 9 |
| Ultra-Ever-Dry | 28 ± 6 | 17 ± 3 |
| Neverwet | 19 ± 2 | 19 ± 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goncalves Dos Santos, A.; Montes-Ruiz Cabello, F.J.; Vereda, F.; Cabrerizo-Vilchez, M.A.; Rodriguez-Valverde, M.A. Oscillating Magnetic Drop: How to Grade Water-Repellent Surfaces. Coatings 2019, 9, 270. https://doi.org/10.3390/coatings9040270
Goncalves Dos Santos A, Montes-Ruiz Cabello FJ, Vereda F, Cabrerizo-Vilchez MA, Rodriguez-Valverde MA. Oscillating Magnetic Drop: How to Grade Water-Repellent Surfaces. Coatings. 2019; 9(4):270. https://doi.org/10.3390/coatings9040270
Chicago/Turabian StyleGoncalves Dos Santos, Angelica, Francisco Javier Montes-Ruiz Cabello, Fernando Vereda, Miguel A. Cabrerizo-Vilchez, and Miguel A. Rodriguez-Valverde. 2019. "Oscillating Magnetic Drop: How to Grade Water-Repellent Surfaces" Coatings 9, no. 4: 270. https://doi.org/10.3390/coatings9040270
APA StyleGoncalves Dos Santos, A., Montes-Ruiz Cabello, F. J., Vereda, F., Cabrerizo-Vilchez, M. A., & Rodriguez-Valverde, M. A. (2019). Oscillating Magnetic Drop: How to Grade Water-Repellent Surfaces. Coatings, 9(4), 270. https://doi.org/10.3390/coatings9040270







