The Effects of an Interlayer Debond on the Flexural Behavior of Three-Layer Beams
Abstract
1. Introduction
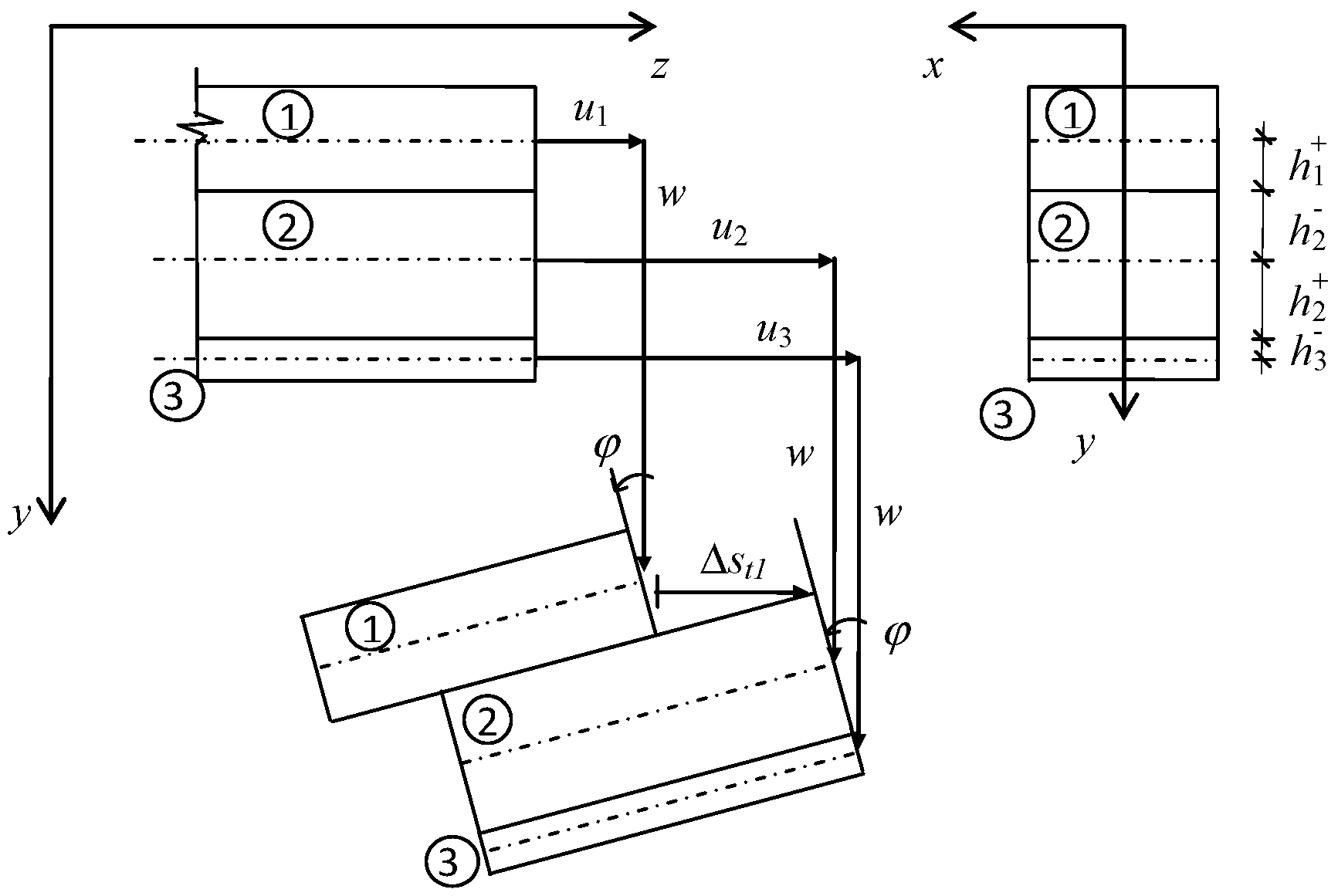
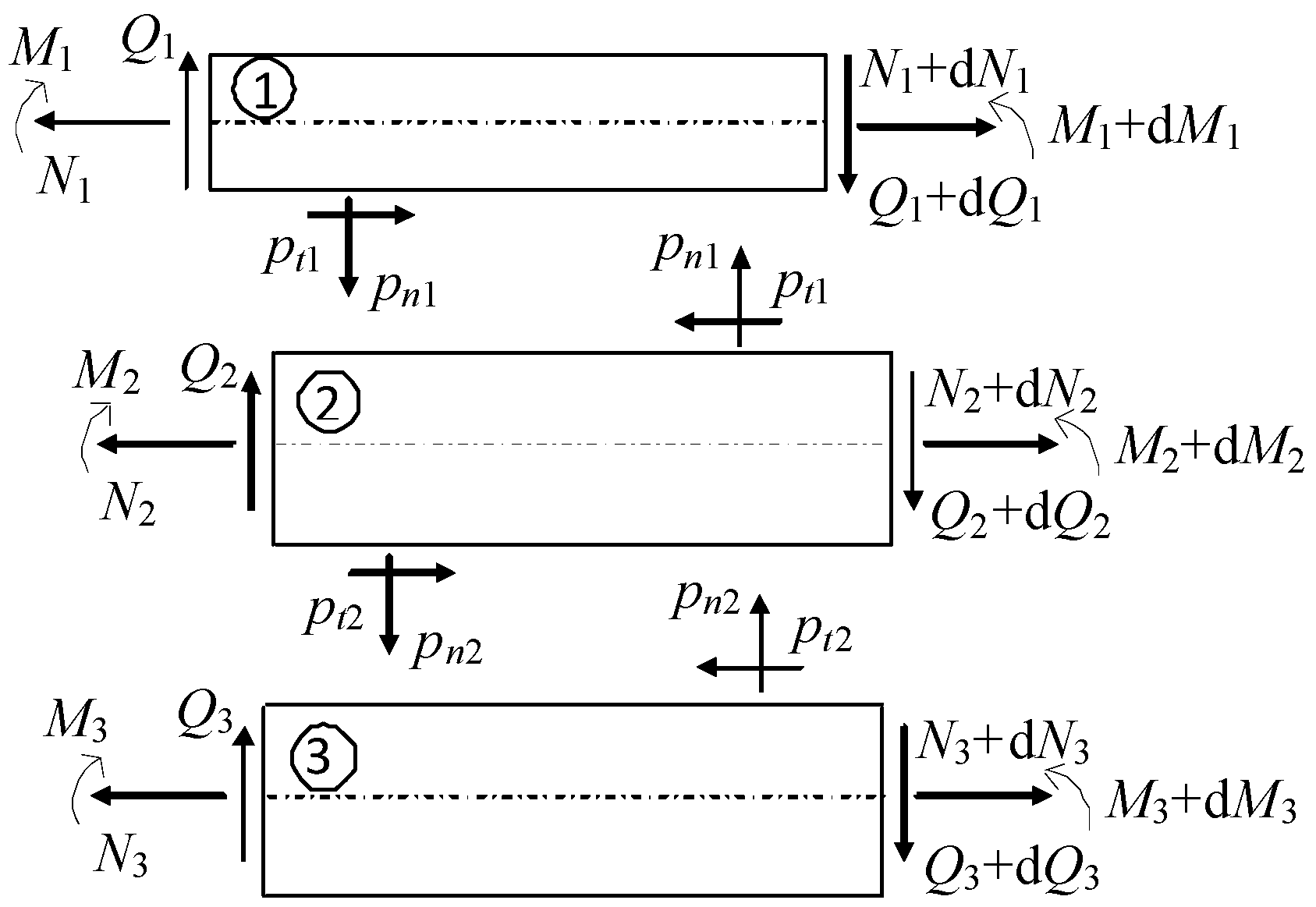
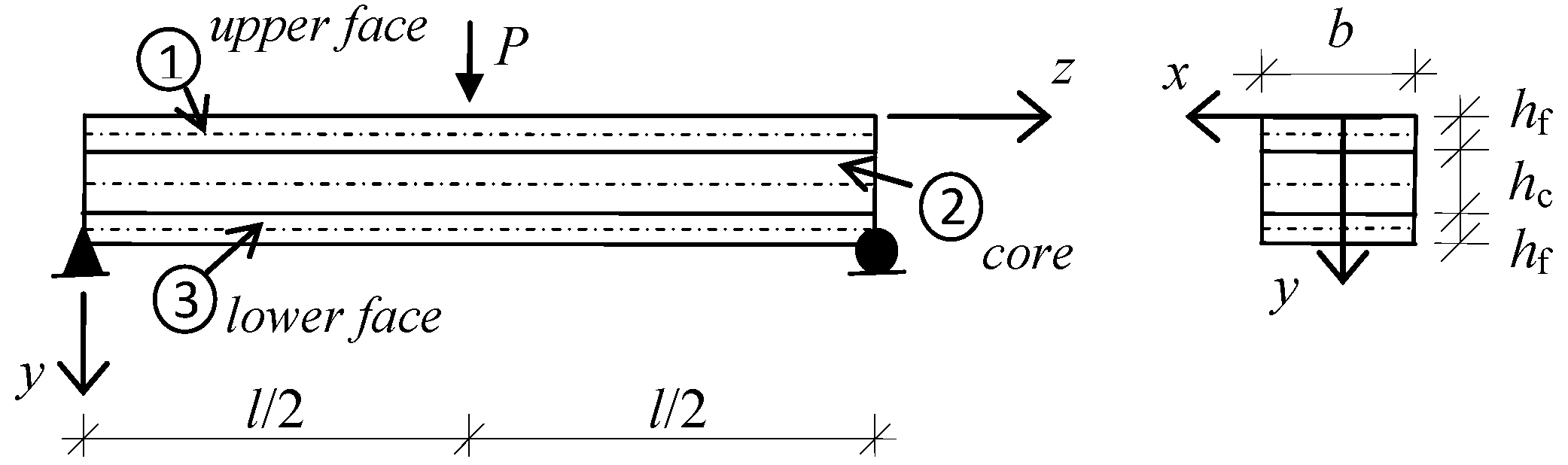
2. Materials and Methods
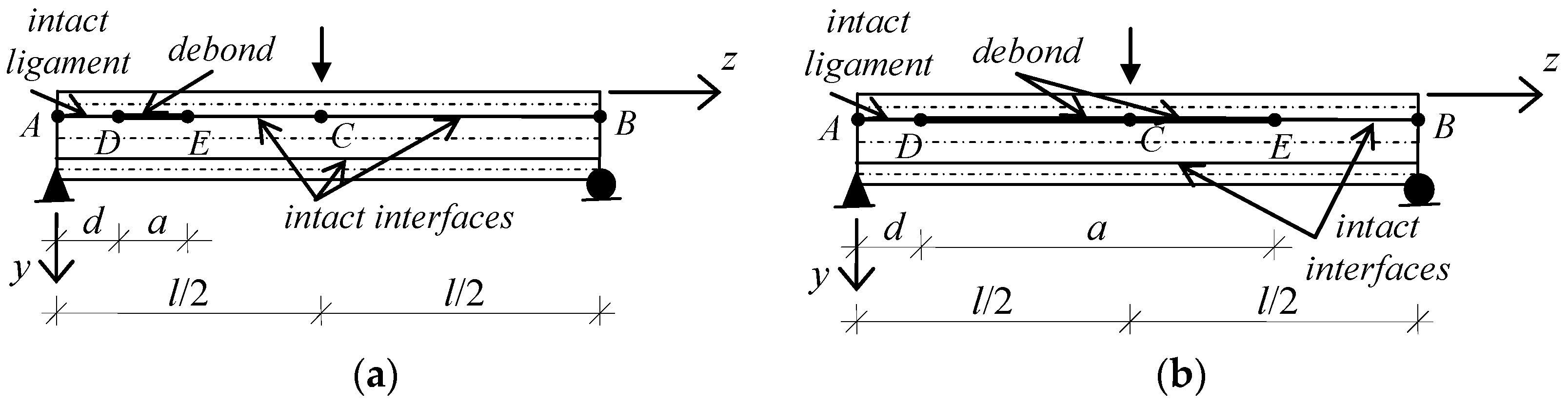
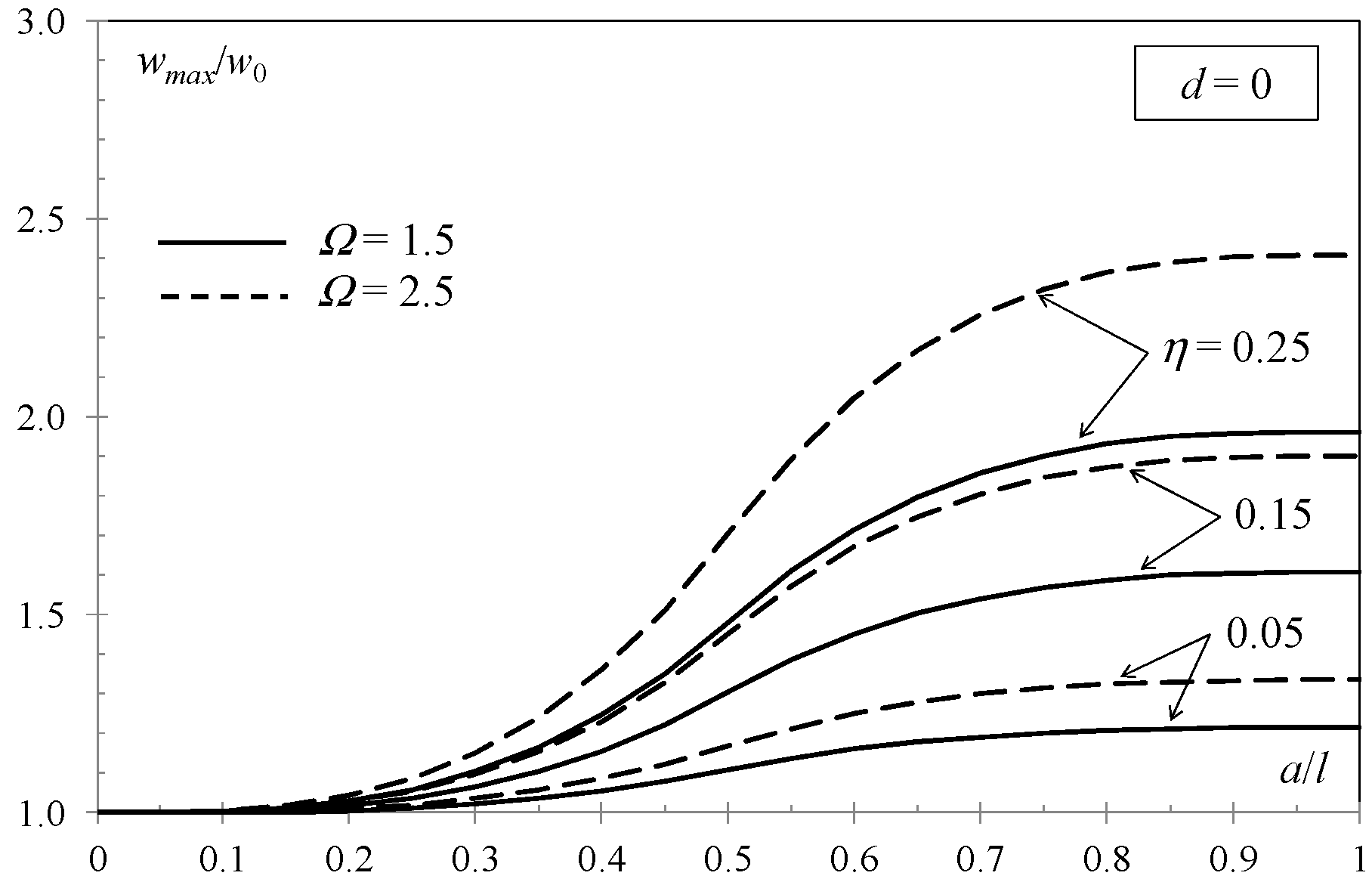
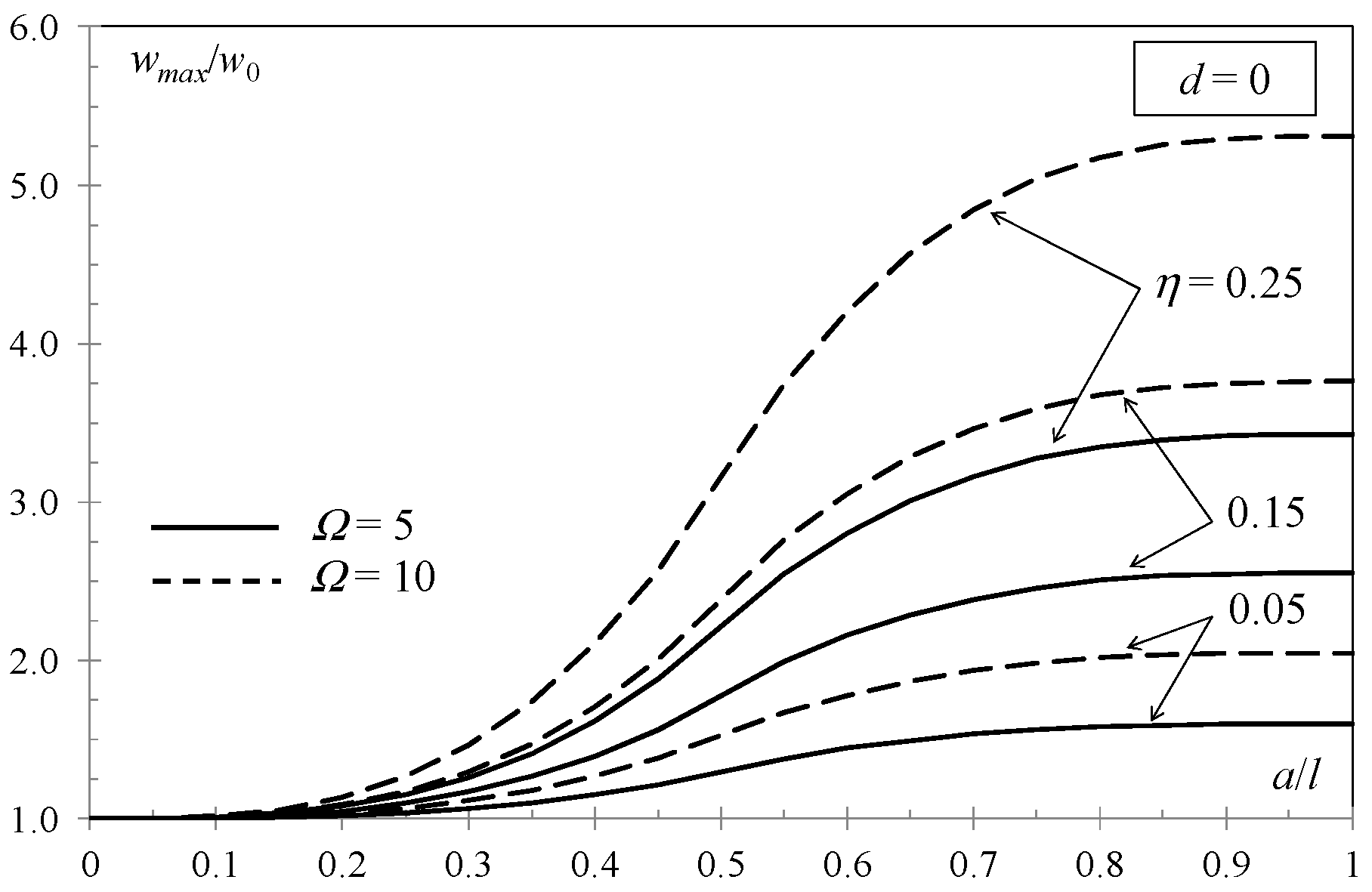
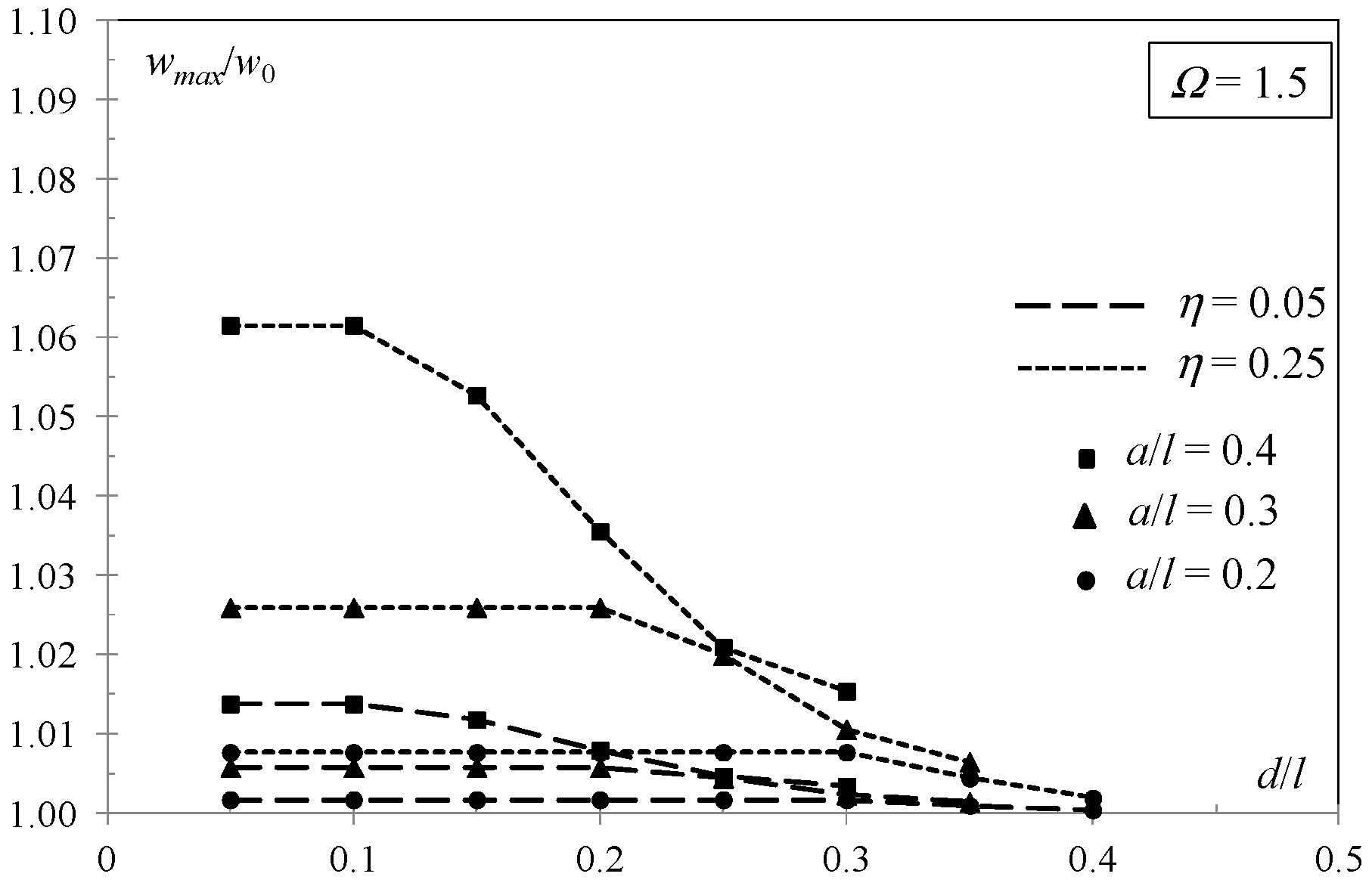
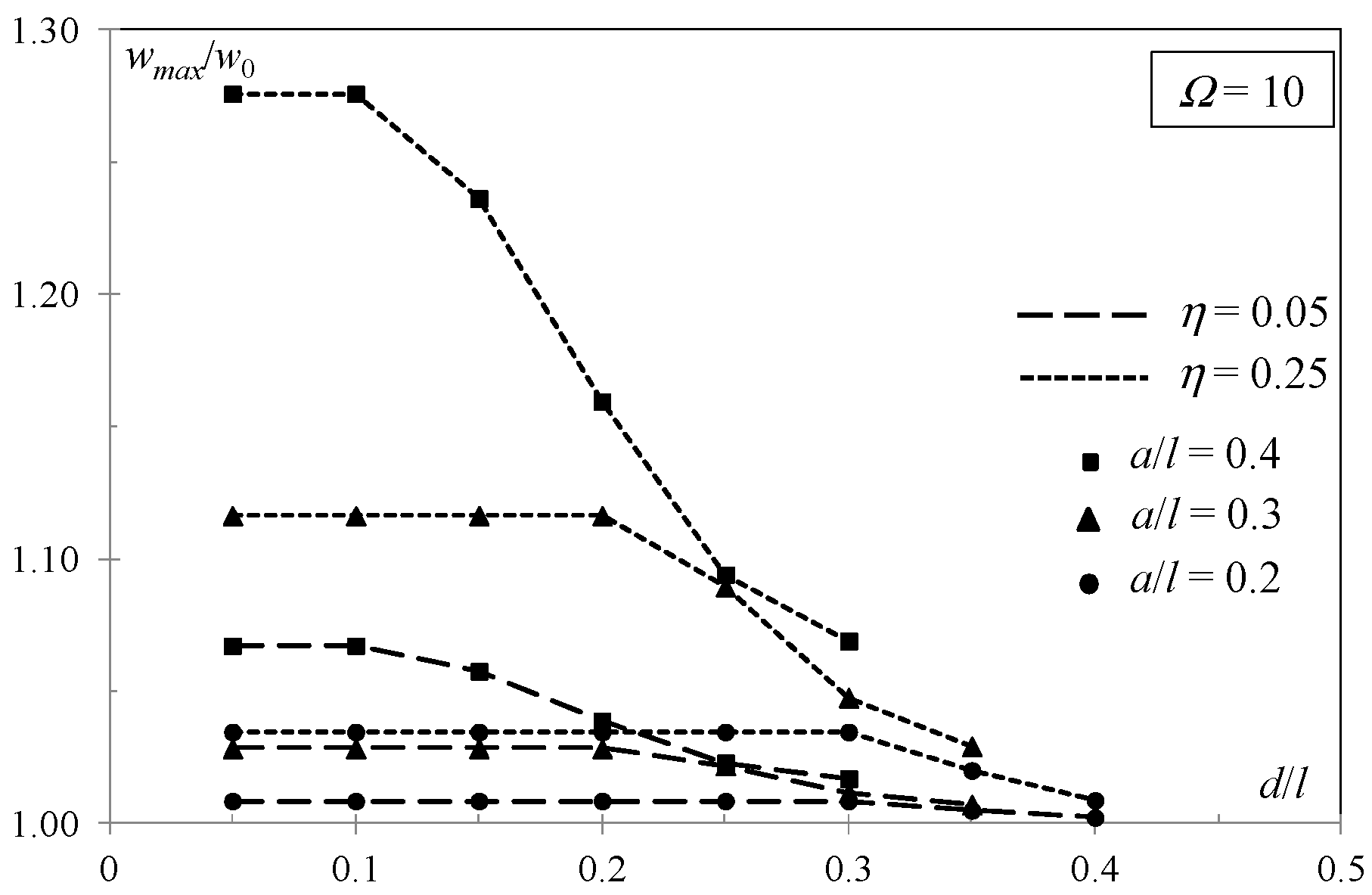
3. Results
4. Discussion and Conclusions
Funding
Conflicts of Interest
Appendix A
References
- Goodman, J.R.; Popov, E.P. Layered beam systems with interlayer slip. J. Struct. Div. 1968, 94, 2535–2548. [Google Scholar]
- McCutcheon, W.J. Stiffness of framing members with partial composite action. J. Struct. Eng. 1986, 112, 1623–1637. [Google Scholar] [CrossRef]
- Chui, Y.H.; Barclay, D.W. Analysis of three-layer beams with non-identical layers and semi-rigid connections. Can. J. Civil Eng. 1998, 25, 271–276. [Google Scholar] [CrossRef]
- Schnabl, S.; Planinc, I.; Saje, M.; Čas, B.; Turk, G. An analytical model of layered continuous beams with partial interaction. Struct. Eng. Mech. 2006, 3, 263–278. [Google Scholar] [CrossRef][Green Version]
- Ranzi, G. Locking problems in the partial interaction analysis of multi-layered composite beams. Eng. Struct. 2008, 30, 2900–2911. [Google Scholar] [CrossRef]
- Sousa, J.B.M., Jr.; da Silva, A.R. Analytical and numerical analysis of multilayered beams with interlayer slip. Eng. Struct. 2010, 32, 1671–1680. [Google Scholar] [CrossRef]
- Monetto, I. Analytical solutions of three-layer beams with interlayer slip and step-wise linear interface law. Compos. Struct. 2015, 120, 543–551. [Google Scholar] [CrossRef]
- Campi, F.; Monetto, I. Analytical solutions of two-layer beams with interlayer slip and bi-linear interface law. Int. J. Solids Struct. 2013, 50, 687–698. [Google Scholar] [CrossRef]
- Pelassa, M.; Massabò, R. Explicit solutions for multi-layered wide plates and beams with perfect and imperfect bonding and delaminations under thermo-mechanical loading. Meccanica 2015, 50, 2497–2524. [Google Scholar] [CrossRef]
- Atashipour, S.R.; Girhammar, U.A.; Challamel, N. Stability analysis of three-layer shear deformable partial composite columns. Int. J. Solids Struct. 2017, 106–107, 213–228. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Pavlov, S.P.; Zhigalov, M.V.; Krysko, A.V. Mathematical model of a three-layer micro- and nano-beams based on the hypotheses of the Grigolyuk–Chulkov and the modified couple stress theory. Int. J. Solids Struct. 2017, 117, 39–50. [Google Scholar] [CrossRef]
- Čas, B.; Planinc, I.; Schnabl, S. Analytical solution of three-dimensional two-layer composite beam with interlayer slips. Eng. Struct. 2018, 173, 269–282. [Google Scholar] [CrossRef]
- Barbieri, L.; Massabò, R.; Berggreen, C. The effects of shear and near tip deformations on interface fracture of symmetric sandwich beams. Eng. Fract. Mech. 2018, 201, 298–321. [Google Scholar] [CrossRef]
- Monetto, I.; Campi, F. Numerical analysis of two-layer beams with interlayer slip and step-wise linear interface law. Eng. Struct. 2017, 144, 201–209. [Google Scholar] [CrossRef]
- Brandinelli, L.; Massabò, R. Mode II weight functions for isotropic and orthotropic double cantilever beams. Int. J. Fract. 2006, 139, 1–25. [Google Scholar] [CrossRef]
- Czechowski, L.; Jankowski, J.; Kotelko, M. Experimental and numeriacl three-point bending tests for sandwich beams. J. KONES 2017, 24, 53–62. [Google Scholar]
- Li, Y.; Bielak, J.; Hegger, J.; Chudoba, R. An incremental inverse analysis procedure for identification of bond-slip laws in composites applied to textile reinforced concrete. Compos. Part Eng. 2018, 137, 111–122. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monetto, I. The Effects of an Interlayer Debond on the Flexural Behavior of Three-Layer Beams. Coatings 2019, 9, 258. https://doi.org/10.3390/coatings9040258
Monetto I. The Effects of an Interlayer Debond on the Flexural Behavior of Three-Layer Beams. Coatings. 2019; 9(4):258. https://doi.org/10.3390/coatings9040258
Chicago/Turabian StyleMonetto, Ilaria. 2019. "The Effects of an Interlayer Debond on the Flexural Behavior of Three-Layer Beams" Coatings 9, no. 4: 258. https://doi.org/10.3390/coatings9040258
APA StyleMonetto, I. (2019). The Effects of an Interlayer Debond on the Flexural Behavior of Three-Layer Beams. Coatings, 9(4), 258. https://doi.org/10.3390/coatings9040258




