Abstract
Debonds at the interfaces between layers of multilayered systems make the degree of the composite action reduce. As a consequence, the global stiffness of such composites decreases. In order to investigate this reduction, even simplified analytical models are preferable to numerical analyses. This paper analyzes the flexural response of a three-point bending three-layer beam having a debonded portion at the upper interface to investigate the effects of the interlayer debond on the flexural stiffness of the three-layer beam and to examine the feasibility of detecting the presence of possible manufacturing or in-service flaws. A more general model proposed and validated previously by the author was specialized to solve the equilibrium problem considered. A parametric analysis was then performed on varying the model parameters and evaluating the maximum deflection to compare with that for perfectly bonded layers as a measure of the reduction of the flexural stiffness due to the presence of the debond. The numerical results obtained show that the flexural behavior of the sandwich beam under consideration is affected strongly by the length of the debond but only moderately by its position along the interface unless the outer faces are quite stiffer than the core.
1. Introduction
Composite beams consisting of structural elements connected together at the common interfaces by appropriate mechanical devices or adhesive joints are widely used in many practical applications, in which the use of materials with unique properties is desirable. Laminated and sandwich beams are only some examples of the employment of multilayer composite beams to develop lightweight structures with high flexural stiffness and strength.
Such enhanced performances depend not only on the mechanical properties of each layer but also on those of the connections that force the parts to act together as a composite, as well as on the geometry of the beam. In such structures, manufacturing flaws as well as in-service debonds at the interfaces between layers can be dangerous, because they lead to a reduction of the degree of the composite action and of the global stiffness and strength of the system as a consequence. Failure can occur even if each element behaves elastically. The investigation of such an additional collapse mechanism is, then, of great importance for the optimal design of composite systems.
This paper deals with the investigation of the effects on the mechanical response of composite systems of a partial composite action between their elements for a prescribed loading condition. In order to do this, even simplified analytical models are preferable to numerical analyses performed for specific geometry, material properties, and interface behavior. In particular, the attention is focused here on the flexural behavior of three-layer beams. This has been the object of some studies in the literature. Starting from the pioneering works by Goodman and Popov [1], McCutcheon [2], and Chui and Barclay [3], other models have been developed (see, e.g., [4,5,6]). Among others, Monetto [7] solved explicitly the problem of partial interaction in three-layer beams with interlayer slip and stepwise linear interface law. This formulation builds on previous work [8] on two-layer composite beams and permits one to derive explicit expressions, having general validity, for all static and kinematic variables of the problem. In spite of its simplicity, this analytical solution can be employed to analyze the response of composite beams for different boundary and loading conditions, also inducing irreversible processes of progressive interfacial debonding. Among more recent papers, References [9,10,11,12,13] present other analytical solutions but for particular geometries or boundary and loading conditions.
In this paper, the analytical solution of the problem of partial interaction in three-layer beams proposed in [7] was employed. Namely, this more general model, proposed previously by the author and validated with many results from the literature for different boundary and loading conditions as well as for interfaces behaving nonlinearly, was here specialized to a specific problem. This is central to achieve the main goal of the present work: The investigation of the effects of an interlayer debond on the flexural stiffness of three-layer beams, as a feasibility study for detecting the presence and possibly determining the extension of possible debonding during the fabrication or employment of a composite beam.
The case study of a sandwich beam simply supported at both ends, subjected to a point load at center and with a debonded portion along the upper interface, was considered. A parametric analysis was then performed on varying the geometrical and mechanical properties of the layers, as well as the debond length and related distance from one end of the beam. The maximum deflection at midspan was then evaluated and compared with that of the beam composed of the same layers but perfectly bonded to measure the reduction of the flexural stiffness due to the presence of the debond, which causes an increase in the displacements as a consequence. The numerical results obtained show that the flexural behavior of the sandwich beam under consideration is strongly affected by the length of the debond but only moderately by its position along the interface unless the outer faces are quite stiffer than the core. This occurs for high face Young’s modulus and/or thickness.
The paper is organized as follows. In Section 2, the composite beam analyzed as a case study to obtain the numerical results is presented; furthermore, the related equilibrium problem is posed; finally, the procedure to employ the explicit functions for all the kinematic and static quantities characterizing the mechanical response of the beam and to determine the arbitrary constants contained in such functions is detailed. The numerical results of the parametric analysis performed are shown and discussed in Section 3, whereas final additional conclusions are drawn in Section 4. In Appendix A, firstly, a brief statement of the main points of a more general model formulation and related fundamental solution detailed in [7] is given; secondly, the procedure to specialize such a more general formulation to the special equilibrium problem described in Section 2 is presented; finally, the derivation of displacements and internal forces functions describing the solution of the equilibrium problem under consideration is detailed.
2. Materials and Methods
The composite beam considered in the present model consists of three layers connected by continuous bonds. The layers have constant cross sections and are made of isotropic, linearly elastic, and homogeneous materials. The lower interface is perfect in both transverse and longitudinal directions: No separation, interpenetration or slip across this interface are possible. The upper interface is perfect in the transverse direction, while it can only ensure partial composite actions in the longitudinal direction. Only interlayer slips can then be allowed at the upper interface, whereas no separation or interpenetration between the layers can occur. Figure 1 shows the undeformed and typical deformed configurations of the three-layer beam under consideration.
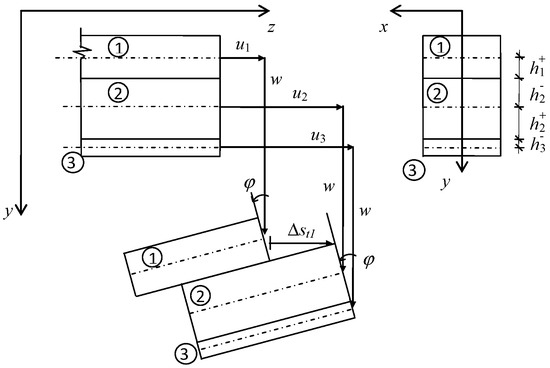
Figure 1.
Composite beam assumed in the present model: Geometry and typical deformed configuration.
Under the assumption of small strains, displacements, and rotations, each layer is modeled as a linearly elastic Euler–Bernoulli beam subjected only to the action of internal forces and interfacial tractions, as shown in Figure 2. This is the situation when point loads are applied, as of interest in this paper. For the imperfect bond, the limit case of vanishing interfacial stiffness is considered; as a consequence, no shear traction is transmitted across the interface.
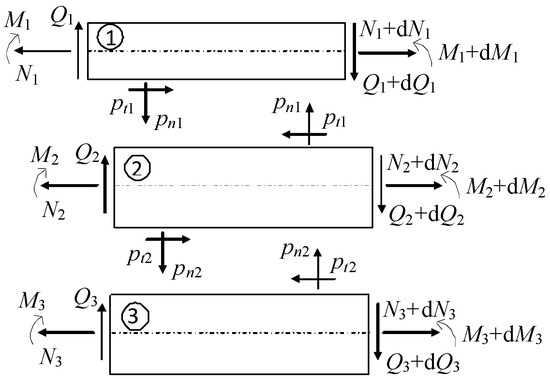
Figure 2.
Composite beam assumed in the present model: Free-body diagram of an infinitesimal element.
The problem of the equilibrium of the composite beam under consideration is governed by the compatibility, equilibrium, and constitutive equations for the three layers together with the bond conditions at the two interfaces. In order to solve this special problem, reference is made to a more general formulation proposed and validated by the author in [7]. In that paper, the governing equations and the solution procedure leading to exact expressions of all the static and kinematic variables were detailed with reference to the most general case of three-layer beams with interlayer slip and stepwise linear interface law at both interfaces and uniformly loaded along their axis. In this paper, these general results were specialized to the particular three-layer beam under consideration shown in Figure 1 and Figure 2. The procedure followed is detailed in Appendix A, where all the closed form solution functions for rotation, deflection, axial displacements, and internal forces so derived can be found as well. The limit case of perfect upper interface was also analyzed.
In this paper, the closed form solution presented in Appendix A was employed to simulate the response in bending of three-layer composite beams with interfacial flaws and analyze the effects of their length and position along the interface on the flexural stiffness for different geometrical and mechanical properties of the layers. The procedure is described with reference to the case study, for which the numerical results are shown and interpreted in Section 3 and Section 4.
A composite symmetric sandwich beam comprising an inner core (layer 2), having thickness hc and Young’s modulus Ec, enclosed by two stiffer outer faces, having equal thickness hf and Young’s modulus Ef, was considered. The beam is simply supported at both ends and subjected to a point load at center, as shown in Figure 3. The lower interface between the core and the lower face (layer 3) was assumed to be perfect also in the longitudinal direction, so no slip can occur along this interface. The upper interface between the core and the upper face (layer 1) was assumed to be perfect as well, except for the presence of a debonded portion having length a at a distance d < l/2 from the left end. Then, the upper interface can exhibit one of the two configurations shown in Figure 4 depending on the value of d + a.
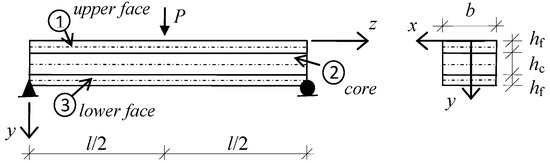
Figure 3.
Simply supported composite sandwich beam case study: Geometry, constraining and loading conditions.
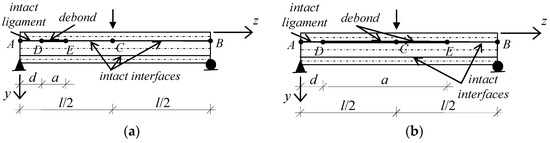
Figure 4.
Simply supported composite sandwich beam case study: Upper interface generic configurations (a) for d + a ≤ l/2 and (b) for d + a > l/2.
Extending the solution procedure described in [14], it is reasonable to divide the beam domain 0 ≤ z ≤ l in four subdomains, l being the beam length: Each subdomain involves adjacent points along the interfaces that behave accordingly to the same regime and are singled out by two distinct discontinuity locations.
With reference to the generic configuration with a small debond (Figure 4a), we have: Portion AD (0 ≤ z ≤ d) with a perfectly bonded upper interface; portion DE (d ≤ z ≤ d + a) with a fully debonded upper interface; and portions EC (d + a ≤ z ≤ l/2) and CB (l/2 ≤ z ≤ l) with a perfectly bonded upper interface. The solution of the equilibrium problem of such a configuration consists of four sets of independent functions for displacements and internal forces, each one referring to a portion of the composite beam. For portions AD, EC, and CB, the explicit expressions for the static and kinematic variables are given by Equations (A10)–(A13) and (A15)–(A17), specialized for the interfacial tractions of Equations (A8) and (A6). Each of these three sets of functions contains 6 arbitrary constants. For portion DE, the explicit expressions for the static and kinematic variables are given by Equations (A10)–(A12) and (A14)–(A17), specialized for the interfacial tractions of Equations (A9) and (A6). This set of functions contains 8 arbitrary constants. The general solution then contains, in total, 26 arbitrary constants, which are determined by imposing the boundary conditions at the ends A and B simply supported and the continuity conditions at the discontinuity locations C (where the point load is applied), D, and E (where the regime experienced by the upper interface changes). In order to do this, it is convenient to define the following static global quantities:
Then, the boundary conditions at end A can be written as:
and at end B as:
where, as an example, wAD denotes the deflection function in portion AD. Furthermore, the continuity conditions at D can be written as:
at E as:
and at C as:
With reference to the generic configuration with a long debond (Figure 4b), we have: Portion AD (0 ≤ z ≤ d) with a perfectly bonded upper interface; portions DC (d ≤ z ≤ l/2) and CE (l/2 ≤ z ≤ d + a) with a fully debonded upper interface; and portion EB (d + a ≤ z ≤ l) with perfectly bonded upper interface. The solution of the equilibrium problem of such a configuration consists of four sets of independent functions for displacements and internal forces, each one referring to a portion of the composite beam. For portions AD and EB, the explicit expressions for the static and kinematic variables are given by Equations (A10)–(A13) and (A15)–(A17), specialized for the interfacial tractions of Equations (A8) and (A6). Each of these two sets of functions contains 6 arbitrary constants. For portions DC and CE, the explicit expressions for the static and kinematic variables are given by Equations (A10)–(A12) and (A14)–(A17), specialized for the interfacial tractions of Equations (A9) and (A6). Each of these two sets of functions contains 8 arbitrary constants. The general solution then contains, in total, 28 arbitrary constants, which are determined by imposing the boundary conditions at the ends A and B, simply supported and the continuity conditions at the discontinuity locations C (where the point load is applied), D, and E (where the regime experienced by the upper interface changes). Also for this configuration, the boundary conditions at ends A and B are given by Equations (2) and (3), while the continuity conditions at D are given by Equation (4). The other conditions differ from those written above. Namely, the continuity conditions at C can be written as:
at E as:
When the arbitrary constants have been determined, the maximum deflection wmax exhibited by the composite beam at midspan under the load point can be evaluated by considering the proper deflection function. For the configuration shown in Figure 4a, wmax is given indifferently by the deflection function wEC or wCB evaluated at C. For the configuration shown in Figure 4b, wmax is given indifferently by the deflection function wDC or wCE evaluated at C. It is straightforward that the value of wmax depends on those of all the geometrical and physical parameters of the model, as discussed in Section 3, where the solution described above is employed to analyze the effects of an interlayer debond at the upper interface of three-layer beams on their flexural behavior.
3. Results
With reference to the sandwich beam shown in Figure 3 and Figure 4, the effects due to the presence of the debond along the upper interface on the flexural stiffness of the system were investigated by performing a parametric analysis. As a measure of the reduction of the flexural stiffness due to the presence of the debond, the maximum deflection at the load point was calculated for different values of the geometrical and mechanical parameters and compared with that of the beam with the same geometry and layer materials but both intact interfaces. In fact, the increase in the displacements due to the presence of the debond results in a decrease in the flexural stiffness of the composite beam.
The following dimensionless parameters which control the response of the composite beam are defined:
which characterize the geometry and layer materials, and:
which characterize the configuration of the upper interface. It is worthwhile to note that the particular case of a composite beam with three equal thickness layers made of the same material corresponds to η = 1 and Ω = 1; ξ = 0 corresponds to the particular case of perfectly bonded layers; and for δ = 0, the system reduces to a standard end notched flexural specimen, analyzed in many analytical models within fracture mechanics (see, e.g., [15]).
Λ = l/hc, η = hf/hc, Ω = Ef/Ec
ξ = a/hc = Λa/l, δ = d/hc = Λd/l
The results shown in what follows were obtained assuming a beam length-to-core thickness ratio Λ = 100 and varying face-to-core thickness ratio η = 0.05, 0.15, and 0.25, and face-to-core Young’s modulus ratio Ω = 1.5, 2.5, 5, and 10 for debonds of different length ξ = 0–Λ (0 ≤ a < l) and position δ = 0–Λ/2 (0 ≤ d < l/2). Such results are presented in terms of the ratio wmax/w0, where for each set of results, wmax and w0 are the maximum deflections in the cases of upper interface with an initial debond and intact upper interface, respectively. It is well known that for a simply supported beam under a point load at midspan:
where P is the point load and K is the section flexural modulus which depends on both the section geometry and material. For the composite section shown in Figure 3, we have, for perfectly bonded layers:
that reduces to:
for a fully debonded upper interface, b being the beam width. It is straightforward that dividing Equation (12) by Equation (13) gives another limit value for the dimensionless maximum deflection, say wlim/w0, which corresponds to the case of fully debonded upper interface; it results in:
w0 = 1/48Pl3/K
A first set of results refers to the composite sandwich beam having a debonded portion at one end of the upper interface between the core and the upper face layers (d = 0). Such results are shown in Figure 5 and Figure 6, where the dimensionless maximum deflection is plotted versus the dimensionless debond length. As expected, the longer the debond, the lower the flexural stiffness of the composite beam in bending is; this leads to an increase in deflections. It is worthwhile to note that for a tending towards l, the dimensionless maximum deflections tend towards the limit value (Equation (14)). However, a minimum debond length for which an additional debond extension induces an important flexural stiffness decrease higher than 1% can be defined. A maximum debond length for which an additional debond extension induces a moderate flexural stiffness decrease lower than 1% can be also defined. Such limit values depend on both the face-to-core stiffness and thickness ratios. Active debonds are in the length range a = 20hc–80hc = 0.2l–0.8l for face layers little stiffer than the core (Ω = 1.5 and 2.5) and a = 15hc–85hc = 0.15l–0.85l for face layers much stiffer than the core (Ω = 5 and 10).
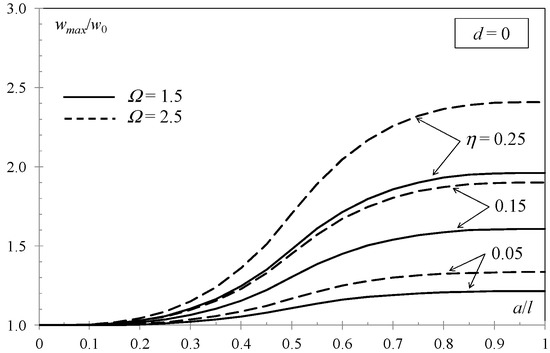
Figure 5.
Simply supported sandwich beam with a debond at one end of the upper interface: Midspan deflection vs. debond length for varying layer material and thickness (Ω = 1.5 and 2.5).
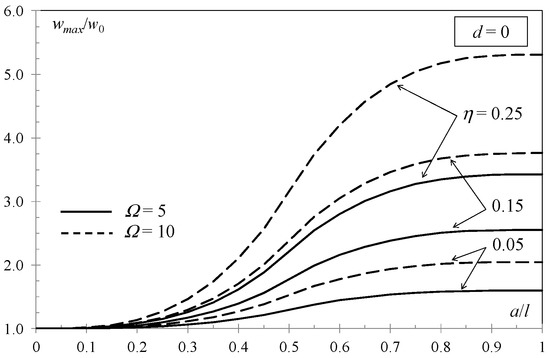
Figure 6.
Simply supported sandwich beam with a debond at one end of the upper interface: Midspan deflection vs. debond length for varying layer material and thickness (Ω = 5 and 10).
A second set of results refers to the composite sandwich beam having an interfacial defect within the upper interface (d ≠ 0). These results are shown in Figure 7 and Figure 8, where the dimensionless maximum deflection is plotted versus the dimensionless length of the intact ligament ahead the interfacial debond. According to these results, for a prescribed debond length, the debond position only moderately affects the composite beam behavior in bending. The decrease in flexural stiffness due to an interfacial debond centered on the beam (e.g., d = 30hc = 0.3l for a = 40hc = 0.4l, d = 35hc = 0.35l for a = 30hc = 0.3l, and d = 40hc = 0.4l for a = 20hc = 0.2l) is minimum independently of layer materials and geometry. Such a decrease becomes more significant for the debond approaching one end of the beam and is maximum for an end debond (d = 0). However, in many cases, the stiffness reduction with respect to that of three perfectly bonded layers results in being independent of the debond position unless the debond approaches midspan. As an example, for faces moderately stiffer than the core (Ω = 1.5), significant reductions are induced by 20hc = 0.2l (circular markers in Figure 7) and 30hc = 0.3l (triangular markers in Figure 7) long debonds at a distance from the end longer than 30hc = 0.3l and 20hc = 0.2l, respectively. Analogous considerations follow from the results related to faces much stiffer than the core (Ω = 10).
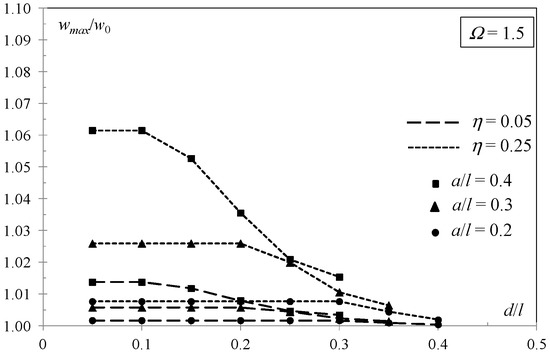
Figure 7.
Simply supported sandwich beam with a debond within the upper interface: Midspan deflection vs. debond distance from the left end for varying layer thickness and debond length (Ω = 1 and 5).
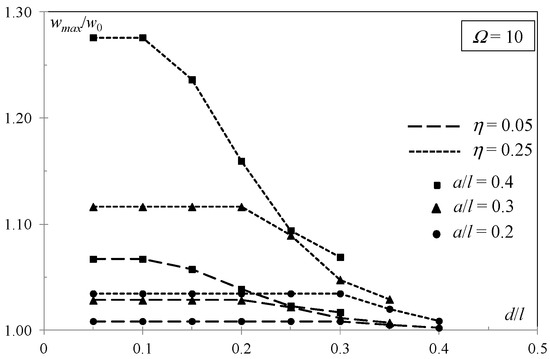
Figure 8.
Simply supported sandwich beam with a debond within the upper interface: Midspan deflection vs. debond distance from the left end for varying layer thickness and debond length (Ω = 10).
4. Discussion and Conclusions
This study deals with the simulation of the mechanical behavior in the bending of three-layer composite beams. The boundary and loading conditions considered are those of standard three point bending tests usually used to measure the flexural Young’s modulus of a material in the shape of a beam: The beam is simply supported at both ends and subjected to a point load at midspan. For simplicity’s sake, a symmetric sandwich beam was analyzed. Its related equilibrium problem was solved by employing a more general model proposed and validated previously by the author; such a fundamental solution actually permits one to also consider sandwich beams with face layers having different thickness, as well as beams composed of three different layers made of different materials.
The attention is focused on the change in flexural stiffness due to the presence of an interface defect. The main aim of the work was to correlate such change with the length and possibly the position along the interface of the defect that caused it. Secondly, the possibility of investigating the presence of interfacial damage and estimating its amount on the basis of a comparison between theoretical results and experimental measures of the maximum deflection was also explored. This is central during a monitoring program for the verification of a manufacturing process of composite beams.
Within this context, a final conclusion can be drawn by examining the distribution of the numerical results shown in Figure 7 and Figure 8. It is evident that a lot of configurations (each one corresponding to a single value of each physical or geometrical parameter Ω, η, ξ and δ) lead to very close results which differ less than 1%. This could make it difficult to distinguish one configuration from the other only on the basis of a measure of the maximum deflection. Then, the accuracy of the test machine plays a fundamental role. This point is worth further investigations through ad hoc test programs on ad hoc designed specimens. In fact, even recent experimental investigations found in the literature focus the attention on other mechanical properties (see, e.g., [16]).
Funding
This research was funded by the Italian Department for University and Scientific and Technological Research (MURST) in the framework of the research MIUR Prin15 (No. 2015LYYXA8), “Multi-Scale Mechanical Models for the Design and Optimization of Micro-Structured Smart Materials and Metamaterials”, coordinated by A. Corigliano.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
The formulation proposed in [7] to solve the equilibrium problem of three-layer beams with interlayer slip assumes that: (i) The layers have constant cross-sections and are made of linearly elastic and homogeneous materials; (ii) the bonds are perfect in the transverse direction, while ensuring partial composite actions in the longitudinal direction so that only interlayer slips are allowed at both interfaces. Under the assumption of small strains, displacements, and rotations, each layer is modeled as a linearly elastic Euler–Bernoulli beam subjected to the action of uniformly distributed loads, related internal forces, and interfacial tractions. Imperfect bonds are described through linear nonproportional relationships between interlayer shear tractions and slips which depend on two coefficients. As underlined by the author in previous papers [7,8,14], this choice makes it possible to describe different types of interfacial regime depending on the values of the two coefficients and to derive explicit solutions as well. Different identification procedures can be adopted to calibrate such an interface constitutive law on the basis of the results of suitable tests (see, e.g., [17]), but this is not of interest to this paper.
According to such a formulation, as detailed in [7], the problem is governed by a system of three coupled linear differential equations with constant coefficients for the three unknowns rotation φ and shear tractions ptj at the interface between layers j and j + 1 (j = 1,2). The first equation follows from the bending problems of the three layers which undergo equal deflections w, and then equal rotations φ = −w′, because of the assumption of perfect connections in the transverse direction, and can be written as:
where primes denote differentiation with respect to z and having defined:
The second and third equations are the bond conditions at the two interfaces. For perfect bonds, we have
Alternatively, for imperfect bonds, described through the following linear nonproportional relationship between interlayer shear traction ptj and slip Δstj at the j-th interface with interfacial coefficients Aj and Bj (j = 1, 2):
we have:
In Equations (A1)–(A5), and measure the distance between the axis of layer i and its top and bottom interfaces with layers i − 1 and i + 1 (i = 1, …, 3); and are, respectively, the axial and bending stiffnesses of the i-th layer to which uniformly distributed axial and transverse loads, respectively, qzi and qyi, are applied (i = 1, …, 3). The system of differential Equations (A1), (A3), and (A5) admits closed form solutions for all possible combinations of the regimes experienced by the two interfaces. In [7], the solution to the case of three-layer beams uniformly loaded and having two imperfect interfaces or only one imperfect interface is detailed. Closed form expressions for axial displacements, interlayer slips, and all the remaining kinematic and static unknowns (deflection, internal forces, and interfacial normal tractions) are derived as well.
This general formulation was then specialized to the special equilibrium problem considered in this paper of three-layer beams subjected to point loads and having a perfect lower interface between layers 2 and 3 also in the longitudinal direction, whereas an imperfect upper interface between layers 1 and 2. Namely, two different regimes in the longitudinal direction for the upper interface were analyzed: A perfect bond, so that no interlayer slips can occur, and an imperfect bond with vanishing interfacial stiffness, then incapable of transmitting shear tractions. The solution procedure for this special problem is detailed in what follows.
In the absence of distributed loads (qzi = qyi = 0 with i = 1, …, 3) and under the assumption of no interlayer slip at the lower interface (Δst2 = 0), Equation (A3b) gives:
from which Equation (A1) reduces to:
In the case of a perfect upper interface (Δst1 = 0), Equations (A3a) and (A6) give:
In the other case of imperfect upper interface with vanishing interfacial stiffness (A1 = B1 = 0) we have:
The stiffnesses being constant, introducing either Equation (A8) or (A9) in Equation (A7) leads to a homogeneous third-order linear differential equation for rotation, whose general solution in both cases is:
with Ch (h = 1, …, 3) as three arbitrary constants. It is straightforward that interfacial shear tractions are obtained, substituting Equation (A10) in Equations (A6) and either (A8) or (A9).
Integration of Equation (A10) then gives deflection:
where C4 is one more arbitrary constant and, for brevity, hereinafter, indicates integration of ∙ with respect to z.
Furthermore, the axial displacement of layer 1 was obtained, integrating the equation governing the axial problem for the same layer. It results in:
where, for brevity, hereinafter, indicates integration of ∙ twice with respect to z. As a consequence of such integrations, the expression of the axial displacement contains two other arbitrary constants Ch (h = 5, 6).
Moreover, if the upper interface is perfect, the axial displacement of layer 2 follows from the condition Δst1 = 0:
whereas, if the upper interface is imperfect, this axial displacement is obtained, integrating the equation governing the axial problem for layer 2:
which contains two other arbitrary constants Ch (h = 7, 8).
Finally, the axial displacement of layer 3 follows from the condition Δst2 = 0:
When rotation, deflection, axial displacements, and interfacial shear tractions have been obtained, closed form expressions for internal forces can also be derived. Through the compatibility and constitutive equations for the three layers (i = 1, 3), axial forces and bending moments are obtained:
Such results are then employed to derive shear forces through the rotational equilibrium equations for the three layers (i = 1, 3):
To conclude, the set of Equations (A10)–(A13) and (A15)–(A17) specialized for the interfacial tractions given by Equations (A8) and (A6) represents the solution for three-layer beams unloaded along their axis and having two perfect interfaces; this set contains 6 arbitrary constants. On the other hand, the set of Equations (A10)–(A12) and (A14)–(A17) specialized for the interfacial tractions given by Equations (A9) and (A6) represents the solution for three-layer beams unloaded along their axis and having a perfect lower interface whereas an imperfect upper interface with vanishing interfacial stiffness; this set contains 8 arbitrary constants. To complete these solutions, all the arbitrary constants were determined by imposing suitable conditions that depend on the specific problem under consideration.
References
- Goodman, J.R.; Popov, E.P. Layered beam systems with interlayer slip. J. Struct. Div. 1968, 94, 2535–2548. [Google Scholar]
- McCutcheon, W.J. Stiffness of framing members with partial composite action. J. Struct. Eng. 1986, 112, 1623–1637. [Google Scholar] [CrossRef]
- Chui, Y.H.; Barclay, D.W. Analysis of three-layer beams with non-identical layers and semi-rigid connections. Can. J. Civil Eng. 1998, 25, 271–276. [Google Scholar] [CrossRef]
- Schnabl, S.; Planinc, I.; Saje, M.; Čas, B.; Turk, G. An analytical model of layered continuous beams with partial interaction. Struct. Eng. Mech. 2006, 3, 263–278. [Google Scholar] [CrossRef][Green Version]
- Ranzi, G. Locking problems in the partial interaction analysis of multi-layered composite beams. Eng. Struct. 2008, 30, 2900–2911. [Google Scholar] [CrossRef]
- Sousa, J.B.M., Jr.; da Silva, A.R. Analytical and numerical analysis of multilayered beams with interlayer slip. Eng. Struct. 2010, 32, 1671–1680. [Google Scholar] [CrossRef]
- Monetto, I. Analytical solutions of three-layer beams with interlayer slip and step-wise linear interface law. Compos. Struct. 2015, 120, 543–551. [Google Scholar] [CrossRef]
- Campi, F.; Monetto, I. Analytical solutions of two-layer beams with interlayer slip and bi-linear interface law. Int. J. Solids Struct. 2013, 50, 687–698. [Google Scholar] [CrossRef]
- Pelassa, M.; Massabò, R. Explicit solutions for multi-layered wide plates and beams with perfect and imperfect bonding and delaminations under thermo-mechanical loading. Meccanica 2015, 50, 2497–2524. [Google Scholar] [CrossRef]
- Atashipour, S.R.; Girhammar, U.A.; Challamel, N. Stability analysis of three-layer shear deformable partial composite columns. Int. J. Solids Struct. 2017, 106–107, 213–228. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Pavlov, S.P.; Zhigalov, M.V.; Krysko, A.V. Mathematical model of a three-layer micro- and nano-beams based on the hypotheses of the Grigolyuk–Chulkov and the modified couple stress theory. Int. J. Solids Struct. 2017, 117, 39–50. [Google Scholar] [CrossRef]
- Čas, B.; Planinc, I.; Schnabl, S. Analytical solution of three-dimensional two-layer composite beam with interlayer slips. Eng. Struct. 2018, 173, 269–282. [Google Scholar] [CrossRef]
- Barbieri, L.; Massabò, R.; Berggreen, C. The effects of shear and near tip deformations on interface fracture of symmetric sandwich beams. Eng. Fract. Mech. 2018, 201, 298–321. [Google Scholar] [CrossRef]
- Monetto, I.; Campi, F. Numerical analysis of two-layer beams with interlayer slip and step-wise linear interface law. Eng. Struct. 2017, 144, 201–209. [Google Scholar] [CrossRef]
- Brandinelli, L.; Massabò, R. Mode II weight functions for isotropic and orthotropic double cantilever beams. Int. J. Fract. 2006, 139, 1–25. [Google Scholar] [CrossRef]
- Czechowski, L.; Jankowski, J.; Kotelko, M. Experimental and numeriacl three-point bending tests for sandwich beams. J. KONES 2017, 24, 53–62. [Google Scholar]
- Li, Y.; Bielak, J.; Hegger, J.; Chudoba, R. An incremental inverse analysis procedure for identification of bond-slip laws in composites applied to textile reinforced concrete. Compos. Part Eng. 2018, 137, 111–122. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).