The Excitation of Ultrasound by Laser Radiation in Water Using an Optical Fiber Laser Converter with a 2D Colloidal Crystalline Coating

Abstract

The technology of applying a colloidal single-layer coating of transparent polystyrene (PS) Ø 1 μm spheres at the tip face of a quartz fiber has been proposed and tested. Such a coating plays, in a light absorbing liquid, the role of a converter of pulsed laser radiation into acoustic radiation. The generation of ultrasound in water using a converter based on a quartz fiber 1 mm in diameter with a 2D colloidal crystalline coating consisted of polystyrene spheres with a diameter of ~1 μm at the fiber end was investigated. When excited by laser radiation (λ = 1.064 µm), coating of polystyrene spheres created in the liquid a laser thermal microstructure with a characteristic size of fractions of ~λ and a maximum temperature up to 10⁻² degree at an energy in a short laser pulse of ~0.005 J. This short-lived thermal microstructure generated sound pulses in the liquid in the approximately 0.2–4 MHz range. The results of the experimental study of this effect are reported. The proposed laser radiation converter with colloidal coating of the optical fiber distal tip by a single layer of transparent spheres can be used for the development of new laser microtools for studying, processing of various objects in microsurgery, microstructuring of the surface, spot cleaning and restoration of objects of art and history.

1. Introduction

The development of efficient converters of optical radiation into acoustic high frequency radiation for medical (sparing surgery, local suppression of bacteria and viruses, acupressure, disinfection) and technological (chemistry, lithography, restoration work) purposes is an important applied problem [1,2,3,4,5,6,7]. Flexible optical fibers can be used for delivery of high power without electrical safety problems. Such converters are mainly based on the “ultrasonic laser” technology, where the converter is a layer of plastic with absorbers readily changing its size [8,9]. However, this technology does not allow generating high-frequency ultrasonic (US) pulses and creating the required spectrum of high-frequency radiation. A possible solution to this problem is to inject radiation into a liquid through a layer of transparent microspheres at the distal end of the fiber, which act as microlenses creating highly concentrated areas of light radiation in the liquid. In the presence of light absorption in the liquid, there arises a system of local heated volumes which leads to an optoacoustic (OA) response due to the thermoelastic effect [10,11,12,13]. From this point of view, the layer of transparent microspheres at the distal tip of the fiber in a light absorbing medium can be considered to be a fiber laser–acoustic converter. The intensity and frequency characteristics of this converter depend on the properties of the exciting radiation (intensity, time-frequency characteristics), on the properties of the liquid (light absorption coefficient, thermophysical characteristics), as well as on the converter parameters: diameter of the microspheres, index of refraction, and mechanical stability of the system [10,11,12,13]. For local use of the tool, it is reasonable to make such a converter at the output end of a flexible fiber. A possible model of such a tool was investigated in [14], where a system of spheres 200 μm in diameter glued onto the surface of a glass plate was used as a converter. A water solution of ink with an absorption coefficient of approximately 100 μm⁻¹ was used as the medium.

In this paper, we present results of the study of ultrasound generation in water using a converter based on a quartz fiber D = 1 mm (D is diameter) with a 2D colloidal crystalline coating of polystyrene (PS) spheres with a diameter d of approximately 1 μm at the fiber tip face. The exciting radiation has the wavelength of 1.064 μm. Distilled water is used as the medium. Water at this wavelength has an optical absorption coefficient α of approximately 0.1 cm⁻¹. This configuration of the experiment allows studying the basic parameters of the system in “primeval” form, avoiding the influence of more complex effects, such as thermal self-defocusing and superheated liquid states. Despite the well studied [10,11,12,13] basic parameters of sound waves excited in a liquid by light, in particular, by laser radiation, the technology for fabricating a converter on a single layer of micron spheres significantly expands the possibilities of exciting high-frequency ultrasound and allows developing new optoacoustic instruments with optical radiation conversion to high-frequency ultrasound with controlled characteristics.

Other opportunities provided by the fiber-optic laser radiation converters with microscale focusing and excitation by laser radiation with a wide spectrum matching the expected spectrum of optoacoustic response are investigated in the paper.

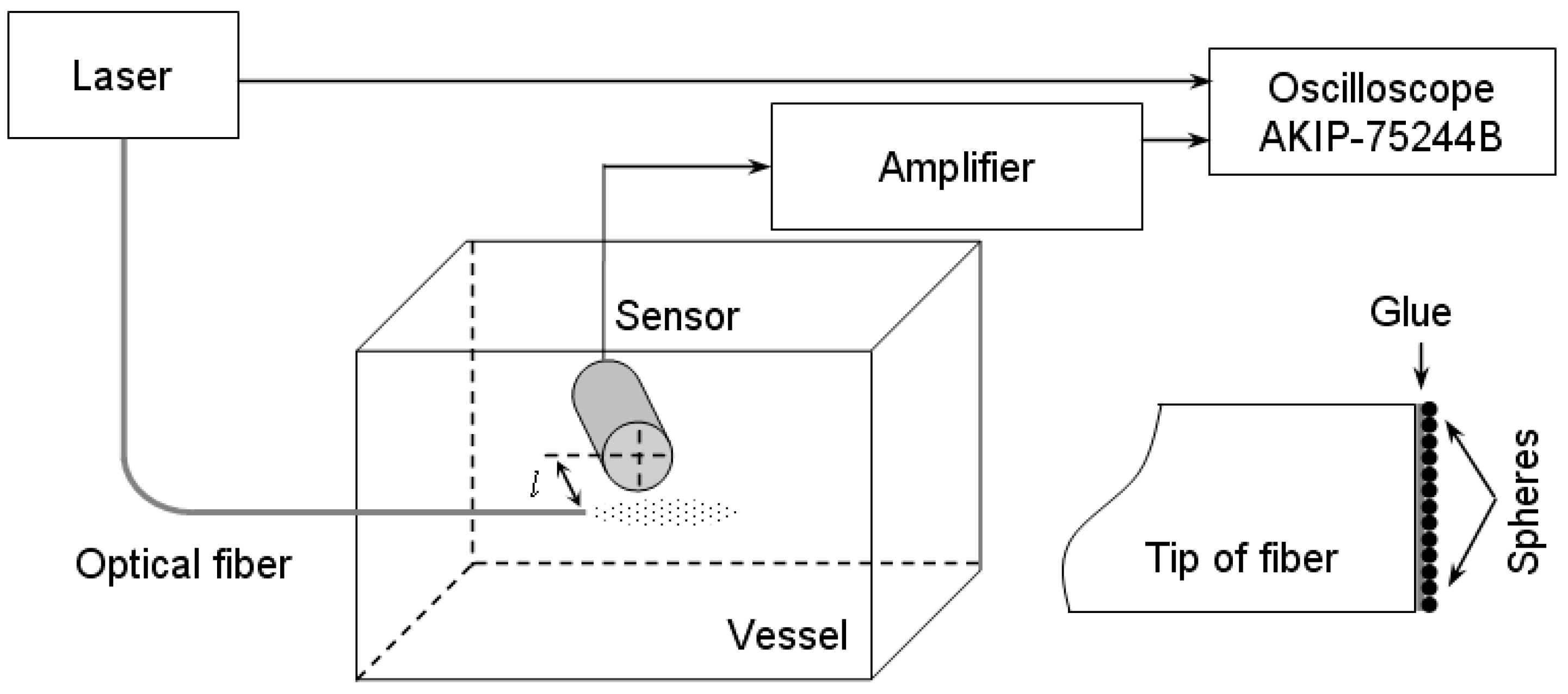
2. Experimental Setup

The experimental setup (Figure 1) was made on the basis of the home made Nd:YAG pulse laser: λ = 1.064 μm. The laser generated in the zero transverse mode regime (beam diameter ~2 mm) a train of pulses with a total duration of ~300 ns with a spike frequency of ~2 × 10⁵ Hz using an optical passive modulator based on a LiF crystal. The radiation temporal structure and spectrum (FFT) are shown in Figure 2a,b, respectively. The total pulse energy was up to E_tot = 0.2 J, the number of spikes up to 40, the total pulse duration ~350 μs, the spike duration τ_spike ~0.3 μs, the leading edge ~50 ns, and the spike energy E_spike up to 0.005 J. The spectrum of the laser pulse was almost continuous and its spectral intensity in the 0.5–4 MHz range fell in the high-frequency region of no more than 10 dB. The repetition rate of laser shots was 0.5 Hz. The modes of laser generation allowed exciting and studying sound waves with a frequency up to ~5 × 10⁷ Hz. The laser beam compressed by a F = 10 cm lens laser beam was inputted into a multimode shell-less silica light fibre guide 1 mm in diameter and about 2 m in long. The fibre focusing was adjusted by maximum energy at the fibre output without fibre damage. The relatively large diameter of the fibre was chosen from ease of 2D sphere coating on the distal tip of the fibre. The conditions of laser irradiation in all cases were the same in all cases.

The original ultrasonic sensor with a diameter of 5 mm and a length of 20 mm had a sensitivity of 8 μV/Pa and an uneven frequency response of ±3 dB in the frequency range of 0.2–4 MHz. The temporal structure of the laser pulse was also recorded using a high-speed photo diode and a digital oscilloscope.

Figure 2 shows typical oscillograms of a laser pulse (Figure 2a) and of an ultrasound signal (Figure 2b).

3. Converter with a Coating of Focusing Spheres

The fiber-optic converter is a layer of transparent spheres of radius r coating the output tip face of the fiber with radius R. Depending on the application technology (and radius), the spheres can either self-organize into a regular structure, or be arranged randomly. The number of spheres is ~R²/r², and each of them “intercepts” a fraction i ~I₀r²/R² of the radiation power I₀ emanating from the fiber.

The coating consisting of spheres 1–200 µm in diameter was applied onto the fiber tip face using a 2-stage technology. First, a single layer of spheres was formed on a flat glass plate. Then the obtained single layer was glued onto the fiber end with a pre-applied thin layer of сyanoacrylate optical adhesive. A single layer of small-sized spheres (up to 10 μm) was deposited onto the plate from a colloidal solution [15]. Large-sized spheres were spread in one layer onto a flat plate [14] (within a limited filling area). Microphotographs of the spheres at the tip of a 1-mm fiber on the adhesive are shown in Figure 3: (Figure 3a) 1 μm polystyrene; (Figure 3b) 10 μm polystyrene; (Figure 3c) 200 μm glass. The pattern of spheres with a diameter of 200 μm (on a flat glass plate) was used in [14] for studying the optoacoustic response in a strongly absorbing liquid. In this work, we investigate ultrasound excited by laser radiation through a quartz optical fiber Ø 1 mm with a converter—a coating at the distal tip of the fiber with Ø 0.96 μm PS spheres.

It was found that if a coating is deposited from a colloidal aqueous solution immediately onto the fiber tip, the spheres detach in the liquid when exciting laser radiation is applied. This problem was solved by using glue, at least when generating a moderately strong ultrasound. However, in this case there arises another problem, namely, the depth at which the spheres should be dipped into the glue. This should be borne in mind when processing and interpreting experimental results.

The сyanoacrylate glue layer properties are less investigated. From optical transmission measurements it can be concluded that the absorption coefficient of сyanoacrylate glue is of the order of magnitude same as that of water at a wavelength of ~1 μm. This also follows from general physical considerations. Indeed, the absorption of light in this region, both in сyanoacrylate and in water, as well as in polystyrene (material of spheres), is determined by H⁺ ion vibrations. Considering that the optical thickness of the сyanoacrylate layer is negligible compared to the thickness of the acoustically emitting water layer, and even to the diameter of the spheres, we can consider the role of the сyanoacrylate layer in the OA response insignificant. The laser radiation intensity (up to ~1.5 MW/cm²) is insufficient for optical damage of the сyanoacrylate film, and together with a small film thickness it is insufficient for nonlinear optical effects. However, it should be recognized that the developed fiber coating is sufficiently suitable for research purposes and it can serve as a model for the development of devices for technological purposes. In particular, glass spheres soldered to the fiber end may be used.

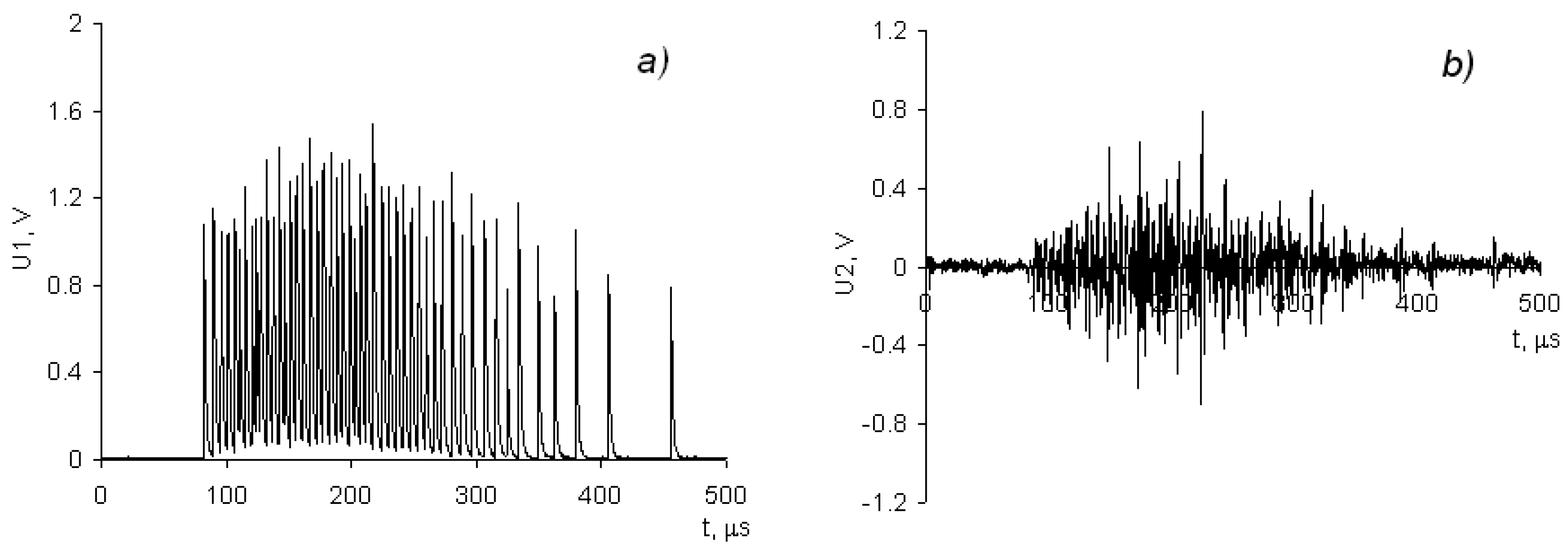
4. Experimental Results

The experiments on exciting ultrasound (US) were performed with an “uncoated” output fiber tip face and “coated” with a single layer of polystyrene spheres 0.96 μm in diameter. Comparison of the signals of a laser pulse and of an ultrasound presented in Figure 2 shows that the response of the ultrasound corresponds to each laser spike.

The spectra of ultrasound S2(f) excited with the “uncoated” fiber (Figure 4a) and with the “coated” (Figure 4b) fiber with a single layer of PS spheres are compared in Figure 4. Each curve corresponds to a separate experimental implementation with laser power 3%, 35% and 100% of full power. Curve 4 in Figure 5 shows a typical laser radiation spectrum S1(f).

The US spectra excited with an uncoated fiber and with a coated fiber are also compared in Figure 5. Hear each curve corresponds to a separate experimental implementation with different length l (l is a distance between laser beam and the acoustic sensor (Figure 1)). Laser power is 100% of the full one.

5. Discussion of Results

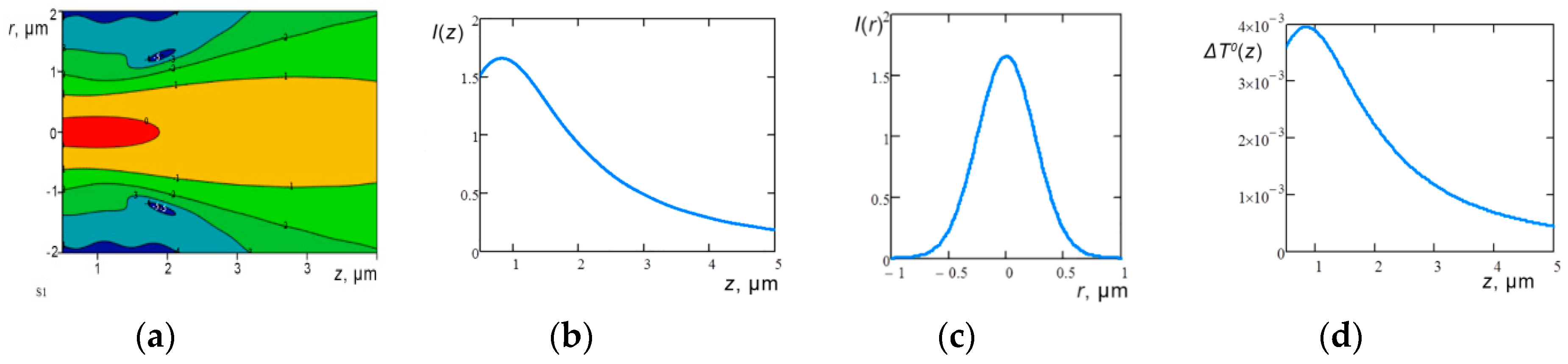
5.1. Focusing: Single Sphere

For understanding the laser field passing through a sphere coating it is useful to calculate focusing by a single sphere and by a regular 2D structure of microspheres. For estimating the action of a single sphere we use here the Gaussian beam approximation [16], which is more clear than the others [17,18,19]. The profiles intensity I(ρ, z) of the focal regions (caustic profiles along and across the beam) for polystyrene spheres in water are given in Figure 6. It is seen that the intensity distribution in the focal field is of a “laser jet” type, with intensity increasing up to two times.

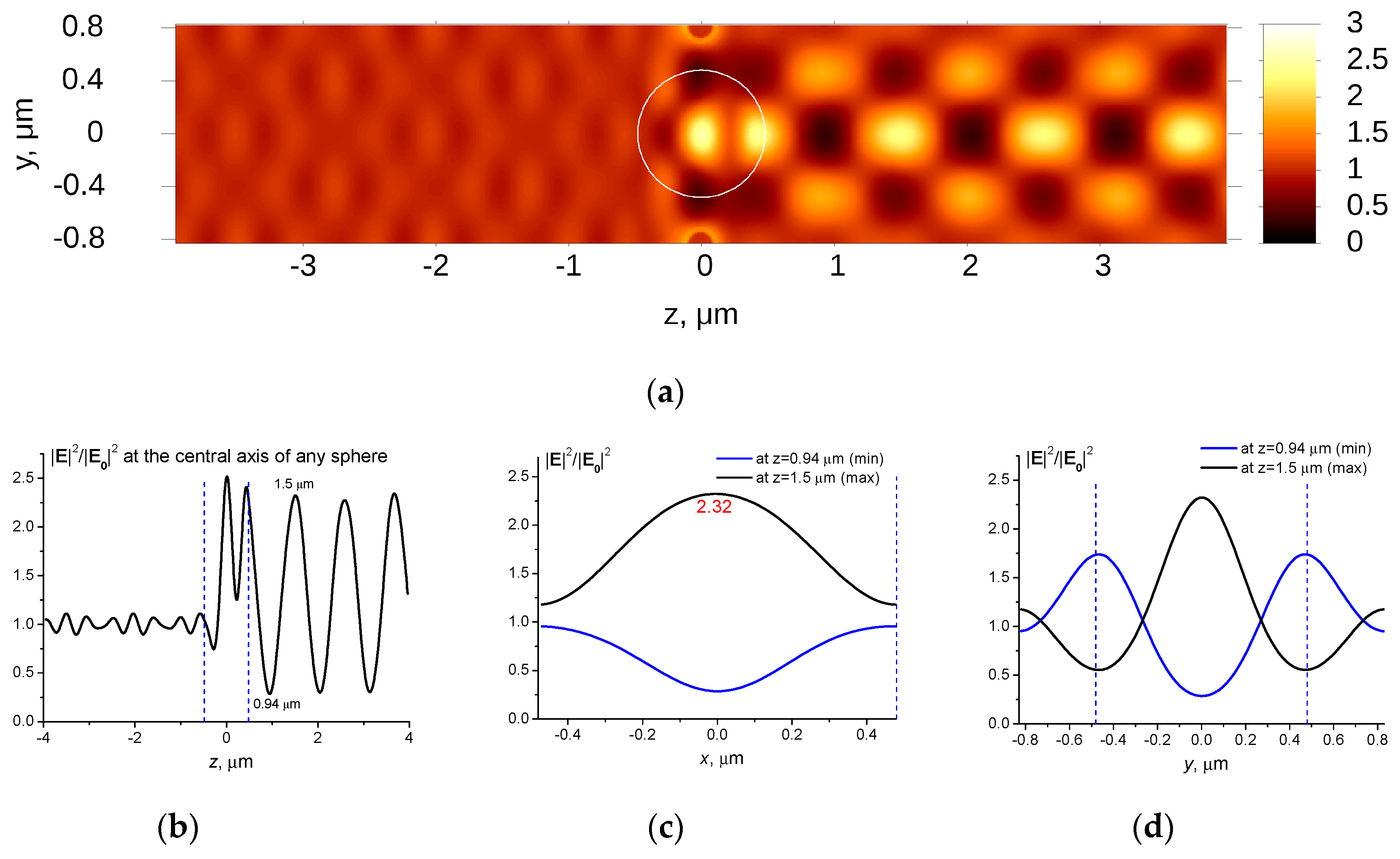
5.2. Diffraction on 2D Spheres Monolayer in Water

A monolayer of spheres (d~λ) deposited on the fiber end face gives a 2D system of laser jets which interfere in the medium and act as a diffraction grating [20] generating a 3D periodical laser field pattern with spatial periodicity on the order of λ. Finite difference time domain (FDTD) calculations of the laser field distribution generated by the monolayer of polysterene spheres deposited on a glass surface and immersed in the water medium were performed. The effects of the aperture and possible defects in the monolayer packing were neglected. Thus, the periodicity of the monolayer was taken into account to minimize the volume of the calculation cell [20,21]. The calculated distribution of the enhancement of the electric field square with respect to the incident beam value is shown in Figure 7. The parameters of the calculations matched our experimental conditions. Namely, the wavelength of the incident light (in vacuum) is λ = 1.064 µm, the sphere diameter is d = 0.96 μm, the refractive indices of the spheres, glass fiber and water are n₁ = 1.58, n_fib = 1.46, and n₀ = 1.33, respectively. The light absorption length in water is much larger than the cuvette size, thus the absorption can be also neglected in the FDTD calculations. However, according to the estimations, а thermal microstructure of laser heated pellets (LHP) with characteristic size on the order of λ, with temperature rise up to 10⁻² degree is created in water by a short laser pulse of 0.005 J energy.

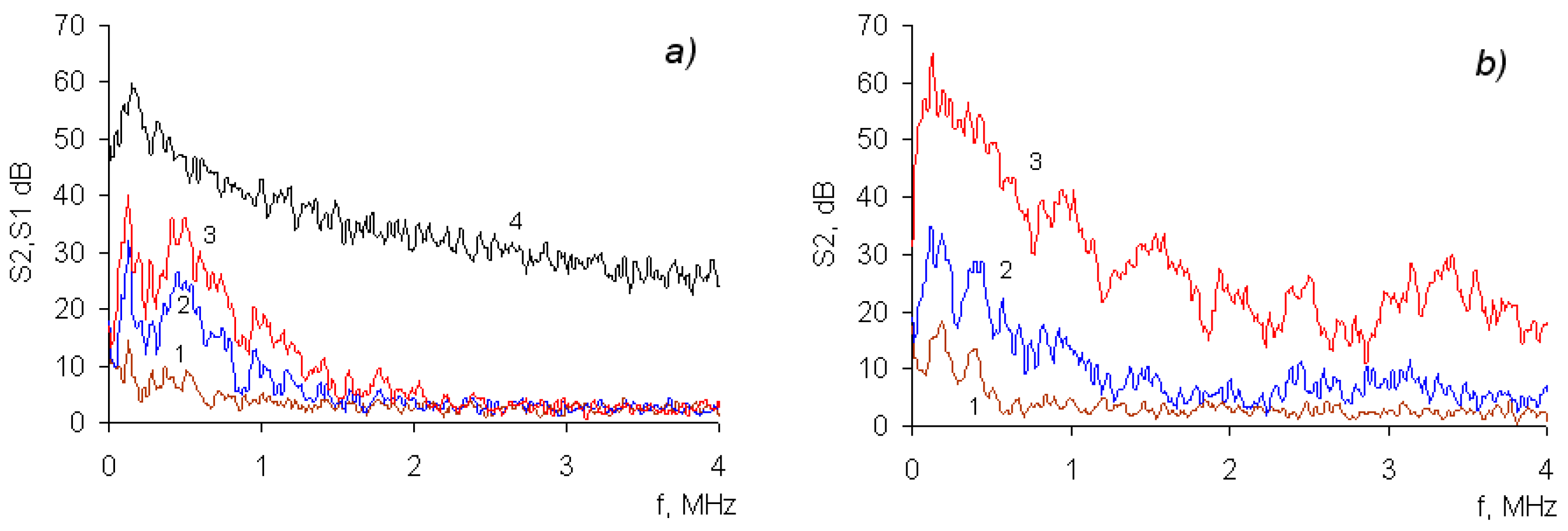
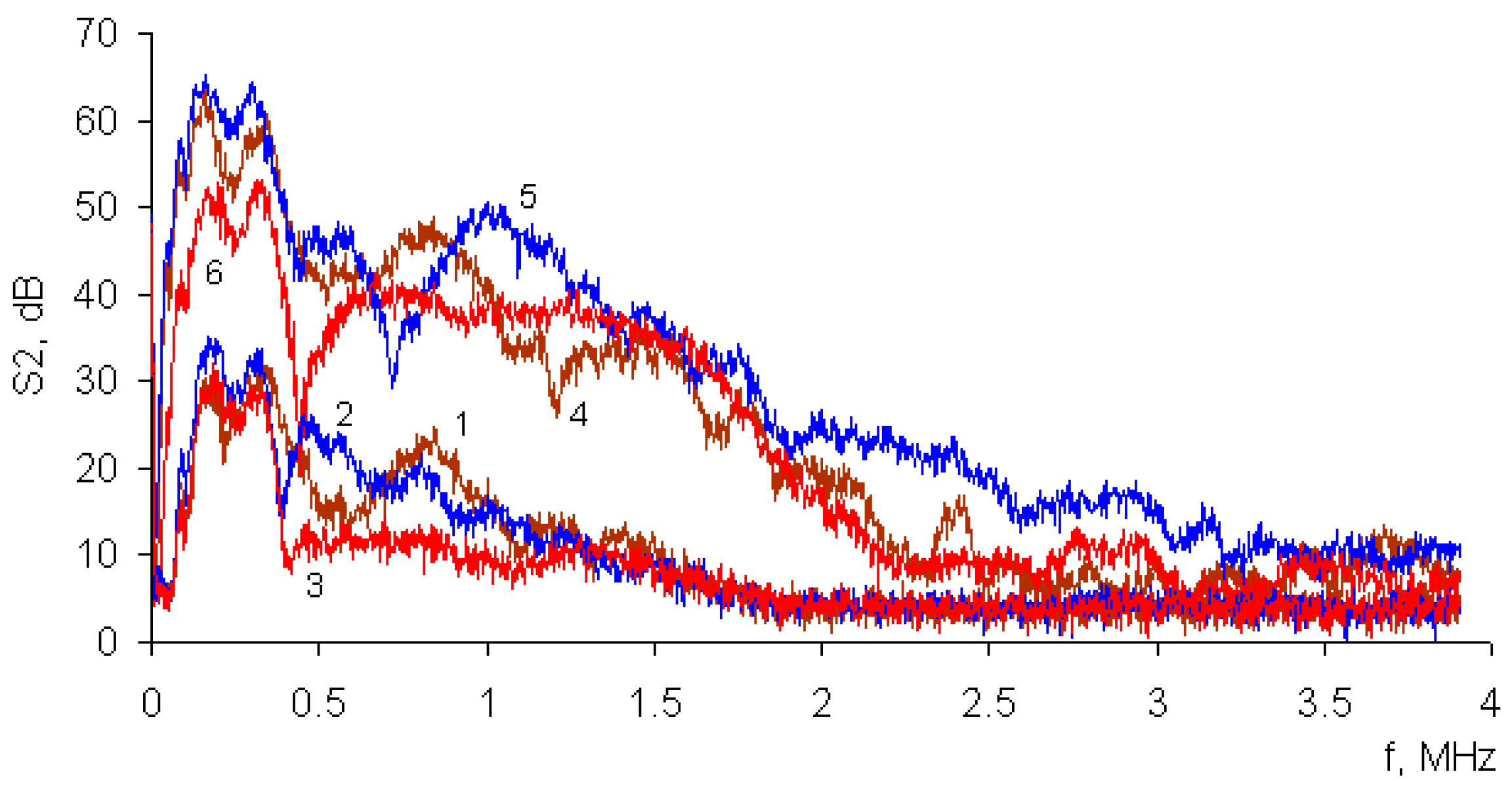
5.3. Generation of Ultrasound

The excitation of ultrasound in a liquid using a fiber with converter is accompanied with a number of features that are worth considering. When the radiating end of a fiber is immersed into a liquid, surface waves on the liquid can be excluded from consideration. Sound waves generated in the beam may hit the fiber end. However, this is a second-order effect; therefore, the emission of sound waves in this case can be considered as the emission from a lumped source in the free space of a liquid. The spatial parameters of the emitter without spheres are determined by the fiber diameter and the length of beam absorption in liquid, whereas in the case of a coated fiber, they also depend on the parameters of the beams focused by the spheres. In this study (pure, weakly absorbing water), in the absence of spheres the emitting region within the experimental cuvette L >> λ_us (λ_us is the wavelength of the ultrasound) can be considered as a rod with a fiber diameter and light intensity decreasing as e^−αx (x is beam length).

In the presence of spheres, the emitting rod is divided into individual LHP areas. The diameter d₀ of these LHP in the waist is fractions of a micron, and their length is of the order of a micron (at a wavelength of λ_us ~1 mm), and their power drops down as e^−αx. The radiation from LHP can be considered as the radiation of a point sources with dimensions d₀ << λ_us.

Three main features can be distinguished in the experimental results on the excitation of ultrasound (Figure 4 and Figure 5):

• A significant increase in the level of ultrasound intensity (up to 20 dB) in the range of 0.5–4 MHz.
• In experiments without coating, radiation with peaks of 0.25 and 0.75 MHz prevails. The same radiation is present in experiments with the coating too.
• When applying coatings, there appears an OA response with peaks in the 1–4 MHz range and with the amplitude comparable to that of the radiation in the region up to 1 MHz.

It is clear that both effects, i.e., the observed overall enhancement of the OA response and the appearance of an OA response in the 1–4 MHz, are associated with the colloidal coating of the fiber tip.

The observed amplification can be related to the specific features of the experiments, when the diameter of the fiber and, therefore, of the beam in the liquid is of order of the wavelength of the generated ultrasound (~0.35–5 mm). In this case, the interference of waves generated in the beam volume, “blocks” the radiation in the direction of ~90°, which leads to sound channeling in the laser beam [22]. When a pellet structure is formed in the heated region, this prohibition is removed, which leads to the appearance of directional pattern petals in the direction close to normal and to amplification of the received ultrasound.

Comparison of the spectral-temporal composition of the laser pulse with the spectrum of the optoacoustic response allows determining the generation mechanism at different frequencies and linking them to different areas in the structure of the laser radiation. The case of ultrasound generation “without spheres” is quite clear. The maximum of the observed US spectrum lies in the 0.7–1.5 MHz region, which corresponds to the “classical” generation mechanism [3,4,5,6] with a characteristic frequency ν₁ = c/D ~1.5 × 10⁶ Hz related to the ultrasound run time through the beam diameter. The frequency-time structure of the laser pulse also meets with the optimal conditions for the excitation of ultrasound in this frequency range.

The case of 2D coating is more interesting as the ultrasound spectrum is enriched in the 1–4 MHz frequency range. This generation region is obviously related to the coating of the fiber end with PS spheres of ~1 μm in diameter, which create a regular structure in the transmitted laser beam with regions of increased intensity and LHP regions in the liquid. The diameter of these LHP structures is 0.5–1 μm. If we assume that the ultrasonic response in this case also corresponds to the “classical” generation mechanism [10,11,12,13], then its maximum response spectrum should be in the frequency band of ~(1–5) GHz, which does not correspond to the considered spectral region. Therefore, the results of the coating experiment show that additional studies are required.

Interestingly, the frequency range of ultrasound radiation in this case is in a good agreement with the LHP cooling time τ₂ = d²/4χ [23] (d is the LHP diameter, χ is thermal diffusivity), which is ~(0.1–0.5) × 10⁻⁶ s.

Preliminary examination shows that 1–4 MHz ultrasound may be associated with cooling an array of heated “pellets” with a characteristic time τ₂. It is interesting that the integrated intensity of such an ultrasound is of the same order of magnitude as the sound associated with heating the area of the laser beam as a whole at the same frequency. The advantage of this generation of ultrasound are both a higher frequency and a higher local heating of the tablets, which can make it possible to obtain and study the effects associated with supercritical liquid overheating with an increase in the laser radiation power and an increase in the optical absorption of the liquid.

6. Conclusions

• The technology of applying a colloidal single-layer coating of transparent PS Ø 1 μm spheres at the end face of a quartz fiber has been proposed and tested. Such a coating plays the role of a converter of pulsed laser radiation into acoustic radiation in a light absorbing liquid.
• When excited by laser radiation, the microspheres produce in the liquid laser jets which interfere and give a regular spatial structure in a laser beam consisting of “pellets” with high intensity and with a diameter of a fraction of a micron and a length of several microns.
• In pure water at λ = 1.064 μm (light absorption ~ 0.1 cm⁻¹), a thermal microstructure is formed with a characteristic size of fractions of ~λ, a maximum temperature up to 10⁻² degree at an energy of a short laser pulse of ~0.005 J. The developed equipment allows accurate recording of ultrasound generation with expected microheating.
• A significant difference between the generation of ultrasound upon excitation in water by laser radiation through an uncoated optical fiber and with a 2D colloidal coating was found experimentally. The ultrasound spectrum in the latter case was enriched in frequency to 1–4 MHz and increased in amplitude by ~20 dB. The mechanism of such a drastic change is still unclear.

The results of the considered work have demonstrated a possibility of creating a new laser micro-tool using a colloidal coating of the optical fiber distal end with a single layer of transparent microspheres for studying, processing of various objects in microsurgery, surface microstructuring, spot cleaning and restoring objects of art and history. The described tool can act on an object by microstructured laser radiation, microstructured thermal field, or point high-frequency ultrasound.