2. Materials and Methods
TiAlN coatings were synthesized by cathodic arc evaporation in an industrial-scale Oerlikon Balzers Ingenia P3e™ platform (Balzers, Liechtenstein). Sapphire with (0001) orientation, as well as cemented carbide substrates, were assembled on the substrate holder. Electrically insulating substrates were chosen for comparison to represent ceramic inserts, which can be based on c-BN, Al2O3 or Si3N4. These ceramic inserts are used for machining of hardened steel, difficult-to-cut materials or cast iron and are frequently coated using PVD techniques in order to reduce tribochemical or adhesive wear.
The deposition system was heated to 450 °C, and the plasma was ignited when the base pressure of the heated system was <3 × 10−3 Pa. Reactive synthesis was carried out with nitrogen gas at the deposition pressure of 3.2 Pa. Three alloyed Ti0.50Al0.50 targets were employed, and the minimum target-to-substrate distance was 16 cm. The substrate bias potential was either floating or −15 V. Coatings were synthesized utilizing a two-fold substrate rotation (periodically interrupted plasma exposure) and a stationary deposition geometry without rotation (continuous plasma exposure). The measured substrate temperatures were 470 and 520 °C, respectively, and the stationary deposition setup exhibited an almost factor 10 higher deposition rate compared to the rotation setup.
Additionally, a hybrid setup was employed; substrates were positioned in front of the arc sources and pneumatically controlled shutters were opened and closed periodically according to the effective deposition time in a rotational setup (where the growing coating surface moves periodically from regions of low plasma density/small fluxes of film-forming species in regions with high plasma density/large fluxes of film-forming species). Hence, the hybrid setup is characterized by a face-to-face geometry as in the stationary deposition setup, while variations in plasma density and fluxes of film-forming species (interrupted plasma exposure), as in the rotational setup, are realized by employing shutters.
Furthermore, Fe foil substrates (99.5% purity) were coated with and without substrate rotation in order to obtain powdered coatings. The Fe foil substrates were etched with a nitric acid in a HNO3/deionized H2O volume ratio of 1/5 and, subsequently, the coating flakes were milled into a powder. Coatings in powder form were used to determine the linear coefficient of thermal expansion as a function of temperature.
The microstructure of coating cross-sections was characterized in scanning transmission electron microscopy (STEM) mode utilizing a FEI HELIOS Nanolab 660 dual-beam focused ion beam (FIB) microscope (Hillsboro, OR, USA) with a STEM III detector at acceleration voltage and current of 30 kV and 50 pA, respectively. Thin lamellae were extracted in growth direction, synthesized by the rotation, stationary and hybrid setup, utilizing Ga ions with an acceleration voltage of 30 kV. First, a 1-µm-thick Pt protection layer was applied with 80 pA current, followed by trench milling, extraction of the lamella with a manipulation needle and application of the lamella on a Cu Omniprobe. Final lamellae thicknesses in the order of 100 nm were realized by sequential thinning utilizing currents of 0.79 and 0.43 nA.
Depth-resolved chemical composition analysis was done by using time-of-flight energy elastic recoil detection analysis (ToF E-ERDA) with 36 MeV
127I
8+ primary projectiles at the tandem accelerator laboratory of Uppsala University. The measurement geometry of a 45° angle between primary ions and detector telescope and a 22.5° angle between specimen and detector telescope was used. Time-energy coincidence spectra were acquired by combination of a ToF setup based on thin carbon foils [
8,
9] and utilizing a gas ionization detection system [
10]. The obtained spectra were evaluated using the CONTES software package [
11]. Homogeneous depth profiles were obtained for Ti, Al and N, while O (<2 at.%) and H (<0.5 at.%) impurities were also detected. Systematic uncertainties were on the order of ±10% (relative deviation), while statistic uncertainties were on the order ±5% (relative deviation). In addition, spatially resolved chemical composition analysis of TiAlN, grown with substrate rotation, was performed utilizing a JEOL JSM-2200FS field emission transmission electron microscope (Tokyo, Japan) at an acceleration voltage of 200 kV. While a high-angle annular dark field (HAADF) detector was employed for morphological characterization, the chemical composition was measured by energy dispersive X-ray spectroscopy (STEM-EDX) with a 30 mm
2 JEOL Si drift detector.
Deposition geometry-dependent roughness values
Ra of the coating surfaces were evaluated with a Keyence VK-9700 laser optical microscope (Osaka, Japan). The evolution of roughness data was in good agreement with macroparticle surface coverage values which can be obtained from scanning electron micrographs [
12]. Hence, the surface roughness represents an indirect measure of the macroparticle surface coverage.
The resistivity of TiAlN coatings was determined by a Van der Pauw setup [
13] using a Keithley 2611B System SourceMeter (Solon, OH, USA) with a current of 5 mA. The measured value for a high power pulsed magnetron sputtered TiN sample was 0.4 μΩ m and in accordance with available literature data in the range of 0.3 [
14] to 1.1 μΩ m [
15]. All resistivity measurements were done at room temperature and ambient atmosphere.
Elastic properties were investigated by nanoindentation and 100 load-displacement curves were acquired per sample, utilizing a Hysitron TI-900 TriboIndenter (Minneapolis, MN, USA). A Berkovich diamond tip with 100 nm radius was used with a maximum load of 10 mN and the indentation modulus was obtained from the unloading part of load-displacement curves according to the method of Oliver and Pharr [
16]. The elastic modulus was calculated from the measured indentation modulus with the Poisson’s ratio of
ν = 0.214 [
17]. Reduction in surface roughness (
Ra < 50 nm) was realized prior to the nanoindentation tests by mechanical grinding with SiC disks and polishing with diamond suspension.
The phase formation, preferred orientation, and crystallite size were investigated by X-ray diffraction (XRD) using a Siemens D5000 system (Munich, Germany). X-ray source and detector were coupled in θ–2θ scans from 30° to 80° with a step size of 0.04° and a scan time of 4 s per step. The crystallite size was estimated from the (200) peak employing the Scherrer equation [
18].
The residual stress state was characterized by XRD stress analysis within a Bruker D8 Discover General Area Diffraction Detection System (Billerica, MA, USA) employing the sin
2Ψ method and assuming a biaxial stress state [
19]. The Cu X-ray source was operated with 40 kV voltage and 40 mA current and the
d spacing of the (200) peak was investigated in Bragg-Brentano geometry [
20] for tilting angles of Ψ = 0, 18.43°, 26.57°, 33.21° and 39.23° (corresponding to sin
2Ψ = 0, 0.1, 0.2, 0.3 and 0.4) with respect to the specimen normal. The residual stress was obtained from the slope of the strain ε plotted as a function of sin
2Ψ and using elastic modulus values
E from nanoindentation experiments according to:
Interpolation served to determine the stress-free lattice spacing
d0 at Ψ
0 with:
For Poisson’s ratio, a constant value of
ν = 0.214 was assumed [
17]. Stress gradients along the layer thickness as well as deviations from the assumed biaxial stress state affect the accuracy of the calculated stress values.
In situ high-energy XRD measurements on the powdered coatings were performed in transmission geometry at Deutsches Elektronen Synchrotron (DESY) in Hamburg, Germany. Stress-free lattice parameters
a0 were determined from the TiAlN (200) peak and linear coefficients of thermal expansion (CTE) α were calculated according to:
Powders grown with substrate rotation and the stationary deposition setup were ground and put into a quartz capillary with a wall thickness of 20 μm and a diameter of 1 mm. The specimens were heated to 600 °C using a Linkam THMS 600 stage (Surrey, UK) in a continuous measurement setup. The stage was constantly purged with Ar to prevent oxidation and powders were illuminated with a monochromatic photon beam (λ = 0.0207 nm). Two-dimensional high energy XRD patterns were acquired every 12 s with a Perkin Elmer 1621 plate detector (Waltham, MA, USA) at a sample-to-detector distance of 771 mm. Data analysis was carried out using the software package FIT2D by integration of the two-dimensional high-energy XRD patterns in
q space and conversion to the total structure factor
S(
q) [
21]. Corrections for absorption, fluorescence and inelastic Compton scattering were made.
Density functional theory [
22] calculations were carried out utilizing the Vienna ab initio simulation package. Projector augmented wave potentials were used with the general gradient approximation [
23] and the ground state was determined by full structural relaxation with convergence criterion of 10
−3 eV, 500 eV energy cut-off and Blöchl corrections [
24]. Total energy minimization was realized as a function of volume with the Birch-Murnaghan equation of states [
25] and a 6 × 6 × 3 k-point mesh was used for reciprocal space integration [
26]. 2 × 2 × 4 supercells of Ti
0.50Al
0.50N (128 atoms) were employed and three different configurations were studied: (a) minimum number of Ti-Al bonds (named C#3 in the original work [
27]); (b) alternating Ti–N and Al–N layers; and (c) random distribution of Ti and Al.
To obtain the equilibrium volume and bulk modulus as a function of temperature and stress state (configuration with minimum number of Ti-Al bonds), the Debye-Grüneisen model [
28,
29] was employed, providing the Helmholtz free energy as a function of volume and temperature. By fitting the Helmholtz free energy vs. volume data to the Birch-Murnagham equation of states [
25] at each temperature, as well as a volume offset to account for a different stress state, equilibrium volume and bulk modulus were acquired. From these data, elastic modulus, assuming Poisson’s ratio of 0.214 [
17], and linear coefficient of thermal expansion were extracted.
3. Results and Discussion
The chemical composition of TiAlN coatings with 5 μm thickness, synthesized on sapphire substrates with periodically interrupted (rotation and hybrid deposition geometry) and continuous plasma exposure (stationary deposition geometry), was identified as 27 ± 2 at.% Ti, 24 ± 2 at.% Al, 48 ± 2 at.% N and <1 at.% O, and the geometry-induced differences were in the range of the statistical uncertainty of ERDA. Hence, the deposition geometry/type of plasma exposure does not influence the chemical composition, while the coating microstructure appears to be significantly different, as demonstrated by the STEM micrographs presented in
Figure 1. Large columns with widths of up to 500 nm are formed in the case of rotation, see
Figure 1a, while finer columns with <100 nm width are observed for the stationary and hybrid deposition geometry, see
Figure 1b,c, respectively. Furthermore, scanning electron micrographs of the coating surface (not shown) provide evidence for a strong angular dependence of the macroparticle surface coverage. These findings are consistent with previous reports, see, for example, [
30]. The density and size of macroparticles incorporated into the growing coating surface are significantly lower in case of continuous plasma exposure compared to the substrate rotation deposition geometry.
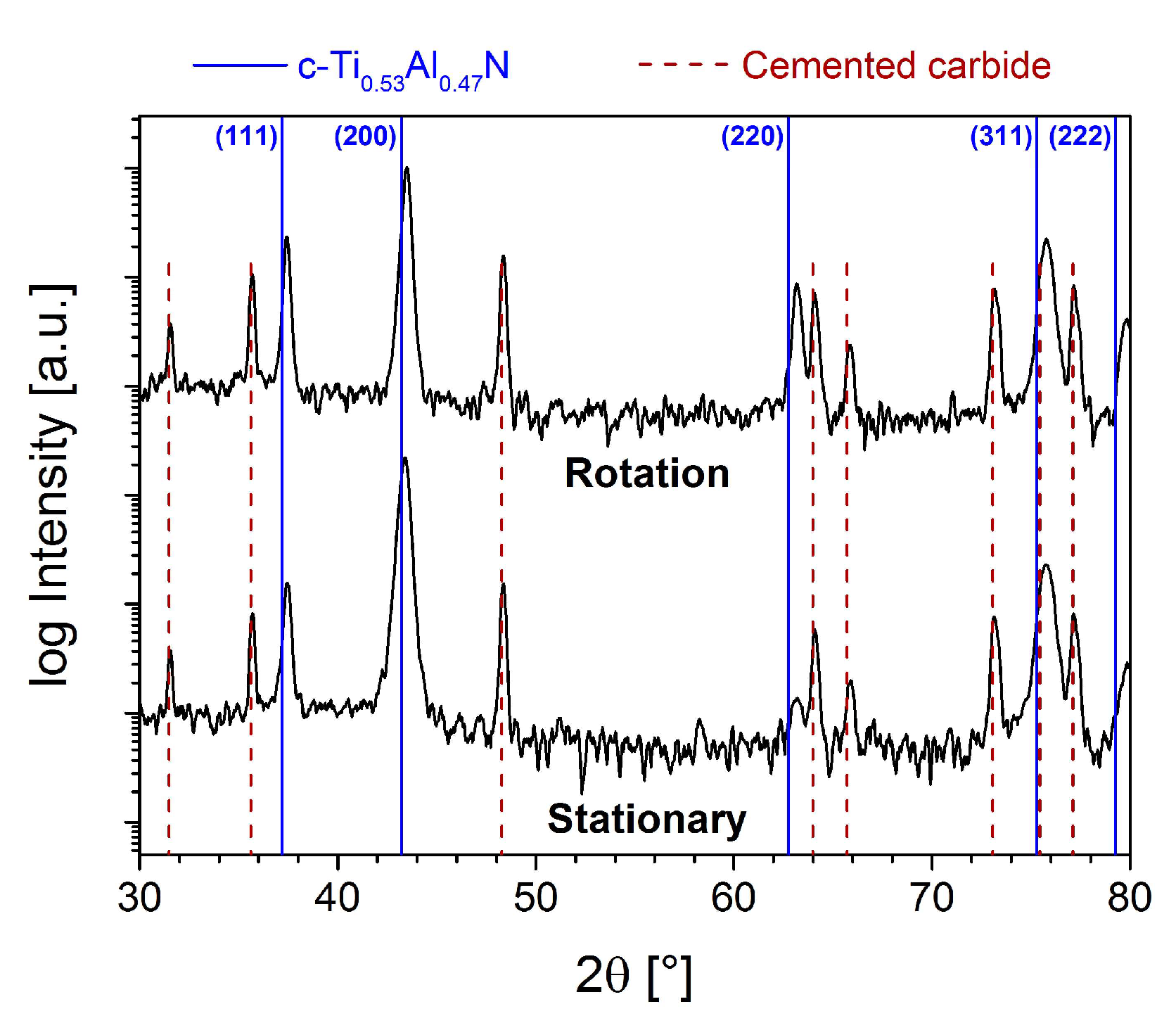
Diffractograms of TiAlN coatings synthesized with the rotation and stationary setup on cemented carbide substrates (10 μm thickness) are presented in
Figure 2, providing evidence for single phase formation of a cubic solid solution structure (NaCl prototype) independent of the deposition geometry. Furthermore, it is evident that the stationary setup results in a stronger (200) preferred orientation compared to the rotation, since the intensity ratios
I(200)/
I(111) are 4.1 and 13.4, respectively. Crystallite sizes of 35 and 24 nm are estimated for substrate rotation and stationary deposition, respectively. Recently, it has been demonstrated that the extent of cubic and wurtzite TiAlN phase stability regions is predominated by the crystallite size [
31]. Based on the present crystallite size data, it is expected that higher critical Al solubilities
x in cubic Ti
1−xAl
xN can be realized by employing substrate rotation, which results in a larger crystallite size than the stationary deposition geometry.
Elastic modulus values of TiAlN are presented as a function of the residual stress state in
Figure 3a. Independent of the substrate or coating thickness, 7%–11% higher elastic modulus values are obtained for TiAlN grown with the stationary deposition geometry in comparison to the rotation setup. All samples were grown at floating potential. Depending on the substrate and thickness, residual stress states are in the range of −0.1 ± 0.1 to 1.0 ± 0.1 GPa and −2.3 ± 0.9 to −4.3 ± 1.5 GPa for the rotation and stationary deposition geometry, respectively. The formation of more compressive stress states in case of the stationary setup can be rationalized based on intense fluxes of film-forming species to the growing coating surface due to the almost factor 10 higher deposition rate compared to the rotation setup. It is well known that chemical composition [
32], chemical configuration [
27], temperature [
33], preferred orientation [
34] and grain size [
35] affect the mechanical properties. However, in the present study, the change in elastic modulus of stationary grown TiAlN as a consequence of composition variations (<1 at.% oxygen incorporation [
32]) or chemical configuration (454–457 GPa elastic modulus for the three different configurations) is estimated to be < 1%. Possible effects of growth temperature, preferred orientation and grain size would result in a decrease of elastic modulus when comparing the rotation to the stationary setup, and this is in contrast to the identified increase in elastic modulus. Hence, these factors cannot serve as an explanation for the 7%–11% difference in elasticity obtained by comparing stationary and rotation deposition geometry.
The experimental and theoretical data depicted in
Figure 3b clearly illustrate that the elastic modulus is stress-dependent, and that the slope of the predicted data at room temperature is similar to that for the experimental data. The relative deviations of the absolute elastic modulus values are in the order of 9%. This very good agreement between theory and experiment emphasizes that the elastic modulus of metastable cubic TiAlN, grown at floating potential, can be predicted from the residual stress state. The data presented here underline that the deposition geometry affects the residual stress state and, thereby, the elastic properties.
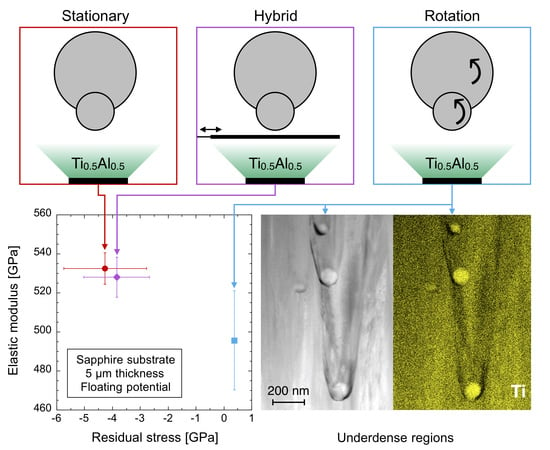
The hybrid deposition geometry can be utilized to compare the interrupted plasma exposure during rotation to the interrupted plasma exposure in the stationary setup. Since both geometries allow for relaxation due to the periodically interrupted plasma exposure, the effect of deposition geometry can be understood. This hybrid setup is characterized by a face-to-face geometry identical to the stationary deposition setup, while shutters enable an interrupted plasma exposure as experienced by the growing film surface during substrate rotation. The stress-dependent elastic modulus data of the stationary and hybrid deposition geometry, presented in
Figure 3c, are identical within the error bars. However, compared to the sample grown during rotation, a significant stress-dependent difference in elastic modulus of 7%–8% was obtained. Hence, the constantly high plasma density and intense fluxes of film-forming species during the shutter opening times cause the formation of compressive residual stresses for the hybrid deposition geometry as in the stationary deposition setup, where the plasma exposure is continuous. Therefore, it can be learned that the exposure time of the substrate to the plasma does not influence the residual stress state significantly, since the stress data from the hybrid geometry (with shutter) is within the error bars identical to the stationary geometry (without shutter).
Experimentally, it has been shown that the elastic modulus is stress-dependent for TiAlN and TiAlVN, synthesized by cathodic arc at negative substrate bias voltages ≤−40 V [
36,
37,
38]. The associated atomic scale mechanisms have recently been addressed by predictions and experimental verification of Cr
0.8Al
0.2N taking ion bombardment explicitly into account [
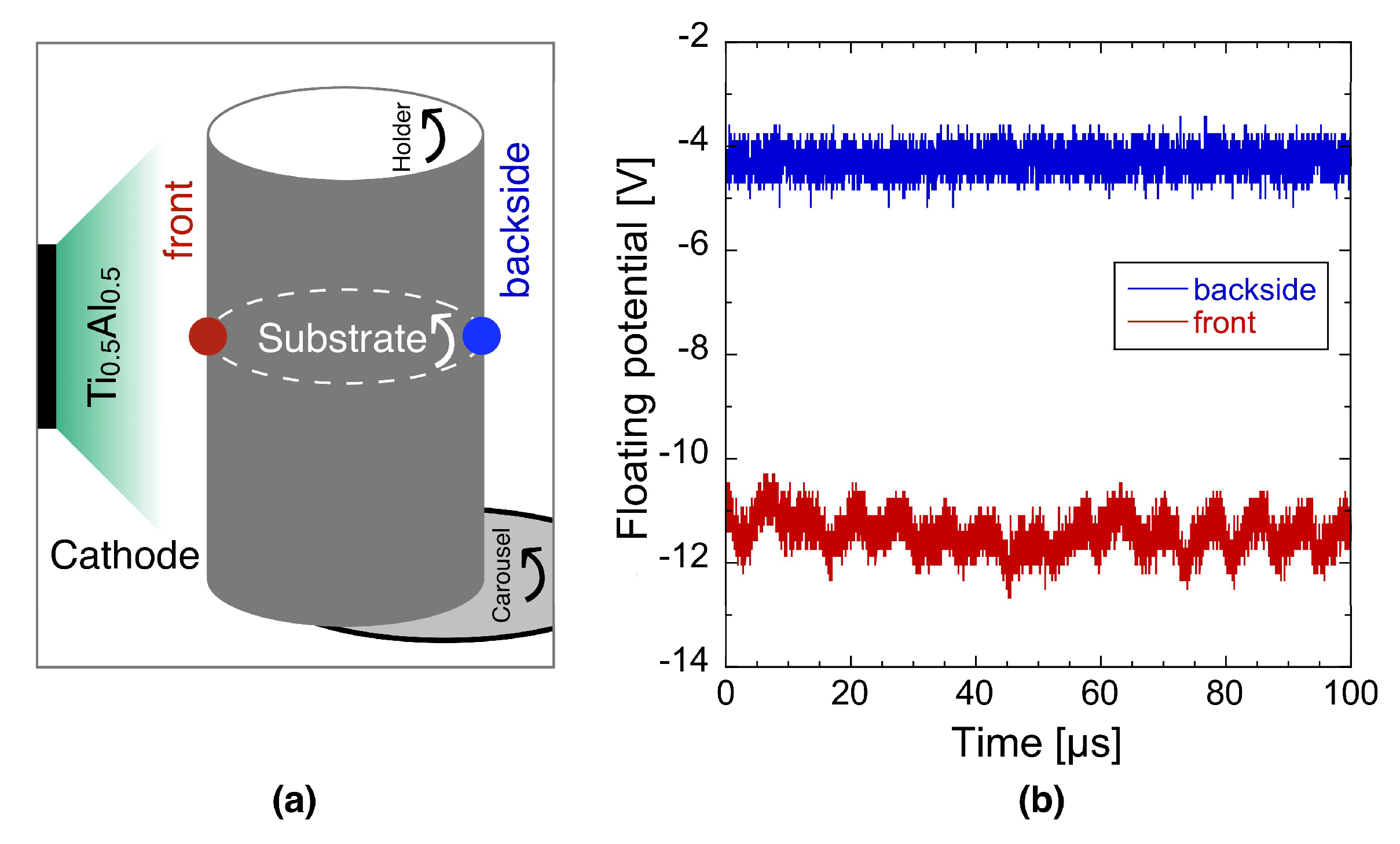
4]. To assess the floating potential that is established during continuous vs. periodically interrupted plasma exposure, flat probe measurements were conducted in front of the intense plasma and at the backside of the substrate holder where the substrate is blocked from the plasma due to the holder, see
Figure 4a. The substrate position-dependent floating potential is presented in
Figure 4b and reveals that the stationary deposition geometry is characterized by a floating potential of −10 to −12 V, while the floating potential during the rotation setup should increase to −4 V, when the substrate is positioned in a region of low plasma density and small fluxes of film-forming species. Therefore, it may be speculated that the constantly “high” floating potential in the stationary deposition geometry explains the 7%–11% higher elastic modulus values compared to the rotation which is characterized not only by variations in the plasma density and fluxes of film-forming species, but also by variations in the floating potential.
This hypothesis was critically appraised by growth experiments utilizing continuous and periodically interrupted plasma exposure with a constant substrate bias potential of −15 V. Provided that the variation in floating potential (during rotation) causes the measured differences in residual stress state and elasticity between coatings produced with rotation and stationary deposition geometry, these differences should be balanced by applying a constant substrate bias potential of −15 V during rotation to mimic the ion bombardment during stationary deposition. Elastic modulus data are presented as a function of residual stress state in
Figure 3d for −15 V substrate bias potential and the elasticity of the coatings grown with the stationary deposition geometry is still 10%–17% higher compared to the substrate rotation. Hence, the significant difference in elastic modulus between the two deposition geometries at floating potential cannot be explained by variations in the floating potential during interrupted plasma exposure.
Another well-known contribution to the residual stress state are thermal stresses which are caused by differences in linear coefficient of thermal expansion of film material and substrate at temperatures different from the deposition temperature. The average linear coefficient of thermal expansion (CTE) was calculated from stress-free lattice parameter data, obtained by in situ high-energy XRD. CTE values are with 8.3 ± 0.4 × 10
−6 K
−1 (rotation) and 8.0 ± 0.4 × 10
−6 K
−1 (stationary) in agreement with both published data [
39,
40,
41] and the predicted value of 7.3 × 10
−6 K
−1. Therefore, TiAlN exhibits a significantly higher linear CTE than the sapphire substrate of 5.0 × 10
−6 K
−1 (in-plane, provided by substrate manufacturer). When cooling the TiAlN coating from the deposition temperature to room temperature, tensile thermal stresses can be expected, as the coating exhibits larger shrinkage than the substrate. The thermal stress contribution (a comprehensive overview of residual stress contributions is provided in [
33]) can be estimated according to:
Based on this estimation, and taking into account the deposition temperatures of 470 and 520 °C, the thermal residual stress contribution of TiAlN during cooling down from the deposition temperature should be 0.9 and 1.0 GPa for the rotation and stationary deposition geometry, respectively. Interestingly, this estimation is in partial agreement with the measured tensile residual stress values of 0.4 ± 0.1 to 1.0 ± 0.1 GPa in case of the rotation deposition geometry at floating substrate bias potential, but in contrast to the values of stationary grown TiAlN with −4.3 ± 1.5 to −2.7 ± 0.6 GPa, see
Figure 3a.
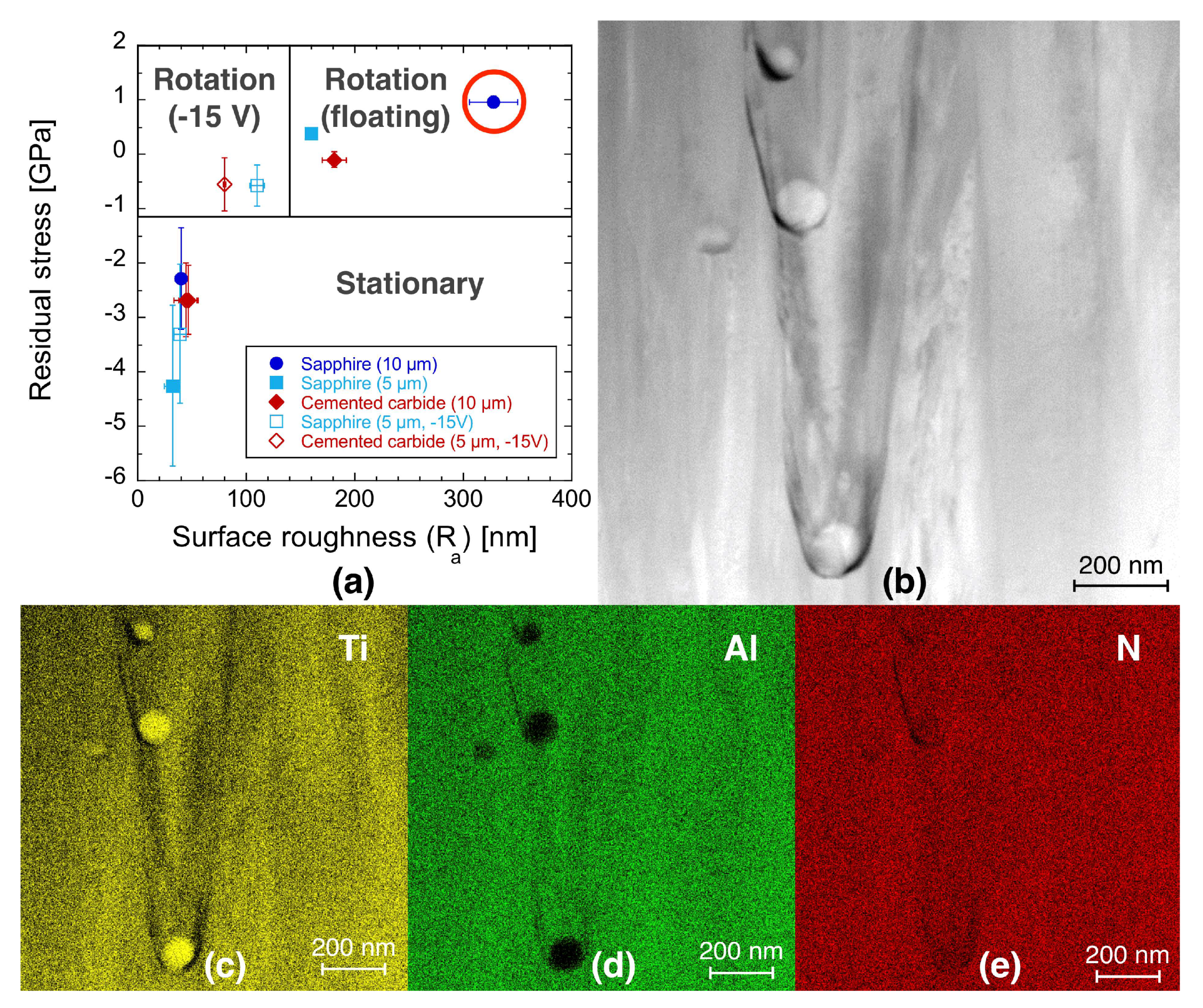
The residual stress state is displayed in
Figure 5a as a function of the average surface roughness, which is an indirect measure of the macroparticle surface coverage and thus macroparticle density. It is evident that there are two regions of tensile/slightly compressive residual stress (>−1 GPa) and strongly compressive residual stress (<−1 GPa). Hence, TiAlN coatings grown at floating potential with periodically interrupted plasma exposure during substrate rotation exhibit the largest macroparticle surface coverage and therefore high roughness values. This can be rationalized by considering that the majority of macroparticles are ejected at an angle >10° with respect to the cathode normal [
30].
To identify the relationship between macroparticle incorporation and the elastic modulus, as well as residual stress state, the cross-sectional morphology and composition of the TiAlN coating with the highest macroparticle surface coverage, highlighted by a circle in
Figure 5a, was investigated by TEM and STEM-EDX. From
Figure 5b–e, it is evident that underdense (dark) boundary regions are formed between the TiN-rich macroparticles and the TiAlN matrix and an average porosity in the order of 1% was determined from transmission electron micrographs. Based on Knudsen [
42], the porosity-dependent elastic modulus can be estimated by:
wherein
E and
P represent elastic modulus and porosity, respectively.
b is an empirical constant and usually assumed to be in the range of
b = 5 to 9 [
42]. Hence, a porosity-induced elastic modulus reduction of 5%–9% has to be expected. The significance of the macroparticle incorporation-induced porosity is also reflected by the coating resistivity which increases by almost factor 2 from 5.3 to 10.4 μΩ m, comparing TiAlN grown with the stationary and rotation deposition geometry (10 μm thickness), respectively. It appears reasonable that such underdense boundary regions act as sites for stress relaxation. Therefore, it is reasonable to assume that the lower elastic modulus and less compressive/tensile residual stress of TiAlN grown with substrate rotation at floating potential originate from a significantly higher macroparticle surface coverage which induces the formation of underdense boundary regions.