1. Introduction
Highway pavements are constantly deteriorating under the combined impacts of traffic loads and climate. The concept of pavement performance, which is used to express the current situation and amount of deterioration, is defined as the ability to explain the effects of deterioration on caused by traffic and climate during the design life [
1]. Pavement distress (cracks, permanent deformations, water-induced distress, etc.) is a very important group of parameters for assessing existing service levels. Regionally, knowledge of the relationship between surface distress and roughness seen in pavements provides very useful information, both for the efficient operation of pavement management systems (PMS), and in the accurate construction of required pavement design analyses.
In the literature, relationships between roughness (expressed as a value in the international roughness index, IRI) and pavement deterioration parameters are investigated using statistic-based modelling techniques, such as linear and nonlinear regression analyses, frequently. It is used to evaluate distress in dozens of different types of pavements and the severity of the distress identification guidelines used for the evaluation of pavements. Therefore, to express a dependent variable within a large number of independent variables, this traditional method is not able to capture relationships with the desired precision. Nowadays, there are also different modelling techniques that can provide meaningful results for the extreme values (high or low) of independent variables and provide complex relationships between data stacks, which also provides practical convenience in modelling with a large number of independent variables. Examples of these are the Artificial Neural Networks (ANN) method, which does not require any assumption of functional distribution similarity of calibration data, and the Multivariate Adaptive Regression Splines (MARS) method, which is similar to the partial regression method.
The studies that model the relationship between surface distress and roughness are observed when the literature is examined. Hozayen and Alrukaibi developed regression relationships based on logical and statistical criteria based on the relationship between roughness, the pavement condition ratio (PCR), cracks, rutting, and raveling [
2]. Researchers have considered only three distress patterns in response to the pavement performance indicators IRI and PCR. Al-Omari and Darter examined the regression equations between IRI and the pavement serviceability ratio (PSR), which are performance indicators in their studies [
3]. Additionally, they investigated the relationships between IRI and rutting, deformations, patches, and cracks (four types of distress) by their regression analysis. Therefore, they determined that a linear relationship is formed between IRI and rutting by combining data (making homogenized sections). Aguiar–Moya et al. [
4] developed a mechanistic-empirical regression model with IRI, longitudinal and transverse cracking, block cracking, fatigue cracking, and rutting, as well as an independent variable for pavement age, precipitation rate, and the mix design parameters. Five surface distress types were taken into consideration. Mactutis et al. [
5] developed a linear regression model between IRI and the mean rut depth and the crack percentage seen on an evaluated surface. To determine the performance change in the model, the measured IRI values were used as input variables. Sandra and Sarkar, in their study, created a linear regression model between IRI and five types of distress, such as cracking, potholes, raveling, patching, and rutting [
6]. Dependent variable estimations were made in addition to a total of fifteen independent variables, which takes into consideration the three different severities of the mentioned types of distress, low, medium, and high. Therefore, it ensured that the model was able to evaluate with sensitivity, regarding the pavement surface evaluation principles described in the distress identification manuals, while also considering the severity levels of distress. The MARS technique, which can be used in combination with repetitive partial fitting and curve fitting techniques from modelling techniques, is also used to investigate the relationship between pavement performance data and surface distress data. Attoh–Okkine et al. [
7], to estimate the IRI dependent variable, developed a prediction model using six independent variables, four of which being surface distress data, such as cracks, environmental factors, age, standard deviation of mean rut depth, and patching.
Moreover, from recent studies, Chandrakasu and Rajiah [
8] determined the relationship between cracks and pothole distress, and IRI in roads with a low traffic volume. The linear regression technique was used in the modelling studies and the calibration of the model, with a very high regression coefficient (0.814), was completed. Chadra et al. developed models using regression and ANN approaches between IRI and five types of surface distress, including rutting, cracks, potholes, patching, and raveling [
9]. Different severity levels of surface distress types are ignored. Through comparing the estimation capabilities of the models created in the study, it was concluded that the most appropriate method is ANN. Mahmood et al. [
10] developed a model that can estimate the pavement condition index (PCI) using long-term pavement performance data (LTPP). Cracking length, cracking area, overlay thickness, age, and the equivalent single axle load (ESAL) data were used as independent variables in the study. During the analysis, the relationships between dependent variables and independent variables were investigated using deterministic and probabilistic modelling techniques. Zhou et al., in their study [
11], made evaluations using the analytic hierarchy processes (AHP) between 14 different types of surface distress and PCI. As a result of the study, three new evaluation indexes were proposed, which can be used in practice, including the Transverse Cracking Evaluation Index (TCEI), the Pavement Patching Condition Index (PPCI), and the Pavement Surface Distress Condition Index.
Studies using the approach of ANN in the investigation of the relationship between surface distress and performance are also striking. Lin et al. developed a model, using the ANN technique, capable of IRI estimation with fourteen surface distress inputs, including the road level, left rutting, right rutting, alligator cracking, cracking, digging/patching, potholes (mild and severe), patching, bleeding, corrugation, stripping, and man-holes (mild and severe) [
12]. The study is one of the rare studies that used a large amount of data as input. Additionally, researchers have examined the sensitivity of changes between IRI and each surface distress.
Moreover, regarding the development of prediction models, there are studies that take into consideration many different parameters other than the surface distress affecting the performance of pavement. During these studies, it was observed that artificial intelligence techniques are frequently preferred due to the large number of independent variables and the fact that some variables cannot be expressed with numerical values. It was seen that the ANN [
13,
14,
15,
16] and the fuzzy logic [
17,
18,
19] approaches, which are quite good for the convenient evaluation of numerical and verbal data, and the Adaptive Neuro Fuzzy Inference System (ANFIS) [
20] approach, which uses both methods together with fuzzy logic and ANN approaches, are very frequently preferred by researchers.
While the surface condition of the pavement gives a lot of information about its current level of performance, obtaining the data requires rather difficult field studies. Innovative approaches applied to simplify field studies are also noteworthy in the literature. Kırbaş and Karaşahin [
21] developed prediction models that can determine the pavement condition index (PCI), which is a performance indicator calculated with the help of the pavement surface distress data, through the vibrations that occur in the vehicle. Lantier et al. [
22] developed a method that can measure the longitudinal and transverse direction slope, evenness, and the depth of water on the pavement surface, with a mobile laser scanning technique. Suanpaga and Yoshikazu [
23] designed a method, with the help of Phase Array type L-band Synthetic Aperture Radar (PALSAR) images, to help determine the IRI values of pavements. It is emphasized that field studies can be completed entirely with the development of this method. Conversely, there are methods developed to determine the types, quantities, and locations of pavement distress by means of vibration meters, laser scanners, and road surface display devices that can be placed on vehicles [
24,
25,
26,
27]. Dondi et al., in their study [
28], proposed a semi-automatic method which can evaluate the surface data obtained by laser scanning and video imaging methods together.
As can be found in studies related to the subject, many different mathematical modelling methods are used in the modelling of the relationship between IRI and surface distress, and a significant mathematical relationship can be obtained between them. However, studies that can expose the sensitivity of the effects of surface distress on the IRI and their changes are very limited.
Mathematical relations between pavement surface distress types and surface roughness are investigated, in the current study, by using the MARS approach in bituminous, hot mixed asphalt (HMA) pavement. Regarding the model developed, ten surface distress types, including alligator cracking, bleeding, block cracking, corrugation, depression, longitudinal and transverse cracking, patching, potholes, rutting, and raveling, as well as a total of twenty-nine individual variables, with differing severity levels of distress, are taken into consideration. Pavement distress and IRI data collected in 3295 highway sections used as rural principal intercity arterial routes are used. As a result of the study, the impacts of the various types of surface distress and the different severities, which are the inputs of the developed model, are evaluated through synthetic input values. Consequently, the increases in sensitivity levels on the IRI according to the distress type, evaluated by area (unit of measure), are determined.
3. Results
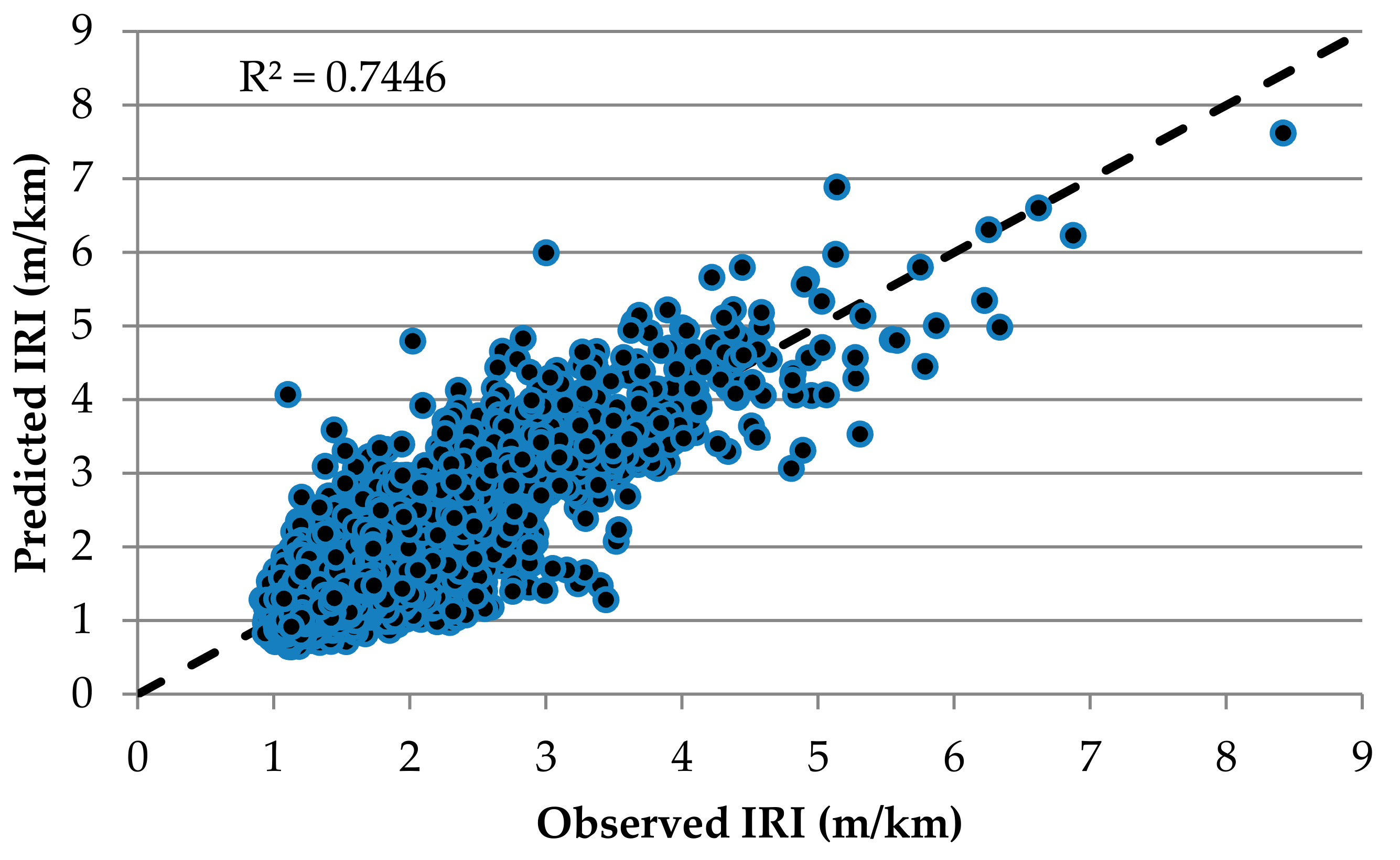
The introduction section of the study emphasized that there are various mathematical approaches to modelling the relationships between the International Roughness Index (IRI) and surface distress. Found in similar studies, IRI prediction models were developed with various quantities of pavement distress being used as input components, and the studies were terminated. Adding to similar studies, in this study, the sensitivity of pavement distress inputs to changes in IRI values were determined with the help of the model developed using the Multivariate Adaptive Regression Splines (MARS) method. The increased rates of IRI value in the current study were determined by changing only one input variable (surface distress data) and keeping the others constant in the model developed. The results were visualized and interpreted using graphics.
The surface distress data was collected according to the distress identification procedure of the PAVER system. Distress input data were standardized using a standardized quantity of distress (SQD) to eliminate the different sample unit size parameters examined according to this system. Hence, in the system, pavement distress types were collected in three different dimensions, including the area, length, and number. It is clear that it would not be right to compare the effects of the types of distress collected in different dimensions (such as length versus area) to the IRI increase, since all distress inputs were standardized by the same mathematical expression. Therefore, pavement distress with only area measurement units, such as: (1) alligator cracking; (2) bleeding; (3) block cracking; (5) corrugation; (6) depression; (11) patching; (15) rutting; and, (19) raveling, were evaluated.
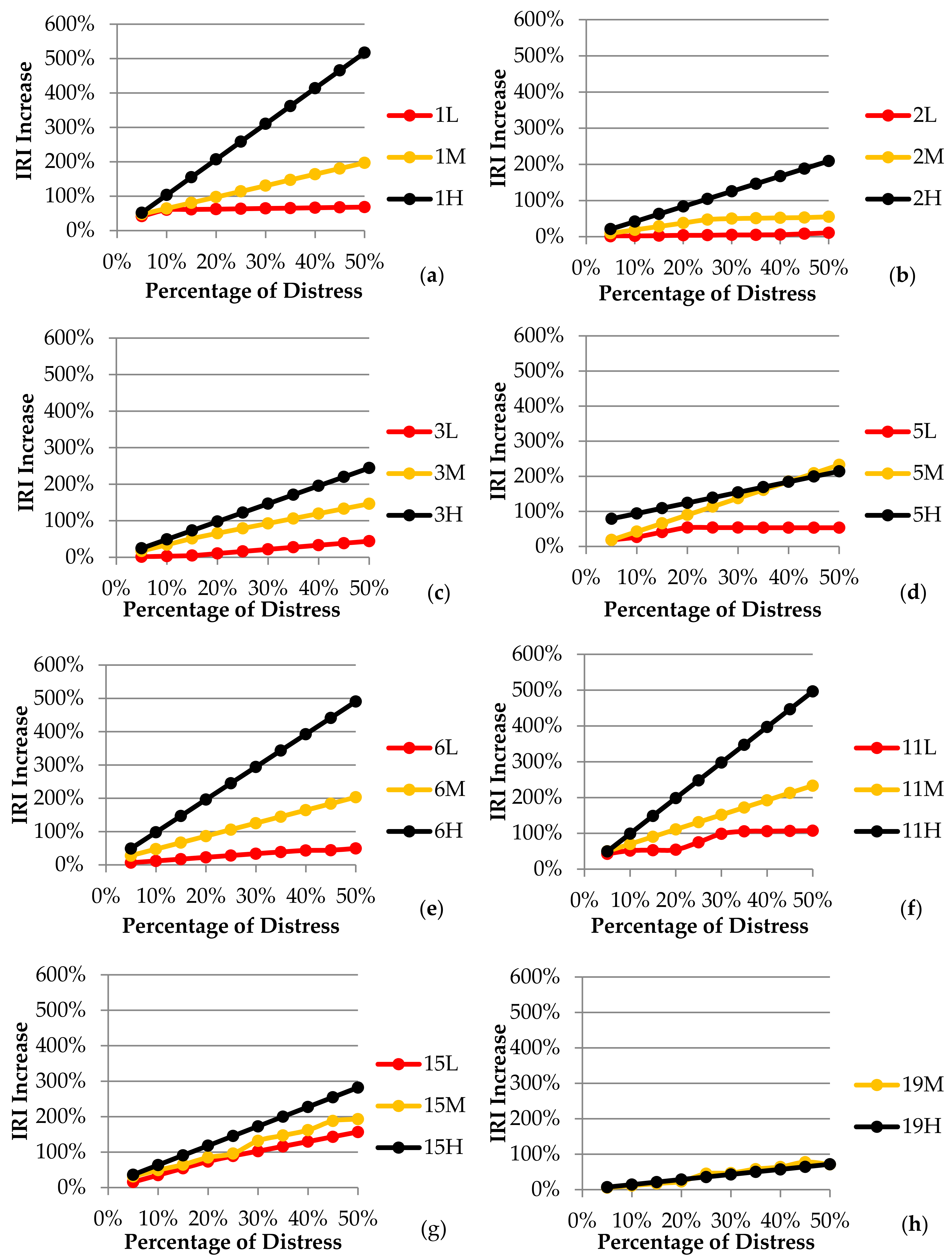
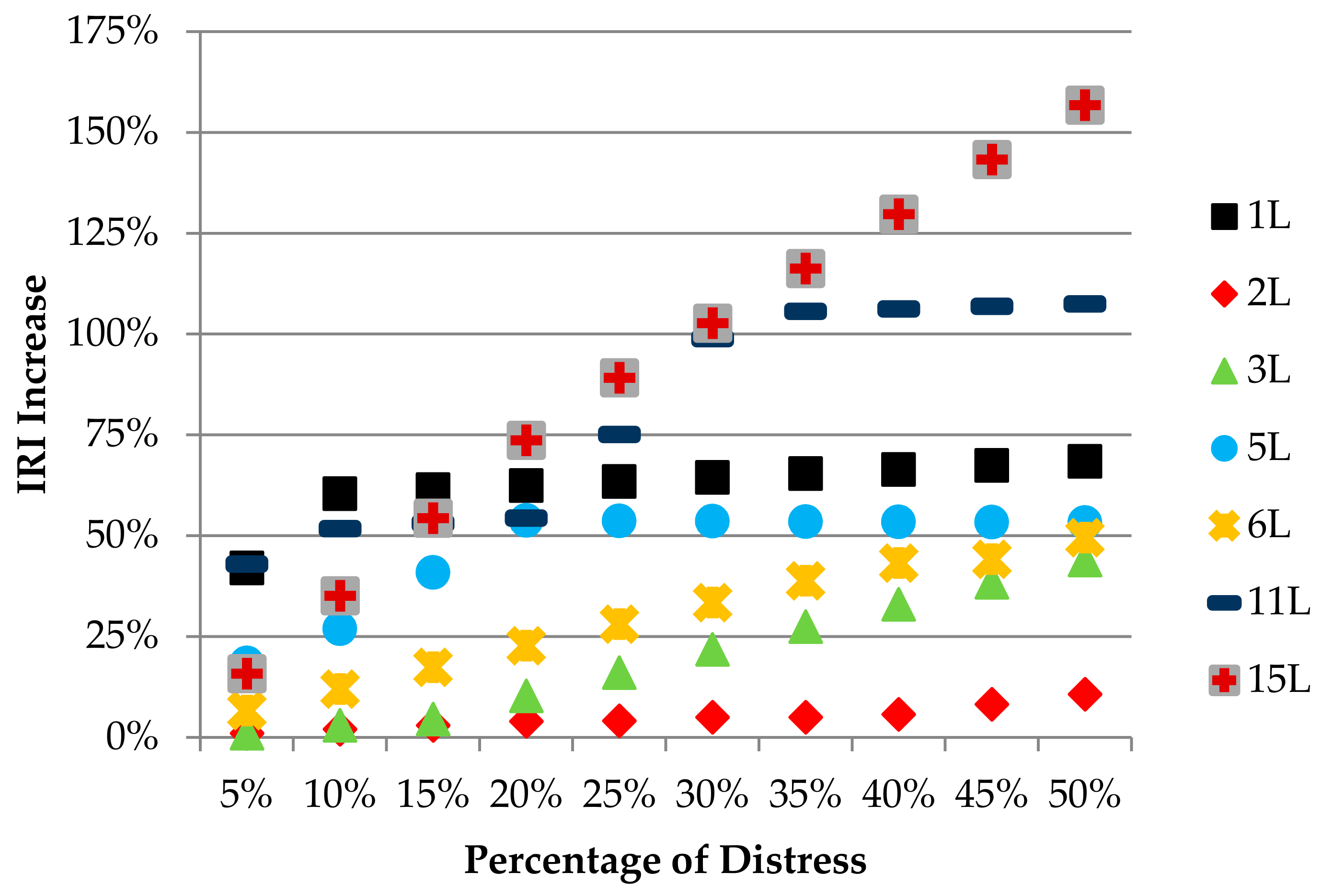
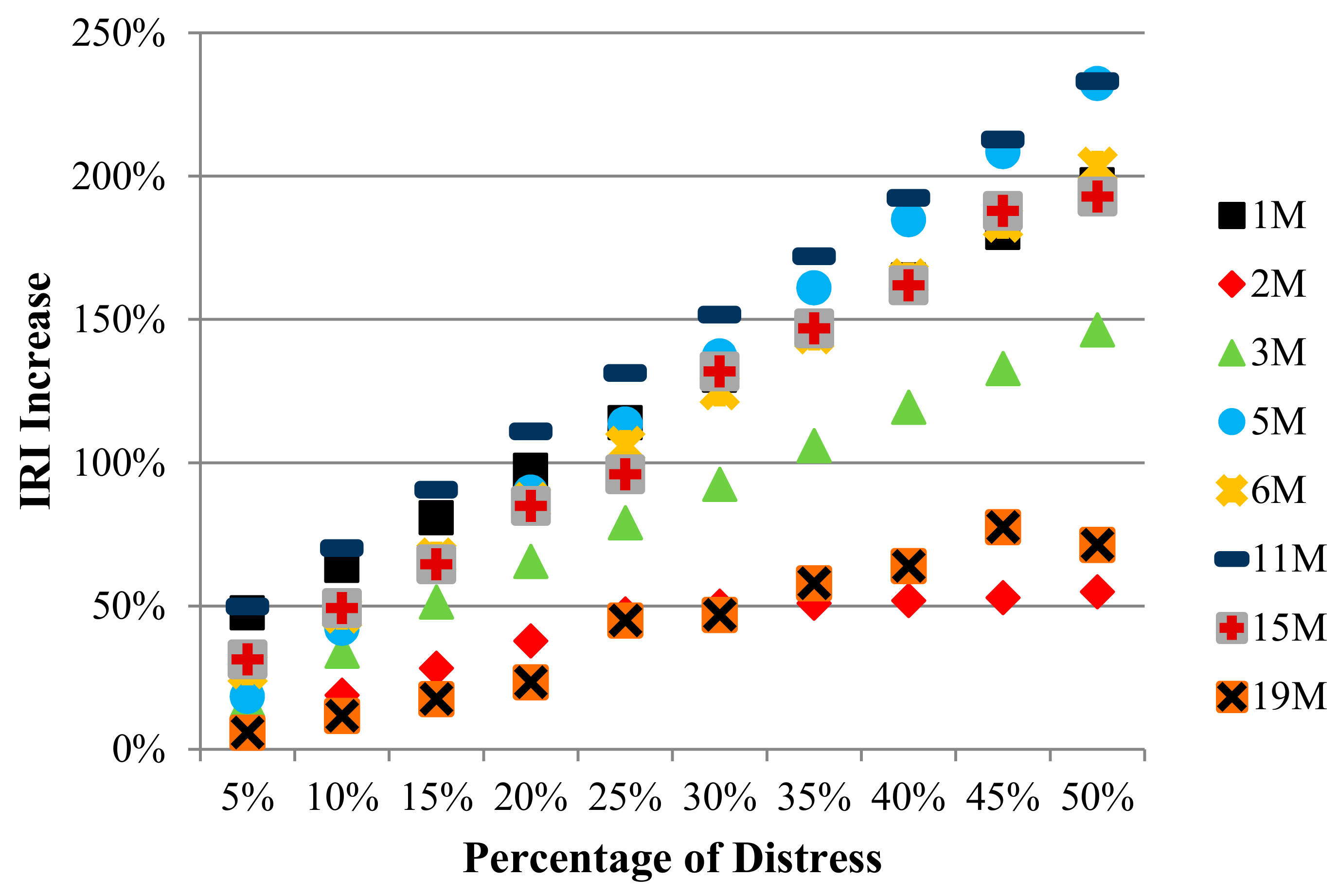
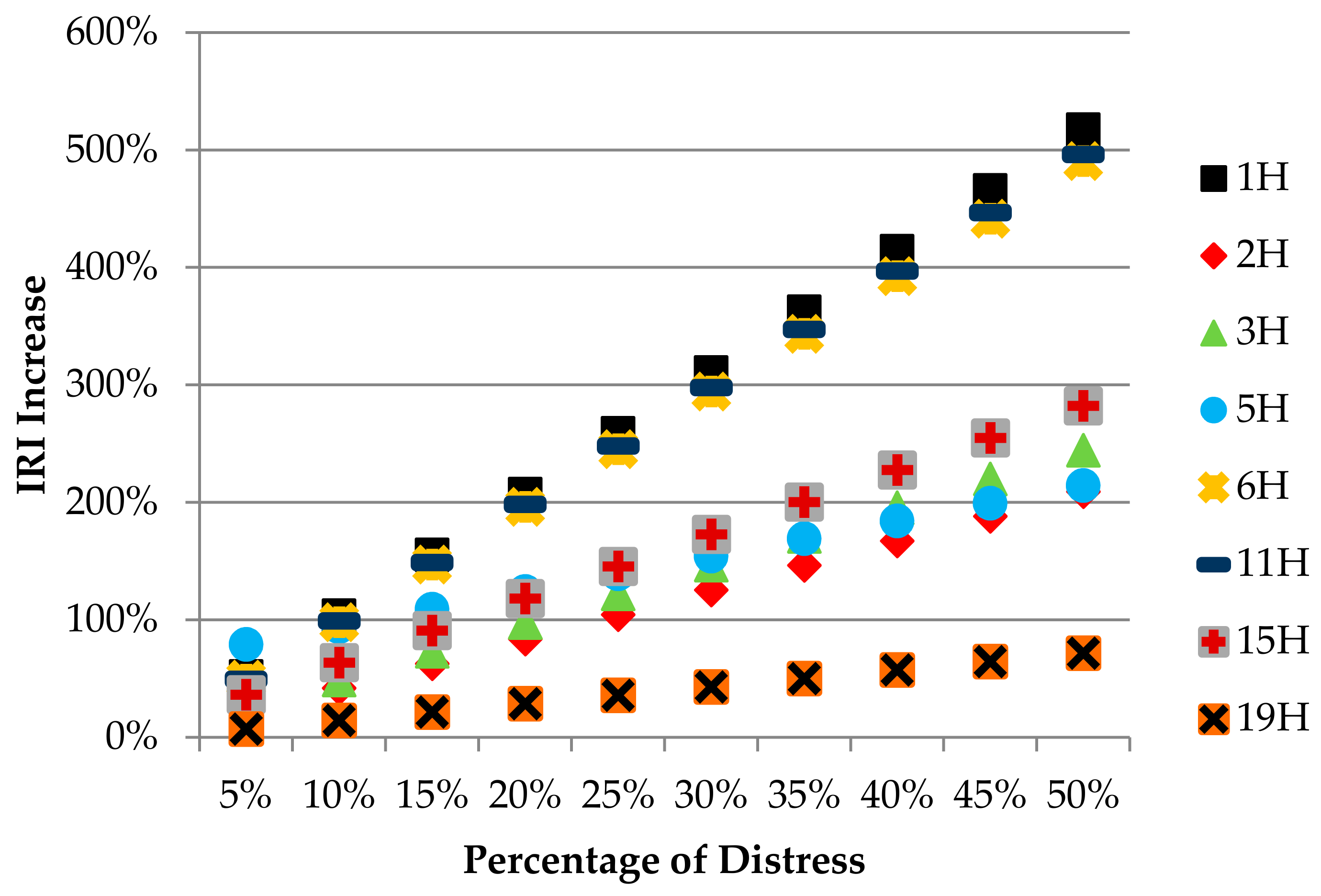
The co-occurrence of different types of distress, severities, and quantities is actually quite common. This is particularly noticeable in sections where the quantity of distress is excessive. It is not expected to encounter the same type and severity of distress in the entire sample unit of an examined pavement. Therefore, the likelihood that the distress evaluated in the eight different types of area measurement units mentioned would occur between a ratio of 5% and 50% on the surface of the pavement—this was taken into consideration. Concerning each of the different severity measures of the distress examined, the effect on the IRI increase versus the various occurrence rates of distress on the pavement surface is shown in
Figure 6.
Figure 6 shows the vertical axes of figures that were adjusted to show the same values in order to compare the effects of pavement distress on IRI increases in terms of different types of distress. It is seen, from all the types of distress examined, that the highest increase in IRI was caused by high severity, followed by medium, and then low severe distress types. It is noteworthy that, for all types of distress, if there was a small quantity of distress in the surface area evaluated (including at different levels of severity), the IRI increases were very low and similar to each other. Nevertheless, in the evaluated surface area, the highest-severity alligator cracking, depression, and patching-type distress were seen to cause an increase in the IRI. It is noted that this increase was up to 500% in the IRI, since the distress occurred in about half of the evaluated area. The assessments for each type of distress are listed below:
(
Figure 6a) The alligator cracking caused a 50% increase in IRI in all severities of distress, if the distress occurred at 5% of the evaluated area. However, if the distress was seen in 50% of the area, it caused an increase in value of about 70% in low severity, 200% in medium severity, and 500% in high severity.
(
Figure 6b) During cases of bleeding-type distress, an increase in low severity by 1%, moderate severity by 9%, and high severity by 21% occurred in IRI when 5% of the distress was seen in the evaluated area. However, if it was observed in 50% of the evaluated area, low severity caused an increase in IRI by 11%, moderate severity by 55%, and high severity by 209%. It is remarkable that there was about 20 times the difference between low-severity distress and high-severity distress in the IRI increase.
(
Figure 6c) IRI was relatively less affected by block cracking-type distress, which was the result of combined states of longitudinal and transverse cracks. When observed at 5% of the evaluated area, low severity caused an increase in IRI by 1%, moderate severity by 17%, and high severity by 24%. Conversely, if it was seen in 50% of the surface area, it caused an increase in the IRI by 44% in low severity, 146% in medium severity, and 244% in high severity. Moderate and high severity distress led to a much greater increase in the IRI than low severity distress.
(
Figure 6d) It is known that the corrugation-type distress, such as a signal waves, result in a disturbance in the transverse direction of the highway pavement. When the distress was observed in 5% of the evaluated area, it was understood that there was an increase in IRI by 18% from low severity, 18% from moderate severity, and 79% from high severity. It is noteworthy that high severity distress resulted in a significant increase in IRI, while low and moderate distress caused a very insignificant increase, according to the model's conclusions. When the distress was observed in 50% of the evaluated area, an increase in IRI value was seen in low intensity by 53%, moderate intensity by 232%, and high intensity by 214%. The difference in the IRI increase that occurred when the distress was seen in the small area shrunk considerably in comparison to the large area. Moreover, the increase in IRI was very close to each other for moderate and high severity distress. The fact that the medium severity IRI increase rate was higher than the high severity IRI increase rate was thought to be due to insufficient data for the calibration of this type of distress used to create the model. This should be considered to be a problem in detecting the sensitivity of the input parameters of the models created from a large number of inputs and it should be kept in mind that the effects of high severity corrugation-type distress on the IRI increase in subsequent studies needs to be verified.
(
Figure 6e) Surface distress of the depression-type affected the increase in IRI negatively in a significant way. When the distress was observed in 5% of the evaluated area, it was understood that it caused an increase in IRI by 7% in low severity, 28% in medium severity, and 49% in high severity. However, if the distress was seen in 50% of the area, it led to an increase in the IRI by 50% in low severity, 203% in medium severity, and 491% in high severity.
(
Figure 6f) Considering the case of 5% of the evaluated area, the patching-type distress caused an increase in IRI by 43% in the low severity, and 50% in the medium and high severity. When observed in 50% of the area, low severity caused an increase in IRI by 107%, moderate severity by 233%, and high severity by 496%. The patching was a type of distress that provided a significant increase in the IRI, especially in the case of a large quantity of evaluated area.
(
Figure 6g) It was seen that the increase in the IRI value of rutting-type distress in the same quantity, low, medium, and high severities, did not make much difference compared to the other types of distress. When the distress was observed in 5% of the evaluated area, it was observed that it caused an increase in IRI by 16% in low severity, 31% in medium severity, and 36% in high severity. If the distress was observed in 50% of the area, it caused an increase of 157% in low severity, 193% in moderate severity, and 282% in high severity.
(
Figure 6h) Finally, raveling-type distress was evaluated in a similar way. As stated in the distress identification standard, raveling-type distress was evaluated at two levels of severity, moderate and high. It was understood that this type of distress led to an increase of IRI by 6%–7% if observed in 5% of the evaluated area and 71%–72% if observed in 50% of the evaluated area for two different severities of distress. Since the raveling-type distress did not change much of the macro roughness seen on the pavement surface, it was determined that the increase in the IRI value in the model was the least impactful type of distress.
Another assessment was made by comparing the effects of distress types on the IRI increase according to each level of severity. When low-severity distress was examined, it was noteworthy that many of the distress types contributed to the IRI increase in similar proportions (between 1% and 40%) when the evaluated area had a small quantity of distress. However, in cases where the quantity of distress was large, rutting and patching-type distress were more likely to cause an increase in IRI than the other types of distress studied. Alligator cracking, depression, corrugation, and block cracking-type distress were seen to have a mean effect on the IRI increase between 40% and 80%. Low severity bleeding, however, seemed to have little or no effect on the increase of IRI. These evaluations are shown graphically in
Figure 7.
Whenever the distress of the medium severity level was examined, in the case where the quantity of distress in the evaluated area was small, it was seen that the distress was close to each other (in the range of 6%–50%). It was seen that there were significant differences in terms of the effects of distress as the quantities of distress grew. It was noticed that a moderate severity level of patching, corrugation, depression, alligator cracking, and rutting-type distress had the most detrimental effects causing IRI increase. As the quantity of distress in the evaluated area increased, it was observed that the effect of block cracking was slightly lower compared to the other types of distress, and raveling and bleeding-type distress affected the IRI increase at the lowest level. These evaluations are shown in
Figure 8.
Whenever the distress of the high severity level was examined, the effects on the increase of IRI (in the range of 7%–79%) were relatively close to each other, as seen in the cases of other severity levels. As the quantity of distress in the evaluated area increased, it was understood that alligator cracking, patching, and depression-type distress were causing a significant increase in IRI. Rutting, block cracking, corrugation, and bleeding-type distress caused relatively less IRI increase and raveling-type distress caused the least increase in IRI between all the examined distresses. All these evaluations are shown graphically in
Figure 9.
4. Discussion
The sensitivity and effects of the International Roughness Index (IRI) increase of eight different types of distress were determined by means of the generated IRI prediction model. Studies evaluating the effects of different types of distress on the IRI increase in the literature are quite limited. In fact, there are almost no studies examining the types of distress that consider different severities. It is thought that this is the strongest side of the study. It is obvious that the study will contribute to the literature and give a new perspective to researchers who are engaged in similar studies. It also contains practical conclusions about which types of distress should be prioritized for maintenance and repair work by the agencies responsible for the operation of road pavements.
The Multivariate Adaptive Regression Splines (MARS) technique was used to model the relationships between surface distress and IRI. Among other situations, this model has not been used for obtaining effective results against some input values for models examining many independent variables. This suggests that MARS is a method that should be preferred when the relationships between surface distress and IRI are determined.
It is understood from the analysis that, as the quantity of impairment increases for each type of distress, the IRI value increases. It is seen that increases in IRI are caused by alligator cracking, depression, and patching-type distress most often. Additionally, it is also noteworthy that the raveling-type distress least increases the IRI and the effects on IRI increases for both medium and high severity levels are close to each other. However, at different levels of severity regarding rutting and block cracking, as the quantity of distress seen in the evaluated section increases, the effect on the increase in IRI seems to increase equally. As expected, the increase in IRI in low and moderate severities of corrugation-type distress resembles that of alligator cracking, depression, and patching-type distress. However, in the case of high severity distress, contrary to what is expected, there is not much effect on the increase of IRI. This is thought to be due to an insufficiency of data used in the model calibration as well as the distress during the measurement, which might be seen in different regions from the direction in which the IRI data was gathered. Assuming that this is a problem in detecting the sensitivity of the input parameters of the models created by a large number of inputs (independent variables), it is necessary to keep in mind that in subsequent studies high severity corrugation-type distress needs to be verified to have an effect on IRI increase.
Although each study cannot be exactly the same as another, similar results were obtained in the study conducted by Lin et al. [
12] wherein the researchers tried to determine the improvement provided to the IRI in case of repair to the distress with the help of a model developed by the Artificial Neural Network (ANN) technique. It seems that the repair of cracking and superficial deformation-type distress has contributed significantly to the improvement of IRI values in this study.
5. Conclusions
Regarding hot mixed asphalt (HMA) pavements, the pavement surface distress effects on the International Roughness Index (IRI) were examined, and are considered to be performance indicators of pavements. To evaluate the types of distress, the surface distress identifications proposed by the PAVER system were used. Relations between IRI and ten different types of distress data (29 different model inputs were formed which considered different levels of severity) was collected in field studies and were digitized by means of the model created using the Multivariate Adaptive Regression Splines (MARS) approach. Through this model, the impact of the changes of input parameters (pavement surface distress) on IRI was determined. Eight different types of pavement distress, including alligator cracking, bleeding, block cracking, corrugation, depression, patching, rutting, and raveling, were collected in area measurement units to make the comparison between parameters more realistic.
During the evaluations for all types of distress, it was observed that the quantity of surface distress in the evaluated area increased as the IRI value increased. It was determined that alligator cracking, depression, and patching-type distress caused the greatest increase in IRI, especially if the distress severity was high, the increase in IRI value was up to 500%, and if it was moderate, the increase in IRI value was up to 200%. The raveling-type distress had the least effect on the increase in IRI and, even in different quantities, the effect of the distress seen in both severities were very close to each other. The other type of distress that had the least effect on IRI increase was bleeding. However, high severity bleeding-type deterioration led to a more than double increase in IRI, as compared to moderate and low severity. However, it was observed that the rates of increase in the IRI regarding the different severity levels of the rutting-type distress were very close to each other. The type of distress that was observed to have the most homogenous change in IRI increase, with increasing quantity of distress observed between different severities and evaluated area, was block cracking.
Since surface distress determinations of pavements made in the field showed that many distress types are seen together, in this study, the effects of surface distress on IRI was investigated by examining the sensitivities of the input parameters of the generated prediction model. During the later stages of the study, it became very clear that using similar analyses with a large number of data sets contributed to the literature and to the evaluation of different types of distress. Additionally, the use of multiple techniques in modelling studies to conduct comparative assessments will ensure that the most appropriate modelling technique to be used for this purpose is identified. Using the help of the findings obtained from this and similar studies, it is thought that significant input can be provided to help the agencies responsible for the upkeep of the pavement to plan maintenance and repair activities.