Abstract
Polytetrafluoroethylene (PTFE) chemically repels water droplets due to the nature of fluorine substituents. This paper presents an experimental study on the impact of PTFE particle size and temperature on the hydrophobicity of a surface. The present study analyzes hydrophobicity due to both the chemical properties of PTFE and the microstructure created by PTFE particles. Herein, studies of the contact angle and the sliding angle of these surfaces are described in supercooled-water conditions ranging from −10 to 0 °C. From the equations governing the surface tension and sliding angle of a droplet on a superhydrophobic surface, it is found that particle size has a much greater effect on hydrophobicity than temperature. An increase in the PTFE particle size greatly reduces the sliding angle, which indicates a lower amount of energy required to remove the droplet from the surface.
1. Introduction
A functional chemical surface has a wide variety of applications including self-cleaning surfaces, drag reduction on ships, and anti-icing technology by repelling supercooled water droplets [1,2,3]. The most effective hydrophobic surfaces found in nature are created using a microstructure, such as that in butterfly wings or the surfaces of lotus plants, and it has been shown that varying the microstructure of such a coating can modify the hydrophobicity of a surface, as well as the wetting properties [4,5,6]. The two extreme conditions for microstructure wetting are the Wenzel state, where the microstructure is filled with fluid, and the Cassie-Baxter state, where fluid is pinned on the entrance and exit corners of the microstructure [7,8,9]. Previous studies have shown that a microstructure comprised of spherical polytetrafluoroethylene (PTFE) nanoparticles is able to produce a superhydrophobic surface, with contact angles greater than 140° [10,11] such as the surface shown in Figure 1. PTFE coatings can be applied to virtually any surface, including metals, wood, and plastics either by electrolytic coating or by mixing PTFE particles with a polymer [12,13,14,15].

Figure 1.
A water repellent characteristic of a superhydrophobic coating.
Because of the nature of PTFE particles, it was assumed that the state of all PTFE coating surfaces was dominated by the Cassie-Baxter state. In this state, the majority of the contact between the fluid and the coating surface is at the liquid–gas interface [8]. Modifying the size of the PTFE particle in a superhydrophobic coating will change the number and size of these interfaces. A larger particle size will force the droplet to stretch over a larger gap and create fewer liquid–gas interfaces. However, at this interface, the contact angle of a fluid droplet is determined primarily by the ambient pressure, the mass of the fluid droplet, and the molecular structure of the compound [16,17], not necessarily the size of the interface, and so the effect of particle size on contact angle is unclear. Contact angle is not the only way to measure the hydrophobicity of a surface. Sliding angle measures the force required to remove a droplet from a surface [14]. This angle, regardless of wetting conditions, is a direct measure of the amount of energy required to remove a droplet from a surface, which can be influenced by the size of PTFE particles. Thus, to accurately measure the effect of PTFE particle size on hydrophobicity, sliding and contact angles must be measured.
This study focuses primarily on supercooled conditions, which encompass a large range of temperatures. Because the properties of the liquid-gas interface, as well as water properties can be influenced by fluid temperature [14], it is necessary to evaluate the hydrophobicity of surfaces over a wide temperature range. Morita and Sakaue [14] have developed a method for the characterization of the hydrophobicity of a surface using both static and dynamic testing. The static test relies on the contact angle of a droplet, while the dynamic test relies on the sliding angle. Herein, both evaluations are used to determine the effects of temperature and PTFE particle size on the hydrophobicity of a surface.
2. Methods and Experiment
Figure 2 schematically describes the theoretical wetted area for a water droplet on a PTFE surface under the Cassie-Baxter wetting condition. The water contact ratio is shown in Equations (1) and (2), where is the contact ratio, n is the number of contact areas between a PTFE particle and fluid droplet, ds is the contact area between the droplet and the PTFE particle, and is the PTFE particle radius.
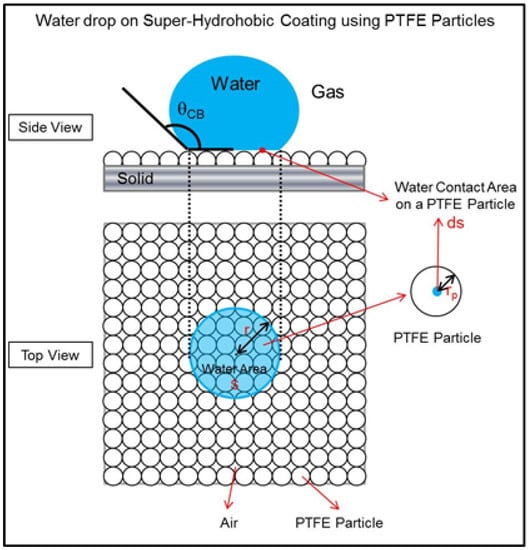
Figure 2.
Schematic description of wetted area related to the PTFE particle size.
If a water droplet is assumed to have infinitesimal thickness dw, it can be modeled as a two- dimensional droplet contacting a superhydrophobic surface (Figure 3). The surface tension of the coating surface, , the surface tension from the supercooled water droplet, , and interfacial tension, , are acting on the surface. All other external forces acting on the droplet can be included in net force, F. The contact angle, can be found by setting the net force acting on the droplet equal to 0. At the boundary points 1 and 2, where the gas, liquid, and solid phases exist, Equation (3) can be derived [14].
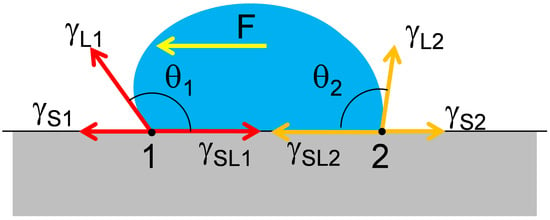
Figure 3.
Schematic description of a water drop on a solid surface.
2.1. Static-Evaluation Method
The static-evaluation method describes the hydrophobicity of a coating, where there is no external force acting on the coating: F = 0. A supercooled-water droplet can be considered as stationary on the coating surface. In this case, the contact angle at both edges of the droplet is the same and can be measured as a function of the work needed to remove the droplet, W, and the surface tension , shown in Equation (4). The predicted measured contact angle, , is shown in Equation (5) [14] where W is the work of adhesion to the surface, and is the area of interaction between the fluid and the solid surface.
Here, is shown as a function of temperature of the supercooled droplet, T, and critical temperature of water, . While the terms containing the critical temperature of water will be very small due to the high critical temperature of water, there is still a temperature dependency that must be investigated. Coefficients B, b, and are given from the IAPWS model, which are 235.8, −0.625, and 1.256 mN·m−1, respectively [18].
2.2. Dynamic-Evaluation Method
In contrast to the static-evaluation method, the dynamic-evaluation method uses an applied force to measure the amount of energy required to remove a droplet from a surface. This force is applied by tilting the surface and allowing the component of gravity parallel to the surface pull on the droplet. In this way, the force on the droplet can be related to the angle at which the surface is tilted. A diagram of the experimental setup with the components of gravity normal and parallel to the solid surface is shown in Figure 4. The angle at which the droplet rolls off the surface, or sliding angle , is shown in Equation (6) [14]:
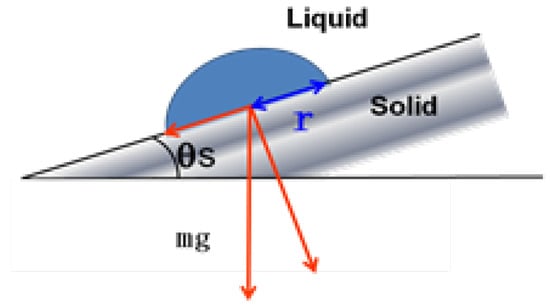
Figure 4.
Schematic description of a water drop on a tilted solid surface.
Here, = 0 when . In this case, when the sliding angle is equal to 0, no energy is required to remove a supercooled-water droplet removed from a hydrophobic surface. A lower indicates a better anti-icing coating, as it implies a lower force necessary to remove the droplet. There is a temperature dependency similar to the one seen in the contact angle equation, but it is multiplied by factors related to the force due to gravity and the difference between advancing and receding contact angles. However, as in the static-evaluation test, the terms containing the temperature dependency will still be small due to the high critical temperature of water.
2.3. Coating Surface and Experimental Setup
Four different coatings were tested with PTFE particle diameters of 1, 5, 10, and 20 μm. These particle diameter sizes were provided by the manufacturer. The particles were also run through a fine mesh to ensure better uniformity in particle size. Scanning electron microscope images of these coatings are shown in Figure 5. Each coating was created by mixing the PTFE particles with a methyl silicone oligomer hardener and hydrofluoroether, a fluorinated solvent, and then applied to a 5 mm × 5 mm aluminum plate via an air paint spray gun.

Figure 5.
Scanning electron microscope pictures of coatings with various particle sizes.
Both the static contact angles and the sliding angles for the various coatings were measured in a temperature-controlled room under supercooled conditions (Figure 6). The temperature was varied from −10 to 0 °C to study conditions where supercooled droplet freezing occurs. An 11 μL droplet of supercooled water was applied on the aluminum plate using a syringe. The angles were determined from image acquisition software from a digital camera. For the static test, the contact angle measurements were taken once the droplet had reached a steady-state position. These angles were measures using Famas analysis software. For the dynamic evaluation, the coated plate was angled after the droplet was applied. Images of the droplet were taken while the plate was rotated until the droplet began to roll on the plate. The frame rate for the camera was 500 frames per second. The angle measurement for both the static and dynamic tests was performed 10 times to reduce uncertainty. During the tests, the humidity in the chamber was minimized to avoid any wetting on the surface of the coatings. Tests were performed so that the droplet was disturbed as little as possible to prevent crystallization.
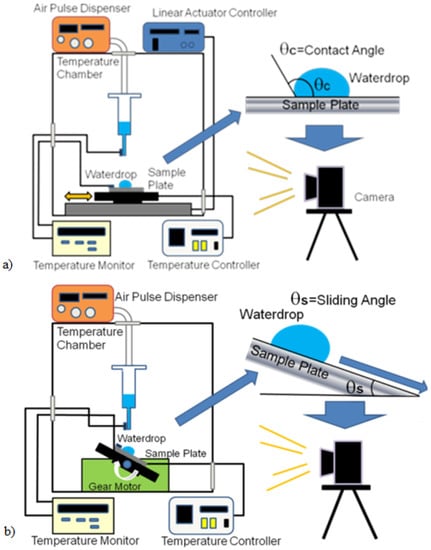
Figure 6.
Schematic description of (a) the static- and (b) dynamic-angle measurement setups.
3. Results and Discussion
3.1. Static-Evaluation Results: Contact Angle under Supercooled Conditions
Figure 7 shows the static contact angle, , for the various hydrophobic coatings evaluated. It was approximately 140° for each coating and the change in the angle was less than 2.2°, well within uncertainty bounds. As shown in Equation (5), the contact angle is a product of the properties of the interface between the liquid and the solid surface and is governed by ambient pressure and molecular forces due to their impact on the work of adhesion. The contact angle does not appear to be at all impacted by the number or size of interfaces between the coating and the droplet surfaces and remains unaffected by changes in the PTFE particle size.
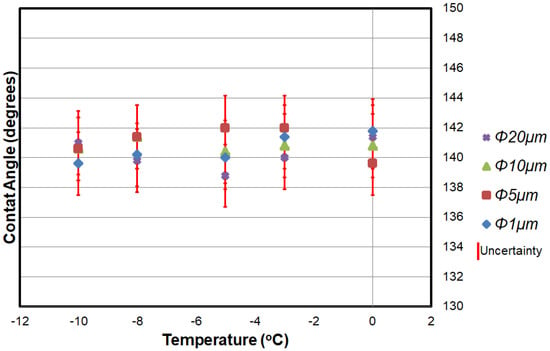
Figure 7.
Static-evaluation results related to the temperature.
The temperature also has little to no impact on the contact angle, due to the fact that the range of temperatures studied (10 °C) is very small compared to the critical temperature of water, and accounts for less than a 2% change in the temperature dependent terms of Equations (4) and (5). While temperature does modify some of the water droplet properties, most of these changes manifest themselves in the viscosity, which does not play a role in a static test where the velocity of the fluid is negligible, as evidenced by the fact that the only fluid property that appears in Equation (5) is critical temperature. This does not mean that the hydrophobicity of the surface is not affected by temperature or particle size, only that it cannot be observed in a static test.
3.2. Dynamic-Evaluation Results: Sliding Angle under Supercooled Conditions
Figure 8 shows the sliding angle, , related to temperature for the various coatings tested. Temperature did have an impact on the results, with a decrease in temperature generally leading to an increase in the sliding angle. However, the coatings with larger particle sizes (10 and 20 μm) had much smaller sliding angles. The greatest decrease in sliding angle came between the 10 and 20 μm where the average contact angle decreased by a factor of a least 1.71, with a decrease of up to 2.4 at lower temperatures.
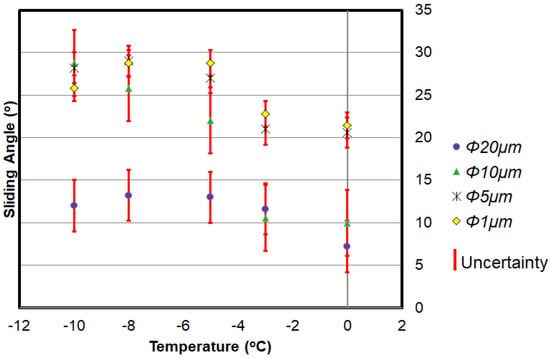
Figure 8.
Dynamic-evaluation results related to the temperature.
The sliding angle was changed much more drastically by PTFE particle size than contact angle, because it is a more direct measure of the force required to remove a water droplet from a surface, shown by the force term in Equation (6). There are several forces acting on the water droplet including solid–liquid and liquid–gas interactions. Because the wetting conditions for PTFE coatings are assumed to be consistent with the Cassie-Baxter state, solid–liquid interactions, which are the main interactions which anchor the droplet to the surface, are only at the tops of the particles (Figure 2). For larger PTFE particle sizes, the area of the surface actually in contact with the droplet is greatly reduced, which leads to substantially less adhesive force keeping the droplet on the surface. As shown in Equations (1) and (2), an increase in the radius of the PTFE particle causes a decrease in n, and thus a decrease in the water contact ratio.
The SEM microscope images also demonstrate this connection between particle size and area in contact with the droplet (Figure 5). The 1 μm is far smoother than the 20 μm coating, and may contain more exposed polymer, as well as much more area in contact with the water droplet. This increased area leads to a decrease in the hydrophobicity of the surface.
A decrease in temperature led to an increase in sliding angle for all particle sizes within uncertainty bounds. As in the static evaluation, temperature dependent terms in Equations (4) and (6) are small due to the high critical temperature of water. Because of this, changes in sliding angle must be due to other effects. An increase in the sliding angle may be due more to changes in droplet properties than changes in the interface. Because the viscosity of water increases with a decrease in temperature [19,20], a decrease in temperature would require an increase in the force required to deform the water and cause it to start rolling. While temperature has an impact on the measured sliding angle, it does not necessarily dramatically impact the hydrophobicity of the surface itself. As shown by Ruijter and others, there is a very weak relationship between the free energy of wetting and temperature [21], and so it is unlikely that a change in hydrophobicity causes this change in sliding angle.
These findings are consistent with the idea that free energy of hydration increases with particle size, leading to more hydrophobic characteristics [22]. It is also consistent with the study performed by Caban-Nevarez and Perez which determined that a decrease in nanocrystalline talc particle size related to a decrease in hydrophobic characteristics [23].
4. Conclusions
Both static and dynamic methods were used to test the effectiveness of hydrophobic coatings of various particle sizes, ranging from 1 to 20 μm in diameter. For the static method, neither temperature nor particle size had an impact on the measured contact angle of the coating. For the dynamic method, an increase in particle size corresponded to a decrease in the sliding angle. This can be attributed to the decreased interface between the coating surface and the droplet. Coatings with larger particle sizes are more hydrophobic under all conditions tested, from −10 to 0 °C. Specifically, coatings composed of particles with a 20 μm diameter had a sliding angle of less than 15°, the lowest out of all the coatings tested. Temperature had much less of an effect on the hydrophobicity of the surface than PTFE particle size, due to the low impact temperature has on the surface tension at the liquid surface interface. While temperature does impact the sliding angle of the surface, this can mostly be attributed to the impact of temperature on water properties such as viscosity. PTFE particle size does not have any noticeable impact on the surface tension either, as evidenced by the lack of change in the contact angle, but an increase in PTFE particle size does dramatically decrease the total area of interaction between the fluid and the solid surface. This decrease in the area of interaction leads to a decrease in the energy required to remove a droplet, and thus an increase in the overall hydrophobicity of the surface.
Author Contributions
K.M. contributed to the concept, evaluation, and writing of the present work; J.G. contributed to the evaluation and writing of the present work; Hirotaka Sakaue contributed to the concept, supervision, and the final edit of the present work.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, D.; Song, B.; Hu, H.; Du, X.; Du, P.; Choi, C.-H.; Rothstein, J.P. Effect of a surface tension gradient on the slip flow along a superhydrophobic air-water interface. Phys. Rev. Fluids 2018, 3, 033303. [Google Scholar] [CrossRef]
- Quere, D. Wetting and roughness. Ann. Rev. Mater. Res. 2008, 38, 71–99. [Google Scholar] [CrossRef]
- Rothstein, J. Slip on superhydrophobic surfaces. Ann. Rev. Fluid Mech. 2010, 42, 89–109. [Google Scholar] [CrossRef]
- Zhang, B.; Chen, X.; Dobnikar, J.; Wang, Z.; Zhang, X. Spontaneous Wenzel to Cassie cewetting transition on structured surfaces. Phys. Rev. Fluids 2016, 1, 073904. [Google Scholar] [CrossRef]
- Amabili, M.; Giacomello, A.; Meloni, S.; Casciola, C.M. Collapse of superhydrophobicity on nanopillared surfaces. Phys. Rev. Fluids 2017, 2, 034202. [Google Scholar] [CrossRef]
- Johnson, R.E.; Detter, R.H. Contact Angle Hysteresis. In Contact Angle, Wettability, and Adhesion; American Chemical Society: Washington, DC, USA, 1964; pp. 112–135. [Google Scholar]
- Diaz, M.E.; Savage, M.D.; Cerro, R.L. Prediction of static contact angles on the basis of molecular forces and adsorption data. Phys. Rev. E 2016, 94, 022801. [Google Scholar] [CrossRef] [PubMed]
- Varchanis, S.; Dimakopoulos, Y.; Tsamopoulos, J. Steady film flow over a substrate with rectangular trenches forming air inclusions. Phys. Rev. Fluids 2017, 2, 124001. [Google Scholar] [CrossRef]
- De Coninck, J.; Dunlop, F.; Huillet, T. Contact angles of a drop pinned on an incline. Phys. Rev. E 2017, 95, 052805. [Google Scholar] [CrossRef] [PubMed]
- Onda, T.; Shibuichi, S.; Satoh, N.; Tsujii, K. Super-water-repellent fractal surfaces. ACS J. Surf. Colloids 1996, 12, 2125–2127. [Google Scholar] [CrossRef]
- Lafuma, A.; Quere, D. Superhydrophobic states. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Menini, R.; Farzaneh, M. Elaboration of Al2O3/PTFE icephobic coatings for protecting aluminum surfaces. Surf. Coat. Technol. 2009, 203, 1941–1946. [Google Scholar] [CrossRef]
- Veeramasuneni, S.; Drelich, J.; Miller, J.; Yamauchi, G. Hydrophobicity of ion-plated PTFE coatings. Prog. Org. Coat. 1997, 31, 265–270. [Google Scholar] [CrossRef]
- Morita, K.; Sakaue, H. Characterization method of hydrophobic anti-icing coatings. Rev. Sci. Instrum. 2015, 86, 115108. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Liu, Y.; Wang, C. Development and evaluation of electroless Ag-PTFE composite coatings with anti-microbial and anti-corrosion properties. Appl. Surf. Sci. 2005, 252, 1620–1627. [Google Scholar] [CrossRef]
- Ling, H.; Katz, J.; Fu, M.; Hultmark, M. Effect of reynolds number and saturation level on gas diffusion in and out of a superhydrophobic surface. Phys. Rev. Fluids 2017, 2, 124005. [Google Scholar] [CrossRef]
- Hernandez-Perez, R.; García-Cordero, J.L.; Escobar, J.V. Simple scaling laws for the evaporation of droplets pinned on pillars: Transfer-rate- and diffusion-limited regimes. Phys. Rev. Fluids 2017, 96, 062803. [Google Scholar] [CrossRef] [PubMed]
- Weisend, N.A. Design of an advanced pneumatic deicer for the composite rotor blade. J. Aircr. 1989, 26, 947–950. [Google Scholar] [CrossRef]
- Zwolinski, B.J.; Eicher, L.D. High-precision viscosity of supercooled water and analysis of the extended range temperature coefficient. J. Phys. Chem. 1971, 75, 2016–2024. [Google Scholar] [CrossRef]
- Hallett, J. The temperature dependence of the viscosity of supercooled water. Proc. Phys. Soc. 1963, 82, 1046. [Google Scholar] [CrossRef]
- De Ruijter, M.; Kölsch, P.; Voué, M.; Coninck, J.D.; Rabe, J. Effect of temperature on the dynamic contact angle. Colloids Surf. A Physicochem. Eng. Asp. 1998, 144, 235–243. [Google Scholar] [CrossRef]
- Chiu, C.C.; Moore, P.B.; Shinoda, W.; Nielsen, S.O. Size-dependent hydrophobic to hydrophilic transition for nanoparticles: A molecular dynamics study. J. Chem. Phys. 2009, 131, 244706. [Google Scholar] [CrossRef] [PubMed]
- Caban-Nevarez, R.; Perales Perez, O.J. Size-dependence hydrophobicity in nanocrystalline talc produced by high-intensity planetary ball milling. MRS Proc. 2015, 1805. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).