Application of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings
Abstract
:1. Introduction
- The in-plane and through-thickness thermal conductivities κx and κy;
- The in-plane and through-thickness dilatation coefficients αx and αy;
- The 4 values of the above mechanical constitutive law Ex, Ey, νxy, νyx.
2. Mechanical Constitutive Law
3. FEM Numerical Method
- Generation of each cell independently with a given material depending on its color + gluing of the different elements;
- Generation of all nodes and edges first to avoid the gluing operation that may be long.
4. Materials Properties
5. Coating Microstructures
6. Numerical Results
6.1. Thermal Aspects
6.2. Strains and Stresses
6.3. Effective Homogenized Properties
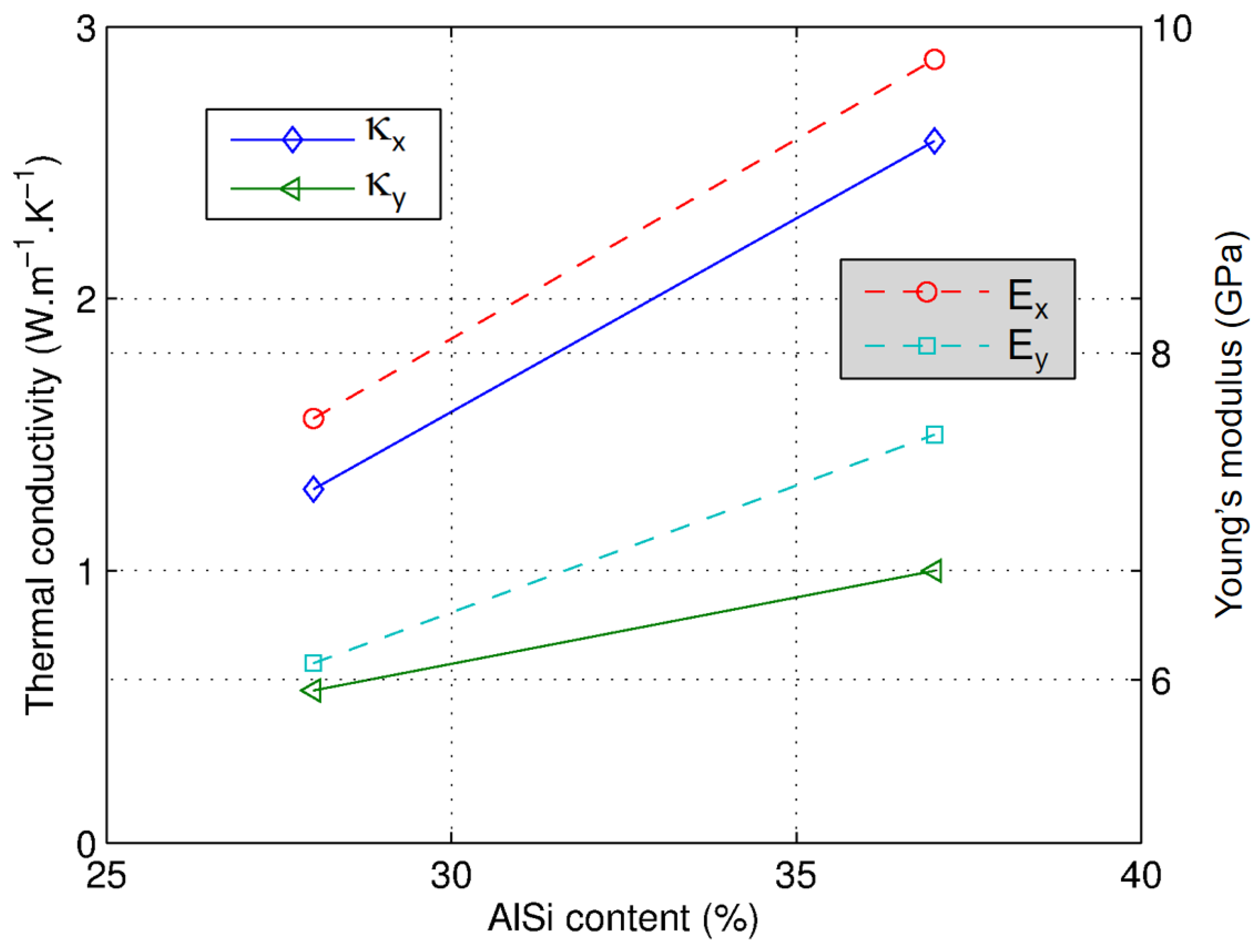
6.4. Effect of the Polyester Content
7. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| κ | thermal conductivity, W·m−1·K−1 |
| α | dilatation coefficient, µm·m−1·K−1 |
| E | Young’s modulus, GPa |
| ν | Poisson’s ratio |
| φ | thermal flux, W |
| ε | strain |
| σ | stress, MPa |
| F | force, N |
| U | displacement, m |
| Subscripts | |
| x | in-plane property |
| y | through-thickness property |
References
- OOF: Finite Element Analysis of Microstructures. Available online: http://www.ctcms.nist.gov/oof/ (accessed on 23 June 2017).
- Langer, S.A.; Fuller, E.; Carter, W.C. OOF: An image-based finite-element analysis of material microstructures. Comput. Sci. Eng. 2001, 3, 15–23. [Google Scholar] [CrossRef]
- Kulkarni, A.; Wang, Z.; Nakamura, T.; Sampath, S.; Goland, A.; Herman, H.; Allen, J.; Ilavsky, J.; Long, G.; Frahm, J.; et al. Comprehensive microstructural characterization and predictive property modeling of plasma-sprayed zirconia coatings. Acta Mater. 2003, 51, 2457–2475. [Google Scholar] [CrossRef]
- Wang, Z.; Kulkarni, A.; Deshpande, S.; Nakamura, T.; Herman, H. Effects of pores and interfaces on effective properties of plasma sprayed zirconia coatings. Acta Mater. 2003, 51, 5319–5334. [Google Scholar] [CrossRef]
- Tan, Y.; Longtin, J.P.; Sampath, S. Modeling thermal conductivity of thermal spray coatings: Comparing predictions to experiments. In Proceedings of the International Thermal Spray Conference, Seattle, WA, USA, 15–18 May 2006. [Google Scholar]
- Michlik, P.; Berndt, C.C. Image-based extended finite element modeling of thermal barrier coatings. Surf. Coat. Techol. 2006, 201, 2369–2380. [Google Scholar] [CrossRef]
- Jadhav, A.D.; Padture, N.P.; Jordan, E.H.; Gell, M.; Miranzo, P.; Fuller, E.R., Jr. Low-thermal-conductivity plasma-sprayed thermal barrier coatings with engineered microstructures. Acta Mater. 2006, 54, 3343–3349. [Google Scholar] [CrossRef]
- Faraoun, H.I.; Seichepine, J.L.; Coddet, C.; Aourag, H.; Zwick, J.; Hopkins, N.; Sporer, D.; Hertter, M. Modelling route for abradable coatings. Surf. Coat. Technol. 2006, 200, 6578–6582. [Google Scholar] [CrossRef]
- Reid, A.C.E.; Langer, S.A.; Lua, R.C.; Coffman, V.R.; Haan, S.I.; Garcia, R.E. Image-based finite element mesh construction for material microstructures. Comput. Mater. Sci. 2008, 43, 989–999. [Google Scholar] [CrossRef]
- Bolot, R.; Seichepine, J.L.; Qiao, J.H.; Coddet, C. Predicting the thermal conductivity of AlSi/Polyester abradable coatings: Effects of the numerical method. J. Therm. Spray Technol. 2011, 20, 39–47. [Google Scholar] [CrossRef]
- Gupta, M.; Curry, N.; Nylén, P.; Markocsan, N.; Vaßen, R. Design of next generation thermal barrier coatings—experiments and modelling. Surf. Coat. Technol. 2013, 220, 20–26. [Google Scholar] [CrossRef]
- Tillmann, W.; Klusemann, B.; Nebel, J.; Svendsen, B. Analysis of the mechanical properties of an arc-sprayed WC-FeCSiMn coating: Nanoindentation and simulation. J. Therm. Spray Technol. 2011, 20, 328–335. [Google Scholar] [CrossRef]
- Klusemann, B.; Denzer, R.; Svendsen, B. Microstructure-based modeling of residual stresses in WC-12Co-sprayed coatings. J. Therm. Spray Technol. 2012, 21, 96–107. [Google Scholar] [CrossRef]
- Wiederkehr, T.; Klusemann, B.; Gies, D.; Müller, H.; Svendsen, B. An image morphing method for 3D reconstruction and FE-analysis of pore networks in thermal spray coatings. Comput. Mater. Sci. 2010, 47, 881–889. [Google Scholar] [CrossRef]
- Bobzin, K.; Kopp, N.; Warda, T.; Öte, M. Determination of the effective properties of thermal spray coatings using 2D and 3D models. J. Therm. Spray Technol. 2012, 21, 1269–1277. [Google Scholar] [CrossRef]
- Qiao, J.H.; Bolot, R.; Liao, H.L.; Coddet, C. Knudsen Effet on the estimation of the effective thermal conductivity of thermal barrier coatings. J. Therm. Spray Technol. 2013, 22, 175–182. [Google Scholar] [CrossRef]
- Qiao, J.H.; Bolot, R.; Liao, H.L.; Bertrand, P.; Coddet, C. A 3D finite-difference model for the effective thermal conductivity of thermal barrier coatings produced by plasma spraying. Int. J. Therm. Sci. 2013, 65, 120–126. [Google Scholar] [CrossRef]
- Qiao, J.H.; Bolot, R.; Liao, H. Finite element modeling of the elastic modulus of thermal barrier coatings. Surf. Coat. Technol. 2013, 220, 170–173. [Google Scholar] [CrossRef]
- Vackel, A.; Dwivedi, G.; Sampath, S. Structurally integrated, damaged-tolerant, thermal spray coatings. JOM 2015, 67, 1540–1553. [Google Scholar] [CrossRef]
- Tan, Y.; Shyam, A.; Choi, W.B.; Lara-Curzio, E.; Sampath, S. Anisotropic elastic properties of thermal spray coatings determined via resonant ultrasound spectroscopy. Acta Mater. 2010, 58, 5305–5315. [Google Scholar] [CrossRef]
- Bolot, R.; Seichepine, J.L.; Coddet, C.; Sporer, D.; Fiala, P.; Bartlett, B. Thermal conductivity of AlSi/Polyester abradable coatings. Weld. Cut. 2009, 8, 104–109. [Google Scholar]
- Duramou, Y.; Bolot, R.; Seichepine, J.-L.; Danlos, Y.; Bertrand, P.; Montavon, G.; Selezneff, S. Relationships between microstructural and mechanical properties of plasma sprayed AlSi-Polyester composite coatings: Application to abradable materials. Key Eng. Mater. 2014, 606, 155–158. [Google Scholar] [CrossRef]
- CES Selector Edupack 2014. Available online: http://www.grantadesign.com/products/ces/ (accessed on 23 June 2017).
- Ekonol® Polyester Fillers for PTFE Seals & Bearings. Available online: http://www.coatingsolutions.saint-gobain.com/ekonol.aspx (accessed on 23 June 2017).
- DSMTS_0016.5. Material Product Data Sheet, Aluminum Silicon Polymer Thermal Spray Powders. Available online: https://www.oerlikon.com/ecomaXL/files/metco/oerlikon_DSMTS-0016.5_AlSi-Poly.pdf (accessed on 23 June 2017).


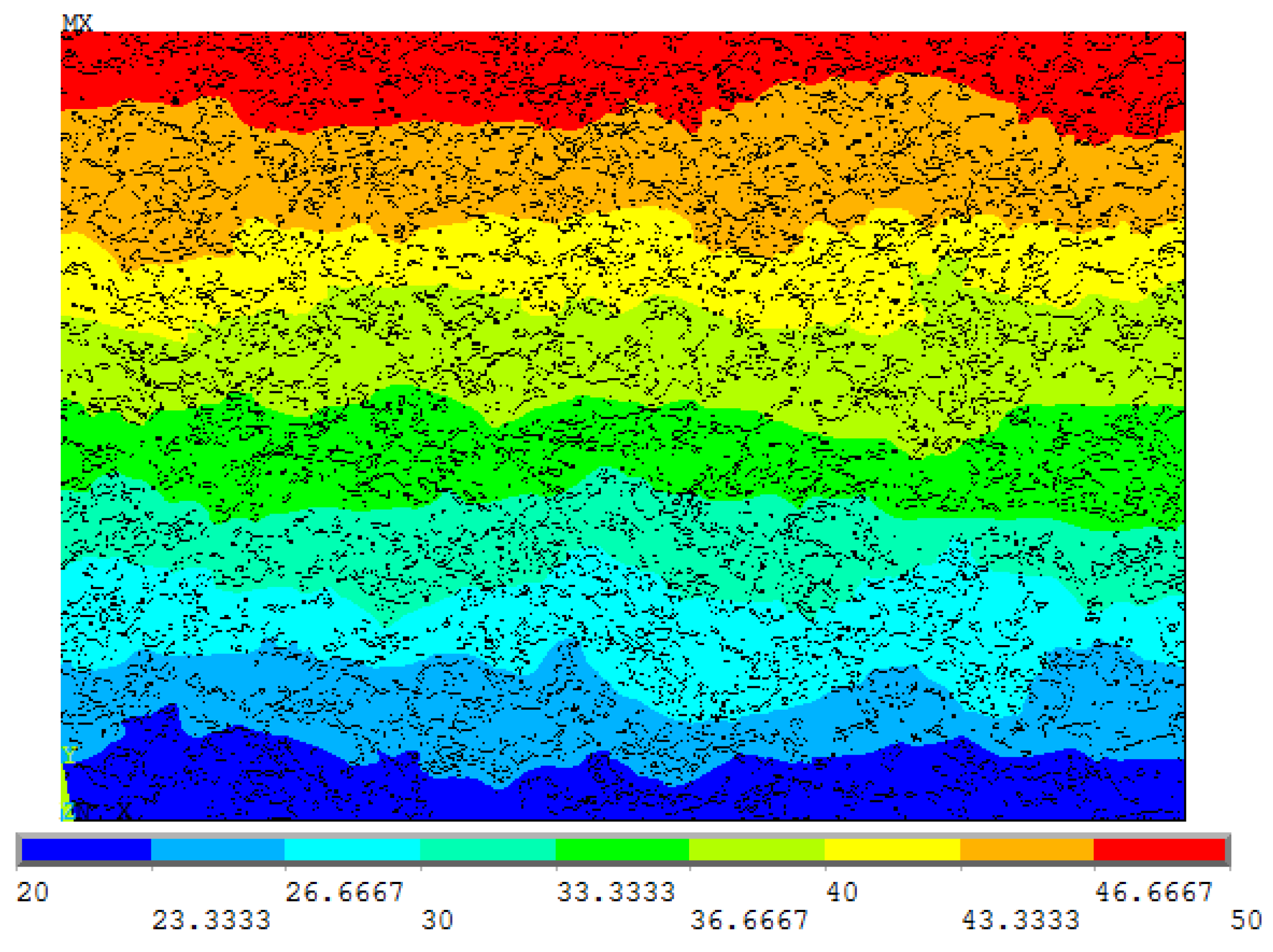


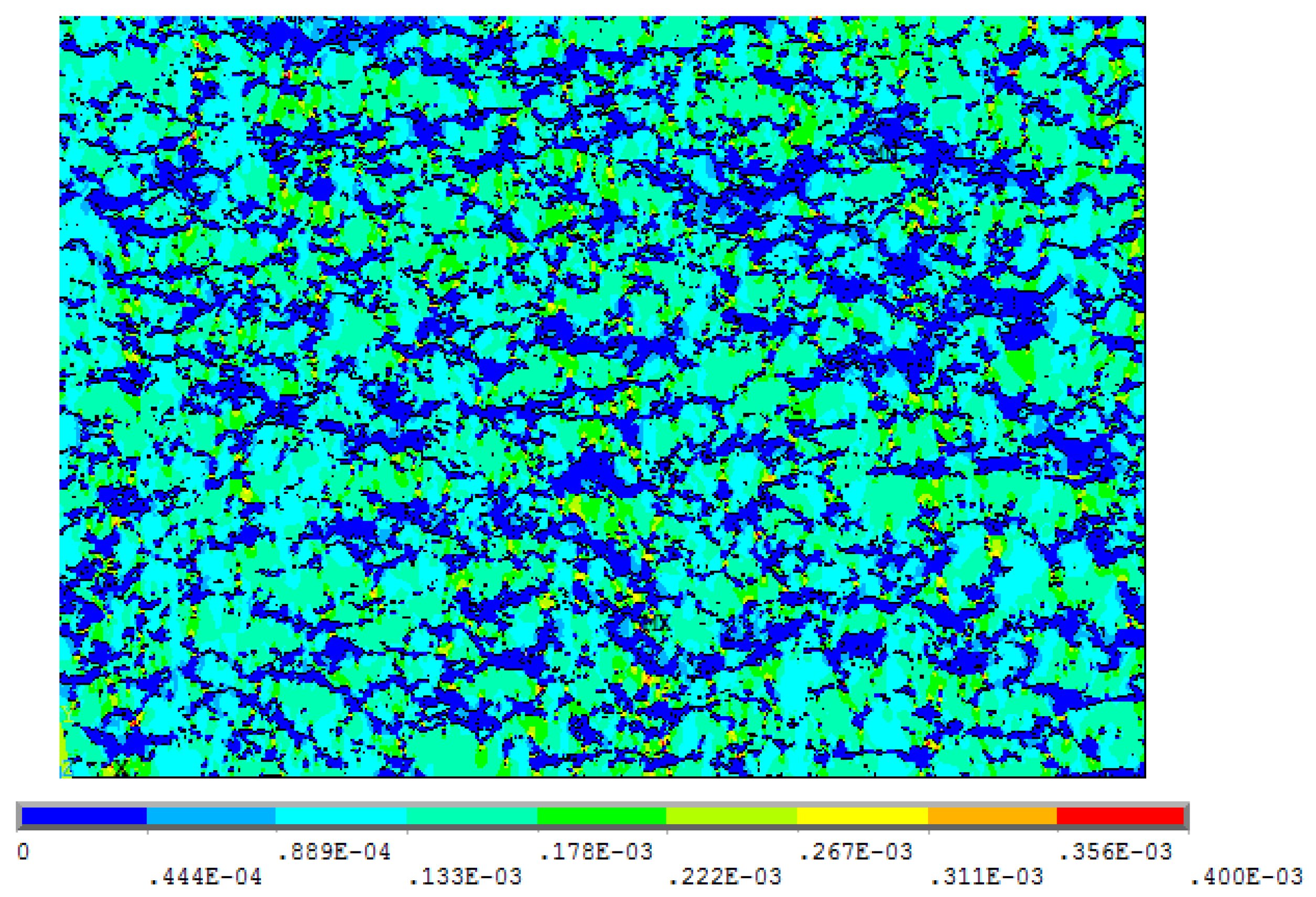
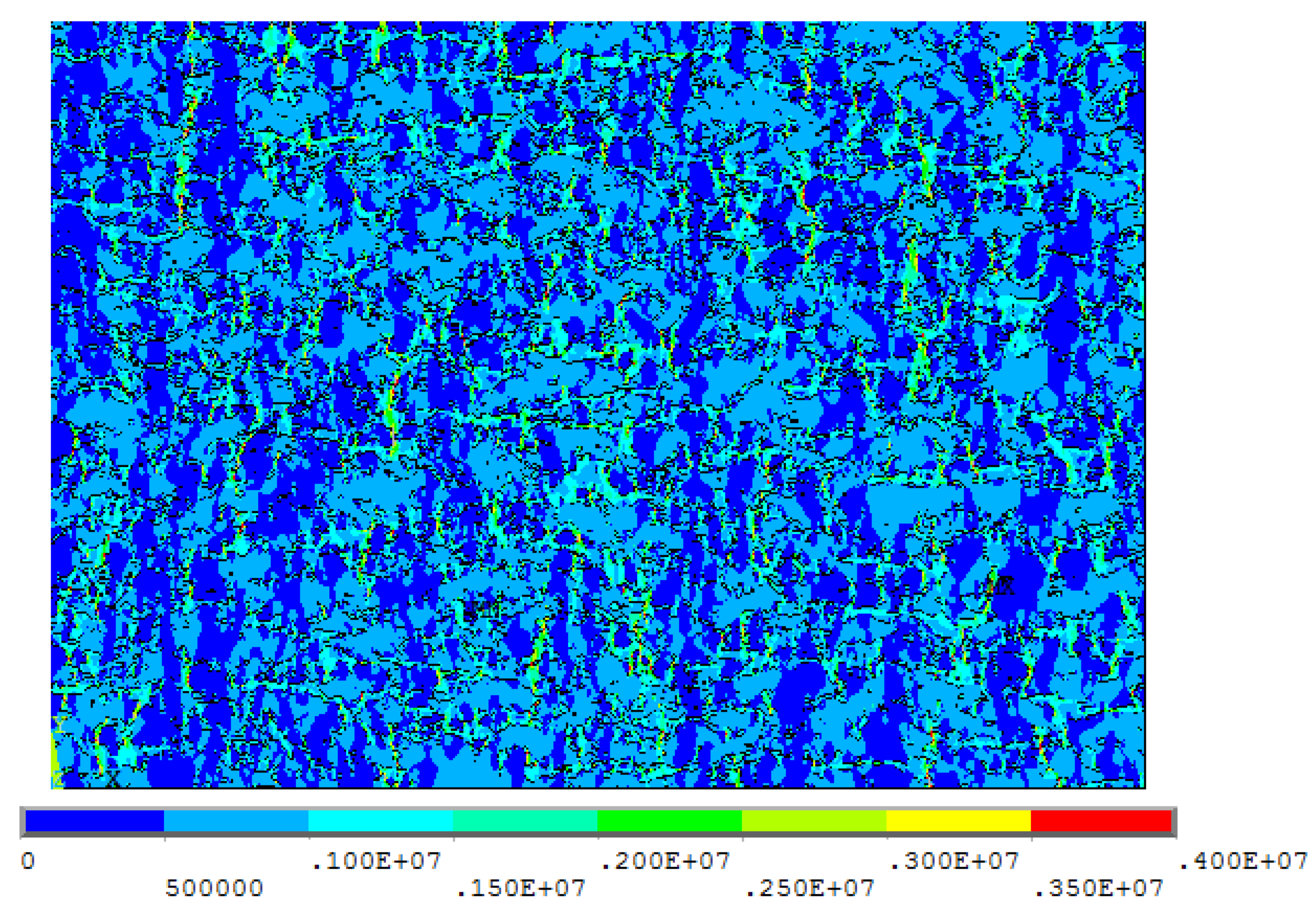

| List of Sets | Top Line | Bottom Line | Left Line | Right Line | Result |
|---|---|---|---|---|---|
| Set 1 | T = 50 °C | T = 20 °C | free | free | κy |
| Set 2 | free | free | T = 50°C | T = 20 °C | κx |
| Set 3 | free | Uy = 0 | Ux = 0 | Ux/W = ε | Ex |
| Set 4 | Uy/H = ε | Uy = 0 | Ux = 0 | free | Ey |
| Set 5 | Uy = 0 | Uy = 0 | Ux = 0 | Ux/W = ε | νxy |
| Set 6 * | Uy/H = ε | Uy = 0 | Ux = 0 | Ux = 0 | νyx |
| Set 7 | free | Uy = 0 | Ux = 0 | Ux = 0 | αx |
| Set 8 | Uy = 0 | Uy = 0 | Ux = 0 | free | αy |
| Loading Case | Applied Formulas |
|---|---|
| Set 1 | |
| Set 2 | |
| Set 3 | |
| Set 4 | |
| Set 5 | |
| Set 6 | |
| Set 7 | |
| Set 8 |
| Material | Thermal Conductivity (W·m−1·K−1) | Young’s Modulus (GPa) | Poisson’s Ratio | Dilatation Coefficient | Density (kg·m−3) |
|---|---|---|---|---|---|
| Al12Si | 130 | 71 | 0.34 | 20.5 | 2660 |
| Polyester | 0.17 [10,21] | 3.5* [22] | 0.4 [23] | 59 [24] | 1440 [24] |
| Effective Property | Value |
|---|---|
| Effective thermal conductivities (W·m−1·K−1) | κy = 0.556 |
| κx = 1.30 | |
| Effective Young’s modulus (GPa) | Ex = 7.6 |
| Ey = 6.1 | |
| Poisson’s ratios | νxy = 0.395 |
| νyx = 0.32 | |
| Dilatation coefficients (µm·m−1·K−1) | αx = 37.2 |
| αy = 44.7 |
| Effective Property | AlSi Content (vol %) | |
|---|---|---|
| 28% | 37% | |
| κx (W·m−1·K−1) | 1.30 | 2.58 |
| κy (W·m−1·K−1) | 0.56 | 1.00 |
| Ex (GPa) | 7.6 | 9.8 |
| Ey (GPa) | 6.1 | 7.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bolot, R.; Aussavy, D.; Montavon, G. Application of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings. Coatings 2017, 7, 91. https://doi.org/10.3390/coatings7070091
Bolot R, Aussavy D, Montavon G. Application of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings. Coatings. 2017; 7(7):91. https://doi.org/10.3390/coatings7070091
Chicago/Turabian StyleBolot, Rodolphe, Delphine Aussavy, and Ghislain Montavon. 2017. "Application of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings" Coatings 7, no. 7: 91. https://doi.org/10.3390/coatings7070091
APA StyleBolot, R., Aussavy, D., & Montavon, G. (2017). Application of FEM to Estimate Thermo-Mechanical Properties of Plasma Sprayed Composite Coatings. Coatings, 7(7), 91. https://doi.org/10.3390/coatings7070091




