Strain Effects by Surface Oxidation of Cu3N Thin Films Deposited by DC Magnetron Sputtering
Abstract
:1. Introduction
2. Materials and Methods
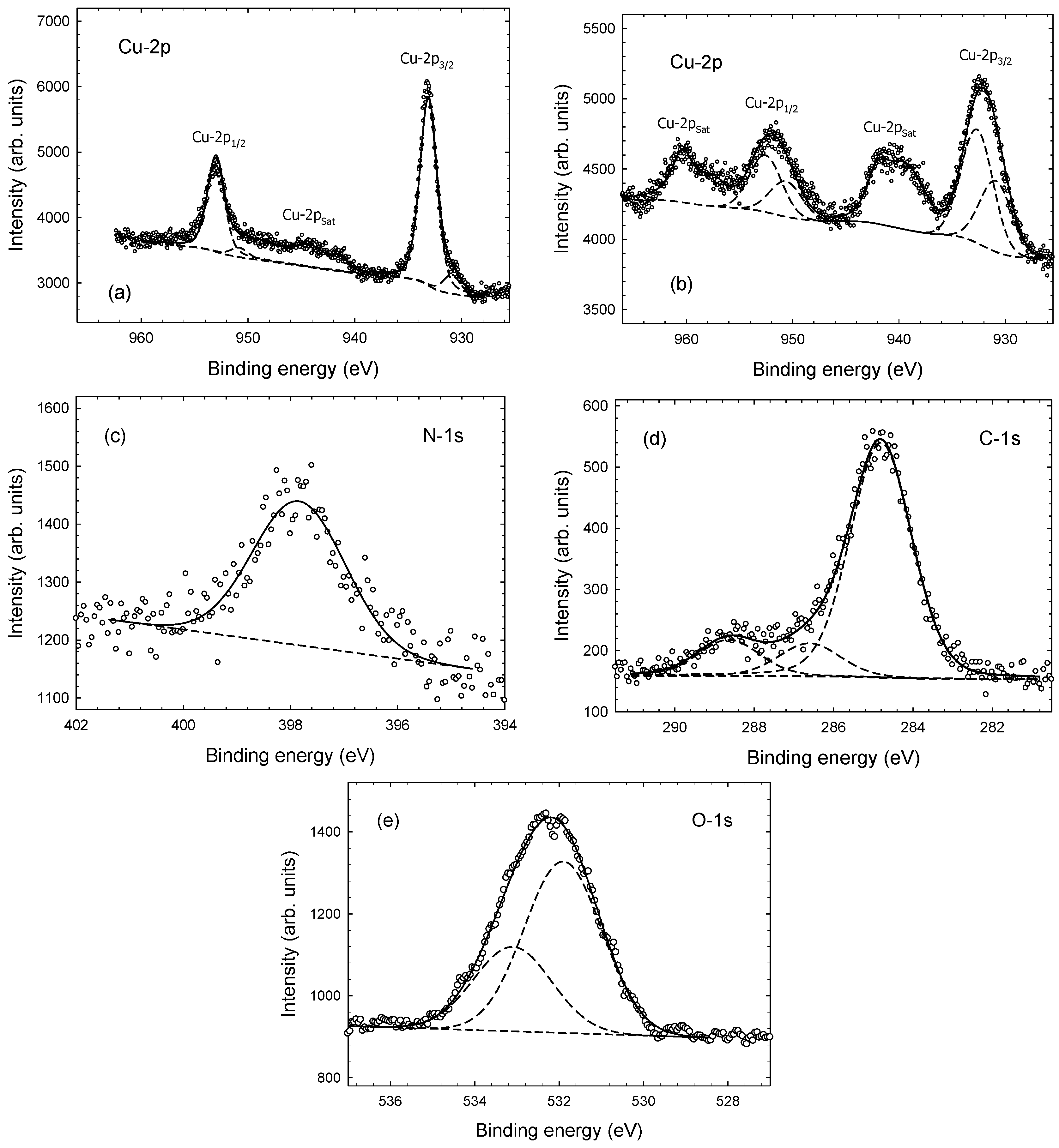
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Maruyama, T.; Morishita, T. Copper nitride and tin nitride thin films for write-once optical recording media. Appl. Phys. Lett. 1996, 69, 890–891. [Google Scholar] [CrossRef]
- Ma, X.D.; Bazhanov, D.I.; Fruchart, O.; Yildiz, F.; Tokoyama, T.; Przybyiski, M.; Stepanyuk, V.S.; Hergert, W.; Kirschner, M. Strain relief guided growth of atomic nanowires in a Cu3N-Cu(110) molecular network. Phys. Rev. Lett. 2009, 102, 205503. [Google Scholar] [CrossRef] [PubMed]
- Borsa, D.M.; Grachev, S.; Presura, C.O.; Boerma, D.O. Growth and properties of Cu3N films and Cu3N/γ′-Fe4N bilayers. Appl. Phys. Lett. 2002, 80, 1823–1825. [Google Scholar] [CrossRef]
- Maya, L. Covalent nitrides for maskless laser writing of microscopic metal lines. MRS Proc. 1992, 282, 203–208. [Google Scholar] [CrossRef]
- Maruyama, T.; Morishita, T. Copper nitride thin films prepared by radio-frequency reactive sputtering. J. Appl. Phys. 1995, 78, 4104–4107. [Google Scholar] [CrossRef]
- Kamat, H.; Wang, X.; Parry, J.; Qin, Y.; Zeng, H. Synthesis and characterization of copper-iron-nitride thin films. MRS Adv. 2016, 1, 203–208. [Google Scholar] [CrossRef]
- Ji, X.; Ju, H.; Zou, T.; Luo, J.; Hong, K.; Yang, H.; Wang, H. Effects of sputtering pressure on Cu3N thin films by reactive radio frequency magnetron sputtering. Adv. Mater. Res. 2015, 1105, 74–77. [Google Scholar] [CrossRef]
- Leng, J.; Chen, L.; Zhu, X.; Sun, Z. Structure and photoelectric properties of Cu3N thin films by reactive magnetron sputtering. Mater. Sci. Forum 2015, 814, 620–624. [Google Scholar] [CrossRef]
- Chen, L.; Leng, J.; Yang, Z.; Meng, Z.; Sun, B. Influence of sputtering power on the structure, optical and electric properties of Cu3N films. Mater. Sci. Forum 2015, 814, 596–600. [Google Scholar] [CrossRef]
- Soukup, L.; Sicha, M.; Fendrych, F.; Jastrabik, L.; Hubicka, Z.; Studnicka, V.; Wagner, T.; Novak, M. Copper nitride thin films prepared by the RF plasma chemical reactor with low pressure supersonic single and multi-plasma jet system. Surf. Coat. Technol. 1999, 116, 321–326. [Google Scholar] [CrossRef]
- Gallardo-Vega, C.; de la Cruz, W. Study of the structure and electrical properties of the copper nitride thin films deposited by pulsed laser deposition. Appl. Surf. Sci. 2006, 252, 8001–8004. [Google Scholar] [CrossRef]
- Sahoo, G.; Meher, S.R.; Jain, M.K. Room temperature growth of high crystalline quality Cu3N thin films by modified activated reactive evaporation. Mater. Sci. Eng. B 2015, 191, 7–14. [Google Scholar] [CrossRef]
- Wrehde, S.; Quaas, M.; Bogdanowicz, R.; Steffen, H.; Wulff, H.; Hippler, R. Reactive deposition of TiNx layers in a DC-magnetron discharge. Surf. Interface Anal. 2008, 40, 790–793. [Google Scholar] [CrossRef]
- Hippler, R.; Steffen, H.; Quaas, M.; Röwf, T.; Tun, T.M.; Wulff, H. Plasma-Assisted Deposition and Crystal Growth of Thin Indium-Tin-Oxide (ITO) Films. In Advances in Solid State Physics 44; Kramer, B., Ed.; Springer: Heidelberg, Germany, 2004; p. 299. [Google Scholar]
- Bräuer, G.; Szyszka, B.; Vergöhl, M.; Bandorf, R. Magnetron sputtering—Milestones of 30 years. Vacuum 2010, 84, 1354–1359. [Google Scholar] [CrossRef]
- Pflug, A.; Siemers, M.; Melzig, T.; Schäfer, L.; Bräuer, G. Simulation of linear magnetron discharges in 2D and 3D. Surf. Coat. Technol. 2014, 260, 411–416. [Google Scholar] [CrossRef]
- Wulff, H.; Steffen, H. Characterization of Thin Films. In Low Temperature Plasmas; Hippler, R., Kersten, H., Schmidt, M., Schoenbach, K.-H., Eds.; Wiley-VCH: Berlin, Germany, 2008; pp. 329–362. [Google Scholar]
- Inorganic Crystal Structure Database (ICSD); Version 1.9.8; FIZ: Karlsruhe, Germany, 2016.
- Zachwieja, U.; Jacobs, H. Ammonothermalsynthese von Kupfernitrid, Cu3N. J. Less Common Met. 1990, 161, 175–184. [Google Scholar] [CrossRef]
- Navío, C.; Capitán, M.J.; Álvarez, J.; Yndurain, F.; Miranda, R. Intrinsic surface band bending in Cu3N(100) ultrathin films. Phys. Rev. B 2007, 76, 085105. [Google Scholar] [CrossRef]
- Moreno-Armenta, M.G.; Soto, G.; Takenchi, N. Ab initio calculations of non-stoichiometric copper nitride, pure and with palladium. J. Alloys Comp. 2011, 509, 1471–1476. [Google Scholar] [CrossRef]
- Pierson, J.F. Structure and properties of copper nitride films formed by reactive magnetron sputtering. Vacuum 2002, 66, 59–64. [Google Scholar] [CrossRef]
- Janssen, G.C.A.M. Stress and strain in polycrystalline thin films. Thin Solid Films 2007, 515, 6654–6664. [Google Scholar] [CrossRef]
- Weihnacht, V.; Brückner, W. Abnormal grain growth in {111} textured Cu thin films. Thin Solid Films 2002, 418, 136–144. [Google Scholar] [CrossRef]
- Rahmati, A.; Ghoohestani, M.; Badehian, H.; Baizaee, M. Ab initio study of the structural, elastic, electronic and optical properties of Cu3N. Mater. Res. 2014, 17, 303–310. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Stokes, R. A Numerical Fourier-analysis method for the correction of widths and shapes of lines on X-ray powder photographs. Proc. Phys. Soc. 1948, 61, 382–391. [Google Scholar] [CrossRef]
- Warren, B.E.; Averbach, B.L. The effect of cold-work distortion on X-ray patterns. J. Appl. Phys. 1950, 21, 595–599. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Addison-Wesley: Boston, MA, USA, 1969. [Google Scholar]
- Klimanek, P. X-ray diffraction analysis of substructures in plastically deformed BCC materials. J. Phys. IV 1993, 3, 2149–2154. [Google Scholar] [CrossRef]
- Krivoglaz, M.A. X-ray and Neutron Diffraction in Nonideal Crystals; Springer: Berlin, Germany, 1966. [Google Scholar]
- Wilkens, M. The determination of density and distribution of dislocations in deformed single crystals from broadened X-ray diffraction profiles. Phys. Stat. Sol. a 1970, 2, 359–370. [Google Scholar] [CrossRef]
- Thejaswini, H.C.; Bogdanowicz, R.; Danilov, V.; Schäfer, J.; Meichsner, J.; Hippler, R. Deposition and characterization of organic polymer thin films using a dielectric barrier discharge with different C2Hm/N2 (m = 2, 4, 6) gas mixtures. Eur. Phys. J. D 2015, 69, 1–6. [Google Scholar]
- Majumdar, A.; Das, G.; Basvani, K.R.; Heinicke, J.; Hippler, R. Role of nitrogen in the formation of HC-N films by CH4/N2 barrier discharge plasma: Aliphatic tendency. J. Phys. Chem. B 2009, 113, 15734–15741. [Google Scholar] [CrossRef] [PubMed]
- Biesinger, M.C.; Lau, L.W.M.; Gerson, A.R.; Smart, R.S.C. Resolving surface chemical states in XPS analysis of first row transition metals, oxides and hydroxides: Sc, Ti, V, Cu and Zn. Appl. Surf. Sci. 2010, 257, 887–898. [Google Scholar] [CrossRef]
- Wurth, W.; Schneider, C.; Treichler, R.; Umbach, E.; Menzel, D. Evolution of adsorbate core-hole states after bound and continuum primary excitation: Relaxation versus decay. Phys. Rev. B 1987, 35, 7741–7744. [Google Scholar] [CrossRef]
- Wagner, C.D.; Zatko, D.A.; Raymond, R.H. Use of the Oxygen KLL Auger lines in identification of surface chemical states by electron spectroscopy for chemical analysis. Anal. Chem. 1980, 52, 1445–1451. [Google Scholar] [CrossRef]

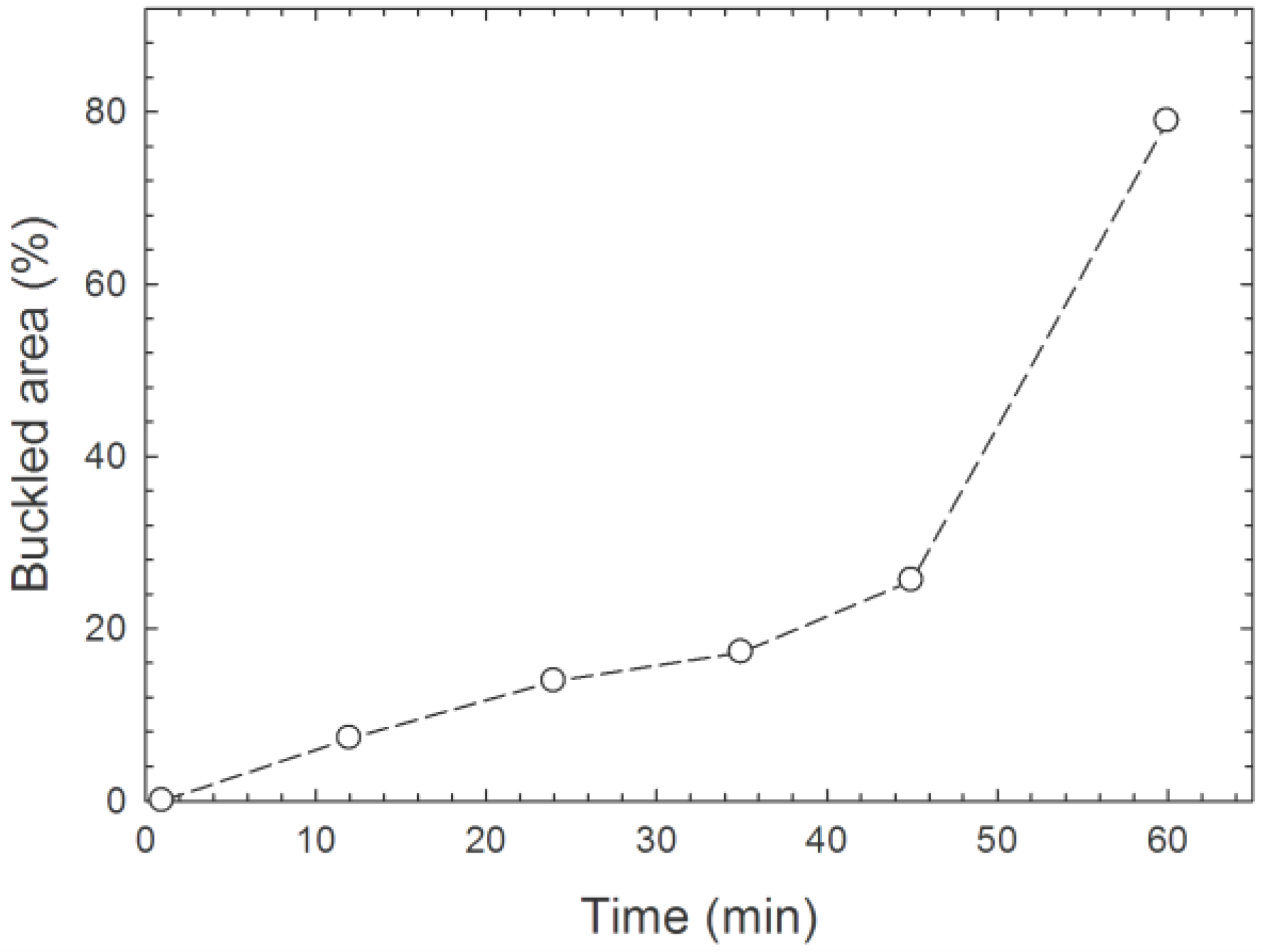

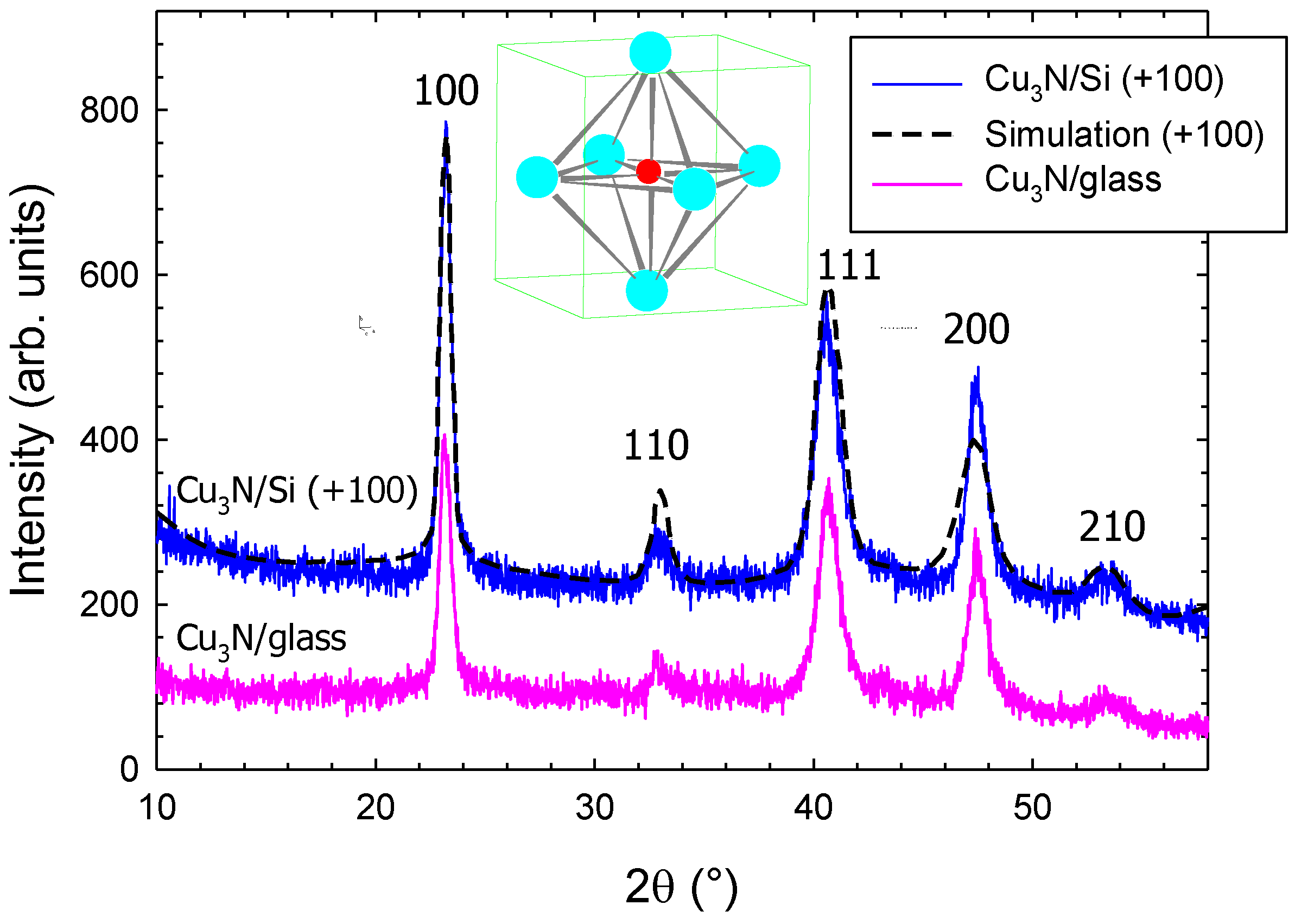
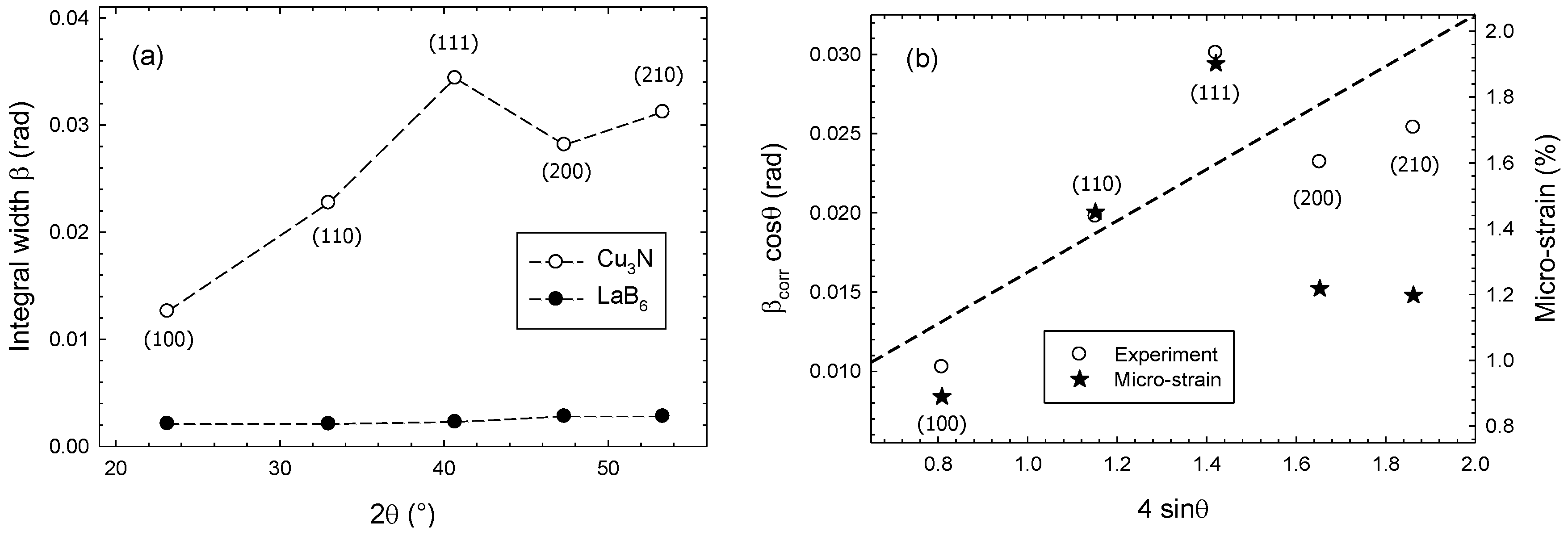
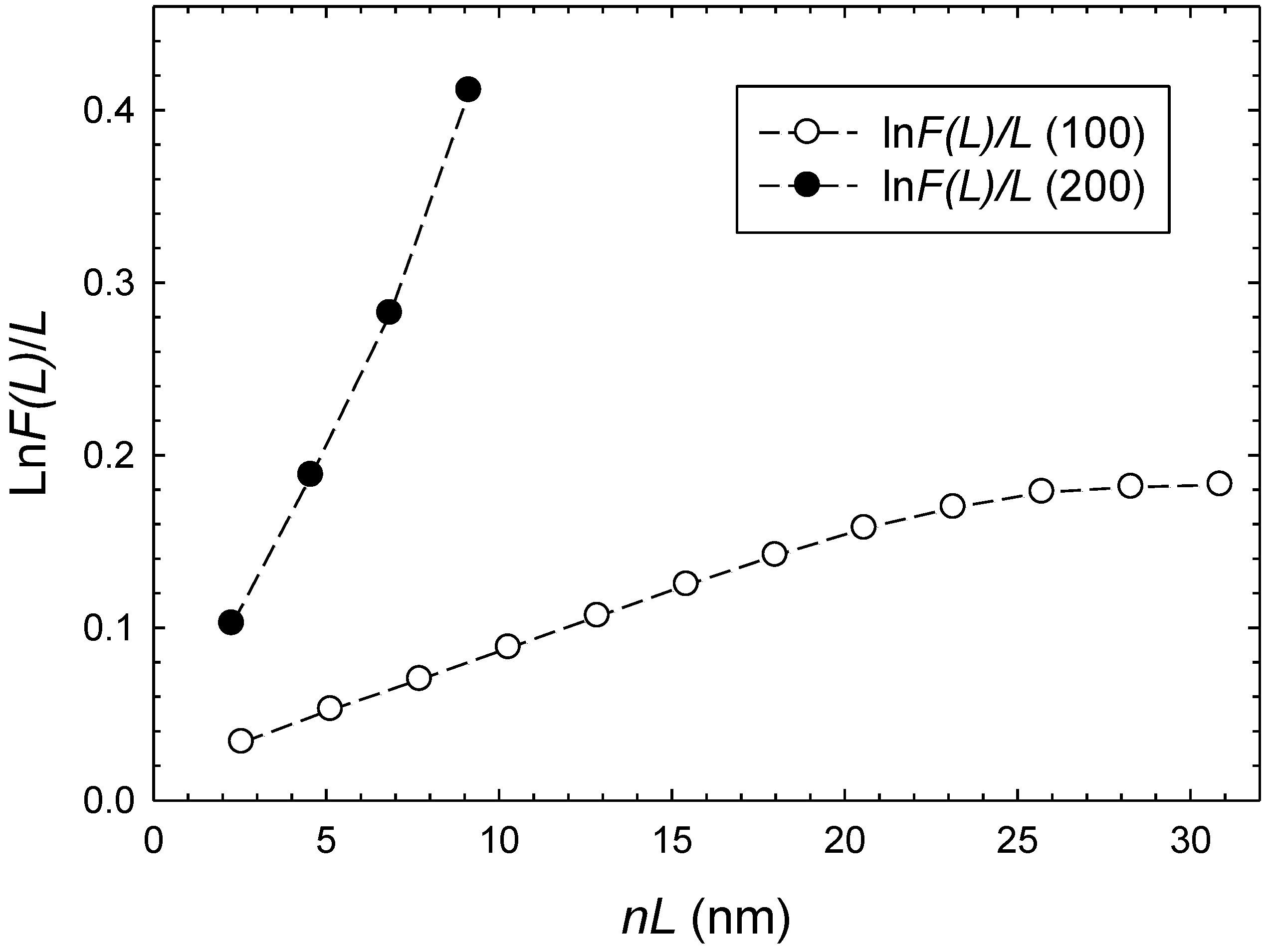
| Sample | HKL | 2θ (°) | D (nm) | Relative Intensity | FWHM (°) |
|---|---|---|---|---|---|
| (a) Cu3N/Si | 100 | 23.166 | 0.3836(4) | 63.0 | 0.621 |
| 110 | 32.993 | 0.2712(8) | 21.9 | 0.938 | |
| 111 | 40.702 | 0.2215(0) | 100.0 | 1.083 | |
| 200 | 47.353 | 0.1918(2) | 60.3 | 1.161 | |
| 210 | 53.355 | 0.1715(7) | 22.2 | 1.200 | |
| (b) Cu3N/glass | 100 | 23.159 | 0.3837(6) | 61.7 | 0.657 |
| 110 | 32.983 | 0.2713(6) | 21.7 | 0.928 | |
| 111 | 40.690 | 0.2215(6) | 100.0 | 1.103 | |
| 200 | 47.338 | 0.1918(8) | 61.0 | 1.243 | |
| 210 | 53.338 | 0.1716(2) | 22.7 | 1.364 |
| Sample | Angle | Cu (%) | N (%) | Cu/N | C (%) | O (%) |
|---|---|---|---|---|---|---|
| CuxN/Si | 90° | 30.4 | 13.8 | 2.2 | 20.4 | 35.5 |
| CuxN/glass | 20° | 10.2 | 4.6 | 2.2 | 41.0 | 44.2 |
| CuxN/glass | 90° | 14.0 | 5.8 | 2.4 | 32.6 | 47.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majumdar, A.; Drache, S.; Wulff, H.; Mukhopadhyay, A.K.; Bhattacharyya, S.; Helm, C.A.; Hippler, R. Strain Effects by Surface Oxidation of Cu3N Thin Films Deposited by DC Magnetron Sputtering. Coatings 2017, 7, 64. https://doi.org/10.3390/coatings7050064
Majumdar A, Drache S, Wulff H, Mukhopadhyay AK, Bhattacharyya S, Helm CA, Hippler R. Strain Effects by Surface Oxidation of Cu3N Thin Films Deposited by DC Magnetron Sputtering. Coatings. 2017; 7(5):64. https://doi.org/10.3390/coatings7050064
Chicago/Turabian StyleMajumdar, Abhijit, Steffen Drache, Harm Wulff, Arun Kumar Mukhopadhyay, Satyaranjan Bhattacharyya, Christiane A. Helm, and Rainer Hippler. 2017. "Strain Effects by Surface Oxidation of Cu3N Thin Films Deposited by DC Magnetron Sputtering" Coatings 7, no. 5: 64. https://doi.org/10.3390/coatings7050064
APA StyleMajumdar, A., Drache, S., Wulff, H., Mukhopadhyay, A. K., Bhattacharyya, S., Helm, C. A., & Hippler, R. (2017). Strain Effects by Surface Oxidation of Cu3N Thin Films Deposited by DC Magnetron Sputtering. Coatings, 7(5), 64. https://doi.org/10.3390/coatings7050064







