Investigation of Droplet Atomization and Evaporation in Solution Precursor Plasma Spray Coating
Abstract
1. Introduction
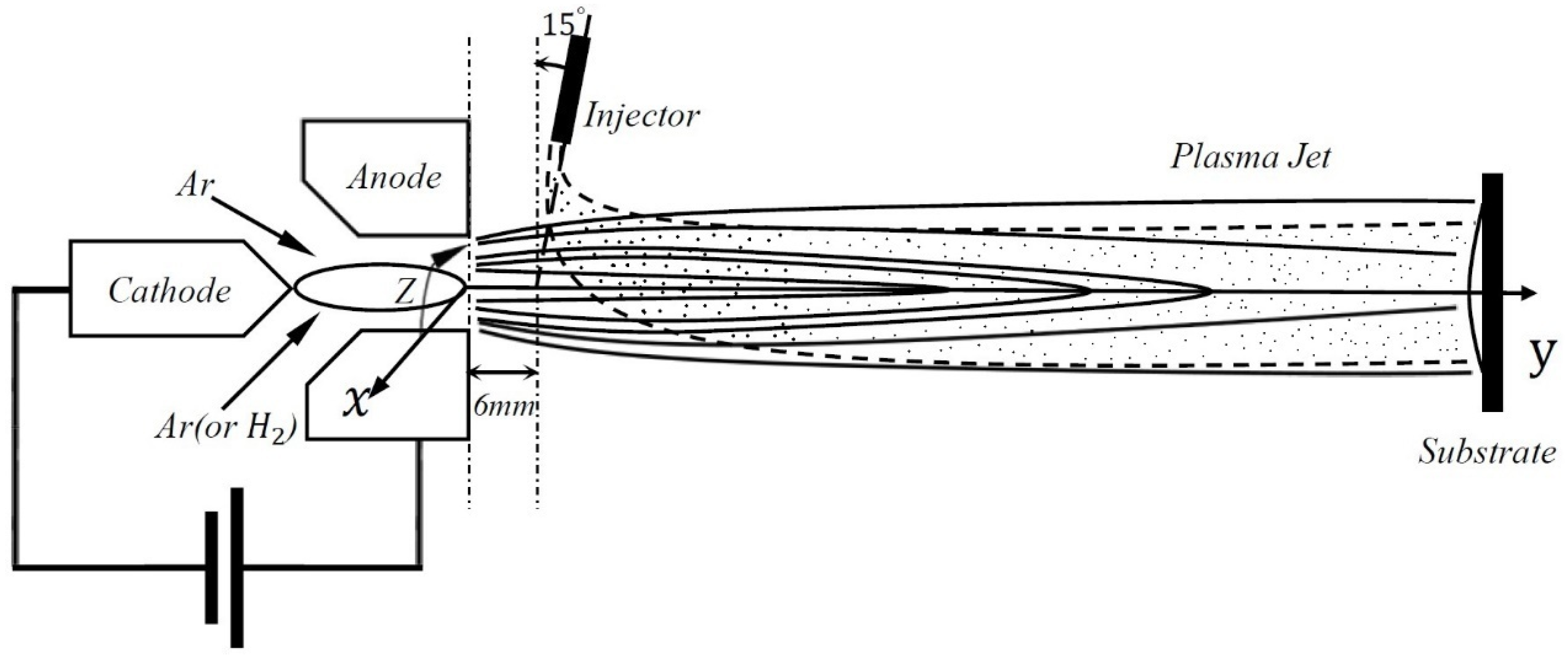
2. Basic Description of the Problem
3. Mathematical Model
3.1. Droplets Tracking and Heating
3.2. Droplet Atomization
3.3. Droplets Evaporation
4. Numerical Treatment and Validation
4.1. Geometry and Boundary Condition
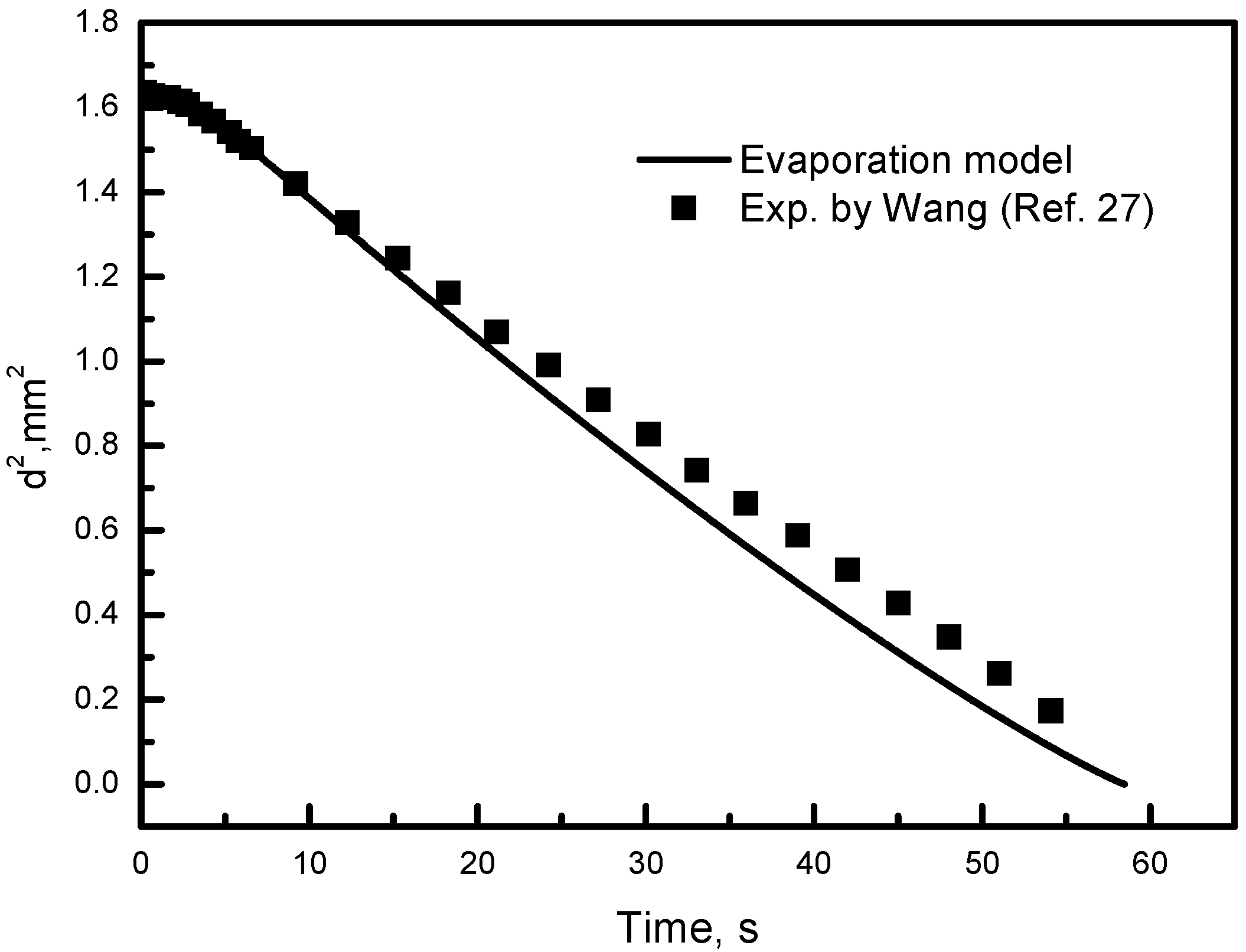
4.2. Validation of Numerical Model
5. Discussion
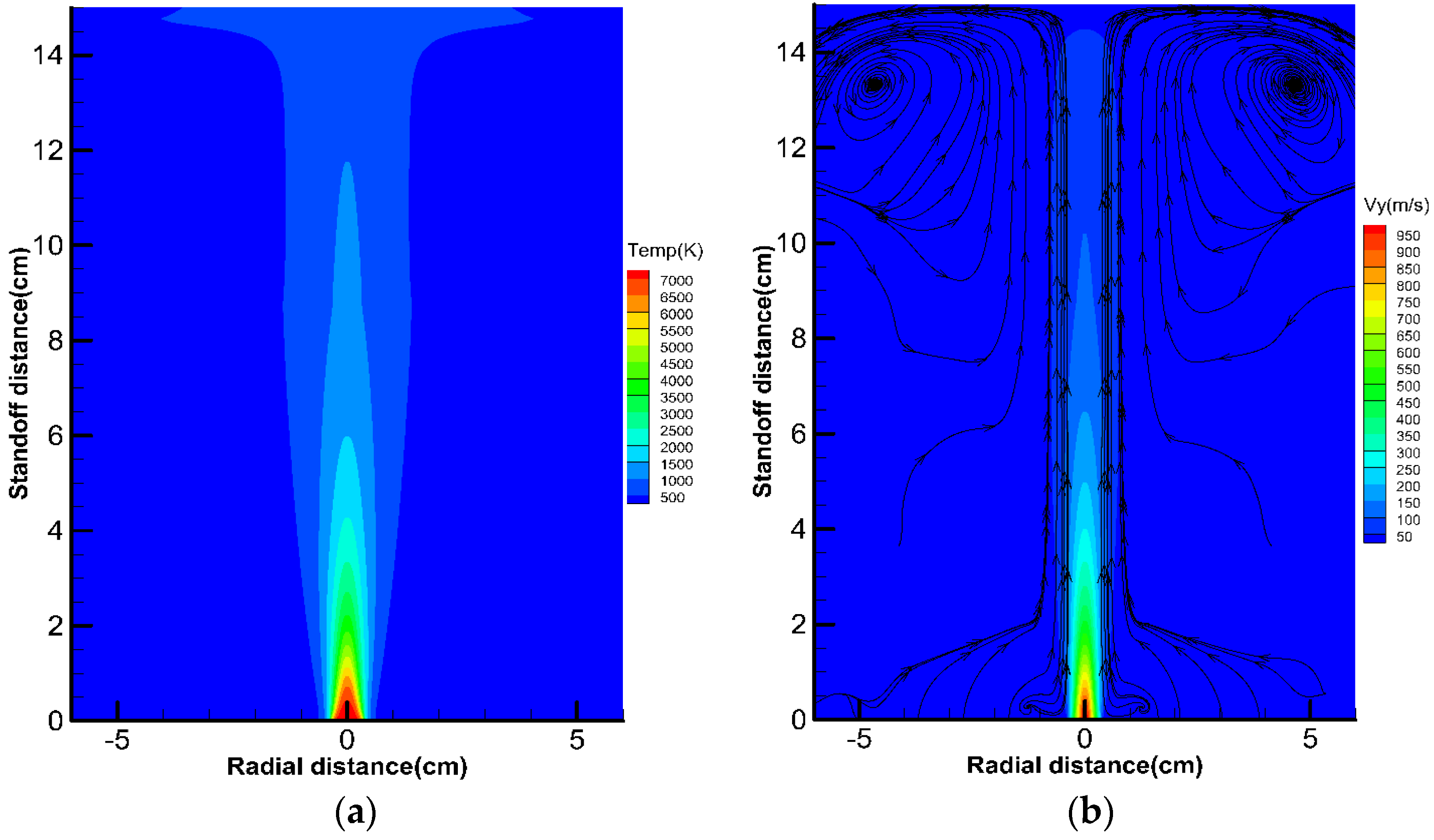
5.1. Results of Plasma Gas Flow Field
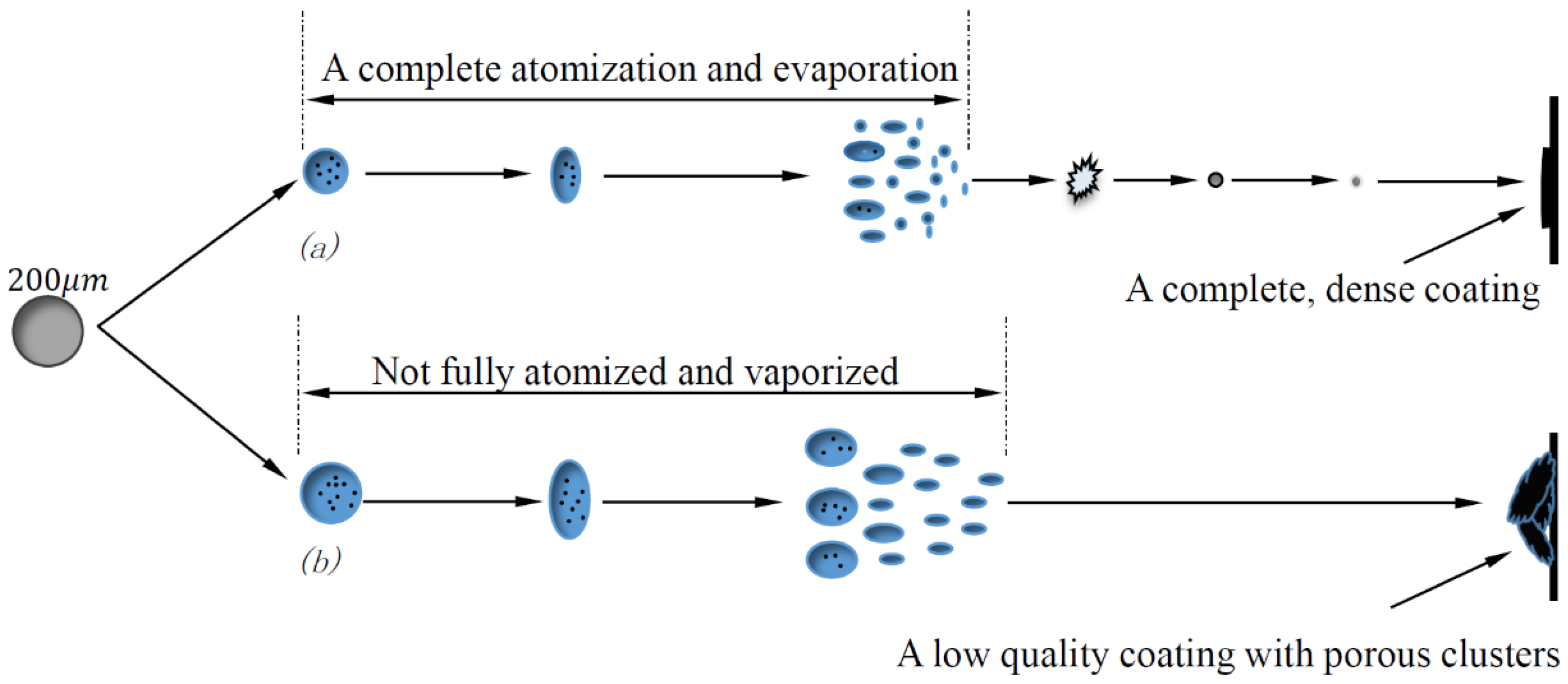
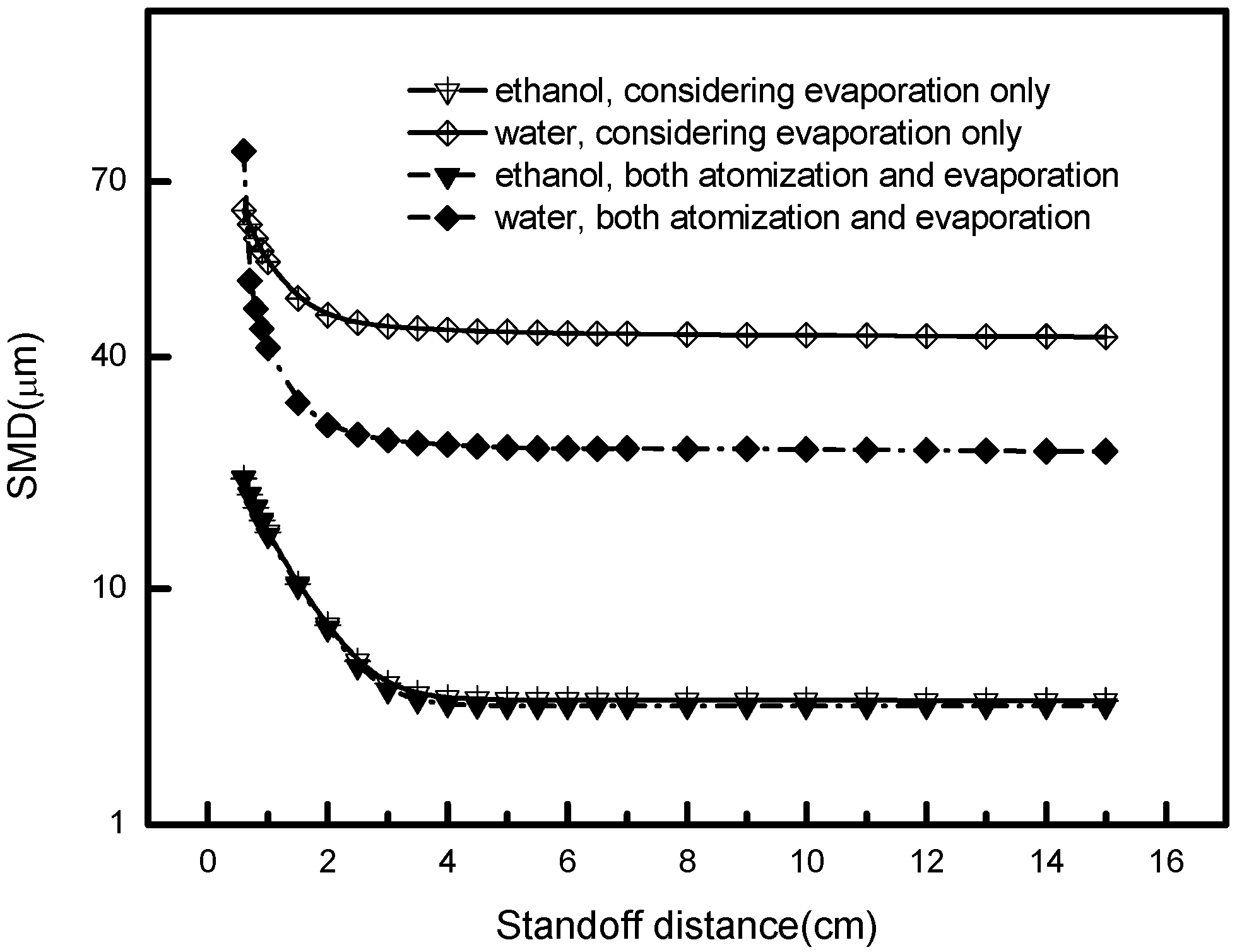
5.2. Acting Mechanism of Atomization and Evaporation
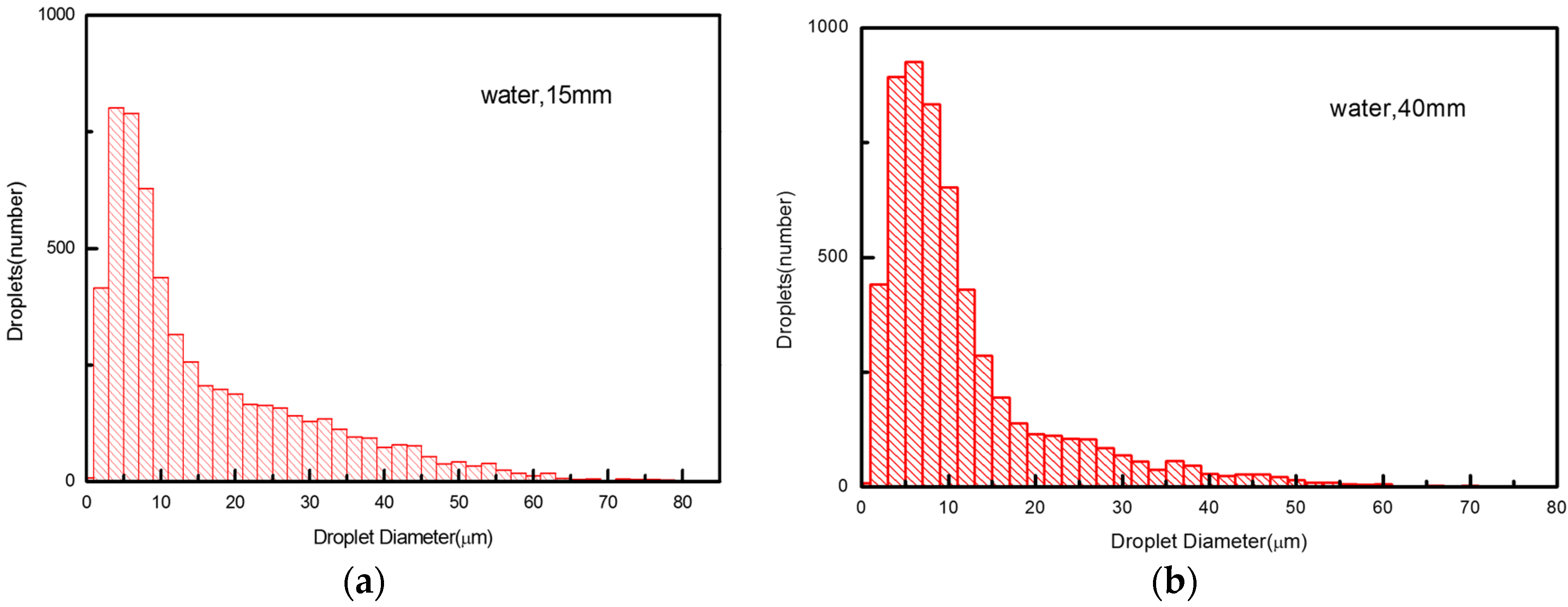
5.3. Droplet Size Distribution
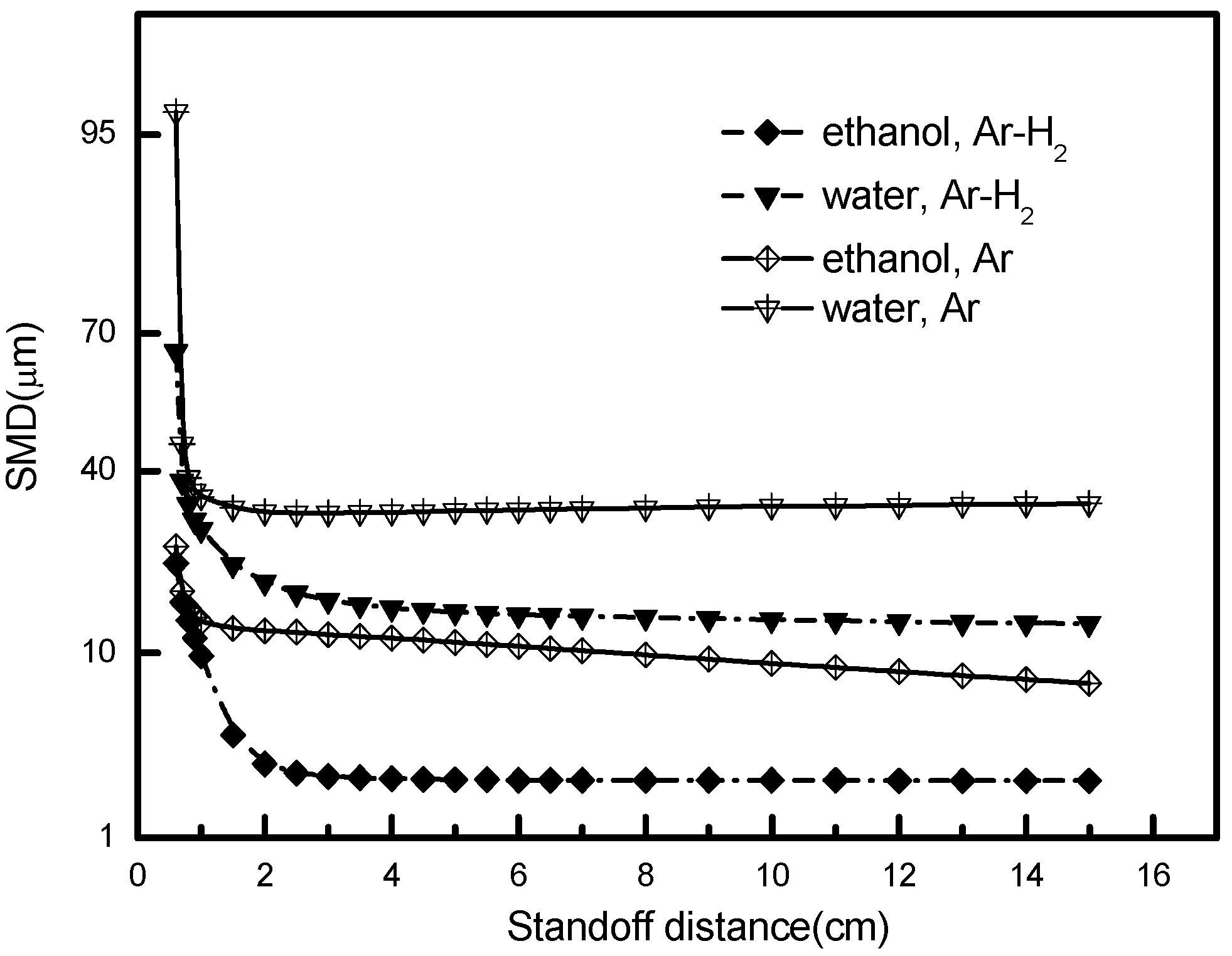
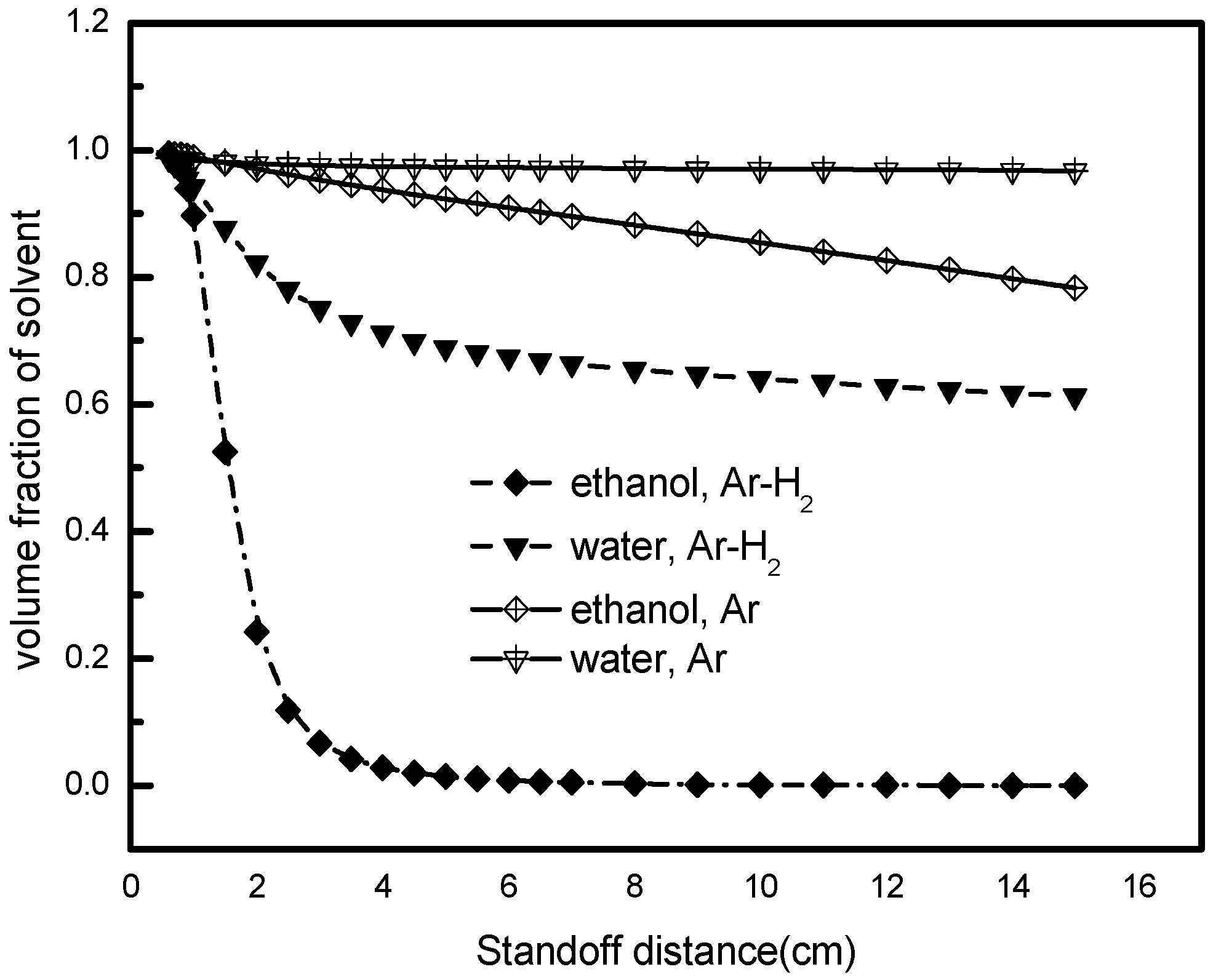
5.4. Effects of Liquid and Gas Types
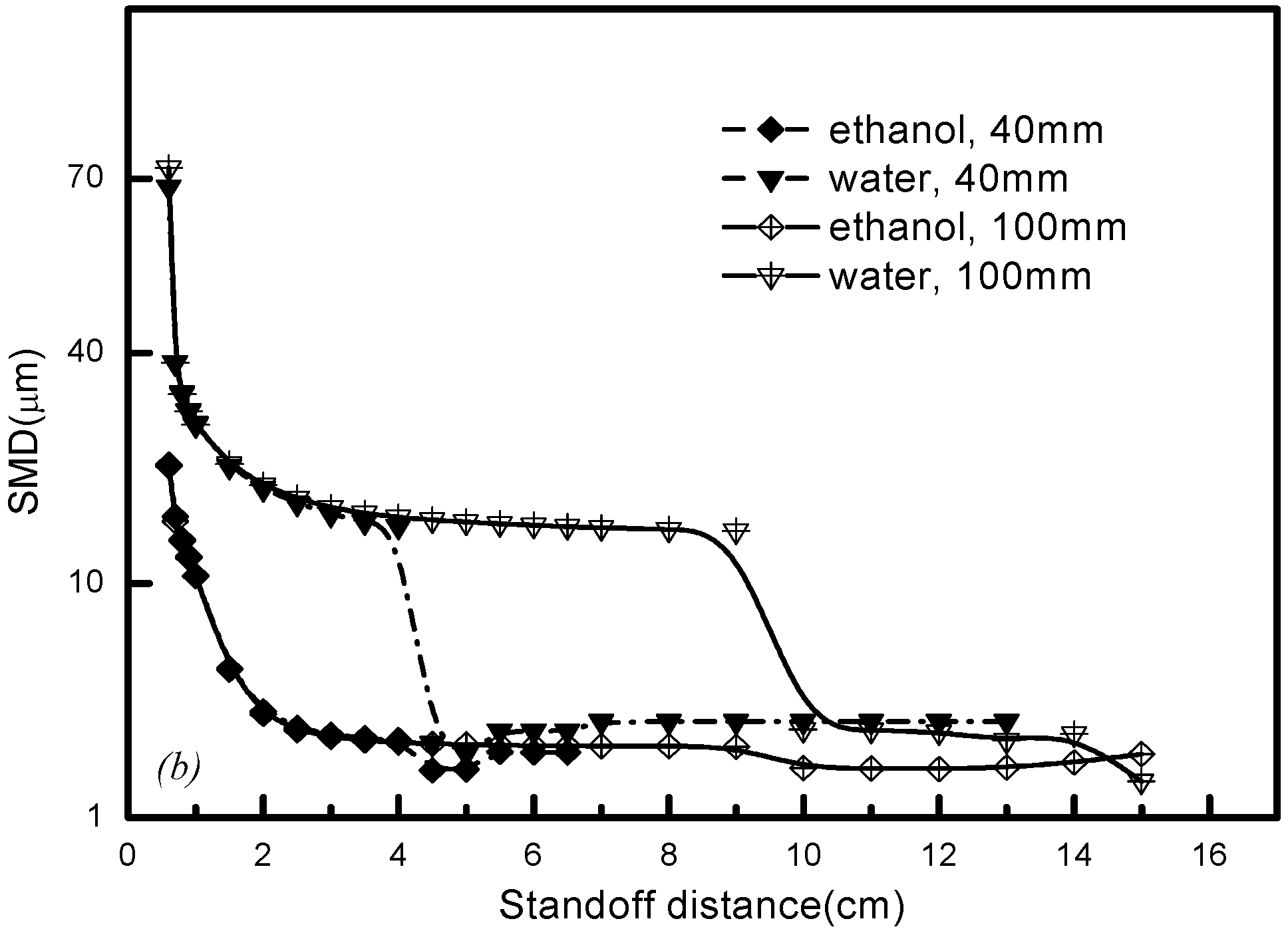
5.5. Effects of Substrate Location
6. Conclusions
- Droplet size and distribution are the main factors impacting the microstructure of the coating surface. Fine droplets resulting from the complete atomization and vaporization contributed to the formation of smaller nanoparticles and a fully melting liquid nanoparticle with low liquid stock vapor is essentially decisive to constructing pure overlapped splats on the material surface.
- Droplet size largely depends on the atomization and evaporation consequences and goes through an instant decrease, corresponding to the axial position of the hot core region and the secondary breakup region. In these areas, atomized and vaporized actions exert inconsistent influences on the modification of droplet size. According to these features, operating parameters, such as types of solvent, could be adjusted from this aspect.
- Ethanol, used as a solvent, undergoes a speedy vaporizing process resulting in a sharp droplet size decrease near the nozzle exit. The evaporation of water or other non-volatility solvent highly depends on the plasma temperature and the length of hot core region. A higher enthalpy plasma gas and a longer length of the hot core region contribute to the effective evaporation. As for ethanol or other solvents with good volatility, the hot core region does not need to be that long; instead, the solvent with suitable atomization properties then become our principal care.
- In comparison with pure Ar gas, Ar-H2 gas mixture reveals more superior performance with respect to the droplet atomizing and vaporizing as a result of the higher specific gas enthalpy, the enhancement of gas velocity, as well as better thermodynamic properties.
- In order to procure an ideal, fine droplet size and uniform distribution near the torch exit, the substrate should be located where the droplet momentum has not yet fully diminished, and in this case it should be put somewhere before the standoff distance of 6 cm.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fauchais, P.; Rat, V.; Coudert, J.F.; Etchart-Salas, R.; Montavon, G. Operating parameters for suspension and solution plasma-spray coatings. Surf. Coat. Technol. 2008, 202, 4309–4317. [Google Scholar] [CrossRef]
- Fauchais, P.; Etchart-Salas, R.; Rat, V.; Coudert, J.-F.; Caron, N.; Wittmann-Ténèze, K. Parameters controlling liquid plasma spraying: Solutions, sols or suspensions. J. Therm. Spray Technol. 2008, 17, 31–59. [Google Scholar] [CrossRef]
- Chen, D.; Jordan, E.H.; Gell, M. The solution precursor plasma spray coatings: Influence of solvent type. Plasma Chem. Plasma Process. 2010, 30, 111–119. [Google Scholar] [CrossRef]
- Muoto, C.K.; Jordan, E.H.; Gell, M.; Aindow, M. Identification of desirable precursor properties for solution precursor plasma spray. J. Therm. Spray Technol. 2011, 20, 802–816. [Google Scholar] [CrossRef]
- Waldbillig, D.; Kesler, O. Effect of suspension plasma spraying process parameters on YSZ coating microstructure and permeability. Surf. Coat. Technol. 2011, 205, 5483–5492. [Google Scholar] [CrossRef]
- Joulia, A.; Bolelli, G.; Gualtierie, E.; Lusvarghi, L.; Valerif, S.; Vardelle, M.; Rossignol, S.; Vardelle, A. Comparing the deposition mechanisms in suspension plasma spray (SPS) and solution precursor plasma spray (SPPS) deposition of yttria-stabilised zirconia (YSZ). J. Eur. Ceram. Soc. 2014, 34, 3925–3940. [Google Scholar] [CrossRef]
- Delbos, C.; Fazilleau, J.; Rat, V.; Coudert, J.F.; Fauchais, P.; Pateyron, B. Phenomena involved in suspension plasma spraying, Part 1: Suspension injection and behaviour. Plasma Chem. Plasma Process. 2006, 26, 371–391. [Google Scholar] [CrossRef]
- Rampon, R.; Filiatre, C.; Bertrand, G. Suspension plasma spraying of YPSZ coatings: Suspension atomization and injection. J. Therm. Spray Technol. 2008, 17, 105–114. [Google Scholar] [CrossRef]
- Bertolissi, G.; Chazelas, C.; Bolelli, G.; Lusvarghi, L.; Vardelle, M.; Vardelle, A. Engineering the microstructure of solution precursor plasma-sprayed coatings. J. Therm. Spray Technol. 2012, 21, 1148–1162. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Goutier, S.; Vardelle, A. Specific measurements of in-flight droplet and particle behavior and coating microstructure in suspension and solution plasma spraying. J. Therm. Spray Technol. 2015, 24, 1498–1505. [Google Scholar] [CrossRef]
- Marchand, C.; Chazelas, C.; Mariaux, G.; Vardelle, A. Liquid precursor plasma spraying: Modeling the interactions between the transient plasma jet and the droplets. J. Therm. Spray Technol. 2007, 16, 705–712. [Google Scholar] [CrossRef]
- Jadidi, M.; Mousavi, M.; Moghtadernejad, S.; Dolatabadi, A. A three-dimensional analysis of the suspension plasma spray impinging on a flat substrate. J. Therm. Spray Technol. 2015, 24, 11–23. [Google Scholar] [CrossRef]
- Farrokhpanah, A.; Coyle, T.W.; Mostaghimi, J. Numerical study of suspension plasma spraying. J. Therm. Spray Technol. 2017, 26, 12–36. [Google Scholar] [CrossRef]
- Huang, P.C.; Heberlein, J.; Pfender, E. Particle behavior in a two-fluid turbulent plasma jet. Surf. Coat. Technol. 1995, 73, 142–151. [Google Scholar] [CrossRef]
- Ozturk, M.; Cetegen, B.M. Modeling of plasma assisted formation of precipitates in zirconia containing liquid precursor droplets. Mater. Sci. Eng. A 2004, 384, 331–351. [Google Scholar] [CrossRef]
- Jabbari, F.; Jadidi, M.; Wuthrich, R.; Dolatabadi, A. A numerical study of suspension injection in plasma-spraying process. J. Therm. Spray Technol. 2014, 23, 3–13. [Google Scholar] [CrossRef]
- Ramshaw, J.D.; Chang, C.H. Computational fluid dynamics modeling of multi-component thermal plasmas. Plasma Chem. Plasma Process. 1992, 12, 299–325. [Google Scholar] [CrossRef]
- Tanner, F.X. Development and validation of a cascade atomization and drop breakup model for high-velocity dense sprays. At. Sprays 2004, 14, 211–242. [Google Scholar] [CrossRef]
- Xiong, H.B.; Qian, L.J.; Lin, J.Z. Simulation of effervescent atomization and nanoparticle characteristics in radio frequency suspension plasma spray. J. Therm. Spray Technol. 2012, 21, 226–239. [Google Scholar] [CrossRef]
- Shao, X.-M.; Zhang, K.; Xiong, H.-B. Modeling of micro- and nanoparticle characteristics in DC suspension plasma spray. J. Therm. Spray Technol. 2015, 24, 309–317. [Google Scholar] [CrossRef]
- Xiong, H.B.; Zheng, L.L.; Sampath, S.; Williamson, R.L.; Fincke, J.R. Three-dimensional simulation of plasma spray: Effects of carrier gas flow and particle injection on plasma jet and entrained particle behavior. Int. J. Heat Mass Transf. 2004, 47, 5189–5200. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Amsden, A.A. The TAB method for numerical calculation of spray droplet break-up. SAE Tech. Pap. 1987, 872089. [Google Scholar]
- Reitz, R.D. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Meillot, E.; Vincent, S.; Caruyer, C.; Damiani, D.; Caltagirone, J.P. Modelling the interactions between a thermal plasma flow and a continuous liquid jet in a suspension spraying process. J. Phys. D Appl. Phys. 2013, 46, 224017. [Google Scholar] [CrossRef]
- Wan, Y.P.; Prasad, V.; Wang, G.-X.; Sampath, S.; Fincke, J.R. Model and powder particle heating, melting, resolidification, and evaporation in plasma spraying processes. J. Heat Transf. 1999, 121, 691–699. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, C.; Zhang, K.; Shao, X. Effects of atomization injection on nanoparticle processing in suspension plasma spray. Nanomaterials 2016, 6, 94. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Theory and Experiment Research on Droplet Evaporation in Cross Flow. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2012. [Google Scholar]
- Pawlowski, L. Suspension and solution thermal spray coatings. Surf. Coat. Technol. 2009, 203, 2807–2829. [Google Scholar] [CrossRef]

| Case | Gas Mixture (Flow Rates, slm) | Specific Enthalpy (MJ/kg) | Solvent | Substrate |
|---|---|---|---|---|
| 1 | Ar(33) | 9.16 | Ethanol | No |
| 2 | Ar-H2(33-10) | 20.46 | Ethanol | No |
| 3 | Ar(33) | 9.16 | Water | No |
| 4 | Ar-H2(33-10) | 20.46 | Water | No |
| 5 | Ar-H2(33-10) | 20.46 | Ethanol | 40 mm |
| 6 | Ar-H2(33-10) | 20.46 | Water | 40 mm |
| 7 | Ar-H2(33-10) | 20.46 | Ethanol | 100 mm |
| 8 | Ar-H2(33-10) | 20.46 | Water | 100 mm |
| Parameter | Value |
|---|---|
| Solid density (kg∙m−3) | 5.89 × 103 |
| Liquid density (kg∙m−3) | 5.89 × 103 |
| Solid thermal conductivity (W∙m−1∙K−1) | 2.0 |
| Liquid thermal conductivity (W∙m−1∙K−1) | 3.0 |
| Solid specific heat (J∙kg−1∙K−1) | 580 |
| Liquid specific heat (J∙kg−1∙K−1) | 713 |
| Melting temperature (K) | 2950 |
| Boiling temperature (K) | 5000 |
| Latent heat of melting (J∙kg−1) | 8 × 105 |
| Latent heat of vaporization (J∙kg−1) | 6 × 106 |
| Parameter | Water | Ethanol |
|---|---|---|
| Molecular Weight (g∙mol−1) | 18 | 46 |
| Density (kg∙m−3) | 1 × 103 | 0.8 × 103 |
| Boiling Point at 1 atm (K) | 373 | 351 |
| specific heat (J kg−1∙K−1) | 4200 | 2400 |
| Critical Temperature (K) | 646 | 516 |
| Critical Pressure (Mpa) | 22 | 6.38 |
| Surface tension (10−3 J/m2) | 72.9 | 22.3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, H.; Sun, W. Investigation of Droplet Atomization and Evaporation in Solution Precursor Plasma Spray Coating. Coatings 2017, 7, 207. https://doi.org/10.3390/coatings7110207
Xiong H, Sun W. Investigation of Droplet Atomization and Evaporation in Solution Precursor Plasma Spray Coating. Coatings. 2017; 7(11):207. https://doi.org/10.3390/coatings7110207
Chicago/Turabian StyleXiong, Hongbing, and Weiqi Sun. 2017. "Investigation of Droplet Atomization and Evaporation in Solution Precursor Plasma Spray Coating" Coatings 7, no. 11: 207. https://doi.org/10.3390/coatings7110207
APA StyleXiong, H., & Sun, W. (2017). Investigation of Droplet Atomization and Evaporation in Solution Precursor Plasma Spray Coating. Coatings, 7(11), 207. https://doi.org/10.3390/coatings7110207





