Abstract
Solution precursor plasma spray (SPPS) is a novel and promising technique in producing nanostructured coatings. This technique involves complex heat, mass and momentum transfer among the liquid feedstock, droplets, plasma jet and the coating material. Nevertheless, the droplet atomization and evaporation in the plasma jet is one of the most essential parts to obtain the desired coating architecture. In the present work, a three-dimensional two-way-coupled Eulerian-Lagrangian code is used to simulate the interactions between the solution precursor and plasma. In order to obtain a more realistic understanding regarding droplet atomization and vaporization, the flash-boiling effect is modeled by an improved vaporization model. This model could provide accurate details for the droplet pyrolysis and help to optimize the solution precursor plasma spray process. We show that the fragmentation of the liquid stock and its vaporization mainly dominate the spraying details and can be decisive to the coating quality. We further investigate their role in SPPS and separately probe their inner link with the flow field relating to the distinctive area when droplets are flying through the thermal flow field. Our studies reveal that ethanol droplets, compared to those of water, show a superior characteristics in SPPS, owing to the low boiling point and low surface tension, conducive to the evaporation and atomization of droplets. In addition, the mixture of the plasma gas with hydrogen breaks the droplets more thoroughly compared to the pure plasma. The numerical results were compared and found to agree well with previous experimental and simulation work.
1. Introduction
Solution precursor plasma spraying (SPPS) is a novel technique that has been widely utilized in nanoparticle processing by plasma spraying over the last decade to obtain high-quality dense nanostructure coatings. In this technique, liquid feedstock plays a crucial role in determining whether nanoparticles carried by it, or formed from the solution, are discharged timely and properly. In comparison with SPS (Suspension Plasma Spraying), SPPS makes use of a solution as the liquid feedstock instead of a suspension, which is considered for its easy handling for sub-micro or micro particles. Besides, during the preprocessing of SPS, nanoparticles need to be produced and resolved into the liquid feedstock forming the suspension, which might pose a serious threat to human health and causes potential powder pollution, affecting the environment. Therefore, SPS is more environmentally friendly and promises a bright future in nanostructure processing for coating material [1].
Many experimental studies have been conducted to explore internal mechanism and factors affecting SPS or SPPS processes. Previous research has illustrated that the process parameters are critical aspect for the entire thermal spray operation [2,3,4,5] and mastering the deposition mechanism and obtaining a proper controlled deposition rate are other important aspects worth our care [6]. These studies have shown that a dense nanostructured coating results from the deposition of overlapping splats under certain conditions. During the entire SPPS, the mass, heat, and momentum transfers between liquid feedstock, droplets, melting particle, and plasma plume needs a perfect adaption to the spraying material and the desirable structure, especially the rate of atomization and evaporation for droplets largely determining the produced or discharged position of sub-micro- and micro-sized particles’ impact upon the substrate [7,8,9,10]. When the droplet encounters an incomplete atomization and evaporation, the processed material cannot be shaped to an ideal state, which will affect the architecture of the coating surface, as the substrate will be fraught with numerous porous clusters instead of completely overlapping splats.
To obtain an insightful understanding of the physical mechanisms underlying behind the phenomenon, study that is more needs to be conducted. The influence of the injection angle, the position of the injected plasma jet, and the interactions between the transient plasma flow and feedstock, droplets, or particles have been considered in many simulation works [11,12,13]. However, particle behavior in SPPS, especially during atomization and evaporation, are still under deep exploration. Some numerical work has focused on the droplet or particle behaviors from the perspective of the scale effect in the plasma gas flow and the physical model of droplets and particles [14,15,16]. However, these studies often ignore the thermal effects in the atomization of the liquid feedstock and the droplets or, if they consider this effect, overlook the flash evaporation of the droplet. This neglect degrades the accuracy and authenticity of the simulation work.
In this paper, we simulate the interactions between the plasma plume and liquid feedstock, droplets, and particles with a comprehensive three-dimensional two-way-coupled Eulerian-Lagrangian code, considering the atomization caused by the aerodynamic force and by droplet evaporation under flash-boiling conditions. The effect of the plasma’s gas composition, types of solvent, and the position of the substrate on the Sauter mean diameter (SMD) and the distribution of the droplet are investigated. The reasonable position of the substrate to obtain a dense and complete coating has been analysed and discussed. The liquid feedstock we focused on in this work are water or ethanol-based solutions of Y2O3-stabilised ZrO2 (YSZ).
2. Basic Description of the Problem
The present work was implemented for a direct-current SPPS system through a radial-injected YSZ solution. Figure 1 shows the schematic information for this system. Gas mixtures, including pure argon (Ar) or argon and hydrogen (Ar-H2) mixtures, are ionized in a plasma gun to generate a high-temperature and high-velocity plasma jet. The YSZ material, usually zyrconyl nitrate and yttrium nitrate salts, is resolved in the solvent of water or ethanol to produce the liquid precursor. A needle-shaped injector, with diameter of 200 μm, is utilized to introduce the droplet from a pressurized liquid reservoir to the plasma jet. These droplets are accelerated and heated up by the plasma gas, then partially or fully atomized and vaporized, as illustrated in Figure 2. Finally, the pyrolysis salt YSZ material impacts the substrate to form the functional zirconia coatings.
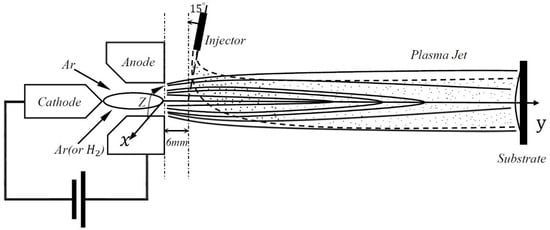
Figure 1.
Schematic of solution precursor plasma spraying with radially-injected droplets.
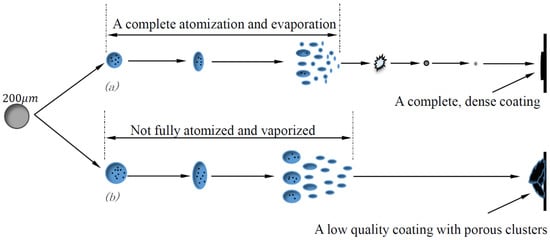
Figure 2.
Different coating quality resulting from fully (a), and not fully atomized and vaporized droplets (b).
Eight cases simulated in our work are listed in Table 1, which hold the same operating conditions as in the experiments by Bertolissi [9]. In these cases, three important factors mostly affecting the droplet states and coating qualities are considered. They are the type of gas mixture, the type of solvent, and the location of substrate, respectively. The detailed physical properties of the plasma gas and liquid are listed in Table 2 and Table 3, respectively. Droplets with an initial diameter of 200 μm are injected into the plasma jet at 6 mm from the nozzle exit with an angle of 15° to the vertical axis. Their initial velocity and temperature is 5 m/s and 300 K, respectively. The injected position of these droplets is decided by random distributions.

Table 1.
Numerical cases of the present work.

Table 2.
Material properties of ZrO2.

Table 3.
Solvent properties of water and ethanol.
3. Mathematical Model
Modeling work of this system includes two parts, i.e., the gas model and the droplet model. For the gas model, we treat the plasma jet as an ideal gas and solve the thermal flow field by an Eulerian method, assuming the flow as being continuous, multicomponent, compressible, and turbulent with a low Mach number in a local thermodynamic equilibrium (LTE). The plasma gas model is then solved by the multiphase Navier-Stokes equations in a well-tested numerical code, and turbulence is modeled here by the k-ε model. Detailed information about this code can be found in [17].
Droplets are modeled by a Lagrangian method. Each droplet them is generated as a computational entity and injected into the plasma jet, and then tracked during its flight before impact on the substrate. The droplet model would predict their position, velocity, temperature, size, and composition. In this study, the droplet tracking and heating states are calculated by a zero-dimensional particle model, and the evaporation of droplets is considered under a flash-boiling condition. The atomization of droplets is illustrated using the cascade atomization and droplet breakup (CAB) model [18].
3.1. Droplets Tracking and Heating
Each droplet is a Lagrangian particle in the plasma jet. Forces imparting on the particles are mainly the drag force, Saffman lift force, and Brownian force. For particle radii smaller than 100 μm, the drag force is prominent. For the particles near the jet edge and the substrate, where the flow shear stress is large, the Saffman lift force is significant, whereas for the sub-micron or nanoparticles, the Brownian force is important. By accounting for these three forces, the particles acceleration rate could be expressed as Equations (1)–(4):
where mp is the particle mass and Vp is velocity. During the particle tracking procedure, the turbulent dispersion of particles is calculated by integrating the trajectory equations for individual particles, using the instantaneous fluid velocity along the particle path. The particle temperature is also calculated with the given surrounding gas thermal conditions. It is assumed that there exists no heat conduction inside the particle, which describes the temperature of individual particle as follows (Equation (5)):
where Tp, Cp, and Qp represents the droplet temperature, specific heat, and the heat flux at the surface, respectively. Detailed explanation of the above particle models for injected droplets can be found in our previous publications [19,20,21].
3.2. Droplet Atomization
The droplets produced by the injector will continually undergo further disintegration and breakup into smaller droplets, because of the aerodynamic force action. Here, the cascade atomization and droplet breakup (CAB) model, as shown in Figure 2, is utilized to determine the droplet size based on the gas aerodynamic force, liquid viscosity, and surface tension.
During the implementation, droplet distortion here is described here by the distortion parameter, ξ = 2x/r, where r represents the radius of the droplet and x denotes the radial variation from the equilibrium position. The value of the distortion parameter can be obtained by Equation (6) [22]:
where ρ denotes the density, μ the viscosity, σ the surface tension, U the relative drop-gas velocity, and the subscripts g and l denote the gas or liquid properties, respectively. Drop distortion will instantaneously vary, and the critical fragmentation condition for the droplet is satisfied if only the distortion parameter, ξ, exceeds 1.
The second core problem this model covers is the profile of product droplet size and distribution. Here, the population dynamics rule the creation procedure of product droplets: From the point of view of number, the assumption is that for each breakup the number of the child droplet is proportional to that of critical parent drops, in which the breakup is in charge of the proportionality constant. According to the above, the rate of droplet creation can be defined and derived, which, in the combination of mass conversation and principle between parent and product droplets, engenders the principal cascade breakup rule (Equation (7)):
where is the mean mass of the child product droplet and ωbu is the breakup frequency, depending on the breakup regimes. As demonstrated by Reitz [23], three distinct breakup mechanisms dominated the fragmentation of drops with respect to the gas Weber number: bag breakup, stripping breakup, and catastrophic breakup regimes. The calculation of the Weber number can be found in [18,24]. In this study, the critical Weber number is below 80, which belongs to the bag breakup, as shown in Figure 2. Here, the critical Weber number reflects the importance of inertia to surface tension. ωbu here has the value of 0.05ωos as suggested by O’Rourke and Amsden [22] and, thus, the drop oscillation frequency ωos could be solved by Equation (8):
We note that the actual size distribution of the child droplet has not been given in addition to the specific . In order to better implementation of the model, a uniform distribution has been employed, by which Equation (7) is replaced by Equation (9),
where r0 and r represent the radii of the parent and child droplets, respectively, and tbu is the characteristic breakup time, derived from Equation (6) when breakup occurs.
3.3. Droplets Evaporation
The droplet will be vaporized at the surface when its temperature increases toward the critical temperature, or the so-called boiling point. When the droplet temperature is slightly higher than the boiling point, the evaporation rate is moderate and its controlling parameter would be the vapor diffusion rate. However, the droplet could be heated dramatically in the plasma jet with the core gas temperature as high as ten thousand degrees, and reach a droplet temperature much higher than the boiling point. Then, flash evaporation occurs and results in a large evaporation rate. In this case, the evaporation rate mainly depends on the heat transfer rate. Here, we use a comprehensive droplet evaporation model to consider both moderate evaporation, as well as flash evaporation.
The evaporation rate mainly depends on the vapor diffusion rate in the boundary layer and heating transfer rate towards the droplet interior. When the surface temperature of the droplets is substantially below the solvent critical temperature, the vapor diffusion rate is relatively low and the heat increment of the droplet is large enough; therefore, it can satisfy the latent heat of vaporization. However, when surface temperature increases to the solvent critical temperature, the saturated vapor pressure also increases quickly, and then the vaporization rate appears to be infinitely high. However, since the droplet cannot, in fact, obtain adequate heat from the plasma gas. Thus, in this case, the vaporization rate is determined by the net heat gain of droplet surface Qnet. Taking both cases mentioned above into account, mv can be given as Equation (10):
where ρg, Dg are the gas density and gas diffusion coefficient, respectively. Sh is the Sherwood number reflecting the convective heat transfer effect (Equation (11)):
where Sc is Schmidt number and Rep is the particle Reynolds number. B is a mass transfer coefficient related to the local mass fraction of vapor in the gas phase Y∞ and the vapor concentration surrounding the droplet surface is Y*, and can be given as Equation (12):
where Y∞ is calculated in the plasma jet simulation, and Y* is calculated by Equation (13):
where Wp and W0 are the molecular weight of the salts and gas, respectively. Pc is the gas pressure and Pv is the vapor pressure [25].
4. Numerical Treatment and Validation
4.1. Geometry and Boundary Condition
The general computational domain and basic boundary condition employed in the calculation of the plasma jet are described as follows: The thermal flow field is solved using a cylindrical coordinate system. The plasma gun wall temperature is set as 300 K, and the wall velocity is 0 with a non-slip condition. The axial length is 15 cm with 66 grid points, while the radial length is 6 cm with 57 grid points, and the scale of the circular direction is 2π with 32 grid points. More details about the boundary condition can be found in [19,20,21].
4.2. Validation of Numerical Model
As in the present work, the simulation of the plasma flow field has been well validated in our previous research [18,19,20,26]. The new modeling of particles, mainly concerning the atomization and vaporization of droplets, is examined here in Figure 3, which displays the evolution of the hot water droplet diameter (d) in the environment of hot gas flow. Our droplet-vaporizing model shows good agreement with the experimental results in the published literature [27]. The maximum deviation between our vaporization model and the experiment is less than 2.6%. After validation, this new particle model could be employed in the plasma spray code, to study the phenomena of atomization and evaporation. Then, the plasma and droplet characteristics could be predicted and their effects on SPPS coatings could be investigated. The influence of plasma operating conditions, droplet size and distributions, and degree of salt pyrolysis are focused on.
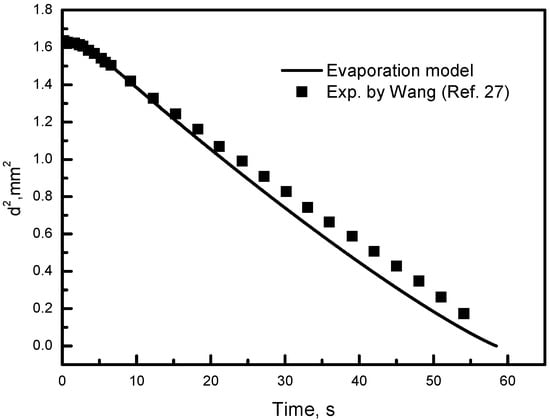
Figure 3.
Numerical and experimental results of droplet evaporation.
5. Discussion
First, the general information regarding the plasma gas flow field is presented. Secondly, we discuss the factors of atomization and vaporization on the droplet state, which clarify the acting mechanism of these two phenomena on the droplet Sauter mean diameter, as well as on the size distribution. After that, the effects of the gas and liquid type are thoroughly discussed, followed by the effects of the substrate location, which identify proper operating conditions to acquire an ideal architecture of SPPS coating without excessive porous clusters.
5.1. Results of Plasma Gas Flow Field
As shown in Figure 4, the hottest region of plasma gas flow ranges within 2 cm of the torch exit. Beyond that, the gas temperature and velocity encounter a quick decrease, due to ambient air entrainment. The engulfed air has much lower temperature and velocity compared to the plasma gas. Mixing of the air and the plasma gas decreases the flow energy and enthalpy, especially in the centerline. Meanwhile, the flow jet becomes wider and wider after spouting from the nozzle exit. Two vortices are identified in the downstream of plasma flow. These vortices are induced by the blocked gas flow around the substrate, which reflect the interaction between the plasma jet and the surrounding air flow.
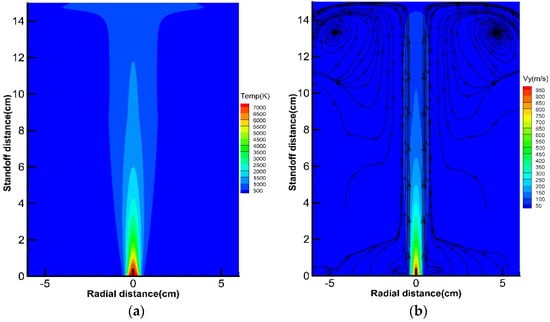
Figure 4.
Gas temperature contour (a), and axial velocity contour with streamlines (b).
5.2. Acting Mechanism of Atomization and Evaporation
Here, we explore the droplet atomization and evaporation behavior in the plasma spray jet using numerical methods. Both of these mechanisms contribute to the droplet disintegration, and good droplet disintegration ensures good salt pyrolysis and good coating quality. The key problem is that we need to know which mechanism is dominant in different circumstances. In this study, we examine the droplet Sauter mean diameter (SMD, or d32) evolution in two cases, i.e., considering both atomization and evaporation, and considering evaporation only, to answer this problem.
Figure 5 depicts the SMD variation for these two cases, for water and ethanol droplets, respectively. For ethanol droplets, the SMD variation is small, either considering atomization or not. This means that the secondary breakup does not play a significant role for the ethanol droplets. The reason is that extremely fine droplets have been formed after injection, and further breakup due to the aerodynamic force could not improve their disintegration degree. Therefore, the vaporizing effect of ethanol droplets matters a great deal, and a higher plasma temperature might give rise to a better coating quality using this liquid.
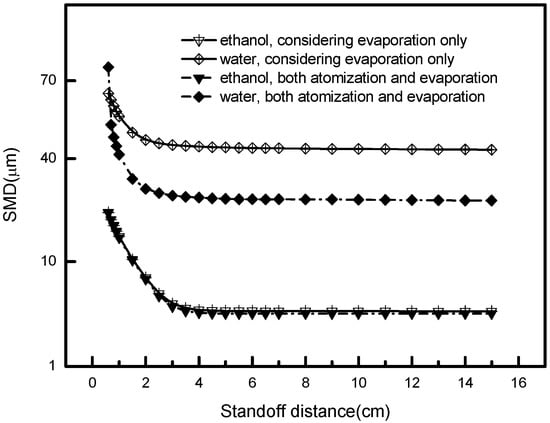
Figure 5.
Effects of atomization and evaporation on the droplet mean size.
On the contrary, the evolution of the droplet size of water presents a different trend compared to ethanol. They strongly depend on the atomization intensity, not only on the evaporation, even near the torch exit. The reason is that water droplets have relatively high surface tension; therefore, the liquid could not be thoroughly disintegrated in the primary breakup region (0–2 cm). Then, the plasma jet in the secondary breakup region (2–6 cm) would further decrease the droplet diameter. For such a liquid, improving the plasma temperature, as well as the velocity, would be necessary for a good degree of disintegration and good coating quality.
The atomization and evaporation in essence depends on the solvent’s aerodynamics and thermal properties, since they are the inherent influential factors that affect the phase transition. Corresponding to the liquid type, different strategies should be adopted, for example, changing the hot core region and the breakup region of the plasma jet. Thereby different droplets behave distinctly in the plasma flow field, attuning to the plasma jet momentum and energy changes, and then exhibiting a sufficient disintegration degree during flight history. To be more specific, when ethanol and other kinds of liquid with a high degree of evaporation are adopted as the liquid feedstock in the plasma flow, the factors affecting the droplets’ disintegration should be primarily taken into account due to their conspicuous length in the hot core region. For water, or its counterparts, both the factors affecting breakup and vaporization need to be integrally considered to adopt proper operating conditions. We will discuss this more detail in Section 5.4 and Section 5.5.
5.3. Droplet Size Distribution
The acting mechanism we mentioned above will lead to a disparate droplet size distribution in the axial cross-section which, in turn, unravels much more underlying details concerning it. As shown in Figure 6 and Figure 7, we examine the droplet size distributions in two cross-sections at the standoff distance of 15 mm in the hot core region and 40 mm in the secondary breakup region, respectively, for water and ethanol droplets in an Ar-H2 atmosphere. We noted that the number of smaller droplets (d ≤ 10 μm) usually outweigh those of the larger ones (d ≥ 20 μm), regardless of liquid or gas types.
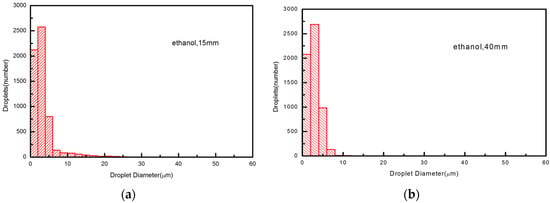
Figure 6.
Ethanol droplet size distribution at different cross-sections at 15 mm (a), and 40 mm (b).
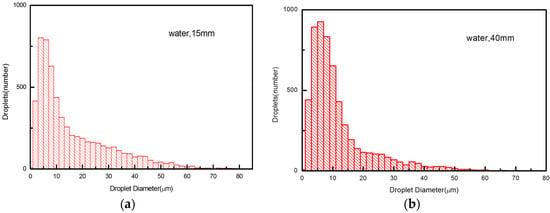
Figure 7.
Water droplet size distribution at different cross-sections at 15 mm (a), and 40 mm (b).
From the results, we see that the number of large ethanol droplets at 15 mm are much smaller than those of water, owing to a thorough primary breakup of the former. In addition, these larger ones even disappear when traveling from 15 to 40 mm as an outcome of violent evaporation. Such a degree of disintegration is favorable for later solvent pyrolysis and the final coating structure.
However, for water droplets, the size distribution and their formation appears to be more complicated. First, their size distribution range is much wider at both cross-sections, compared to ethanol. The reason is poor primary breakup of water droplets at injection. Secondly, the number of large droplets decreases, but the number of small droplets increases when traveling from 15 to 40 mm. The decrease of large droplets is due to the aerodynamic secondary breakup, which transforms the large droplets to smaller droplets, and also due to the evaporation, which shrinks both large and small droplets. Meanwhile, the increase of small droplets means that the breakup influence is more dominant than that of evaporation for the case of water.
Therefore, the resemblance and disparity of the droplets’ size distribution shown here is an integrated reflection of the acting mechanism mentioned above. After explaining the acting mechanisms on the mean diameter and size distributions, further investigation on the gas and liquid conditions, as well as the substrate location, on the SMD diameter and the pyrolysis degree is conducted.
5.4. Effects of Liquid and Gas Types
Essentially, the physics of atomization and evaporation is an extension of the liquid feedstock’s properties controlling the transport of momentum and energy between the droplets and plasma gas. Thus, mastering the role of the physical properties, including liquid and gas, is necessary to generate an insightful understanding of the evolution of droplets development.
Figure 8 depicts the SMDs of ethanol and water droplets in different plasma atmospheres. It reveals that ethanol has a smaller droplet size than water for the same plasma gas, due to its low surface tension and low boiling point. For the same liquid, Ar-H2 plasma produces a smaller droplet size than Ar plasma, since the presence of hydrogen enlarges the gas heat capacity and, thus, more thermal heat can be transferred to the droplets. In the current study, the minimum droplet diameter obtained in Ar gas is 14 and 33 μm for water and ethanol, respectively. However, in Ar-H2 gas, we could obtain much smaller minimum diameters as 2.5 and 20 μm, for water and ethanol, respectively. The shift from Ar to Ar-H2 leads to the enhancement of the plasma dynamic velocity and thermal enthalpy, eventually boosting the fragmentation of droplets [9]. This is essential for water-based SPPS coatings: Only Ar-H2 plasma could render the favorable occurrence of complete water disintegration.
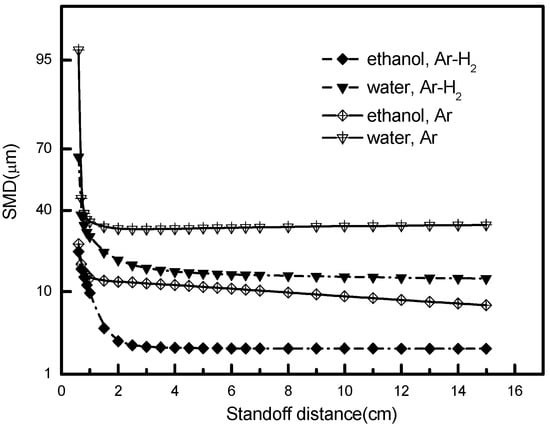
Figure 8.
Droplet Sauter mean diameter in the Ar or Ar-H2 plasma gas.
In addition to the droplet size and distribution, the solvent fraction is another important characteristic for the droplets’ degree of pyrolysis. The lower the solvent fraction, the higher the salt degree of pyrolysis will be. The solvent fraction here refers to the proportion of solvent in the droplet. It depends on the extent of droplet evaporation. Figure 9 shows that the solvent fraction experiences a visible decay, principally caused by the vaporization effect. Such decay depends on the liquid and plasma gas conditions. The volume fraction of ethanol decreases more rapidly compared to that of water, and Ar-H2 plasma produces further decay of the solvent than Ar plasma, mainly because the Ar-H2 atmosphere provides higher specific enthalpy, compared to pure Ar gas. Another reason is that the composite hydrogen in the plasma gas results in the higher velocity and dynamic pressure, which enlarges the shear rate of the gas and helps to break up the liquid into fine and desirable droplets downstream of the nozzle exit [7]. Therefore, it could be concluded that droplet evolution in SPPS prefer a solvent with low surface tension and a low boiling point in gas mixture with H2, which agrees with the previous observations in Section 5.3.
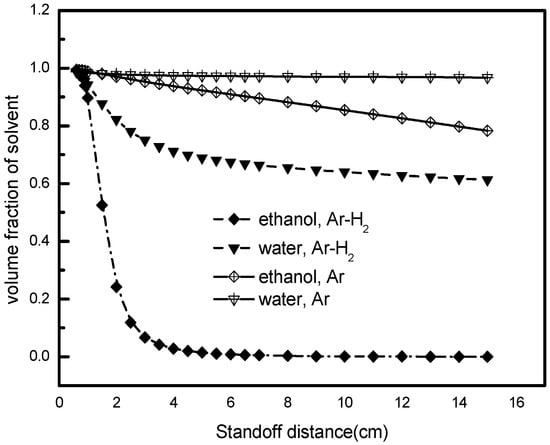
Figure 9.
Evolution of the solvent volume fraction in the Ar or Ar-H2 plasma gas.
5.5. Effects of Substrate Location
Apart from the effects of solvent and plasma gas properties, the substrate is another major factor affecting the droplet state in-flight history. The substrate should be set in a position where there is enough time left for the droplet to vaporize and the salts to pyrolyze, without forming the overheating nanoparticle that completely vaporizes before hitting the substrate [9,28]. As shown in Figure 10, the substrate mostly affects the water droplet size downstream of the torch outlet, but for ethanol droplets it does not, because ethanol droplets remain in a maturely-evolved situation before hitting the substrate so that the substrate cannot impose an overwhelming effect on the droplet size. From Figure 10, it can be seen that a sharply atomized rate and fine droplet size will occur when we locate the substrate in the specific secondary breakup region if the standoff distance is less than 6 cm. Thus, substrate location needs to be carefully assessed in the combination with the solvent properties and gas mixture types in order to achieve a desirable coating structure.
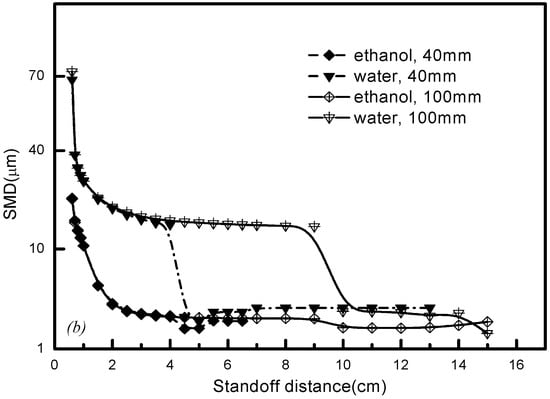
Figure 10.
Effects of substrate location on the droplet size in Ar-H2 plasma gas.
6. Conclusions
In this work, we focused on the droplet size, distribution, and composition during SPSS coating, uncovering the acting mechanism between atomization and evaporation and also discussing the influential effects behind them, including solvent and plasma types, and substrate position, which give insights for yielding fully-atomized and vaporized droplets and constructing a well-proportioned, uniform coating without undue porous clusters stacked by non-pyrolysis salts. An improved droplet vaporization model is integrated in the current code to model the interactions between droplets and the plasma jet, which is validated by a previous single-droplet vaporizing experimental work with reasonable agreement. The main conclusions are listed as follows:
- Droplet size and distribution are the main factors impacting the microstructure of the coating surface. Fine droplets resulting from the complete atomization and vaporization contributed to the formation of smaller nanoparticles and a fully melting liquid nanoparticle with low liquid stock vapor is essentially decisive to constructing pure overlapped splats on the material surface.
- Droplet size largely depends on the atomization and evaporation consequences and goes through an instant decrease, corresponding to the axial position of the hot core region and the secondary breakup region. In these areas, atomized and vaporized actions exert inconsistent influences on the modification of droplet size. According to these features, operating parameters, such as types of solvent, could be adjusted from this aspect.
- Ethanol, used as a solvent, undergoes a speedy vaporizing process resulting in a sharp droplet size decrease near the nozzle exit. The evaporation of water or other non-volatility solvent highly depends on the plasma temperature and the length of hot core region. A higher enthalpy plasma gas and a longer length of the hot core region contribute to the effective evaporation. As for ethanol or other solvents with good volatility, the hot core region does not need to be that long; instead, the solvent with suitable atomization properties then become our principal care.
- In comparison with pure Ar gas, Ar-H2 gas mixture reveals more superior performance with respect to the droplet atomizing and vaporizing as a result of the higher specific gas enthalpy, the enhancement of gas velocity, as well as better thermodynamic properties.
- In order to procure an ideal, fine droplet size and uniform distribution near the torch exit, the substrate should be located where the droplet momentum has not yet fully diminished, and in this case it should be put somewhere before the standoff distance of 6 cm.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (No. 11472245).
Author Contributions
Hongbing Xiong designed the study and Weiqi Sun conducted the simulation. Weiqi Sun wrote the draft and Hongbing Xiong edited the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fauchais, P.; Rat, V.; Coudert, J.F.; Etchart-Salas, R.; Montavon, G. Operating parameters for suspension and solution plasma-spray coatings. Surf. Coat. Technol. 2008, 202, 4309–4317. [Google Scholar] [CrossRef]
- Fauchais, P.; Etchart-Salas, R.; Rat, V.; Coudert, J.-F.; Caron, N.; Wittmann-Ténèze, K. Parameters controlling liquid plasma spraying: Solutions, sols or suspensions. J. Therm. Spray Technol. 2008, 17, 31–59. [Google Scholar] [CrossRef]
- Chen, D.; Jordan, E.H.; Gell, M. The solution precursor plasma spray coatings: Influence of solvent type. Plasma Chem. Plasma Process. 2010, 30, 111–119. [Google Scholar] [CrossRef]
- Muoto, C.K.; Jordan, E.H.; Gell, M.; Aindow, M. Identification of desirable precursor properties for solution precursor plasma spray. J. Therm. Spray Technol. 2011, 20, 802–816. [Google Scholar] [CrossRef]
- Waldbillig, D.; Kesler, O. Effect of suspension plasma spraying process parameters on YSZ coating microstructure and permeability. Surf. Coat. Technol. 2011, 205, 5483–5492. [Google Scholar] [CrossRef]
- Joulia, A.; Bolelli, G.; Gualtierie, E.; Lusvarghi, L.; Valerif, S.; Vardelle, M.; Rossignol, S.; Vardelle, A. Comparing the deposition mechanisms in suspension plasma spray (SPS) and solution precursor plasma spray (SPPS) deposition of yttria-stabilised zirconia (YSZ). J. Eur. Ceram. Soc. 2014, 34, 3925–3940. [Google Scholar] [CrossRef]
- Delbos, C.; Fazilleau, J.; Rat, V.; Coudert, J.F.; Fauchais, P.; Pateyron, B. Phenomena involved in suspension plasma spraying, Part 1: Suspension injection and behaviour. Plasma Chem. Plasma Process. 2006, 26, 371–391. [Google Scholar] [CrossRef]
- Rampon, R.; Filiatre, C.; Bertrand, G. Suspension plasma spraying of YPSZ coatings: Suspension atomization and injection. J. Therm. Spray Technol. 2008, 17, 105–114. [Google Scholar] [CrossRef]
- Bertolissi, G.; Chazelas, C.; Bolelli, G.; Lusvarghi, L.; Vardelle, M.; Vardelle, A. Engineering the microstructure of solution precursor plasma-sprayed coatings. J. Therm. Spray Technol. 2012, 21, 1148–1162. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Goutier, S.; Vardelle, A. Specific measurements of in-flight droplet and particle behavior and coating microstructure in suspension and solution plasma spraying. J. Therm. Spray Technol. 2015, 24, 1498–1505. [Google Scholar] [CrossRef]
- Marchand, C.; Chazelas, C.; Mariaux, G.; Vardelle, A. Liquid precursor plasma spraying: Modeling the interactions between the transient plasma jet and the droplets. J. Therm. Spray Technol. 2007, 16, 705–712. [Google Scholar] [CrossRef]
- Jadidi, M.; Mousavi, M.; Moghtadernejad, S.; Dolatabadi, A. A three-dimensional analysis of the suspension plasma spray impinging on a flat substrate. J. Therm. Spray Technol. 2015, 24, 11–23. [Google Scholar] [CrossRef]
- Farrokhpanah, A.; Coyle, T.W.; Mostaghimi, J. Numerical study of suspension plasma spraying. J. Therm. Spray Technol. 2017, 26, 12–36. [Google Scholar] [CrossRef]
- Huang, P.C.; Heberlein, J.; Pfender, E. Particle behavior in a two-fluid turbulent plasma jet. Surf. Coat. Technol. 1995, 73, 142–151. [Google Scholar] [CrossRef]
- Ozturk, M.; Cetegen, B.M. Modeling of plasma assisted formation of precipitates in zirconia containing liquid precursor droplets. Mater. Sci. Eng. A 2004, 384, 331–351. [Google Scholar] [CrossRef]
- Jabbari, F.; Jadidi, M.; Wuthrich, R.; Dolatabadi, A. A numerical study of suspension injection in plasma-spraying process. J. Therm. Spray Technol. 2014, 23, 3–13. [Google Scholar] [CrossRef]
- Ramshaw, J.D.; Chang, C.H. Computational fluid dynamics modeling of multi-component thermal plasmas. Plasma Chem. Plasma Process. 1992, 12, 299–325. [Google Scholar] [CrossRef]
- Tanner, F.X. Development and validation of a cascade atomization and drop breakup model for high-velocity dense sprays. At. Sprays 2004, 14, 211–242. [Google Scholar] [CrossRef]
- Xiong, H.B.; Qian, L.J.; Lin, J.Z. Simulation of effervescent atomization and nanoparticle characteristics in radio frequency suspension plasma spray. J. Therm. Spray Technol. 2012, 21, 226–239. [Google Scholar] [CrossRef]
- Shao, X.-M.; Zhang, K.; Xiong, H.-B. Modeling of micro- and nanoparticle characteristics in DC suspension plasma spray. J. Therm. Spray Technol. 2015, 24, 309–317. [Google Scholar] [CrossRef]
- Xiong, H.B.; Zheng, L.L.; Sampath, S.; Williamson, R.L.; Fincke, J.R. Three-dimensional simulation of plasma spray: Effects of carrier gas flow and particle injection on plasma jet and entrained particle behavior. Int. J. Heat Mass Transf. 2004, 47, 5189–5200. [Google Scholar] [CrossRef]
- O’Rourke, P.J.; Amsden, A.A. The TAB method for numerical calculation of spray droplet break-up. SAE Tech. Pap. 1987, 872089. [Google Scholar]
- Reitz, R.D. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Meillot, E.; Vincent, S.; Caruyer, C.; Damiani, D.; Caltagirone, J.P. Modelling the interactions between a thermal plasma flow and a continuous liquid jet in a suspension spraying process. J. Phys. D Appl. Phys. 2013, 46, 224017. [Google Scholar] [CrossRef]
- Wan, Y.P.; Prasad, V.; Wang, G.-X.; Sampath, S.; Fincke, J.R. Model and powder particle heating, melting, resolidification, and evaporation in plasma spraying processes. J. Heat Transf. 1999, 121, 691–699. [Google Scholar] [CrossRef]
- Xiong, H.; Zhang, C.; Zhang, K.; Shao, X. Effects of atomization injection on nanoparticle processing in suspension plasma spray. Nanomaterials 2016, 6, 94. [Google Scholar] [CrossRef] [PubMed]
- Wang, J. Theory and Experiment Research on Droplet Evaporation in Cross Flow. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2012. [Google Scholar]
- Pawlowski, L. Suspension and solution thermal spray coatings. Surf. Coat. Technol. 2009, 203, 2807–2829. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).