Electrodeposition of Alloys and Compounds in the Era of Microelectronics and Energy Conversion Technology
Abstract
:1. Introduction
2. Electrodeposition at the Macroscopic Scale
2.1. Thermodynamics and Redox Potential
2.2. Kinetics and Growth Rate
3. Electrodeposition at the Atomic Scale
3.1. Ion Transport
3.2. Mechanism of Electron Transfer
3.3. Kinetics of Film Growth
3.4. Growth and Film Morphology
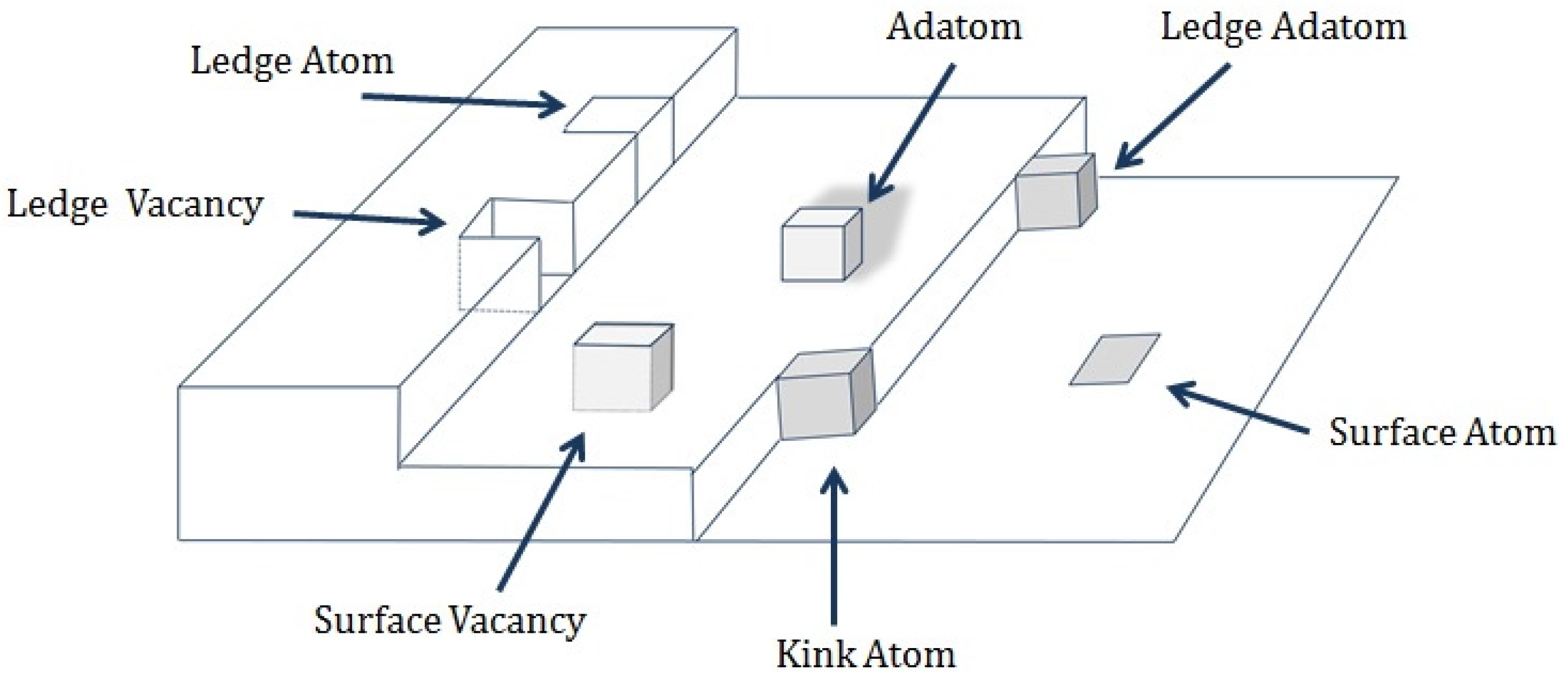
4. Overview and Taxonomy of Alloy Deposition Processes
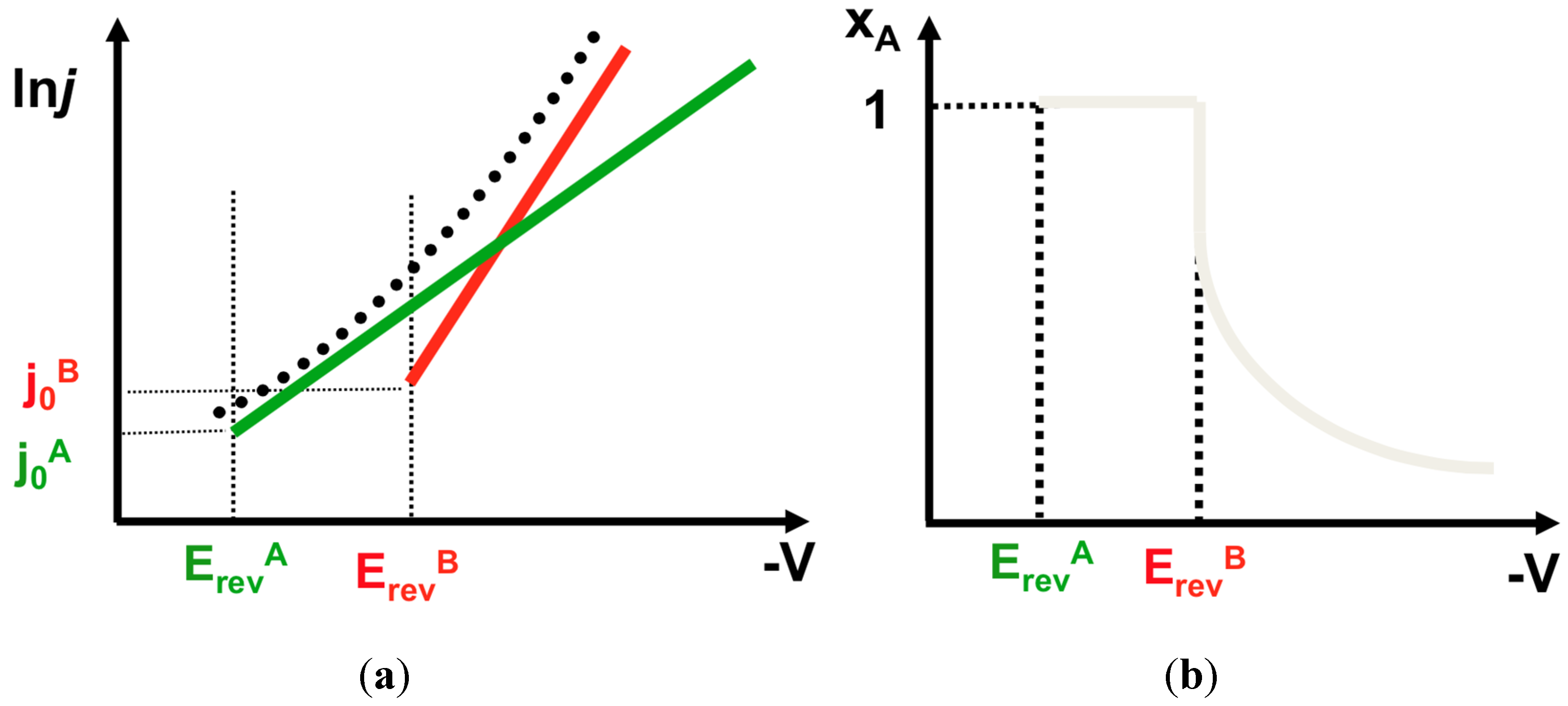
4.1. Interactions in the Bulk Electrolyte
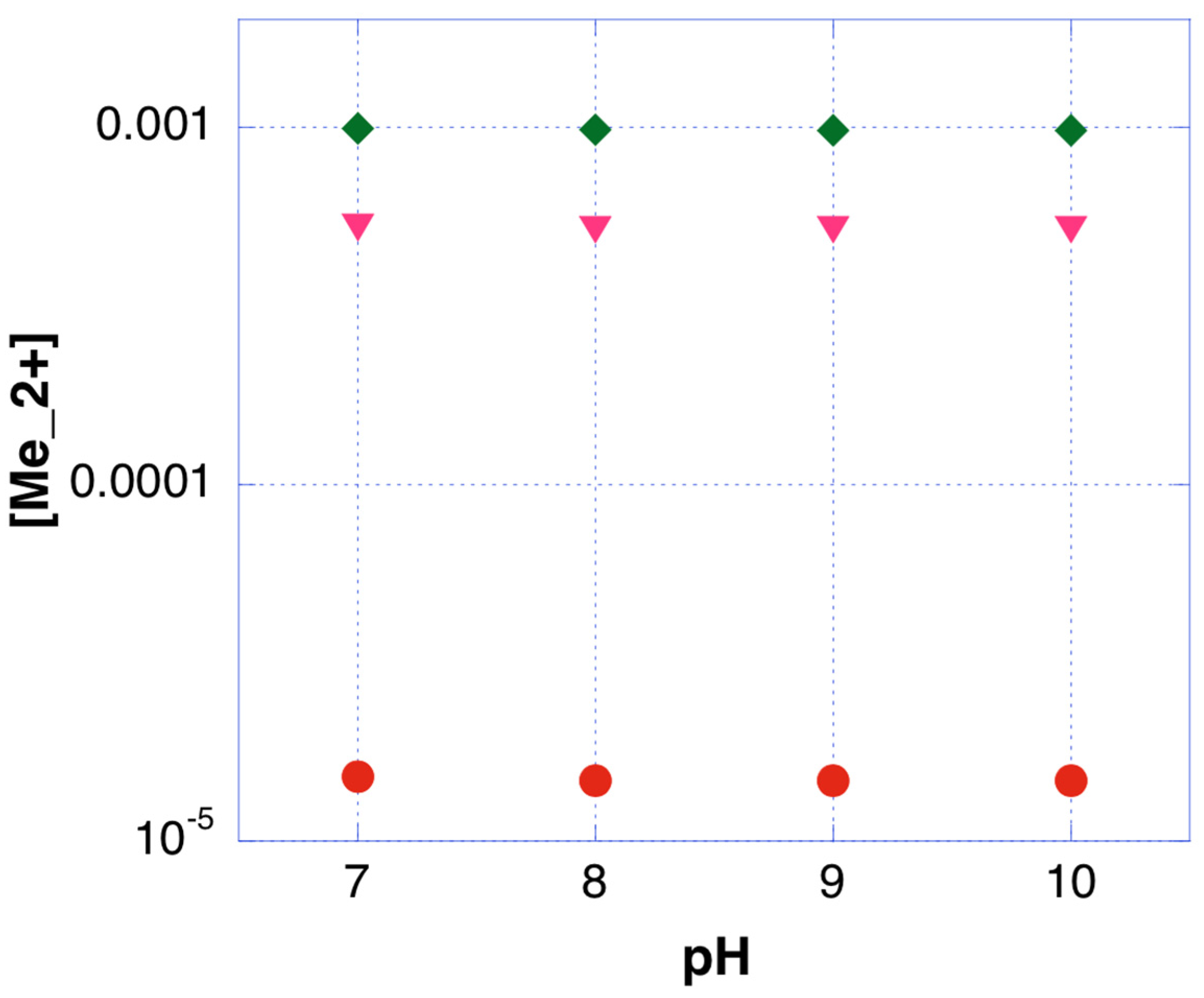
4.2. Interactions in the Solid
4.3. Interactions at the Interface
4.4. Peculiarities of Alloy Deposition
5. Surface-Limited Electrochemical Processes for Materials Synthesis
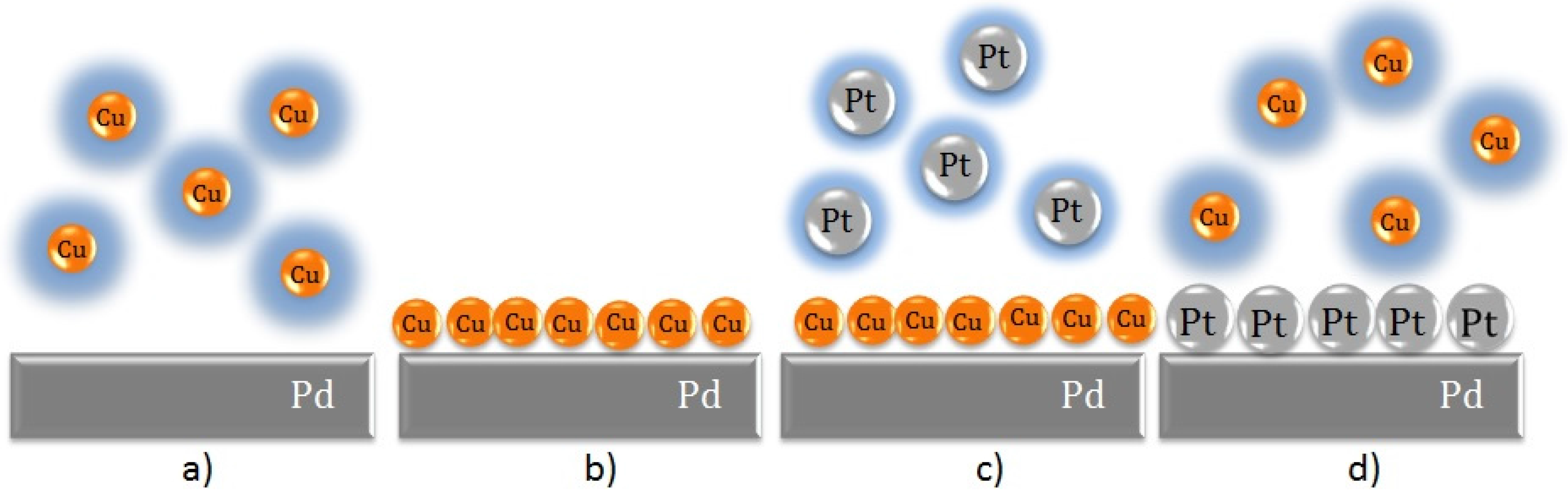
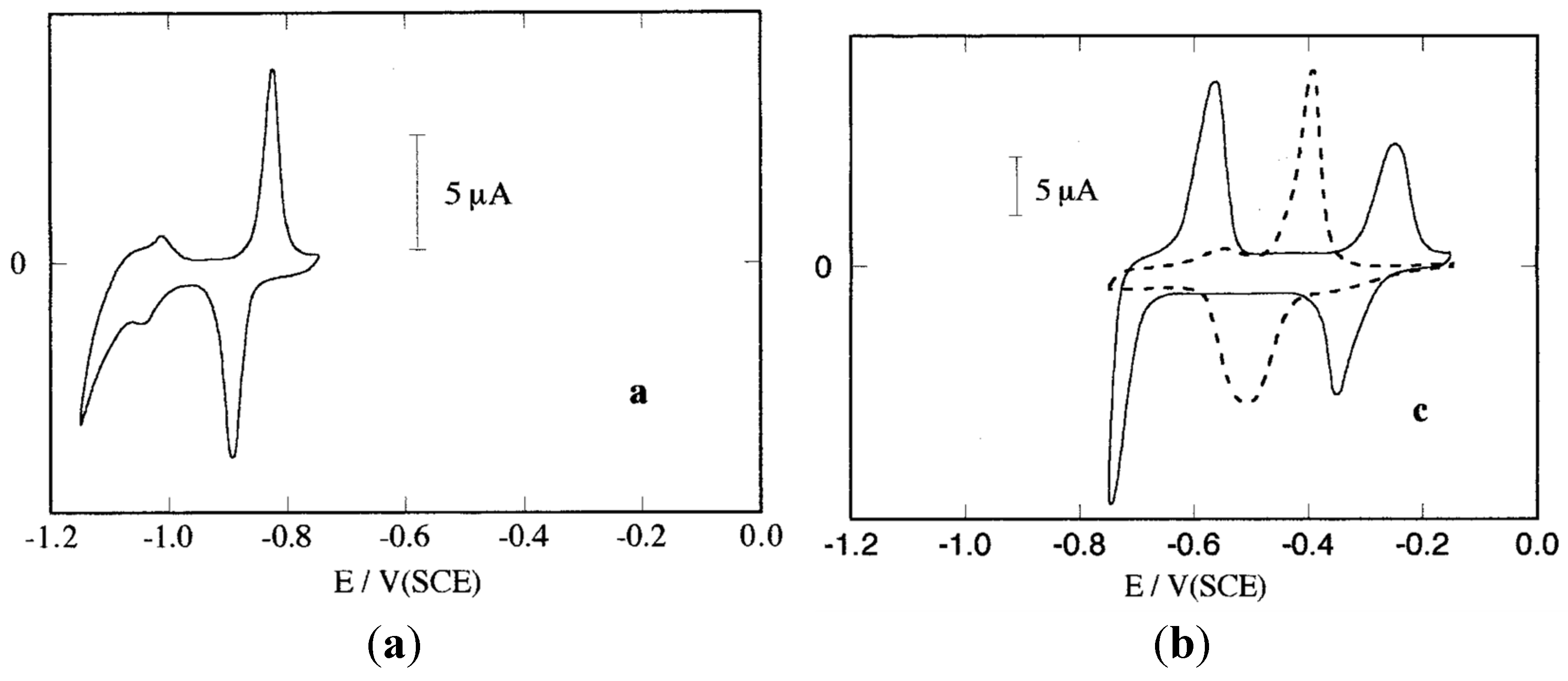
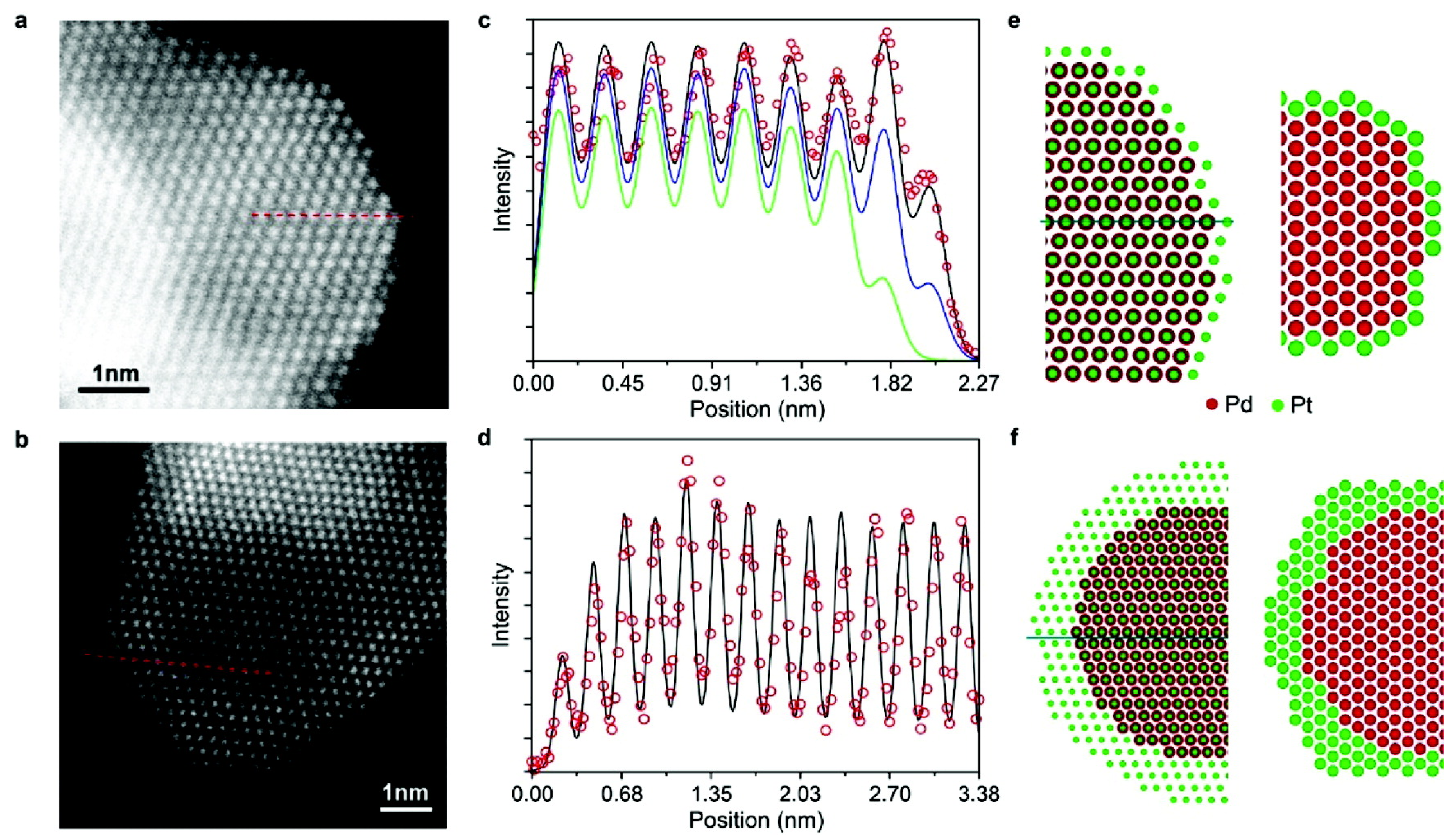
6. Final Remarks
Acknowledgement
Conflicts of Interest
References
- Gamburg, Y.D.; Zangari, G. Theory and Practice of Metal Electrodeposition; Springer: New York, NY, USA, 2011. [Google Scholar]
- Dini, J.W. Electrodeposition: The Materials Science of Coatings and Substrates; Noyes Publications: Park Ridge, NJ, USA, 1993. [Google Scholar]
- Schlesinger, M.; Paunovic, M. Modern Electroplating, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Plieth, W. Electrochemistry for Materials Science; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Mallory, G.O.; Hajdu, J.B. Electroless Plating: Fundamentals and Applications; William Andrew Publishing: Norwich, NY, USA, 1990. [Google Scholar]
- Zangari, G. Electrochemistry over matter. Electrochem. Soc. Interface 2011, 31–32. [Google Scholar]
- Hunt, L.B. The early history of gold plating. Gold Bull. 1973, 6, 16–27. [Google Scholar] [CrossRef]
- Romankiw, L.T. A path: From electroplating through lithographic masks in electronics to LIGA in MEMS. Electrochim. Acta 1997, 42, 2985–3005. [Google Scholar] [CrossRef]
- Krongelb, S.; Romankiw, L.T.; Tornello, J.A. Electrochemical process for advanced package fabrication. IBM J. Res. Dev. 1998, 42, 575–586. [Google Scholar] [CrossRef]
- Zangari, G.; Fukunaka, Y. Electrochemical processing and materials tailoring for advanced energy technology. J. Electrochem. Soc. 2014, 161, Y5–Y7. [Google Scholar] [CrossRef]
- Moffat, T.P.; Josell, D. Superconformal electrodeposition for 3-dimensional interconnects. Isr. J. Chem. 2010, 50, 312–320. [Google Scholar] [CrossRef]
- Heremans, J. Solid state magnetic field sensors and applications. J. Phys. D Appl. Phys. 1993, 26, 1149–1168. [Google Scholar] [CrossRef]
- Brankovic, S.R.; Yang, X.; Klemmer, T.J.; Seigler, M. Pulse electrodeposition of 2.4 T Co37Fe63 alloys at nanoscale for magnetic recording application. IEEE Trans. Magn. 2006, 42, 132–139. [Google Scholar] [CrossRef]
- Xiao, F.; Hangarter, C.; Yoo, B.; Rheem, Y.; Lee, K.H.; Myung, N.V. Recent progress in electrodeposition of thermoelectric thin films and nanostructures. Electrochim. Acta 2008, 53, 8103–8117. [Google Scholar] [CrossRef]
- Yan, R.; Gargas, D.; Yang, P. Nanowire photonics. Nat. Photonics 2009, 3, 569–576. [Google Scholar] [CrossRef]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Lombardi, I.; Marchionna, S.; Zangari, G.; Pizzini, S. Effect of Pt particle size and distribution on photoelectrochemical hydrogen evolution by p-Si photocathodes. Langmuir 2007, 23, 12413–12420. [Google Scholar] [CrossRef] [PubMed]
- Vukmirovic, M.B.; Bliznakov, S.T.; Sasaki, K.; Wang, J.X.; Adzic, R.R. Electrodeposition of metals in catalyst synthesis: The case of platinum monolayer electrocatalysts. Electrochem. Soc. Interface 2011, 20, 33–40. [Google Scholar]
- Potentials and Thermodynamics of Cells. In Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Bard, A.J.; Faulkner, L.R. (Eds.) Wiley: New York, NY, USA, 2000.
- Guo, L.; Oskam, G.; Radisic, A.; Hoffmann, P.M.; Searson, P.C. Island growth in electrodeposition. J. Phys. D Appl. Phys. 2011, 44. [Google Scholar] [CrossRef]
- Heusler, K.E. Multicomponent electrodes. Electrochim. Acta 1996, 41, 411–418. [Google Scholar] [CrossRef]
- Kinetics of Electrode Reactions. In Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Bard, A.J.; Faulkner, L.R. (Eds.) Wiley: New York, NY, USA, 2000.
- Vetter, K.J. Electrochemical Kinetics: Theoretical Aspects; Academic Press: London, UK, 1967. [Google Scholar]
- Pleskov, Y.V. The Rotating Disk Electrode; Springer: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Giesen, M.; Beltramo, G.; Dieluweit, S.; Müller, J.; Ibach, H.; Schmickler, W. The thermodynamics of electrochemical annealing. Surf. Sci. 2005, 595, 127–137. [Google Scholar] [CrossRef]
- Marcus, R.A. Chemical and electrochemical electron-transfer theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Hush, N.S. Distance dependence of electron transfer rates. Coordination Chem. Rev. 1985, 64, 135–157. [Google Scholar] [CrossRef]
- Gileadi, E. The enigma of metal deposition. J. Electroanal. Chem. 2011, 660, 247–253. [Google Scholar] [CrossRef]
- Pinto, L.; Spohr, E.; Quaino, P.; Santos, E.; Schmickler, W. Why silver deposition is so fast: Solving the enigma of metal deposition. Angew. Chem. Int. Ed. 2013, 52, 7883–7885. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Lagally, M.G. Atomistic processes in the early stages of thin-film growth. Science 1997, 276, 377–383. [Google Scholar] [CrossRef] [PubMed]
- Morin, S.; Lachenwitzer, A.; Magnussen, O.M.; Behm, R.J. Potential-controlled step flow to 3D step decoration transition: Ni electrodeposition on Ag (111). Phys. Rev. Lett. 1999, 83, 5066–5069. [Google Scholar] [CrossRef]
- Kern, K. Surface Roughening: experimental aspects. In The Chemical Physics of Solid Surfaces and Heterogeneous Catalysis; King, D.A., Woodruff, D.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1993. [Google Scholar]
- Wu, Q.; Barkey, D. Faceting and roughening transitions on copper single crystals in acid sulfate plating baths with chloride. J. Electrochem. Soc. 2000, 147, 1038–1045. [Google Scholar] [CrossRef]
- Budevski, E.; Bostanov, V.; Staikov, G. Electrocrystallization. Annu. Rev. Mater. Sci. 1980, 10, 85–112. [Google Scholar] [CrossRef]
- Bockris, J.O’M.; Despic, A.R. The mechanism of deposition and dissolution of metals. In Physical Chemistry—An Advanced Treatise; Eyring, H., Ed.; Academic Press: New York, NY, USA; London, UK, 1970. [Google Scholar]
- Venables, J.A. Atomic processes in crystal growth. Surf. Sci. 1994, 299, 798–817. [Google Scholar] [CrossRef]
- Scharifker, B.; Hills, G. Theoretical and experimental studies of multiple nucleation. Electrochim. Acta 1983, 28, 879–889. [Google Scholar] [CrossRef]
- Hyde, M.E.; Compton, R.G. A review of the analysis of multiple nucleation with diffusion controlled growth. J. Electroanal. Chem. 2003, 549, 1–12. [Google Scholar] [CrossRef]
- Budevski, E.B.; Staikov, G.T.; Lorenz, W.J. Electrochemical Phase Formation and Growth: An Introduction to the Initial Stages of Metal Deposition; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- He, Y.; Borguet, E. Effect of local environment on nanoscale dynamics at electrochemical interfaces: Anisotropic growth and dissolution in the presence of a step providing evidence for a Schwoebel–Ehrlich barrier at solid/liquid interfaces. Faraday Discuss. 2002, 121, 17–25. [Google Scholar] [CrossRef] [PubMed]
- Bergstresser, T.R.; Merchant, H.D. Surface morphology of electrodeposits. In Defect Structures, Morphology and Properties of Electrodeposits; Merchant, H.D., Ed.; The Minerals, Metals and Materials Society: Warrendale, PA, USA, 1995. [Google Scholar]
- Léger, C.; Servant, L.; Bruneel, J.L.; Argoul, F. Growth patterns in electrodeposition. Phys. A Stat. Mech. Appl. 1999, 263, 305–314. [Google Scholar] [CrossRef]
- Witten, T.A., Jr.; Sander, L.M. Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 1981, 47, 1400. [Google Scholar] [CrossRef]
- Schwarzacher, W. Kinetic roughening of electrodeposited films. J. Phys. Condens. Matter 2004, 16. [Google Scholar] [CrossRef]
- Chen, C.-P.; Jorne, J. The dynamics of morphological instability during electrodeposition. J. Electrochem. Soc. 1991, 138, 3305–3311. [Google Scholar] [CrossRef]
- Sieradzki, K.; Dimitrov, N. Electrochemical defect-mediated thin-film growth. Science 1999, 284, 138–141. [Google Scholar] [CrossRef] [PubMed]
- Andricacos, P.C.; Uzoh, C.; Dukovic, J.O.; Horkans, J.; Deligianni, H. Damascene copper electroplating for chip interconnections. IBM J. Res. Dev. 1998, 42, 567–574. [Google Scholar] [CrossRef]
- Landolt, D. Fundamental aspects of alloy plating. Plat. Surf. Finish. 2001, 88, 70–79. [Google Scholar]
- Brenner, A. Electrodeposition of Alloys: Principles and Practice; Academic Press: New York, NY, USA; London, UK, 1963. [Google Scholar]
- Brankovic, S.R.; Zangari, G. Electrochemical Surface Processes and Opportunities for Material Synthesis. In Electrochemical Engineering across Scales: From Molecules to Processes; VCH-Wiley: Weinheim, Germany, 2015. [Google Scholar]
- Mallett, J.J.; Shao, W.; Liang, D.; Zangari, G. Underpotential codeposition of Cu–Au alloys. Electrochem. Solid-State Lett. 2009, 12, D57–D60. [Google Scholar] [CrossRef]
- Mallett, J.J.; Svedberg, E.B.; Sayan, S.; Shapiro, A.J.; Wielunski, L.; Madey, T.E.; Chen, P.J.; Egelhoff, W.F.; Moffat, T.P. Compositional Control in Electrodeposited CoxPt1−x Films. Electrochem. Solid-State Lett. 2005, 8, C15–C18. [Google Scholar] [CrossRef]
- Mallett, J.J.; Svedberg, E.B.; Sayan, S.; Shapiro, A.J.; Wielunski, L.; Madey, T.E.; Egelhoff, W.F.; Moffat, T.P. Compositional control in electrodeposition of FePt films. Electrochem. Solid-State Lett. 2004, 10, C121–C124. [Google Scholar] [CrossRef]
- Mallett, J.J.; Bertocci, U.; Bonevich, J.E.; Moffat, T.P. Compositional control in electrodeposited Pt100−xCux Alloys. J. Electrochem. Soc. 2009, 156, D531–D542. [Google Scholar] [CrossRef]
- Liang, D.; Mallett, J.J.; Zangari, G. Electrodeposition of Fe-Pt films with low oxide content using an alkaline complexing electrolyte. ACS Appl. Mater. Interfaces 2010, 2, 961–964. [Google Scholar] [CrossRef] [PubMed]
- Liang, D.; Mallett, J.J.; Zangari, G. Underpotential codeposition of Fe-Pt alloys from an alkaline complexing electrolyte: Electrochemical studies. J. Electrochem. Soc. 2011, 158, D149–D157. [Google Scholar] [CrossRef]
- Liang, D.; Zangari, G. Electrochemical deposition of Fe-Pt magnetic alloy films with large magnetic anisotropy. ECS Trans. 2013, 50, 35–47. [Google Scholar] [CrossRef]
- Liang, D.; Rajput, P.; Zegenhagen, J.; Zangari, G. Nanoscale structuring in Au–Ni films grown by electrochemical underpotential Co-deposition. Chem. Electro. Chem. 2014, 1, 787–792. [Google Scholar] [CrossRef]
- Lincot, D. Electrodeposition of semiconductors. Thin Solid Films 2005, 487, 40–48. [Google Scholar] [CrossRef]
- Andricacos, P.C.; Romankiw, L.T. Magnetically soft materials in data storage: Their properties and electrochemistry. Adv. Electrochem. Sci. Eng. 1994, 3, 227–321. [Google Scholar]
- Dahms, H.; Croll, I.M. The Anomalous Codeposition of Iron-Nickel Alloys. J. Electrochem. Soc. 1965, 112, 771–775. [Google Scholar] [CrossRef]
- Matlosz, M. Competitive adsorption effects in the electrodeposition of iron-nickel alloys. J. Electrochem. Soc. 1993, 140, 2272–2279. [Google Scholar] [CrossRef]
- Zech, N.; Podlaha, E.J.; Landolt, D. Anomalous codeposition of iron group metals: I. Experimental results. J. Electrochem. Soc. 1999, 146, 2886–2891. [Google Scholar] [CrossRef]
- Zech, N.; Podlaha, E.J.; Landolt, D. Anomalous codeposition of iron group metals: II. Mathematical model. J. Electrochem. Soc. 1999, 146, 2892–2900. [Google Scholar] [CrossRef]
- Podlaha, E.J.; Landolt, D. Induced codeposition I. An experimental investigation of Ni-Mo alloys. J. Electrochem. Soc. 1996, 143, 885–892. [Google Scholar] [CrossRef]
- Podlaha, E.J.; Landolt, D. Induced codeposition II. A mathematical model describing the electrodeposition of Ni-Mo alloys. J. Electrochem. Soc. 1996, 143, 893–899. [Google Scholar] [CrossRef]
- Younes, O.; Gileadi, E. Electroplating of Ni/W alloys I. Ammoniacal citrate baths. J. Electrochem. Soc. 2002, 149, C100–C111. [Google Scholar] [CrossRef]
- Younes-Metzler, O.; Zhu, L.; Gileadi, E. The anomalous codeposition of tungsten in the presence of nickel. Electrochim. Acta 2003, 48, 2551–2562. [Google Scholar] [CrossRef]
- Naor, A.; Eliaz, N.; Gileadi, E. Electrodeposition of rhenium–nickel alloys from aqueous solutions. Electrochim. Acta 2009, 54, 6028–6035. [Google Scholar] [CrossRef]
- Georgiev, G.S.; Georgieva, V.T.; Plieth, W. Markov chain model of electrochemical alloy deposition. Electrochim. Acta 2005, 51, 870–876. [Google Scholar] [CrossRef]
- Plieth, W. Kinetic models for alloy and semiconductor electrodeposition. Electrochim. Acta 2007, 53, 245–249. [Google Scholar] [CrossRef]
- Kolb, D.M. Advances in Electrochemical Engineering; Gerischer, H., Tobias, W., Eds.; Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Sudha, V.; Sangaranarayanan, M.V. Underpotential deposition of metals–progress and prospects in modeling. J. Chem. Sci. 2005, 117, 207–218. [Google Scholar] [CrossRef]
- Brankovic, S.R.; Wang, J.X.; Adzic, R.R. Metal monolayer deposition by replacement of metal adlayers on electrode surfaces. Surf. Sci. 2001, 474, L173–L179. [Google Scholar] [CrossRef]
- Fayette, M.; Liu, Y.; Bertrand, D.; Nutariya, J.; Vasiljevic, N.; Dimitrov, N. From Au to Pt via surface limited redox replacement of Pb UPD in one-cell configuration. Langmuir 2011, 27, 5650–5658. [Google Scholar] [CrossRef] [PubMed]
- Nutariya, J.; Fayette, M.; Dimitrov, N.; Vasiljevic, N. Growth of Pt by surface limited redox replacement of underpotentially deposited hydrogen. Electrochim. Acta 2013, 112, 813–823. [Google Scholar] [CrossRef]
- Gokcen, D.; Bae, S.E.; Brankovic, S.R. Stoichiometry of Pt submonolayer deposition via surface-limited redox replacement reaction. J. Electrochem. Soc. 2010, 157, D582–D587. [Google Scholar] [CrossRef]
- Innocenti, M.; Bellandi, S.; Lastraioli, E.; Loglio, F.; Foresti, M.L. Selective electrodesorption based atomic layer deposition (SEBALD): A novel electrochemical route to deposit metal clusters on Ag (111). Langmuir 2011, 27, 11704–11709. [Google Scholar] [CrossRef] [PubMed]
- Nişancı, F.B.; Öznülüer, T.; Demir, Ü. Photoelectrochemical properties of nanostructured ZnO prepared by controlled electrochemical underpotential deposition. Electrochim. Acta 2013, 108, 281–287. [Google Scholar] [CrossRef]
- Stickney, J.L. Electrochemical Atomic Layer Epitaxy (EC-ALE): Nanoscale Control in the Electrodeposition of Compound Semiconductors. In Advances in Electrochemical Science and Engineering; Alkire, R.C., Kolb, D.M., Eds.; Wiley: New York, NY, USA; Volume 7, pp. 1–105.
- Dimitrov, N.; Vasilic, R.; Vasiljevic, N. A kinetic model for redox replacement of UPD layers. Electrochem. Solid-state Lett. 2007, 10, D79–D83. [Google Scholar] [CrossRef]
- Innocenti, M.; Pezzatini, G.; Forni, F.; Foresti, M.L. CdS and ZnS deposition on Ag (111) by electrochemical atomic layer epitaxy. J. Electrochem. Soc. 2001, 148, C357–C362. [Google Scholar] [CrossRef]
- Wang, J.X.; Inada, H.; Wu, L.; Zhu, Y.; Choi, Y.M.; Liu, P.; Zhou, W.-P.; Adzic, R.A. Oxygen reduction on well-defined core-shell nanocatalysts: particle size, facet, and Pt-shell thickness effect. J. Am. Chem. Soc. 2009, 131, 17298–17302. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zangari, G. Electrodeposition of Alloys and Compounds in the Era of Microelectronics and Energy Conversion Technology. Coatings 2015, 5, 195-218. https://doi.org/10.3390/coatings5020195
Zangari G. Electrodeposition of Alloys and Compounds in the Era of Microelectronics and Energy Conversion Technology. Coatings. 2015; 5(2):195-218. https://doi.org/10.3390/coatings5020195
Chicago/Turabian StyleZangari, Giovanni. 2015. "Electrodeposition of Alloys and Compounds in the Era of Microelectronics and Energy Conversion Technology" Coatings 5, no. 2: 195-218. https://doi.org/10.3390/coatings5020195
APA StyleZangari, G. (2015). Electrodeposition of Alloys and Compounds in the Era of Microelectronics and Energy Conversion Technology. Coatings, 5(2), 195-218. https://doi.org/10.3390/coatings5020195




