Next Article in Journal
Thermal Aging-Induced Alterations in Surface and Interface Topography of Bio-Interactive Dental Restorative Materials Assessed by 3D Non-Contact Profilometry
Previous Article in Journal
IMTS-YOLO: A Steel Surface Defect Detection Model Integrating Multi-Scale Perception and Progressive Attention
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Coatings
Volume 16
Issue 1
10.3390/coatings16010052
coatings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A First-Principles Study of Lithium Adsorption and Diffusion on Graphene and Defective-Graphene as Anodes of Li-Ion Batteries

by
Lina Si
,
Yijian Yang
,
Yuhao Wang
,
Qifeng Wu
,
Rong Huang
,
Hongjuan Yan
*,
Mulan Mu
,
Fengbin Liu
and
Shuting Zhang
*
School of Mechanical and Materials Engineering, North China University of Technology, Beijing 100144, China
*
Authors to whom correspondence should be addressed.
Coatings 2026, 16(1), 52; https://doi.org/10.3390/coatings16010052 (registering DOI)
Submission received: 3 November 2025 / Revised: 23 December 2025 / Accepted: 25 December 2025 / Published: 3 January 2026
(This article belongs to the Section Surface Engineering for Energy Harvesting, Conversion, and Storage)
Browse Figures
Review Reports Versions Notes

Abstract

Defective graphene has emerged as a promising strategy to enhance electrochemical performance of pristine graphene (p-Gr) as anodes in lithium-ion batteries (LIBs). Herein, we perform a comprehensive first-principles study based on density functional theory (DFT) to systematically investigate the Li adsorption, charge transfer, and diffusion behaviors of p-Gr and defective graphene (d-Gr) with single vacancy (SV Gr) and double vacancy (DV5-8-5 Gr) defects, aiming to clarify the mechanism by which defects modulate Li storage performance. Structural optimization reveals that SV Gr undergoes notable out-of-plane distortion after Li adsorption, while DV5-8-5 Gr retains planar geometry but exhibits more significant C-C bond length variations compared to p-Gr. Binding energy results confirm that defects enhance Li adsorption stability, with DV5-8-5 Gr showing the strongest Li–graphene interaction, followed by SV Gr and p-Gr. Bader charge analysis and charge density difference plots further validate that defects enhance charge transfer from Li ions to graphene. Using the nudged elastic band (NEB) method, we find that defects reduce Li diffusion barriers: DV5-8-5 Gr exhibits a lower barrier than p-Gr. Our findings demonstrate that DV5-8-5 Gr exhibits the most favorable Li storage performance, providing a robust theoretical basis for designing high-performance graphene anodes for next-generation LIBs.

1. Introduction

The rapid development of electric vehicles, portable electronic devices, and large-scale energy storage systems has driven an urgent demand for lithium-ion batteries (LIBs) with high energy density, long cycle life, and excellent safety [1,2,3]. As a key component of LIBs, the anode material plays a crucial role in determining the overall performance of the battery. Graphene, with its unique two-dimensional (2D) structure, high electrical conductivity, large specific surface area, and outstanding mechanical properties, has been recognized as a promising candidate for LIB anodes [4,5]. However, pristine graphene anodes suffer from two critical limitations: relatively low theoretical lithium storage capacity and significant volume expansion during the lithium insertion/extraction process, both of which hinder their practical application [6].
Defective graphene has recently emerged as a viable solution to enhance the lithium storage performance of graphene-based anodes [7,8]. Graphene commonly exhibits two typical point defects: single vacancy (SV) and divacancy (DV) defects. SV defects are formed by removing one carbon atom, while DV defects are created by removing a C-C dimer [8,9]. These defects can effectively tailor the electronic structure of graphene, create additional active sites for lithium adsorption, and strengthen the interaction between lithium ions and the graphene matrix [10]. This makes defective graphene a more attractive option for LIB anodes, as it has the potential to overcome the limitations of pristine graphene and achieve higher energy density and improved cycling stability [11].
In recent years, extensive experimental studies have focused on the lithium insertion behavior of graphene and defective graphene [12,13,14,15,16]. A wide range of graphene-based anode materials has been synthesized, and their electrochemical performance has been characterized. For example, Pan et al. reported that graphene sheets can achieve a maximum reversible capacity of 1054 mAh/g [14]. Another study demonstrated that defective graphene anodes exhibit increased capacity during cycling, which is attributed to the presence of defects and the unique structure that facilitates lithium storage [15]. Lee et al. further revealed that defects promote the diffusion of Li ions perpendicular to the graphene basal plane, while diffusion parallel to the plane is restricted by steric hindrance from aggregated Li ions adsorbed on abundant defect sites [16]. Despite these advances, challenges such as maintaining long-term cycling stability persist.
Theoretically, first-principles calculations based on density functional theory (DFT) have become a powerful tool to study the lithium adsorption energy, diffusion pathways, and electronic properties of graphene and defective graphene systems. A series of DFT studies has been carried out to explore how defects tune Li–graphene interactions. Early work confirmed that defects enhance Li storage compared to pristine graphene [11,17,18,19]. For example, Zhou et al. [11] analyzed Li behavior on graphene with point defects (Stone–Wales (SW55-77) and double vacancy (DV5-8-5)), showing DV5-8-5 stabilizes Li at octagon-ring hollow sites; a separate study further demonstrated single vacancy (SV) defects boost Li adsorption stability via enhanced binding energy [17]. However, these studies focused on individual defect types and lacked systematic comparison. Cheng et al. [19] investigated Li adsorption and diffusion on graphene with vacancy defects of different sizes, and their results showed that, unlike pristine graphene, these defective structures could adsorb Li atoms stably and dispersedly. Studies on defect density (e.g., Datta et al. [20]) reported that increasing DV density raises Li storage capacity to 1675 mAh/g by enhancing charge transfer and creating additional adsorption sites. Zheng et al. [21] quantified Li+ diffusion barriers (0.32 eV for pristine graphene, 10.68 eV for cross-plane penetration). Zhou et al. [22] extended their investigation to grain boundary defects, and their work showed that the (2,0)|(2,0) boundary exhibits strong Li binding. Fan et al. [23] focused on the effect of the Li/C ratio on Li adsorption and Li diffusion between graphene layers. These DFT studies collectively establish that defects enhance graphene’s Li storage performance. However, no prior study has systematically compared the two most common vacancy defects (SV and DV5-8-5) to clarify how their distinct structural/electronic features modulate the intrinsic mechanisms of Li adsorption, charge transfer, and diffusion on graphene. 15
In this work, we conducted a comprehensive first-principles study to systematically investigate the lithium insertion behavior of pristine graphene (p-Gr) and defective graphene (d-Gr) as LIB anodes. We thoroughly examined the effects of various defects on lithium adsorption energy and Li diffusion on the surfaces of p-Gr and d-Gr. The objective is to provide a solid theoretical basis for the design and optimization of high-performance graphene-based anodes for next-generation LIBs.

2. Computational Method

First-principles calculations were performed using the MedeA Vienna Ab initio Simulation Package (VASP) [24]. The electron–ion interactions were described by the projected augmented wave (PAW) pseudopotential [25]. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional was adopted for the exchange-correlation potential [26]. To account for van der Waals interactions, which are crucial for describing the weak interactions between Li ions and graphene, the DFT-D3 method with Becke–Johnson (BJ) damping was employed [27,28]. A gamma-centered k-grid with a 3 × 3 × 1 mesh was used for Brillouin zone integration, and a plane-wave energy cutoff of 400 eV was applied. The spin-polarized calculation employed in the present study is considered a possible magnetism of defective graphene. Geometry optimizations were performed using the conjugate gradient method until the residual force on each atom was less than 0.02 eV/Å and the energy change per atom was less than 10−5 eV.
We investigated the lithium intercalation properties of p-Gr and d-Gr, considering two common defects in d-Gr: SV and DV5-8-5 defects, both of which are experimentally prevalent, structurally well-defined vacancy defects [7,8]. Additionally, other defect types (e.g., SW defects, grain boundary defects) will be explored in future work. The primitive unit cell of graphene consists of two carbon atoms arranged in a 2D honeycomb lattice with a hexagonal structure. Based on this primitive cell, a 6 × 6 hexagonal supercell with dimensions of 14.682 Å × 14.682 Å was used as the p-Gr model. To eliminate interactions between the model and its periodic replicas along the z-axis, a 15 Å vacuum layer was introduced perpendicular to the graphene surface. Periodic boundary conditions were applied in all three directions. d-Gr models were constructed by introducing vacancies into the p-Gr supercell: single-vacancy graphene (SV Gr) was obtained by removing one carbon atom and optimizing the structure; double-vacancy graphene (DV5-8-5 Gr) was obtained by removing two adjacent carbon atoms, followed by structural optimization to form a 5-8-5 ring configuration, which is the most stable structure for double vacancies in graphene.
Top and front views of different graphene models with Li ions adsorbed at various sites are shown in Figure 1. The VESTA Version 3 software was used to generate the atomic structures in Figure 1 and subsequent figures [29]. For Li ion adsorption on p-Gr, three typical sites were considered: hollow site (Li1), above the center of a carbon hexagon ring; top site (Li2), directly above a carbon atom; and bridge site (Li3), above the midpoint of a C-C bond. For Li ion adsorption of SV Gr, three typical adsorption sites were evaluated: hollow site (Li4): above the center of a carbon hexagon ring; top site (Li5), directly above a carbon atom; center site (Li6), directly above the removed carbon atom (vacancy center). For Li ion adsorption of DV5-8-5 Gr, three typical adsorption sites were examined: hollow site (Li7): above the center of a carbon hexagon ring; top site (Li8), directly above a carbon atom; and center site (Li9), above the center of the octagon ring. The initial position of each Li ion was set 1.5 Å above the graphene surface. All structures were fully relaxed to obtain the lowest- energy configurations by first-principles calculations.
The lithium adsorption behavior on different graphene structures was evaluated by calculating the binding energy (Eb) using the following formula [30]:
Eb = Ediff-Gr + ELi − Etot
where Ediff-Gr is the energy of the graphene system (p-Gr, SV Gr, or DV5-8-5 Gr) without Li insertion, Etot is the energy of the Li-adsorbed graphene system, and ELi is the energy of an isolated Li ion. The isolated Li atoms were placed in a 14.682 Å × 14.682 Å × 17 Å cubic supercell (sufficient to avoid self-interactions) with the same DFT parameters as the graphene systems. A positive Eb indicates a thermodynamically favorable Li intercalation process, and a larger Eb value corresponds to more stable Li adsorption.
To analyze the charge redistribution induced by Li adsorption, the charge density difference (Δρ) is calculated using the following formula [30]:
Δρ = ρtot − ρdiff-Gr − ρLi
where ρtot is the charge density of the Li-adsorbed graphene system, ρdiff-Gr is the charge density of the graphene system without Li adsorption, and ρLi is the charge density of an isolated Li ion.

3. Results and Discussions

3.1. The Lowest-Energy Li Adsorption Structures and Binding Energy Analysis

To identify the energetically favorable Li adsorption sites, we examined non-equivalent adsorption positions on different graphene surfaces and calculated their binding energies. Figure 2, Figure 3 and Figure 4 show the lowest-energy structures of Li adsorbed on p-Gr, SV Gr, and DV5-8-5 Gr surfaces, respectively. For p-Gr (Figure 2), compared with the pre-optimization structures (Figure 1a), the position of the Li1 ion (hollow site) remains nearly unchanged after structural optimization, indicating that the hollow site is inherently a stable adsorption position for p-Gr. In contrast, the Li2 (top site) and Li3 (bridge site) ions, initially located above a single carbon atom and the midpoint of a C-C bond, respectively, diffuse to new positions above the center of carbon hexagon rings. The vertical distance between Li ions and the p-Gr surface adjusts from the initial 1.5 Å to approximately 1.67 Å. Throughout the optimization process, the p-Gr structure maintains a planar configuration.
For SV Gr (Figure 3), compared with the pre-optimization structures, the Li4, Li5, and Li6 ions all migrate toward the center site (i.e., the position above the removed carbon atom) after structural optimization. Meanwhile, full structural relaxation causes the SV Gr layer to evolve into a configuration consisting of a pentagon ring and a nonagon ring. The vertical distance between Li ions and the SV Gr surface adjusts from the initial 1.5 Å to approximately 1.93 Å. It is further observed that the presence of vacancies (defects) and Li adsorption significantly alter the geometric structure of graphene [31]. Specifically, the insertion of Li ions disrupts the force balance within the SV Gr lattice, causing several carbon atoms to protrude from the original graphene plane, resulting in a non-planar surface with a distortion height ranging from approximately 0.3 to 0.5 Å. A relevant study has demonstrated that such surface protrusions can form “anchoring sites,” which in turn accelerate the lateral migration of lithium ions [32].
For DV5-8-5 Gr (Figure 4), after structural optimization, the Li8 and Li9 ions diffuse to the center site above the carbon octagon ring, while the Li7 ion is adsorbed above the center of a carbon hexagon ring adjacent to the octagon ring. The vertical distance between Li ions and the DV5-8-5 Gr surface adjusts from the initial 1.5 Å to approximately 1.54 Å. To verify whether DV5-8-5 Gr retains its planar structure after Li adsorption, we calculated the out-of-plane displacement (Δz) before/after Li adsorption, defined as the difference in z-coordinate between each C atom in DV5-8-5 Gr and the average z-plane of the graphene sheet. The Δz of C atoms within an 8 Å radius of the defect site (the region most sensitive to Li-induced distortion) was calculated and summarized the maximum and average Δz values in Table 1. For DV5-8-5 Gr, after Li adsorption, the maximum out-of-plane displacement of C atoms is only 0.04 Å, which is far below the threshold for meaningful distortion. From the above results, it is clear that in contrast to SV Gr, the geometric configuration of DV5-8-5 Gr remains unaltered after optimization, retaining a planar structure.
To further analyze the structural changes of graphene layers before and after Li adsorption, we investigated the variations in C-C bond lengths in the graphene plane near the adsorbed Li ions. Before Li adsorption, the C-C bond lengths of the carbon hexagon ring in the p-Gr lattice beneath the Li1 ion are approximately 1.413 Å, which is consistent with previous reports [7]. After Li adsorption, the bond lengths increase slightly to around 1.415 Å, with a maximum change of only 0.002 Å. This negligible variation indicates that Li adsorption has little effect on the lattice structure of p-Gr.
Table 2 presents the C-C bond lengths of the carbon nonagon ring in SV Gr near the Li6 ion. Before Li adsorption, the C-C bond lengths around the vacancy range from 1.388 Å to 1.404 Å. After Li adsorption, the maximum change in C-C bond lengths reaches approximately 0.129 Å (far more significant than that in p-Gr). This result aligns with the structural analysis of the lowest-energy Li-adsorbed SV Gr: the SV Gr structure undergoes substantial changes upon Li adsorption, leading to notable variations in C-C bond lengths.
Table 3 lists the C-C bond lengths of the carbon octagon ring in DV5-8-5 Gr near the Li8 ion. Before Li adsorption, the C-C bond lengths of the octagon ring range from 1.461 Å to 1.468 Å. After Li adsorption, the maximum change in C-C bond lengths is approximately 0.159 Å, and the lattice edge with the largest bond length variation is one of the edges of the adjacent pentagon ring. This is not random but reflects targeted lattice relaxation: The DV5-8-5 defect inherently disrupts graphene’s periodic honeycomb lattice, creating localized strain at the 5-8-5 ring junctions. Li adsorption exacerbates this strain by transferring charge to nearby C atoms, inducing repulsive electrostatic interactions between negatively charged C atoms.
Figure 5 shows the calculated binding energies for all Li-adsorbed configurations. For p-Gr, the binding energies are relatively low (approximately 0.41 eV), which is attributed to the stable π-electron cloud of pristine graphene, hindering the formation of stable chemical bonds with Li ions. In contrast, the binding energies of Li adsorbed on both types of defective graphene (SV Gr and DV5-8-5 Gr) are significantly higher than those on p-Gr, with DV5-8-5 Gr exhibiting the highest binding energy. For SV Gr, the binding energies at the three adsorption sites are relatively consistent, approximately 0.38 eV higher than those on p-Gr. This enhancement is due to the unpaired electrons introduced by the single vacancy, which modify the electron density around carbon atoms—creating regions with higher local electron density that facilitate the formation of strong chemical bonds with Li ions. For DV5-8-5 Gr, the binding energies at the Li8 and Li9 sites are relatively similar (about 0.02 eV higher than that at the Li7 site), while being approximately 0.74 eV higher than those on SV Gr. Compared with SV Gr, DV5-8-5 Gr introduces more significant local structural effects and electronic perturbations, leading to a stronger interaction between Li ions and the graphene matrix, resulting in even higher binding energies.
In summary, the binding energy follows the order: DV5-8-5 Gr > SV Gr > p-Gr. This indicates that the DV5-8-5 Gr structure is the most stable and most favorable for Li ion adsorption. The binding energy is influenced by factors such as defect type and Li adsorption position. By controlling the type and distribution of defects in graphene, the cycling stability and Li storage capacity of graphene-based anodes can be effectively improved, providing valuable insights for the development of high-performance LIBs.

3.2. Charge Density Difference Analysis and Bader Charge Analysis

To elucidate the electronic interaction mechanisms during Li-ion intercalation in p-Gr and d-Gr, systematic analyses of charge density difference (Δρ) plots were conducted, with representative results presented in Figure 6. As illustrated in Figure 6a, the Δρ plots of Li ions adsorbed at the Li1, Li2, and Li3 sites (after structural optimization) exhibit essential consistency. Upon Li-ion adsorption, the electron density surrounding Li ions decreases, accompanied by partial electron transfer from Li ions to adjacent carbon atoms. Concurrently, the electron density between neighboring C-C bonds is reduced, leading to weakened C-C interactions.
For SV Gr and DV5-8-5 Gr (Figure 6b,c), distinct charge distributions are observed at the vacancy sites. Taking SV Gr (Figure 6b) as an example, the combination of vacancy defects and Li-ion intercalation induces more pronounced electron cloud redistribution compared to p-Gr. A similar trend is evident in DV5-8-5 Gr (Figure 6c): vacancy defects disrupt the periodicity of graphene’s electronic structure, enhancing the polarizability of the local atomic environment. Consequently, Li ions anchored at vacancies exert a stronger attraction on adjacent electron clouds, forming new charge density patterns that differ distinctly from those in the surrounding regions.
Bader charge analysis—an established first-principles-based method for quantifying charge transfer via topological analysis of electron density [33]—was employed to further characterize the charge redistribution behavior. Table 4 summarizes the calculated charge transfer values for different graphene systems. For Li-ion adsorption on the graphene systems studied, the charge transferred from Li to the graphene layer falls within a narrow range: approximately +0.894|e| for p-Gr, ~0.905|e| for SV Gr, and ~0.910|e| for DV5-8-5 Gr. The above observations are consistent with the findings from previous literature.
The magnitude of the Bader charge transfer on the defective graphene surface shows a negligible difference from that on the defect-free graphene surface. The Bader charge state of carbon atoms is approximately −0.79|e|. The interaction between the adsorbed Li atom and its nearest neighbor C atoms is predominantly ionic, and valence electrons of the adsorbed Li atoms are transferred to the nearest neighbor C atoms.

3.3. Diffusion of Li on Different Graphene

Finally, the nudged elastic band (NEB) method [34] was employed to investigate the diffusion barriers associated with Li atom migration between various adsorption sites. Before calculating the NEB path, the initial and final structures were fully relaxed. For both pristine graphene and defective graphene systems, we constructed the NEB pathways with five intermediate images (excluding the initial and final states). This number is determined based on preliminary tests: increasing the number to seven images resulted in a barrier difference of less than 0.02 eV compared to five images, confirming that five images are sufficient to capture the energy profile accurately without high computational cost. After the initial elastic band calculation is finished, a refinement step sets up the same number of linearly interpolated images between two images bracketing the expected saddle point. With a small number of images, the transition barrier can be over- or underestimated; creating a finer distance between the images by increasing their number also increases the computational cost and affects convergence. The refinement overcomes this situation by closer examination of the region around the suspected transition states. The convergence was judged by two criteria: (1) force convergence: the maximum force on any atom in the intermediate images was converged to 0.05 eV/Å; (2) energy convergence: the energy difference between consecutive iterations was less than 1 × 10−4 eV, ensuring stable convergence of the energy profile.
The diffusion barrier (ΔE), which is defined as the energy difference between the saddle point and the local potential energy minimum, was calculated. The diffusion path schematic diagrams and the energy curves for Li diffusion between adjacent adsorption sites are presented in Figure 7. For p-Gr, the hollow site is confirmed as the most thermodynamically stable adsorption position. Accordingly, Li diffusion was considered as the migration from one hollow site S1 to a neighboring hollow site S2 (Figure 7a,b), yielding a ΔE of approximately 0.30 eV. As illustrated in Figure 7a, the bridge site B1, located directly above the midpoint of a C-C bond, was identified as the saddle point along this diffusion pathway, consistent with the typical migration mechanism of Li on defect-free graphene lattices [11].
For SV Gr (Figure 7c,d), Li diffusion was examined along the path (S1-B1-S2-B2-S3). The calculated ΔE for the diffusion pathways (S1-B1-S2) and (S2-B2-S3) are about 0.25 eV and 0.24 eV. Similar to p-Gr, the saddle point along this migration route corresponds to a bridge site (B1) above the midpoint of a C-C bond adjacent to the vacancy. For DV5-8-5 Gr (Figure 7e,f), Li diffusion was simulated along two paths (S1-B1-S2-B2-S3 and S1-B3-S4). The computed energy barriers (ΔEs) for the diffusion pathways (S1-B1-S2), (S2-B2-S3), and (S1-B3-S4) are ~0.21 eV, ~0.13 eV, and ~0.17 eV, respectively. As can be seen from the above results, the diffusion barrier between hexagon sites around the defect is about 0.13 eV for DV5-8-5 Gr, and 0.24 eV for SV Gr, which is less than that of p-Gr (0.30 eV).
The reduced diffusion barrier in d-Gr can be attributed to the defect-induced local structural distortion that reconfigures the graphene lattice, creating a “low-energy channel” for Li-ion migration [35]. The progressively lower ΔE in DV5-8-5 Gr (vs. SV Gr and p-Gr) further suggests that larger defect regions induce more significant lattice distortion and electronic modulation, making them more effective in facilitating Li-ion mobility, and this trend is consistent with previous DFT studies on defect-engineered graphene anodes [36].

4. Conclusions

In this work, we conducted a systematic first-principles investigation to explore the effects of SV and DV5-8-5 defects on the Li adsorption, charge transfer, and diffusion behaviors of graphene anodes for LIBs. The key conclusions are summarized as follows: Pristine graphene (p-Gr) maintains a planar structure after Li adsorption, with Li ions preferentially anchoring at hollow sites. In contrast, SV Gr undergoes significant out-of-plane distortion and notable C-C bond changes due to Li adsorption. DV5-8-5 Gr retains planar geometry but exhibits the largest C-C bond length variation among the three systems. Binding energy results confirm that defects enhance Li adsorption stability, with DV5-8-5 Gr showing the strongest Li–graphene interaction, followed by SV Gr and p-Gr. The NEB method demonstrates that defects reduce Li diffusion barriers.
Our results suggest that intentional introduction of point defects, particularly DV5-8-5 defects, is recommended when utilizing graphene as an LIB anode material, which simultaneously achieves stronger Li binding and faster Li diffusion compared to SV defects or pristine graphene.

Author Contributions

Writing—original draft preparation, conceptualization, investigation, methodology, and writing—review and editing, L.S.; data curation and formal analysis, Y.Y., Y.W., Q.W. and R.H.; supervision and writing—review and editing, H.Y., M.M. and S.Z.; funding acquisition, F.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the support of the National Natural Science Foundation of China (Grant No. 52575193), the Joint Funds of the National Natural Science Foundation of China (Grant No. U23A2025), and the Beijing Natural Science Foundation (Grant No. 3212003).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
  2. Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
  3. Si, L.N.; Song, B.; Yan, H.J.; Zhang, S.T.; Chen, Q.H. A first-principles study of the lithium insertion behaviors in graphene/Si composites anodes. Comp. Mater. Sci. 2024, 233, 112754. [Google Scholar] [CrossRef]
  4. Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
  5. Stoller, M.D.; Park, S.; Zhu, Y.; An, J.; Ruoff, R.S. Graphene-based ultracapacitors. Nano Lett. 2008, 8, 3498–3502. [Google Scholar] [CrossRef] [PubMed]
  6. Huang, X.; Yin, Z.Y.; Wu, S.X.; Qi, X.Y.; He, Q.Y.; Zhang, Q.C.; Yan, Q.Y.; Boey, F.; Zhang, H. Graphene-based materials: Synthesis, characterization, properties, and applications. Small 2011, 7, 1876–1902. [Google Scholar] [CrossRef] [PubMed]
  7. Qin, W.; Lu, W.C.; Xue, X.Y.; Ho, K.M.; Wang, C.Z. Lithium diffusion in silicon encapsulated with graphene. Nanomaterial 2021, 11, 3397. [Google Scholar] [CrossRef]
  8. Bhatt, M.D.; Kim, H.; Kim, G. Various defects in graphene: A review. RSC Adv. 2022, 33, 21520–21547. [Google Scholar] [CrossRef]
  9. Si, L.N.; Huang, R.; Liu, F.B.; Chen, Q.H.; Ouyang, P.X.; Dou, Z.L. Study on the influence of defective graphene on the Li diffusion performance in Si/defective graphene composite anodes: An ab initio molecular dynamics study. ACS Omega 2025, 10, 19502–19509. [Google Scholar] [CrossRef]
  10. Wang, G.X.; Shen, X.P.; Yao, J.; Park, J.S. Graphene nanosheets for enhanced lithium storage in lithium ion batteries. Carbon 2009, 47, 2049–2053. [Google Scholar] [CrossRef]
  11. Zhou, L.J.; Hou, Z.F.; Wu, L.M. First-principles study of lithium adsorption and diffusion on graphene with point defects. J. Phys. Chem. C 2012, 116, 21780–21787. [Google Scholar] [CrossRef]
  12. Zhu, J.P.; Duan, R.; Zhang, S.; Jiang, N.; Zhang, Y.Y.; Zhu, J. The application of graphene in lithium ion battery electrode materials. SpringerPlus 2014, 3, 585. [Google Scholar] [CrossRef]
  13. Luo, R.P.; Lv, W.Q.; Wen, K.C.; He, W.D. Overview of Graphene as Anode in Lithium-ion Batteries. J. Electron. Sci. Technol. 2018, 16, 57–68. [Google Scholar]
  14. Pan, D.; Wang, S.; Zhao, B.; Wu, M.; Zhang, H.; Wang, Y.; Jiao, Z. Li storage properties of disordered graphene nanosheets. Chem. Mater. 2009, 21, 3136–3142. [Google Scholar] [CrossRef]
  15. Li, G.; Xu, S.W.; Li, B.; Yin, M.S.; Shao, F.; Li, H.; Xia, T.; Yang, Z.; Su, Y.J.; Zhang, Y.F.; et al. In-plane defect engineering enabling ultra-stable graphene paper-based hosts for lithium metal anodes. ChemElectroChem 2021, 8, 3273–3281. [Google Scholar] [CrossRef]
  16. Yao, F.; Gunes, F.; Ta, H.Q.; Lee, S.M.; Chae, S.J.; Sheem, K.Y.; Cojocaru, C.S.; Xie, S.S.; Lee, Y.H. Diffusion Mechanism of Lithium Ion through Basal Plane of Layered Graphene. J. Am. Chem. Soc. 2012, 134, 8646–8654. [Google Scholar] [CrossRef] [PubMed]
  17. Pašti, I.A.; Jovanović, A.; Dobrota, A.S.; Mentus, S.V.; Johansson, B.; Skorodumova, N.V. Atomic adsorption on graphene with a single vacancy: Systematic DFT study through the periodic table of elements. Phys. Chem. Chem. Phys. 2017, 20, 858. [Google Scholar] [CrossRef] [PubMed]
  18. Yildirim, H.; Kinaci, A.; Zhao, Z.J.; Chan, M.K.Y.; Greeley, J.P. First-principles analysis of defect-mediated Li adsorption on graphene. ACS Appl. Mater. Interfaces 2014, 6, 21141. [Google Scholar] [CrossRef]
  19. Cheng, Z.; Zhang, X.; Zhang, H.; Liu, H.; Yu, X.; Dai, X.; Liu, G.; Chen, G. Large vacancy-defective graphene for enhanced lithium storage. Carbon Trends 2023, 10, 100237. [Google Scholar] [CrossRef]
  20. Datta, D.; Li, J.; Koratker, N.; Shenoy, V.B. Enhanced lithiation in defective graphene. Carbon 2014, 80, 305–310. [Google Scholar] [CrossRef]
  21. Zheng, J.; Ren, Z.; Guo, P.; Fang, L.; Fan, J. Diffusion of Li+ ion on graphene: A DFT study. Appl. Surf. Sci. 2011, 258, 1651–1655. [Google Scholar] [CrossRef]
  22. Zhou, L.; Hou, Z.; Wu, L.; Zhang, Y. First-principles studies of lithium adsorption and diffusion on graphene with grain boundaries. J. Phys. Chem. C 2014, 118, 28055–28062. [Google Scholar] [CrossRef]
  23. Fan, X.; Zheng, W.T.; Kuo, J.L. Adsorption and diffusion of Li on pristine and defective graphene. ACS Appl. Mater. Interfaces 2012, 4, 2432–2438. [Google Scholar] [CrossRef]
  24. Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
  25. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  26. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  27. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  28. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  29. Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
  30. Zhou, F.; Liao, N.B.; Zhang, M.; Xue, W. Lithiation behavior of graphene-silicon composite as high performance anode for lithium-ion battery: A first principles study. Appl. Surf. Sci. 2019, 463, 610–615. [Google Scholar] [CrossRef]
  31. Odbadrakh, K.; McNutt, N.W.; Nicholson, D.M.; Rios, O.; Keffer, D.J. Lithium diffusion at Si-C interfaces in silicon-graphene composites. Appl. Phys. Lett. 2014, 105, 053906. [Google Scholar] [CrossRef]
  32. Ni, K.; Wang, X.; Tao, Z.; Yang, J.; Shu, N.; Ye, J.; Pan, F.; Xie, J.; Tan, Z.; Sun, X.; et al. In Operando Probing of Lithium-Ion Storage on Single-Layer Graphene. Adv. Mater. 2019, 31, 1808091. [Google Scholar] [CrossRef] [PubMed]
  33. Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
  34. Mills, G.; Jónsson, H. Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems. Phys. Rev. Lett. 1994, 72, 1124–1127. [Google Scholar] [CrossRef] [PubMed]
  35. Uthaisar, C.; Barone, V. Edge effects on the characteristics of Li diffusion in graphene. Nano Lett. 2010, 10, 2838–2842. [Google Scholar] [CrossRef]
  36. Uthaisar, C.; Barone, V.; Peralta, J. Lithium adsorption on zigzag graphene nanoribbons. J. Appl. Phys. 2009, 106, 113715. [Google Scholar] [CrossRef]
Coatings 16 00052 g001
Figure 1. Various Li adsorption sites in p-Gr (a), SV Gr (b), and DV5-8-5 Gr (c) before structure optimization. The green and dark gray spheres represent the Li and C atoms.
Figure 1. Various Li adsorption sites in p-Gr (a), SV Gr (b), and DV5-8-5 Gr (c) before structure optimization. The green and dark gray spheres represent the Li and C atoms.
Coatings 16 00052 g001
Coatings 16 00052 g002
Figure 2. The lowest-energy structures of Li adsorbed on p-Gr surface with adsorption sites of Li1 (a), Li2 (b), and Li3 (c). The green and dark gray spheres represent the Li and C atoms.
Figure 2. The lowest-energy structures of Li adsorbed on p-Gr surface with adsorption sites of Li1 (a), Li2 (b), and Li3 (c). The green and dark gray spheres represent the Li and C atoms.
Coatings 16 00052 g002
Coatings 16 00052 g003
Figure 3. The lowest-energy structures of Li adsorbed on SV Gr surface with adsorption sites of Li4 (a), Li5 (b), and Li6 (c). The green and dark gray spheres represent the Li and C atoms.
Figure 3. The lowest-energy structures of Li adsorbed on SV Gr surface with adsorption sites of Li4 (a), Li5 (b), and Li6 (c). The green and dark gray spheres represent the Li and C atoms.
Coatings 16 00052 g003
Coatings 16 00052 g004
Figure 4. The lowest-energy structures of Li adsorbed on DV5-8-5 Gr surface with adsorption sites of Li7 (a), Li8 (b), and Li9 (c). The green and dark gray spheres represent the Li and C atoms.
Figure 4. The lowest-energy structures of Li adsorbed on DV5-8-5 Gr surface with adsorption sites of Li7 (a), Li8 (b), and Li9 (c). The green and dark gray spheres represent the Li and C atoms.
Coatings 16 00052 g004
Coatings 16 00052 g005
Figure 5. Binding energies (Eb, eV) of Li at different adsorption sites on p-Gr, SV Gr, and DV5-8-5 Gr.
Figure 5. Binding energies (Eb, eV) of Li at different adsorption sites on p-Gr, SV Gr, and DV5-8-5 Gr.
Coatings 16 00052 g005
Coatings 16 00052 g006
Figure 6. The charge density difference plots when Li dopant is at various sites on p-Gr (a), SV Gr (b), and DV5-8-5 Gr (c).
Figure 6. The charge density difference plots when Li dopant is at various sites on p-Gr (a), SV Gr (b), and DV5-8-5 Gr (c).
Coatings 16 00052 g006
Coatings 16 00052 g007
Figure 7. The diffusion path schematic diagrams and energy barrier ΔE along Li migration path on p-Gr (a,b), SV Gr (c,d), and DV5-8-5 Gr (e,f) surfaces.
Figure 7. The diffusion path schematic diagrams and energy barrier ΔE along Li migration path on p-Gr (a,b), SV Gr (c,d), and DV5-8-5 Gr (e,f) surfaces.
Coatings 16 00052 g007
Table 1. The maximum and average Δz values in DV5-8-5 Gr.
Table 1. The maximum and average Δz values in DV5-8-5 Gr.
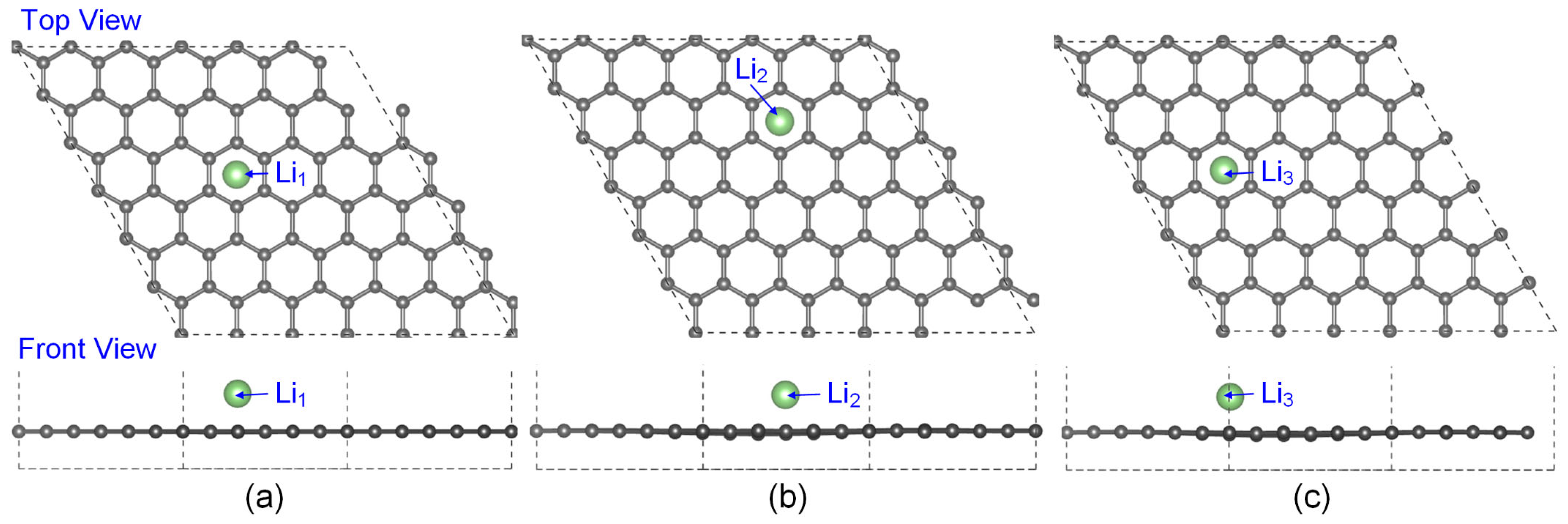
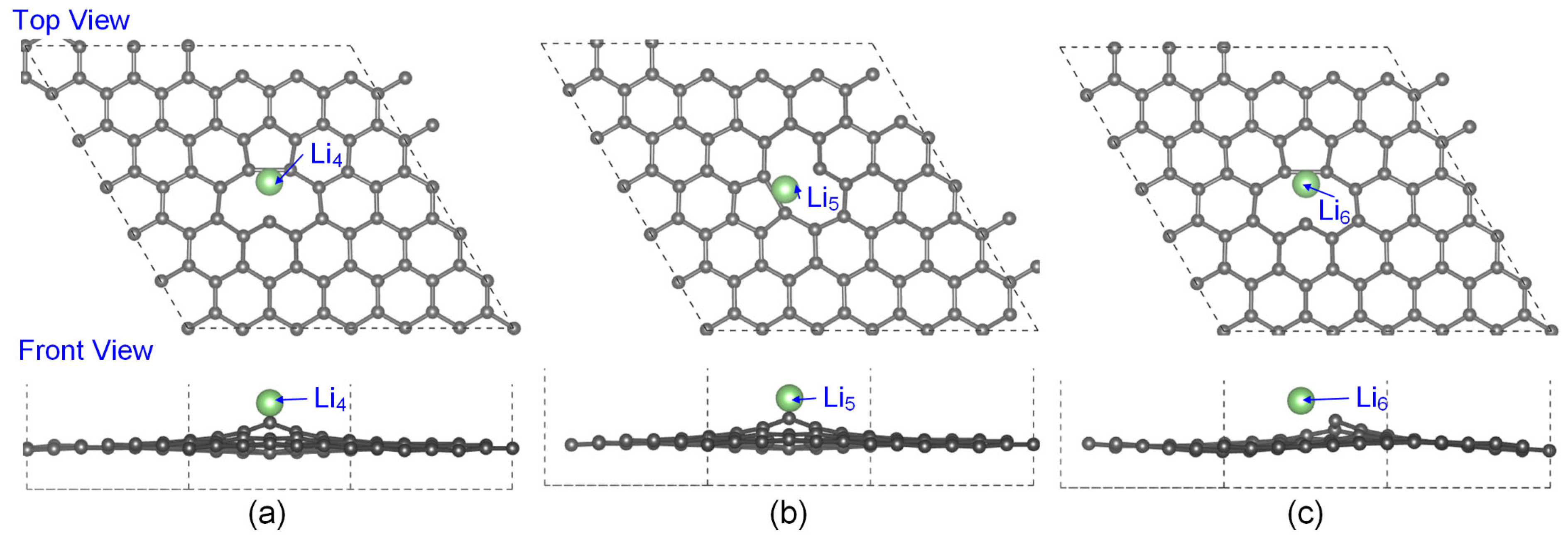
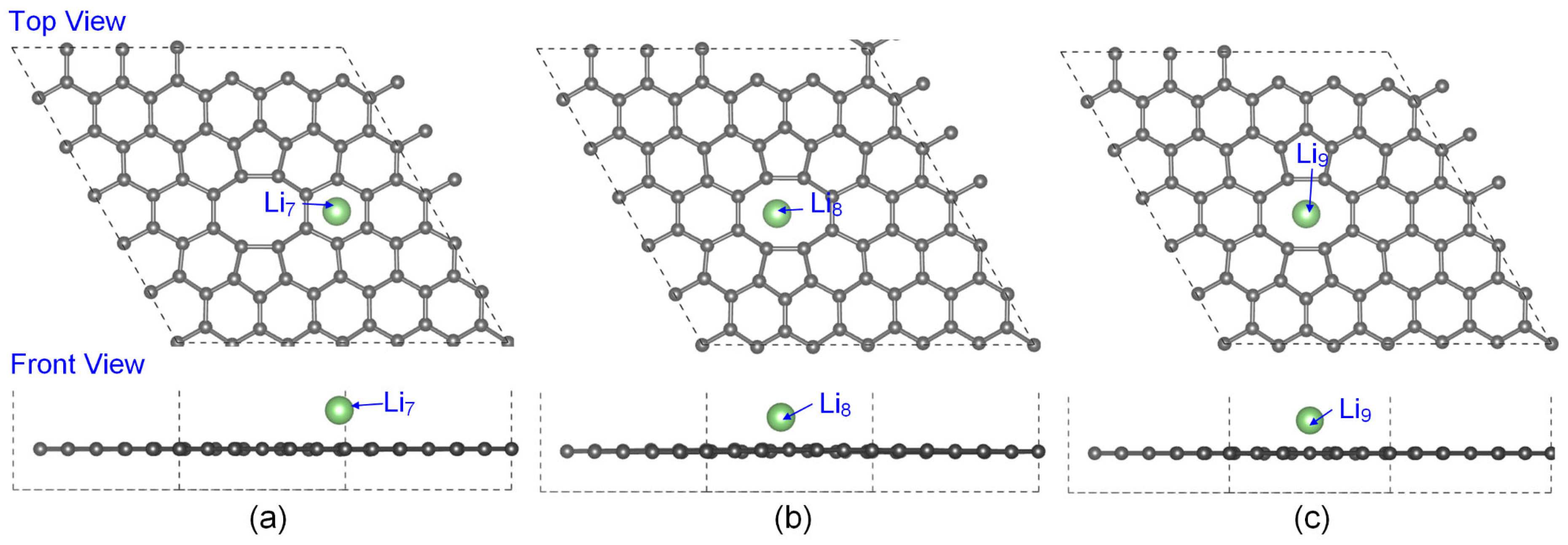
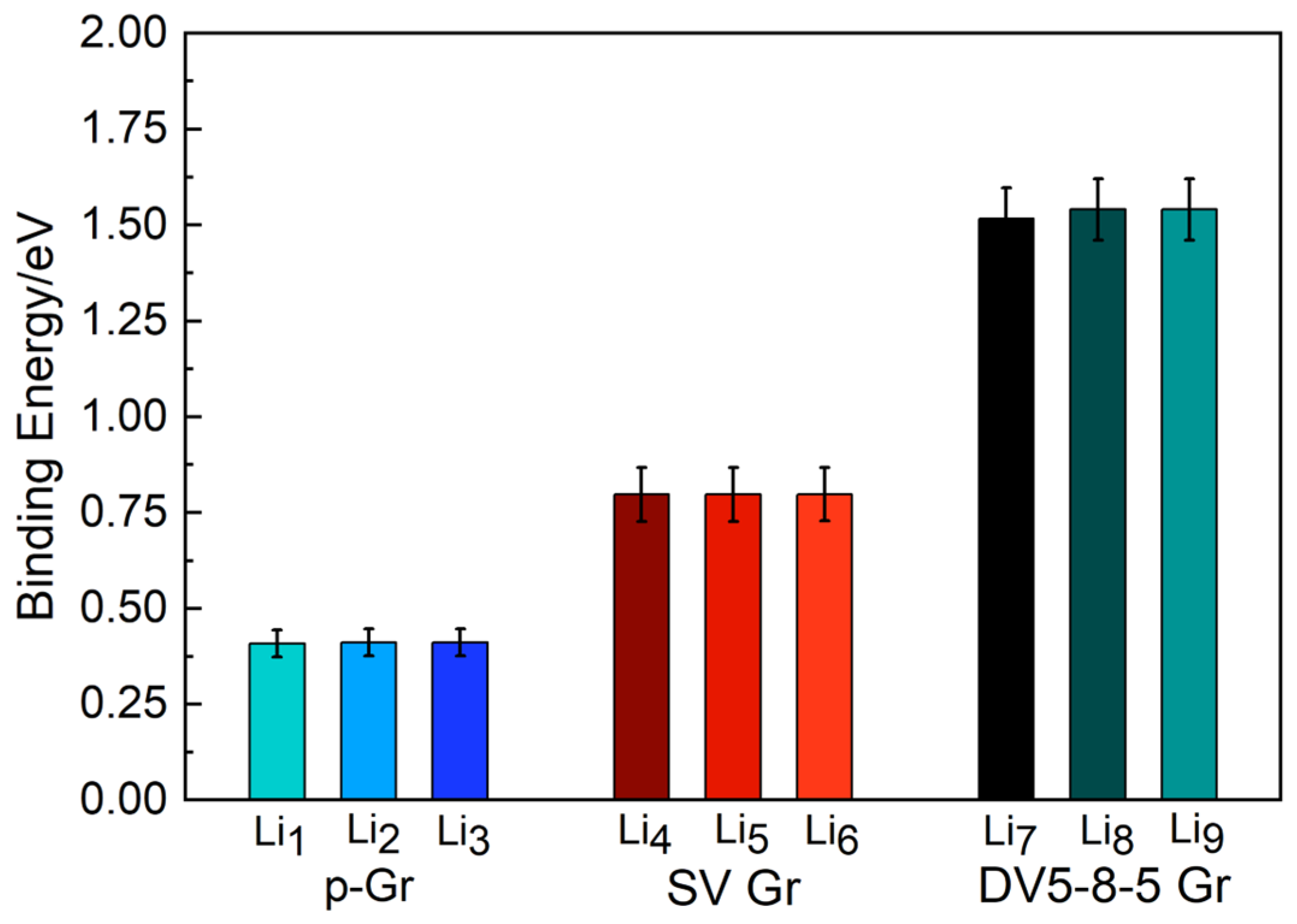
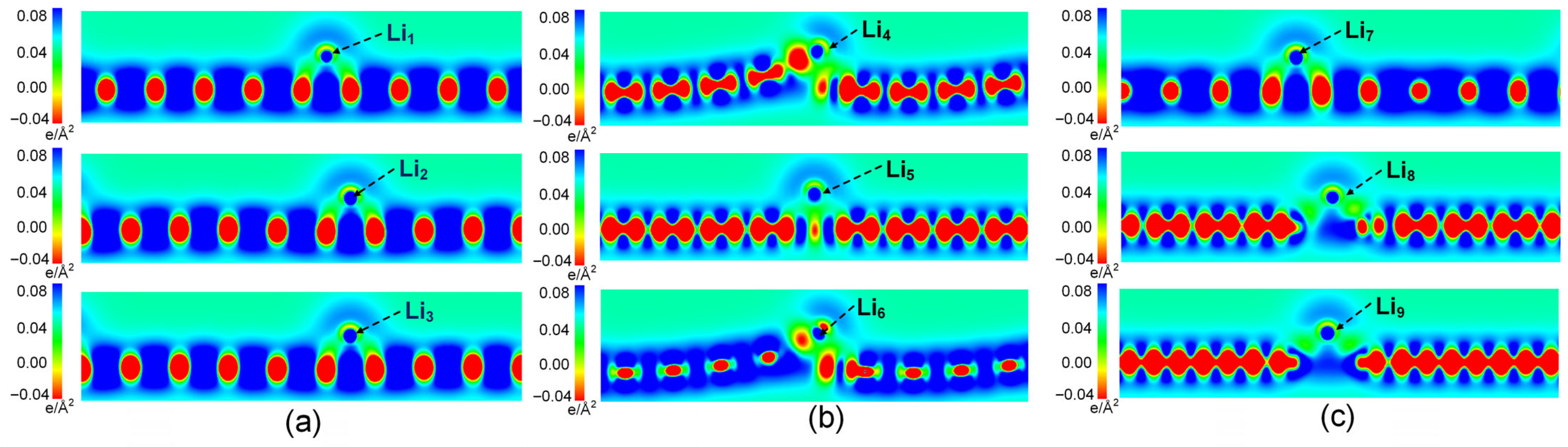
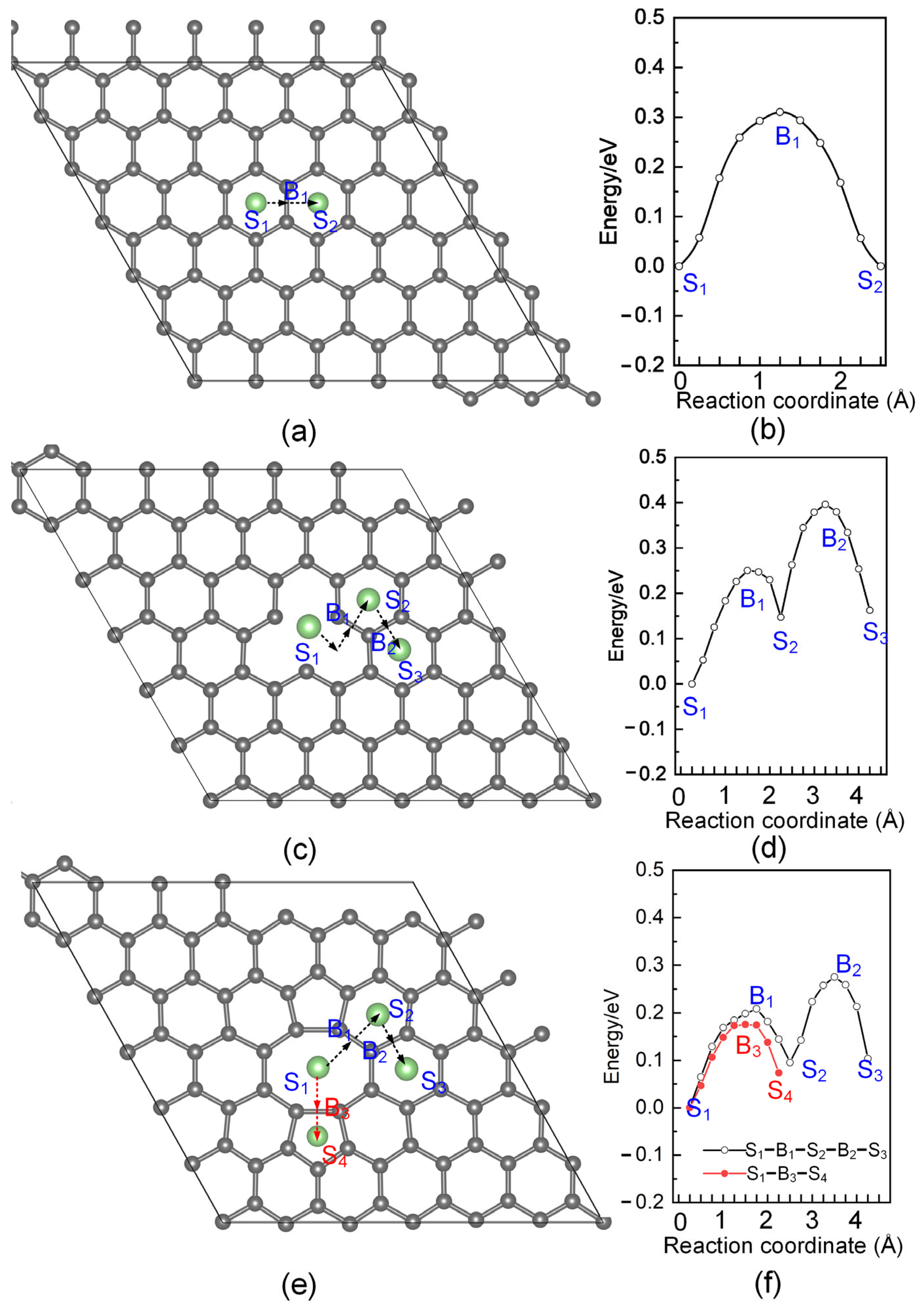
SystemMax Δz of C Atoms (Å)Avg Δz of C Atoms (Å)
DV5-8-5 Gr (before Li adsorption)0.030.01
DV5-8-5 Gr (after Li adsorption)0.040.02
Table 2. The C-C bond lengths (L) of the carbon nonagon ring in SV Gr right beneath Li6 ion.
Table 2. The C-C bond lengths (L) of the carbon nonagon ring in SV Gr right beneath Li6 ion.
Nonagon RingBond Length/ÅBefore Li AdsorptionAfter Li AdsorptionVariation
Coatings 16 00052 i001LC1-C21.3881.4090.021
LC2-C31.4041.4410.037
LC3-C41.4041.4300.025
LC4-C51.3881.5180.129
LC5-C61.4041.4620.058
LC6-C71.3891.5180.129
LC7-C81.4041.4290.025
LC8-C91.4041.4410.037
LC9-C11.3891.4090.020
Table 3. The C-C bond lengths (L) of the carbon octagon ring in DV5-8-5 Gr right beneath Li8 ion.
Table 3. The C-C bond lengths (L) of the carbon octagon ring in DV5-8-5 Gr right beneath Li8 ion.
Octagon RingBond Length/ÅBefore Li AdsorptionAfter Li AdsorptionVariation
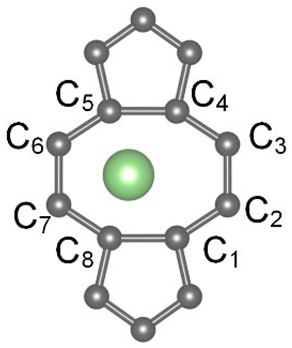Coatings 16 00052 i002LC1-C21.4611.471 0.010
LC2-C31.4621.463 0.001
LC3-C41.4621.472 0.010
LC5-C61.4611.476 0.015
LC6-C71.4621.465 0.003
LC7-C81.4621.476 0.014
LC8-C11.4681.626 0.158
LC4-C51.4681.627 0.159
Table 4. The charge transfer of Li and C atoms for various graphene structures.
Table 4. The charge transfer of Li and C atoms for various graphene structures.
Different Graphene StructureAdsorption Sites∆QLi∆QC
p-GrLi1+0.893−0.783
Li2+0.895−0.784
Li3+0.894−0.784
SV GrLi4+0.905−0.795
Li5+0.905−0.796
Li6+0.905−0.795
DV5-8-5 GrLi7+0.910−0.798
Li8+0.911−0.800
Li9+0.912−0.804
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Si, L.; Yang, Y.; Wang, Y.; Wu, Q.; Huang, R.; Yan, H.; Mu, M.; Liu, F.; Zhang, S. A First-Principles Study of Lithium Adsorption and Diffusion on Graphene and Defective-Graphene as Anodes of Li-Ion Batteries. Coatings 2026, 16, 52. https://doi.org/10.3390/coatings16010052

AMA Style

Si L, Yang Y, Wang Y, Wu Q, Huang R, Yan H, Mu M, Liu F, Zhang S. A First-Principles Study of Lithium Adsorption and Diffusion on Graphene and Defective-Graphene as Anodes of Li-Ion Batteries. Coatings. 2026; 16(1):52. https://doi.org/10.3390/coatings16010052

Chicago/Turabian Style

Si, Lina, Yijian Yang, Yuhao Wang, Qifeng Wu, Rong Huang, Hongjuan Yan, Mulan Mu, Fengbin Liu, and Shuting Zhang. 2026. "A First-Principles Study of Lithium Adsorption and Diffusion on Graphene and Defective-Graphene as Anodes of Li-Ion Batteries" Coatings 16, no. 1: 52. https://doi.org/10.3390/coatings16010052

APA Style

Si, L., Yang, Y., Wang, Y., Wu, Q., Huang, R., Yan, H., Mu, M., Liu, F., & Zhang, S. (2026). A First-Principles Study of Lithium Adsorption and Diffusion on Graphene and Defective-Graphene as Anodes of Li-Ion Batteries. Coatings, 16(1), 52. https://doi.org/10.3390/coatings16010052

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop