Next Article in Journal
Experimental Study on Overlay Tester of Asphalt Mixture Based on Discrete Element Method
Previous Article in Journal
Novel Poly(butylene succinate-dilinoleic succinate) Films in Packaging Systems for Fresh Cut Chicory
Previous Article in Special Issue
An Advanced Fatigue Life Predicting Model for High-Strength Steel Sucker Rods Integrating Material Strength Parameters
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Coatings
Volume 15
Issue 9
10.3390/coatings15091096
coatings-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Insight into the Cooperative Strengthening of Interstitial Atoms(C/N/O) and Cr in Dilute Fe-Cr System

by
Fang Wang
1,*,
Tengge Mi
1,
Pinghu Chen
1,
Hongmei Zhu
1,
Yong Chen
1,
Pengbo Zhang
2,
Ruiqing Li
3 and
Changjun Qiu
1,*
1
Key Laboratory of Hunan Province of Equipment Safety Service Technology Under Extreme Environment, School of Resource Environment and Safety Engineering, College of Mechanical Engineering, University of South China, Hengyang 421001, China
2
School of Physics, Dalian Maritime University, Dalian 116026, China
3
Light Alloys Research Institute, Central South University, Changsha 410083, China
*
Authors to whom correspondence should be addressed.
Coatings 2025, 15(9), 1096; https://doi.org/10.3390/coatings15091096
Submission received: 19 August 2025 / Revised: 4 September 2025 / Accepted: 16 September 2025 / Published: 18 September 2025
(This article belongs to the Special Issue Microstructure, Fatigue and Wear Properties of Steels, 2nd Edition)
Browse Figures
Versions Notes

Abstract

Solution strengthening is an effective strategy to improve the properties of martensitic steels (MSs). However, the microscopic mechanism of solution strengthening between Cr and interstitial atoms (IAs; C/N/O) remains elusive in dilute Fe-Cr system. Herein, this research aimed to ascertain the stability of Cr and IAs, and the interaction mechanisms between Cr and IAs by energy analysis and four-level electronic structure analysis (projected density of states, Electron Localization Function, crystal orbital Hamiltonian population, and charge density difference) in Fe-Cr alloys based on the first-principles calculations. First, studies on the thermostability of Cr and IAs show that Cr tends to occupy a central substitution site, IAs prefer to occupy octahedral interstitial sites (O-sites), whereas Fe53Cr1N/O is the most stable structure in the Cr-rich region. Therefore, the Fe53Cr1X (X=C/N/O) is selected to investigate the interaction between Cr and IAs. Moreover, the formation energy of IAs in the Fe-Cr system is significantly lower than the solid solution of IAs in the pure Fe system, indicating that there is a cooperative effect between Cr and IAs. Then, the four-level electronic structure analyses of Fe53Cr1X reveal the strong bonding between IAs and Cr, implying that the system has high stability. Furthermore, compared to the pure iron system, the increase in the dissociation temperature of IAs in the Fe-Cr system again verifies the enhancement of stability by cooperative strengthening. The results provide a theoretical basis for understanding the solid solution strengthening of IAs and Cr in martensitic steels.

Graphical Abstract

1. Introduction

Martensitic steels (MSs) are widely applied in the machinery industry, aerospace, marine engineering, and other fields for its excellent comprehensive properties (high strength, high hardness, and outstanding corrosion resistance) [1,2,3]. Laser cladding is one of the effective means to manufacture high-strength MS [4,5,6]. As a key element of MS, solute Cr has an important effect on its corrosion resistance, especially its tendency to segregate at grain boundaries, which affects the mechanical properties of the alloy [7,8]. Moreover, interstitial atoms (IAs, mainly referring to C, N, and O), as the key alloy elements or impurities of MS, are inevitably doped during the process of laser cladding [9,10,11]. Our previous experimental results indicate that high-strength stainless steel with excellent properties can be produced by laser cladding rapid solidification technology, which is closely related to the solid solution of IAs, their interaction with solute Cr, and the formation of Cr complex clusters [12,13,14]. However, it is still a challenge to explore the microstructure and interaction between solute Cr and IAs in MS at the atomic scale so as to reveal the microscopic principle of solid solution strengthening.
First-principles calculations are a useful method for investigating the atomic-level interaction between atoms (Cr and IAs) in the Fe-Cr system [15,16,17]. Many researchers have focused on the effect of a solid solution of solute Cr on the Fe-Cr system [18,19,20,21,22,23]. The interaction between Fe-Cr and its effect on magnetism has been investigated by Klaver et al., Paduani et al., and Liu et al.; their results indicate that the repulsive effect between Cr and Fe leads to ordering and solid solution strengthening [18], Cr has an important effect on the ferromagnetic moment [19], and the short-range ordered Fe-Cr structure will delay the passivation behavior of the alloys [20]. Moreover, the effect of Cr on the vacancy or point defect has been investigated by Piochaud et al. They revealed that the first nearest-neighbors Cr of the point defects drive the evolution of the formation energies [21]. Furthermore, the effect of Cr on the stability of Fe-Cr systems has been examined by Wang et al. and Yang et al. They found that Cr is more prone to interstitial diffusion compared with vacancy diffusion [22]; when Cr atoms are symmetrically distributed, the system has the highest stability [23]. Based on the above research results, it can be seen that the solute Cr has a significant effect on the thermal stability of the Fe-Cr system. Additionally, IAs may also play an important role during the process of solution strengthening of the Fe-Cr system, which needs to be further explored.
A large number of studies have shown that a solid solution of IAs has an important influence on the stability and properties of the Fe-Cr system. It also has a strong relationship to the interaction between IAs and Cr. Some investigations have been conducted on the interaction between interstitial C/N/O and Cr. Sandberg et al. [24], Wallenius et al. [25], and Smirnova et al. [26] reported that the Cr-C interaction is repulsive, and a C solid solution can slightly increase the elastic properties of the Fe-Cr system. Moreover, Lv et al. and Uesugi et al. confirmed that the thermal stability of the Fe-Cr system is enhanced by interstitial C/N [27], and the metallic radius of the element Cr affects the interaction in Cr-C/N clusters [28]. In addition, the interaction between Cr and N has been explored by Zhou et al. and Tong et al., who revealed that the lattice constants and cell volumes produce a large increase after N solid solution, that N enhanced the stability of the Fe-Cr-Mn system [29], that Cr-N clusters are formed due to their strong interaction, and that Cr-N tends to form short-range ordered clusters to enhance the stability of austenitic stainless steel [30]. Additionally, the interaction between Cr and O has been investigated by Wang et al., Zhang et al., and Mathayan et al. They reported that Cr reduces the O migration barrier, the O-Cr shows an attractive interaction [31,32], and Cr atoms present a strong influence on the O trapping at defects in Fe-Cr alloy [33]. Despite the previous studies, there are still two aspects to be further investigated regarding the solid solution strengthening of Cr and IAs, i.e., (1) the effect of solutes (Cr or IAs) on the microstable configuration in the Fe-Cr system; (2) how the interaction mechanism between interstitial C/N/O and Cr affects the thermostability of the Fe-Cr system, which is important for the solid solution strengthening of MS.
The solid solution strengthening of the Fe-Cr system was thoroughly investigated in our work using first-principles calculations. First, the stability of Cr and its effect on the Fe-Cr system were studied with the Birch–Murnaghan equation of state (EOS) fitting method. Then, the occupancy stability and the diffusion of IAs were studied by energy analysis and the CI-NEB method. At last, the interaction between IAs and Cr in the Fe-Cr system was investigated by energy analysis and four-level electronic structure analysis (projected density of states, Electron Localization Function, crystal orbital Hamiltonian population, and charge density difference). These findings could give important information for understanding the solid solution strengthening of Cr and IAs in the Fe-Cr system.

2. Computational Methods

The calculations were based on the Vienna ab initio Simulation Package (VASP) [34] of the first-principles density functional theory (DFT). The exchange correlation function was represented by the Perdew–Burke–Ernzerhof (PBE) pseudopotential of the generalized gradient approximation (GGA) [35,36,37]. The interaction between electrons and ions was realized by the projector-augmented wave (PAW) method [38,39]. A 3 × 3 × 3 supercell with 54 atoms was employed for BCC Fe. Calculations adopted the Gamma center Monkhorst-Pack scheme [40] with a 3 × 3 × 3 K-points mesh in the Brillouin zone by using the VASPKIT 1.5.1 [41] software, and the selection of the K-points mesh was based on the convergence test of K-points (Table A1 and Figure A1). The cutoff energy was selected at 600 eV in order to guarantee computation convergence based on the cutoff energy convergence test (Figure A2). The energy convergence criterion of electron self-consistent calculation (SCF) is 10−6 eV/atom, and the convergence criterion of interatomic force is −0.02 eV/Å. The structure optimization was performed by completely relaxing atom positions, cell shape, and cell volume. The climbing image nudged elastic band (CI-NEB) approach [42,43] was adopted to find the transition pathways of IAs (C/N/O) in the Fe-Cr system. All calculations employed spin polarization to account for the ferromagnetic state of BCC Fe. After the complete relaxation and the convergence of the static calculation of the supercell, the Birch-Murnaghan equation of state fitting method [44,45] was used to improve the accuracy of the calculation of the ground state energy and obtain the ground state physical properties. Lobster 5.1.1 software was used to calculate the crystal orbital Hamiltonian population (COHP) and analyze the chemical bonding characteristics between Cr and IAs [46,47].
The formation energy (Ef) of Fe-Cr-X alloys is defined as Equation (1) [48,49]:
Fe 54 − m Cr m X n − ( 54 − m ) × E ( Fe ) − m E ( Cr ) − n E   X
where the total energy of the Fe-Cr supercell with m Cr atoms and n interstitial X (C, N, or O) is denoted by E(Fe54−mCrmXn). The energy of a single Fe atom of the ideal Fe is represented by E(Fe), the energy of a single Cr of the perfect Cr is represented by E(Cr), the energy of a single C atom in the graphite solid is represented by E(C), and the energy of a single O/N atom of O2/N2 molecule is represented by E(O)/E(N). It should be noted that m is 0, 1, or 2 and n is 0 or 1 in the current and the following equations. Positive formation energy implies that the structure is difficult to construct, whereas negative formation energy suggests that it is easily formed.
The binding energy between Cr and an interstitial X (X=C/N/O) in the Fe-Cr system can be estimated using the following Equation (2):
E b Cr m − X = E ( Fe 54 − m Cr m ) + E ( Fe 54 X ) − E ( Fe 54 − m Cr m X ) + E ( Fe 54 )
where E(Fe54−mCrm) signifies the total energy of the Fe supercell replaced by m Cr atoms, E(Fe54X) signifies the energy of the Fe supercell with an IA, E(Fe54−mCrmX) signifies the whole energy of the Fe-Cr-X alloy, and E(Fe54) signifies the energy of the perfect BCC Fe. By definition, a positive binding energy indicates attraction between Cr and interstitial X, while a negative binding energy denotes repulsion.
The lattice distortion energy (Eld) is used to examine and quantitatively express the contribution of lattice distortion generated by solute atoms, which can be described as Equation (3) [50,51,52]
E ld = E Fe 54 − m Cr m X n − E ( Fe 54 )
where E(Fe54−mCrmXn) and E(Fe54) represent the total energy of the Fe-Cr-X alloys with lattice distortion and the total energy of the equilibrium lattice without solute atoms, respectively.
In Equation (4), the charge density difference (Δρ(Fe54−mCrmX)) is defined as the difference between the charge density of the Fe-Cr-X alloys, the Fe-Cr system, and the X atom [51,53], as follows:
Δ ρ = ρ Fe 54 − m Cr m X - ρ Fe 54 − m Cr m − ρ ( X )
where ρ(Fe54−mCrm), ρ(X), and ρ(Fe54−mCrmX) signify the charge density of the Fe-Cr supercell, the charge density of interstitial X (X = C/N/O), and the whole charge density of the Fe-Cr-X system, respectively.

3. Results and Discussion

3.1. The Effect of Cr Occupation on Structural Stability in Fe-Cr System

The method of constructing the Fe-Cr system is to directly replace Fe atoms with Cr in a perfect BCC Fe supercell. Due to the large atomic radius of the Cr atom, it is found that Cr tends to occupy substitution sites [18,21,54]. There are two types of occupancy for one Cr atom, as shown in Figure 1: the central position (a) and the angular position (b). There are five types of occupancy for two Cr atoms in the unit cell, as shown in Figure 1c–g.
To investigate the effect of Cr solid solution on the BCC Fe supercell, using the perfect Fe54 supercell as a reference, the BM-EOS fitting method is used to compare the physical properties of the Fe-Cr system in the ground state, as illustrated in Table 1. From the perspective of lattice changes, replacing Fe with Cr will result in a certain degree of lattice distortion and an increase in the unit cell volume. Moreover, the volume change and lattice distortion of a unit cell containing two Cr atoms are greater than those containing one Cr. Lattice distortion also leads to a decrease in the bulk modulus. Overall, the absolute value of lattice distortion energy is positively correlated with the change in the lattice volume and negatively correlated with the value of the bulk modulus. However, lattice distortion can hinder dislocation slip and increase material strength and hardness, which is one of the microscopic mechanisms of solid solution strengthening [55]. Furthermore, from an energy perspective, the formation energy of the Fe-Cr system is negative after the Cr solid solution, indicating that it is easy for the Fe-Cr system to form. The two structures containing one Cr have similar energy, indicating their similar stability, while the formation energy of Cr1-1 is lower and more stable. Among the five structures containing two Cr atoms, Cr2-3, presenting the lowest formation energy and the lowest lattice distortion energy, is the most stable structure. Last, but not least, from the perspective of magnetic influence, the average magnetic moment of the iron supercells decreases after the solid solution of Cr, and the decrease in the magnetic moment is greater in the case of two Cr atoms than one Cr. This indicates that Cr-Fe exhibits antiferromagnetic coupling, and the increase in the antiferromagnetic element Cr suppresses the ferromagnetism of the Fe-based phase, resulting in a decrease in the average magnetic moment. Nevertheless, the antiferromagnetic coupling of Fe-Cr at a low Cr concentration is the root of the enhanced stability of the Fe-Cr system [56,57].

3.2. The Effect of IAs (C/N/O) on the Thermostability in Fe-Cr System

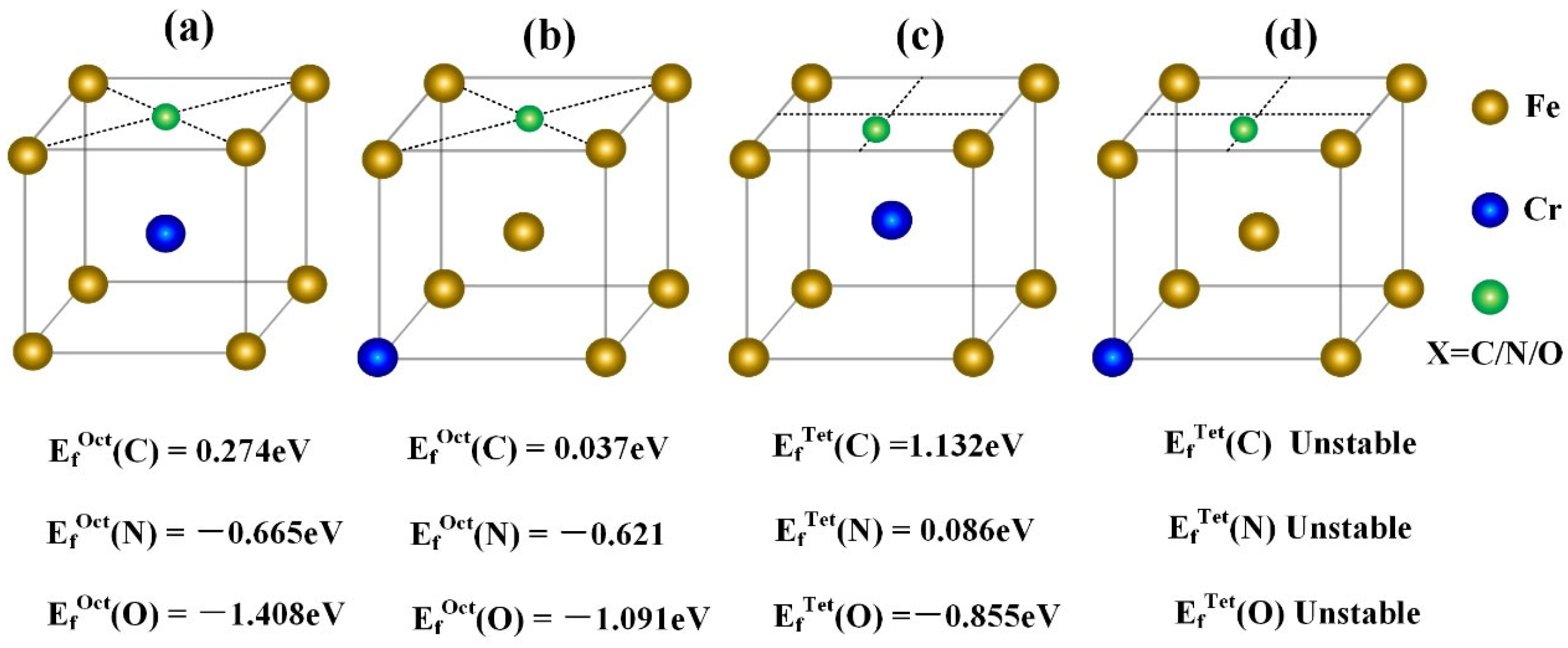
3.2.1. Site Preference of IAs at Interstitial Sites

IAs (C/N/O) tend to inhabit the following interstitial sites: octahedral interstitial sites (O-sites) and tetrahedral interstitial sites (T-sites) for the smaller atomic radius [49,58,59]. To determine the occupancy stability of IAs, the occupancy of IAs in Fe53Cr1 is studied. As shown in Figure 2, the results indicate that the formation energy of T-sites is higher than that of O-sites, or that IAs are unstable at T-sites. Particularly, when the IAs are in the T-site in the structure shown in Figure 2d, it is found that it is difficult for the structures to exist stably in this position, and are thus eventually optimized to the adjacent O-site. It is revealed that C/N/O atoms prefer to inhabit O-sites. Furthermore, at the O-sites, the formation energy of C is positive, indicating that C can be dissolved under certain conditions. However, the negative formation energies of N and O indicate that N/O is easily solid soluble in Fe-Cr supercells, and the lower formation energies of O suggest that O is more easily solid soluble. Therefore, the IAs at O-sites in the Fe-Cr system will be discussed in the following section.

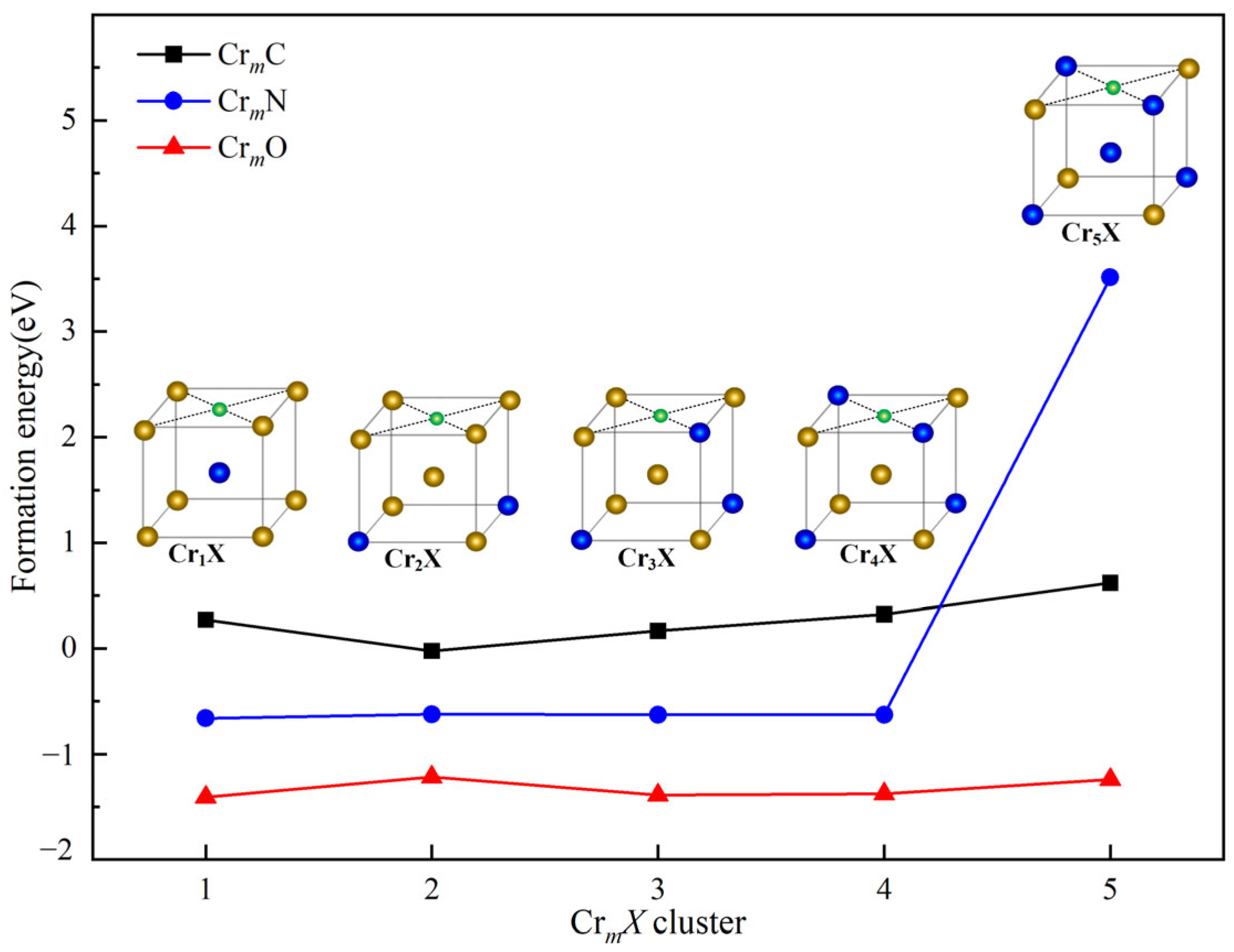
3.2.2. The Effect of IAs on the Stability in Cr-Rich Regions of Fe-Cr System

Previous investigations have shown that the formation of ordered compounds between IAs and Cr is closely related to the formation of Cr-rich clusters and Cr segregation [60]. Therefore, to further understand the interaction between IAs and Cr, it is necessary to understand the stability of IAs in the Cr-rich region. As can be seen in Figure 3, compared with the X (X = C, N, or O) at the O-site in pure Fe54, the formation energy of IAs in the Cr-rich region is significantly lower (except for Cr5N), indicating that IAs tend to form Cr-rich clusters with Cr and Fe54−mCrmX (m represents the number of Cr elements; m = 0–5), and are more stable than Fe54X. In other words, Cr and IAs (C, N, or O) have a cooperative effect to enhance the stability of the Fe-Cr system. Specifically, for interstitial C, as the number of Cr elements increases, the formation energy of the CrmC cluster decreases first and then increases, where Cr2C has the lowest formation energy and is negative (−0.024eV), while the formation energies in the other cases are positive, indicating that CrmC clusters can be formed under certain conditions. Moreover, for interstitial N, when m = 1–4, the formation energies are all negative, and the formation energy of Cr1N is the smallest (−0.665 eV), indicating that N can form a stable structure with Cr in the Cr-rich region. However, the formation energy of Cr5N is much higher than the other cases. This shows that N tends to form a precipitation phase with Cr and cannot exist stably with an excessive Cr concentration, which is consistent with experimental research on the precipitation behavior of N and Cr in the Cr-rich region [30]. Furthermore, for the interstitial O, compared with interstitial C/N, the CrmO cluster has a lower formation energy, which is negative, indicating that O is more likely to form Cr-rich clusters and Cr1O has the lowest formation energy (−1.408 eV).

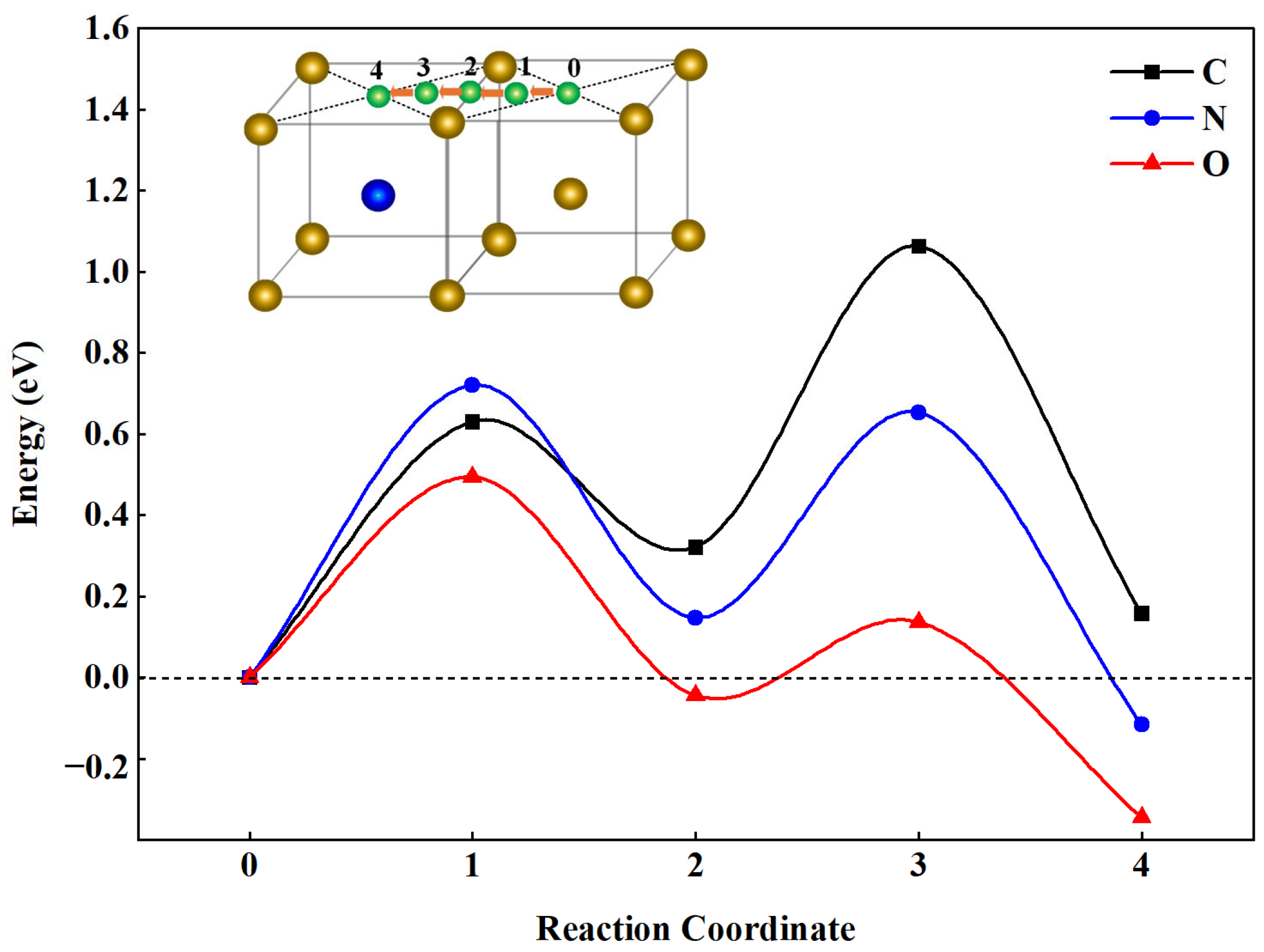
3.2.3. The Diffusion of IA (C/N/O) in Fe-Cr System

The diffusion behavior of IAs in the Fe-Cr system is closely related to Cr segregation and short-range ordered Cr clusters [13,61]. Therefore, it is crucial to analyze the migration of IAs (C, N, or O) to the Cr region. The diffusion process of IAs from the central O-site far from Cr to the nearest central O-site near Cr is studied by the CI-NEB method. The migration path is from 0 to 4, with 1 and 3 at T-sites and 2 at the edge O-site. As exhibited in Figure 4, the migration energy (Em) of interstitial N and O decreases significantly when they are close to Cr, while the migration energy of C increases significantly when it is close to Cr. Additionally, N/O has lower energy and is more stable in the first nearest O-site (1). Specifically, when it is close to Cr, the Em of O decreases from 0.493 eV at 1 to 0.136 eV at 3, indicating that it is very easy for O to diffuse to the Cr region. The Em of N decreases from 0.719 eV at 1 to 0.652 eV at 3, indicating that N also tends to diffuse to the Cr region (Table A2). However, the Em of C increases significantly from 0.834 eV at 1 to 1.420 eV at 3, indicating that it is difficult for C to diffuse to Cr region and can remain stable at a long distance from Cr. These results are consistent with the site occupation stability. In summary, the results of the occupation tendency and diffusion of IAs in the Cr region show that Cr1N/O is the most stable, and Cr1C has a strong repulsive effect. Therefore, Fe53Cr1X is selected as the stable configuration to investigate the interaction between Cr and IAs in the succeeding investigation.

3.3. The Interaction Mechanism Between IA (C/N/O) and Cr in Fe53Cr1X

3.3.1. The Occupancy Stability of C/N/O IAs in Fe53Cr1X

The occupancy stability of C/N/O IAs in Fe53Cr1X is investigated by comparing the energies of seven different configurations, as depicted in Figure 5. The formation energies of the seven configurations of Fe53Cr1C1 are all positive, and the binding energies are all negative, demonstrating that Cr and C have a repulsive interaction, which decreases as the distance between Cr and C increases (Table A3). When the distance between Cr and C is greater than 3Å, the binding energy is close to zero. In other words, there is essentially no contact between them, and Cr-C remains stable across long distances, which is in line with prior research findings [24]. The formation energies of Fe53Cr1N1 are negative, indicating that Cr-N can enhance the stability of the system. The negative binding energies of configuration 4 indicate that there is a repulsive effect between Cr and N, while configuration 1 has a positive binding energy, implying an attractive effect between Cr and N, making it the most stable. In addition, there is no linear relationship between the interaction effect and the distance of Cr-N. The formation energies of Fe53Cr1O1 are negative and lower than C/N, indicating that Cr-O is easier to form and more stable. The binding energy of Cr-O is positive and the largest at configuration 1 (the distance between Cr and O is 1.78Å), which shows a strong attraction to make it the most stable configuration. As the distance increases, its attraction weakens and eventually turns into repulsion. This indicates that Cr-O tends to be more stable at short distances (within 2 Å).

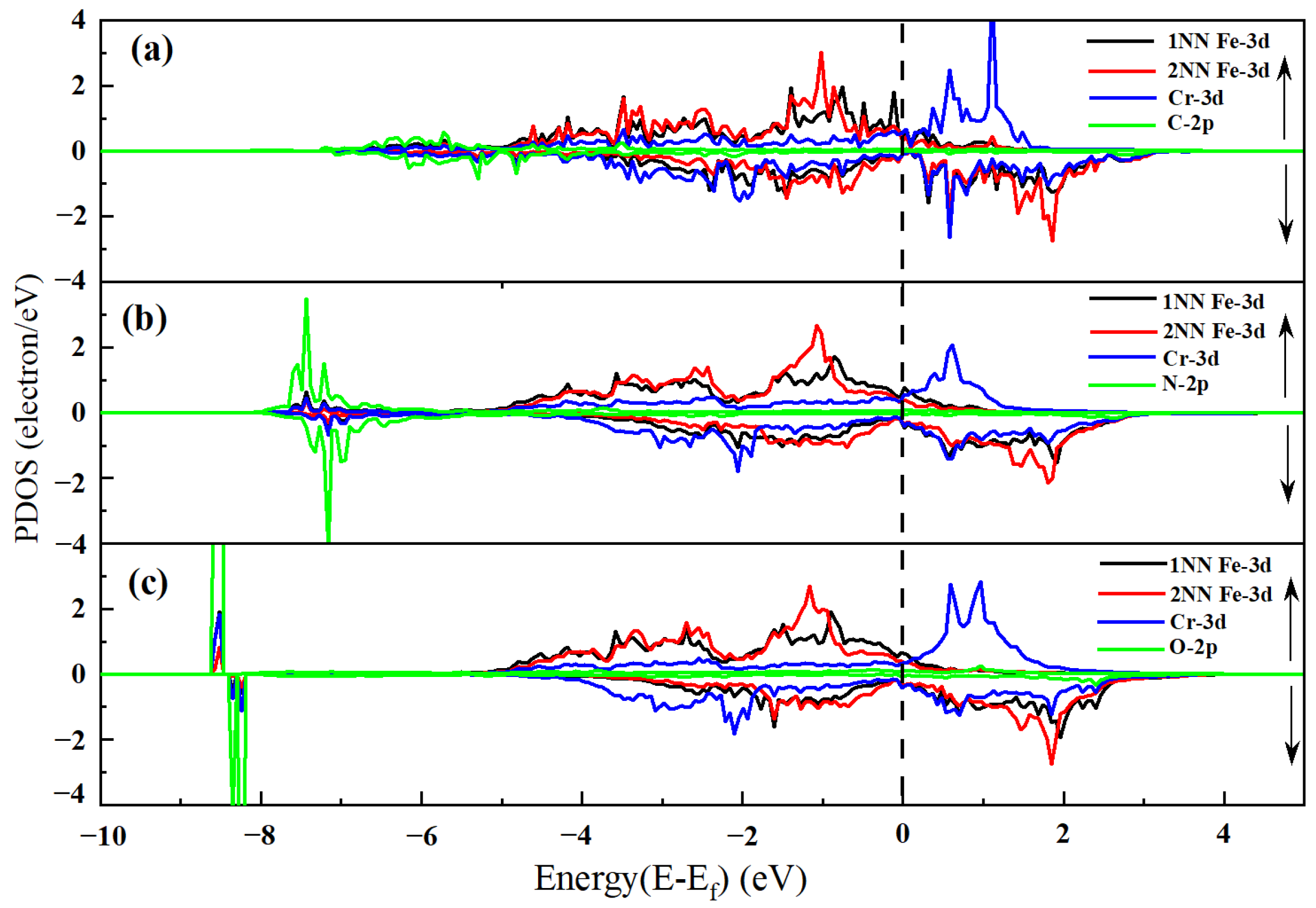
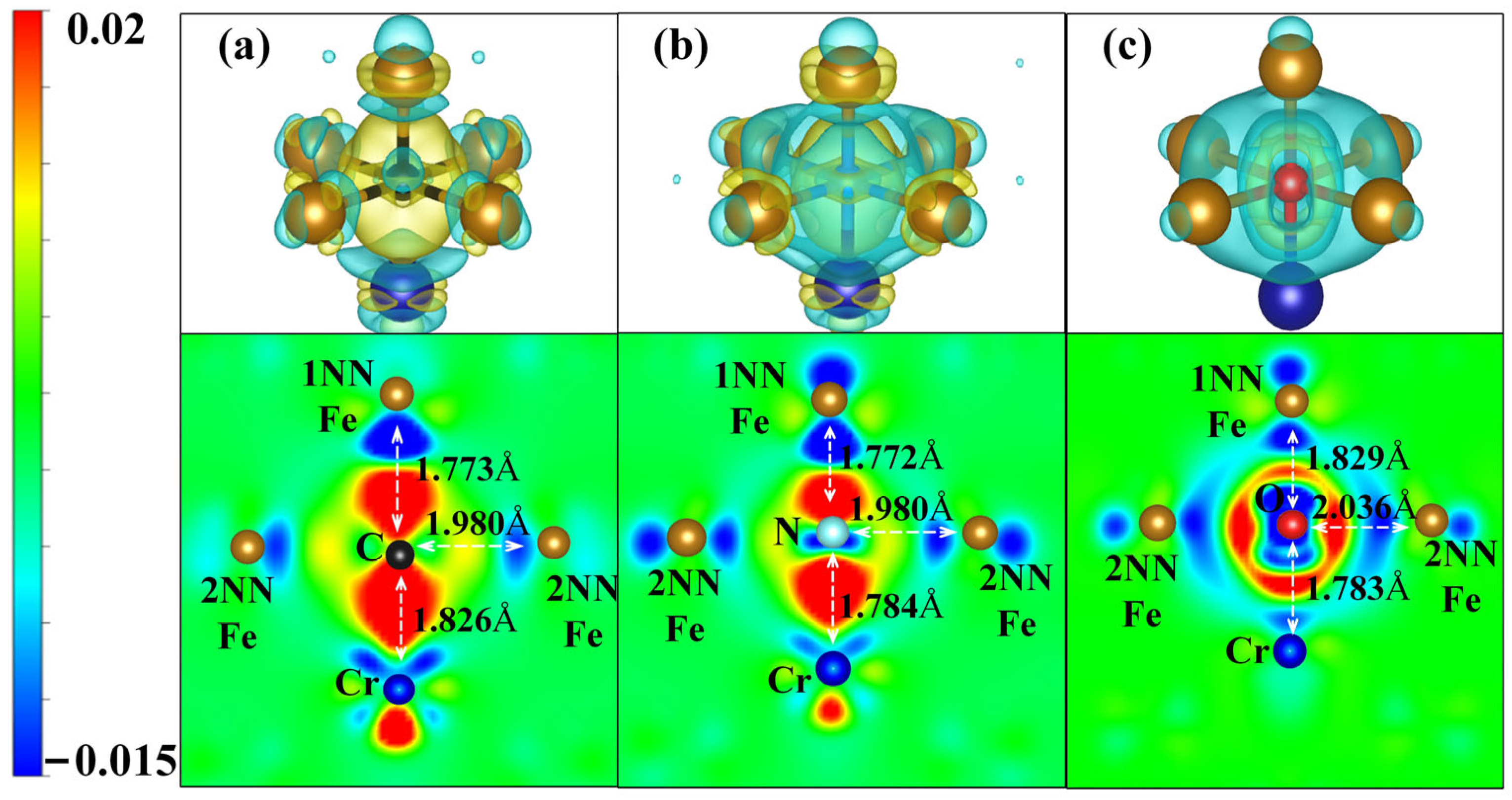
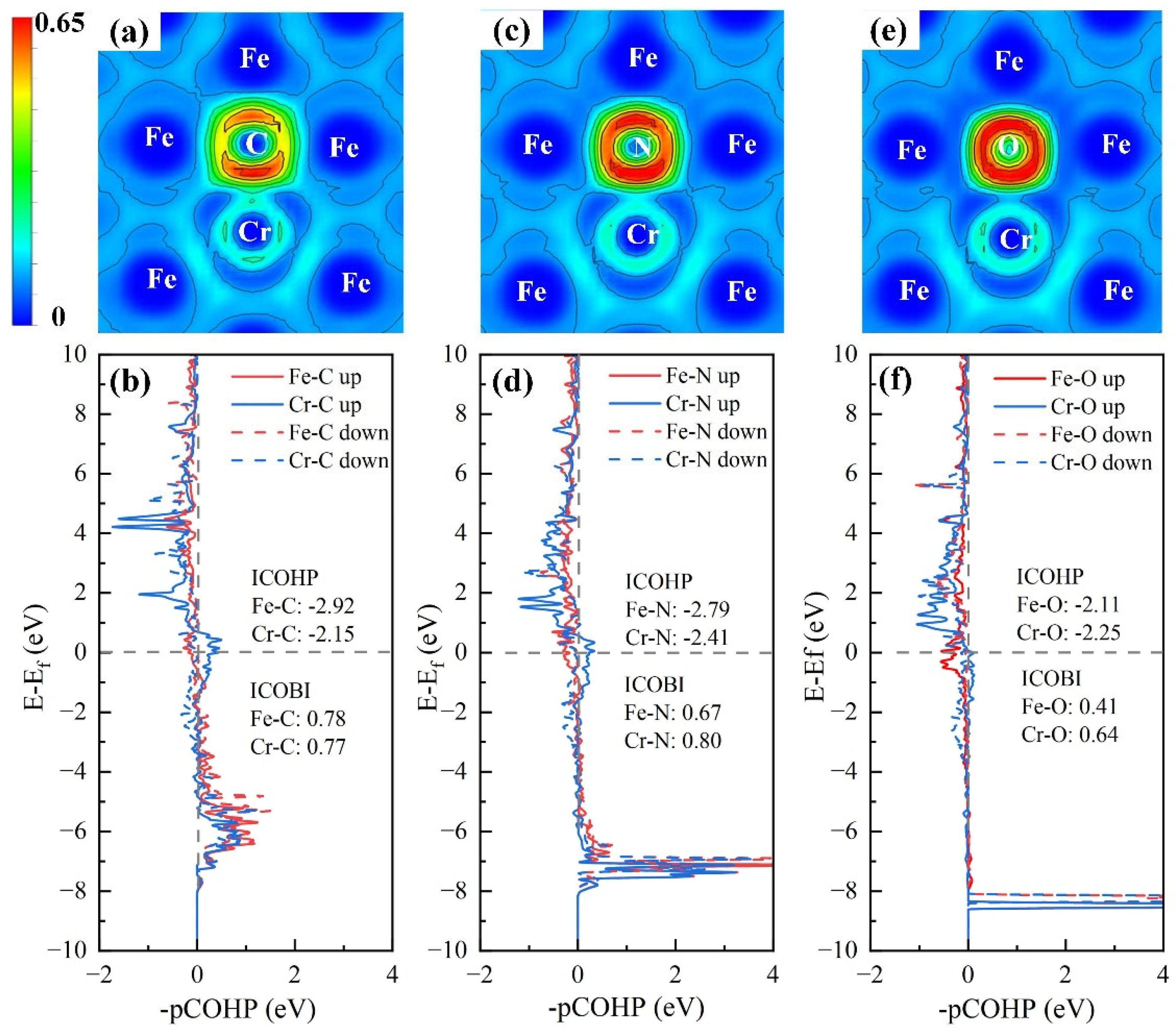
3.3.2. An In-Depth Analysis of the Interaction Mechanism Between IAs and Cr

To gain a deeper understanding of the bonding characteristics between IAs and Cr, as well as their neighboring Fe atoms, the PDOS of Cr, IAs, and their first and second nearest-neighboring (1NN and 2NN) Fe atoms are calculated, as shown in Figure 6. It can be clearly observed that the density of states (DOS) of the Fe-Cr system is filled with electrons at the Fermi level, which reveals the metallic properties of the system. The asymmetry of spin densities reveals the ferromagnetism of the Fe-Cr system. In general, the PDOS results show that the 2p orbitals of IAs are obviously hybrid with the 3d orbitals of Cr and neighboring Fe atoms. Specifically, the 2p orbital of interstitial C and the 3d orbital of Cr, and the 3d orbital of ortho-Fe, have multiple hybrid peaks between −6.5 eV and −5.7 eV, and the DOS in the hybrid region is significantly lower than that of N/O, showing covalent bond characteristics. The 2p orbital of the interstitial N and the 3d orbital of the Cr, and the 3d orbital of the ortho-Fe, have three obvious hybrid peaks between −8 eV and −7 eV, and the DOS energy is higher than C, showing the characteristics of polar covalent bonds. In the 2p orbital of interstitial O and the 3d orbital of Cr, and the 3d orbital of the ortho-Fe form, there is an isolated hybrid peak with the highest DOS at −8.5 eV, exhibiting typical ionic bond characteristics.
To verify the bonding between IAs and Cr, and neighboring Fe, a charge density difference (CDD) analysis is carried out on Fe-Cr supercells with IA solid solution, as shown in Figure 7. On the whole, charge accumulation occurs around the IAs, while charge depletion occurs around the Fe and Cr atoms, indicating that the IAs are bonded with the neighboring metal atoms. In detail, the dumbbell-shaped charge accumulation appears around the interstitial C/N, indicating that C/N forms covalent bonds with Cr and ortho-Fe, and the charge depletion around metal atoms bonded with N is higher than that around C, indicating that polar covalent bonds are formed around N. The spherical charge distribution around O indicates that O forms a typical ionic bond with Cr and ortho-Fe.
To gain further insight into the chemical bonding characteristics and bonding strength of IAs with Cr and its neighboring Fe atom, and to evaluate the effect of IAs on the stability of the Fe-Cr system, Electron Localization Function (ELF) and COHP analyses are carried out, as shown in Figure 8. On the one hand, according to the ELF values of the 2D slices in Figure 8 a–c, it can be seen that the electrons around the C/N atom are localized and N has a greater electron localization than C, showing typical covalent bond characteristics. There is a slight asymmetry, indicating that the interaction between Cr-C and Cr-N causes the rearrangement of electrons around Cr. While the electron around the O atom is highly localized, the ELF value between O-Cr and O-Fe is very low, showing obvious ionic bond characteristics. On the other hand, the COHP results demonstrate that the Fe-Cr system containing IAs has considerable bonding contributions below the Fermi level, and the ICOHP values at the Fermi level are all negative, indicating that the Fe-Cr system has a high stability after the IA solid solution, and the bonding ranges of the three alloys are consistent with the PDOS results. Specifically, the ICOHP absolute value of Fe-C is higher than that of Cr-C, implying that the bonding effect between interstitial C and Fe is stronger. Similarly, the ICOHP absolute value of Fe-N is greater than that of Cr-N, indicating that the bonding between interstitial N and Fe is stronger. Compared to C/N, Cr-O has a higher ICOHP absolute value than Fe-O, revealing a stronger bonding effect between interstitial O and Cr. According to the absolute value of ICOHP, the bonding strength between IAs and Cr follows Cr-N>Cr-O>Cr-C. The value of ICOBI can reflect the contribution of covalent bonds and ionic bonds in chemical bonds [62]. In Fe53Cr1C1 and Fe53Cr1N1, the ICOBI values of interstitial C/N, Cr, and Fe atom pairs are between 0.67 and 0.80, indicating that the chemical bond has both covalent and ionic components. Similarly, the ICOBI values of interstitial Cr-O and Fe-O pairs are 0.64 and 0.41, respectively, indicating that there are both covalent and ionic components, but the ionic component accounts for a large proportion. This is consistent with the results of PDOS and ELF.
In summary, the solid solution of IAs and Cr can concurrently enhance the stability of the Fe-Cr system, indicating a cooperative strengthening effect between Cr and IAs. To verify the thermodynamic stability of the system, the dissociation temperature of IAs in the Fe-Cr system is calculated using the Polanyi–Wigner formula [49,63]. As shown in Table 2, compared with the pure iron system, the dissociation temperature (Tdis) increases on account of the interaction between IAs and Cr, especially for Cr-O, where the Tdis increases by 52K, suggesting that the stability of the system is improved. This result is also consistent with our earlier experimental findings that nano-sized carbides are formed after laser cladding, endowing MS with exceptional strength and corrosion resistance [64]. Additionally, this result aligns with previous theoretical findings by Lv et al., Zhang et al., and Tong et al., who also reported that C solid solution enhances the thermal stability of the Fe-Cr system [27], Cr-O shows a strong attractive interaction in the Fe-Cr system [32], and Cr-N has strong interactions and tends to form short-range ordered clusters to enhance the stability of austenitic stainless steel [30]. Furthermore, the relevant experimental findings also confirm these results. It is found that the short-range ordered structure composed of interstitial atoms and Cr can strengthen the properties of austenitic alloys [13], and the ordered interstitial complexes formed by the combination of IAs and the main elements of the alloy after the laser additive process can improve the strength and ductility of the alloy at the same time [65]. The cooperative strengthening effect can be attributed to the strong orbital hybridization and intense bonding between interstitial atoms and Cr based on the four-level electronic structure analysis. Specifically, the electronegativity difference between C and Cr is the smallest among the three, while the orbital hybridization range is wider, resulting in the strong covalent bonds between Cr and C. The electronegativity difference between O and Cr is the largest, and orbital hybridization shows an isolated hybrid peak, leading to strong polar bonds (with a higher ionic component) between Cr and O. Although the electronegativity difference between N and Cr falls between C and O, their special electronic properties make them tend to form metal coordination bonds; hence, the bonding strength between Cr and N is the highest among the three, showing a cooperative solid solution strengthening effect. The increase in the dissociation temperature of IAs in the Fe-Cr system, and the strong bond cooperation between Cr and IAs, reveal that the cooperative effect of IAs and Cr enhances the stability of the system, which improves the solubility of IAs in the Fe-Cr system. This provides a theoretical basis for the design of high-performance steel.

4. Conclusions

In this work, the stability of Cr and IAs, and the interaction mechanism between IAs and Cr in the Fe-Cr system, were systematically investigated in-depth by DFT calculations. The results show that the solute Cr induces significant lattice distortion, which improves the stability of the pure Fe system while weakening its magnetic properties. IAs prefer to inhabit O-sites in the Fe-Cr system. IAs have different stability rules in Cr-rich regions. The results of the interaction between IAs and Cr show that Cr-C is repulsive, Cr-C tends to be stable at a long distance, while N/O is most stable at the first neighboring O-site of Cr. Moreover, the diffusion of IAs towards the Cr region further verifies these results. After the solution of IAs and Cr, the formation energy of the system is lower than their solution in the pure iron system alone, indicating that there is an obvious cooperative strengthening effect between IAs and Cr. Moreover, the four-level electronic structure analyses are employed to illustrate the interaction between IAs and Cr. The PDOS results indicate significant hybridization between the 3d orbital of Cr and the 2p orbital of IAs. Additionally, the CDD results reveal that Cr loses electrons while interstitial atoms gain electrons. Furthermore, the ELF and COHP analysis results demonstrate intensive bonding between Cr and IAs, confirming that the strong cooperative effect between IAs and Cr improves the stability of the Fe-Cr system. Finally, the increase in the dissociation temperature of IAs in the Fe-Cr system further demonstrates that the stability of the system is enhanced by cooperative solid solution strengthening.

Author Contributions

F.W.: Conceptualization, Supervision, Writing—review and editing, and Writing—original draft. T.M.: Conceptualization, Investigation, Methodology, and Resources. P.C.: Formal analysis, Supervision, and Writing—review and editing. H.Z.: Supervision, Writing—review and editing, and Funding acquisition. Y.C.: Supervision and Writing—review and editing. P.Z.: Software, Supervision, and Writing—review and editing. R.L.: Supervision and Writing—review and editing. C.Q.: Conceptualization, Formal analysis, Writing—review and editing, and Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant No. 51474130); the National Natural Science Foundation of China (Grant No. 52375341).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data are contained within the article.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
MSsmartensitic steels
IAsinterstitial atoms
O-sitesoctahedral interstitial sites
T-sitestetrahedral interstitial sites
DFTdensity functional theory
PBEPerdew–Burke–Ernzerhof
GGAgeneralized gradient approximation
SCFself-consistent calculation
EOSequation of state
ELFElectron Localization Function
COHPcrystal orbital Hamiltonian population
CDDcharge density difference
BCC Febody-centered cubic iron
CI-NEBclimbing image nudged elastic band
VASPVienna ab initio Simulation Package
PAWprojector-augmented wave
1NNthe first nearest neighbor
2NNthe second nearest neighbor
PDOSprojected density of states

Appendix A

Coatings 15 01096 g0a1
Figure A1. K-points convergence test of Fe54 and the red square represents the chosen K-mesh of this paper.
Figure A1. K-points convergence test of Fe54 and the red square represents the chosen K-mesh of this paper.
Coatings 15 01096 g0a1
Table A1. Details of K-point convergence test of Fe54.
Table A1. Details of K-point convergence test of Fe54.
K-MeshEnergy per Atom (eV)Energy Error (meV)K-Spacing Value (2π/Å)
2 × 2 × 2−8.428−191.3150.050
3 × 3 × 3−8.2360.8150.040
4 × 4 × 4−8.238−0.8890.030
5 × 5 × 5−8.2360.6300.025
6 × 6 × 6−8.2370.0000.020
Coatings 15 01096 g0a2
Figure A2. Cutoff energy convergence test of Fe54; the red square represents the chosen cutoff energy of this paper.
Figure A2. Cutoff energy convergence test of Fe54; the red square represents the chosen cutoff energy of this paper.
Coatings 15 01096 g0a2
Table A2. Migration energy barrier (Em) of each reaction coordinate of diffusion process in Fe53Cr1C1, Fe53Cr1N1, and Fe53Cr1O1.
Table A2. Migration energy barrier (Em) of each reaction coordinate of diffusion process in Fe53Cr1C1, Fe53Cr1N1, and Fe53Cr1O1.
Reaction CoordinateEm(eV)
Fe53Cr1C1Fe53Cr1N1Fe53Cr1O1
00.0000.0000.000
10.8340.7190.493
20.3210.148−0.044
31.4200.6520.136
40.158−0.116−0.345
Table A3. Formation energy (∆Ef), binding energy (Eb), and bond lengths (d) between interstitial atoms and Cr of different configurations in Fe53Cr1C1/Fe53Cr1N1/Fe53Cr1O1.
Table A3. Formation energy (∆Ef), binding energy (Eb), and bond lengths (d) between interstitial atoms and Cr of different configurations in Fe53Cr1C1/Fe53Cr1N1/Fe53Cr1O1.
ConfigurationsEf (eV)Eb (eV)d (Å)
Fe53Cr1C1Fe53Cr1N1Fe53Cr1O1Fe53Cr1C1Fe53Cr1N1Fe53Cr1O1Cr-CCr-NCr-O
10.264 −0.665 −1.408 −0.265 0.0740.216 1.830 1.784 1.783
20.243 −0.543 −1.236 −0.244 −0.0480.044 2.061 1.965 1.932
30.263 −0.523 −1.323 −0.264 −0.0680.131 1.830 1.782 1.780
40.221 −0.429 −1.160 −0.221 −0.162−0.032 2.061 1.991 1.944
50.088 −0.467 −1.015 −0.089 −0.124−0.177 3.224 3.261 3.265
60.037 −0.621 −1.091 −0.038 0.030−0.101 3.586 3.587 3.598
70.030 −0.548 −1.117 −0.031 −0.043−0.075 4.272 4.317 4.317

References

  1. Li, J.H.; Zhan, D.P.; Jiang, Z.H.; Zhang, H.S.; Yang, Y.K.; Zhang, Y.P. Progress on improving strength-toughness of ultra-high strength martensitic steels for aerospace applications: A review. J. Mater. Res. Technol. 2023, 23, 172–190. [Google Scholar] [CrossRef]
  2. Sun, H.; Liu, M.; Zeng, Y.; Liu, J. Influence of Chromium Content in Alloys on Corrosion in Saline Water Saturated with Supercritical CO2. Processes 2025, 13, 1334. [Google Scholar] [CrossRef]
  3. Singh, R.; Singh, J.; Chauhan, B.S.; Bansal, A.; Aggarwal, V. Microstructure and mechanical properties of the microwave welded dissimilar joints between SS-430 and plain carbon steel. Phys. Scr. 2025, 100, 055902. [Google Scholar] [CrossRef]
  4. Ei-Labban, H.F.; Mahmoud, E.R.I.; Al-Wadai, H. Formation of VC-composite surface layer on high C-Cr bearing tool steel by laser surface cladding. J. Manuf. Process. 2015, 20, 190–197. [Google Scholar] [CrossRef]
  5. Russell, Z.; Amegadzie, M.Y.; David, A.M.S.; Plucknett, K.P. Scratch Resistance and Damage Mechanisms Arising in Titanium Carbide-Nickel Aluminide-Based Laser DED Clads on D2 Tool Steel. Coatings 2025, 15, 330. [Google Scholar] [CrossRef]
  6. Saharudin, M.F.; Zulkifli, N.W.M.; Goh, Y.; Ibrahim, M.Z.; Morina, A.; Mehtab, R. Investigation of the tribological and mechanical properties of FeCrMoCB coating on AISI 52100 bearing steel. Tribol. Int. 2025, 203, 1100401. [Google Scholar] [CrossRef]
  7. Bolli, E.; Fava, A.; Ferro, P.; Kaciulis, S.; Mezzi, A.; Montanari, R.; Varone, A. Cr Segregation and Impact Fracture in a Martensitic Stainless Steel. Coatings 2020, 10, 843. [Google Scholar] [CrossRef]
  8. Liu, Z.-b.; Yang, Z.; Liang, J.-x.; Yang, Z.-y.; Sheng, G.-m. Atomic-scale characterization of multiple precipitating species in a precipitation-hardened martensitic stainless steel. J. Iron Steel Res. Int. 2022, 29, 207–214. [Google Scholar] [CrossRef]
  9. Ye, Z.; Lei, Y.; Zhang, J.; Zhang, Y.; Li, X.; Xu, Y.; Wu, X.; Liu, C.S.; Hao, T.; Wang, Z. Effects of oxygen concentration and irradiation defects on the oxidation corrosion of body-centered-cubic iron surfaces: A first-principles study. Chin. Phys. B 2022, 31, 086802. [Google Scholar] [CrossRef]
  10. Wang, C.Y.; Luo, K.Y.; Wang, J.; Lu, J.Z. Carbide-facilitated nanocrystallization of martensitic laths and carbide deformation in AISI 420 stainless steel during laser shock peening. Int. J. Plast. 2022, 150, 103191. [Google Scholar] [CrossRef]
  11. Song, Y.; Lu, Y.; Li, Y.; Sun, H.; Li, H.; Xu, H.; Wang, Y. Effect of nitrogen on the thermal deformation behavior of maternsitic stainless bearing steel. Mater. Tehnol. 2024, 58, 809–818. [Google Scholar] [CrossRef]
  12. Zhu, H.M.; Hu, W.F.; Li, Y.Z.; Li, B.C.; Qiu, C.J. Effect of Tempering Temperature on Microstructure and Properties of Laser-cladded Martensitic Stainless Steel Layer. Chin. J. Lasers 2019, 46, 1202001. [Google Scholar] [CrossRef]
  13. Chen, Y.; Zhu, H.; Zhang, P.; Wang, Z.; Wang, M.; Sha, G.; Lin, H.; Ma, J.; Zhang, Z.; Song, Y.; et al. An exceptionally strong, ductile and impurity-tolerant austenitic stainless steel prepared by laser additive manufacturing. Acta Mater. 2023, 250, 118868. [Google Scholar] [CrossRef]
  14. Zhu, H.M.; Ben, X.; Li, B.C.; Shen, L.Z.; Pan, C.L.; Qiu, C.J. Influence of Al microalloying on microstructure and mechanical properties of laser directed energy deposited AISI 420 steel. Mater. Today Commun. 2025, 42, 111355. [Google Scholar] [CrossRef]
  15. Moriyama, J.; Takakuwa, O.; Yamaguchi, M.; Ogawa, Y.; Tsuzaki, K. The contribution of Cr and Ni to hydrogen absorption energy in Fe-Cr-Ni austenitic systems: A first-principles study. Comp. Mater. Sci. 2024, 232, 112650. [Google Scholar] [CrossRef]
  16. Shahboub, A.; Chen, P.; Deng, C.; Ding, W.; Zheng, M. Investigation of the anti-corrosion behavior of Fe-Cr oxide layer in LBE: A first-principles study. J. Nucl. Mater. 2025, 605, 155592. [Google Scholar] [CrossRef]
  17. Shao, Z.; Li, K.; Zhang, Y.; Liao, Z.; Li, C. Effect of Cr/Ni on the structural stability and mechanical properties of Fe-Cr-Ni-Mn alloys. Mater. Today Commun. 2025, 47, 113186. [Google Scholar] [CrossRef]
  18. Klaver, T.P.C.; Drautz, R.; Finnis, M.W. Magnetism and thermodynamics of defect-free Fe-Cr alloys. Phys. Rev. B 2006, 74, 094435. [Google Scholar] [CrossRef]
  19. Paduani, C.; Krause, J.C. A first-principles study of Cr impurities in iron. Braz. J. Phys. 2006, 36, 1262–1266. [Google Scholar] [CrossRef]
  20. Liu, M.; Aiello, A.; Xie, Y.; Sieradzki, K. The Effect of Short-Range Order on Passivation of Fe-Cr Alloys. J. Electrochem. Soc. 2018, 165, C830–C834. [Google Scholar] [CrossRef]
  21. Piochaud, J.B.; Klaver, T.P.C.; Adjanor, G.; Olsson, P.; Domain, C.; Becquart, C.S. First-principles study of point defects in an fcc Fe-10Ni-20Cr model alloy. Phys. Rev. B 2014, 89, 024101. [Google Scholar] [CrossRef]
  22. Wang, L.P.; Yang, W.; Ma, Z.B.; Zhu, J.H.; Li, Y.T. First-principles study of chromium diffusion in the ferritic Fe-Cr alloy. Comp. Mater. Sci. 2020, 181, 109733. [Google Scholar] [CrossRef]
  23. Yang, Z.H.; Zhang, C.; Wang, S.; Xue, C.P.; Tian, G.Y.; Su, H.; Yan, C.M.; Yan, Z.F.; Liu, X.G.; Wang, J.S. Towards quantum corrosion chemistry: Screening perfect Cr, Ni sites and stoichiometry on top of an Fe(110) surface using DFT. RSC Adv. 2023, 13, 9945–9953. [Google Scholar] [CrossRef] [PubMed]
  24. Sandberg, N.; Henriksson, K.O.E.; Wallenius, J. Carbon impurity dissolution and migration in bcc Fe-Cr: First-principles calculations. Phys. Rev. B 2008, 78, 094110. [Google Scholar] [CrossRef]
  25. Wallenius, J.; Sandberg, N.; Henriksson, K. Atomistic modelling of the Fe-Cr-C system. J. Nucl. Mater. 2011, 415, 316–319. [Google Scholar] [CrossRef]
  26. Smirnova, E.A.; Ponomareva, A.V.; Shulyatev, D.A. Investigation of interstitial carbon in the disordered bcc FeCr alloys. J. Alloy Compd. 2024, 994, 174686. [Google Scholar] [CrossRef]
  27. Lv, Z.; Liu, T.; Wu, Z.; Guan, K.; Li, Y. Structural, electronic and magnetic properties of Fe20Cr6Mn6 austenitic alloys with interstitial carbon and nitrogen atoms from density functional theory. J. Magn. Magn. Mater. 2020, 504, 166663. [Google Scholar] [CrossRef]
  28. Uesugi, T.; Ashino, S.; Takigawa, Y.; Higashi, K. Interactions between Interstitial and Substitutional Elements of Solute Diatomic and Triatomic Clusters in α-Fe from First-principles Calculations. ISIJ Int. 2024, 64, 1206–1217. [Google Scholar] [CrossRef]
  29. Zhou, Y.; Li, Y.; Wang, W.; Qian, L.; Xiao, S.; Lv, Z. Effect of interstitial nitrogen in Fe18Cr6Mn8 austenitic alloys from density functional theory. J. Magn. Magn. Mater. 2018, 463, 57–63. [Google Scholar] [CrossRef]
  30. Tong, K.; Ye, F.; Wang, Y.K. Short-range ordered structure and phase stability of supersaturated nitrided layer on austenitic stainless steel. Acta Mater. 2019, 175, 314–323. [Google Scholar] [CrossRef]
  31. Wang, X.; Posselt, M.; Fassbender, J. Influence of substitutional atoms on the diffusion of oxygen in dilute iron alloys. Phys. Rev. B 2018, 98, 064103. [Google Scholar] [CrossRef]
  32. Zhang, P.B.; Zou, T.T.; Sun, D.; Yin, Y.; Zhao, J.J. Oxygen interaction with alloying elements (Cr/Ni) and vacancies in dilute austenitic iron alloys: A first-principles study. Fusion. Eng. Des. 2021, 163, 112123. [Google Scholar] [CrossRef]
  33. Mathayan, V.; Gnanasekaran, J.; Chelladurai, L.; Balakrishnan, S.; Ramalingam, R.; Panigrahi, B.K.; Gangavarapu, A. Oxygen trapping in defect clusters in Fe and FeCr alloy by ion channeling and ab-initio study. J. Nucl. Mater. 2020, 532, 152032. [Google Scholar] [CrossRef]
  34. Kresse, G. Ab-intio molecular-dynamics for liquid-metals. J. Non-Cryst. Solids. 1995, 193, 222–229. [Google Scholar] [CrossRef]
  35. Kresse, G.; Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  36. Kresse, G.; Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  37. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  38. Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  39. Blochl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  40. Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
  41. Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
  42. Henkelman, G.; Uberuaga, B.P.; Jonsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  43. Henkelman, G.; Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
  44. Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 1947, 71, 809. [Google Scholar] [CrossRef]
  45. Katsura, T.; Tange, Y. A Simple Derivation of the Birch-Murnaghan Equations of State (EOSs) and Comparison with EOSs Derived from Other Definitions of Finite Strain. Minerals 2019, 9, 745. [Google Scholar] [CrossRef]
  46. Dronskowski, R.; Bloechl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
  47. Nelson, R.; Ertural, C.; George, J.; Deringer, V.L.; Hautier, G.; Dronskowski, R. LOBSTER: Local orbital projections, atomic charges, and chemical-bonding analysis from projector-augmented-wave-based density-functional theory. J. Comput. Chem. 2020, 41, 1931–1940. [Google Scholar] [CrossRef] [PubMed]
  48. Lv, Z.; Zhang, Q.; Li, R.; Hong, Y.; Zhang, X. Combined Effects of Carbon and Nitrogen in Fe20Cr6Mn6CN Alloys from First-Principles Calculation. J. Mater. Eng. Perform. 2021, 30, 8322–8335. [Google Scholar] [CrossRef]
  49. Wang, F.; Mi, T.; Chen, P.; Zhu, H.; Chen, Y.; Zhang, P.; Li, R.; Qiu, C. Synergistic Effect of Hetero Interstitial Atoms (C/N/O) on the Thermodynamic Stability in BCC Fe: A DFT Study. Coatings 2025, 15, 929. [Google Scholar] [CrossRef]
  50. Zhang, L.; Fu, C.-C.; Lu, G.-H. Energetic landscape and diffusion of He in α-Fe grain boundaries from first principles. Phys. Rev. B 2013, 87, 134107. [Google Scholar] [CrossRef]
  51. Luo, W.D.; Hou, T.P.; Liang, X.; Cheng, S.; Zheng, Y.H.; Li, Y.; Ye, X.F.; Wu, K.M. Structure and stability investigation of oxygen interaction with Fe in bcc-Fe. Vacuum 2023, 212, 112005. [Google Scholar] [CrossRef]
  52. Zou, C.; Li, J.; Wang, W.Y.; Zhang, Y.; Tang, B.; Wang, H.; Lin, D.; Wang, J.; Kou, H.; Xu, D. Revealing the local lattice strains and strengthening mechanisms of Ti alloys. Comp. Mater. Sci. 2018, 152, 169–177. [Google Scholar] [CrossRef]
  53. Raebiger, H.; Lany, S.; Zunger, A. Charge self-regulation upon changing the oxidation state of transition metals in insulators. Nature 2008, 453, 763–766. [Google Scholar] [CrossRef] [PubMed]
  54. Martinez, E.; Fu, C.-C. Cr interactions with He and vacancies in dilute Fe-Cr alloys from first principles. Phys. Rev. B 2011, 84, 014203. [Google Scholar] [CrossRef]
  55. Razumovskiy, V.I.; Ruban, A.V.; Korzhavyi, P.A. First-principles study of elastic properties of Cr- and Fe-rich Fe-Cr alloys. Phys. Rev. B 2011, 84, 024106. [Google Scholar] [CrossRef]
  56. Olsson, P.; Abrikosov, I.A.; Wallenius, J. Electronic origin of the anomalous stability of Fe-rich bcc Fe-Cr alloys. Phys. Rev. B 2006, 73, 104416. [Google Scholar] [CrossRef]
  57. Nguyen-Manh, D.; Lavrentiev, M.Y.; Dudarev, S.L. Ab initio and Monte Carlo modeling in Fe-Cr system: Magnetic origin of anomalous thermodynamic and kinetic properties. Comp. Mater. Sci. 2008, 44, 1–8. [Google Scholar] [CrossRef]
  58. Barouh, C.; Schuler, T.; Fu, C.-C.; Nastar, M. Interaction between vacancies and interstitial solutes (C, N, and O) in α-Fe: From electronic structure to thermodynamics. Phys. Rev. B 2014, 90, 054112. [Google Scholar] [CrossRef]
  59. Kadowaki, M.; Saengdeejing, A.; Muto, I.; Chen, Y.; Masuda, H.; Katayama, H.; Doi, T.; Kawano, K.; Miura, H.; Sugawara, Y.; et al. First-principles analysis of the inhibitive effect of interstitial carbon on an active dissolution of martensitic steel. Corros. Sci. 2020, 163, 108251. [Google Scholar] [CrossRef]
  60. Fedorov, M.; Wróbel, J.S.; London, A.J.; Kurzydlowski, K.J.; Fu, C.C.; Tadic, T.; Dudarev, S.L.; Nguyen-Manh, D. Precipitation of Cr-rich clusters in Fe-Cr alloys: Effects of irradiation from first principles modeling and experimental observations. J. Nucl. Mater. 2023, 587, 154715. [Google Scholar] [CrossRef]
  61. Yang, Z.-X.; Liu, W.-B.; Zhang, C.-Y.; He, X.-F.; Sun, Z.-Y.; Jia, L.-X.; Shi, T.-T.; Yun, D. Phase field simulation of grain boundary segregation and radiation-enhanced segregation in Fe-Cr alloys. Acta Phys. Sin.-Chim. Ed. 2021, 70, 20201840. [Google Scholar] [CrossRef]
  62. Müller, P.C.; Ertural, C.; Hempelmann, J.; Dronskowski, R. Crystal Orbital Bond Index: Covalent Bond Orders in Solids. J. Phys. Chem. C 2021, 125, 7959–7970. [Google Scholar] [CrossRef]
  63. Fernandez, N.; Ferro, Y.; Kato, D.J.A.M. Hydrogen diffusion and vacancies formation in tungsten: Density Functional Theory calculations and statistical models. Acta Mater. 2015, 94, 307–318. [Google Scholar] [CrossRef]
  64. Zhu, H.M.; Li, Y.Z.; Li, B.C.; Zhang, Z.Y.; Qiu, C.J. Effects of Low-Temperature Tempering on Microstructure and Properties of the Laser-Cladded AISI 420 Martensitic Stainless Steel Coating. Coatings 2018, 8, 415. [Google Scholar] [CrossRef]
  65. Zhao, D.; Yang, Q.; Wang, D.; Yan, M.; Wang, P.; Jiang, M.; Liu, C.; Diao, D.; Lao, C.; Chen, Z.; et al. Ordered nitrogen complexes overcoming strength-ductility trade-off in an additively manufactured high-entropy alloy. Virtual Phys. Prototy. 2020, 15, 532–542. [Google Scholar] [CrossRef]
Coatings 15 01096 g001
Figure 1. The configurations of Fe53Cr1 and Fe52Cr2 simplified as Cr1 and Cr2 in the unit cell. (a) Cr1-1; (b) Cr1-2; (c) Cr2-1; (d) Cr2-2; (e) Cr2-3; (f) Cr2-4; (g) Cr2-5.
Figure 1. The configurations of Fe53Cr1 and Fe52Cr2 simplified as Cr1 and Cr2 in the unit cell. (a) Cr1-1; (b) Cr1-2; (c) Cr2-1; (d) Cr2-2; (e) Cr2-3; (f) Cr2-4; (g) Cr2-5.
Coatings 15 01096 g001
Coatings 15 01096 g002
Figure 2. The configurations of C, N, and O in T-sites and O-sites, and their formation energy in Fe53Cr1. (a) the central position Cr and O-site X (X=C/N/O); (b) the angular position Cr and O-site X; (c) the central position Cr and T-site X; (d) the angular position Cr and T-site X.
Figure 2. The configurations of C, N, and O in T-sites and O-sites, and their formation energy in Fe53Cr1. (a) the central position Cr and O-site X (X=C/N/O); (b) the angular position Cr and O-site X; (c) the central position Cr and T-site X; (d) the angular position Cr and T-site X.
Coatings 15 01096 g002
Coatings 15 01096 g003
Figure 3. The O-site interstitial X (X = C/N/O) formation energy varies with the Cr numbers (m = 0–5) in the unit cell of Fe54−mCrmX. Note that m = 0 represents the O-site interstitial X in pure Fe lattice.
Figure 3. The O-site interstitial X (X = C/N/O) formation energy varies with the Cr numbers (m = 0–5) in the unit cell of Fe54−mCrmX. Note that m = 0 represents the O-site interstitial X in pure Fe lattice.
Coatings 15 01096 g003
Coatings 15 01096 g004
Figure 4. Schematic diffusion pathway (0–4) of C/N/O and the migration energy barrier in the Fe-Cr supercell during the diffusion process. Note that 0 denotes the initial central O-site, 4 denotes the final OCI-site, 1 and 3 represent the transition states, and 2 is the stable edge O-site. The dashed line serves as a reference line, indicating zero diffusion energy.
Figure 4. Schematic diffusion pathway (0–4) of C/N/O and the migration energy barrier in the Fe-Cr supercell during the diffusion process. Note that 0 denotes the initial central O-site, 4 denotes the final OCI-site, 1 and 3 represent the transition states, and 2 is the stable edge O-site. The dashed line serves as a reference line, indicating zero diffusion energy.
Coatings 15 01096 g004
Coatings 15 01096 g005
Figure 5. Configurations of IAs (C, N, or O) inhabiting O-sites in Fe53Cr1, and their binding energy (Eb) and formation energy (Ef). (a) Occupation of interstitial C/N/O in Fe-Cr system; (b) Ef and Eb of Fe53Cr1C1 with different configurations; (c) Ef and Eb of Fe53Cr1N1 with different configurations; (d) Ef and Eb of Fe53Cr1O1 with different configurations; (e) the most stable occupation of IAs (C, N, or O) from energy analysis.
Figure 5. Configurations of IAs (C, N, or O) inhabiting O-sites in Fe53Cr1, and their binding energy (Eb) and formation energy (Ef). (a) Occupation of interstitial C/N/O in Fe-Cr system; (b) Ef and Eb of Fe53Cr1C1 with different configurations; (c) Ef and Eb of Fe53Cr1N1 with different configurations; (d) Ef and Eb of Fe53Cr1O1 with different configurations; (e) the most stable occupation of IAs (C, N, or O) from energy analysis.
Coatings 15 01096 g005
Coatings 15 01096 g006
Figure 6. (a) PDOS of Fe53Cr1C1; (b) PDOS of Fe53Cr1N1; (c) PDOS of Fe53Cr1O1. The upward arrow indicates spin up, and the downward arrow indicates spin down.
Figure 6. (a) PDOS of Fe53Cr1C1; (b) PDOS of Fe53Cr1N1; (c) PDOS of Fe53Cr1O1. The upward arrow indicates spin up, and the downward arrow indicates spin down.
Coatings 15 01096 g006
Coatings 15 01096 g007
Figure 7. (a) The CDD of the <110> plane in Fe53Cr1C1; (b) the CDD of the <110> plane in Fe53Cr1N1; (c) the CDD of the <110> plane in Fe53Cr1O1. The value of CDD ranged from −0.015 to 0.02 e/Å3.
Figure 7. (a) The CDD of the <110> plane in Fe53Cr1C1; (b) the CDD of the <110> plane in Fe53Cr1N1; (c) the CDD of the <110> plane in Fe53Cr1O1. The value of CDD ranged from −0.015 to 0.02 e/Å3.
Coatings 15 01096 g007
Coatings 15 01096 g008
Figure 8. Two-dimensional slices of the ELF of the <110> plane in Fe53Cr1C1, Fe53Cr1N1, and Fe53Cr1O1 at configuration 1. (a) the ELF of Fe53Cr1C1; (b) COHP of Cr-C pair and 1NN Fe-C pair in Fe53Cr1C1; (c) the ELF of Fe53Cr1N1; (d) COHP of Cr-N pair and 1NN Fe-N pair in Fe53Cr1N1; (e) the ELF of Fe53Cr1O1; (f) COHP of Cr-O pair and 1NN Fe-O pair in Fe53Cr1O1.
Figure 8. Two-dimensional slices of the ELF of the <110> plane in Fe53Cr1C1, Fe53Cr1N1, and Fe53Cr1O1 at configuration 1. (a) the ELF of Fe53Cr1C1; (b) COHP of Cr-C pair and 1NN Fe-C pair in Fe53Cr1C1; (c) the ELF of Fe53Cr1N1; (d) COHP of Cr-N pair and 1NN Fe-N pair in Fe53Cr1N1; (e) the ELF of Fe53Cr1O1; (f) COHP of Cr-O pair and 1NN Fe-O pair in Fe53Cr1O1.
Coatings 15 01096 g008
Table 1. Calculated ground state physical properties of the pure Fe54 and Fe-Cr system, including the volume change in the supercell per solute atom (∆V) and bulk modulus (B) predicted by the four-parameter BM-EOS fitting, average magnetic moment (M), formation energy (Ef), and lattice distortion energy (Eld).
Table 1. Calculated ground state physical properties of the pure Fe54 and Fe-Cr system, including the volume change in the supercell per solute atom (∆V) and bulk modulus (B) predicted by the four-parameter BM-EOS fitting, average magnetic moment (M), formation energy (Ef), and lattice distortion energy (Eld).
Alloys∆V (Å3)B (GPa)M (μB)Ef (eV)Eld (eV)
Fe540.000189.2402.200--
Cr1-12.518183.8862.158−0.648−1.465
Cr1-22.503184.0792.158−0.646−1.463
Cr2-15.266179.3182.114−0.661−2.776
Cr2-24.473181.642.109−0.557−2.762
Cr2-35.577177.9422.112−0.782−2.897
Cr2-45.268178.3232.108−0.777−2.892
Cr2-55.267178.672.115−0.662−2.777
Table 2. Comparison of dissociation temperatures (Tdis) of interstitial X (C, N, or O) in Fe53Cr1X and Fe54X. Dissolution energy (Edis) equals to the sum of biding energy (Eb) and migration energy (Em), and the heating rate is 1 K/s.
Table 2. Comparison of dissociation temperatures (Tdis) of interstitial X (C, N, or O) in Fe53Cr1X and Fe54X. Dissolution energy (Edis) equals to the sum of biding energy (Eb) and migration energy (Em), and the heating rate is 1 K/s.
EbEmEdisTdis (K)
Single C-0.926 *0.926325
Single N-0.784 *0.784281
Single O-0.557 *0.557202
Cr1C→Cr + C−0.2651.2620.997347
Cr1C→Cr + N0.0740.7680.842302
Cr1O→Cr + O0.2230.4810.704254
* Ref. [49].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Wang, F.; Mi, T.; Chen, P.; Zhu, H.; Chen, Y.; Zhang, P.; Li, R.; Qiu, C. Theoretical Insight into the Cooperative Strengthening of Interstitial Atoms(C/N/O) and Cr in Dilute Fe-Cr System. Coatings 2025, 15, 1096. https://doi.org/10.3390/coatings15091096

AMA Style

Wang F, Mi T, Chen P, Zhu H, Chen Y, Zhang P, Li R, Qiu C. Theoretical Insight into the Cooperative Strengthening of Interstitial Atoms(C/N/O) and Cr in Dilute Fe-Cr System. Coatings. 2025; 15(9):1096. https://doi.org/10.3390/coatings15091096

Chicago/Turabian Style

Wang, Fang, Tengge Mi, Pinghu Chen, Hongmei Zhu, Yong Chen, Pengbo Zhang, Ruiqing Li, and Changjun Qiu. 2025. "Theoretical Insight into the Cooperative Strengthening of Interstitial Atoms(C/N/O) and Cr in Dilute Fe-Cr System" Coatings 15, no. 9: 1096. https://doi.org/10.3390/coatings15091096

APA Style

Wang, F., Mi, T., Chen, P., Zhu, H., Chen, Y., Zhang, P., Li, R., & Qiu, C. (2025). Theoretical Insight into the Cooperative Strengthening of Interstitial Atoms(C/N/O) and Cr in Dilute Fe-Cr System. Coatings, 15(9), 1096. https://doi.org/10.3390/coatings15091096

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop