SEM Image Segmentation Method for Copper Microstructures Based on Enhanced U-Net Modeling
Abstract
1. Introduction
2. Related Work
3. Materials
3.1. Material Preparation
3.2. Dataset
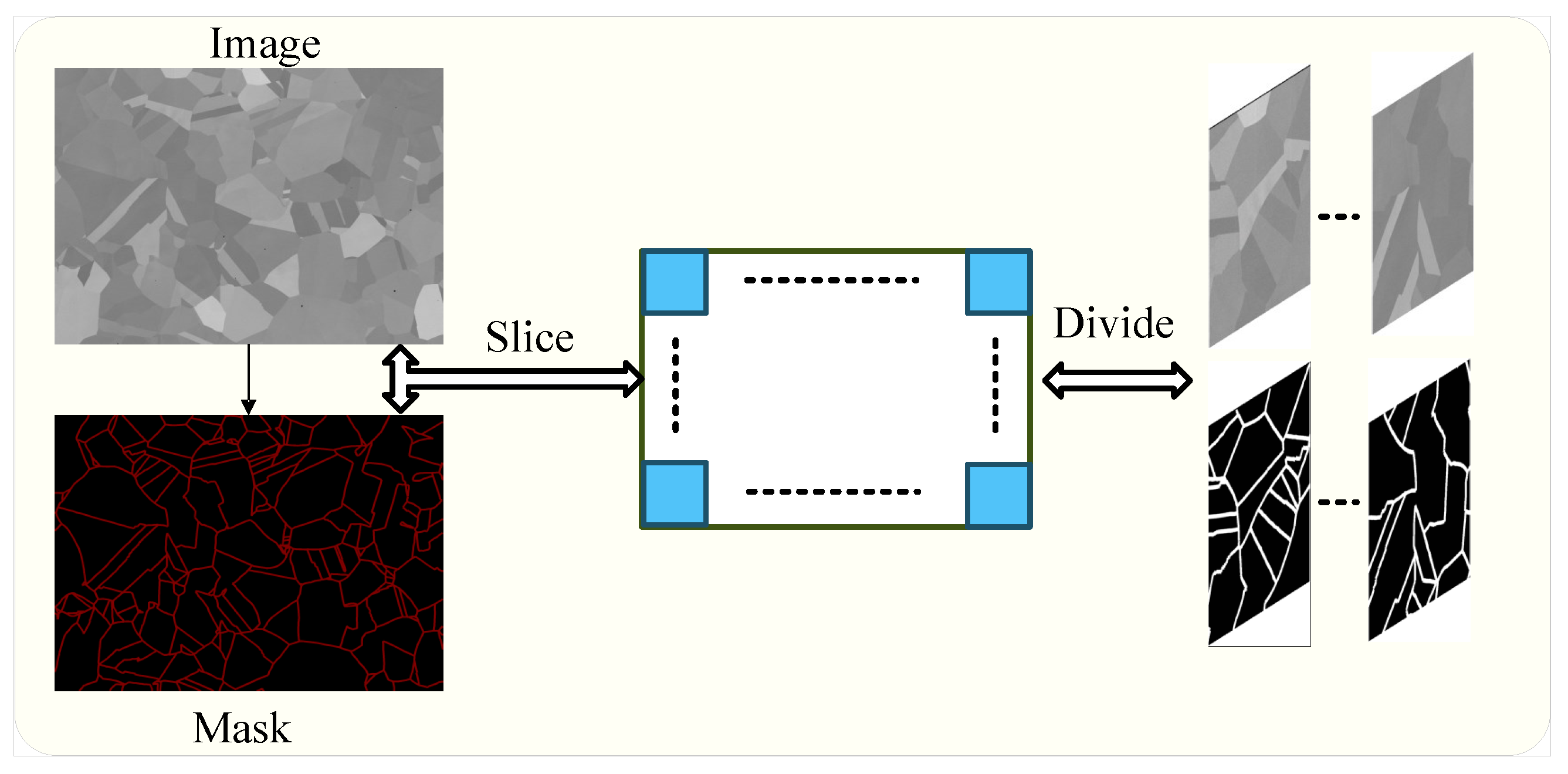
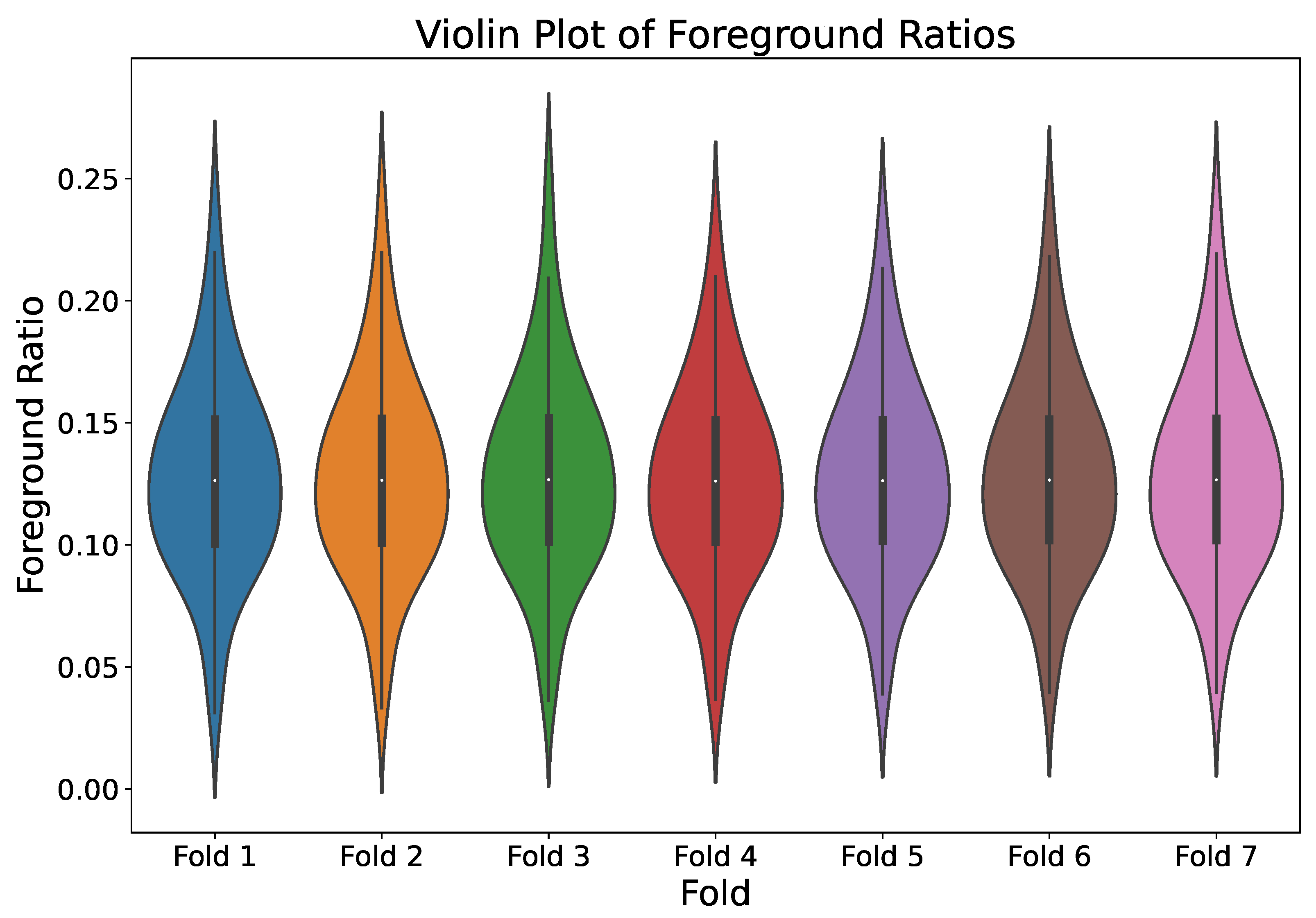
3.2.1. Dataset Description
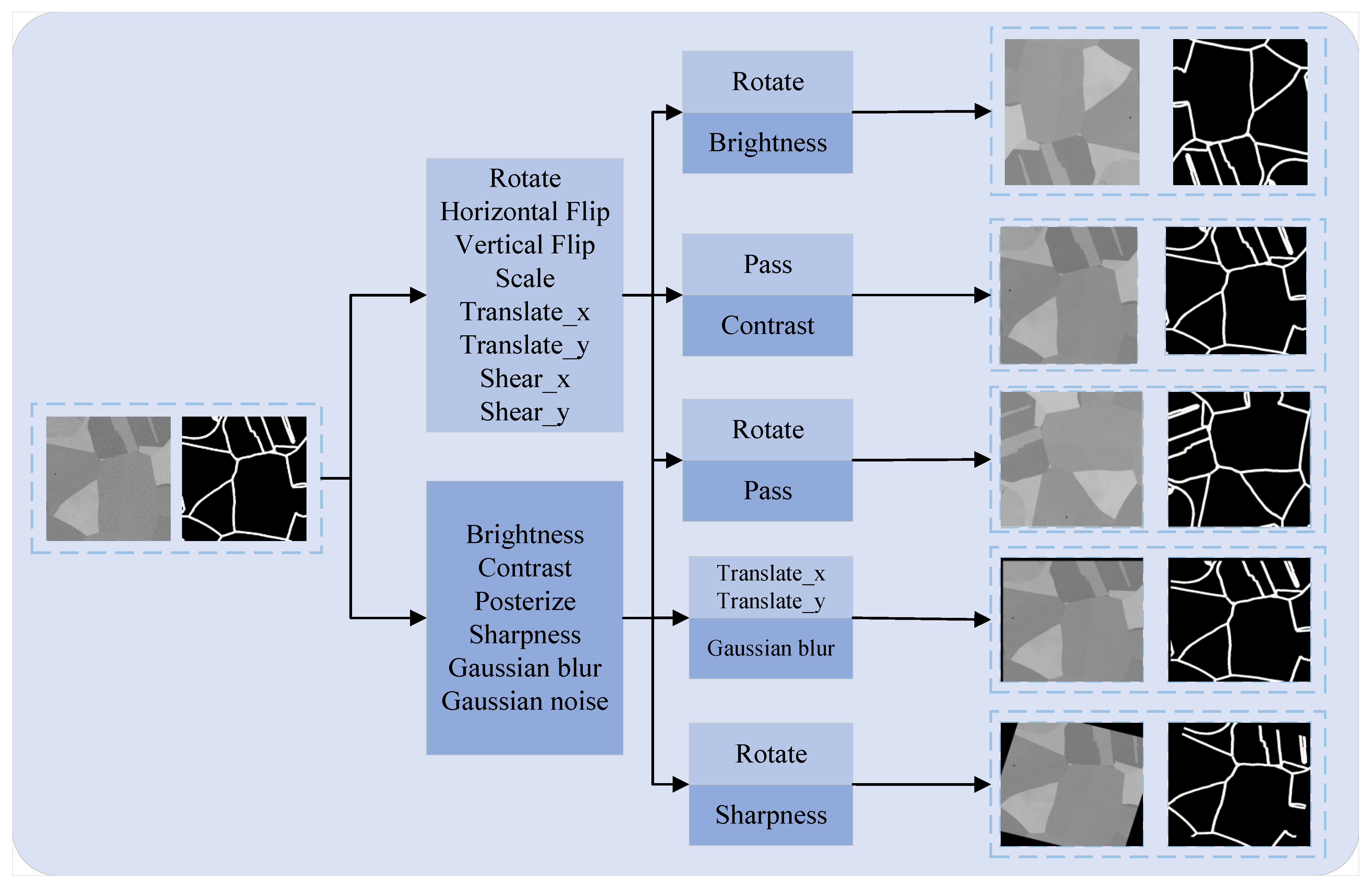
3.2.2. Dataset Augmentation
4. Methods
4.1. Preventing Overfitting
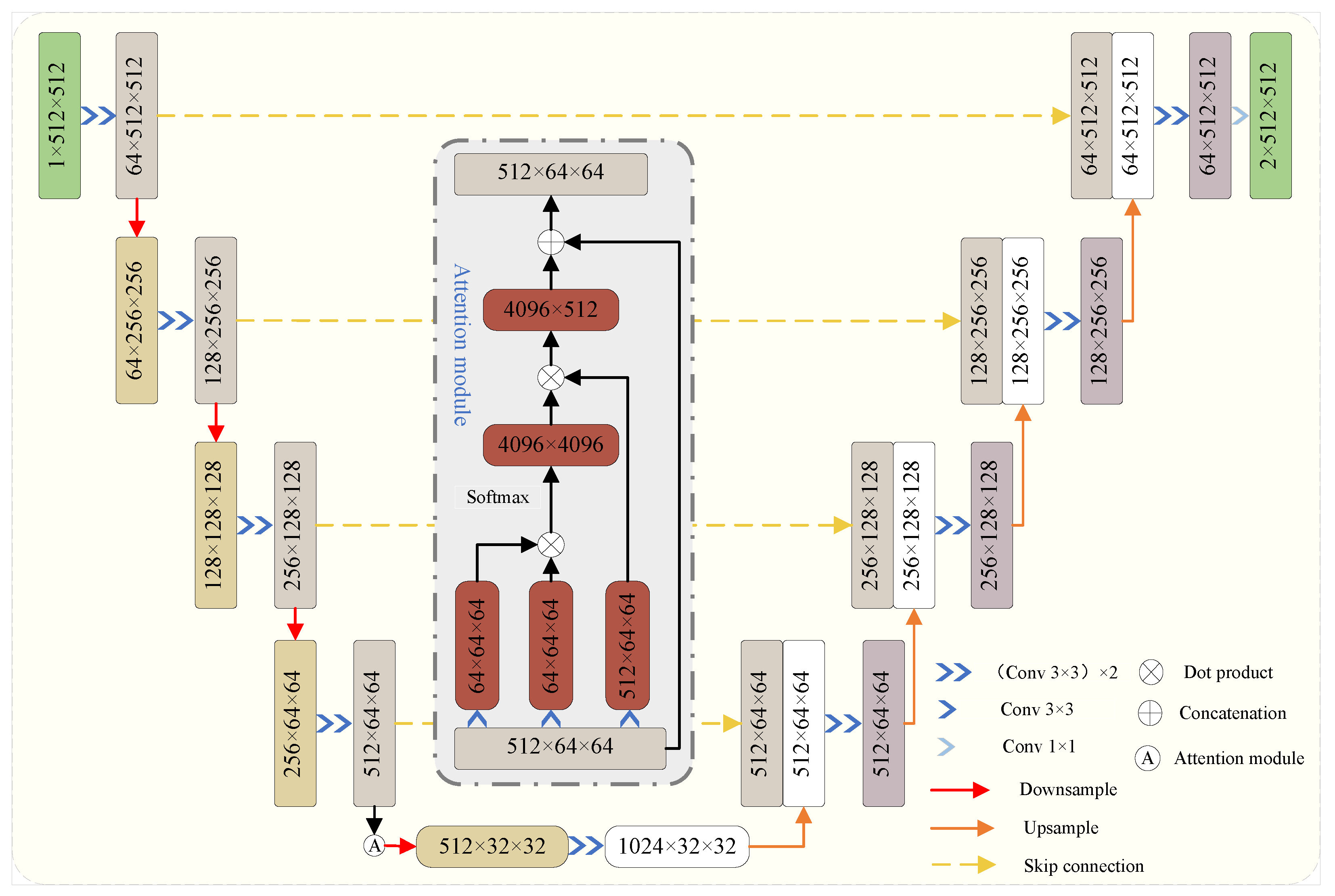
4.2. Model Introduction and Improvement
4.3. Evaluation Criteria and Computational Resources
5. Experimental Results and Discussion
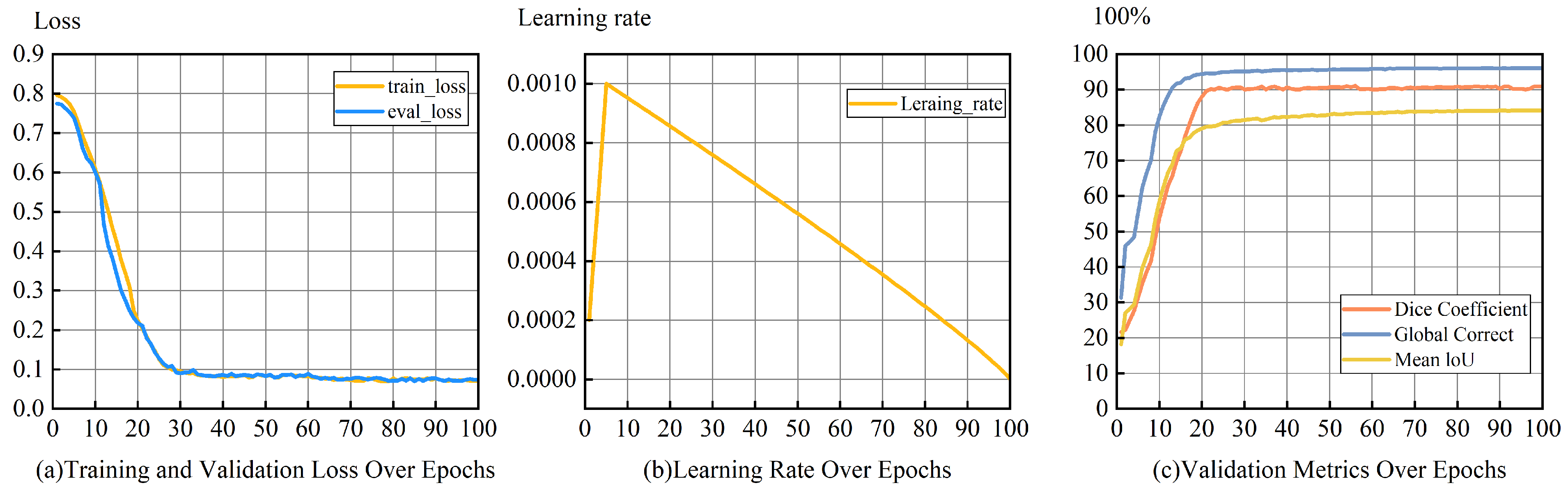
5.1. Quantitative Analysis
5.2. Qualitative Analysis
5.3. Ablation Experiment
5.4. Comparison Results with Other Methodological Methods
6. Conclusions
- 1.
- Diverse Material Applications: Validated on pure copper, CUNet could be extended to ceramics or composites by adapting data augmentation and leveraging transfer learning to accommodate varied microstructures.
- 2.
- Computational Efficiency: Training (1 h 31 min) and inference (13.0 FPS) times limit real-time use. Model pruning or quantization could enhance efficiency while maintaining accuracy.
- 3.
- Model Interpretability: The self-attention mechanism’s opacity could be addressed using explainable AI techniques, such as attention visualization, to enhance trust in materials science applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rusanovsky, M.; Beeri, O.; Oren, G. An End-to-End Computer Vision Methodology for Quantitative Metallography. Sci. Rep. 2022, 12, 4776. [Google Scholar] [CrossRef]
- Ragone, M.; Shahabazian-Yassar, R.; Mashayek, F.; Yurkiv, V. Deep Learning Modeling in Microscopy Imaging: A Review of Materials Science Applications. Prog. Mater. Sci. 2023, 138, 101165. [Google Scholar] [CrossRef]
- Luo, Y.X.; Dong, Y.L.; Yang, F.Q.; Lu, X.Y. Ultraviolet Single-Camera Stereo-Digital Image Correlation for Deformation Measurement up to 2600 °C. Exp. Mech. 2024, 64, 1343–1355. [Google Scholar] [CrossRef]
- Paredes-Orta, C.A.; Mendiola-Santibañez, J.D.; Manriquez-Guerrero, F.; Terol-Villalobos, I.R. Method for Grain Size Determination in Carbon Steels Based on the Ultimate Opening. Measurement 2019, 133, 193–207. [Google Scholar] [CrossRef]
- Shah, A.; Schiller, J.A.; Ramos, I.; Serrano, J.; Adams, D.K.; Tawfick, S.; Ertekin, E. Automated Image Segmentation of Scanning Electron Microscopy Images of Graphene Using U-Net Neural Network. Mater. Today Commun. 2023, 35, 106127. [Google Scholar] [CrossRef]
- Zhang, L.; Xu, Z.; Wei, S.; Ren, X.; Wang, M. Grain size automatic determination for 7050 Al alloy based on a fuzzy logic method. Rare Met. Mater. Eng. 2016, 45, 548–554. [Google Scholar] [CrossRef]
- Campbell, A.; Murray, P.; Yakushina, E.; Marshall, S.; Ion, W. New methods for automatic quantification of microstructural features using digital image processing. Mater. Des. 2018, 141, 395–406. [Google Scholar] [CrossRef]
- Shen, C.; Wang, C.; Wei, X.; Li, Y.; van der Zwaag, S.; Xu, W. Physical Metallurgy-Guided Machine Learning and Artificial Intelligent Design of Ultrahigh-Strength Stainless Steel. Acta Mater. 2019, 179, 201–214. [Google Scholar] [CrossRef]
- Azimi, S.M.; Britz, D.; Engstler, M.; Fritz, M.; Mücklich, F. Advanced steel microstructural classification by deep learning methods. Sci. Rep. 2018, 8, 2128. [Google Scholar] [CrossRef]
- Goetz, A.; Durmaz, A.R.; Müller, M.; Thomas, A.; Britz, D.; Kerfriden, P.; Eberl, C. Addressing materials’ microstructure diversity using transfer learning. npj Comput. Mater. 2022, 8, 27. [Google Scholar] [CrossRef]
- Ajioka, F.; Wang, Z.L.; Ogawa, T.; Adachi, Y. Development of high accuracy segmentation model for microstructure of steel by deep learning. ISIJ Int. 2020, 60, 954–959. [Google Scholar] [CrossRef]
- Durmaz, A.R.; Müller, M.; Lei, B.; Thomas, A.; Britz, D.; Holm, E.A.; Gumbsch, P.; Mücklich, F.; Gumbsch, P. A deep learning approach for complex microstructure inference. Nat. Commun. 2021, 12, 6272. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, J.H.; Liu, C.N.; Ban, X.J.; Ma, B.Y.; Wang, H.; Xue, W.; Guo, Y. Boundary learning by using weighted propagation in convolution network. J. Comput. Sci. 2022, 62, 101709. [Google Scholar] [CrossRef]
- Zhu, X.; Zhu, Y.; Kang, C.; Liu, M.; Yao, Q.; Zhang, P.; Huang, G.; Qian, L.; Zhang, Z.; Yao, Z. Research on automatic identification and rating of ferrite–pearlite grain boundaries based on deep learning. Materials 2023, 16, 1974. [Google Scholar] [CrossRef]
- Wittwer, M.; Gaskey, B.; Seita, M. An Automated and Unbiased Grain Segmentation Method Based on Directional Reflectance Microscopy. Mater. Charact. 2021, 174, 110978. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A Survey on Image Data Augmentation for Deep Learning. J. Big Data 2019, 6, 60. [Google Scholar] [CrossRef]
- Liu, Z.; Lv, Q.; Li, Y.; Yang, Z.; Shen, L. MedAugment: Universal Automatic Data Augmentation Plug-in for Medical Image Analysis. arXiv 2023, arXiv:2306.17466. [Google Scholar]
- Gholamiangonabadi, D.; Kiselov, N.; Grolinger, K. Deep Neural Networks for Human Activity Recognition with Wearable Sensors: Leave-One-Subject-Out Cross-Validation for Model Selection. IEEE Access 2020, 8, 133982–133994. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. TransUNet: Transformers Make Strong Encoders for Medical Image Segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Wang, H.; Xu, X.; Liu, Y.; Lu, D.; Liang, B.; Tang, Y. Real-time defect detection for metal components: A fusion of enhanced Canny–Devernay and YOLOv6 algorithms. Appl. Sci. 2023, 13, 6898. [Google Scholar] [CrossRef]
- Luengo, J.; Moreno, R.; Sevillano, I.; Charte, D.; Peláez-Vegas, A.; Fernández-Moreno, M.; Mesejo, P.; Herrera, F. A tutorial on the segmentation of metallographic images: Taxonomy, new MetalDAM dataset, deep learning-based ensemble model, experimental analysis and challenges. Inf. Fusion 2022, 78, 232–253. [Google Scholar] [CrossRef]



| True Value | Predicted Positive Class | Predicted Negative Class |
|---|---|---|
| Positive Class Label | TP | FN |
| Negative Class Label | FP | TN |
| Batch Size | Epochs | Learning Rate | Optimizer | Momentum | Weight Decay |
|---|---|---|---|---|---|
| 12 | 100 | 0.001 | SGD | 0.9 | 1 × 10−4 |
| Method | Evaluation | Dataset Score |
|---|---|---|
| Without MedAugment | Global Correct | 0.9074 |
| Dice | 0.8558 | |
| MIoU | 0.8370 | |
| With MedAugment | Global Correct | 0.9202 |
| Dice | 0.8657 | |
| MIoU | 0.8481 | |
| Without Stratified Cross-Validation | Global Correct | 0.9074 |
| Dice | 0.8558 | |
| MIoU | 0.8370 | |
| With Stratified Cross-Validation | Global Correct | 0.9140 |
| Dice | 0.8812 | |
| MIoU | 0.8381 |
| Model | Encoder Layer | Global Correct | Dice | MIoU | Time | FPS | |||
|---|---|---|---|---|---|---|---|---|---|
| U-Net | 0.9074 | 0.8558 | 0.8370 | 1 h 26 min | 14.0 | ||||
| Improved U-Net1 | ✓ | 0.8962 | 0.8561 | 0.8084 | 2 h 16 min | 10.5 | |||
| Improved U-Net2 | ✓ | 0.8983 | 0.8552 | 0.8193 | 1 h 51 min | 11.5 | |||
| Improved U-Net3 | ✓ | 0.9049 | 0.8571 | 0.8231 | 1 h 44 min | 12.0 | |||
| CUNet | ✓ | 0.9341 | 0.8783 | 0.8417 | 1 h 31 min | 13.0 | |||
| Improved U-Net5 | ✓ | ✓ | ✓ | ✓ | 0.8668 | 0.8374 | 0.8108 | 4 h 46 min | 7.0 |
| Methods | Global Correct | Dice | mIoU |
|---|---|---|---|
| CUNet (Ours) | 0.9589 | 0.9108 | 0.8415 |
| U-Net | 0.9074 | 0.8558 | 0.8050 |
| U-Net++ | 0.9247 | 0.8692 | 0.8250 |
| Canny | 0.5124 | 0.4551 | 0.4000 |
| Watershed | 0.3425 | 0.6157 | 0.5500 |
| Mipar | 0.7629 | 0.7961 | 0.7800 |
| DeepLabV3+ | 0.8907 | 0.8835 | 0.8200 |
| SAM | 0.9017 | 0.9043 | 0.8350 |
| Segnet | 0.8399 | 0.8011 | 0.7900 |
| U-Net+SE | 0.8918 | 0.8672 | 0.8100 |
| U-Net+CBAM | 0.9114 | 0.8864 | 0.8300 |
| U-Net+PAN | 0.8157 | 0.8536 | 0.8000 |
| Mask-RCNN | 0.8951 | 0.8713 | 0.8147 |
| AttentionUnet | 0.9200 | 0.8843 | 0.8316 |
| TransUnet | 0.9300 | 0.8918 | 0.8287 |
| Methods | Global Correct CI Width | Dice CI Width | mIoU CI Width |
|---|---|---|---|
| CUNet (Ours) | 0.0124 | 0.0148 | 0.0178 |
| U-Net | 0.0288 | 0.0306 | 0.0330 |
| U-Net++ | 0.0236 | 0.0262 | 0.0280 |
| Canny | 0.0556 | 0.0594 | 0.0638 |
| Watershed | 0.0728 | 0.0576 | 0.0594 |
| Mipar | 0.0450 | 0.0428 | 0.0450 |
| DeepLabV3+ | 0.0306 | 0.0288 | 0.0306 |
| SAM | 0.0280 | 0.0262 | 0.0280 |
| Segnet | 0.0384 | 0.0400 | 0.0384 |
| U-Net+SE | 0.0288 | 0.0306 | 0.0306 |
| U-Net+CBAM | 0.0262 | 0.0280 | 0.0280 |
| U-Net+PAN | 0.0400 | 0.0384 | 0.0384 |
| Mask-RCNN | 0.0288 | 0.0288 | 0.0306 |
| AttentionUnet | 0.0236 | 0.0262 | 0.0262 |
| TransUnet | 0.0220 | 0.0236 | 0.0236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Zhu, J.; Cao, Z.; Yang, M.; Wang, Y. SEM Image Segmentation Method for Copper Microstructures Based on Enhanced U-Net Modeling. Coatings 2025, 15, 969. https://doi.org/10.3390/coatings15080969
Yang S, Zhu J, Cao Z, Yang M, Wang Y. SEM Image Segmentation Method for Copper Microstructures Based on Enhanced U-Net Modeling. Coatings. 2025; 15(8):969. https://doi.org/10.3390/coatings15080969
Chicago/Turabian StyleYang, Shiqi, Jianpeng Zhu, Zhenfeng Cao, Minglai Yang, and Ying Wang. 2025. "SEM Image Segmentation Method for Copper Microstructures Based on Enhanced U-Net Modeling" Coatings 15, no. 8: 969. https://doi.org/10.3390/coatings15080969
APA StyleYang, S., Zhu, J., Cao, Z., Yang, M., & Wang, Y. (2025). SEM Image Segmentation Method for Copper Microstructures Based on Enhanced U-Net Modeling. Coatings, 15(8), 969. https://doi.org/10.3390/coatings15080969






