Modeling Enthalpy of Formation with Machine Learning for Structural Evaluation and Thermodynamic Stability of Organic Semiconductors
Abstract
1. Introduction
2. Methodology
2.1. ML Analysis
2.2. Correlations and Feature Scores
3. Results and Discussion
3.1. Descriptor Designing
3.2. Model Evaluation
3.3. SHapley Impact
3.4. Cross Validation
3.5. Hyperparameter Tuning
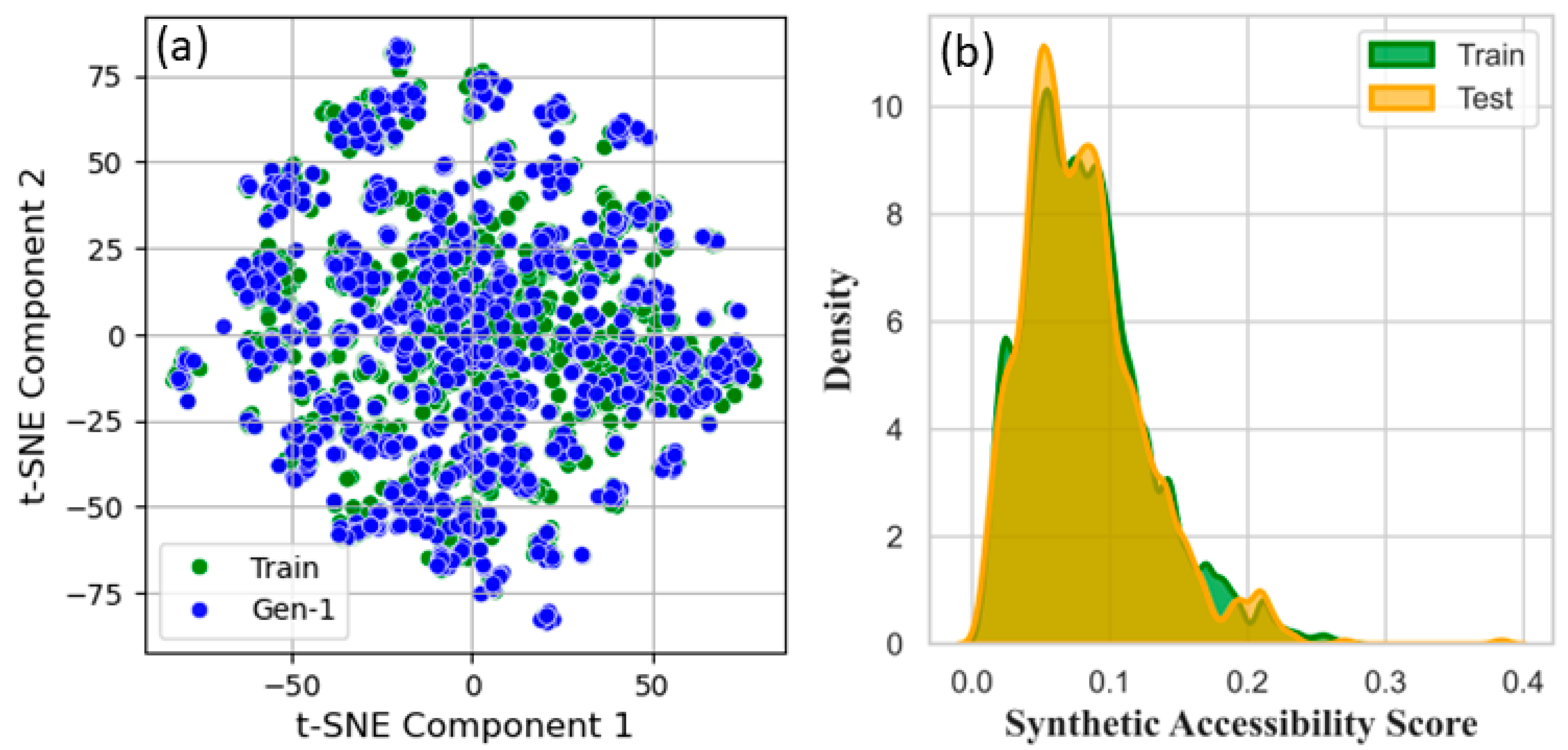
3.6. Data Clustering
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gopalakrishnan, V.; Balaji, D.; Dangate, M.S. Conjugated Polymer Photovoltaic Materials: Performance and Applications of Organic Semiconductors in Photovoltaics. ECS J. Solid State Sci. Technol. 2022, 11, 35001. [Google Scholar] [CrossRef]
- Güleryüz, C.; Sumrra, S.H.; Hassan, A.U.; Mohyuddin, A.; Waheeb, A.S.; Awad, M.A.; Jalfan, A.R.; Noreen, S.; Kyhoiesh, H.A.K.; El Azab, I.H. A machine learning and DFT assisted analysis of benzodithiophene based organic dyes for possible photovoltaic applications. J. Photochem. Photobiol. A Chem. 2025, 460, 116157. [Google Scholar] [CrossRef]
- Wu, T.; Tan, L.; Feng, Y.; Zheng, L.; Li, Y.; Sun, S.; Liu, S.; Cao, J.; Yu, Z. Toward Ultrathin: Advances in Solution-Processed Organic Semiconductor Transistors. ACS Appl. Mater. Interfaces 2024, 16, 61530–61550. [Google Scholar] [CrossRef]
- Jia, Y.; Chen, G.; Zhao, L. Defect detection of photovoltaic modules based on improved VarifocalNet. Sci. Rep. 2024, 14, 15170. [Google Scholar] [CrossRef]
- Dong, J.; Yan, C.; Chen, Y.; Zhou, W.; Peng, Y.; Zhang, Y.; Wang, L.-N.; Huang, Z.-H. Organic semiconductor nanostructures: Optoelectronic properties, modification strategies, and photocatalytic applications. J. Mater. Sci. Technol. 2022, 113, 175–198. [Google Scholar] [CrossRef]
- Salzmann, I.; Heimel, G.; Oehzelt, M.; Winkler, S.; Koch, N. Molecular Electrical Doping of Organic Semiconductors: Fundamental Mechanisms and Emerging Dopant Design Rules. Acc. Chem. Res. 2016, 49, 370–378. [Google Scholar] [CrossRef] [PubMed]
- Joly, D.; Delgado, J.L.; Atienza, C.; Martín, N. Light-Harvesting Materials for Organic Electronics. In Photonics, Volume 2: Nanophotonic Structures and Materials; Wiley: Hoboken, NJ, USA, 2015; pp. 311–341. ISBN 978-1-119-01401-0. [Google Scholar]
- Weis, M. Organic Semiconducting Polymers in Photonic Devices: From Fundamental Properties to Emerging Applications. Appl. Sci. 2025, 15, 4028. [Google Scholar] [CrossRef]
- Güleryüz, C.; Hassan, A.U.; Güleryüz, H.; Kyhoiesh, H.A.K.; Mahmoud, M.H.H. A machine learning assisted designing and chemical space generation of benzophenone based organic semiconductors with low lying LUMO energies. Mater. Sci. Eng. B 2025, 317, 118212. [Google Scholar] [CrossRef]
- Kunkel, C.; Margraf, J.T.; Chen, K.; Oberhofer, H.; Reuter, K. Active discovery of organic semiconductors. Nat. Commun. 2021, 12, 2422. [Google Scholar] [CrossRef]
- Wang, X.; Wang, W.; Yang, C.; Han, D.; Fan, H.; Zhang, J. Thermal transport in organic semiconductors. J. Appl. Phys. 2021, 130, 170902. [Google Scholar] [CrossRef]
- Wang, X.; Peng, B.; Chan, P. Thermal Annealing Effect on the Thermal and Electrical Properties of Organic Semiconductor Thin Films. MRS Adv. 2016, 1, 1637–1643. [Google Scholar] [CrossRef]
- Tong, W.; Li, H.; Liu, D.; Wu, Y.; Xu, M.; Wang, K. Study on the changes in the reverse recovery characteristics of high-power thyristor under 14.1 MeV fusion neutron irradiation. Fusion Eng. Des. 2025, 211, 114744. [Google Scholar] [CrossRef]
- Miao, Z.; Gao, C.; Shen, M.; Wang, P.; Gao, H.; Wei, J.; Deng, J.; Liu, D.; Qin, Z.; Wang, P.; et al. Organic light-emitting transistors with high efficiency and narrow emission originating from intrinsic multiple-order microcavities. Nat. Mater. 2025, 24, 917–924. [Google Scholar] [CrossRef]
- Güleryüz, C.; Sumrra, S.H.; Hassan, A.U.; Mohyuddin, A.; Elnaggar, A.Y.; Noreen, S. A machine learning analysis to predict the stability driven structural correlations of selenium-based compounds as surface enhanced materials. Mater. Chem. Phys. 2025, 339, 130786. [Google Scholar] [CrossRef]
- Bronstein, H.; Nielsen, C.B.; Schroeder, B.C.; McCulloch, I. The role of chemical design in the performance of organic semiconductors. Nat. Rev. Chem. 2020, 4, 66–77. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Chen, Y.; Xie, B.; Wu, H.; Cheng, L.; Guo, Y.; Cai, C.; Chen, X. Microdynamic behaviors of Au/Ni-assisted chemical etching in fabricating silicon nanostructures. App. Surf. Sci. 2025, 696, 122915. [Google Scholar] [CrossRef]
- Gao, S.; Wang, H.; Huang, H.; Dong, Z.; Kang, R. Predictive models for the surface roughness and subsurface damage depth of semiconductor materials in precision grinding. IJEM 2025, 7, 035103. [Google Scholar] [CrossRef]
- Tian, X.; Xun, R.; Chang, T.; Yu, J. Distribution function of thermal ripples in h-BN, graphene and MoS2. Phys. Lett. A 2025, 550, 130597. [Google Scholar] [CrossRef]
- Wang, H.; Hou, Y.; He, Y.; Wen, C.; Giron-Palomares, B.; Duan, Y.; Gao, B.; Vavilov, V.P.; Wang, Y. A Physical-Constrained Decomposition Method of Infrared Thermography: Pseudo Restored Heat Flux Approach Based on Ensemble Bayesian Variance Tensor Fraction. IEEE Trans. Ind. Inform. 2023, 20, 3413–3424. Available online: https://ieeexplore.ieee.org/document/10242241 (accessed on 14 June 2025). [CrossRef]
- Armeli, G.; Peters, J.-H.; Koop, T. Machine-Learning-Based Prediction of the Glass Transition Temperature of Organic Compounds Using Experimental Data. ACS Omega 2023, 8, 12298–12309. [Google Scholar] [CrossRef]
- Qin, X.; Wang, Q.; Zhao, X.; Xia, S.; Wang, L.; Zhang, Y.; He, C.; Chen, D.; Jiang, B. PCS: Property-composition-structure chain in Mg-Nd alloys through integrating sigmoid fitting and conditional generative adversarial network modeling. Scr. Mater. 2025, 265, 116762. [Google Scholar] [CrossRef]
- Mckinney, W. Pandas: A Foundational Python Library for Data Analysis and Statistics. Python High Perform. Sci. Comput. 2011, 14, 1–9. [Google Scholar]
- Schäfer, C. Extensions for Scientists: NumPy, SciPy, Matplotlib, Pandas. In Quickstart Python: An Introduction to Programming for STEM Students; Schäfer, C., Ed.; Springer Fachmedien: Wiesbaden, Germany, 2021; pp. 45–53. ISBN 978-3-658-33552-6. [Google Scholar]
- Scalfani, V.F.; Patel, V.D.; Fernandez, A.M. Visualizing chemical space networks with RDKit and NetworkX. J. Cheminform. 2022, 14, 87. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar] [CrossRef]
- Hasan, D.M.; Mallah, S.H.; Waheeb, A.S.; Güleryüz, C.; Hassan, A.U.; Kyhoiesh, H.A.K.; Elnaggar, A.Y.; Azab, I.H.E.; Mahmoud, M.H.H. Chemical modification-induced enhancements in quantum dot photovoltaics: A theoretical and molecular descriptive analysis. Struct. Chem. 2025. [Google Scholar] [CrossRef]
- Li, X.H.; Jalbout, A.F.; Solimannejad, M. Definition and application of a novel valence molecular connectivity index. J. Mol. Struct. Theochem 2003, 663, 81–85. [Google Scholar] [CrossRef]
- Müller, M.; Hansen, A.; Grimme, S. An atom-in-molecule adaptive polarized valence single-ζ atomic orbital basis for electronic structure calculations. J. Chem. Phys. 2023, 159, 164108. [Google Scholar] [CrossRef]
- Okoye, K.; Hosseini, S. Correlation Tests in R: Pearson Cor, Kendall’s Tau, and Spearman’s Rho. In R Programming: Statistical Data Analysis in Research; Okoye, K., Hosseini, S., Eds.; Springer Nature: Singapore, 2024; pp. 247–277. ISBN 978-981-97-3385-9. [Google Scholar]
- Saarela, M.; Jauhiainen, S. Comparison of feature importance measures as explanations for classification models. SN Appl. Sci. 2021, 3, 272. Available online: https://link.springer.com/article/10.1007/s42452-021-04148-9 (accessed on 25 December 2024). [CrossRef]
- Li, Q.; Yang, Y.; Wen, Y.; Tian, X.; Li, Y.; Xiang, W. A Fast Overcurrent Protection IC for SiC MOSFET Based on Current Detection. IEEE Trans. Power Electron. 2024, 39, 4986–4990. [Google Scholar] [CrossRef]
- Hu, Q.-N.; Liang, Y.-Z.; Yin, H.; Peng, X.-L.; Fang, K.-T. Structural Interpretation of the Topological Index. 2. The Molecular Connectivity Index, the Kappa Index, and the Atom-type E-State Index. J. Chem. Inf. Comput. Sci. 2004, 44, 1193–1201. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- Marques Ramos, A.P.; Prado Osco, L.; Elis Garcia Furuya, D.; Nunes Gonçalves, W.; Cordeiro Santana, D.; Pereira Ribeiro Teodoro, L.; Antonio da Silva Junior, C.; Fernando Capristo-Silva, G.; Li, J.; Henrique Rojo Baio, F.; et al. A random forest ranking approach to predict yield in maize with uav-based vegetation spectral indices. Comput. Electron. Agric. 2020, 178, 105791. [Google Scholar] [CrossRef]
- Berrouachedi, A.; Jaziri, R.; Bernard, G. Deep Extremely Randomized Trees. In Neural Information, Proceedings of the Neural Information Processing, Sydney, NSW, Australia, December 12–15, 2019; Gedeon, T., Wong, K.W., Lee, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 717–729. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Fox, E.W.; Hill, R.A.; Leibowitz, S.G.; Olsen, A.R.; Thornbrugh, D.J.; Weber, M.H. Assessing the accuracy and stability of variable selection methods for random forest modeling in ecology. Environ. Monit. Assess. 2017, 189, 316. [Google Scholar] [CrossRef]
- Mallah, S.H.; Güleryüz, C.; Sumrra, S.H.; Hassan, A.U.; Güleryüz, H.; Mohyuddin, A.; Kyhoiesh, H.A.K.; Noreen, S.; Elnaggar, A.Y. Benzothiophene semiconductor polymer design by machine learning with low exciton binding energy: A vast chemical space generation for new structures. Mater. Sci. Semicond. Process. 2025, 190, 109331. [Google Scholar] [CrossRef]
- Liebscher, E. Estimating the Density of the Residuals in Autoregressive Models. Stat. Inference Stoch. Process. 1999, 2, 105–117. [Google Scholar] [CrossRef]
- Zhou, Y.; Fan, S.; Zhu, Z.; Su, S.; Hou, D.; Zhang, H.; Cao, Y. Enabling High-Sensitivity Calorimetric Flow Sensor Using Vanadium Dioxide Phase-Change Material with Predictable Hysteretic Behavior. IEEE Trans. Electron. Devices 2025, 72, 1360–1367. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, C.-A. Model averaging prediction by K-fold cross-validation. J. Econom. 2023, 235, 280–301. [Google Scholar] [CrossRef]
- Young, S.R.; Rose, D.C.; Karnowski, T.P.; Lim, S.-H.; Patton, R.M. Optimizing deep learning hyper-parameters through an evolutionary algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15 November 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 1–5. [Google Scholar]
- Cess, C.G.; Haghverdi, L. Compound-SNE: Comparative alignment of t-SNEs for multiple single-cell omics data visualization. Bioinformatics 2024, 40, btae471. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noreen, S.; Aljaafreh, M.J.; Sumrra, S.H. Modeling Enthalpy of Formation with Machine Learning for Structural Evaluation and Thermodynamic Stability of Organic Semiconductors. Coatings 2025, 15, 758. https://doi.org/10.3390/coatings15070758
Noreen S, Aljaafreh MJ, Sumrra SH. Modeling Enthalpy of Formation with Machine Learning for Structural Evaluation and Thermodynamic Stability of Organic Semiconductors. Coatings. 2025; 15(7):758. https://doi.org/10.3390/coatings15070758
Chicago/Turabian StyleNoreen, Sadaf, Mamduh J. Aljaafreh, and Sajjad H. Sumrra. 2025. "Modeling Enthalpy of Formation with Machine Learning for Structural Evaluation and Thermodynamic Stability of Organic Semiconductors" Coatings 15, no. 7: 758. https://doi.org/10.3390/coatings15070758
APA StyleNoreen, S., Aljaafreh, M. J., & Sumrra, S. H. (2025). Modeling Enthalpy of Formation with Machine Learning for Structural Evaluation and Thermodynamic Stability of Organic Semiconductors. Coatings, 15(7), 758. https://doi.org/10.3390/coatings15070758





