Energy Sustainability, Resilience, and Climate Adaptability of Modular and Panelized Buildings with a Lightweight Envelope Integrating Active Thermal Protection. Part 1—Parametric Study and Computer Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Overview of Scientific and Professional Studies
2.1.1. Research Area—Active Thermal Protection
2.1.2. Research Area—Computer Simulation and Modelling of Energy Phenomena in Buildings
2.2. Analysis Strategy, Validation Methods, and Optimization of ATP in Lightweight Building Envelope
2.2.1. Theoretical Foundations
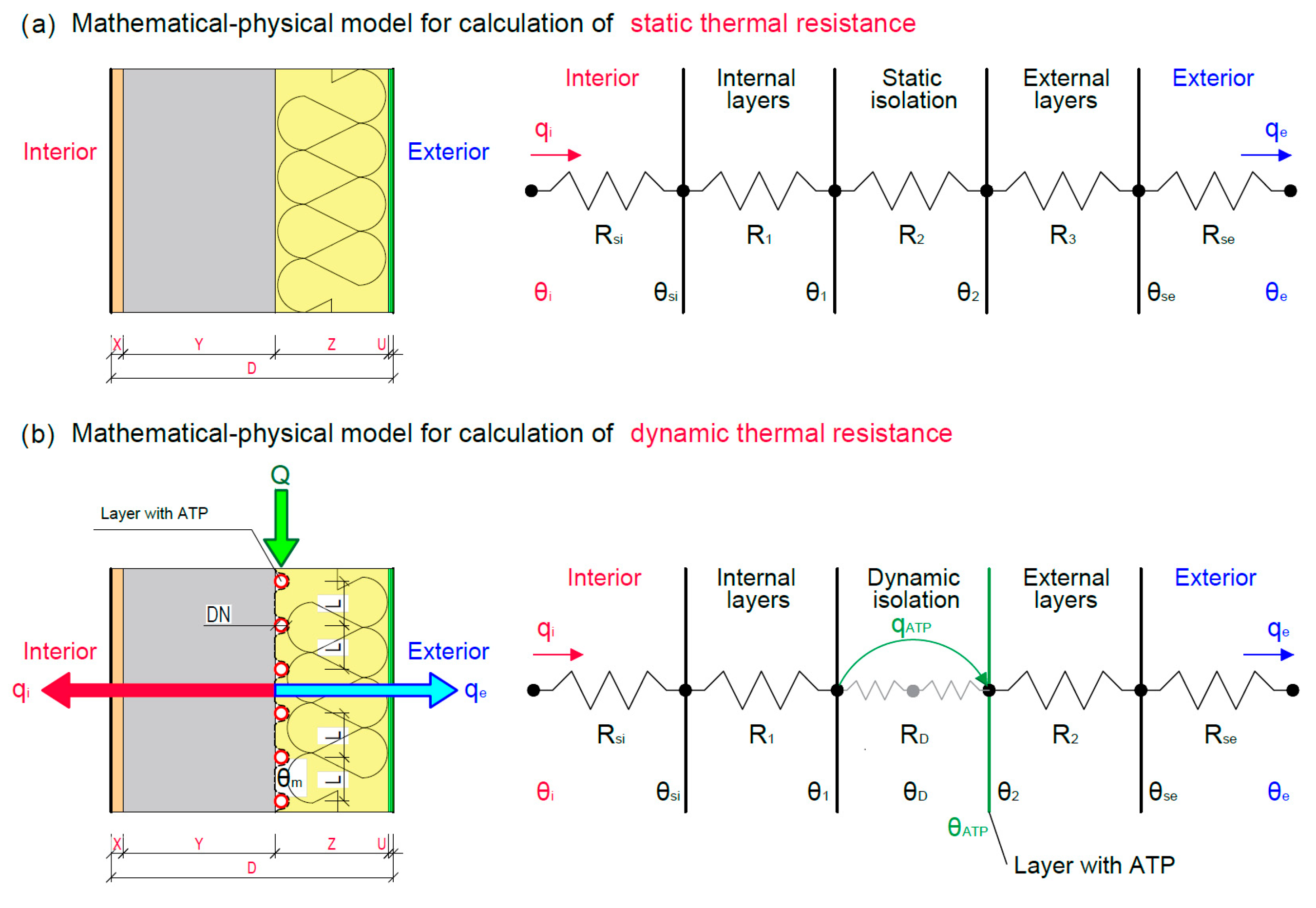
2.2.2. Mathematical–Physical Model of a Lightweight Building Envelope
qj = −λ∇θ.n
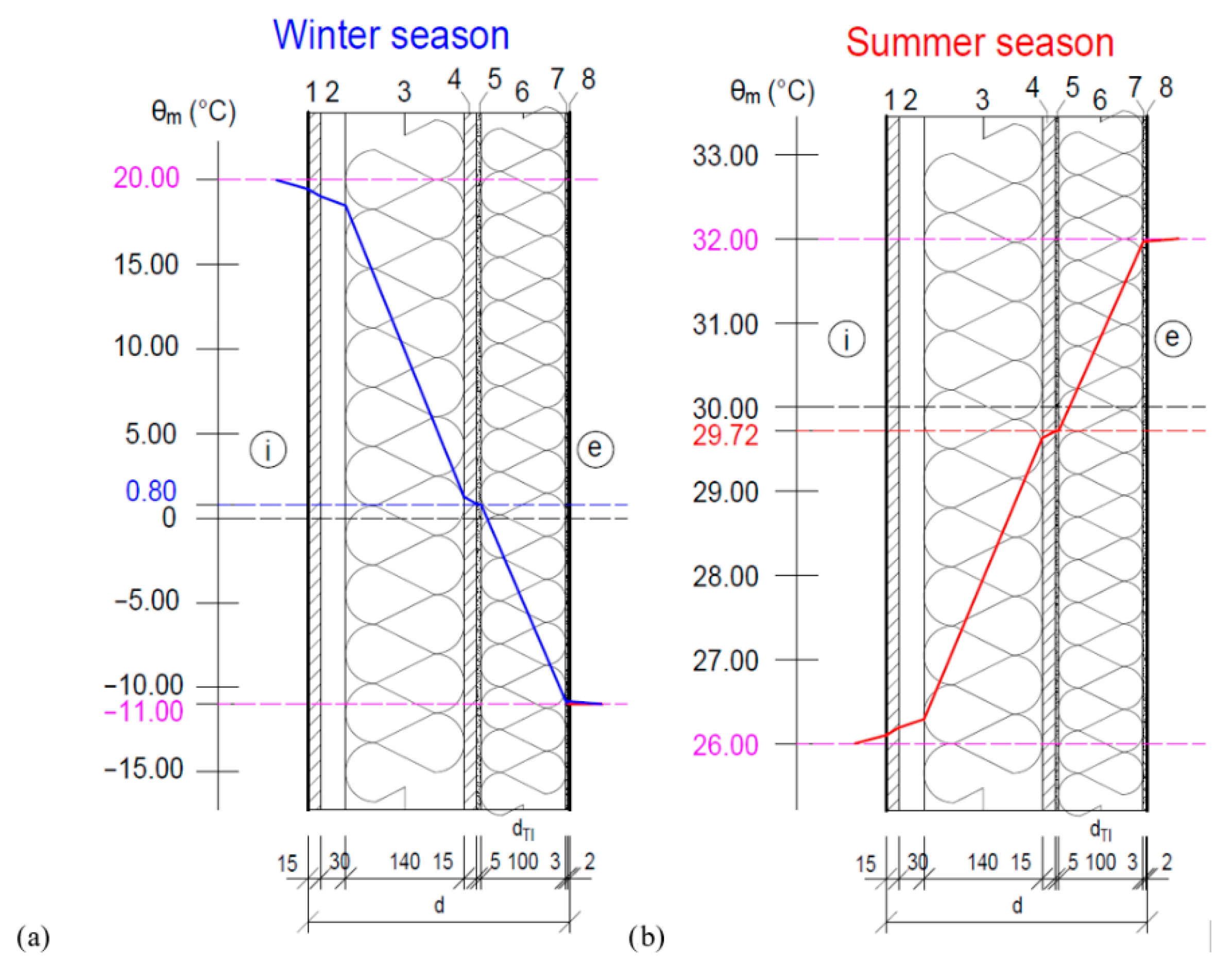
- indoor temperature θi = 20 °C;
- outdoor temperature θe = −11 °C.
- indoor temperature θi = 26 °C;
- outdoor temperature θe = 32 °C.
- heat transfer coefficient at the internal surface horizontally hi = 8 W/(m2K);
- heat transfer coefficient on the external surface in winter he = 23 W/(m2K).
2.2.3. Parametric Study of the Energy Potential of a Lightweight Envelope with TB
- θi—indoor temperature (θi = 20 °C);
- θe—outdoor temperature (θe = −11 °C).
- θi—indoor temperature (θi = 26 °C, extreme requirement θi = 20 °C);
- θe—outdoor temperature (θe = 32 °C, extreme temperature due to climate change θe = 36 °C).
2.2.4. Computer Simulation of a Lightweight Building Envelope with ATP
- Convection on the interior layer:
- θi—interior temperature (20 °C);
- hi—heat transfer coefficient on the inner surface horizontally (hi = 8 W/(m2·K)).
- 2.
- Convection on the exterior layer:
- θe—exterior temperature (−11 °C);
- he—heat transfer coefficient on the outer surface in winter (he = 23 W/(m2·K)).
- 3.
- Water temperature in the pipes:
- θTL—heat transfer fluid temperature (6 °C).
3. Results
3.1. Results of the Parametric Study
3.2. Results of the Computer Simulation
4. Discussion
5. Conclusions
- it is necessary to properly define the thermal–moisture properties of all layers that make up the construction;
- it is essential to identify the parameters of the model that will be subject to changes;
- the boundary conditions such as convection on the inner and outer surfaces of the wall and the temperature of the heat transfer fluid in the pipes, must be defined;
- proper mesh generation is essential.
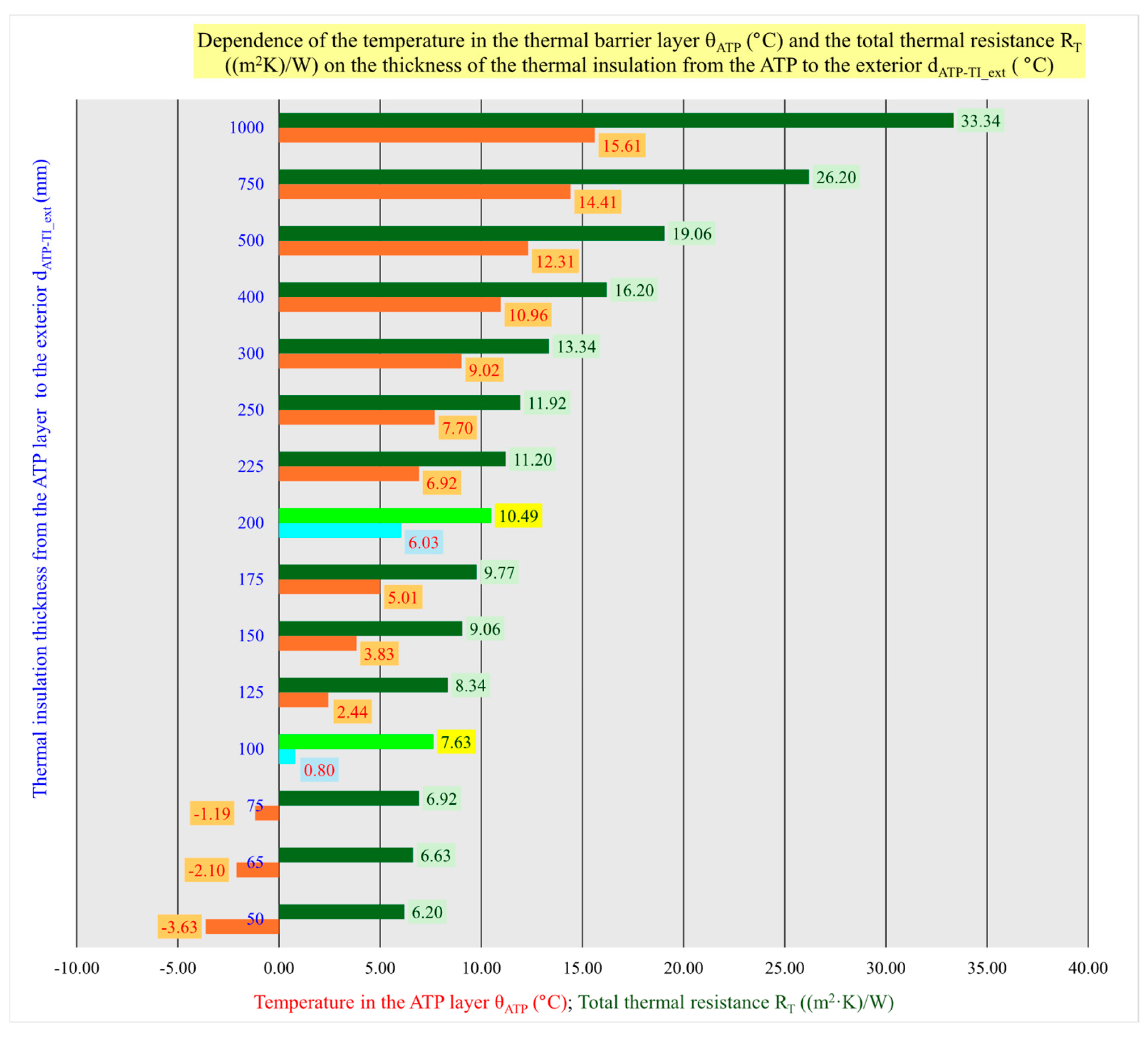
- thermal insulation thickness of d = 100 mm towards the exterior in front of the ATP layer in the energy function TB is optimal in terms of radiant flux, temperature differences in the structure, and thermal resistance as long as the average temperature of the heat transfer medium is approximately θm,ATP = +6 °C;
- thermal insulation thickness d = 100 mm represents the optimum solution for the investigated lightweight building envelope construction for modular and panelized buildings, also from the point of view that when the energy function TB is shut down the mean temperature of the heat transfer medium in the ATP would be θm,ATP = +0.8 °C, so this internal ATP circuit does not need to be filled with a frost-resistant heat transfer medium;
- for a thermal insulation thickness of d = 100 mm, an axial distance between the pipes of L = 150 mm is the most appropriate, because at an axial distance of L = 100 mm there is excessive heat production, which increases heat loss. At an axial distance of L = 200 mm the continuity and uniformity of the thermal barrier between the pipes is almost broken.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANSYS | Name of engineering simulation software |
| AOTR | Average operative temperature reduction |
| ATFR | Average temperature fluctuation reduction |
| ATP | Active thermal protection |
| BEPS | Building energy performance simulation |
| CFD | Computational fluid dynamics |
| CNKI | China national knowledge infrastructure |
| CO2 | Carbon dioxide |
| DHW | Domestic hot water |
| EPS | Expanded polystyrene |
| EU | European Union |
| FE | Mathematical–physical model (computer code) of a software package ABAQUS for finite element analysis and computer-aided engineering |
| HVAC | Heating, ventilation, and air conditioning |
| IEA | International energy agency |
| IFC | Industry foundation classes |
| MPC | Model predictive control |
| MITR | Maximum indoor temperature reduction |
| nZEB | Near-zero energy buildings |
| PCM | Phase change materials |
| RES | Renewable energy sources |
| SDGs | Sustainable Development Goals |
| STN | Slovak technical norm |
| TABEs | Thermally activated building envelopes |
| TB | Thermal barrier |
| TL | Time lag |
| TOP | Temperature operative |
| UN | United Nations |
| WIHP | Wall-implanted heat pipe |
References
- Directive (EU) 2024/1275 of the European Parliament and the Council (of 24 April 2024) on the Energy Performance of Buildings. Available online: https://eur-lex.europa.eu/eli/dir/2024/1275/oj/eng (accessed on 23 March 2025).
- United Nations Office at Vienna (UNOV). Available online: https://unis.unvienna.org/unis/en/topics/sustainable_development_goals.html (accessed on 23 March 2025).
- Kalús, D. UTILITY MODEL SK 5749 Y1 (UTILITY MODEL): Method of Operation of a Combined Construction-Energy System of Buildings and Equipment. Date of Entry into Force of the Utility Model: 1.4.2011. In Vestník ÚPV SR č.: 5/2011, 23p. Spôsob Prevádzky Kombinovaného Stavebno-Energetického Systému Budov a Zariadenie: Číslo Prihlášky 5027-2010, Zverejnená 8. 11. 2010 vo Vestníku ÚPV SR č. 11/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 23p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5027-2010 (accessed on 23 March 2025).
- Kalús, D. UTILITY MODEL SK 5729 Y1 (UTILITY MODEL): Samonosný Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla. [Self-Supporting Thermal Insulation Panel for Systems with Active Heat Transfer Control]. Date of Entry into Force of the Utility Model: 28.2.2011. In Vestník ÚPV SR No. 4/2011, Banská Bystrica, Slovak Republic, 32 p. Samonosný Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla: Číslo Prihlášky UV 5030-2010, Zverejnená 7. 10. 2010 vo Vestníku ÚPV SR č. 10/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 32p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5030-2010 (accessed on 23 March 2025).
- Kalús, D. UTILITY MODEL SK 5725 Y1 (UTILITY MODEL): Tepelnoizolačný Panel pre Systémy s Aktívnym Riadením Prechodu Tepla: Číslo Prihlášky UV 5031-2010, Zverejnená 7.10. 2010 vo Vestníku ÚPV SR č. 10/2010; Úrad Priemyselného Vlastníctva Slovenskej Republiky: Banská Bystrica, Slovakia, 2011; 63p. Available online: https://wbr.indprop.gov.sk/WebRegistre/UzitkovyVzor/Detail/5031-2010 (accessed on 23 March 2025).
- Kalús, D. EUROPEAN PATENT EP 2 572 057 B1. Heat-Insulating Panel with Active Regulation of Heat Transfer. International Application Number: PCT/SK2011/000004, International Publication Number: WO 2011/146025 (24.11.2011 Gazette 2011/47). 15 October 2014. 67p. Available online: https://register.epo.org/application?number=EP11716446&tab=main&lng=en10 (accessed on 23 March 2025).
- Kalús, D.; Gašparík, J.; Janík, P.; Kubica, M.; Šťastný, P. Innovative building technology implemented into facades with active thermal protection. Sustainability 2021, 13, 4438. [Google Scholar] [CrossRef]
- Kalús, D.; Mučková, V.; Koudelková, D. Energy, Economic and Environmental Assessment of Thermal Barrier Application in Building Envelope Structures. Coatings 2021, 11, 1538. [Google Scholar] [CrossRef]
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M.; Šťastný, P. Parametric study of the energy potential of a building’s envelope with integrated energy-active elements. Acta Polytech. 2022, 62, 595–606. [Google Scholar] [CrossRef]
- Kalús, D.; Koudelková, D.; Mučková, V.; Sokol, M.; Kurčová, M. Contribution to the Research and Development of Innovative Building Components with Embedded Energy-Active Elements. Coatings 2022, 12, 1021. [Google Scholar] [CrossRef]
- Mučková, V.; Kalús, D.; Koudelková, D.; Kurčová, M.; Straková, Z.; Sokol, M.; Ingeli, R.; Šťastný, P.; Janík, P. Contribution to Active Thermal Protection Research—Part 1 Analysis of Energy Functions by Parametric Study. Energies 2023, 16, 4391. [Google Scholar] [CrossRef]
- Kalús, D.; Mučková, V.; Koudelková, D.; Kurčová, M.; Straková, Z.; Sokol, M.; Ingeli, R.; Šťastný, P.; Janík, P. Contribution to Active Thermal Protection Research—Part 2 Verification by Experimental Measurement. Energies 2023, 16, 4595. [Google Scholar] [CrossRef]
- Mučková, V.; Kalús, D.; Koudelková, D.; Kurčová, M.; Straková, Z.; Sokol, M.; Ingeli, R.; Šťastný, P. Analysis of the Dynamic Thermal Barrier in Building Envelopes. Coatings 2023, 13, 648. [Google Scholar] [CrossRef]
- Isomax–Terrasol Building Technologies. Successor to Isomax—Solinterra. Available online: https://www.solinterra.si/en/about-solinterra.html (accessed on 23 March 2025).
- Krecké, E.; Ulbrich, R.; Radlak, G. Connection of Solar and Near-Surface Geothermal Energy in Isomax Technology. In Proceedings of the CESB 07 PRAGUE Conference, Prague, Czech Republic, 24–26 September 2007; pp. 622–628. Available online: https://www.yumpu.com/en/document/read/4706674/connection-of-solar-and-near-surface-geothermal-energy-in-isomax- (accessed on 23 March 2025).
- Xu, X.; Wang, S.; Wang, J.; Xiao, F. Active pipe-embedded structures in buildings for utilizing low-grade energy sources: A review. Energy Build. 2010, 42, 1567–1581. [Google Scholar] [CrossRef]
- Krzaczek, M.; Kowalczuk, Z. Thermal Barrier as a technique of indirect heating and cooling for residential buildings. Energy Build. 2011, 43, 823–837. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Z.; Duan, C. A new type of passive solar energy utilization technology—The wall is implanted with heat pipes. Energy Build. 2014, 84, 111–116. [Google Scholar] [CrossRef]
- Li, A.; Xu, X.; Sun, Y. A study on pipe-embedded wall integrated with ground source-coupled heat exchanger for enhanced building energy efficiency in diverse climate regions. Energy Build. 2016, 121, 139–151. [Google Scholar] [CrossRef]
- Koenders, S.J.; Loonen, R.C.; Hensen, J.L. Investigating the potential of a closed-loop dynamic insulation system for opaque building elements. Energy Build. 2018, 173, 409–427. [Google Scholar] [CrossRef]
- Krzaczek, M.; Florczuk, J.; Tejchman, J.J. Improved energy management technique in pipe-embedded wall heating/cooling system in residential buildings. Appl. Energy 2019, 254, 113711. [Google Scholar] [CrossRef]
- Congedo, P.M.; Baglivo, C.; Seyhan, A.K.; Marchetti, R. Worldwide dynamic predictive analysis of building performance under long-term climate change conditions. J. Build. Eng. 2021, 42, 103057. [Google Scholar] [CrossRef]
- Fawaier, M.; Bokor, B. Dynamic insulation systems of building envelopes: A review. Energy Build. 2022, 270, 112268. [Google Scholar] [CrossRef]
- Karanafti, A.; Theodosiou, T.; Tsikaloudaki, K. Assessment of buildings’ dynamic thermal insulation technologies—A review. Appl. Energy 2022, 326, 119985. [Google Scholar] [CrossRef]
- Al-Yasiri, Q.; Szabó, M. Building envelope-combined phase change material and thermal insulation for energy-effective buildings during harsh summer: Simulation-based analysis. Energy Sustain. Dev. 2023, 72, 326–339. [Google Scholar] [CrossRef]
- Ibrahim, M.; Wurtz, E.; Biwole, P.H.; Achard, P. Transferring solar energy from the south to the north facade through embedded water pipes. Energy 2014, 78, 834–845. [Google Scholar] [CrossRef]
- Xie, J.; Xu, X.; Li, A.; Zhu, Q. Experimental validation of frequency-domain finite-difference model of active pipe-embedded building envelope in time domain by using Fourier series analysis. Energy Build. 2015, 99, 177–188. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Thermal performance of double skin façade with built-in pipes utilizing evaporative cooling water in cooling season. Sol. Energy 2016, 137, 55–65. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Dynamic thermal performance of pipe-embedded building envelope utilizing evaporative cooling water in the cooling season. Appl. Therm. Eng. 2016, 106, 1103–1113. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, A.; Xie, J.; Li, W.; Xu, X. Experimental validation of a semi-dynamic simplified model of active pipe-embedded building envelope. Int. J. Therm. Sci. 2016, 108, 70–80. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Energy saving potential of pipe-embedded building envelope utilizing low-temperature hot water in the heating season. Energy Build. 2017, 138, 318–331. [Google Scholar] [CrossRef]
- Shen, C.; Li, X. Potential of utilizing different natural cooling sources to reduce the building cooling load and cooling energy consumption: A case study in Urumqi. Energies 2017, 10, 366. [Google Scholar] [CrossRef]
- Shekar, V.; Krarti, M. Control strategies for dynamic insulation materials applied to commercial buildings. Energy Build. 2017, 154, 305–320. [Google Scholar] [CrossRef]
- Alongi, A.; Angelotti, A.; Mazzarella, L. Analytical modelling of Breathing Walls: Experimental verification using the Dual Air Vented Thermal Box lab facility. Energy Procedia 2017, 140, 36–47. [Google Scholar] [CrossRef][Green Version]
- Palme, M.; Salvati, A. UWG-TRNSYS Simulation Coupling for Urban Building Energy Modeling. Available online: http://bura.brunel.ac.uk/handle/2438/16798 (accessed on 15 March 2018).
- Asad, H.S.; Kit, Y.R.; Ming, L.E. Energy modeling with nonlinear-autoregressive exogenous neural network. InE3S Web Conf. 2019, 111, 03059. [Google Scholar] [CrossRef]
- Kisilewicz, T.; Fedorczak-Cisak, M.; Barkanyi, T. Active thermal insulation as an element limiting heat loss through external walls. Energy Build. 2019, 205, 109541. [Google Scholar] [CrossRef]
- Rupp, S.; Krarti, M. Analysis of multi-step control strategies for dynamic insulation systems. Energy Build. 2019, 204, 109459. [Google Scholar] [CrossRef]
- Alongi, A.; Angelotti, A.; Mazzarella, L. Experimental validation of a steady periodic analytical model for Breathing Walls. Build. Environ. 2020, 168, 106509. [Google Scholar] [CrossRef]
- Čurpek, J.; Čekon, M. Climate response of a BiPV façade system enhanced with latent PCM-based thermal energy storage. Renew. Energy 2020, 152, 368–384. [Google Scholar] [CrossRef]
- Drgoňa, J.; Arroyo, J.; Figueroa, I.C.; Blum, D.; Arendt, K.; Kim, D.; Ollé, E.P.; Oravec, J.; Wetter, M.; Vrabie, D.L.; et al. All you need to know about model predictive control for buildings. Annu. Rev. Control 2020, 50, 190–232. [Google Scholar] [CrossRef]
- Bokor, B.; Akhan, H.; Eryener, D.; Horváth, M. Nocturnal passive cooling by transpired solar collectors. Appl. Therm. Eng. 2021, 188, 116650. [Google Scholar] [CrossRef]
- Motuzienė, V.; Čiuprinskas, K.; Rogoža, A.; Lapinskienė, V. A review of the life cycle analysis results for different energy conversion technologies. Energies 2022, 15, 8488. [Google Scholar] [CrossRef]
- He, Y.; Zhou, H.; Fahimi, F. Modeling and demand-based control of responsive building envelope with integrated thermal mass and active thermal insulations. Energy Build. 2022, 276, 112495. [Google Scholar] [CrossRef]
- Cui, B.; Dong, J.; Lee, S.; Im, P.; Salonvaara, M.; Hun, D.; Shrestha, S. Model predictive control for active insulation in building envelopes. Energy Build. 2022, 267, 112108. [Google Scholar] [CrossRef]
- Arıcı, M.; Bilgin, F.; Krajčík, M.; Nižetić, S.; Karabay, H. Energy saving and CO2 reduction potential of external building walls containing two layers of phase change material. Energy 2022, 252, 124010. [Google Scholar] [CrossRef]
- Rogoža, A.; Misevičiūtė, V. Research of technological possibilities of heat pumps’ application in district heating of residential buildings. Moksl.–Liet. Ateitis/Sci.–Future Lithuania 2022, 14, 1–7. [Google Scholar] [CrossRef]
- Yan, B.; Han, X.; Malkawi, A.; Dokka, T.H.; Howard, P.; Knowles, J.; Hegli, T.; Edwards, K. Comprehensive assessment of operational performance of coupled natural ventilation and thermally active building systems via an extensive sensor network. Energy Build. 2022, 260, 111921. [Google Scholar] [CrossRef]
- Gopalan, A.; Antony, A.S.M.; Suresh, R.; Sahoo, S.; Livingston, L.M.; Titus, A.; Nanammal, V.; Mohanavel, V.; Sathyamurthy, R. Performance enhancement of building energy through the combination of dynamic insulation panels and phase changing materials. Energy Rep. 2022, 8, 945–958. [Google Scholar] [CrossRef]
- Wang, P.; Liu, Z.; Zhang, X.; Hu, M.; Zhang, L.; Fan, J. Adaptive dynamic building envelope integrated with phase change material to enhance the heat storage and release efficiency: A state-of-the-art review. Energy Build. 2023, 286, 112928. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, H.; Liu, J.; Yang, J.; Huang, H.; Ding, Y.; Xie, L. Dynamic performance and energy efficiency of reflective and insulating composite coating on building exterior wall. Build. Simul. 2023, 16, 2245–2259. Available online: https://link.springer.com/article/10.1007/s12273-022-0932-x (accessed on 15 March 2018). [CrossRef]
- Procházka, J.; Procházková, D.; Rusko, M.; Rockel, G.; Iľko, J. Methodology for Selecting a Source of Electrical Energy Suitable for the Site. In Proceedings of the 34th International DAAAM Symposium on Intelligent Manufacturing and Automation; DAAAM International: Vienna, Austria, 2023. [Google Scholar] [CrossRef]
- Ponechal, R.; Jandačka, J.; Ďurica, P. Evaluation of Residential Buildings Savings for Various Envelope Retrofits and Heating Energy Sources: A Simulation Study. Buildings 2024, 14, 332. [Google Scholar] [CrossRef]
- Gorás, M.; Domanický, J.; Káposztásová, D.; Vranay, F.; Vranayová, Z. Innovative Approaches to Bridging Energy Supply and Demand Gaps Through Thermal Energy Storage: A Case Study. Energies 2024, 17, 6197. [Google Scholar] [CrossRef]
- Yan, D.; Hong, T.; Dong, B.; Mahdavi, A.; D’Oca, S.; Gaetani, I.; Feng, X. IEA EBC Annex 66: Definition and simulation of occupant behavior in buildings. Energy Build. 2017, 156, 258–270. [Google Scholar] [CrossRef]
- Santos-Herrero, J.M.; Lopez-Guede, J.M.; Flores-Abascal, I. Modeling, simulation and control tools for nZEB: A state-of-the-art review. Renew. Sustain. Energy Rev. 2021, 142, 110851. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Zhang, J.; Zhang, Z.; Li, S.; Chen, K.; Xiao, X. Thermal performances and invisible thermal barrier formation mechanism of arc-shaped metal-fin-enhanced thermally activated building envelopes with directional heat charging feature. Build. Simul. 2023, 17, 1461–1489. Available online: https://link.springer.com/article/10.1007/s12273-024-1141-6 (accessed on 18 April 2023). [CrossRef]
- Zhou, S.; Razaqpur, A.G. CFD modeling and experimental validation of the thermal performance of a novel dynamic PCM Trombe wall: Comparison with the companion static wall with and without PCM. Appl. Energy 2024, 353, 121985. [Google Scholar] [CrossRef]
- Mendes, V.F.; Cruz, A.S.; Gomes, A.P.; Mendes, J.C. A systematic review of methods for evaluating the thermal performance of buildings through energy simulations. Renew. Sustain. Energy Rev. 2024, 189, 113875. [Google Scholar] [CrossRef]
- Poljak, M.; Ponechal, R. Optimisation of Attic Space Ventilation in a Listed Church: Integration of Microclimatic Monitoring and Dynamic Simulations. In Proceedings of the International Conference on Protection of Historical Constructions, Naples, Italy, 26–28 March 2025; Springer Nature: Cham, Switzerland, 2025; pp. 470–477. Available online: https://link.springer.com/chapter/10.1007/978-3-031-87312-6_58 (accessed on 2 January 2025).
- Li, Y.; Chen, H.; Yu, P.; Yang, L. A Review of Artificial Intelligence Applications in Architectural Design: Energy-Saving Renovations and Adaptive Building Envelopes. Energies 2025, 18, 918. [Google Scholar] [CrossRef]
- Li, F.; Peng, T.; Chen, J.; Wu, J.; Cao, J.; Luo, H.; Wang, Z. Prediction and strategies of buildings’ energy consumption: A review of modeling approaches and energy-saving technologies. Int. J. Green Energy 2025, 15, 1740. [Google Scholar] [CrossRef]
- Chang, S.J.; Kang, Y.; Yun, B.Y.; Yang, S.; Kim, S. Assessment of the Effect of Climate Change on the Hygrothermal Performance of Cross-Laminated Timber Building Envelopes with Modular Construction. Case Stud. Therm. Eng. 2021, 28, 101703. [Google Scholar] [CrossRef]
- Volpe, S.; Sangiorgio, V.; Petrella, A.; Coppola, A.; Notarnicola, M.; Fiorito, F. Building envelope prefabricated with 3D printing technology. Sustainability 2021, 13, 8923. [Google Scholar] [CrossRef]
- Maracchini, G.; D’Orazio, M. Improving the livability of lightweight emergency architectures: A numerical investigation on a novel reinforced-EPS based construction system. Build. Environ. 2022, 208, 108601. [Google Scholar] [CrossRef]
- Blanchet, P.; Perez, C.; Cabral, M.R. Wood building construction: Trends and opportunities in structural and envelope systems. Curr. For. Rep. 2024, 10, 21–38. Available online: https://link.springer.com/article/10.1007/s40725-023-00196-z (accessed on 12 April 2024). [CrossRef]
- Sarmento, R.; Posani, M.; Fernandes, P.; Rodrigues, A.M.; Gomes, M.G. Energy efficiency in modular emergency shelters: Impact of envelope finishings and shadowing. J. Build. Eng. 2024, 94, 110029. [Google Scholar] [CrossRef]
- Jia, Y.H.; Niu, Z.R.; Qiao, W.T.; Zhang, X.; Wang, R.Q.; Mei, S.Q. Thermal performance study on the outer wall of a new ultra-low energy modular wall prefabricated building. J. Build. Eng. 2024, 98, 111382. [Google Scholar] [CrossRef]
- Hu, Y.; Ai, Z.; Zhang, G.; Zong, J.; Liu, Z. Analyzing the impact of design factors on external walls in lightweight modular construction based on life-cycle analysis: Energy, economic, and environmental trade-offs. J. Build. Eng. 2025, 103, 112090. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, T.; Gasparri, E.; Lucchi, E. A Modular Agrivoltaics Building Envelope Integrating Thin-Film Photovoltaics and Hydroponic Urban Farming Systems: A Circular Design Approach with the Multi-Objective Optimization of Energy, Light, Water and Structure. Sustainability 2025, 17, 666. [Google Scholar] [CrossRef]
- Parracho, D.F.R.; Nour El-Din, M.; Esmaeili, I.; Freitas, S.S.; Rodrigues, L.; Poças Martins, J.; Corvacho, H.; Delgado, J.M.P.Q.; Guimarães, A.S. Modular Construction in the Digital Age: A Systematic Review on Smart and Sustainable Innovations. Buildings 2025, 15, 765. [Google Scholar] [CrossRef]
- Gong, Q.; Ding, W.; Liu, X.; Zeng, Y.; Adu, E.; Shao, H. Multi-objective Optimization Framework for the Building Envelope of Public Rental Housing in China’s Cold Regions. J. Build. Eng. 2025, 104, 112261. [Google Scholar] [CrossRef]
- Li, Y.; Chen, L. A study on a database of modular façade retrofitting building envelopes. Energy Build. 2020, 214, 109826. [Google Scholar] [CrossRef]
- Huang, B.; Wang, Y.; Lu, W.; Cheng, M. Fabrication and energy efficiency of translucent concrete panel for building envelope. Energy 2022, 248, 123635. [Google Scholar] [CrossRef]
- Pless, S.; Podder, A.; Kaufman, Z.; Klammer, N.; Dennehy, C.; Muthumanickam, N.K.; Rothgeb, S.; Louis, J.; Swanson, C.; Wallace, H.; et al. The Energy in Modular (EMOD) Buildings Method: A Guide to Energy-Efficient Design for Industrialized Construction of Modular Buildings; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2022. [Google Scholar] [CrossRef]
- Kysela, P.; Ponechal, R.; Michálková, D. Airtightness of a critical joint in a timber-based building affected by the seasonal climate change. Buildings 2023, 13, 698. [Google Scholar] [CrossRef]
- Sah, T.P.; Lacey, A.W.; Hao, H.; Chen, W. Prefabricated concrete sandwich and other lightweight wall panels for sustainable building construction: State-of-the-art review. J. Build. Eng. 2024, 89, 109391. [Google Scholar] [CrossRef]
- Mohammed, M.A.; Budaiwi, I.M.; Al-Osta, M.A.; Abdou, A.A. Thermo-Environmental Performance of Modular Building Envelope Panel Technologies: A Focused Review. Buildings 2024, 14, 917. [Google Scholar] [CrossRef]
- Pan, Y.; Zhu, M.; Lv, Y.; Yang, Y.; Liang, Y.; Yin, R.; Yan, Y.; Jia, X.; Wang, X.; Zeng, F.; et al. Building energy simulation and its application for building performance optimization: A review of methods, tools, and case studies. Adv. Appl. Energy 2023, 10, 100135. [Google Scholar] [CrossRef]
- Alhammad, M.; Eames, M.; Vinai, R. Enhancing building energy efficiency through building information modeling (BIM) and building energy modeling (BEM) integration: A systematic review. Buildings 2024, 14, 581. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Z.; Chen, X.; Yang, J.; Song, C.; Chen, Y. UAV-BIM-BEM: An automatic unmanned aerial vehicles-based building energy model generation platform. Energy Build. 2025, 328, 115120. [Google Scholar] [CrossRef]
- Lydon, G.P.; Caranovic, S.; Hischier, I.; Schlueter, A. Coupled simulation of thermally active building systems to support a digital twin. Energy Build. 2019, 202, 109298. [Google Scholar] [CrossRef]
- Ponechal, R.; Krušinský, P.; Kysela, P.; Pisca, P. Simulations of airflow in the roof space of a Gothic sanctuary using CFD models. Energies 2021, 14, 3694. [Google Scholar] [CrossRef]
- Ponechal, R.; Barňák, P.; Ďurica, P. Comparison of simulation and measurement in a short-term evaluation of the thermal comfort parameters of an office in a low-carbon building. Buildings 2022, 12, 349. [Google Scholar] [CrossRef]
- An, J.; Wu, Y.; Gui, C.; Yan, D. Chinese prototype building models for simulating the energy performance of the nationwide building stock. Build. Simul. 2023, 16, 1559–1582. Available online: https://link.springer.com/article/10.1007/s12273-023-1058-5 (accessed on 15 November 2023). [CrossRef]
- Liu, Z.; Zhang, X.; Sun, Y.; Zhou, Y. Advanced controls on energy reliability, flexibility, and occupant-centric control for smart and energy-efficient buildings. Energy Build. 2023, 297, 113436. [Google Scholar] [CrossRef]
- Kiaulakis, A.; Vilutienė, T.; Šarka, V.; Šarkienė, E.; Rogoža, A. The Conceptual Model of the BIM4NZEB-DS System for Selecting Technological Variants of Rational Passive Energy Efficiency Measures for a Sustainable Building. Vilnius Univ. Proc. 2023, 37, 41–47. Available online: https://www.zurnalai.vu.lt/proceedings/article/view/33495 (accessed on 21 September 2023). [CrossRef]
- Zhang, Z.; Yao, J.; Zheng, R. Multi-Objective optimization of building energy saving based on the randomness of energy-related occupant behavior. Sustainability 2024, 16, 1935. [Google Scholar] [CrossRef]
- Muhič, S.; Čikić, A.; Perić, M. Building with an Active Thermal Protection in Combination with a High Share of Renewable Energy Sources Use. In Proceedings of the 2024 9th International Conference on Smart and Sustainable Technologies (SpliTech), Bol and Split, Croatia, 25–28 June 2024; IEEE: New York City, NY, USA, 2024; pp. 1–4. Available online: https://ieeexplore.ieee.org/abstract/document/10612420 (accessed on 15 July 2024).
- Kozlovska, M.; Petkanic, S.; Vranay, F.; Vranay, D. Enhancing energy efficiency and building performance through BEMS-BIM integration. Energies 2023, 16, 6327. [Google Scholar] [CrossRef]
- Al Khiro, H.A.; Boukhanouf, R. Analytical and computer modelling of a thermo-mechanical vapour compression system for space air conditioning in buildings. Energy Convers. Manag. 2025, 323, 119252. [Google Scholar] [CrossRef]
- Fawaier, M.; Róbert, G.; Bokor, B. Simulation study of dynamic building insulation with transpired solar collectors. Energy Rep. 2024, 12, 1325–1343. [Google Scholar] [CrossRef]
- Straková, Z.; Takács, J. Indoor Air Quality and Mechanical Ventilation for Technology Buildings. Pollack Period.—Int. J. Eng. Inf. Sci. 2017, 12, 141–150. [Google Scholar] [CrossRef]
- Funtík, T.; Makýš, P.; Ďubek, M.; Erdélyi, J.; Honti, R.; Cerovšek, T. The Status of Building Information Modeling Adoption in Slovakia. Buildings 2023, 13, 2997. [Google Scholar] [CrossRef]
- Straková, Z.; Vojtaššák, J.; Beňovský, P.; Koudelková, D. CFD Simulations—Efficient Tool for Designers of Industrial HVAC Applications. Period. Polytech. Mech. Eng. 2019, 63, 201–206. [Google Scholar] [CrossRef]
- Zhangabay, N.; Oner, A.; Rakhimov, M.; Tursunkululy, T.; Abdikerova, U. Thermal Performance Evaluation of a Retrofitted Building with Adaptive Composite Energy-Saving Facade Systems. Energies 2025, 18, 1402. [Google Scholar] [CrossRef]
- STN 73 0540-2+Z1 + Z2:2019; Tepelná Ochrana Budov. Tepelnotechnické Vlastnosti Stavebných Konštrukcií a Budov Časť 2 Funkčné Požiadavky. (Thermal Protection of Buildings. Thermal Performance of Building Structures and Buildings Part 2 Functional Requirements). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2019.
- Benča, Š. Výpočtové Postupy MKP pri Riešení Lineárnych úloh Mechaniky (FEM Computational Procedures for Solving Linear Mechanics Problems); STU v Bratislave: Bratislava, Slovakia, 2004; 150p, ISBN 80-227-2032-1. Available online: https://kis.stuba.sk/arl-stu/sk/detail-stu_us_cat-stu84989-Vypoctove-postupy-MKP-pri-rieseni-linearnych-uloh-mechaniky/ (accessed on 11 February 2004).
- STN EN 1264-1; Vykurovacie a Chladiace Systémy Zabudované pod Povrchom s Vodou ako Teplonosnou Látkou. Časť 1: Termíny, Definície a Symboly (Heating and Cooling Systems Embedded in the Floor with Water as the Heat Carrier. Part 1: Terms, Definitions, and Symbols). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2001.
- STN EN 1264-2+A1; Vykurovacie a Chladiace Systémy Zabudované pod Povrchom s Vodou ako Teplonosnou Látkou. Časť 2: Podlahové Vykurovanie, Skúšobné Metódy na Určenie Tepelného Výkonu Pomocou Výpočtových Experimentálnych Metód (Heating and Cooling Systems Embedded in the Floor with Water as the Heat Carrier. Part 2: Underfloor Heating, Test Methods for Determining Thermal Output Using Computational Experimental Methods). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2001.
- STN EN 1264-3; Vykurovacie a Chladiace Systémy Zabudované pod Povrchom s Vodou ako Teplonosnou Látkou. Časť 3: Dimenzovanie (Heating and Cooling Systems Embedded in the Floor with Water as the Heat Carrier. Part 3: Design). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2001.
- STN EN 1264-4; Vykurovacie a Chladiace Systémy Zabudované pod Povrchom s Vodou ako Teplonosnou Látkou. Časť 4: Inštalácia (Heating and Cooling Systems Embedded in the Floor with Water as the Heat Carrier. Part 4: Installation). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2001.
- STN EN 1264-5; Vykurovacie a Chladiace Systémy Zabudované pod Povrchom s Vodou ako Teplonosnou Látkou. Časť 5: Vykurovacie a Chladiace Systémy Zabudované v Podlahách, Stropoch a Stenách, Určenie Tepelného Výkonu (Heating and Cooling Systems Embedded in the Floor with Water as the Heat Carrier. Part 5: Heating and Cooling Systems Embedded in Floors, Ceilings, and Walls, Determination of Thermal Output). Slovenská Technická Norma (Slovak Technical Standard): Bratislava, Slovakia, 2001.
- Sacks, R.; Eastman, C.; Lee, G.; Teicholz, P. BIM Handbook, a Guide to Building Information Modeling for Owners, Managers, Designers, Engineers, and Contractors, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2018. [Google Scholar] [CrossRef]
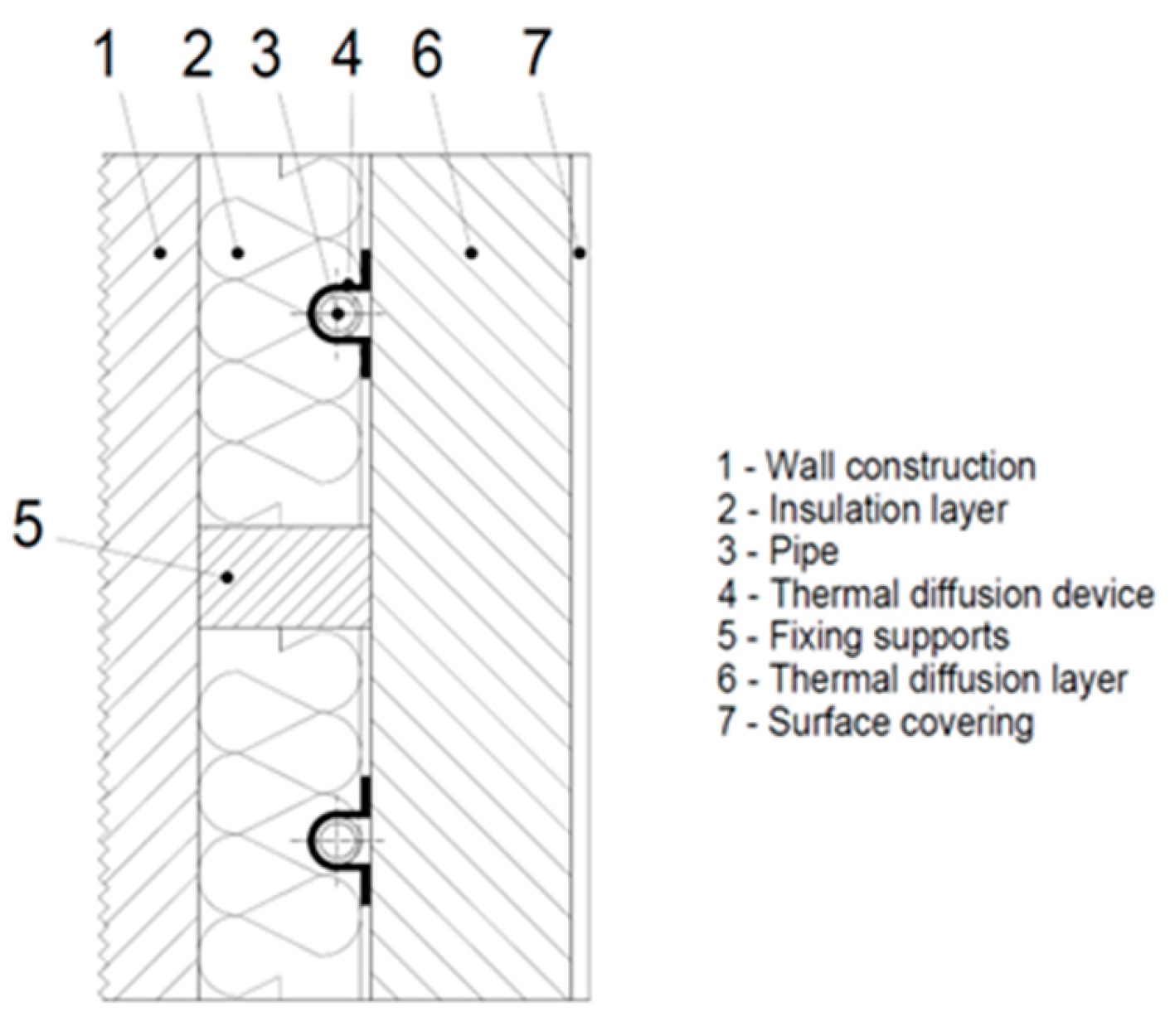
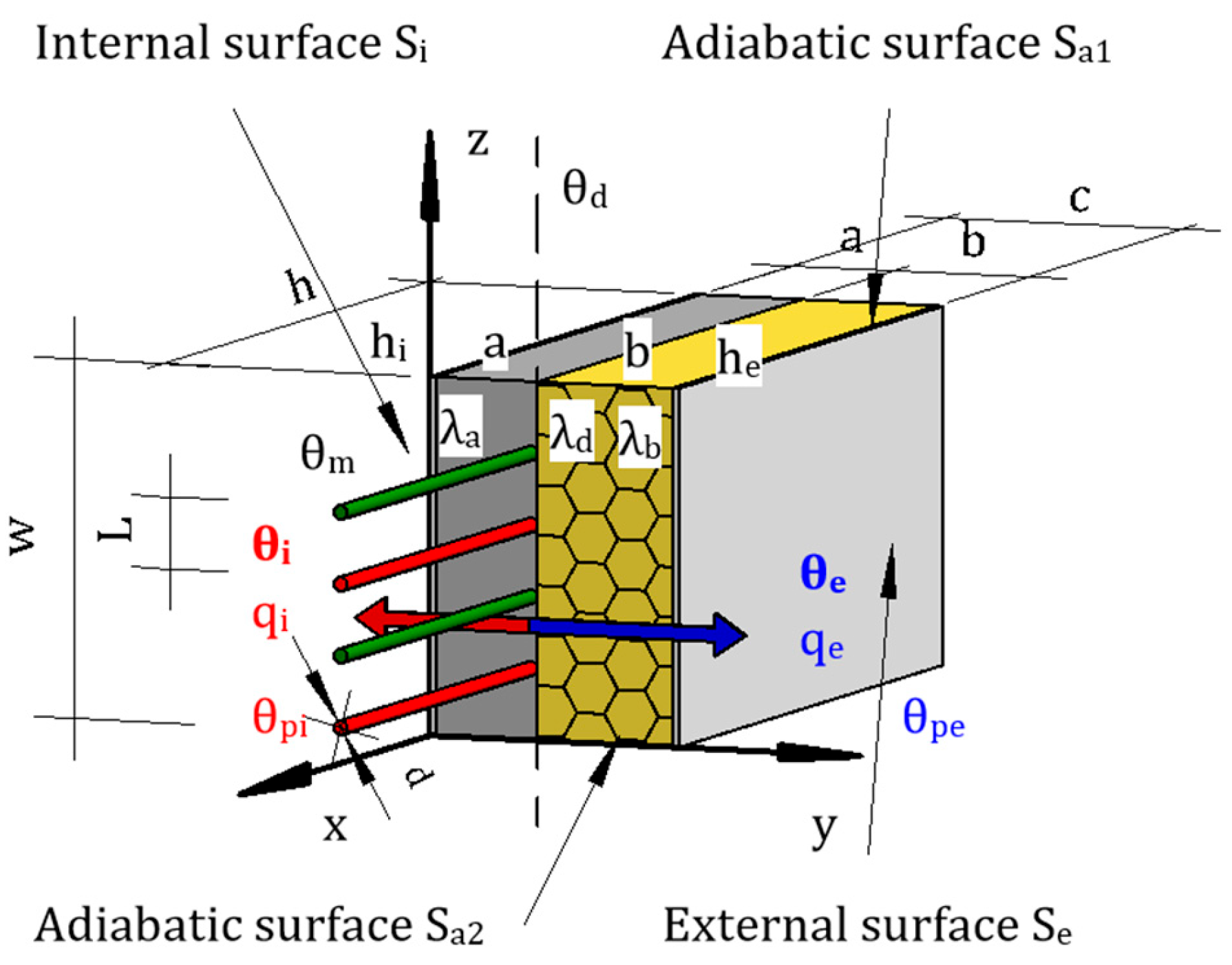
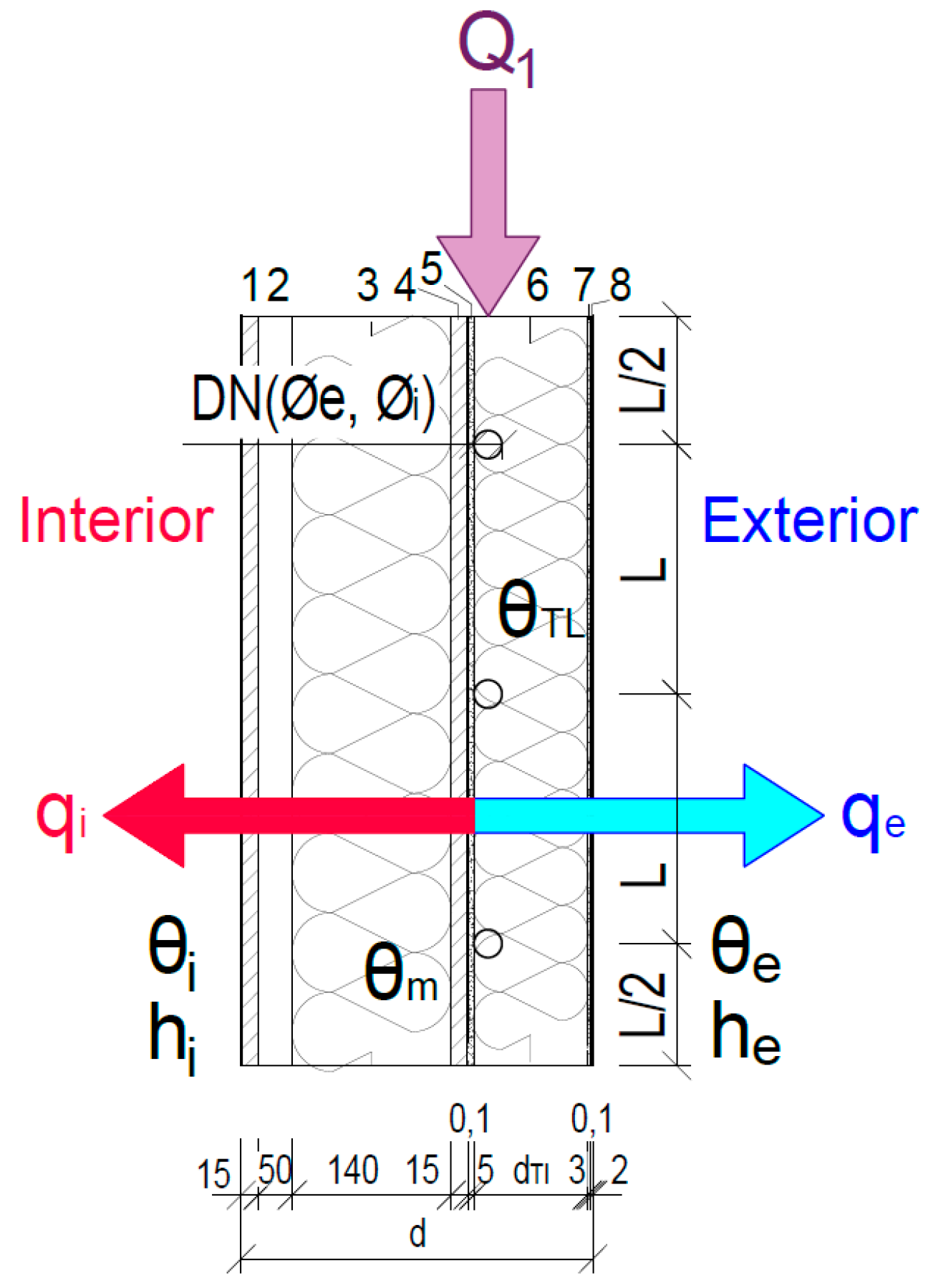
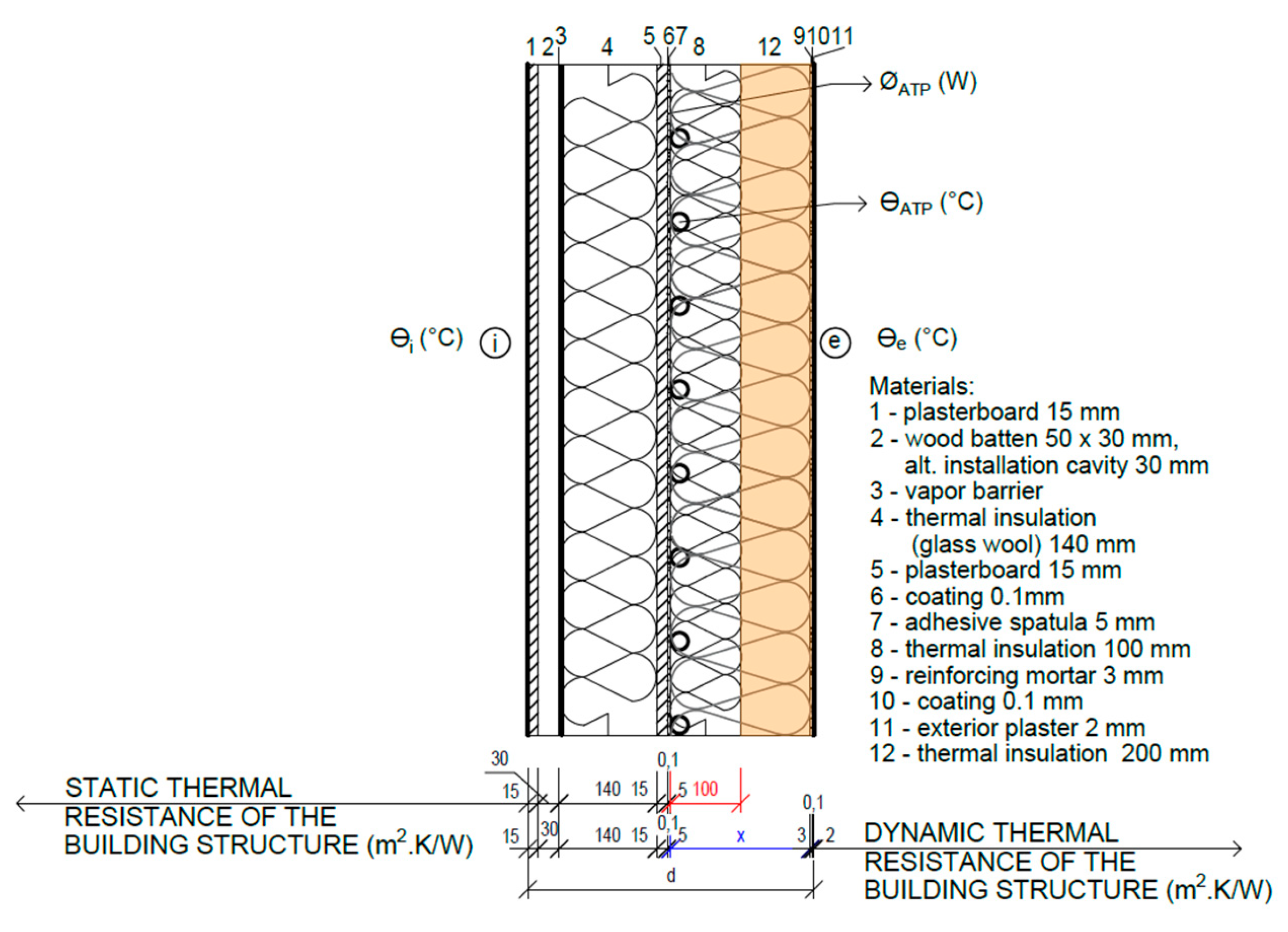

| Material Name | Thickness | Density | Thermal Conductivity Coefficient | Specific Heat Capacity | |
|---|---|---|---|---|---|
| Symbol | d | ρ | λ | c | |
| Unit | m | kg/m3 | W/(m·K) | J/(kg·K) | |
| 1. | Gypsum board | 0.015 | 840 | 0.142 | 960 |
| 2. | Lat | 0.05 | 600 | 0.22 | 2510 |
| 3. | Thermal insulation (glass wool) | 0.140 | 21 | 0.033 | 840 |
| 4. | Gypsum board | 0.015 | 840 | 0.142 | 960 |
| 5. | Adhesive plaster | 0.005 | 1300 | 0.800 | 1020 |
| 6. | Thermal insulation (EPS) | dTI * | 100 | 0.035 | 1020 |
| 7. | Reinforcing plaster | 0.003 | 1300 | 0.800 | 1020 |
| 8. | Exterior plaster | 0.002 | 1800 | 0.800 | 920 |
| 9. | Pe-Xa pipe | (Øe x Øi) ** | 920 | 0.350 | 1470 |
| Parameter Name | Symbol | Unit in ANSYS | |
|---|---|---|---|
| 1. | Thickness of Thermal Insulation | dTI | m |
| 2. | Outer Diameter of Pipe | Øe | m |
| 3. | Inner Diameter of Pipe | Øi | m |
| 4. | Axial Distance of the ATP Pipes | L | m |
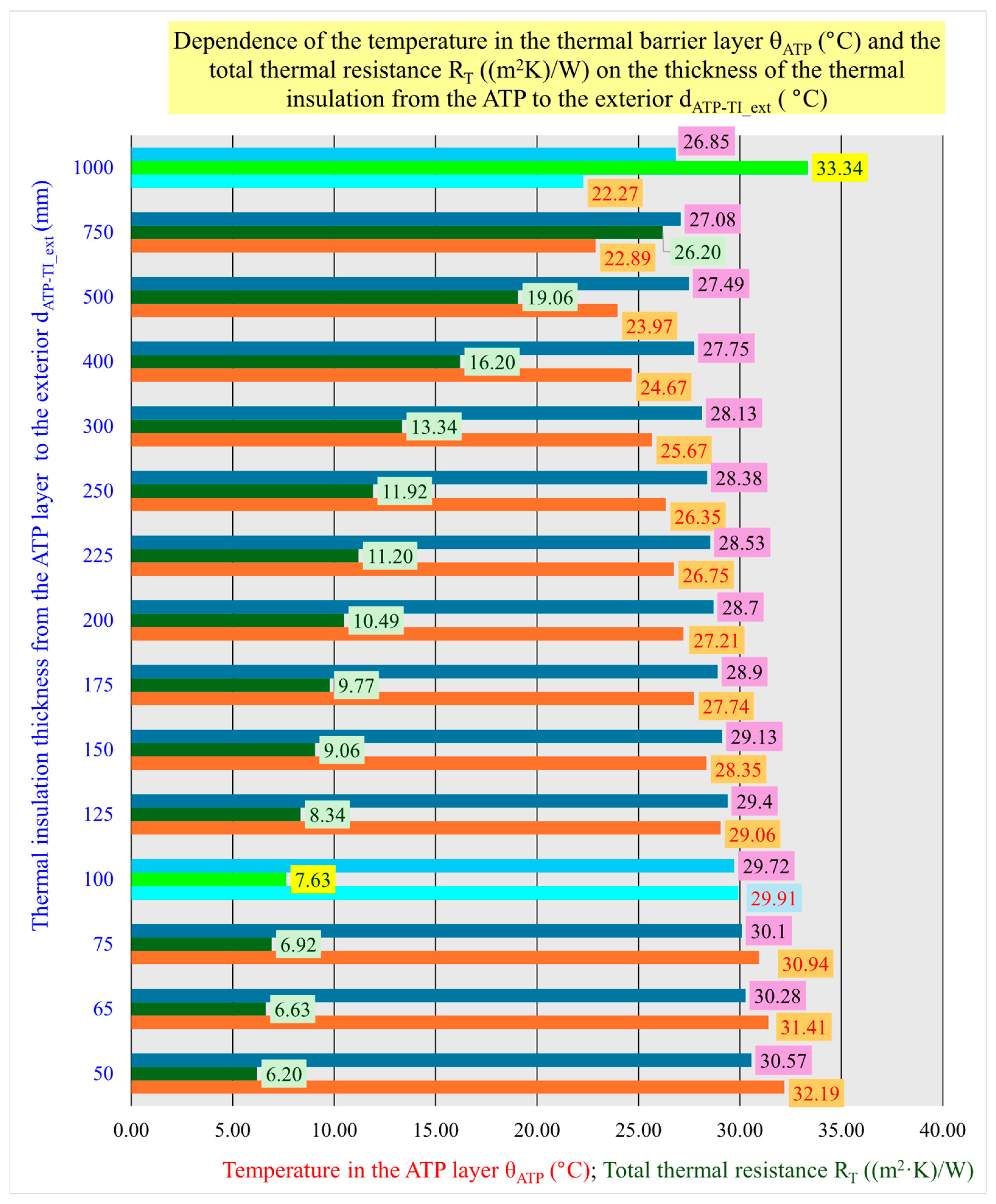
| Thermal insulation thickness from the ATP layer to the exterior dATP-TI_ext (mm) | 50 | 65 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 300 | 400 | 500 | 750 | 1000 |
| Temperature in the ATP layer θATP (°C) | −3.63 | −2.10 | −1.19 | 0.80 | 2.44 | 3.83 | 5.01 | 6.03 | 6.92 | 7.70 | 9.02 | 10.96 | 12.31 | 14.41 | 15.61 |
| Total thermal resistance RT ((m2·K)/W) | 6.20 | 6.63 | 6.92 | 7.63 | 8.34 | 9.06 | 9.77 | 10.49 | 11.20 | 11.92 | 13.34 | 16.20 | 19.06 | 26.20 | 33.34 |
| Total heat transfer coefficient UT (W/(m2·K)) | 0.161 | 0.151 | 0.145 | 0.131 | 0.120 | 0.110 | 0.102 | 0.095 | 0.089 | 0.084 | 0.075 | 0.062 | 0.052 | 0.038 | 0.030 |
| Thermal insulation thickness from the ATP layer to the exterior dATP-TI_ext (mm) | 50 | 65 | 75 | 100 | 125 | 150 | 175 | 200 | 225 | 250 | 300 | 400 | 500 | 750 | 1000 |
| Temperature in the ATP layer θATP (°C), θi = +20 °C, θe = +36 °C | 32.19 | 31.41 | 30.94 | 29.91 | 29.06 | 28.35 | 27.74 | 27.21 | 26.75 | 26.35 | 25.67 | 24.67 | 23.97 | 22.89 | 22.27 |
| Temperature in the ATP layer θATP (°C), θi = +26 °C, θe = +32 °C | 30.57 | 30.28 | 30.1 | 29.72 | 29.4 | 29.13 | 28.9 | 28.7 | 28.53 | 28.38 | 28.13 | 27.75 | 27.49 | 27.08 | 26.85 |
| Total thermal resistance RT ((m2·K)/W) | 6.20 | 6.63 | 6.92 | 7.63 | 8.34 | 9.06 | 9.77 | 10.49 | 11.20 | 11.92 | 13.34 | 16.20 | 19.06 | 26.20 | 33.34 |
| Total heat transfer coefficient UT (W/(m2·K)) | 0.161 | 0.151 | 0.145 | 0.131 | 0.120 | 0.110 | 0.102 | 0.095 | 0.089 | 0.084 | 0.075 | 0.062 | 0.052 | 0.038 | 0.030 |
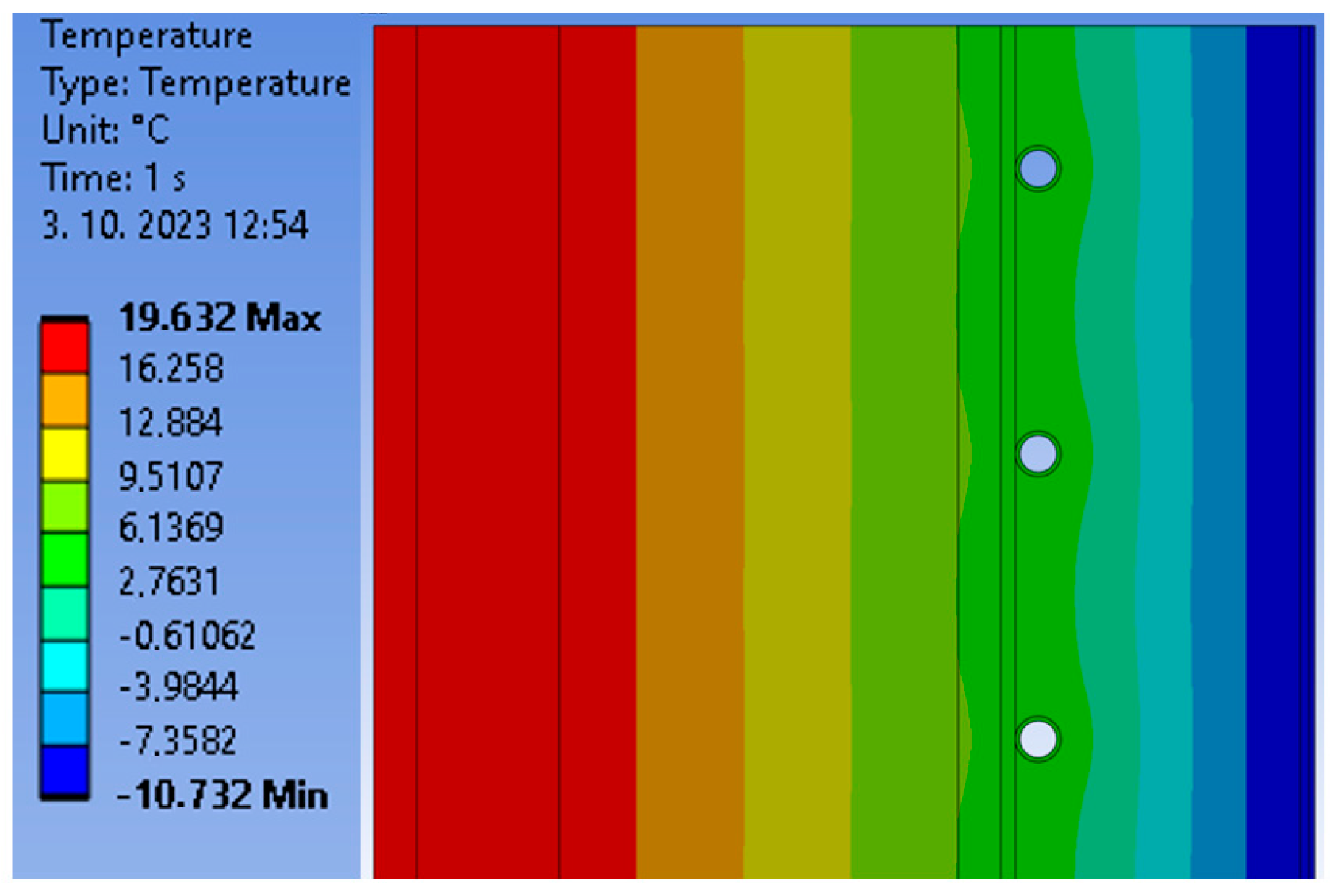
| Thermal Insulation Thickness | Axial Distance of the Pipe | Average Total Radiant Flux Density | Radiant Flux Density on the Outer Surface of the Pipe | Radiant Flux Density on the Inner Surface of the Pipe | Average Total Temperature in the Structure | Minimum Temperature at the Pipe Junction | Maximum Temperature at the Pipe Junction | |
|---|---|---|---|---|---|---|---|---|
| dTI (m) | L (m) | q (W/m2) | qext (W/m2) | qint (W/m2) | θ (°C) | θm-min (°C) | θm-max (°C) | |
| 1. | 0.10 | 0.10 | 4.00 | 6.29 | 7.95 | 8.51 | 5.75 | 5.98 |
| 2. | 0.10 | 0.15 | 4.10 | 8.53 | 10.78 | 8.31 | 5.21 | 5.87 |
| 3. | 0.10 | 0.20 | 4.16 | 10.29 | 12.96 | 8.12 | 4.63 | 5.79 |
| 4. | 0.15 | 0.10 | 3.37 | 4.67 | 5.83 | 7.18 | 6.07 | 6.10 |
| 5. | 0.15 | 0.15 | 3.37 | 4.32 | 5.44 | 7.09 | 5.88 | 6.05 |
| 6. | 0.15 | 0.20 | 3.38 | 4.08 | 5.15 | 7.01 | 5.66 | 6.01 |
| 7. | 0.20 | 0.10 | 2.97 | 4.39 | 5.46 | 6.09 | 6.14 | 6.23 |
| 8. | 0.20 | 0.15 | 2.95 | 4.42 | 5.49 | 6.09 | 6.14 | 6.23 |
| 9. | 0.20 | 0.20 | 2.95 | 4.40 | 5.45 | 6.06 | 6.13 | 6.21 |
| Axial distance of the pipe | ||||
| 100 mm | 150 mm | 200 mm | ||
| Thickness of thermal insulation | 100 mm |  |  |  |
| 150 mm | 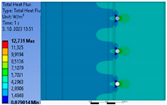 | 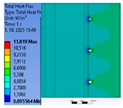 |  | |
| 200 mm |  |  |  | |
| Axial distance of the pipe | ||||
| 100 mm | 150 mm | 200 mm | ||
| Thickness of thermal insulation | 100 mm |  |  |  |
| 150 mm |  |  |  | |
| 200 mm | 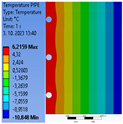 | 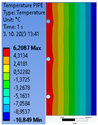 |  | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mučková, V.; Kalús, D.; Muhič, S.; Straková, Z.; Mudrá, M.; Predajnianska, A.; Füri, M.; Bolček, M. Energy Sustainability, Resilience, and Climate Adaptability of Modular and Panelized Buildings with a Lightweight Envelope Integrating Active Thermal Protection. Part 1—Parametric Study and Computer Simulation. Coatings 2025, 15, 756. https://doi.org/10.3390/coatings15070756
Mučková V, Kalús D, Muhič S, Straková Z, Mudrá M, Predajnianska A, Füri M, Bolček M. Energy Sustainability, Resilience, and Climate Adaptability of Modular and Panelized Buildings with a Lightweight Envelope Integrating Active Thermal Protection. Part 1—Parametric Study and Computer Simulation. Coatings. 2025; 15(7):756. https://doi.org/10.3390/coatings15070756
Chicago/Turabian StyleMučková, Veronika, Daniel Kalús, Simon Muhič, Zuzana Straková, Martina Mudrá, Anna Predajnianska, Mária Füri, and Martin Bolček. 2025. "Energy Sustainability, Resilience, and Climate Adaptability of Modular and Panelized Buildings with a Lightweight Envelope Integrating Active Thermal Protection. Part 1—Parametric Study and Computer Simulation" Coatings 15, no. 7: 756. https://doi.org/10.3390/coatings15070756
APA StyleMučková, V., Kalús, D., Muhič, S., Straková, Z., Mudrá, M., Predajnianska, A., Füri, M., & Bolček, M. (2025). Energy Sustainability, Resilience, and Climate Adaptability of Modular and Panelized Buildings with a Lightweight Envelope Integrating Active Thermal Protection. Part 1—Parametric Study and Computer Simulation. Coatings, 15(7), 756. https://doi.org/10.3390/coatings15070756






