Study of Lithium-Ion Battery Charge State Estimation Based on BP Neural Network Fusion Optimized Sparrow Algorithm
Abstract
1. Introduction
2. SOC Prediction Model of Lithium Battery Based on BP Neural Network
3. BP Neural Network Based on ISSN Optimization
3.1. Sparrow’s Algorithm to Optimize BP Neural Networks
- (1)
- Generation of the Sparrow Population
- (2)
- Calculation of Fitness for Each Sparrow in the Population
- (3)
- In the population, producers with higher fitness values are prioritized in obtaining energy during the search process. At the same time, producers are responsible for leading the entire population, guiding the population toward the food source. The position update for producers follows the formula below:
3.2. Optimizing the Sparrow Algorithm
- (1)
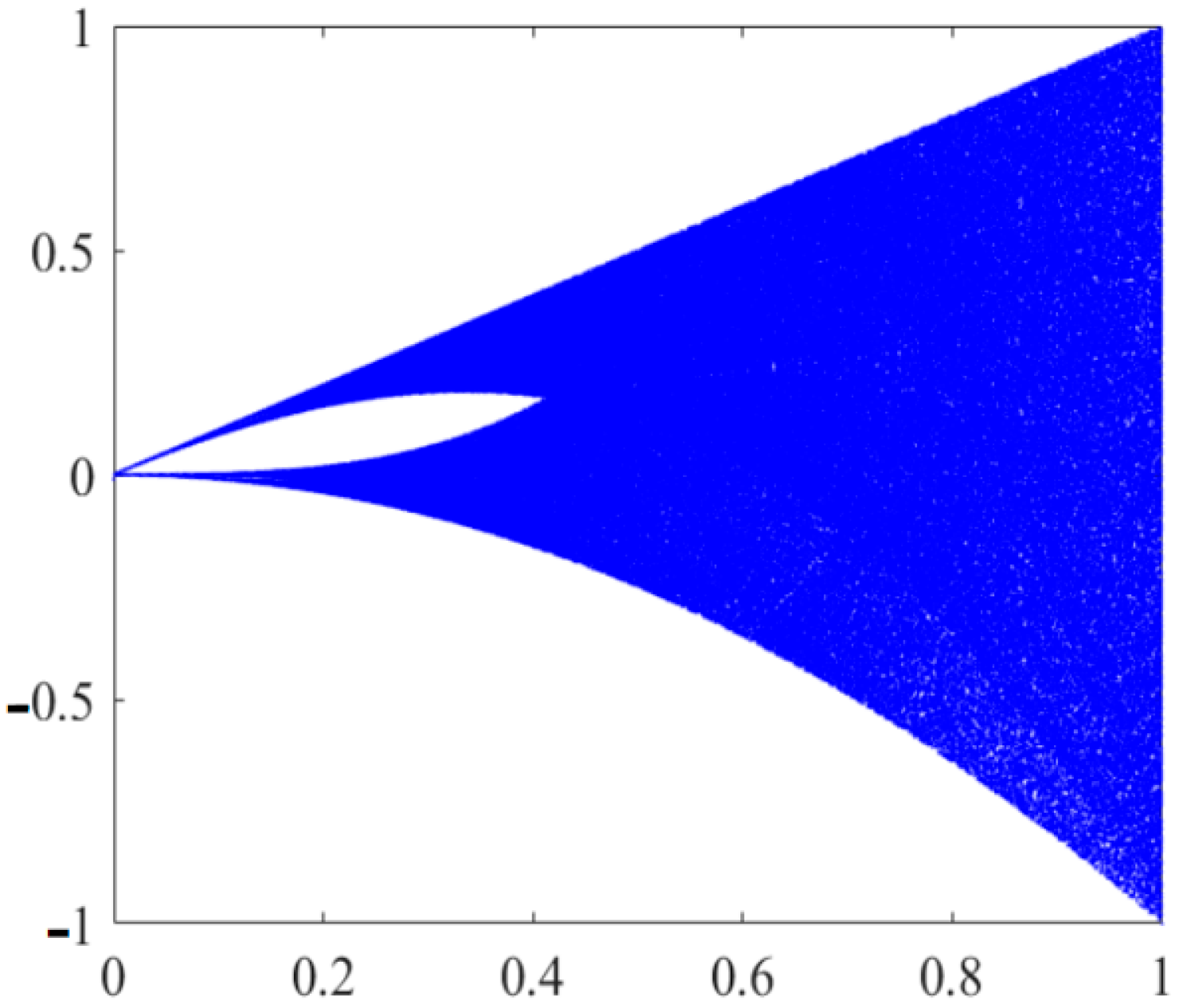
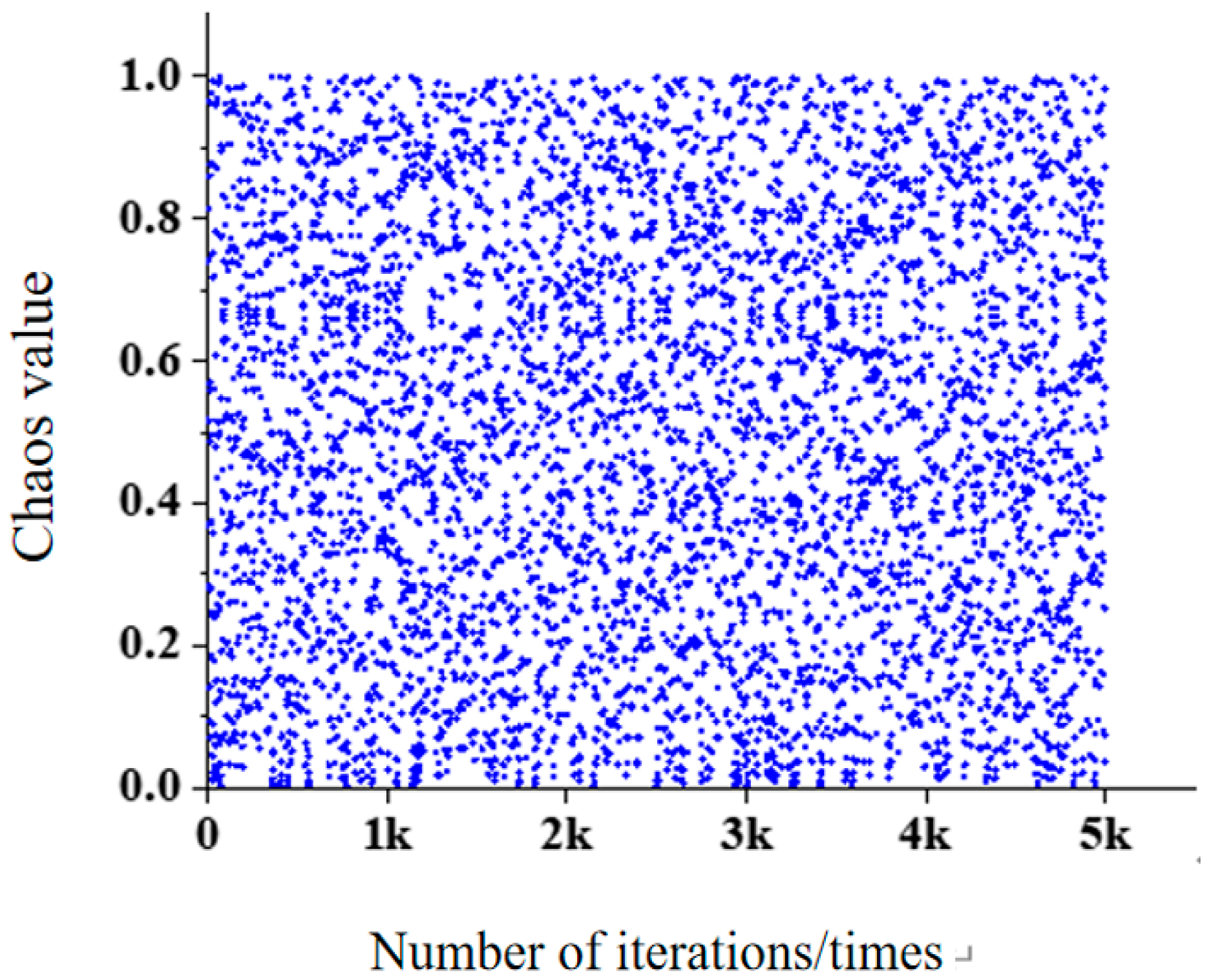
- Tent Chaos Mapping
- (2)
- Sine–cosine algorithm
- (3)
- Firefly Perturbation Strategy
3.3. Comparison of Optimization Algorithms
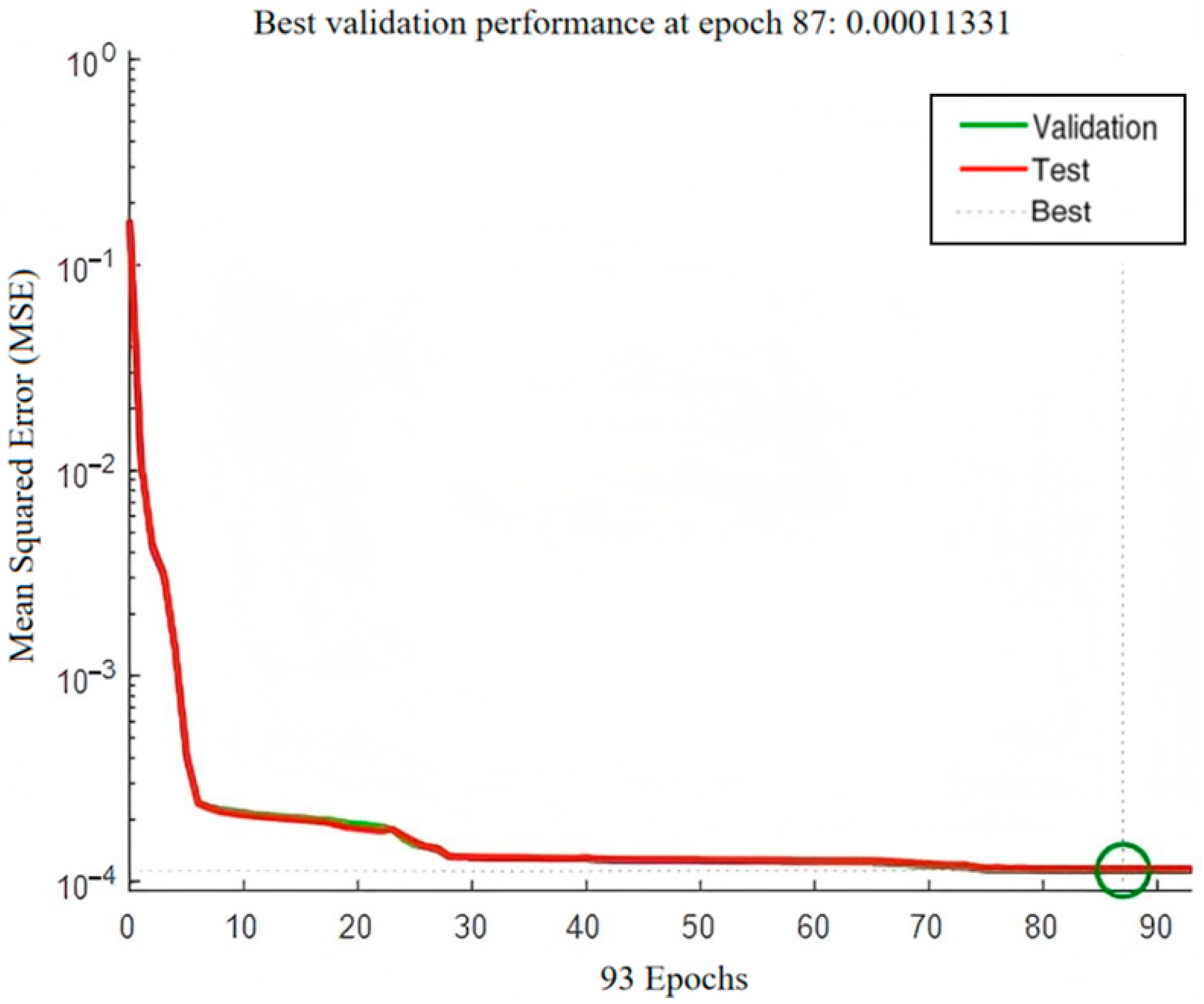
3.4. Model Training and Convergence
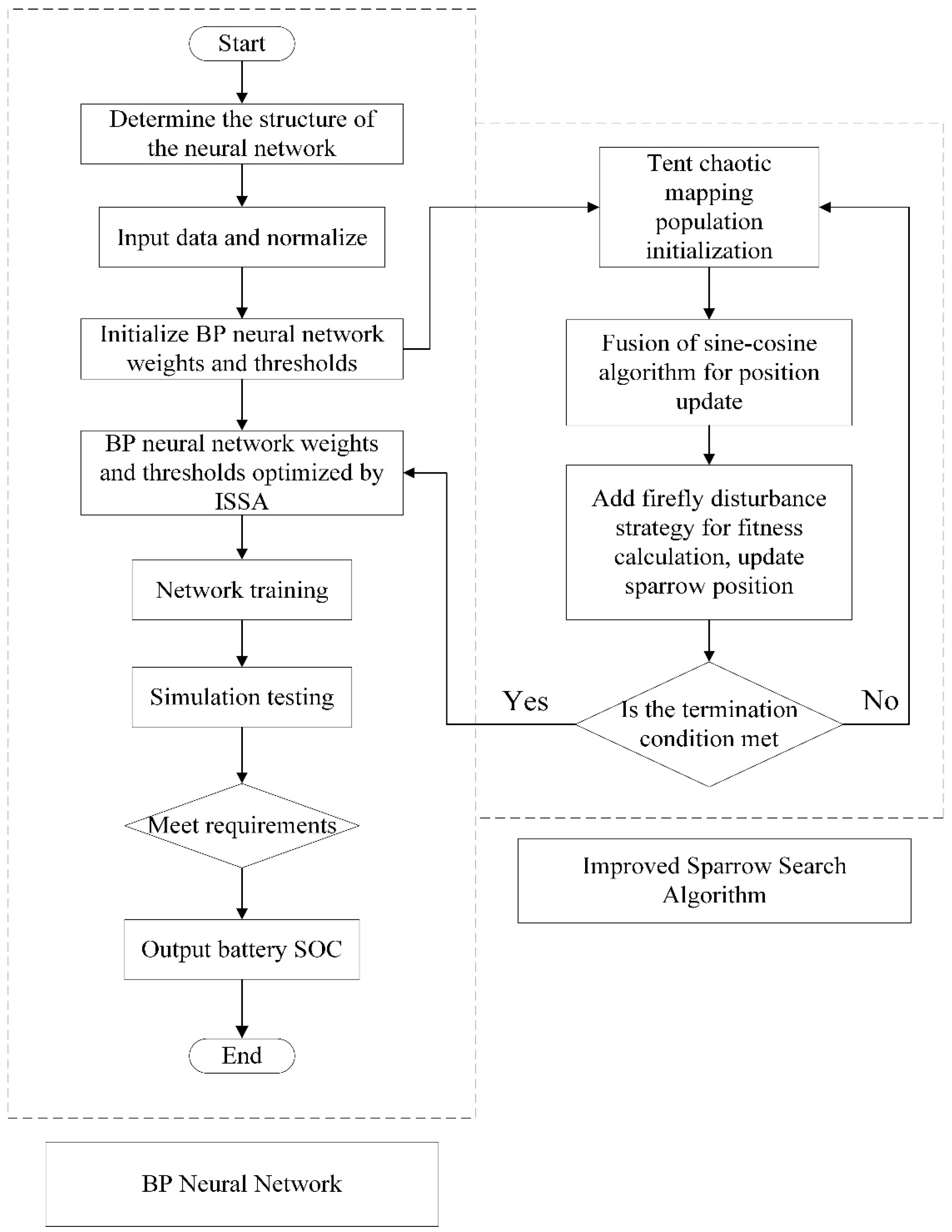
3.5. ISSNBP-Based Model Realization Process
- (1)
- Normalize the input and output data, and set the basic parameters of the BP neural network, such as the maximum number of iterations, learning rate, etc.
- (2)
- Set the basic parameters of the Sparrow Search Algorithm, including the maximum number of iterations, population size, safety threshold, upper and lower bounds of initial values, etc.
- (3)
- Initialize the population using Tent chaotic mapping, and calculate the fitness of each sparrow individual in every generation.
- (4)
- Update each individual in the sparrow population, selecting individuals with high fitness values as producers.
- (5)
- Introduce the sine–cosine algorithm into the update of producers, update the positions of producers, and select individuals with high fitness as producers.
- (6)
- Update the positions of followers and alerters in the sparrow population, and calculate their fitness.
- (7)
- Add firefly disturbance to the updated population, calculate the fitness of the updated sparrow population, and update the positions of the sparrows.
- (8)
- Calculate the fitness, determine the optimal position of the population, and input the optimal structural parameters into the BP neural network for training.
- (9)
- Judge whether the training requirements are met based on the training error. If not, continue training the network; if met, stop the calculation and output the battery’s SOC value.
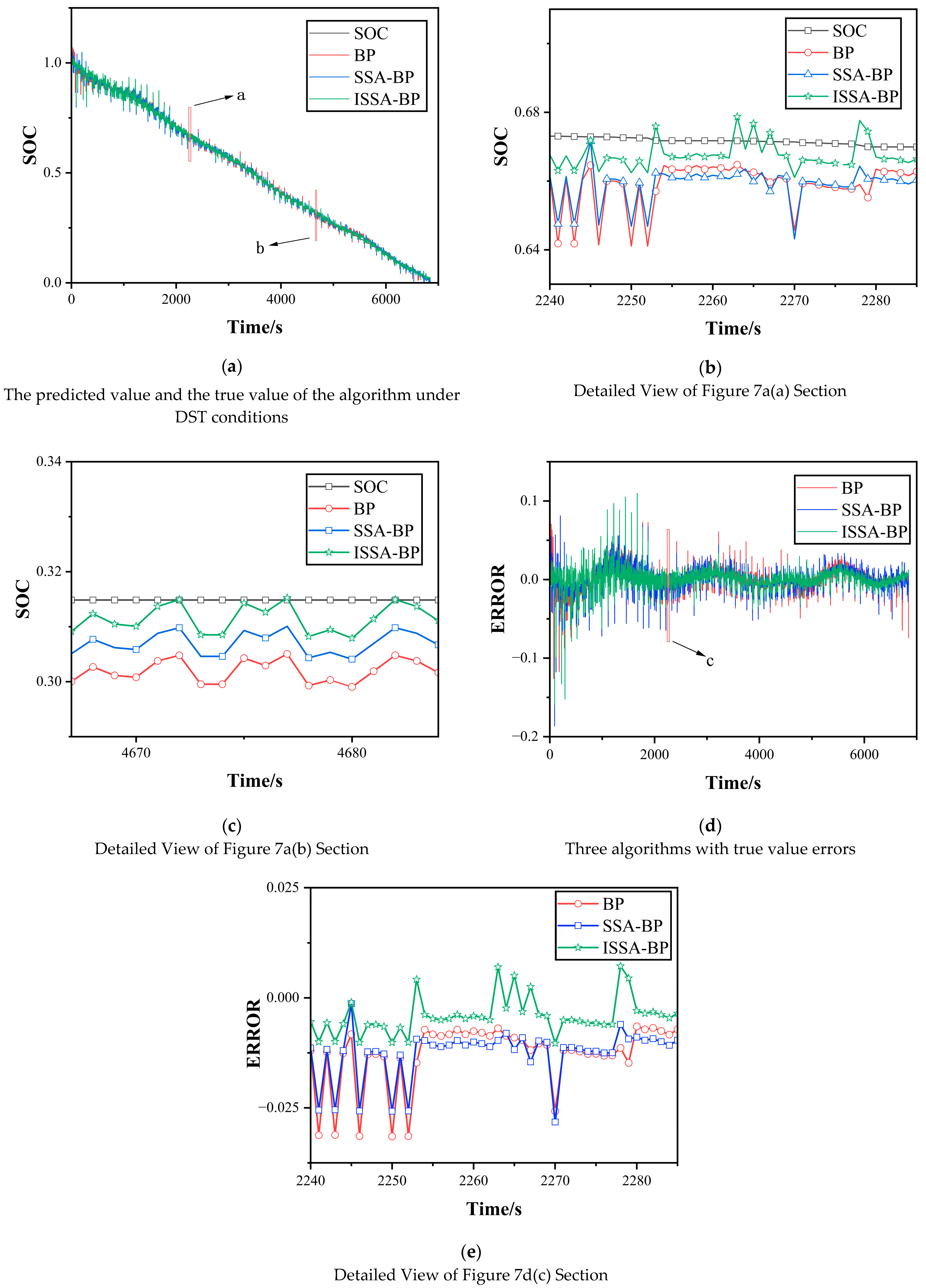
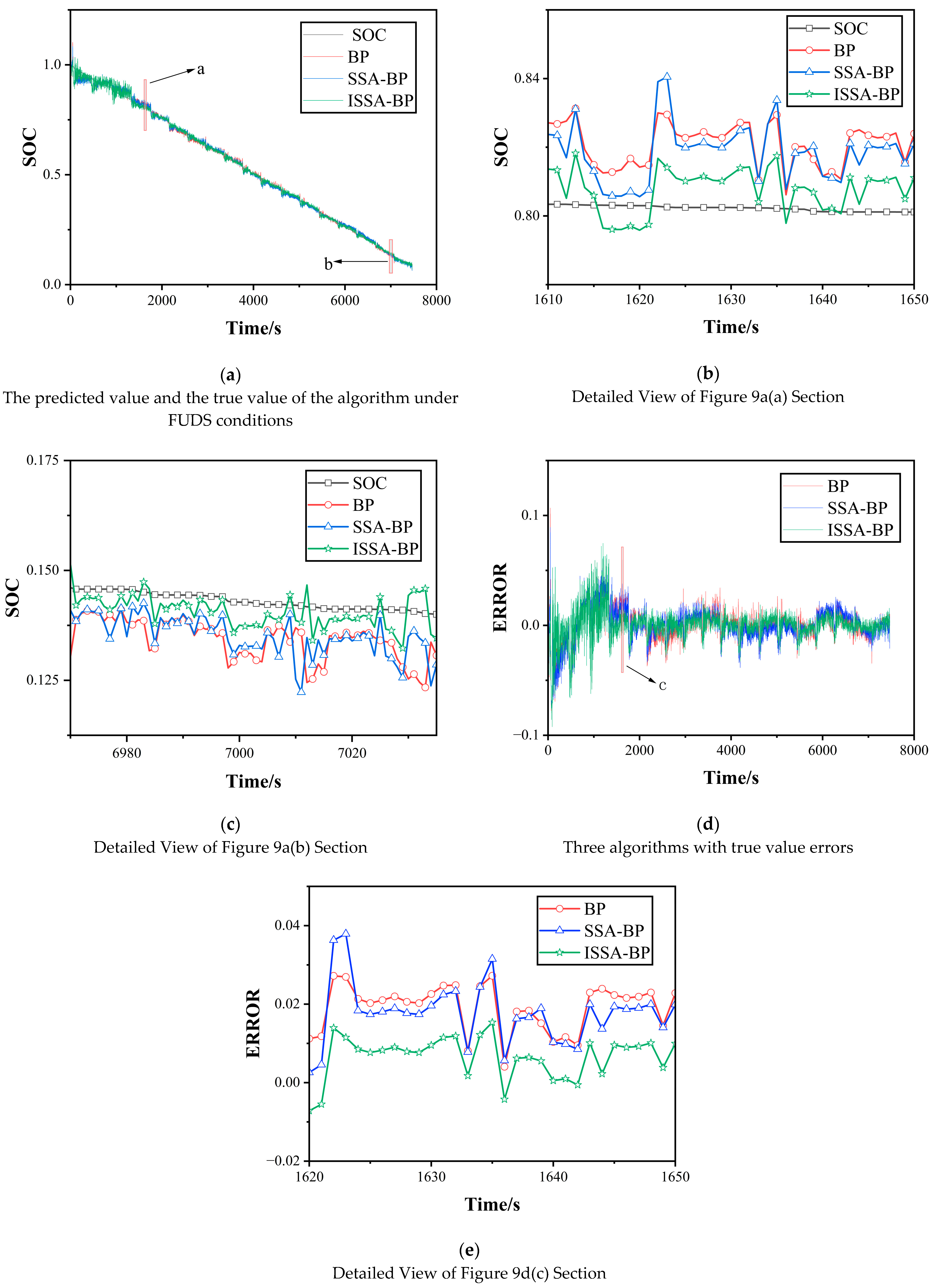
4. Simulation Experiment and Analysis
4.1. Sampling Data Selection
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BMS | Battery management system |
| SOC | State of charge |
| SSA | Sparrow Search Algorithm |
| BP | Backpropagation |
| DST | Dynamic Stress Test |
| UDDS | Urban Dynamometer Driving Schedule |
| FUDS | Federal Urban Driving Schedule |
| MAE | Mean absolute error |
| MSE | Mean squared error |
| RMSE | Root Mean Squared Error |
References
- Jiang, M.; Li, D.; Li, Z.; Chen, Z.; Yan, Q.; Lin, F.; Yu, C.; Jiang, B.; Wei, X.; Yan, W.; et al. Advances in battery state estimation of battery management system in electric vehicles. J. Power Sources 2024, 612, 234781. [Google Scholar] [CrossRef]
- Bentley, P.; Bhangu, B.; Bingham, C.; Stone, D. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles. IEEE Trans. Veh. Technol. 2005, 54, 783–794. [Google Scholar]
- Zhu, X.Q.; Wang, Z.P.; Wang, H. Review of research on thermal runaway and safety management of lithium-ion power battery. Chin. J. Mech. Eng. 2020, 56, 18–91. [Google Scholar]
- Yu, Q.; Huang, Y.; Tang, A.; Wang, C.; Shen, W. OCV-SOC-Temperature Relationship Construction and State of Charge Estimation for a Series–Parallel Lithium-Ion Battery Pack. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6362–6371. [Google Scholar] [CrossRef]
- Chouhan, S.; Guha, A. Incremental State-of-Charge determination of a Lithium-ion battery based on Capacity update using Particle Filtering framework. In Proceedings of the 2023 IEEE Transportation Electrification Conference & Expo (ITEC), Detroit, MI, USA, 21–23 June 2023; pp. 1–6. [Google Scholar]
- Xu, Y.; Hu, M.; Fu, C.; Cao, K.; Su, Z.; Yang, Z. State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics 2019, 8, 1012. [Google Scholar] [CrossRef]
- Tong, S.; Klein, M.P.; Park, J.W. On-line optimization of battery open circuit voltage for improved state-of-charge and state-of-health estimation. J. Power Sources 2015, 293, 416–428. [Google Scholar] [CrossRef]
- Xu, X.; Huang, C.-S.; Chow, M.-Y.; Luo, H.; Yin, S. Data-driven SOC Estimation with Adaptive Residual Generator for Li-ion Battery. In Proceedings of the IECON 2020 the 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 2612–2616. [Google Scholar]
- Zhang, X.; Jin, Y.; Zhang, R.; Dong, H. Lithium Battery SOC Prediction Based on mproved BP eural etwork Algorithm. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 882–886. [Google Scholar]
- Wang, W.; Wang, X.; Xiang, C.; Wei, C.; Zhao, Y. Unscented Kalman Filter-Based Battery SOC Estimation and Peak Power Prediction Method for Power Distribution of Hybrid Electric Vehicles. IEEE Access 2018, 6, 35957–35965. [Google Scholar] [CrossRef]
- Mao, X.; Song, S.; Ding, F. Optimal BP neural network algorithm for state of charge estimation of lithium-ion battery using PSO with Levy flight. J. Energy Storage 2022, 49, 104139. [Google Scholar] [CrossRef]
- Zhou, K.; Li, R.; Xu, S.; Li, S.; Zhou, Y.; Liu, X.; Yao, J. State of Charge Prediction Algorithm of Lithium-Ion Battery Based on PSO-SVR Cross Validation. IEEE Access 2020, 8, 10234–10242. [Google Scholar]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Haus, B.; Mercorelli, P. Polynomial Augmented Extended Kalman Filter to Estimate the State of Charge of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2020, 69, 1452–1463. [Google Scholar] [CrossRef]
- Mohammadi, F. Lithium-ion battery State-of-Charge estimation based on an improved Coulomb-Counting algorithm and uncertainty evaluation. J. Energy Storage 2022, 48, 104061. [Google Scholar] [CrossRef]
- Zhao, F.; Li, P.; Li, Y.; Li, Y. The Li-ion Battery State of Charge Prediction of Electric Vehicle Using Deep Neural Network. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 773–777. [Google Scholar]
- Shen, Y. Adaptive online state-of-charge determination based on neuro-controller and neural network. Energy Convers. Manag. 2010, 51, 1093–1098. [Google Scholar] [CrossRef]
- El Fallah, S.; Kharbach, J.; Hammouch, Z.; Rezzouk, A.; Jamil, M.O. State of charge estimation of an electric vehicle’s battery using Deep Neural Networks: Simulation and experimental results. J. Energy Storage 2023, 62, 106904. [Google Scholar] [CrossRef]
- Bhattacharyya, H.S.; Yadav, A.; Choudhury, A.B.; Chanda, C.K. Convolution Neural Network-Based SOC Estimation of Li-ion Battery in EV Applications. In Proceedings of the 2021 5th International Conference on Electrical, Electronics, Communication, Computer Technologies and Optimization Techniques (ICEECCOT), Mysuru, India, 10–11 December 2021; pp. 587–592. [Google Scholar]
- Qi, Y.; Jiang, A.; Gao, Y. A Gaussian convolutional optimization algorithm with tent chaotic mapping. Sci. Rep. 2024, 14, 31027. [Google Scholar] [CrossRef]
- Ren, X.; Chen, S.; Wang, K.; Tan, J. Design and application of improved sparrow search algorithm based on sine cosine and firefly perturbation. Math. Biosci. Eng. 2022, 19, 11422–11452. [Google Scholar] [CrossRef]
- Wei, F.; Feng, Y.; Shi, X.; Hou, K. Improved sparrow search algorithm with adaptive multi-strategy hierarchical mechanism for global optimization and engineering problems. Cluster Comput. 2025, 28, 215. [Google Scholar] [CrossRef]
- Fei, T.; Wang, H.; Liu, L.; Zhang, L.; Wu, K.; Guo, J. Research on multi-strategy improved sparrow search optimization algorithm. Math. Biosci. Eng. 2023, 20, 17220–17241. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, P.; Zhang, L.; Qi, Q.; Zhou, Q.; Chen, Y.; Hu, Y.; Ma, B. Enhanced Sparrow Search Algorithm With Mutation Strategy for Global Optimization. IEEE Access 2021, 9, 159218–159261. [Google Scholar]
- Sun, L.; Si, S.; Ding, W.; Wang, X.; Xu, J. Multiobjective sparrow search feature selection with sparrow ranking and preference information and its applications for high-dimensional data. Appl. Soft Comput. 2023, 147, 110837. [Google Scholar] [CrossRef]
- Dong, J.; Dou, Z.; Si, S.; Wang, Z.; Liu, L. Optimization of Capacity Configuration of Wind–Solar–Diesel–Storage Using Improved Sparrow Search Algorithm. J. Electr. Eng. Technol. 2022, 17, 1–14. [Google Scholar] [CrossRef]
- Guo, X.; Hu, Y.; Song, C.; Zhao, F.; Jiang, J. An improved sparrow search algorithm based on multiple strategies. In Proceedings of the 2024 5th International Conference on Computing, Networks and Internet of Things (CNIOT ‘24), Tokyo, Japan, 24–26 May 2024; Association for Computing Machinery: New York, NY, USA, 2024; pp. 112–118. [Google Scholar]
- Gao, B.; Shen, W.; Guan, H.; Zheng, L.; Zhang, W. Research on Multistrategy Improved Evolutionary Sparrow Search Algorithm and its Application. IEEE Access 2022, 10, 62520–62534. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, Q.; Li, D.; Rao, W. An improved sparrow search algorithm with multi-strategy integration. Sci. Rep. 2025, 15, 3314. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Qin, J.; Hu, Z.; He, J.; Tang, D. Multi-Objective Antenna Design Based on BP Neural Network Surrogate Model Optimized by Improved Sparrow Search Algorithm. Appl. Sci. 2022, 12, 12543. [Google Scholar] [CrossRef]
- Dang, M.; Zhang, C.; Yang, Z.; Wang, J.; Li, Y.; Huang, J. An estimation method for the state-of-charge of lithium-ion battery based on PSO-LSTM. AIP Adv. 2023, 13, 115204. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, J.; Xu, L.; Wang, L.; Li, W.; Wang, F. SOC estimation of lead–carbon battery based on GA-MIUKF algorithm. Sci. Rep. 2024, 14, 3347. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Joint SOH-SOC Estimation Model for Lithium-Ion Batteries Based on GWO-BP Neural Network. Energies 2023, 16, 132. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, S.; Cao, W.; Xie, Y.; Fernandez, C. State of health prediction of lithium-ion batteries based on SSA optimized hybrid neural network model. Electrochim. Acta 2024, 487, 144146. [Google Scholar] [CrossRef]



| Algorithm | Advantages | Disadvantages |
|---|---|---|
| PSO | Fast convergence Simple implementation | Prone to local optima |
| GA | Strong global search ability Adaptive crossover mechanisms | Slow convergence Sensitive to noise |
| GWO | Good balance between exploration and exploitation | Performance degrades in high dimensions |
| SSA | Good global exploration Fewer control parameters Accurate | Sensitive to initial population quality |
| ISSA | High accuracy Improved robustness Better convergence | Increased complexity due to hybridization |
| BP | SSA-BP | ISSA-BP | |
|---|---|---|---|
| MAE | 0.0122 | 0.0109 | 0.0073 |
| MSE | 2.8494 × 10−4 | 2.2003 × 10−4 | 1.1927 × 10−4 |
| RMSE | 0.0169 | 0.0148 | 0.0109 |
| BP | SSA-BP | ISSA-BP | |
|---|---|---|---|
| MAE | 0.0111 | 0.0102 | 0.0079 |
| MSE | 2.0756 × 10−4 | 1.9204 × 10−4 | 1.1193 × 10−4 |
| RMSE | 0.0144 | 0.0139 | 0.0106 |
| BP | SSA-BP | ISSA-BP | |
|---|---|---|---|
| MAE | 0.0108 | 0.0107 | 0.0081 |
| MSE | 2.3585 × 10−4 | 2.3547 × 10−4 | 1.5821 × 10−4 |
| RMSE | 0.0154 | 0.0153 | 0.0126 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, S.; Wei, T.; Wang, L.; Li, X.; Chen, D.; Jia, Z.; Zhang, R. Study of Lithium-Ion Battery Charge State Estimation Based on BP Neural Network Fusion Optimized Sparrow Algorithm. Coatings 2025, 15, 697. https://doi.org/10.3390/coatings15060697
Han S, Wei T, Wang L, Li X, Chen D, Jia Z, Zhang R. Study of Lithium-Ion Battery Charge State Estimation Based on BP Neural Network Fusion Optimized Sparrow Algorithm. Coatings. 2025; 15(6):697. https://doi.org/10.3390/coatings15060697
Chicago/Turabian StyleHan, Shaojian, Tianhao Wei, Liyong Wang, Xiaojie Li, Dongdong Chen, Zhenhua Jia, and Rui Zhang. 2025. "Study of Lithium-Ion Battery Charge State Estimation Based on BP Neural Network Fusion Optimized Sparrow Algorithm" Coatings 15, no. 6: 697. https://doi.org/10.3390/coatings15060697
APA StyleHan, S., Wei, T., Wang, L., Li, X., Chen, D., Jia, Z., & Zhang, R. (2025). Study of Lithium-Ion Battery Charge State Estimation Based on BP Neural Network Fusion Optimized Sparrow Algorithm. Coatings, 15(6), 697. https://doi.org/10.3390/coatings15060697









