Review of Research on Prediction Models for Residual Life of Concrete Structures
Abstract
:1. Introduction
2. Aging and Failure Mechanisms of Concrete Structures
2.1. Rebar Corrosion and the Decline of Concrete’s Mechanical Properties
2.2. Crack Propagation and Structural Damage
2.3. Chloride Ion Penetration and Concrete Corrosion
3. Classification of Lifespan Prediction Models
3.1. Physical Lifespan Prediction Models
3.1.1. Carbonation Depth Model
3.1.2. Chloride Ion Penetration Model
- represents the chloride ion concentration at time t and depth ,
- is the initial concentration, typically the chloride ion concentration in the concrete,
- is the surface concentration, corresponding to the concentration at the concrete surface exposed to water or air,
- is the chloride diffusion coefficient,
- erf denotes the error function.
- represents the initial chloride ion diffusion coefficient,
- is the reference time,
- is the coefficient for time-dependent decay.
3.2. Empirical Models
3.2.1. Empirical Formulas
3.2.2. Applicability and Limitations of Empirical Models
3.2.3. Integrating Empirical Models with Real-Time Data
3.3. Statistical Lifespan Prediction Models
3.3.1. Regression Analysis Models
3.3.2. Bayesian Networks for Lifespan Prediction
3.4. Machine Learning-Based Lifespan Prediction Models
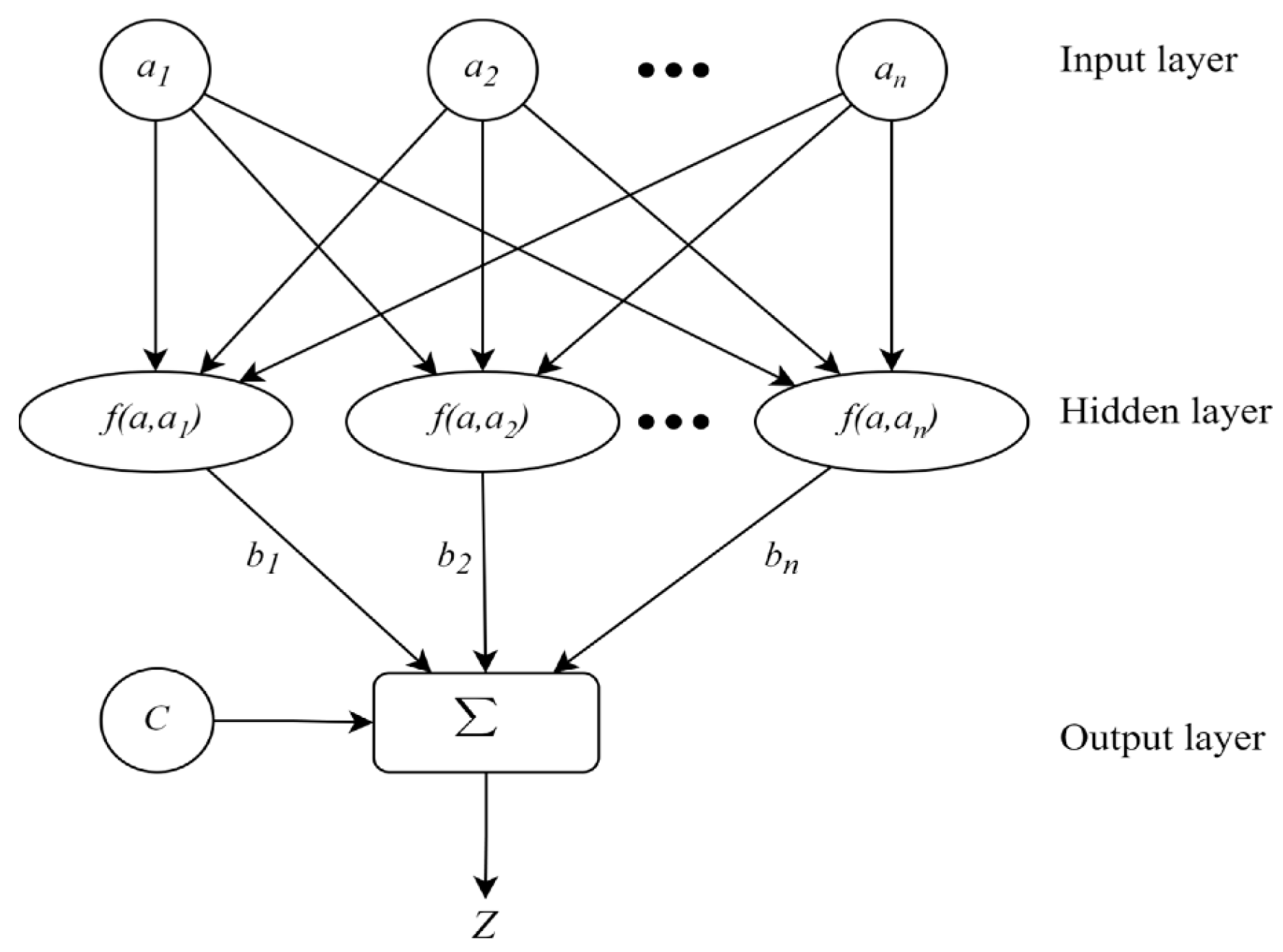
3.4.1. Artificial Neural Networks (ANNs)
3.4.2. Support Vector Machines (SVMs)
3.4.3. Random Forests and Decision Trees
4. Model Validation and Prediction
4.1. Validation Methods
4.2. Expansion and Application of Evaluation Metrics
4.3. Sensitivity Analysis and Uncertainty Analysis
5. Application Cases of Models
6. Analysis of Advantages and Disadvantages of Existing Models
7. Research Progress and Development Trends
8. Conclusions
- Combining real-time monitoring data with advanced machine learning algorithms to improve prediction accuracy and robustness;
- Exploring hybrid models that integrate the strengths of both physical and data-driven models to enhance adaptability in complex environments;
- Developing more precise nonlinear and multiscale modeling techniques to accommodate environmental and material variations;
- Optimizing model validation and evaluation methods to improve their reliability and applicability in practical engineering projects;
- By combining experimental data with field monitoring data, future research should continue to explore how to effectively integrate these two sources in order to further optimize the predictive capability of models and improve the accuracy of concrete structure durability assessments.
Funding
Conflicts of Interest
References
- Imbabi, M.S.; Carrigan, C.; McKenna, S. Trends and developments in green cement and concrete technology. Int. J. Sustain. Built Environ. 2012, 1, 194–216. [Google Scholar] [CrossRef]
- Shi, X.; Xie, N.; Fortune, K.; Gong, J. Durability of steel reinforced concrete in chloride environments: An overview. Constr. Build. Mater. 2012, 30, 125–138. [Google Scholar] [CrossRef]
- Athibaranan, S.; Karthikeyan, J.; Rawat, S. Investigation on service life prediction models of reinforced concrete structures exposed to chloride laden environment. J. Build. Pathol. Rehabil. 2022, 7, 1–15. [Google Scholar] [CrossRef]
- Peng, R.; Qiu, W.; Jiang, M. Frost resistance performance assessment of concrete structures under multi-factor coupling in cold offshore environment. Build. Environ. 2022, 226, 109733. [Google Scholar] [CrossRef]
- Zhang, K.; Guo, A.; Yu, Y.; Yang, B.; Yu, B.; Xie, C. Freeze–thaw damage degradation model and life prediction of air-entrained concrete in multi-year permafrost zone. Materials 2023, 16, 7703. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Li, Y.; Wen, L.; Guo, H. Effects of curing conditions with different temperature and humidity on damage evolution of concrete during freeze–thaw cycling. Mater. Struct. 2022, 55, 80. [Google Scholar] [CrossRef]
- Zhang, X.G.; Wang, J. Probabilistic Model of Corrosion in Reinforced Concrete Structures Considering Coupling Effects of Influence Factors. Adv. Mater. Res. 2013, 671, 740–745. [Google Scholar] [CrossRef]
- Zhang, P.; Cong, Y.; Vogel, M.; Liu, Z.; Müller, H.S.; Zhu, Y.; Zhao, T. Steel reinforcement corrosion in concrete under combined actions: The role of freeze-thaw cycles, chloride ingress, and surface impregnation. Constr. Build. Mater. 2017, 148, 113–121. [Google Scholar] [CrossRef]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Dinesh, A.; Prasad, B.R. Predictive models in machine learning for strength and life cycle assessment of concrete structures. Autom. Constr. 2024, 162, 105412. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, G.; Ye, H.; Zeng, Q.; Zhang, Z.; Tian, Z.; Jin, X.; Jin, N.; Chen, Z.; Wang, J. Corrosion of steel rebar in concrete induced by chloride ions under natural environments. Constr. Build. Mater. 2023, 369, 130504. [Google Scholar] [CrossRef]
- Ju, X.; Wu, L.; Lin, C.; Yang, X.; Yang, C. Prediction of chloride concentration with elevation in concrete exposed to cyclic drying-wetting conditions in marine environments. Constr. Build. Mater. 2021, 278, 122370. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, J.; Yu, Q.; Gu, X. Corrosion evolution of steel bars in RC structures based on Markov chain modeling. Struct. Saf. 2021, 88, 102037. [Google Scholar] [CrossRef]
- Sun, B.; Xiao, R.; Ruan, W.; Wang, P. Corrosion-induced cracking fragility of RC bridge with improved concrete carbonation and steel reinforcement corrosion models. Eng. Struct. 2020, 208, 110313. [Google Scholar] [CrossRef]
- Zhang, Y.; Su, R.K.L. Corner cracking model for non-uniform corrosion-caused deterioration of concrete covers. Constr. Build. Mater. 2020, 234, 117410. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, X.; Wu, L. Prediction model of chloride diffusion in concrete considering the coupling effects of coarse aggregate and steel reinforcement exposed to marine tidal environment. Constr. Build. Mater. 2019, 216, 40–57. [Google Scholar] [CrossRef]
- Hájková, K.; Šmilauer, V.; Jendele, L.; Červenka, J. Prediction of reinforcement corrosion due to chloride ingress and its effects on serviceability. Eng. Struct. 2018, 174, 768–777. [Google Scholar] [CrossRef]
- Wang, W.; Lu, C. Time-varying law of rebar corrosion rate in fly ash concrete. J. Hazard. Mater. 2018, 360, 520–528. [Google Scholar] [CrossRef]
- Ann, K.Y.; Ahn, J.H.; Ryou, J.S. The importance of chloride content at the concrete surface in assessing the time to corrosion of steel in concrete structures. Constr. Build. Mater. 2009, 23, 239–245. [Google Scholar] [CrossRef]
- Zhou, Y.; Gencturk, B.; Willam, K.; Attar, A. Carbonation-induced and chloride-induced corrosion in reinforced concrete structures. J. Mater. Civ. Eng. 2015, 27, 04014245. [Google Scholar] [CrossRef]
- Saeki, T. Effect of carbonation on chloride penetration in concrete. In Proceedings of the Third International RILEM Workshop on Testing and Modelling Chloride Ingress into Concrete, Madrid, Spain, 9–10 September 2002; pp. 1–14. [Google Scholar]
- Zhou, Y.; Tian, H.; Sui, L.; Xing, F.; Han, N. Strength deterioration of concrete in sulfate environment: An experimental study and theoretical modeling. Adv. Mater. Sci. Eng. 2015, 2015, 951209. [Google Scholar] [CrossRef]
- Scott, A.; Alexander, M.G. The influence of binder type, cracking and cover on corrosion rates of steel in chloride-contaminated concrete. Mag. Concr. Res. 2007, 59, 495–505. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, L.; Ma, Y.; Wu, B.; Ren, L.; Gui, S.; Su, X. Probabilistic fatigue life prediction of corroded PC beams considering spatial variability of pitting corrosion. Eng. Struct. 2024, 306, 117721. [Google Scholar] [CrossRef]
- Wu, J.; Xu, J.; Diao, B.; Jin, L.; Du, X. Fatigue life prediction for the reinforced concrete (RC) beams under the actions of chloride attack and fatigue. Eng. Struct. 2021, 242, 112543. [Google Scholar] [CrossRef]
- Ge, B.; Kim, S. Probabilistic service life prediction updating with inspection information for RC structures subjected to coupled corrosion and fatigue. Eng. Struct. 2021, 238, 112260. [Google Scholar] [CrossRef]
- Bhargava, K.; Ghosh, A.K.; Mori, Y.; Ramanujam, S. Model for cover cracking due to rebar corrosion in RC structures. Eng. Struct. 2006, 28, 1093–1109. [Google Scholar] [CrossRef]
- Choe, D.E.; Gardoni, P.; Rosowsky, D.; Haukaas, T. Probabilistic capacity models and seismic fragility estimates for RC columns subject to corrosion. Reliab. Eng. Syst. Saf. 2008, 93, 383–393. [Google Scholar] [CrossRef]
- Jianyu, Y.; Xin, Y.; Cong, J.; Weijun, Y. Effect of NaCl solution and simulated concrete pore solution environment on the efficiency of steel bar energized corrosion. Materials 2022, 15, 7040. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Li, L.; Ma, H.; Lu, Y.; Hu, D. Study on time range of definite integral in derivation process of chloride ion diffusion theoretical model of concrete. Constr. Build. Mater. 2024, 428, 135876. [Google Scholar] [CrossRef]
- Chen, D.; Guo, W.; Quan, X.; Duan, B.; Guo, L. Mesoscopic statistics-based probability characteristics of chloride transport and reliability-based corrosion initiation life of bridge tower. Thin-Walled Struct. 2024, 198, 111680. [Google Scholar] [CrossRef]
- Guo, Z.; Guo, R.; Lin, S. Multi-factor fuzzy prediction model of concrete surface chloride concentration with trained samples expanded by random forest algorithm. Mar. Struct. 2022, 86, 103311. [Google Scholar] [CrossRef]
- Taffese, W.Z.; Espinosa-Leal, L. Prediction of chloride resistance level of concrete using machine learning for durability and service life assessment of building structures. J. Build. Eng. 2022, 60, 105146. [Google Scholar] [CrossRef]
- Liu, J.; Liao, C.; Jin, H.; Jiang, Z.; Zhou, H. Numerical and experimental research on the effect of rainfall on the transporting behavior of chloride ions in concrete. Constr. Build. Mater. 2021, 302, 124160. [Google Scholar] [CrossRef]
- Shao, W.; Nie, Y.; Liang, F.; Shi, D. A novel comprehensive evaluation method for the corrosion initiation life of RC hollow piles in chloride environments. Constr. Build. Mater. 2020, 249, 118801. [Google Scholar] [CrossRef]
- Safehian, M.; Ramezanianpour, A.A. Assessment of service life models for determination of chloride penetration into silica fume concrete in the severe marine environmental condition. Constr. Build. Mater. 2013, 48, 287–294. [Google Scholar] [CrossRef]
- Papadakis, V.G.; Vayenas, C.G.; Fardis, M.N. Fundamental modeling and experimental investigation of concrete carbonation. Mater. J. 1991, 88, 363–373. [Google Scholar]
- Wang, D.; Tan, Q.; Wang, Y.; Liu, G.; Lu, Z.; Zhu, C.; Sun, B. Carbonation depth prediction and parameter influential analysis of recycled concrete buildings. J. CO2 Util. 2024, 85, 102877. [Google Scholar] [CrossRef]
- Cao, H.; Xu, Z.; Peng, X. An Improved Fick Model for Predicting Carbonation Depth of Concrete. Coatings 2024, 14, 1345. [Google Scholar] [CrossRef]
- Yu, H.; Sun, W.; Ma, H. Research on Theoretical Models of Chloride Ion Diffusion in Concrete I—Non-steady State Homogeneous and Non-homogeneous Diffusion Problems Based on Infinite Bodies. Nanjing Univ. Aeronaut. Astronaut. 2009, 41, 276–280. [Google Scholar]
- Yu, H.; Sun, W.; Ma, H. Research on Theoretical Models of Chloride Ion Diffusion in Concrete II—Non-steady State Homogeneous and Non-homogeneous Diffusion Problems Based on Finite Bodies. Nanjing Univ. Aeronaut. Astronaut. 2009, 41, 408–413. [Google Scholar]
- Chen, W.; Zhang, J.; Zhang, J. A variable-order time-fractional derivative model for chloride ions sub-diffusion in concrete structures. Fract. Calc. Appl. Anal. 2013, 16, 76–92. [Google Scholar] [CrossRef]
- Lu, Z.H.; Lun, P.Y.; Li, W.; Luo, Z.; Li, Y.; Liu, P. Empirical model of corrosion rate for steel reinforced concrete structures in chloride-laden environments. Adv. Struct. Eng. 2019, 22, 223–239. [Google Scholar] [CrossRef]
- Chen, X.; Ming, Y.; Fu, F.; Chen, P. Numerical and empirical modeling for the assessment of service life of RC structures in marine environment. Int. J. Concr. Struct. Mater. 2022, 16, 11. [Google Scholar] [CrossRef]
- Mangat, P.S.; Molloy, B.T. Prediction of free chloride concentration in concrete using routine inspection data. Mag. Concr. Res. 1994, 46, 279–287. [Google Scholar] [CrossRef]
- Mangat, P.S.; Molloy, B.T. Prediction of long term chloride concentration in concrete. Mater. Struct. 1994, 27, 338–346. [Google Scholar] [CrossRef]
- Luping, T.; Gulikers, J. On the mathematics of time-dependent apparent chloride diffusion coefficient in concrete. Cem. Concr. Res. 2007, 37, 589–595. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Q.; Wang, X.; Peng, X.; Qin, F. Review of Prediction Models for Chloride Ion Concentration in Concrete Structures. Buildings 2025, 15, 149. [Google Scholar] [CrossRef]
- Ashrafian, A.; Panahi, E.; Salehi, S.; Amiri, M.J.T. On the implementation of the interpretable data-intelligence model for designing service life of structural concrete in a marine environment. Ocean. Eng. 2022, 256, 111523. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, L.; Wang, Y.; Li, Q.; Xiao, Z. Prediction model of long-term chloride diffusion into plain concrete considering the effect of the heterogeneity of materials exposed to marine tidal zone. Constr. Build. Mater. 2018, 159, 297–315. [Google Scholar] [CrossRef]
- Prieto, M.; Tanner, P.; Andrade, C. Multiple linear regression model for the assessment of bond strength in corroded and non-corroded steel bars in structural concrete. Mater. Struct. 2016, 49, 4749–4763. [Google Scholar] [CrossRef]
- Jin, R.; Chen, Q.; Soboyejo, A.B.O. Non-linear and mixed regression models in predicting sustainable concrete strength. Constr. Build. Mater. 2018, 170, 142–152. [Google Scholar] [CrossRef]
- Hanif, M.U.; Ibrahim, Z.; Ghaedi, K.; Hashim, H.; Javanmardi, A. Damage assessment of reinforced concrete structures using a model-based nonlinear approach–A comprehensive review. Constr. Build. Mater. 2018, 192, 846–865. [Google Scholar] [CrossRef]
- Atienza, D.; Larrañaga, P.; Bielza, C. Hybrid semiparametric Bayesian networks. TEST 2022, 31, 299–327. [Google Scholar] [CrossRef]
- Guo, H.; Dong, Y. Dynamic Bayesian network for durability of reinforced concrete structures in long-term environmental exposures. Eng. Fail. Anal. 2022, 142, 106821. [Google Scholar] [CrossRef]
- Guo, H.; Dong, Y.; Bastidas-Arteaga, E. Mixed Bayesian Network for reliability assessment of RC structures subjected to environmental actions. Struct. Saf. 2024, 106, 102392. [Google Scholar] [CrossRef]
- Aneja, S.; Sharma, A.; Gupta, R.; Yoo, D.Y. Bayesian regularized artificial neural network model to predict strength characteristics of fly-ash and bottom-ash based geopolymer concrete. Materials 2021, 14, 1729. [Google Scholar] [CrossRef]
- Kellouche, Y.; Ghrici, M.; Boukhatem, B. Service life prediction of fly ash concrete using an artificial neural network. Front. Struct. Civ. Eng. 2021, 15, 793–805. [Google Scholar] [CrossRef]
- Chen, L. Hybrid structured artificial network for compressive strength prediction of HPC concrete. J. Appl. Sci. Eng. 2022, 26, 989–999. [Google Scholar]
- BKA, M.A.R.; Ngamkhanong, C.; Wu, Y.; Kaewunruen, S. Recycled aggregates concrete compressive strength prediction using artificial neural networks (ANNs). Infrastructures 2021, 6, 17. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, K.; Lu, G.; Guo, W.; Liu, J.; Zhang, N.; Yang, C. Life-cycle seismic performance analysis of an offshore small-to-medium span bridge based on interpretable machine learning. In Structures; Elsevier: Amsterdam, The Netherlands, 2024; Volume 70, p. 107511. [Google Scholar]
- Wang, X.; Yang, Q.; Peng, X.; Qin, F. A review of concrete carbonation depth evaluation models. Coatings 2024, 14, 386. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Support vector machine based reliability analysis of concrete dams. Soil Dyn. Earthq. Eng. 2018, 104, 276–295. [Google Scholar] [CrossRef]
- Fan, C.L. Detection of multidamage to reinforced concrete using support vector machine-based clustering from digital images. Struct. Control. Health Monit. 2021, 28, e2841. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Kashani, A.; Arashpour, M. Chloride diffusion modeling of concrete using tree-based forest models. Struct. Concr. 2023, 24, 5614–5634. [Google Scholar] [CrossRef]
- Liu, Q.; Andersen, L.V.; Wu, M. Prediction of concrete abrasion depth and computational design optimization of concrete mixtures. Cem. Concr. Compos. 2024, 148, 105431. [Google Scholar] [CrossRef]
- Concha, N.C.; Oreta, A.W.C. Investigation of the effects of corrosion on bond strength of steel in concrete using neural network. Comput. Concr. 2021, 28, 77–91. [Google Scholar]
- Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Śliwa-Wieczorek, K.; Czarnecki, S. Application of novel machine learning techniques for predicting the surface chloride concentration in concrete containing waste material. Materials 2021, 14, 2297. [Google Scholar] [CrossRef]
- Ding, S.; Li, H.; Su, C.; Yu, J.; Jin, F. Evolutionary artificial neural networks: A review. Artif. Intell. Rev. 2013, 39, 251–260. [Google Scholar] [CrossRef]
- Rothacher, Y.; Strobl, C. Identifying informative predictor variables with random forests. J. Educ. Behav. Stat. 2024, 49, 595–629. [Google Scholar] [CrossRef]
- Karbassi, A.; Mohebi, B.; Rezaee, S.; Lestuzzi, P. Damage prediction for regular reinforced concrete buildings using the decision tree algorithm. Comput. Struct. 2014, 130, 46–56. [Google Scholar] [CrossRef]
- Ann, K.Y.; Pack, S.W.; Hwang, J.P.; Song, H.W.; Kim, S. Service life prediction of a concrete bridge structure subjected to carbonation. Constr. Build. Mater. 2010, 24, 1494–1501. [Google Scholar] [CrossRef]
- Papadakis, V.G.; Demis, S. Estimation and validation of concrete strength and service life using software packages based on predictive models. In Proceedings of the 12th International Conference on Durability of Building Materials and Components, Porto, Portugal, 12–15 April 2011. [Google Scholar]
- Xu, W.; Li, W.; Wang, D.; Ji, Y. Mechanical performance degradation investigation on FRP reinforced concrete based on neural network design method. Sci. Rep. 2024, 14, 11807. [Google Scholar] [CrossRef]
- Wang, S.; Wu, R.; Gong, F.; Xia, J.; Zhao, Y.; Zeng, B. Service life evaluation of marine concrete structures considering spatial and temporal characteristics: A framework based on multi training-MCS-NLS. Eng. Struct. 2025, 322, 119193. [Google Scholar] [CrossRef]
- Fan, J.; Zhu, H.; Yi, C.; Li, Z. Research on durability evaluation of concrete in complex attack environment. AIP Adv. 2019, 9, 115019. [Google Scholar] [CrossRef]
- Nanukuttan, S.V.; Basheer, P.A.M.; McCarter, W.J.; Tang, L.; Holmes, N.; Chrisp, T.M.; Starrs, G.; Magee, B. The performance of concrete exposed to marine environments: Predictive modelling and use of laboratory/on site test methods. Constr. Build. Mater. 2015, 93, 831–840. [Google Scholar] [CrossRef]
- Pang, L.; Li, Q. Service life prediction of RC structures in marine environment using long term chloride ingress data: Comparison between exposure trials and real structure surveys. Constr. Build. Mater. 2016, 113, 979–987. [Google Scholar] [CrossRef]
- Al-Obaidi, S.; Bamonte, P.; Luchini, M.; Mazzantini, I.; Ferrara, L. Durability-based design of structures made with ultra-high-performance/ultra-high-durability concrete in extremely aggressive scenarios: Application to a geothermal water basin case study. Infrastructures 2020, 5, 102. [Google Scholar] [CrossRef]
- Chen, S.; Duffield, C.; Miramini, S.; Raja, B.N.K.; Zhang, L. Life-cycle modelling of concrete cracking and reinforcement corrosion in concrete bridges: A case study. Eng. Struct. 2021, 237, 112143. [Google Scholar] [CrossRef]
- Sharp, M.E. Simple metrics for evaluating and conveying prognostic model performance to users with varied backgrounds. In Proceedings of the Annual Conference of the PHM Society, San Diego, CA, USA, 27 September–1 October 2013; Volume 5. [Google Scholar]
- Bennett, N.D.; Croke, B.F.W.; Guariso, G.; Guillaume, J.H.A.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.H.; Norton, J.P.; Perrin, C.; et al. Characterising performance of environmental models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
- Gupta, H.V.; Clark, M.P.; Vrugt, J.A.; Abramowitz, G.; Ye, M. Towards a comprehensive assessment of model structural adequacy. Water Resour. Res. 2012, 48, W08301. [Google Scholar] [CrossRef]
- Yu, J.; Wang, N.; Wang, M.; Zhang, J. Hou, D. Recyclable rubber-cement composites produced by interfacial strengthened strategy from polyvinyl alcohol. Constr. Build. Mater. 2020, 264, 120541. [Google Scholar] [CrossRef]
- Kostić, S.; Vasović, N.; Sunarić, D. Slope stability analysis based on experimental design. Int. J. Geomech. 2016, 16, 04016009. [Google Scholar] [CrossRef]
- Kefei, L.; Torrent, R. Analytical and Experimental Service Life Assessment of Hong Kong-Zhuhai-Macau Link; Civil Engng. Dept., Tsinghua University: Beijing, China, 2016. [Google Scholar]
- Sarmiento, S.; Thöns, S.; Gonzalez, J.; Björnsson, I.; Sas, G. Comparison and Joint Evaluation of Importance, Redundancy and Robustness Indicators Applied to Aging Prestressed Concrete Bridges. Nord. Concr. Res. 2024, 70, 147–171. [Google Scholar] [CrossRef]
- Carević, V.; Ignjatović, I. Evaluation of concrete cover depth for green concretes exposed to carbonation. Struct. Concr. 2021, 22, E1009–E1021. [Google Scholar] [CrossRef]
- Yu, B.; Ning, C.; Li, B. Probabilistic durability assessment of concrete structures in marine environments: Reliability and sensitivity analysis. China Ocean. Eng. 2017, 31, 63–73. [Google Scholar] [CrossRef]
- Strauss, A.; Vidovic, A.; Zambon, I.; Grossberger, H.; Bergmeister, K. Monitoring information and probabilistic-based prediction models for the performance assessment of concrete structures. J. Perform. Constr. Facil. 2016, 30, 04015081. [Google Scholar] [CrossRef]
- Franceschini, L.; Vecchi, F.; Belletti, B.; Andrade, C.; Peiretti, H.C. Analytical method for the evaluation of the residual service life of prestressed concrete beams subjected to corrosion deterioration. Struct. Concr. 2022, 23, 121–137. [Google Scholar] [CrossRef]
- Vishwanath, B.S.; Banerjee, S. Considering uncertainty in corrosion process to estimate life-cycle seismic vulnerability and risk of aging bridge piers. Reliab. Eng. Syst. Saf. 2023, 232, 109050. [Google Scholar] [CrossRef]
- Cho, H.K.; Lee, H.S.; Wang, X.Y.; Ismail, M.; Park, W.J. Evaluation of CO2 emission–absorption of fly-ash-blended concrete structures using cement-hydration-based carbonation model. Mater. Struct. 2015, 48, 3949–3963. [Google Scholar] [CrossRef]
- Shafikhani, M.; Chidiac, S.E. Quantification of concrete chloride diffusion coefficient—A critical review. Cem. Concr. Compos. 2019, 99, 225–250. [Google Scholar] [CrossRef]
- Liang, M.T.; Chang, J.J.; Yu, T.W. Studies of the effect of diffusion-induced chloride binding on chlorination life predictions for existing reinforced concrete bridges. J. Mar. Sci. Technol. 2012, 20, 10. [Google Scholar]
- Martın-Pérez, B.; Zibara, H.; Hooton, R.D.; Thomas, M.D.A. A study of the effect of chloride binding on service life predictions. Cem. Concr. Res. 2000, 30, 1215–1223. [Google Scholar] [CrossRef]
- Sergi, G.; Yu, S.W.; Page, C.L. Diffusion of chloride and hydroxyl ions in cementitious materials exposed to a saline environment. Mag. Concr. Res. 1992, 44, 63–69. [Google Scholar] [CrossRef]
- Xue, P.F.; Mao, D.L. Corrected diffusion model of chloride in concrete and its engineering application. Adv. Mater. Res. 2011, 189, 1886–1891. [Google Scholar] [CrossRef]
- Chen, E.; Berrocal, C.G.; Löfgren, I.; Lundgren, K. Comparison of the service life, life-cycle costs and assessment of hybrid and traditional reinforced concrete through a case study of bridge edge beams in Sweden. Struct. Infrastruct. Eng. 2022, 19, 39–57. [Google Scholar] [CrossRef]
- Yamamoto, M.; Nakarai, K.; Yoshizumi, Y.; Torrent, R. Relationship between chloride ingress and concrete cover quality of inland structures exposed to deicing salts. Case Stud. Constr. Mater. 2024, 20, e03075. [Google Scholar] [CrossRef]
- Li, J.A.; Feng, D. Fatigue life evaluation of bridge stay cables subject to monitoring traffic and considering road roughness. Eng. Struct. 2023, 293, 116572. [Google Scholar] [CrossRef]
- Fathalla, E.; Tanaka, Y.; Maekawa, K. Fatigue lifetime prediction of newly constructed RC road bridge decks. J. Adv. Concr. Technol. 2019, 17, 715–727. [Google Scholar] [CrossRef]
- Balestra, C.E.T.; Reichert, T.A.; Vizzotto, A.L.P.; Pansera, W.A.; Savaris, G. General model for service life analysis of reinforced concrete structures subject to chloride penetration. Constr. Build. Mater. 2021, 305, 124727. [Google Scholar] [CrossRef]
- Shreir, L.L. (Ed.) Corrosion: Metal/Environment Reactions; Newnes-Butterworths: London, UK, 1976. [Google Scholar]
- Li, C.Q.; Mahmoodian, M. Risk based service life prediction of underground cast iron pipes subjected to corrosion. Reliab. Eng. Syst. Saf. 2013, 119, 102–108. [Google Scholar] [CrossRef]
- Dasar, A.; Patah, D.; Hamada, H.; Yamamoto, D.; Sagawa, Y. Life performance of 40-year-old RC beams with different concrete covers and bar diameters in natural corrosion environments. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 46, pp. 2031–2046. [Google Scholar]
- Chen, D.; Mei, G.; Xiao, L. Analysis of chloride invasion process in undersea RC circular lined tunnel based on nonlinear ADE theory: Analytical solution, numerical verification and experimental prediction. Constr. Build. Mater. 2022, 343, 128140. [Google Scholar] [CrossRef]
- Keßler, S. Probabilistic corrosion condition assessment of a tunnel structure. Struct. Concr. 2020, 21, 1345–1355. [Google Scholar] [CrossRef]
- Meng, T.; Yu, H.; Zhao, Y.; Ruan, S. Strength/Service life-oriented environmental assessment of normal and recycled concrete with nano-SiO2 in a natural and a marine environment: A pioneer case study in Zhejiang Province. J. Build. Eng. 2023, 64, 105623. [Google Scholar] [CrossRef]
- Canestro, E.; Strauss, A.; Sousa, H. Multiscale modelling of the long-term performance of prestressed concrete structures–Case studies on T-Girder beams. Eng. Struct. 2021, 231, 111761. [Google Scholar] [CrossRef]
- Zheng, L.; Pornsing, C. Prediction of airport road service life based on concrete structure characteristics. Case Stud. Constr. Mater. 2024, 20, e02814. [Google Scholar] [CrossRef]
- Mortagi, M.; Ghosh, J. Climate change considerations for seismic vulnerability assessment of aging highway bridges. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2020, 6, 04020005. [Google Scholar] [CrossRef]
- Jeon, C.H.; Kwon, T.H.; Kim, J.; Jung, K.S.; Park, K.T. Health Index-Based Maintenance of Prestressed Concrete Bridges Considering Building Information Modeling Application. Buildings 2024, 14, 4032. [Google Scholar] [CrossRef]
- Ying, J.; Chen, W.; Wang, W.; Tian, Z.; Liang, L.; Chen, B. Multiscale study on high-temperature mechanical behaviors and durability of recycled concrete reinforced by polycarboxylate-modified 3D porous graphene. Constr. Build. Mater. 2024, 450, 138676. [Google Scholar] [CrossRef]
- Kaveh, H.; Alhajj, R. Recent advances in crack detection technologies for structures: A survey of 2022-2023 literature. Front. Built Environ. 2024, 10, 1321634. [Google Scholar] [CrossRef]
- Wang, Z.; Maekawa, K. Lifetime assessment of structural concrete–multi-scale integrated hygro-thermal-chemo-electrical-mechanistic approach and statistical evaluation. Struct. Infrastruct. Eng. 2022, 18, 933–949. [Google Scholar] [CrossRef]
- Azimi, M.; Eslamlou, A.D.; Pekcan, G. Data-driven structural health monitoring and damage detection through deep learning: State-of-the-art review. Sensors 2020, 20, 2778. [Google Scholar] [CrossRef] [PubMed]



| Corrosion Product | Conditions for Corrosion Occurrence | Effect on Concrete Cover | Effect on Corrosion Process | Relative Effect During Continuous Corrosion Process |
|---|---|---|---|---|
| Carbonate Products [20] | Reaction of carbon dioxide with calcium hydroxide, forming calcium carbonate | Reduces the alkalinity of the concrete, compromising the concrete cover of the reinforcement | Lowers the pH of concrete; the steel protection layer gradually fails, promoting steel corrosion | Moderate |
| Chloride Products [21] | Chloride ions penetrate, particularly in marine or high-salinity environments | Increases the permeability of concrete, diminishing its protective capacity | Directly breaks down the steel passivation layer, initiates corrosion, causes pitting (localized corrosion) | High |
| Sulfate Products [22] | Sulfates react with cement hydration products to form expansive compounds | Causes expansion and cracking, damaging the concrete structure | Expanding reactions create cracks, increasing permeability and accelerating corrosion | Low |
| Corrosion rate at 40 mm cover (µA/cm2) | |||
| Cement Type | Crack width | Percentage change | |
| 0.2 mm | 0.7 mm | ||
| Ordinary Portland Cement | 1.20 | 1.48 | 23% |
| 7% Silica Fume Blended Cement | 0.59 | 1.03 | 75% |
| 30% Fly Ash Blended Cement | 0.39 | 0.50 | 28% |
| 50% Ground Granulated Blast Furnace Slag Blended Cement | 0.35 | 0.53 | 51% |
| Corrosion rate at 20 mm cover (µA/cm2) | |||
| Cement Type | Crack width | Percentage change | |
| 0.2 mm | 0.7 mm | ||
| Ordinary Portland Cement | 2.65 | 3.23 | 22% |
| 7% Silica Fume Blended Cement | 0.67 | 1.12 | 67% |
| 30% Fly Ash Blended Cement | 0.64 | 0.71 | 11% |
| 50% Ground Granulated Blast Furnace Slag Blended Cement | 0.39 | 0. 51 | 31% |
| Carbonation Conditions | Statistical Indicators | Fick Model | New Model |
|---|---|---|---|
| 20 °C Carbonation | Mean error value (%) | 1.80% | 0.78% |
| Standard deviation σ (%) | 1.91% | 0.35% | |
| 30 °C Carbonation | Mean error value (%) | 6.67% | 2.67% |
| Standard deviation σ (%) | 7.70% | 3.39% |
| Model | Disadvantages | Advantages |
|---|---|---|
| The model in reference [45]: : chloride concentration in the pore fluid at depth from the concrete surface after time of exposure to a chloride environment; : free chloride concentration at the concrete surface; erf: error function; : the coefficient of Cl− diffusion. | 1. Assumes chloride diffusion is uniform, ignoring the pores and cracks in concrete, which affects accuracy. 2. Assumes the diffusion coefficient remains constant, whereas it actually changes with time and environmental conditions. 3. In extreme environments such as high or low temperatures, the model’s applicability and accuracy decrease. | 1. The formula is based on Fick’s second law, with a simple structure that is easy to apply. 2. It is consistent with experimental data for short-term and medium-term exposures (90 to 520 days). 3. Suitable for different types of concrete and exposure environments. |
| The model in reference [46]: : chloride concentration at distance x and time ; : chloride concentration at the concrete surface; erf: error function; : the initial chloride diffusion coefficient; m: the empirical coefficient that represents the time-dependent variation of the diffusion coefficient. | 1. The m coefficient depends on the mix ratio and environment, requiring calibration. 2. Extensive experimental data are needed for validation and adjustment. 3. Long-term predictions (e.g., decades) face uncertainties regarding diffusion coefficient behavior. | 1. Incorporating time-dependent diffusion coefficients enhances long-term chloride concentration predictions. 2. Predictions align well with actual data, especially in marine environments. 3. Suitable for various concrete mixes and environmental conditions. |
| The model in reference [47]: : chloride concentration inside the concrete; : chloride concentration at the surface of the concrete; : depth of chloride penetration; : exposure time; : initial chloride diffusion coefficient; : age factor representing how diffusion changes with concrete age; : initial exposure time (when the concrete starts being exposed); : reference time for the initial measurements. | 1. Assumes chloride binding is time-independent and linear, which may not reflect actual behavior. 2. When the age factor is high, it may underestimate chloride penetration depth, leading to overly conservative predictions. 3. For short-term exposure, the model may overestimate the diffusion coefficient, leading to inaccurate predictions. | 1. Introduces a time-dependent diffusion coefficient, more accurately reflecting the change in chloride diffusion over time. 2. Provides a more accurate prediction of chloride penetration, especially under long-term exposure conditions like marine environments. 3. Aligns better with measured chloride penetration profiles in real-world applications. |
| The model in reference [48]: : the chloride ion concentration at position and time ; : the stabilized surface chloride ion concentration; : the coefficient representing the influence of water–cement ratio on the stabilized surface chloride ion concentration; : the impact of sulfate ions on the chloride ion concentration on the concrete surface; erf: error function; : the chloride diffusion coefficient of the concrete measured at the hydration age. | 1. The model features complex mathematical expressions, requires large computational resources, and is highly sensitive to input parameters, requiring precise measurements. 2. In real marine environments, the diffusion coefficient undergoes dynamic changes due to the inhomogeneity and variability of the medium, and the boundary conditions are uncertain, which adds challenges to its field application. | 1. The model is particularly suitable for describing diffusion processes involving dynamic changes in both time and space variables. 2. It can be applied to diffusion processes under complex boundary conditions, taking into account the changes in substances over time. |
| Reference | Type | Advantages | Disadvantages | Applicable Conditions |
|---|---|---|---|---|
| Reference [70] | Neural Networks | Strong adaptability, no gradient information required, optimization potential | Sensitive to network architecture, difficult to optimize, risk of overfitting | Complex and nonlinear problems with large datasets |
| Reference [65] | SVMs | High prediction accuracy, adaptable to complex problems, strong optimization capability | Requires many parameters, computationally complex | Small high-dimensional datasets |
| Reference [71] | Random Forests | Handles high-dimensional data, easy to apply | Lack of interpretability, long computation time | Exploratory analysis when relationships are unclear |
| Reference [72] | Decision Trees | Can handle multiple data types, requires little data preprocessing | Instability, prone to bias | Data need clear classification, applicable to structured data |
| Context | Model Prediction Accuracy | Importance of Field Data | |
|---|---|---|---|
| Reference [78] | Field validation of chloride ion diffusion in UK harbors | At 1.17 and 6.17 years, model predictions closely matched the monitoring data. At year 18, the model slightly underestimated chloride ion diffusion at deeper layers, with about 10% error. | Highlights the role of field data in validating the model’s performance over time, showing discrepancies at deeper layers at later years. |
| Reference [79] | Study of chloride ion diffusion coefficients in aging structures along the South China Sea | For the HPW6 structure, the measured chloride ion surface concentration was 1.78%, while the model predicted 4.13%. | Demonstrates how field data from actual aging structures provides critical validation for model predictions, emphasizing real-world applications. |
| Reference [80] | Geothermal power plant concrete exposed to chloride- and sulfate-rich geothermal water | Field data show that, after 18 years, chloride ions had penetrated into deeper layers in normal concrete and began corroding the reinforcement; ultra-high-durability concrete performed better at the same time, although the diffusion occurred slightly earlier, but the overall trend was consistent with the model. | Field data confirmed that the actual chloride diffusion rate was faster than predicted in normal concrete, validating the importance of monitoring for accurate durability modeling. |
| Reference [81] | Lifecycle modeling of concrete cracking and reinforcement corrosion in Changfeng Creek Bridge, China | The study predicts, through lifecycle modeling, that reducing the maintenance cycle (e.g., shortening it from 12 years to 4 years) can significantly extend the service life of the bridge. Field data from regular monitoring revealed an extension of approximately 15 years. | This case highlights the importance of field monitoring in ensuring the long-term durability of infrastructure and optimizing models. |
| Model Type | Advantages | Disadvantages | Applicable Scenarios |
|---|---|---|---|
| Physical Models | Strong theoretical foundation, capable of simulating long-term degradation processes, incorporates environmental factors | Computationally complex, requires accurate data, limited applicability | Suitable for simpler controlled environments, such as laboratory settings or less complex engineering projects |
| Empirical Models | Simple, fast, cost-effective, highly adaptable | Limited precision, reliant on past data, not applicable to all situations | Ideal for scenarios with available data, especially for quick preliminary assessments |
| Statistical Models | Based on data-driven predictions, adaptable to complex environments, capable of handling uncertainty | Requires high-quality data, difficult to interpret | Best for data-rich complex environments with numerous variables and uncertainties |
| Machine Learning Models | High accuracy, capable of handling complex data and problems, real-time prediction updates | Requires large amounts of data and computational resources, difficult to interpret model mechanisms | Best suited for environments that require high-precision predictions, real-time monitoring, and substantial data support |
| Hybrid Models | Strong theoretical foundation, capable of simulating long-term degradation processes, incorporates environmental factors | Complex models that require multidisciplinary knowledge for integration | Ideal for engineering projects that need to consider multiple factors, complex structures, or dynamic environments |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, L.; Peng, X.; Yang, Q.; Xia, K.; Xu, B. Review of Research on Prediction Models for Residual Life of Concrete Structures. Coatings 2025, 15, 693. https://doi.org/10.3390/coatings15060693
Qi L, Peng X, Yang Q, Xia K, Xu B. Review of Research on Prediction Models for Residual Life of Concrete Structures. Coatings. 2025; 15(6):693. https://doi.org/10.3390/coatings15060693
Chicago/Turabian StyleQi, Linyuan, Xi Peng, Qiuwei Yang, Kangshuo Xia, and Bin Xu. 2025. "Review of Research on Prediction Models for Residual Life of Concrete Structures" Coatings 15, no. 6: 693. https://doi.org/10.3390/coatings15060693
APA StyleQi, L., Peng, X., Yang, Q., Xia, K., & Xu, B. (2025). Review of Research on Prediction Models for Residual Life of Concrete Structures. Coatings, 15(6), 693. https://doi.org/10.3390/coatings15060693








