Composition Optimization of Coating Machine Oven Manufacturing Services Based on Improved Sparrow Search Algorithm

Abstract

Aiming at the problem of the low collaborative efficiency of outsourced processing of coating machine oven parts under the network collaborative manufacturing mode, this paper proposes a composition optimization method for coating machine oven-manufacturing services based on an improved sparrow search algorithm. We establish a framework for the service composition optimization problem on the oven manufacturing service platform; complete an evaluation of the manufacturing service quality of service indicators (QoS) and energy consumption indicators; construct a dual-objective service composition optimization mathematical model considering the QoS and energy consumption indicators; and embed the Tent chaotic mapping, elite reverse learning, and Lévy flight improvement differential evolution strategies into the sparrow search algorithm. We named this algorithm the LCSSA_DE algorithm, using it to solve the mathematical model of the manufacturing service combination problem of coating machine ovens, and obtain the optimal manufacturing service combination recommendation scheme. The experimental results demonstrate that this algorithm can effectively improve the convergence speed compared with the suboptimal multi-objective artificial vulture optimization algorithm (MOAVOA), with the average convergence time improved by 7.26%, avoiding falling into the local optimum during the search, while 69%–77% of the test points are more in line with the preference criteria of the Pareto frontier, and can be adapted to the optimization of the coating machine oven manufacturing service composition optimization problem at different scales.

1. Introduction

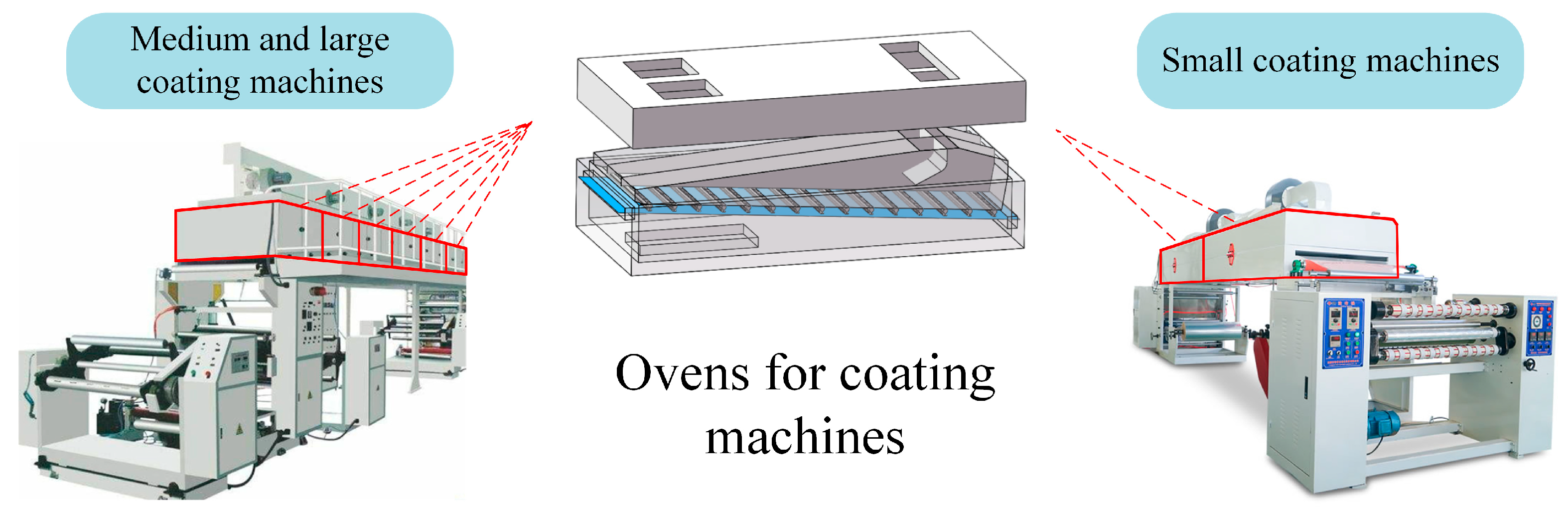
Coating machines are important pieces of equipment for packaging printing, new energy, and other industries; the overall coating machine market size in 2024 reached USD 10 billion, and the global market is predicted to reach USD 15 billion in 2025. The oven is a core component of the drying system of coating machines (shown in Figure 1), the drying effect of which has a direct impact on the quality of the final printed product. However, the current production and assembly process of these ovens still has problems such as resources are overly dispersed, poor industrial synergy, and a low efficiency of manufacturing resource utilization. In order to solve this problem, new networked manufacturing modes based on the Internet, such as computer-integrated manufacturing, manufacturing grids, agile manufacturing, networked manufacturing, cloud manufacturing, etc., have been continuously proposed, adopting crowdsourcing and utilizing networked manufacturing service synergy platforms to achieve the optimal allocation of oven manufacturing services with the industrial agglomeration of coating equipment manufacturing, which greatly improves the efficiency of the synergies between industrial chains and shortens the oven processing production cycle.

In the crowdsourcing manufacturing environment, manufacturing service combinations are the main routes of oven manufacturing. Manufacturing service combination optimization is a nondeterministic polynomial problem, which needs to take into account the influence of both functional and nonfunctional factors. Guo et al. [1] proposed a comprehensive composition optimization framework, which converts three interrelated optimization models into a Karush–Kuhn–Tucker condition-based mathematical planning problem with equilibrium constraints, which effectively optimizes the operation of networked IDC. Li et al. [2] proposed a matching method based on Markov decision process and cross-entropy for the demand problem of complex machine tools in a single collaborative manufacturing task to achieve the matching of manufacturing tasks to manufacturing services. Xiao et al. [3] proposed a decision-making method for accurately matching manufacturing resources based on multidimensional information fusion. Zeng et al. [4] proposed an optimization algorithm named improved-TC to solve the problems of the slow convergence and instability of existing methods in large-scale environments. Liu et al. [5] proposed an optimal selection method for manufacturing resources in roll-guided clouds based on a composite algorithm of scalable clustering and the fuzzy analytic hierarchy process (FAHP), which utilizes an improved extended clustering algorithm combined with the FAHP to achieve optimal co-manufacturing resource selection for optimal guide-roll production equipment. Tabalvandani et al. [6] proposed two new reliability and cost models to formulate the web-service combination problem as a multi-objective optimization problem, proposing a multi-objective particle swarm optimization algorithm to solve the composition problem in a large search space in a multi-cloud environment (MCE). Shi et al. [7] achieved the optimal selection of a set of manufacturing resources for sewing machine housings using an extended comprehensive evaluation method based on the ontological modeling of manufacturing resources. However, a composition optimization method for manufacturing services for coating machine ovens has not been proposed yet, and this paper addresses this, carrying out the relevant research.

In terms of the construction of a service composition optimization model, Jing et al. [8] developed a QoS scheduling model incorporating cloud characteristics to ensure that failures can be tolerated during task execution. Li et al. [9] proposed a topology-aware neural model for collaborative QoS prediction to make accurate QoS predictions. Zhang et al. [10] introduced multi-stage multiscale feature fusion with individual evaluations to a deep learning model for accurate QoS prediction. Yu et al. [11] developed a prediction model using the similarity property of temporal QoS values, which integrates the attributes of QoS and candidate services to make the prediction of QoS values more accurate. Shi et al. [12] proposed a bi-layer planning-based service composition optimization method, which proposed a bi-objective model based on QoS and flexibility, and applied this model in the field of sewing-machine housing parts manufacturing. Zhao et al. [13] used a collaborative filtering algorithm to compute the missing QoS values of candidate manufacturing services and used a composition optimization model with QoS constraints to generate optimal service combination recommendations. Song et al. [14] proposed a parameter estimation method for manufacturing service uncertainty models based on Gaussian mixture regression at edge measurement, which can adaptively model service uncertainty. However, most current models for manufacturing service composition optimization problems only consider QoS indicators such as time, cost, and quality, and do not take into account the energy consumption attribute that is currently valued by most service demanders.

In the selection of manufacturing service composition-optimization decisions, meta-heuristic algorithms are widely used to solve manufacturing service composition optimization problems, typical algorithms are gray wolf optimization (GWO) [15], dung beetle optimization (DBO) [16], cuckoo search algorithm (CS) [17], particle swarm optimization (PSO) [18], balanced composite motion optimization (BCMO) [19], and sparrow search algorithm (SSA) [20], and in terms of the recent use of meta-heuristics, Kumar et al. [21] applied the BCMO algorithm for day-ahead cost-based generation scheduling in a multi-power MG to enable microgrids to operate in a cost-effective manner. Li et al. [22] proposed an enhanced dung beetle optimization for nonlinear optimization problems with multiple constraints in the manufacturing industry, and the experiments showed that the algorithm has strong optimization accuracy and optimization stability. Tuan et al. [23] applied the BCMO algorithm to the prediction of landslides by proposing and evaluating a new method called BCMO-DeepNeuralNets, which leads to a more accurate understanding of the associated risks. These algorithms have their own advantages and disadvantages; taking BCMO algorithm as an example, it has the advantages of simple control parameters, strong adaptability, and the ability to simultaneously take into account the global search and local search, etc. However, it still has the problems of slow convergence speed, high computational complexity, and sensitivity to the initial population when dealing with complex problems and large-scale high-dimensional optimization problems. As for meta-heuristic algorithm improvement, Wang et al. [24] proposed a hybrid algorithm named bee colony simplex for the CSCO problem, which applies global best bootstrap and chaotic search strategies to avoid local optimization. Mirjalili et al. [25] proposed a multi-objective grey wolf optimization algorithm (MOGWO) for multi-objective problems and proved the superiority of the proposed algorithm, while Wang et al. [26] proposed a multi-objective sparrow search algorithm (MOSSA) and proved that the MOSSA algorithm demonstrates a good performance in solving multi-objective problems. The SSA algorithm, with its unique search mechanism, has shown a good performance on classical test functions for low-dimensional optimization problems, which are widely used in intelligent path planning for shop floor drones [27], optimal control of chilled water systems [28], node localization problems for heterogeneous wireless sensor networks [29], etc. The SSA algorithm provides new ideas for solving the service composition optimization problem of coating machine ovens, but it still faces dilemmas such as fast convergence and a tendency to fall into the local optimization.

Although there is a large amount of theoretical support for the construction of manufacturing service composition-optimization models and manufacturing service composition-preference decisions, there is still less research on manufacturing service composition optimization for coating machine ovens. In summary, the following deficiencies remain in the composition optimization of coating machine-oven parts manufacturing services:

• Most manufacturing service composition-optimization methods only consider QoS indicators such as time, cost, and quality, and do not take into account the energy consumption attributes valued by service demanders.
• Many meta-heuristic algorithms have insufficient optimization-seeking ability in solving the service composition-optimization problem and are prone to fall into local optimums, resulting in the less precise selection of the final service portfolio.

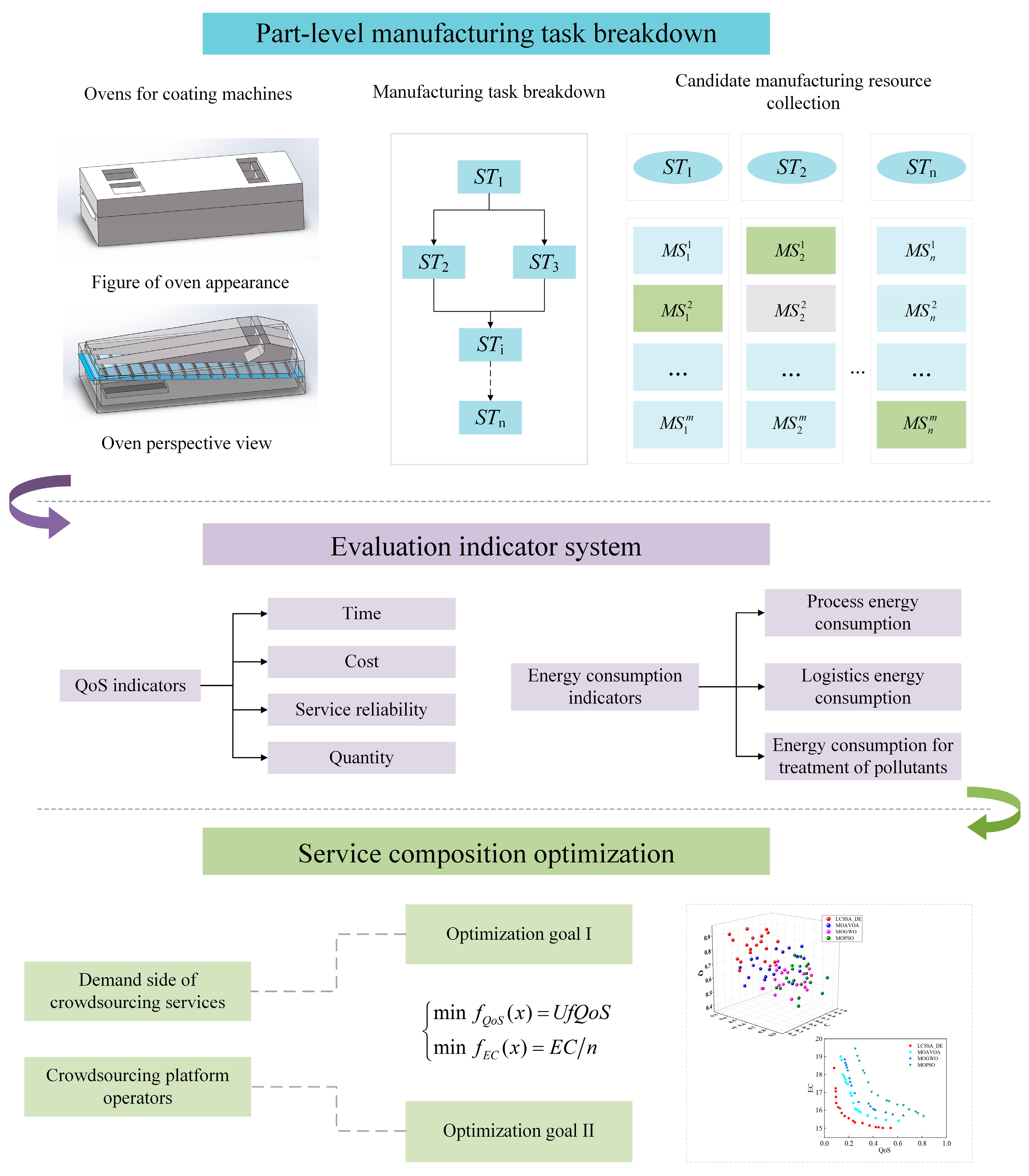
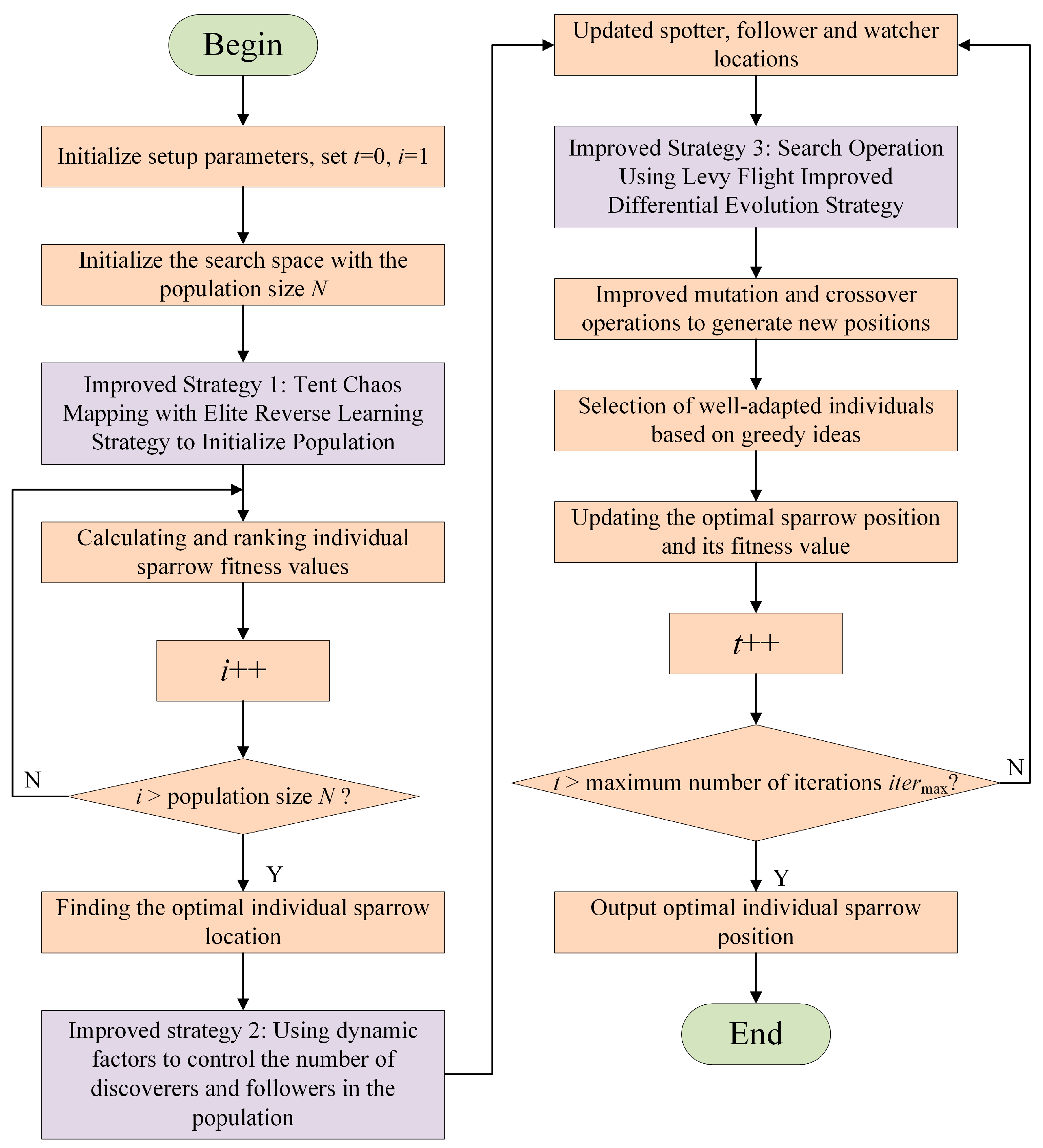
To this end, this paper proposes a composition optimization method for coating machine-oven manufacturing services based on the improved sparrow search algorithm, and the specific workflow is shown in Figure 2.

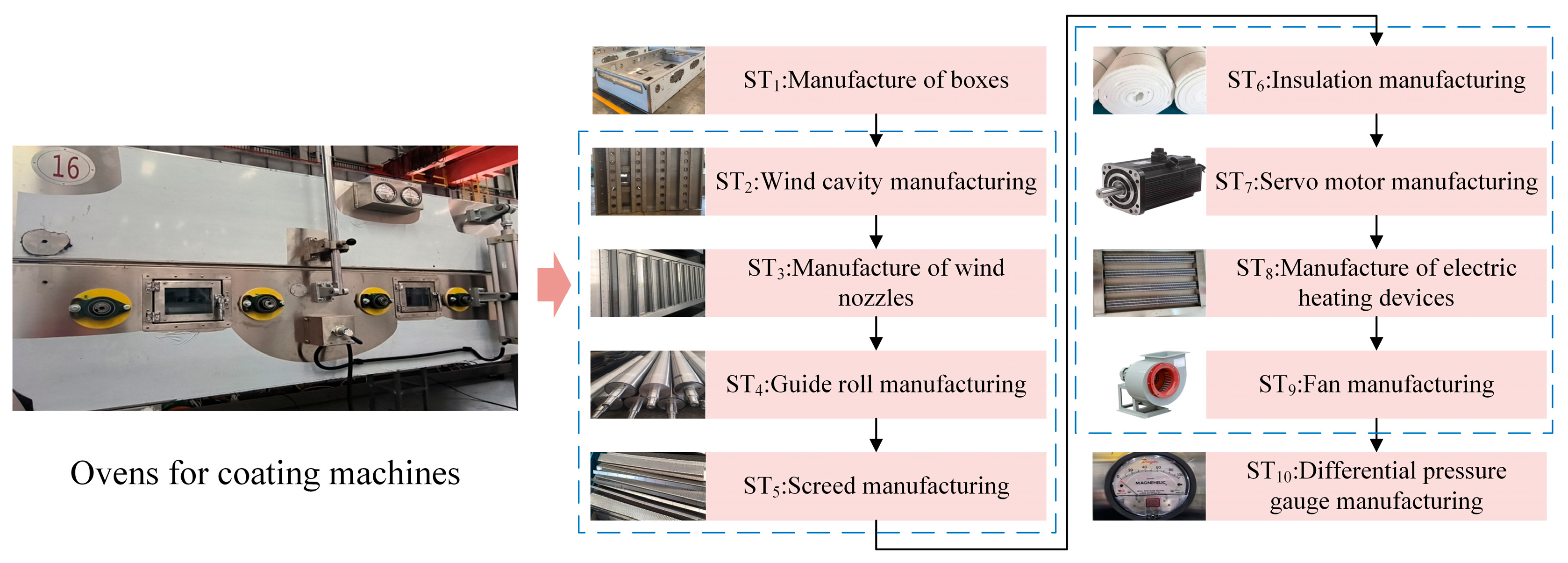
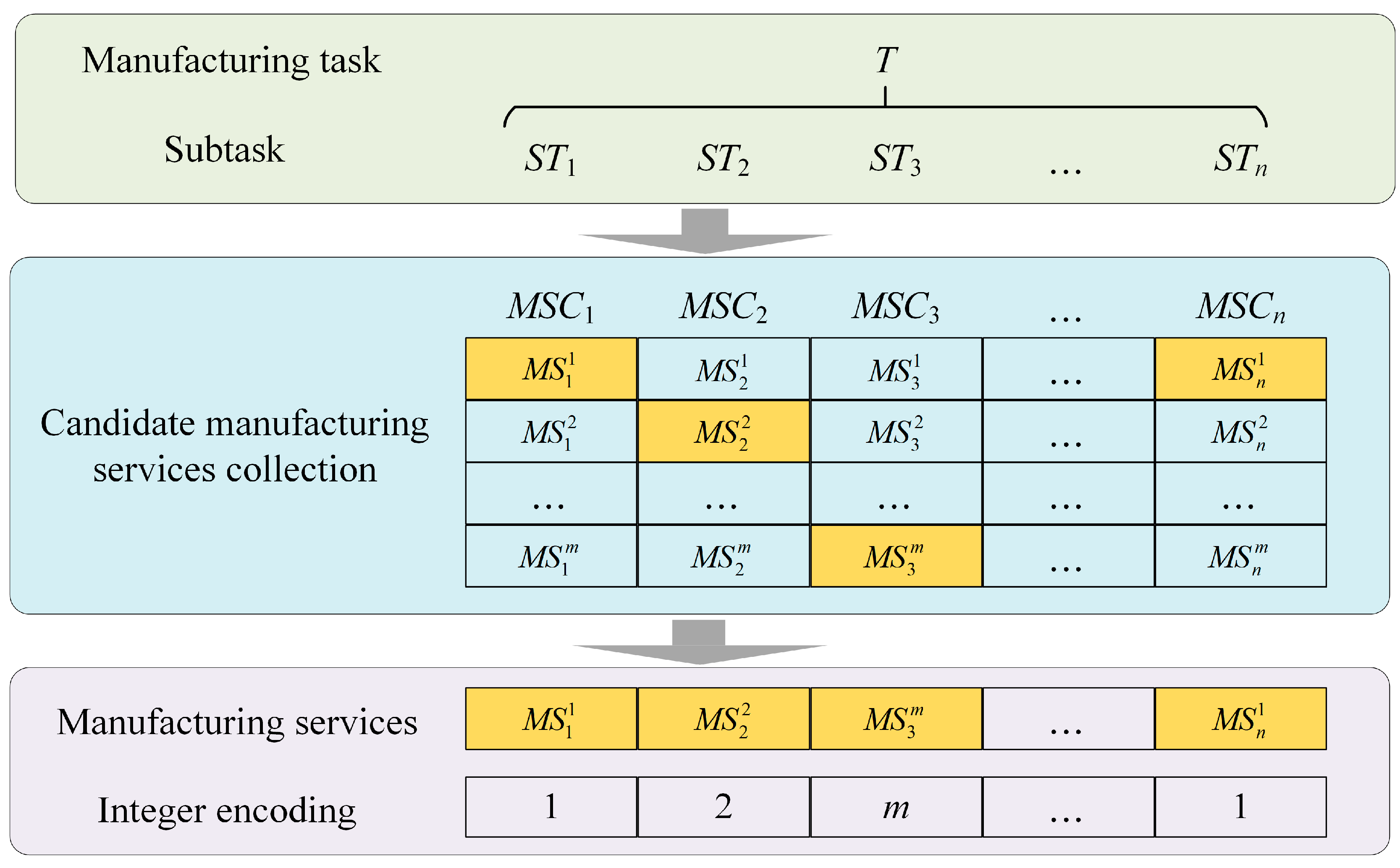
• Based on the actual production research, the service-optimization problem framework in the oven-crowdsourcing manufacturing platform is identified to understand the subtasks of coating machine-oven parts manufacturing.
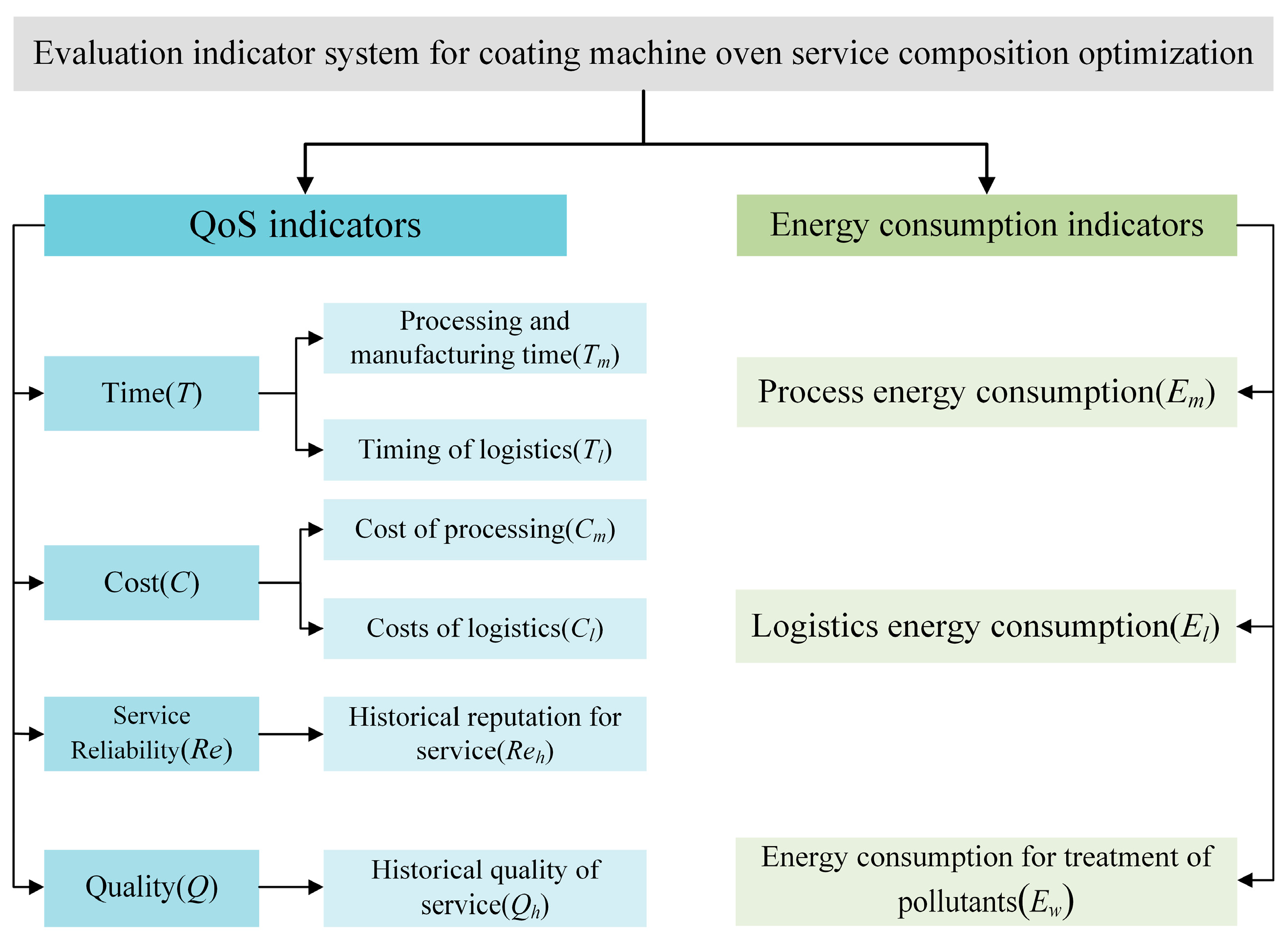
• Evaluation of service quality indicators QoS and energy consumption indicators of manufacturing services is completed, and a mathematical model of dual-objective service composition optimization considering QoS and energy consumption indicators is established.
• L in the LCSSA_DE algorithm denotes the Lévy flight strategy, C denotes the chaotic mapping strategy, and DE denotes the differential evolution strategy; the algorithm is used to solve the mathematical model of this service composition optimization problem and to obtain the optimal manufacturing service combination scheme.

The experimental results demonstrate that the LCSSA_DE algorithm has lower adaptation compared to the remaining three compared algorithms and the average convergence time at the test scale is improved by 7.26% compared to the suboptimal algorithm; meanwhile, the Pareto front of the LCSSA_DE algorithm is more in line with the preference criteria for modeling, demonstrates better stability across multiple test functions, and has advantages in the large-scale scaling problem.

2. Materials and Methods

2.1. Materials

In this paper, the classic coating machine oven is taken as the research object, and the manufacturing task of the coating machine oven is split into sub-tasks at the part level. Through the actual production research, the manufacturing process of the coating machine oven can be divided into box manufacturing, air cavity manufacturing, air nozzle manufacturing, guide roller manufacturing, air leveling plate manufacturing, insulation layer manufacturing, electric heating device manufacturing, servo motor manufacturing, fan manufacturing, and differential pressure gauge manufacturing, the manufacturing process is shown in Figure 3, in which the blue dashed box in the parts of the sub-tasks can be categorized as the same component.

2.2. A Framework for the Oven Crowdsourcing Manufacturing Service Composition Optimization Problem

In the crowdsourcing manufacturing mode, the production of the oven can be split into part-level manufacturing services in the form of a combination, the crowdsourcing platform receives the demand-side manufacturing requirements issued by the demand side, the demand will be transformed into the corresponding part manufacturing sub-tasks, which can be completed independently by a manufacturing resource, but also by a combination of multiple manufacturing resources to complete. Subsequently, the manufacturing resources provided by the service provider that meet the criteria are screened out and integrated, so as to obtain the optimal manufacturing service combination that meets the expectations, and the specific process is shown in Figure 4.

• Completion of coating machine oven part-level manufacturing sub-task decomposition: In the oven crowdsourcing manufacturing service platform, the oven manufacturing task T_h submitted by the contractor can be decomposed into n oven crowdsourcing manufacturing sub-tasks ST, and each ST corresponds to a collection of candidate manufacturing services that can complete the sub-task. For the sake of calculation convenience, it is assumed that the number of manufacturing services in each collection of candidate services is m. Selecting a manufacturing service from each collection of candidate manufacturing services can complete the oven manufacturing task. Select one manufacturing service from each candidate manufacturing service set to form a manufacturing service combination to complete the oven manufacturing task. The mapping relationship between sub-tasks and candidate manufacturing service sets is shown in Equation (1), where CMSS represents the set of candidate manufacturing services corresponding to ST, MS is the manufacturing service, and MSC is the set of manufacturing services to accomplish the complete oven manufacturing task T_h.

$$\begin{gathered} T_h=\left[\begin{array}{c}S{T}_1\\ S{T}_2\\ ⋮\\ S{T}_n\end{array}\right]\to \left[\begin{array}{c}CMS{S}_1\\ CMS{S}_2\\ ⋮\\ CMS{S}_n\end{array}\right]=\left[\begin{array}{cccc}M{S}_1^1& M{S}_1^2& \dots & M{S}_1^m\\ M{S}_2^1& M{S}_2^2& \dots & M{S}_2^m\\ ⋮& ⋮& \ddots & ⋮\\ M{S}_n^1& M{S}_n^2& \dots & M{S}_n^m\end{array}\right] \\ MSC=\left[\begin{array}{cccccc}M{S}_1^1& M{S}_2^1& \dots & M{S}_3^1& \dots & M{S}_n^1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\end{array}\right] \end{gathered}$$

(1)

2.

Construct the evaluation indicator system for the composition optimization of the coating machine oven: Constructing a reasonable and comprehensive evaluation indicator system can optimize the resource allocation more effectively. The composition-optimization evaluation indicator system constructed in this paper takes into account the time, cost, quality, and service reliability indicators that the service demand side, service provider, and crowdsourcing platform side are concerned about, and at the same time, it takes into account the energy consumption indicators of the oven manufacturing process, based on which it constructs a dual-objective service composition optimization model of coating machine oven QoS and energy consumption indicators.

3.

Manufacturing service composition optimization method: Manufacturing resources are combined to complete the oven manufacturing task, using the improved sparrow search algorithm LCSSA_DE to solve the service composition optimization model, to obtain the optimal manufacturing service-composition scheme.

2.3. Oven Service Portfolio Evaluation Indicator System

The participants in the collaborative manufacturing of the oven include the manufacturing service demand side, the manufacturing service provider, and the collaborative platform operator, and the common interests of the three parties need to be considered in the optimization of the manufacturing service portfolio of the oven; at the same time, the green and low-carbon aspects have become an important factor in the selection of products. Therefore, this paper divides the evaluation indicator system into two dimensions: QoS indicators and energy consumption indicators, and the established evaluation indicator system for the service portfolio of coating machine oven is shown in Figure 5.

The QoS indicators of the oven service portfolio evaluation index system include time T, cost C, service reliability Re, and quality Q. The time indicators include processing time T_m and logistics time T_l; the cost indicators include processing cost C_m and logistics cost C_l; the service reliability indicators are expressed by the historical word of mouth of the manufacturing service, and the quality indicators are the historical service quality of the manufacturing service. The energy consumption indicator EC includes processing energy consumption E_m, logistics energy consumption E_l, and pollutant treatment energy consumption E_w.

2.4. A Dual-Objective Service Composition Optimization Model Considering QoS Indicators and Energy Consumption Indicators

The attribute values of QoS need to be normalized first. According to the actual meaning represented by the indicators, QoS indicators can be classified into positive and negative attribute indicators; among the said indicators, service reliability Re and quality Q belong to positive attribute indicators, and time T and cost C belong to school-level attribute indicators. The calculation Formula (2) for the normalization process is as follows:

$$\overline{q_k}=\left\{\begin{array}{l}{\displaystyle \frac{q^k-q_{\min }^k}{q_{\max }^k-q_{\min }^k}},\mathrm{if}{q}_k\mathrm{is}\mathrm{a}\mathrm{positive}\mathrm{attribute}\\ {\displaystyle \frac{q_{\max }^k-q^k}{q_{\max }^k-q_{\min }^k}},\mathrm{if}{q}_k\mathrm{is}\mathrm{a}\mathrm{negative}\mathrm{attribute}\end{array}\right.$$

(2)

After completing the selection of service portfolio attribute indicators, it is necessary to calculate the values of each attribute of the complete service portfolio. Based on the relational characteristics of manufacturing service combinations, manufacturing service combinations can be categorized into two forms: tandem-structure manufacturing service combinations and hybrid-structure manufacturing service combinations. It is worth noting that any hybrid structure can be deconstructed into tandem primitives by the structural normalization method; on this basis, this paper constructs a unified QoS aggregation calculation framework for the tandem model, and the aggregation formula of each QoS indicator in tandem mode is as follows:

• Time T, the accumulation operation is performed, and the aggregation formula is shown in Equation (3):

  $$T={\displaystyle \sum _{i=1}^n{q}^T}\left(M{S}_i\right)/n$$

  (3)
• Cost C, perform the cumulative operation and the aggregation formula is shown in Equation (4):

  $$C={\displaystyle \sum _{i=1}^n{q}^C}\left(M{S}_i\right)/n$$

  (4)
• The service reliability Re performs the cumulative multiplication operation and the aggregation formula is shown in Equation (5):

  $$Re={\displaystyle \sum _{i=1}^n{q}^{Re}}\left(M{S}_i\right)$$

  (5)
• The mass Q performs the accumulation operation and the aggregation formula is shown in Equation (6):

  $$Q={\displaystyle \sum _{i=1}^n{q}^Q}\left(M{S}_i\right)/n$$

  (6)

In order to ensure the consistency of the overall QoS utility value, the service reliability and quality attributes are processed to ensure that it is better when the QoS utility value is smaller, and the resulting QoS indicator for the manufacturing service portfolio is calculated as shown in Equation (7):

$$UfQoS={\displaystyle \sum _{k=1}^4{\omega }_k}{Q}_k\left(\left\{{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^{m}M}}{S}_{i,j}\right\}\right)={\omega }_1\times \overline{T}+{\omega }_2\times \overline{C}+{\omega }_3\times (1-\overline{Re})+{\omega }_4\times (1-\overline{Q})$$

(7)

where ω₁, ω₂, ω₃, and ω₄ are the weights of time, cost, service reliability, and quality, respectively, and ω₁, ω₂, ω₃, and ω₄ ∈ [0, 1] and ω₁ + ω₂ + ω₃ + ω₄ = 1. It is believed that the weights of cost and quality among the four indicators are relatively high after communicating with the related enterprises, so ω₁ = 0.2, ω₂ = 0.3, ω₃ = 0.2, ω₄ = 0.3 are taken.

Under the consistency criterion that the smaller the utility value is, the better the service combination is, the constraints on the QoS value of the manufacturing service combination are as follows: the total time is less than the maximum limit of the service combination allowed by the service demander in terms of time Tmax, the total cost is less than the maximum limit of the service combination allowed by the service demander in terms of cost Cmax, the reliability of the service is greater than the lowest level of the historical reliability Remin, and the quality is greater than the historical minimum level of quality Qmin. In summary, the objective function of the oven QoS indicator is shown in Equation (8):

$$\left\{\begin{array}{l}\min f_{QoS}(x)=UfQoS\\ s.t.\hspace{0.17em}\hspace{0.17em}\overline{T}\le {\overline{T}}_{\max }\\ \hspace{1em}\hspace{1em}\overline{C}\le {\overline{C}}_{\max }\\ \hspace{1em}\hspace{1em}\overline{Re}\ge {\overline{Re}}_{\min }\\ \hspace{1em}\hspace{1em}\overline{Q}\ge {\overline{Q}}_{\min }\end{array}\right.$$

(8)

The formula for calculating the energy consumption indicator for the resulting manufacturing service portfolio is shown in Equation (9):

$$EC=E_m+E_l+E_w={\displaystyle \sum _{i=1}^n{e}_i^m\cdot t_i^m+e_i^l\cdot r_i\cdot \lambda +e_i^w\cdot t_i^w}$$

(9)

In the formula, e_i^m denotes the unit processing energy consumption of the ith manufacturing service; t_i^m denotes the processing time of the corresponding service; e_i^l denotes the unit processing energy consumption of the ith manufacturing service; r_i and λ are the logistics distance and fuel type coefficients of the corresponding service, respectively; e_i^w denotes the unit waste treatment energy consumption of the ith service; and t_i^w denotes the processing time of the corresponding service. In summary, the oven energy consumption indicator objective function is shown in Equation (10):

$$\left\{\begin{array}{l}\min f_{EC}(x)=EC/n\\ s.t.EC=E_m+E_l+E_w\le E{C}_{\max }\end{array}\right.$$

(10)

In summary, on the basis of the QoS optimization objective and energy consumption optimization objective, combined with the previous formula, the objective function of the oven manufacturing service composition optimization problem that simultaneously considers the QoS indicator and the energy consumption indicator is formed, and the specific representation is shown in Equation (11):

$$\left\{\begin{array}{l}\min f_{QoS}(x)=UfQoS\\ \min f_{EC}(x)=EC/n\\ s.t.\hspace{0.17em}\hspace{0.17em}\overline{T}\le {\overline{T}}_{\max },\overline{C}\le {\overline{C}}_{\max },\overline{Re}\ge {\overline{Re}}_{\min },\overline{Q}\ge {\overline{Q}}_{\min }\\ \hspace{1em}\hspace{1em}EC=E_m+E_l+E_w\le E{C}_{\max }\end{array}\right.$$

(11)

2.5. LCSSA_DE Algorithm

On the basis of the original SSA algorithm, the improved LCSSA_DE algorithm is used to solve the mathematical model of coating machine oven service composition-optimization and obtain the optimal manufacturing service combination scheme.

2.5.1. Setting the Sparrow Code Location

Each sparrow coordinate vector is encoded in the form of an integer array whose length is equal to the number of subtasks. As shown in Figure 6, each subtask ST needs to select a manufacturing service MS from the corresponding set of candidate manufacturing services, and if the specific composition of the selected set of manufacturing service combinations is {${MS}_1^1$, ${MS}_2^2$, ${MS}_3^m$, …, ${MS}_n^1$}, the final corresponding sparrow individual coordinate integer encoding of the service combination is expressed as {1, 2, m, …, 1}.

2.5.2. Initializing Sparrow Population Based on Tent Chaos Mapping with Elite Reverse Learning Strategy

Aiming at the problems of insufficient population diversity and insufficient synergy with the subsequent stages of the algorithm in the process of initializing the population parameters of the traditional SSA algorithm, an initialization population strategy based on tent chaotic mapping [30] and elite reverse learning [31] is proposed. Tent chaotic mapping is a simple and effective chaotic mapping method, which can effectively enhance the stochasticity of the population and improve the global search ability of the algorithm, and it is simple, efficient, and easy to implement. Tent chaotic mapping is used to replace the original random initialization population process, as shown in Equation (12):

$$x_{i+1}=\left\{\begin{array}{cc}\begin{array}{cc}{x}_i/a& x_i<a\\ \left(1-x_i\right)/\left(1-a\right)& x_i\ge a\end{array}& ,a\in \left(0,1\right)\end{array}\right.$$

(12)

After initializing the population using tent chaotic mapping, the initial population is further optimized by the elite reverse learning strategy. Elite reverse learning is an improved reverse learning method which improves the performance of the algorithm by utilizing the information of elite individuals, which can effectively improve the quality of the initial population, accelerate the convergence speed of the algorithm, and enhance the adaptability of the algorithm. In this paper, the elite reverse strategy is used thereby generating the reverse learning population individuals $x_i^o$, as shown in Equation (13):

$$x_i^o=k(lb+ub)-x_i$$

(13)

where x_i is the information of the current individual; lb and ub represent the upper and lower boundaries of the decision space solution, respectively; and k is a random number between [0, 1]. After elite backward learning to optimize the population generated by tent chaotic mapping, the greedy selection strategy is used to retain the individuals with better fitness values to obtain the final version of the initialized sparrow population.

2.5.3. Calculation of Fitness and Dynamic Factor Assignment

The fitness value of each individual sparrow is calculated and ranked, the fitness value of individual sparrows in the initial population is calculated, and the individual sparrow with the optimal fitness value in the initial population is obtained using a roulette wheel. The number of discoverers and followers in the search process is rationally allocated by means of the dynamic factor r; the specific formula for the dynamic factor r is shown in Equation (14):

$$r=\gamma \sin \left({\displaystyle \frac{\pi }{2}}\cdot \left(ite{r}_{\max }-t\right)/\left(ite{r}_{\max }\right)\right)$$

(14)

where iter_max is the maximum number of iterations and γ is the scale factor. At the beginning of the sparrow individual iteration, a larger scale factor is used to control the number of discoverers and thus realizing the global search; in the middle and late iteration, the scale factor is controlled to accelerate the decrease to achieve a more accurate local search by increasing the number of followers.

2.5.4. Updating Sparrow Population Spotter, Follower, and Alert Locations

The core of the sparrow search algorithm is to divide the sparrow population into discoverers, followers, and vigilantes, and iteratively obtain the optimal sparrow individuals by simulating the foraging process of sparrow individuals with three different identities.

Discoverers with better fitness values are prioritized for food during search. The discoverer can search for food in a wider range of places than the follower. During each iteration, the position update formula of the discoverer is shown in Equation (15):

$$X_{i,j}^{t+1}=\left\{\begin{array}{ll}{X}_{i,j}^t\cdot \exp \left({\displaystyle \frac{-i}{\alpha \cdot {\mathrm{iter}}_{\max }}}\right)& \mathrm{if}{R}_2<ST\\ X_{i,j}^t+Q\cdot L& \mathrm{if}{R}_2\ge ST\end{array}\right.$$

(15)

where t and iter_max are the current and maximum iteration times, respectively; α is a random number generated in (0, 1] and satisfies the uniform distribution; Q is a random number obeying the normal distribution; and L denotes a matrix of 1 × d. R₂ and ST are the alert value and the safety threshold, respectively, and satisfy the values of R₂ ∈ [0, 1], ST ∈ [0.5, 1], when R₂ < ST it means that the current state is safe and the discoverer is able to search and guide other individuals to obtain a higher fitness value than its own, and when R₂ > ST, it means that the alert value has exceeded the safety threshold, requiring alarm and evacuation to a safer area. The discoverer is able to search and guide other individuals to obtain higher adaptation values than its own, and when R2 > ST it means that the alert value has exceeded the safety threshold, and it needs to call the police and evacuate to a safer area.

Once the finder finds a food source, the follower will immediately leave the current position to go to the food source found by the finder and compete for the food to the best of its ability. The follower’s position update formula is shown in Equation (16):

$$X_{i,j}^{t+1}=\left\{\begin{array}{cc}Q\cdot \exp \left({\displaystyle \frac{X_{worst}^t-X_{i,j}^t}{i^2}}\right)& \mathrm{if}i>n/2\\ X_{best}^{t+1}+|X_{i,j}^t-X_{best}^{t+1}|\cdot A^{+}\cdot L& \mathrm{if}i\le n/2\end{array}\right.$$

(16)

where X_best is the optimal position currently found by the producer; X_worst denotes the current worst position; A is a 1 × d matrix; and A⁺ = A^T(AA^T)⁻¹. When i > n/2, it means that the i follower with the lowest adaptation value needs to go to another region to continue searching for food.

Individual sparrows responsible for early warning account for 10%–20% of the total, and their task is to sound the alarm when the alert value exceeds the safety threshold and lead the whole group to evacuate to a safer area, and their position updating formula is shown in Equation (17):

$$X_{i,j}^{t+1}=\left\{\begin{array}{cc}{X}_{best}^t+\beta \cdot \left|X_{i,j}^t-X_{best}^t\right|& \mathrm{if}{f}_i>f_g\\ X_{i,j}^t+K\cdot \left({\displaystyle \frac{\left|X_{i,j}^t-X_{worst}^t\right|}{(f_i-f_w)+\epsilon }}\right)& \mathrm{if}{f}_i=f_g\end{array}\right.$$

(17)

where X_best is the current global optimal position; β and K are step control parameters; β is a random number obeying a normal distribution; and K ∈ rand [−1, 1]. f_i is the fitness value of the current individual, f_g and f_w are the current global optimal and worst fitness values, and ε is a tiny constant to avoid division by zero error. f_i > f_g indicates that the individual sparrow is at the edge and may be attacked by predators, and f_i = f_g indicates that the individual sparrow in the middle of the population is aware of the danger and needs to approach the rest of the individuals to reduce the risk of predation.

2.5.5. Differential Evolutionary Strategies Based on Levy Flight Improvement

Lévy flight is a random walk strategy [32] with unique step-size distribution characteristics, which updates the positions of the previous discoverer, follower, and vigilant to significantly enhance the global search capability of the SSA algorithm, improve the convergence speed, and enhance the robustness of the algorithm. Perturbation is performed using the Lévy flight improved differential evolution strategy while updating the global optimum. The mutation operation is performed and the formula for generating a mutated individual v_i(t) from an individual x_i(t) is shown in Equation (18):

$${\nu }_i(t)=x_{best}(t)+F\cdot \left(x_{r1}(t)-x_{r2}(t)\right)$$

(18)

where x_best(t) is the current optimal individual; x_r1(t) and x_r2(t) are two randomly selected ones in the current generation; and F is the variation factor. The differential evolution strategy of the Lévy flight improvement is to replace the variation factor with the step size of the Lévy flight, so as to balance the global search ability and local search ability of the algorithm.

The formula for the mutation operation using the Lévy flight improved differential evolution strategy is shown in Equation (19):

$${\nu }_i(t)=x_{best}(t)+\epsilon \cdot Levy(s)\cdot \left(x_{r1}(t)-x_{r2}(t)\right)$$

(19)

where ε is an adjustable coefficient. Appropriately adjusting the value of this parameter can prevent the Lévy flight step from being too large or too small; here, we set the value to 1 so as to always maintain an efficient search process.

A Lévy flight refers to a random path that conforms to the Lévy distribution: levy~t^3−β, 1 < β ≤ 3. The step size s of the Lévy flight is simulated using Mantegna, and the formula is shown in Equation (20):

$$s={\displaystyle \frac{u}{{\left|v\right|}^{1/\beta }}}$$

(20)

where u~N(0, σ²), v~N(0, 1) are random numbers obeying normal distribution and the standard deviation satisfies Equation (21):

$$\sigma ={\left\{{\displaystyle \frac{\mathrm{\Gamma }(1+\beta \sin (\frac{\pi \beta }{2}))}{\beta \mathrm{\Gamma }(\frac{1+\beta }{2})2^{\frac{\beta -1}{2}}}}\right\}}^{{\displaystyle \frac{1}{\beta }}}$$

(21)

where Γ is the gamma function; β is the step size distribution control parameter, the smaller the value of β, the more significant the Levy distribution heavy-tailed characteristics, the high probability of long-distance jumps, which is conducive to jumping out of the local optimum, but the convergence is slow; the β value is larger, the step size is limited, and it is easy to fall into the local optimum. In order to balance the search ability, convergence speed, and stability, β = 1.5 is taken.

The crossover operation is performed between the parent individual x_i(t) and the variant individual v_i(t) to obtain the crossover individual u_i(t), as shown in Equation (22):

$$u_{ij}(t)=\left\{\begin{array}{ll}{\nu }_{ij}(t)& \mathrm{if}\mathrm{rand}[0,1]\le CR\mathrm{or}j=j_{rand}\\ x_{ij}(t)& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{otherwise}\end{array}\right.$$

(22)

where j = j_rand is an integer randomly chosen within [1,d] to ensure that u_i(t) obtains at least one element from the mutant individual v_i(t); the CR value is the crossover factor, which is taken as CR = 0.5 × (1 + Rand); and Rand is a random number between [0, 1].

The selection operation is to choose the better individual as the population individual of the next generation between the parent individual x_i(t) and the crossover individual u_i(t) by using a greedy selection strategy, and the selection expression is Equation (23):

$$x_i(t+1)=\left\{\begin{array}{ll}{u}_i(t)& \mathrm{if}f(u_i(t))<f(x_i(t))\\ x_i(t)& \hspace{1em}\hspace{1em}\mathrm{otherwise}\end{array}\right.$$

(23)

2.5.6. LCSSA_DE Algorithm Flow

According to the previous description of the method details, the flow of the proposed LCSSA_DE algorithm is shown in Figure 7: where N is 50% of the maximum population size, the current iteration number is t, the maximum iteration number is e, and i is the current population size.

3. Results

To verify the superiority and feasibility of the improved method, algorithm performance comparison, arithmetic analysis, and scale-up examples were designed. The above operations were accomplished using MATLAB software with version R2024b, Intel(R) Core(TM) i5-12400F, 2.50 GHz CPU, 16.0 GB of runtime space, NVIDIA GeForce GT 1050Ti graphic card, 1TB HDD hard disk, and Windows 11 professional 24H2 operating system.

3.1. Algorithm Performance Comparison

Two sets of arithmetic cases with different experimental sizes were selected to test the generational distance (GD) and spread indicator; ZDT1-3 in the Zitzler–Deb–Thiele test function set (ZDT) and UF1-7 in the unconstrained function set (UF) were selected as test functions to test the GD and the inverted generational distance (IGD).

• Generation distance (GD) is an indicator used to evaluate the convergence of multi-objective optimization algorithms [33]. The smaller the value of GD, indicating that the solution found is closer to the real Pareto solution set, the better the convergence performance. The specific expression is shown in Equation (24):

  $$GD(X,P)={\displaystyle \frac{{\displaystyle \sum _{X^{*}\in P}dist(X^{*},X)}}{\left|P\right|}}$$

  (24)

  where P is the obtained solution on the Pareto front; X denotes the generated ensemble sample; and dist(X*,X) is the Euclidean distance.
• The IGD indicator evaluates the convergence and diversity of the algorithm by calculating the average minimum distance from points on the real PF to the set of nondominated solutions obtained by the algorithm [34], with smaller values indicating that the solution set is closer to the real PF and more evenly distributed. The core of this is to evaluate convergence and diversity at the same time. The IGD formula is shown in Equation (25):

  $$IGD(X,P^{*})={\displaystyle \frac{{\displaystyle \sum _{X^{*}\in P^{*}}dist(X^{*},X)}}{\left|P^{*}\right|}}$$

  (25)

  where P* is the solution on the true Pareto boundary and dist(X*,X) is the Euclidean distance.
• Spread indicator is a kind of evaluation indicator to measure the uniformity of the distribution of Pareto front, which reflects the distribution of the non-dominated solution set in the whole target space; when the spread is closer to 0, it indicates that the distribution of the solutions is more uniform. The formula of spread is shown in Equation (26):

  $$S={\displaystyle \frac{{\displaystyle {\sum }_{i=1}^{N-1}‖d_i-\overline{d}‖}}{(N-1)\overline{\mathrm{d}}}}$$

  (26)

  where N is the number of non-dominated solutions; d_i is the Euclidean distance between the i-th and i + 1-th solution; and $\overline{d}$ denotes the average distance.

In this paper, using the self-constructed dataset of the group, the manufacturing resource composition-optimization process is simulated for the manufacturing requirements of oven parts, and the effectiveness of the LCSSA_DE algorithm in the composition optimization of oven manufacturing resources is analyzed by comparing the evaluation indicators of the selected algorithms. The classic algorithms in the field of multi-objective optimization, MOGWO algorithm and the multi-objective particle swarm optimization (MOPSO) [35] algorithm and the advanced algorithm proposed in recent years, the multi-objective African vultures optimization algorithm (MOAVOA) [36] for algorithm comparison, and the initial conditions of each algorithm are set in the same experimental environment as shown in

Table 1. Parameterization of individual algorithms.

Arithmetic	Parameters
LCSSA_DE	Maximum number of iterations: 300, population size: 50, early warning value: 0.8; percentage of detector sparrows: 0.2, percentage of alert sparrows: 0.1, crossover factor CR: 0.75
MOGWO	Maximum number of iterations: 300, population size: 50, control parameters ainitial: 2, afinal: 0
MOPSO	Maximum number of iterations: 300, population size: 50, learning factors c1, c2: 1.49445. Inertia weight: 0.729
MOAVOA	Maximum number of iterations: 300, population size: 50, number of grids per dimension: 30, expansion rate: 0.1, leader selection pressure: 4, deletion selection pressure: 2

.

3.1.1. Effectiveness of LCSSA_DE in Solving the Oven-Manufacturing Service Composition Optimization Problem

The experimental scale is divided into two groups, S-10-20 and S-10-40, i.e., the number of subtasks is 10, and the number of candidate services corresponding to each subtask in the two groups is divided into 20, 40, and the experimental data are in the form of factory-collected data plus self-fabricated data. Each algorithm is run independently for 20 times. Since the real Pareto frontier of the oven-manufacturing service composition optimization problem is unknown, this paper takes the Pareto frontier obtained from the algorithm running results as the real Pareto frontier in order to calculate the indicator value. The Pareto frontiers obtained by the four algorithms are shown in Figure 8.

The algorithm performance is measured using the GD and spread indicators for the service composition optimization problem for both sets of scales, and the results are shown in

Table 2. GD vs. spread at both scales.

Arithmetic	GD Mean(std)		Spread Mean(std)
	S-10-20	S-10-40	S-10-20	S-10-40
LCSSA_DE	7.62 × 10−2 (1.45 × 10−4)	8.13 × 10−2 (3.43 × 10−4)	7.68 × 10−1 (3.06 × 10−3)	7.52 × 10−1 (2.66 × 10−3)
MOGWO	8.98 × 10−2 (2.59 × 10−4)	9.56 × 10−2 (3.06 × 10−4)	8.81 × 10−1 (3.18 × 10−3)	7.69 × 10−1 (4.62 × 10−3)
MOPSO	1.41 × 10−1 (4.03 × 10−3)	2.82 × 10−1 (3.04 × 10−2)	8.34 × 10−1 (2.33 × 10−3)	8.95 × 10−1 (2.80 × 10−3)
MOAVOA	8.42 × 10−2 (4.20 × 10−4)	1.17 × 10−1 (2.45 × 10−4)	7.78 × 10−1 (2.67 × 10−3)	8.24 × 10−1 (2.83 × 10−3)

.

Figure 8 is analyzed with Table 2. In Figure 8, it can be seen that the LCSSA_DE algorithm solves the manufacturing service combination solution significantly better than the remaining three algorithms, with nearly 69% of points better than the other algorithms at the first set of scales and nearly 77% of points better than the other algorithms at the second set of scales, and the average convergence time of the LCSSA_DE algorithm improves by 7.26% at both scales compared to the second-best algorithm; from the data in Table 2, the LCSSA_DE algorithm outperforms the rest of the algorithms in terms of GD and spread values on the service combination problem at two different scales. Taken together, most of the solutions generated by the LCSSA_DE algorithm are able to exhibit a wide range of convergence and diversity, and the algorithm performs well.

3.1.2. Effectiveness of LCSSA_DE on Benchmark Functions

This paper evaluates the effectiveness of the LCSSA_DE algorithm on 10 well-known benchmark functions. The selected benchmark functions include ZDT1-3 and UF1-7, the test function is set, the number of decision variables is 30, and the comparison algorithms and experimental setups used are consistent with the previous paper.

The evaluation was completed using GD and IGD indicators, all the algorithms were run independently for 30 times, and the results are shown in

Table 3. Comparison of GD with different test functions.

GD	Mean(std)
	LCSSA_DE	MOGWO	MOPSO	MOAVOA
ZDT1	1.01 × 10−4 (7.06 × 10−5)	9.33 × 10−5 (1.97 × 10−5)	2.39 × 10−4 (8.19 × 10−5)	2.88 × 10−4 (1.37 × 10−4)
ZDT2	6.60 × 10−5 (3.82 × 10−6)	7.75 × 10−5 (1.15 × 10−5)	8.67 × 10−5 (3.96 × 10−5)	7.68 × 10−4 (1.23 × 10−5)
ZDT3	2.59 × 10−4 (1.54 × 10−5)	2.62 × 10−4 (2.68 × 10−5)	4.14 × 10−4 (3.44 × 10−5)	3.24 × 10−4 (2.23 × 10−5)
UF1	9.18 × 10−3 (1.37 × 10−3)	1.05 × 10−2 (1.55 × 10−3)	1.27 × 10−2 (1.77 × 10−3)	6.62 × 10−3 (4.80 × 10−4)
UF2	4.86 × 10−3 (6.40 × 10−5)	4.99 × 10−3 (1.51 × 10−4)	6.54 × 10−3 (3.82 × 10−4)	5.82 × 10−3 (1.44 × 10−4)
UF3	4.24 × 10−2 (4.23 × 10−3)	5.95 × 10−2 (4.71 × 10−3)	7.92 × 10−2 (8.42 × 10−3)	6.35 × 10−2 (4.60 × 10−3)
UF4	5.09 × 10−3 (4.66 × 10−4)	5.20 × 10−3 (6.28 × 10−4)	8.56 × 10−3 (1.16 × 10−3)	6.12 × 10−3 (7.40 × 10−4)
UF5	2.54 × 10−1 (6.25 × 10−2)	3.14 × 10−1 (1.17 × 10−1)	7.14 × 10−1 (1.36 × 10−1)	9.28 × 10−2 (3.68 × 10−2)
UF6	1.73 × 10−1 (3.61 × 10−2)	3.06 × 10−1 (9.68 × 10−2)	5.42 × 10−1 (1.65 × 10−1)	2.66 × 10−1 (7.83 × 10−2)
UF7	6.94 × 10−3 (7.60 × 10−4)	7.55 × 10−3 (9.90 × 10−4)	8.61 × 10−3 (1.22 × 10−3)	7.80 × 10−3 (5.20 × 10−4)

and

Table 4. Comparison of IGD with different test functions.

IGD	Mean(std)
	LCSSA_DE	MOGWO	MOPSO	MOAVOA
ZDT1	5.06 × 10−4 (4.32 × 10−5)	6.31 × 10−4 (1.39 × 10−4)	6.47 × 10−4 (1.33 × 10−4)	8.42 × 10−4 (8.53 × 10−5)
ZDT2	7.20 × 10−4 (8.92 × 10−5)	8.73 × 10−4 (1.25 × 10−4)	8.17 × 10−4 (9.43 × 10−5)	5.44 × 10−4 (5.12 × 10−5)
ZDT3	6.12 × 10−4 (3.72 × 10−5)	9.56 × 10−4 (1.18 × 10−4)	1.12 × 10−3 (5.69 × 10−5)	8.97 × 10−4 (1.63 × 10−4)
UF1	3.48 × 10−3 (8.50 × 10−4)	5.77 × 10−3 (1.30 × 10−3)	6.63 × 10−3 (2.17 × 10−3)	3.36 × 10−3 (6.40 × 10−4)
UF2	1.57 × 10−3 (3.10 × 10−4)	1.69 × 10−3 (5.01 × 10−4)	3.36 × 10−3 (1.44 × 10−3)	3.26 × 10−3 (3.39 × 10−4)
UF3	1.18 × 10−2 (5.57 × 10−3)	1.31 × 10−2 (8.19 × 10−3)	2.84 × 10−2 (1.29 × 10−2)	1.81 × 10−2 (6.45 × 10−3)
UF4	1.68 × 10−3 (5.60 × 10−4)	2.36 × 10−3 (6.02 × 10−4)	2.20 × 10−3 (1.30 × 10−3)	1.77 × 10−3 (7.40 × 10−4)
UF5	1.39 × 10−1 (2.04 × 10−2)	1.71 × 10−1 (5.06 × 10−2)	3.24 × 10−1 (1.12 × 10−1)	1.99 × 10−1 (5.16 × 10−1)
UF6	2.75 × 10−2 (6.60 × 10−3)	2.57 × 10−2 (5.50 × 10−3)	4.08 × 10−2 (1.50 × 10−2)	3.34 × 10−2 (1.16 × 10−2)
UF7	2.38 × 10−3 (5.60 × 10−4)	2.66 × 10−3 (7.60 × 10−4)	6.32 × 10−3 (2.23 × 10−3)	1.04 × 10−2 (1.32 × 10−3)

.

As can be seen from the data in Table 3, in terms of GD indicators, the LCSSA_DE algorithm achieves the best results for all except ZDT1, UF1, and UF5, the MOGWO algorithm achieves the best IGD value only for ZDT1, MOAVOA achieves the best value only for UF1 and UF5, and the MOPSO algorithm does not achieve the best value. It can be seen from the data in Table 4 that in terms of the IGD indicator, the LCSSA_DE algorithm achieves optimal results on all benchmark test functions except ZDT2, UF1, and UF6. The MOGWO algorithm achieves the best IGD value on UF6, the MOAVOA algorithm achieves the best value only on ZDT2 and UF1, and the MOPSO algorithm does not achieve the best value. It can be seen that the LCSSA_DE algorithm is superior to the remaining algorithms in terms of GD indicator and IGD indicator for the selected benchmark functions.

Figure 9 and Figure 10 show the performance differences of the four algorithms under different test functions through box and line plots, where the box position reflects the level of GD and IGD indicators, the box length indicates the data dispersion, and the small black circles are noted as the mean values of 30 independent experiments. Based on the analysis of the box and line plots, it can be seen that in terms of the GD indicator, Figure 9b,c,e,g,i,j show that the LCSSA_DE algorithm is in the lowest decile and has narrower boxes on most of the benchmark functions, indicating optimal convergence stability; meanwhile, the MOGWO algorithm shows optimal results only on the ZDT1 function shown in Figure 9a, and the MOAVOA algorithm shows better results only on the UFI function and the UF5 function shown in Figure 9d,h.

The boxplots of the IGD indicator show that the LCSSA_DE algorithm in Figure 10a,c,e,f,h,j is in the lowest quartile on the corresponding six benchmark functions and the interquartile range (IQR) is 29.7% smaller than that of the suboptimal algorithm, and the test function on Figure 10d,e is slightly better than that of the MOAVOA algorithm, while the MOAVOA algorithm and the MOGWO algorithms have better test function results only on Figure 10b,i. The stability of the benchmarking performance of the LCSSA_DE algorithm is confirmed.

Friedman’s test is performed on the data of the two performance indicators and the results are shown in

Table 5. Friedman test results for GD and IGD.

Arithmetic	GD		IGD
	Order of Averages	Rankings	Order of Averages	Rankings
LCSSA_DE	1.3	1	1.4	1
MOGWO	2.7	3	2.9	3
MOPSO	3.6	4	3.5	4
MOAVOA	2.3	2	2.1	2
N	10		10
DF	3		3
Chi-square	16.58		13.36
p-value	0.00179		0.00412

. According to the test results of the table, it can be seen that the mean rank of the GD value is only 1.3 and that of the IGD is only 1.4, and the LCSSA_DE algorithm performs better than the other three algorithms on the selected benchmark function.

3.2. Examples of Scaling Up

In order to further verify the applicability of the LCSSA_DE algorithm to the coating machine oven-manufacturing problem, this paper sets up an experiment as an example of the cross-enterprise crowdsourcing manufacturing process of a coating oven manufacturing enterprise in Shaanxi Province. The experimental data are based on the self-constructed database of the enterprise’s past historical orders, and for the sake of generality, the attribute value parameters of the QoS normalization of the candidate services are randomly initialized in a specific range of values, as shown in

Table 6. Range of values for attribute indicators.

Indicator	Quality of Service Indicators QoS				EC Indicators
	T	C	Re	Q
range of values	[0.28, 0.96]	[0.22, 0.91]	[0.45, 0.97]	[0.53, 0.95]	[5,20]
causality	negative	negative	Positive	Positive	negative

.

Extend this case to nine different-sized coating machine oven manufacturing problems. If each oven-part manufacturing subtask corresponds to 20 candidate services, the 10 subtasks can be expanded to (10–20), (10–40), (10–80), (20–20), (20–40), (20–80), (30–20), (30–40), and (30–80), totaling nine groups. Figure 11a–i and Figure 12a–i represent the corresponding expansion scales above. Figure of the QoS distribution for the above scale-up problem obtained using the self-built database brought into Equation (11) and normalized by applying the equation. In this case, both service reliability and quality are positive indicators and can be uniformly classified as Q. Figure 11a,e,g,h show that the LCSSA_DE algorithm outperforms the other compared algorithms at 55% of all points, Figure 11c,d show that the LCSSA_DE algorithm outperforms the other compared algorithms at 60% of all points, and Figure 11i shows that the LCSSA_DE algorithm outperforms the other algorithms at 65% of all points; Figure 11f shows that the LCSSA_ DE algorithm works best with 85% of all points outperforming the other algorithms, and Figure 11b shows that the LCSSA_DE algorithm works worst with 35% of all points outperforming the other algorithms. In summary, most of the red data points obtained by the LCSSA_DE algorithm are located at the top, indicating that the LCSSA_DE algorithm has lower time and cost and higher quality in dealing with the coating machine oven-manufacturing problem, which meets the modeling criteria and proves the applicability of the LCSSA_DE algorithm in the coating machine oven-manufacturing problem.

QoS indicator and energy consumption indicator are the two subjects of the dual-objective model; the two together determine the degree of the model’s advantages and disadvantages. In order to verify the distribution of decision-making under the mutual influence of the two subjects, the self-built database is brought into the formula, and the distribution of the solution set is obtained as shown in Figure 11, which shows that the smaller the indicators of the two subjects are, the better the algorithm is according to the previous modeling. In Figure 12, the solution sets generated by the LCSSA_DE algorithm are represented by red circles, and it can be seen that they constitute the outermost Pareto boundaries in the other seven scales except for the scale of Figure 12e (10–20) and under the scale of Figure 12a (20–40); and a comparison of the nine subpictures reveals that the distributions of the LCSSA_DE algorithm in Figure 12g–i have a more obvious advantage over the distributions in Figure 12b–d,f. This shows that as the problem size increases, the solution set of the LCSSA_DE algorithm is always concentrated in the ideal range, and the larger the problem size, the more obvious the advantage of the algorithm, indicating its applicability in dealing with large-scale problems. However, the solution set of the MOPSO algorithm is mostly distributed in the upper right, which indicates that the method has a weak optimization-seeking ability in solving this bi-objective model, while the solution set distribution of the MOGWO algorithm is in between the MOAVOA algorithm and the MOPSO algorithm, with a moderate optimization-seeking ability, and the solution set distribution of the MOAVOA algorithm is better than that of the MOGWO algorithm, but it is still a bit short compared with the LCSSA_DE algorithm.

The maximum size of 30–80 was chosen for the example simulation, and the two optimal manufacturing service combinations for this size were obtained as shown in

Table 7. Optimized manufacturing service portfolio.

Serial Number	Manufacturing Services Portfolio	T	C	Q	EC
1	${MS}_1^1$-${MS}_2^3$-${MS}_3^6$-${MS}_4^2$-${MS}_5^1$-${MS}_6^6$-${MS}_7^{10}$-${MS}_8^5$-${MS}_9^2$-${MS}_{10}^7$	0.31	0.26	0.92	10.35
2	${MS}_1^1$-${MS}_2^5$-${MS}_3^6$-${MS}_4^4$-${MS}_5^1$-${MS}_6^6$-${MS}_7^{12}$-${MS}_8^7$-${MS}_9^2$-${MS}_{10}^{10}$	0.33	0.23	0.91	10.42

.

4. Discussion

In Section 2, the set of candidate manufacturing services corresponding to each part manufacturing process is obtained by analyzing the part-level manufacturing processes of the coating machine ovens, laying the foundation for the subsequent discussion on improving the manufacturing efficiency of the coating machine ovens. After that, considering the common interests of the demand-side of oven crowdsourcing service and the operator of the oven crowdsourcing platform, the evaluation indicator system of oven manufacturing service composition-optimization is proposed, and the dual-objective service composition-optimization model for ovens is established by combining the QoS indicator and the energy consumption indicator; in view of the problems of the SSA algorithm, such as the slower convergence and the ease of falling into the local optimum, the LCSSA_DE algorithm is used to solve this model, which is worthy of attention. It is worth noting that the proposed LCSSA_DE algorithm may not be the optimal solution. In this paper, through the three parts of algorithm performance comparison, arithmetic analysis and scale expansion examples were employed to verify the effectiveness of the proposed method in solving the optimal solution, and to obtain the optimal manufacturing service portfolio of the oven.

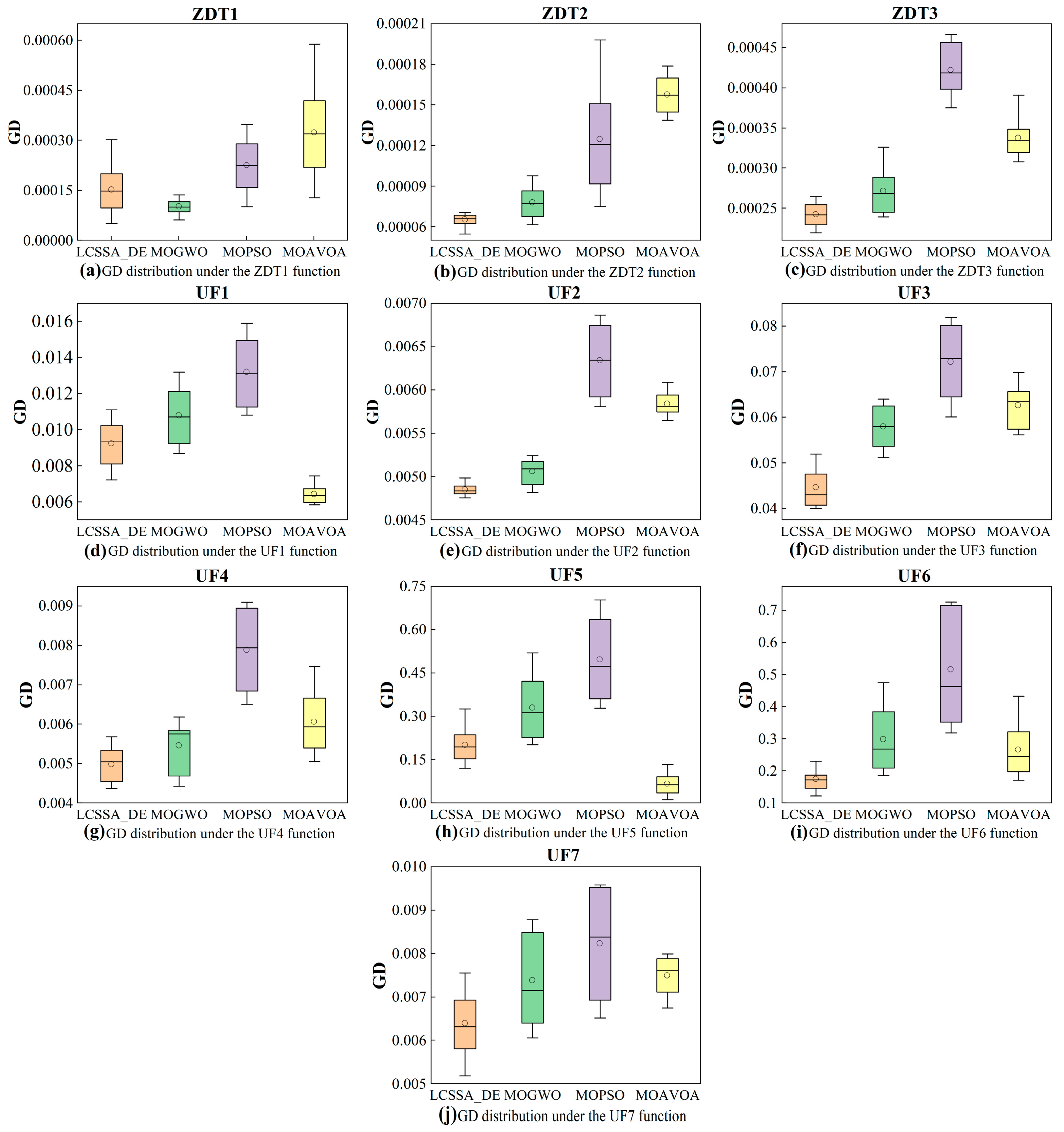
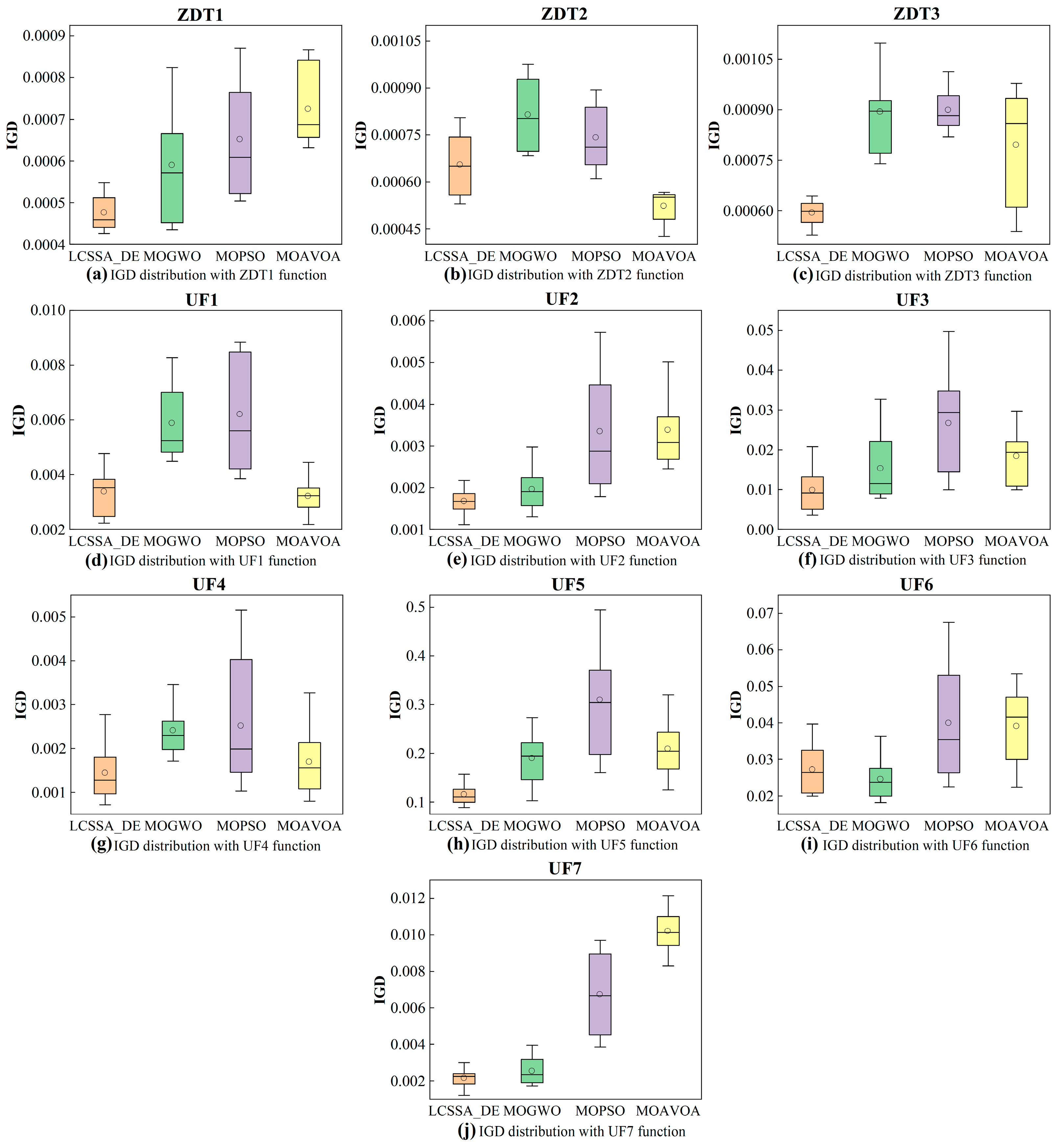
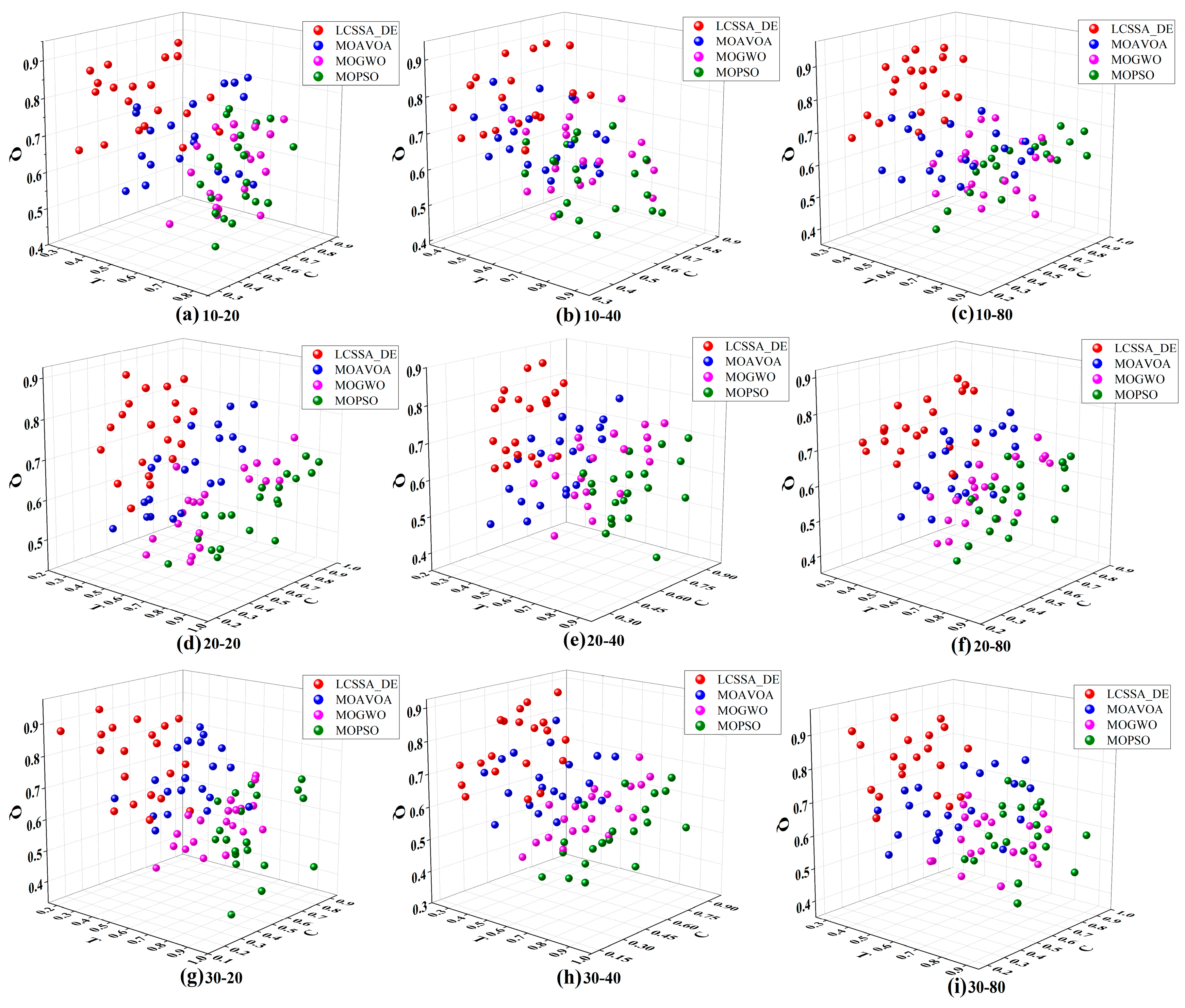
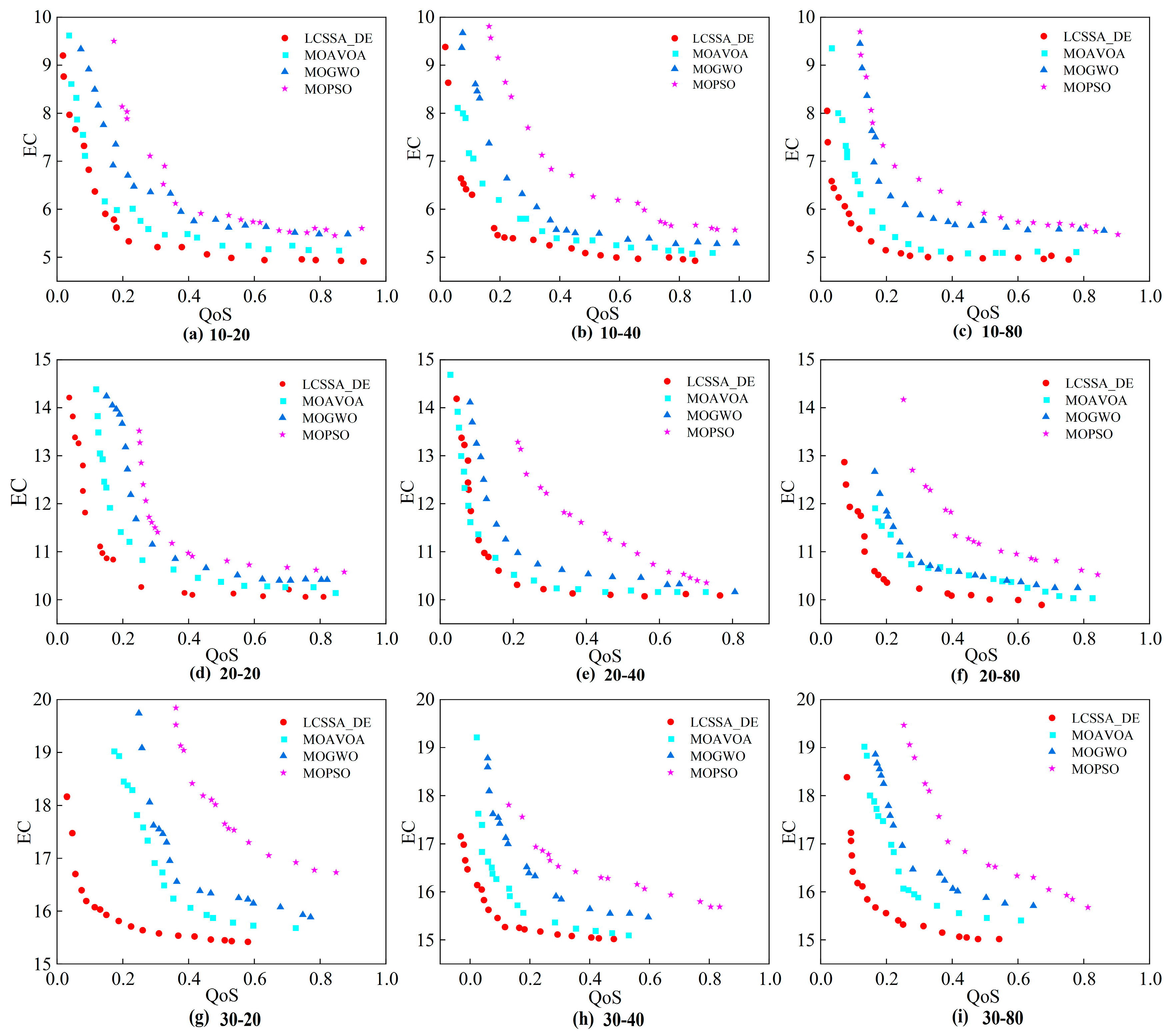
As can be seen from the results in Figure 8, Figure 9 and Figure 10, although the LCSSA_DE algorithm can effectively solve the problems of lower efficiency, slow convergence, and having fallen into local optimization when solving the model, there are 23%–31% of the points where the distribution of the Pareto front surface is still not optimal, 3/10 of the test functions have a GD indicator that is not optimal, and 2/10 of the test functions have IGD indicators that are not optimal. 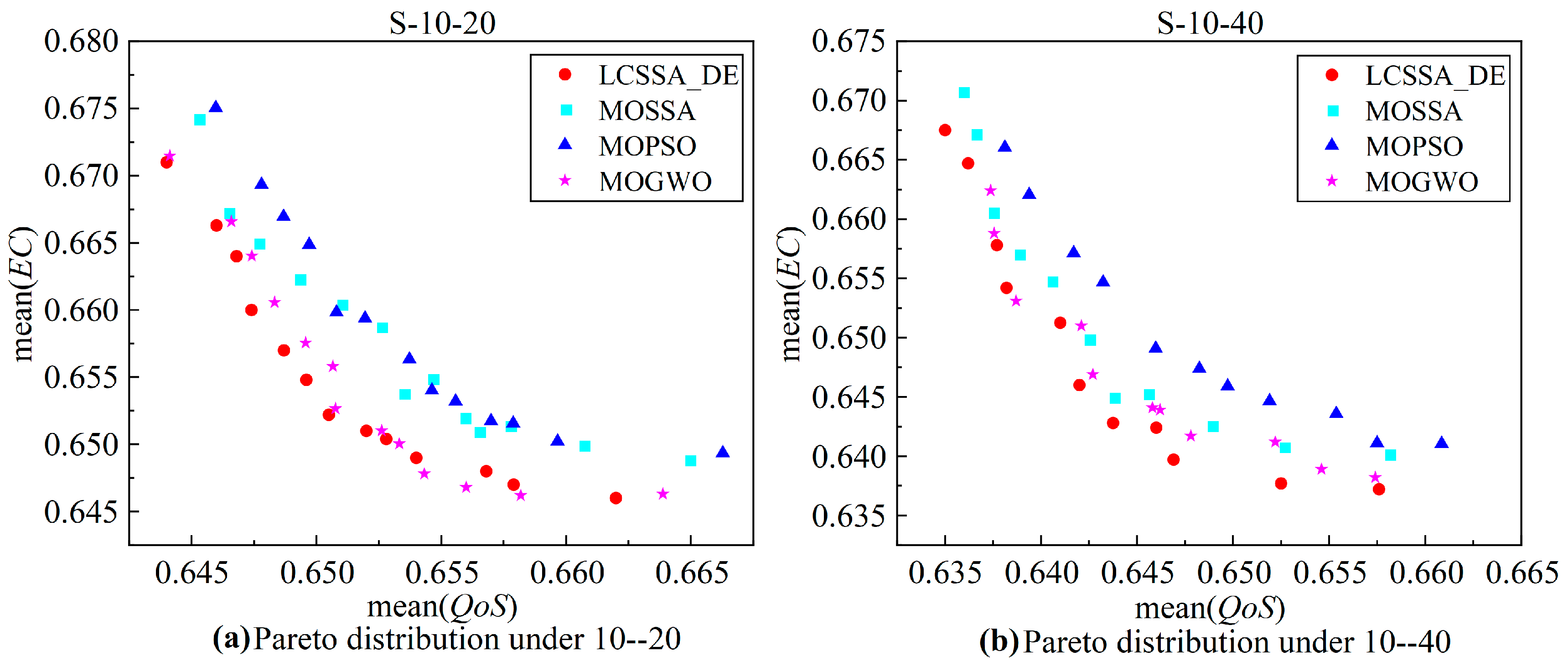By analyzing Figure 11 and Figure 12, it can be seen that although the LCSSA_DE algorithm has advantages over the comparison algorithms for several datasets on the manufacturing scale-up problem, there are still some datasets with poor distributions; in addition, the current theoretical analysis only applies to the research of the self-built database, the conclusion is not necessarily applicable to the actual production site or other manufacturing parts, for the manufacturing process of more complex parts of the resource optimization model to solve the problem still need to be further explored. As shown in Equation (11), according to the modeling criteria, both QoS indicators and energy consumption indicators are consistent with the smaller the better under the constraints of meeting the secondary and tertiary indicators, and this objective function can be similarly applied to other manufacturing parts. At the same time, in the actual production, the establishment of the evaluation indicator system still has many uncertainties, service substitutability and other flexibility indicators also have a certain impact on the preferred combination of manufacturing services, and the more accurate establishment of energy consumption indicators will further affect the algorithm’s solution results. For example, direct and indirect energy consumption are considered in the establishment of energy consumption per unit of processing, and the integrated energy consumption of production equipment is also considered, which also points out the direction for subsequent research.

In addition, the application of machine learning in the service composition optimization problem is gradually maturing [37], and it can be used for capacity optimization in combination with neural networks and other technologies; while the parameters of the quality indicators and the parameters of the energy consumption indicators depend on the quality of the raw materials and other factors of the complex production environment, the machine learning model can be dynamically adapted to the parameters of the optimization model based on these factors. At the same time, the machine’s operating status, historical production data, maintenance records, and other capacity-related characteristics affect the variation in the parameters in the model, and the introduction of machine learning allows for the better prediction of this set of variations in order to improve the productivity of coating machine ovens. In short, through the combination of machine learning and coating machine oven service composition-optimization, can significantly improve the optimization efficiency and adaptability. In the face of the actual production conditions of a dynamic and complex environment, this combination will have a wider range of applications.

5. Conclusions

This paper takes coating machine ovens as the research object, for the service composition optimization of the coating machine ovens, proposes an effective method to derive the composition optimization decision of the oven manufacturing services, which improves the production quality of the oven, shortens the production time, reduces the cost, and improves the production efficiency of the coating machines. At the same time, it considers the common interests of the demand-side of the crowdsourcing service and the operator of the crowdsourcing platform, and offers new ideas for the solution of this kind of part-level multi-objective optimization problems. However, there are still many uncertainties in the manufacturing production problems at different scales in this study, and the set of manufacturing resources corresponding to machining processes and parts in the actual production process is more complex; at the same time, the dual-objective indicators proposed for the oven are not comprehensive, and more QoS indicators and energy consumption indicators are often considered in the actual production. Therefore, in the subsequent research, the part-level splitting of the coating machine ovens can be more refined to collect and summarize a more comprehensive collection of manufacturing services for the coating machine ovens; additionally, the indicators in the modeling can be improved to make the experimental conclusions closer to the real production situation. In this paper, the following conclusions are obtained through field research, completing the part-level splitting of the manufacturing task of the coating machine oven, obtaining the candidate matching set of the oven, and then through the steps of establishing the evaluation system, modeling, solving, and validation:

• Under the specific experimental scale, the LCSSA_DE algorithm has lower adaptation, with 69% to 77% points better than other algorithms, and has faster convergence speed, with 7.26% improvement in convergence speed compared to the suboptimal algorithm; in addition, analyzing the comparison of the GD indicator and the spread indicator under the two scales, the LCSSA_DE algorithm’s values are better than the other algorithms, and it exhibits a wide range of convergence and diversity, and the algorithm performs well.
• Under the test function with the same number of iterations and population size, compared with the MOAVOA algorithm, the MOGWO algorithm and the MOPSO algorithm, the LCSSA_DE algorithm has a lower GD value under seven conditions, with a minimum value of 6.60 × 10⁻⁵ under the ZDT2 function; and a lower IGD value under eight conditions, with a minimum value of 5.06 × 10⁻⁴ under the ZDT1 function; it further illustrates the effectiveness of the LCSSA_DE algorithm in solving such problems.
• Expanding the problem to nine different sizes of manufacturing problems of coating machine ovens and comparing the four algorithms normalized to the QoS values of the problem, which can positively reflect the benefits of the demand-side of crowdsourcing services, on the basis of 10 processes, 20 processes, and 30 processes, the LCSSA_DE algorithms’ time indicators are all concentrated in (0.3–0.67), (0.29–0.7), and (0.28–0.68); cost indicators are all concentrated in (0.25–0.67), (0.22–0.7), and (0.22–0.68); quality indicators are all concentrated in (0.63–0.95), (0.6–0.92), (0.61–0.94). Meanwhile, by comparing the bi-objective manufacturing service portfolio optimization, the LCSSA_DE algorithm obtains a smaller value of the energy consumption indicator, which is increasing with the increase in the population size, and most of the solutions for the LCSSA_DE algorithm are concentrated in the lower-left optimal part.