Performance and Mechanism on Sand Mold Ultrasonic Milling
Abstract
1. Introduction
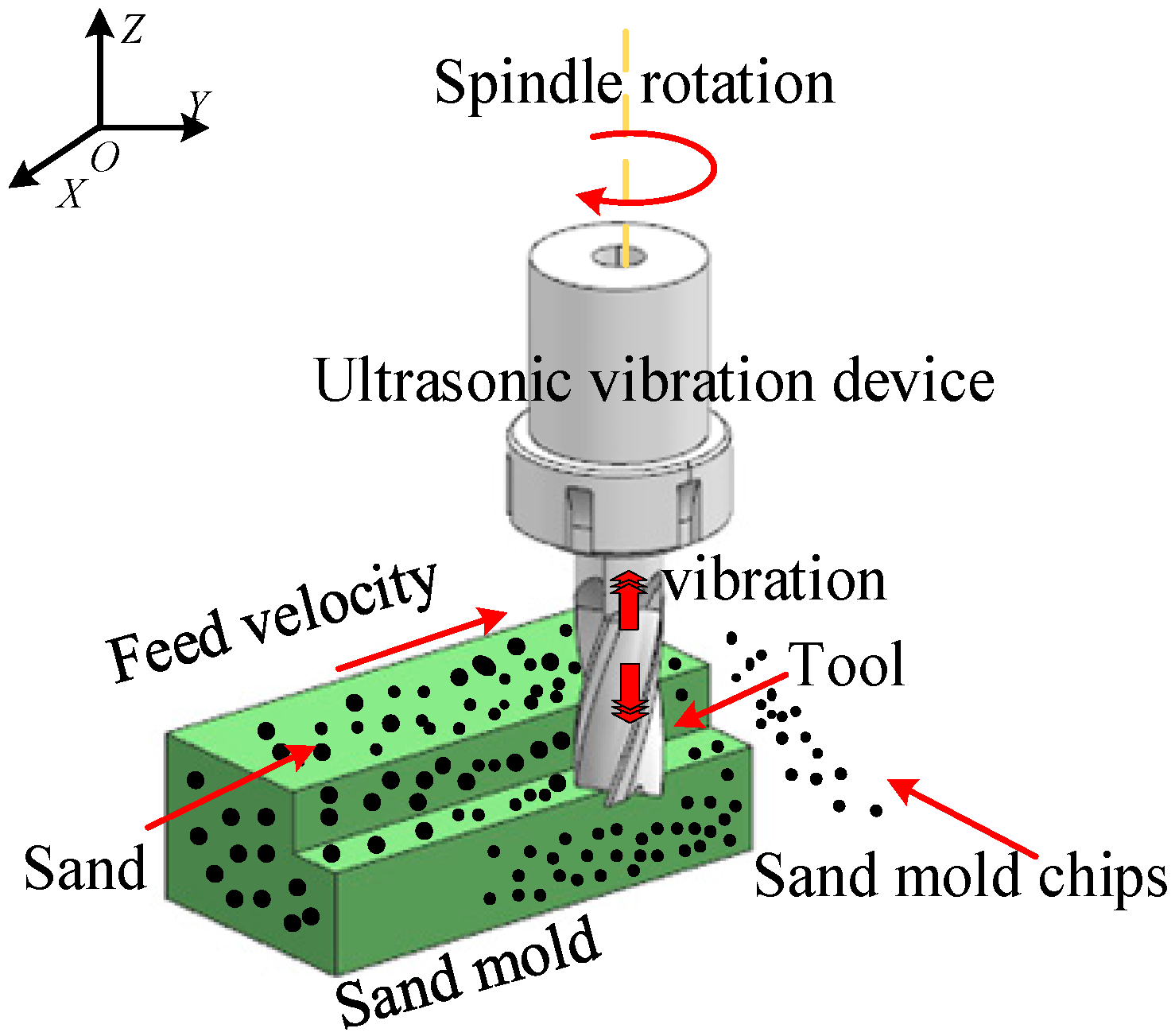
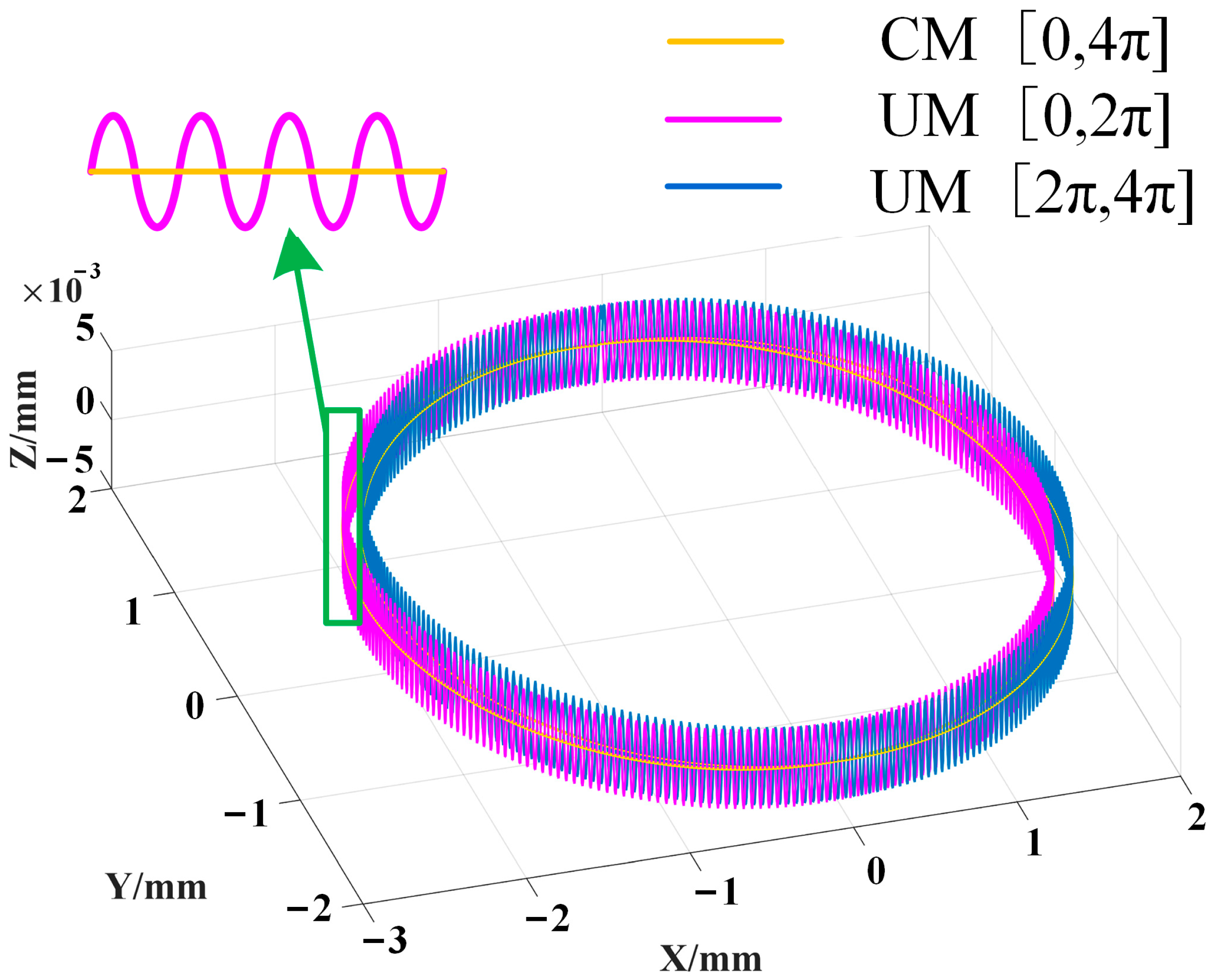
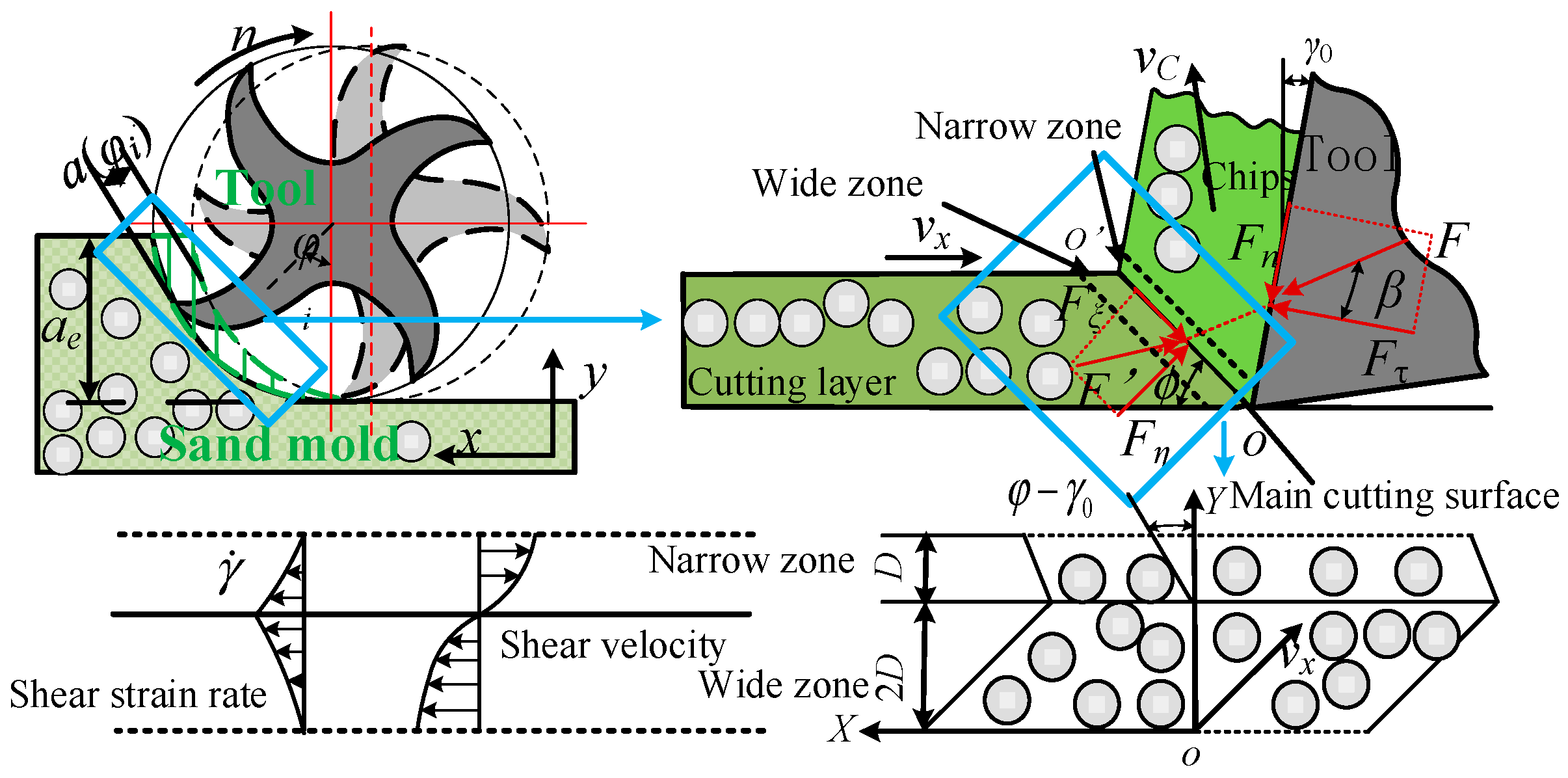
2. Characteristics of Sand Mold UM
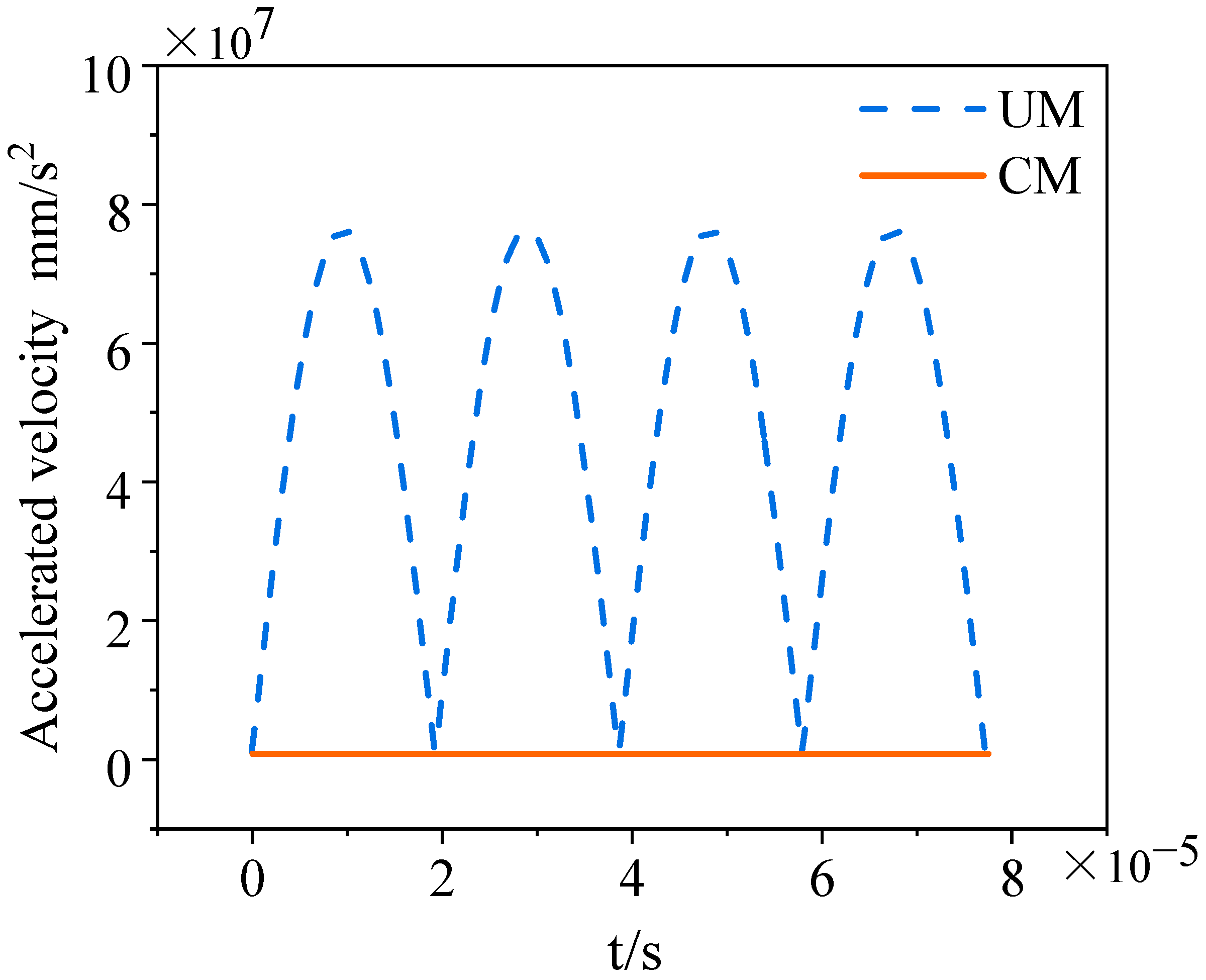
3. Dynamic Milling Force of Sand Mold UM
4. Sand Mold UM Experiment
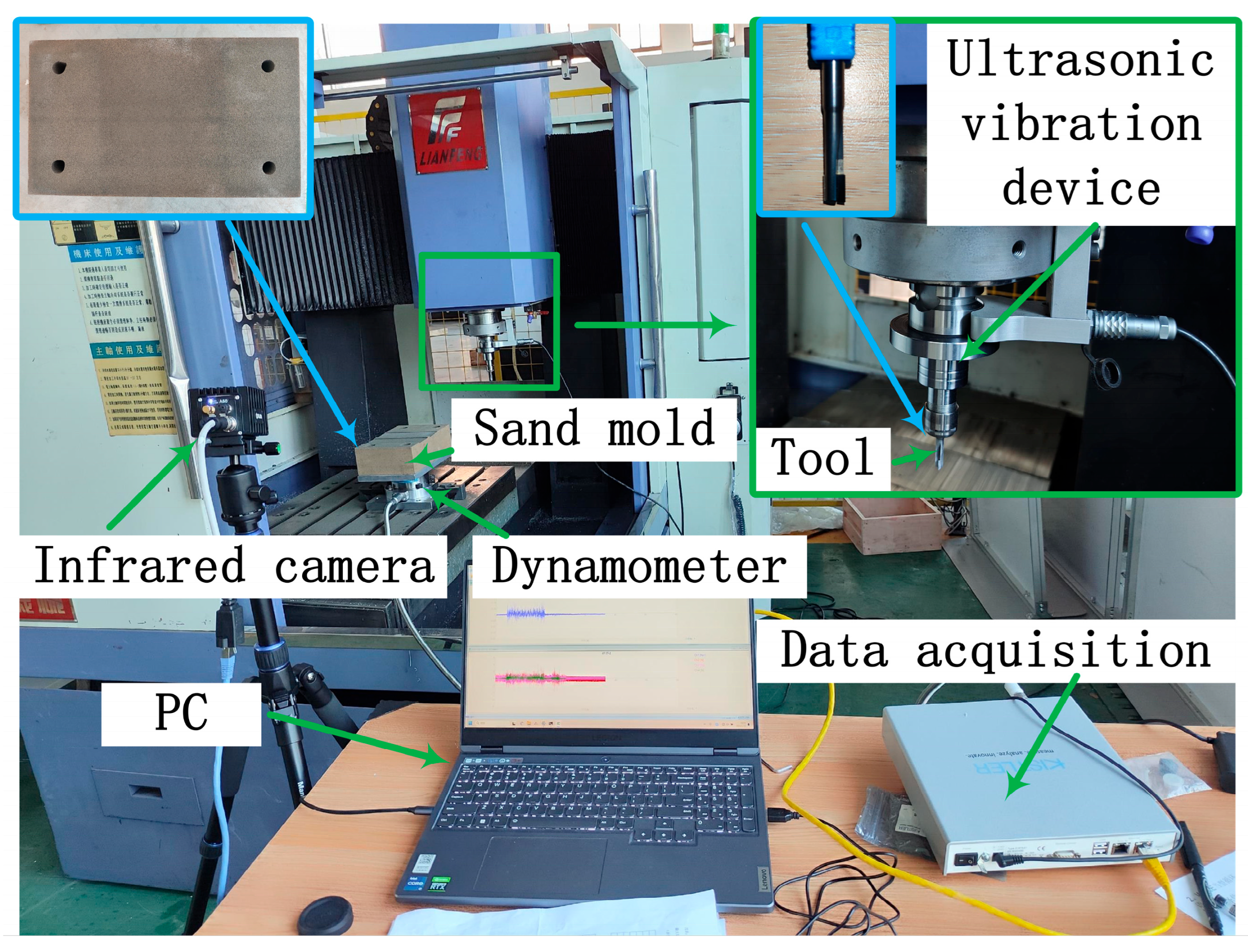
4.1. Experimental Setup and Procedure
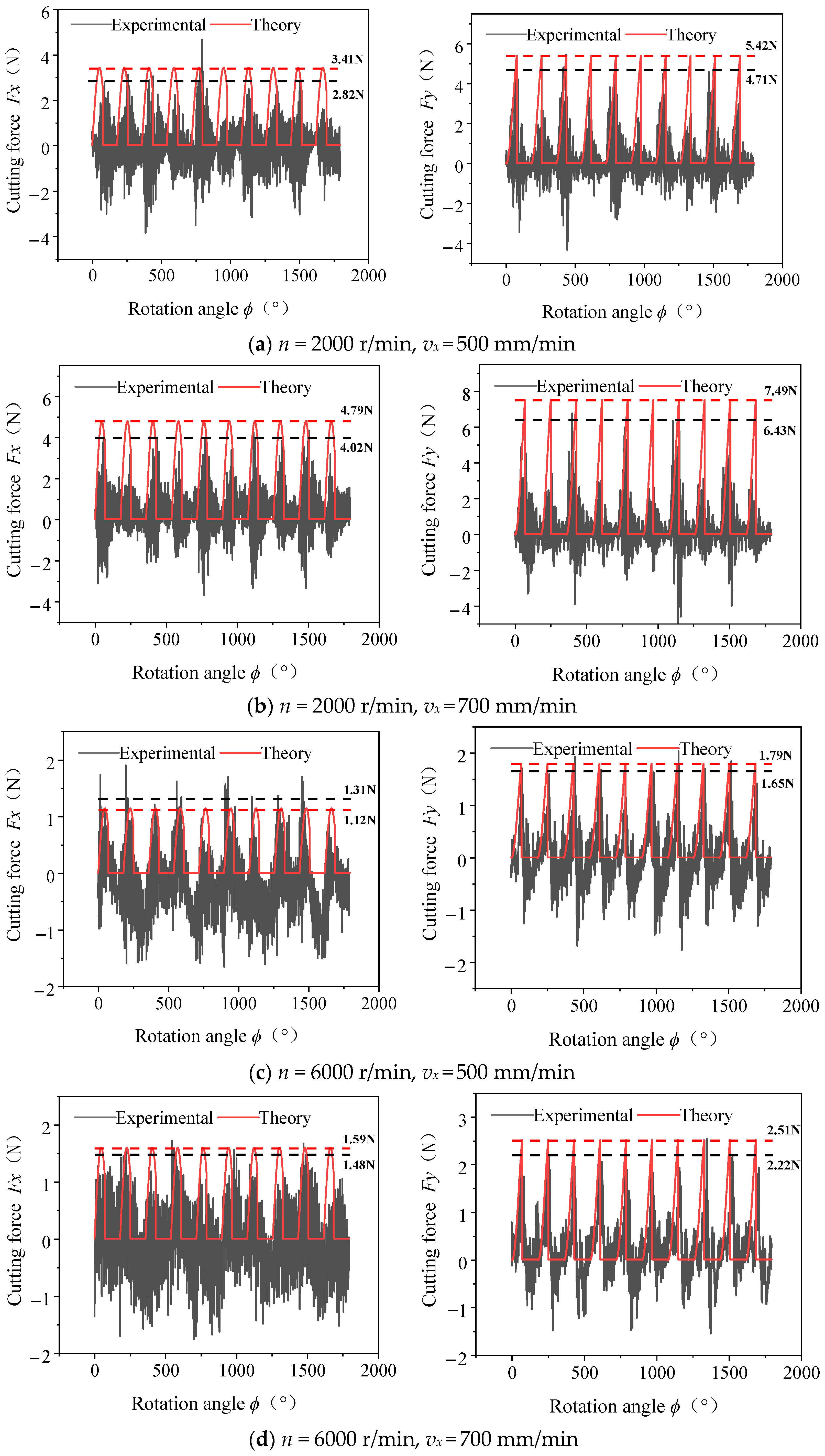
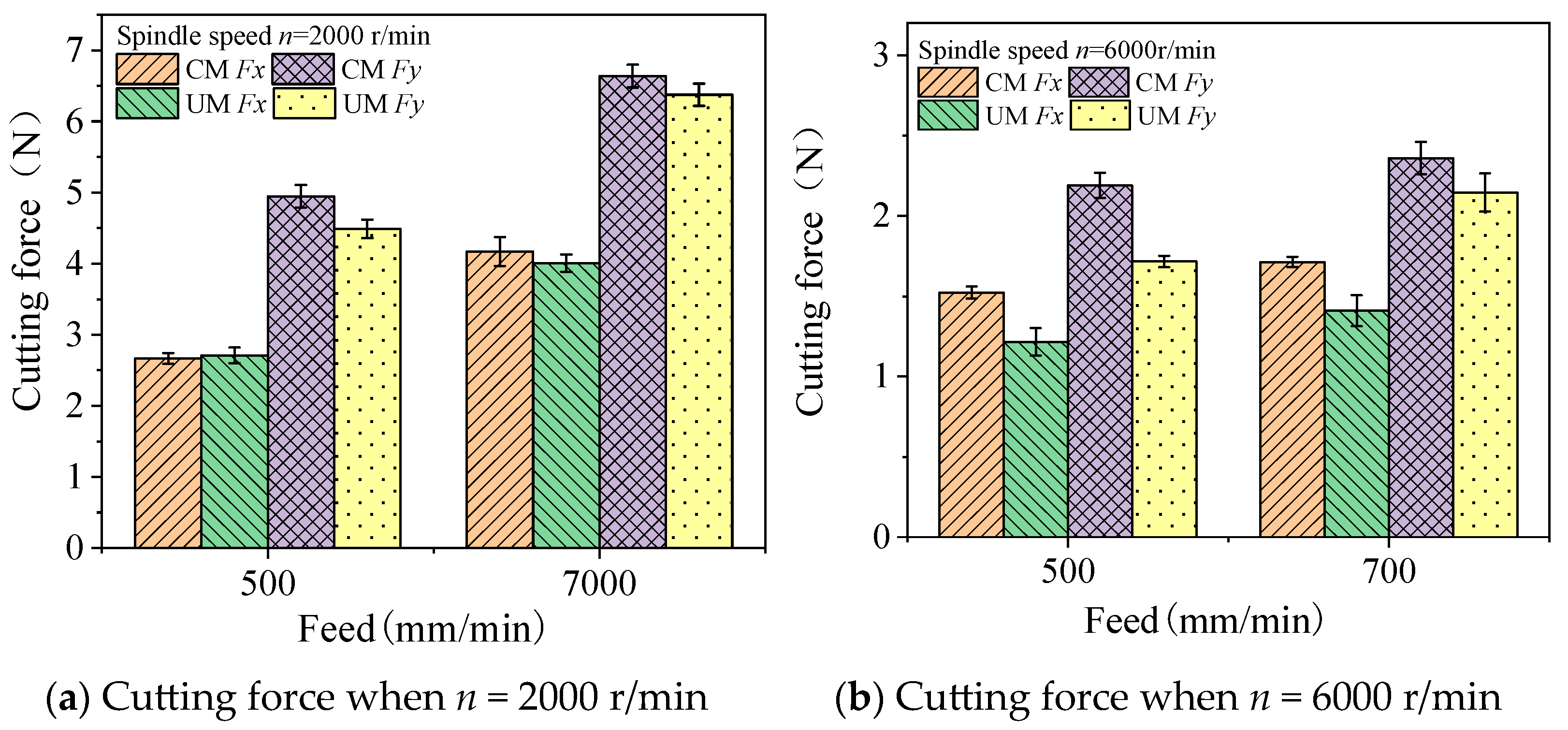
4.2. Analysis of the Milling Force on the Sand Mold
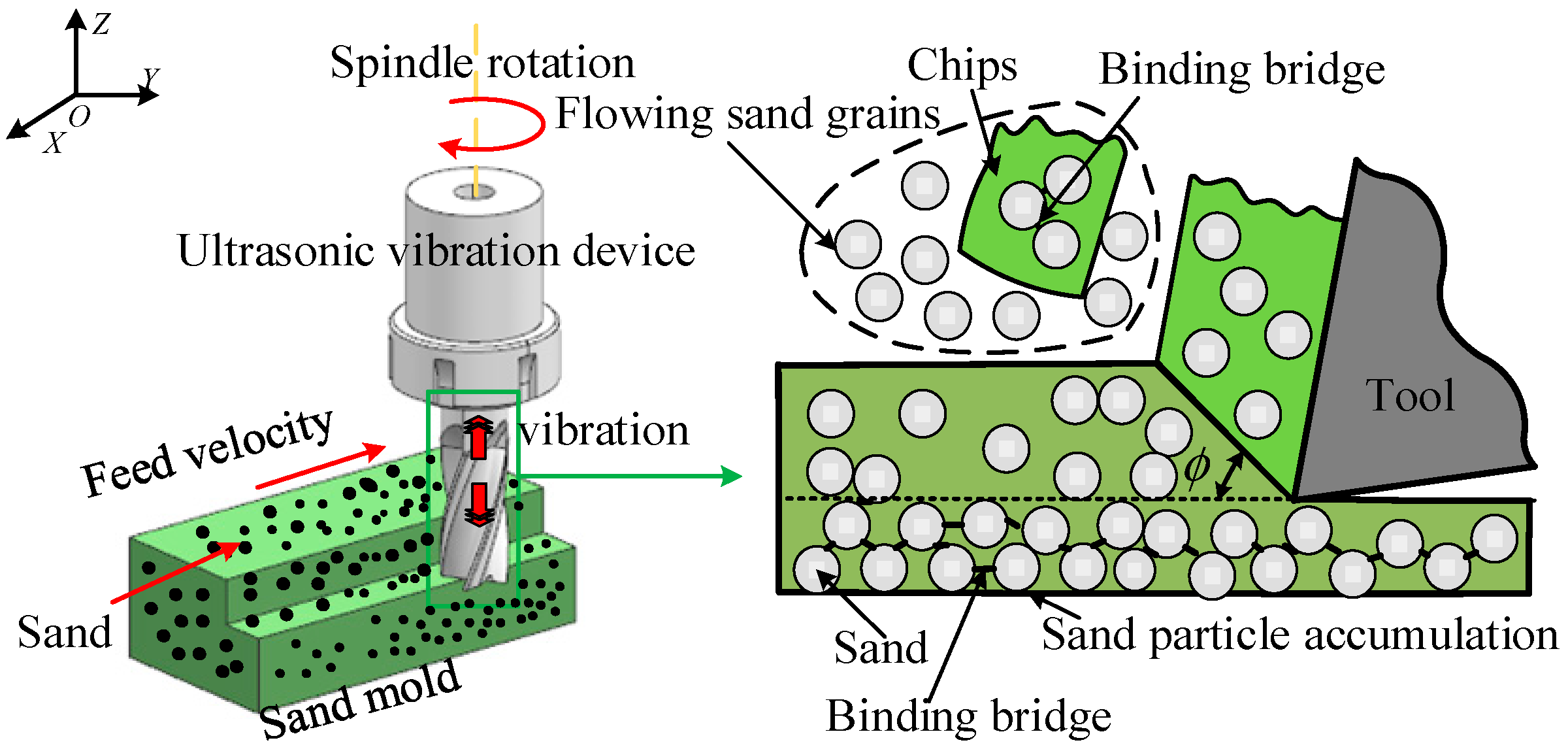
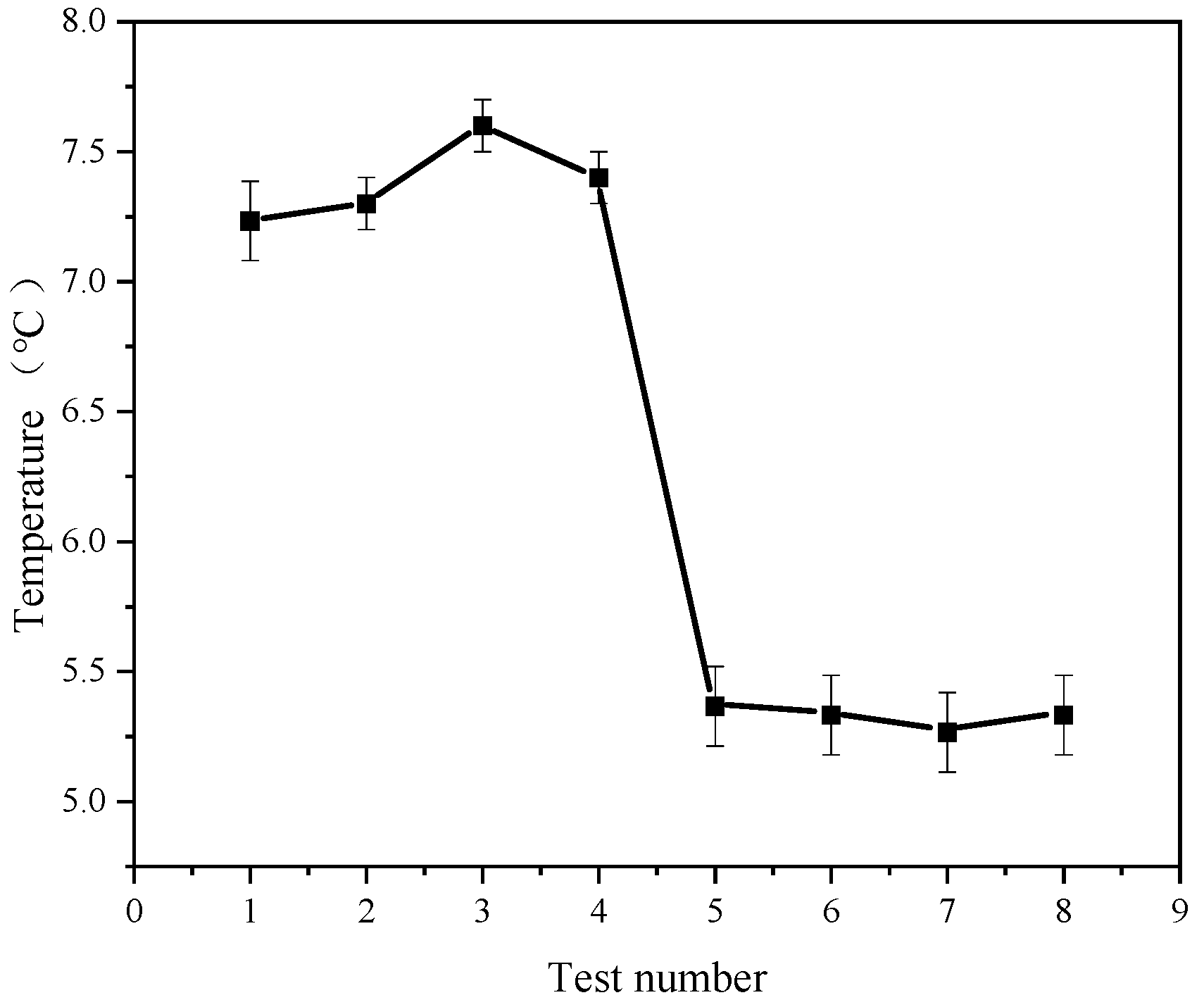
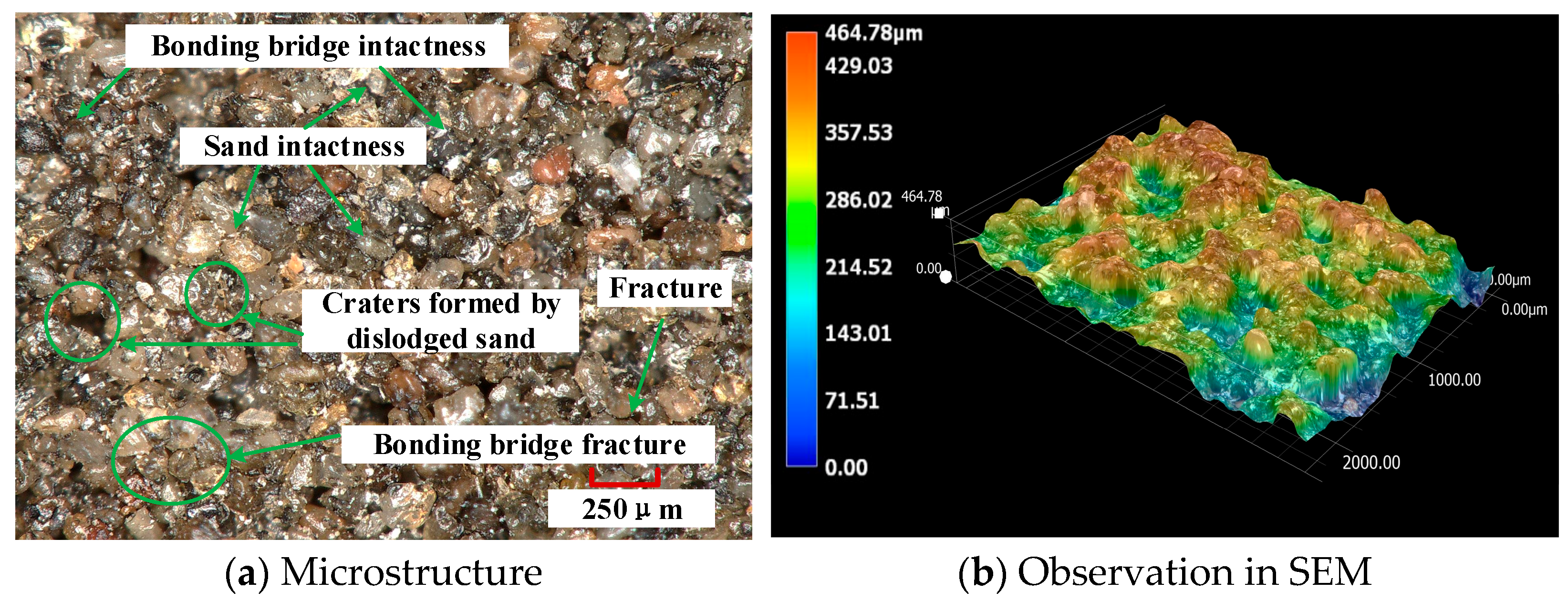
4.3. Analysis of the Microstructure After Milling
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, K.; Xu, Z.; Zhang, S.; Xiao, W. Research Progress in Sand Casting Process for Titanium Alloy. Spec. Cast. Nonferrous Alloys 2023, 43, 1598–1606. [Google Scholar]
- Chen, X. Research on Manufacturing Technology of Die Casting Mold Based on Digital Forming. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Xiang, Q.; Zhang, W.; Mao, J.; Qiu, K.; Li, R. Exploration and Practice of Applying the Digital No-Pattern Casting Technology to Produce Art Casting. Foundry Equip. Technol. 2014, 1, 15–18. [Google Scholar]
- Xie, D.; Yu, H.; Xu, Z.; Rao, J.; Nie, M.; Liang, X. Effect of NC Milling Process Parameters on Surface Quality of the Coated Sand Mold. Foundry Technol. 2018, 39, 1228–1232. [Google Scholar]
- Shan, Z.; Zhu, F. A Model for Predicting Dynamic Cutting Forces in Sand Mould Milling with Orthogonal Cutting. Chin. J. Mech. Eng. 2018, 31, 103. [Google Scholar] [CrossRef]
- Shan, Z.; Zhu, F. Wear Mechanism and Prediction Model of Polycrystalline Diamond Tool in Milling Sand Mould. J. Mech. Eng. 2018, 54, 124–132. [Google Scholar] [CrossRef]
- Zhang, G.; Shan, Z.; Liu, F.; Liu, L.; Liang, H.; Ming, Y. Influence of Milling Forming Parameters on the Milling Force of Frozen Sand Mold. Foundry Technol. 2023, 44, 665–670. [Google Scholar]
- Rao, J.; Xu, Z.; Xie, Y.; Zhao, K.; Nie, M.; Liang, X. Sand Model Milling Force Prediction Calculation and Fracture Surface Analysis. Foundry 2016, 65, 228–232+236. [Google Scholar]
- Rizal, S.M.; Suprayitno, S.; Aji, R.Y.P. Parameter Design of Sand Casting to Minimize Shrinkage Defects, Porosity Defects and Incomplete Defects. Mater. Sci. Forum 2024, 11223–11229. [Google Scholar] [CrossRef]
- Zhang, D.; Peng, Z.; Geng, D.; Jiang, X.; Liu, Y.; Zhou, Z.; Yin, X. Development of High-Speed Wave-Motion Ultrasonic Machining Technology with High Efficiency and Low Damage. Aeronaut. Manuf. Technol. 2022, 65, 22–33. [Google Scholar]
- Asmael, M.; Safaei, B.; Zeeshan, Q.; Zargar, O.; Nuhu, A.A. Ultrasonic Machining of Carbon Fiber-Reinforced Plastic Composites: A Review. Int. J. Adv. Manuf. Technol. 2021, 113, 3079–3120. [Google Scholar] [CrossRef]
- Bie, W.; Zhao, B.; Chen, F.; Wang, X.; Zhao, C.; Niu, Y. Progress of Ultrasonic Vibration-Assisted Machining Surface Micro-Texture and Serviceability. Diam. Abras. Eng. 2023, 43, 401–416. [Google Scholar]
- Kabir, S.; Ansary, R.S.; Li, Y.; Zhang, M.; Cong, W. Rotary ultrasonic surface machining of silicon: Effects of ultrasonic power and tool rotational speed. Manuf. Lett. 2024, 41, 518–525. [Google Scholar] [CrossRef]
- Zhu, S.; Sun, Y.; Wang, F.; Gong, H. Investigation on the Surface Integrity of 40Cr Steel Machined by Rotary Ultrasonic Flank Milling. Micromachines 2024, 15, 189. [Google Scholar] [CrossRef]
- Huang, W.; Cao, S.; Li, H.N.; Zhou, Q.; Wu, C.; Zhu, D.; Zhuang, K. Tool Wear in Ultrasonic Vibration-Assisted Drilling of CFRP: A Comparison with Conventional Drilling. Int. J. Adv. Manuf. Technol. 2021, 115, 1809–1820. [Google Scholar] [CrossRef]
- Delgado Arroyo, D.; Richter, T.; Schroepfer, D.; Boerner, A.; Rhode, M.; Lindner, T.; Preuß, B.; Lampke, T. Influence of Milling Conditions on AlxCoCrFeNiMoy Multi-Principal-Element Alloys. Coatings 2023, 13, 662. [Google Scholar] [CrossRef]
- Potyondy, D.O.; Cundall, P.A. A bonded-particle model for rock. Int. J. Rock Mech. Min. Sci. 2004, 41, 1329–1364. [Google Scholar] [CrossRef]
- Kazerani, T.; Zhao, J. Micromechanical parameters in bonded particle method for modelling of brittle material failure. Int. J. Numer. Anal. Methods Geomech. 2010, 34, 1877–1895. [Google Scholar] [CrossRef]
- Wang, G.; Xiong, G.; Fang, H. General Ontological Relationships for Particle Flow. Sci. China 1998, 28, 282–288. [Google Scholar]
- Zhang, D.Z.; Rauenzahn, R.M. Stress Relaxation in Dense and Slow Granular Flows. J. Rheol. 2000, 44, 1019–1041. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, S. Soil Mechanics; China Architecture & Building Press: Beijing, China, 2001. [Google Scholar]
- Astakhov, V.P.; Osman, M.O.M.; Hayajneh, M.T. Re-evaluation of the Basic Mechanics of Orthogonal Metal Cutting: Velocity Diagram, Virtual Work Equation and Upper-Bound Theorem. Int. J. Mach. Tools Manuf. 2001, 41, 393–418. [Google Scholar] [CrossRef]
- Pu, X. Physical Simulation and Process Parameter Optimization of Nickel Base Superalloy Cutting. Master’s Thesis, Southwest Petroleum University, Chengdu, China, 2016. [Google Scholar]
- Hou, M.; Shan, Z.; Dong, X.; Ding, B. Prediction of Sand Mold Cutting Force and Identification of Cutting Force Coefficients. J. Phys. Conf. Ser. 2021, 1885, 042002. [Google Scholar]




| Number | Speed | Feed | Cut | Depth | Ultrasonic |
|---|---|---|---|---|---|
| (r/min) | (mm/min) | (mm) | (mm) | Open | |
| 1 | 2000 | 500 | 3 | 2.5 | Yes |
| 2 | 2000 | 500 | 3 | 2.5 | No |
| 3 | 2000 | 700 | 3 | 2.5 | Yes |
| 4 | 2000 | 700 | 3 | 2.5 | No |
| 5 | 6000 | 500 | 3 | 2.5 | Yes |
| 6 | 6000 | 500 | 3 | 2.5 | No |
| 7 | 6000 | 700 | 3 | 2.5 | Yes |
| 8 | 6000 | 700 | 3 | 2.5 | No |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, B.; Shan, Z.; Zhu, Z.; Ding, D.; Zhao, Q. Performance and Mechanism on Sand Mold Ultrasonic Milling. Coatings 2025, 15, 633. https://doi.org/10.3390/coatings15060633
Zhuang B, Shan Z, Zhu Z, Ding D, Zhao Q. Performance and Mechanism on Sand Mold Ultrasonic Milling. Coatings. 2025; 15(6):633. https://doi.org/10.3390/coatings15060633
Chicago/Turabian StyleZhuang, Bailiang, Zhongde Shan, Zhuozhi Zhu, Di Ding, and Qi Zhao. 2025. "Performance and Mechanism on Sand Mold Ultrasonic Milling" Coatings 15, no. 6: 633. https://doi.org/10.3390/coatings15060633
APA StyleZhuang, B., Shan, Z., Zhu, Z., Ding, D., & Zhao, Q. (2025). Performance and Mechanism on Sand Mold Ultrasonic Milling. Coatings, 15(6), 633. https://doi.org/10.3390/coatings15060633




