The Effect of Substrate Roughness and Impact Angle on Droplet Spreading in Spraying
Abstract
1. Introduction
2. Numerical Models and Methods
2.1. Mathematical Model of Droplet Spreading Process
2.2. Solution Method
3. Simulation Results and Discussion
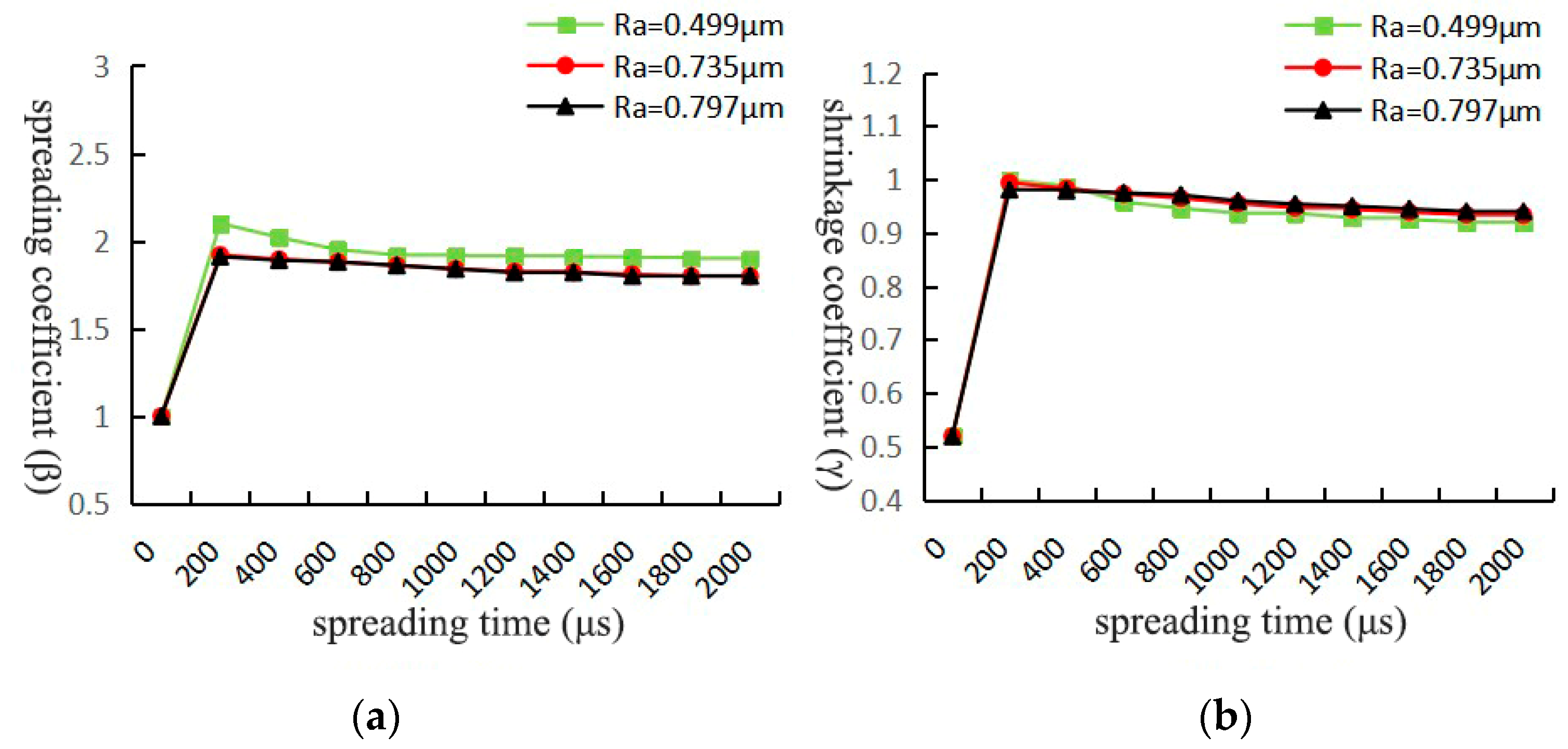
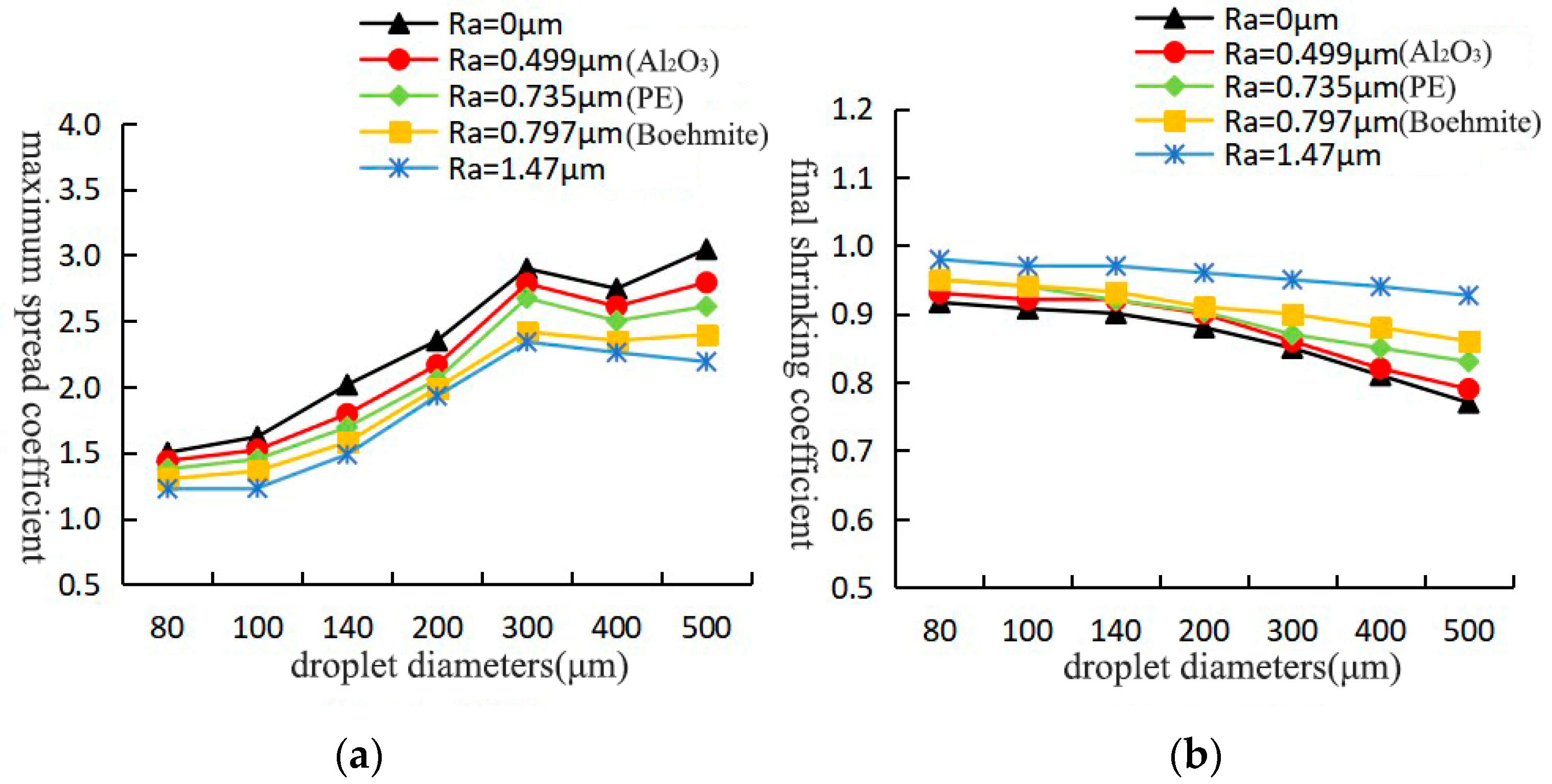
3.1. Effect of Substrate Surface Roughness on the Spreading Process
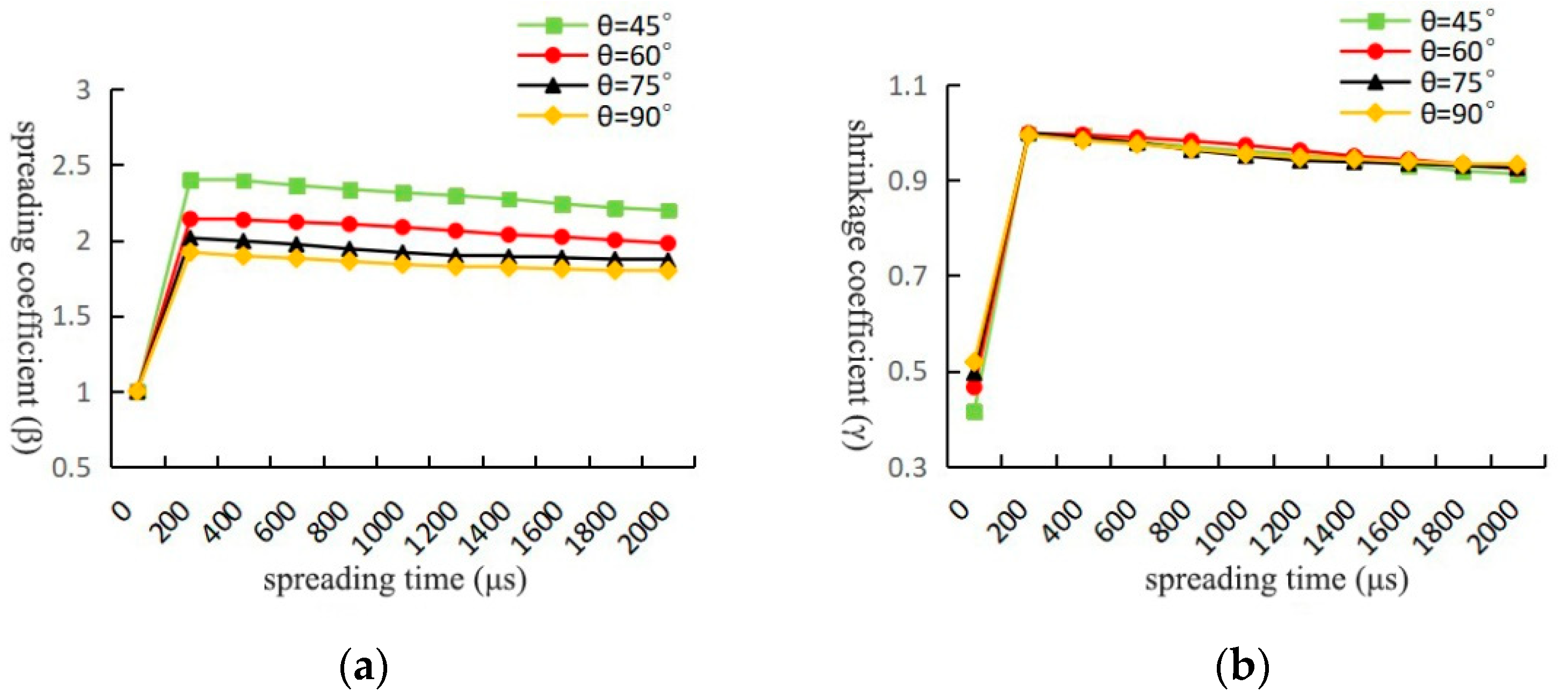
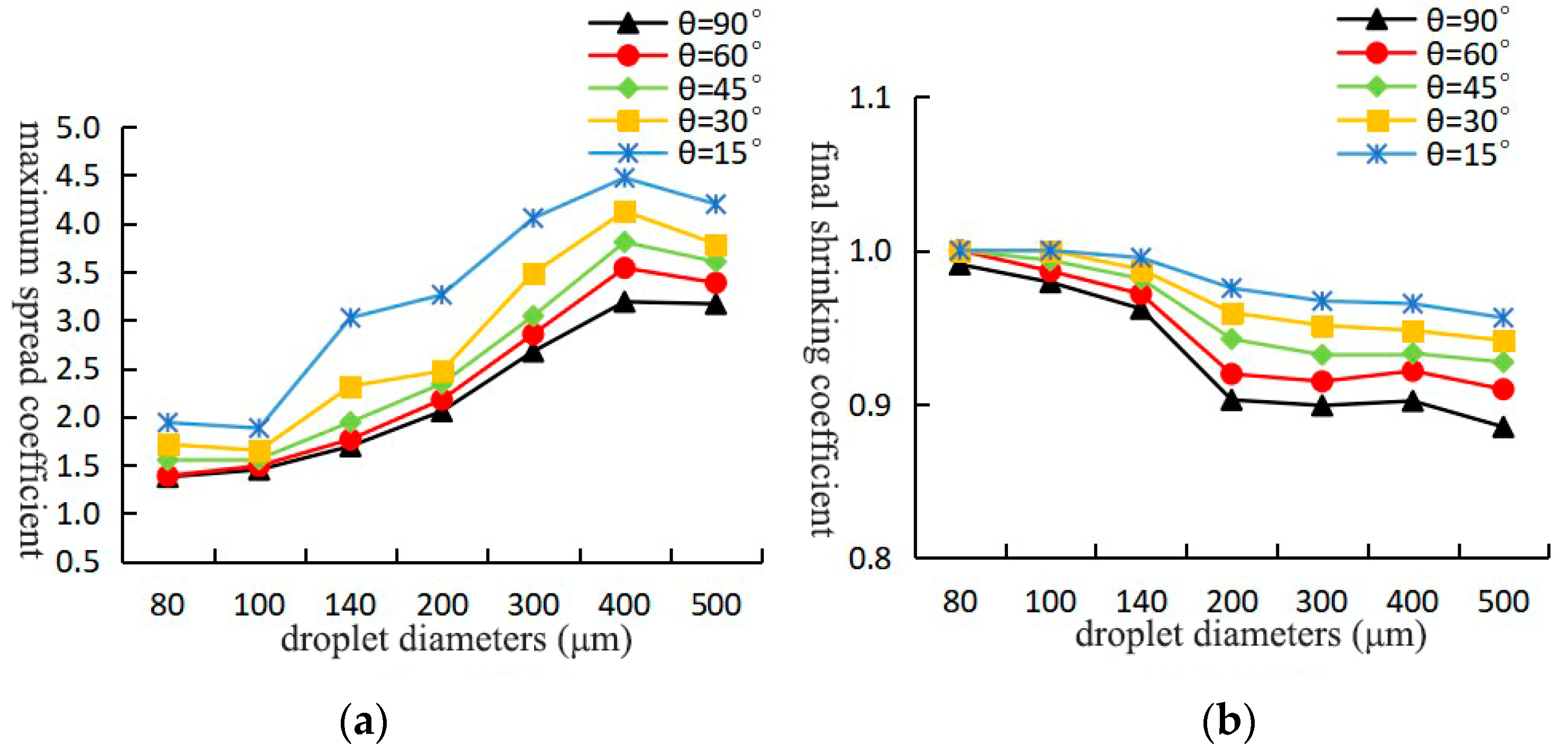
3.2. Effect of Droplet Impingement Angle on Spreading Process
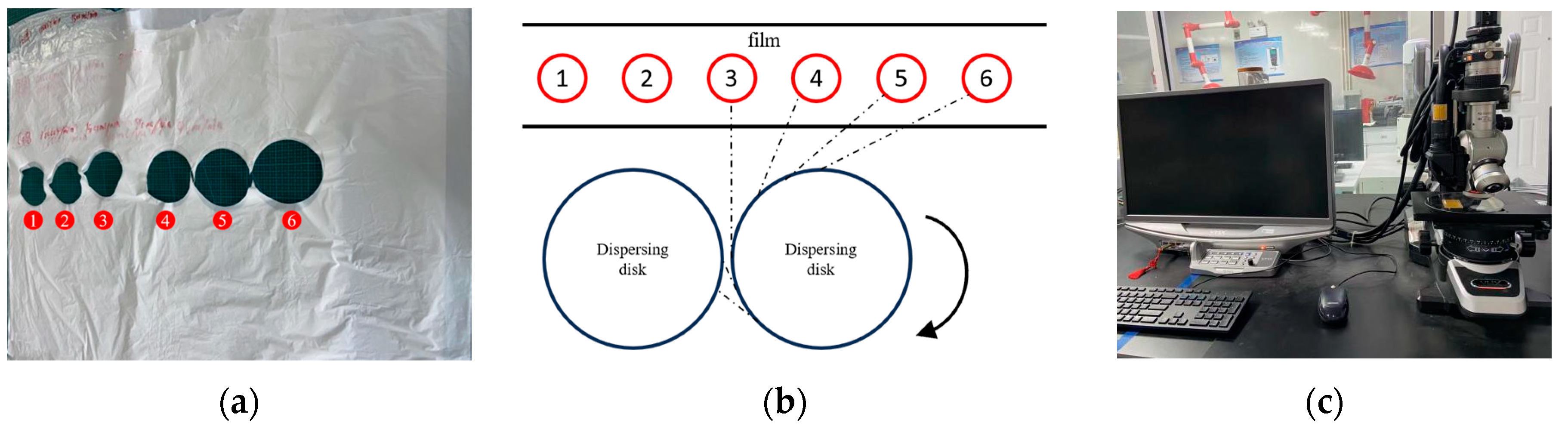
4. Experimental Verification
4.1. Experimental Equipment
4.2. Results
4.2.1. Effect of Substrate Roughness on Spreading of PVDF Slurry Droplets
4.2.2. Effect of Impact Angle on Spreading of PVDF Slurry Droplets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meinshausen, M.; Meinshausen, N.; Hare, W.; Raper, S.C.B.; Frieler, K.; Knutti, R.; Frame, D.J.; Allen, M.R. Greenhouse-gas emission targets for limiting global warming to 2 °C. Nature 2009, 458, 1158–1162. [Google Scholar] [CrossRef]
- Twidell, J. Renewable Energy Resources; Routledge: London, UK, 2021. [Google Scholar]
- Wen, Z.; Fang, W.; Chen, L.; Guo, Z.; Zhang, N.; Liu, X.; Chen, G. Anticorrosive copper current collector passivated by self-assembled porous membrane for highly stable lithium metal batteries. Adv. Funct. Mater. 2021, 31, 2104930. [Google Scholar] [CrossRef]
- Hao, Z.; Zhao, Q.; Tang, J.; Zhang, Q.; Liu, J.; Jin, Y.; Wang, H. Functional separators towards the suppression of lithium dendrites for rechargeable high-energy batteries. Mater. Horiz. 2021, 8, 12–32. [Google Scholar] [CrossRef]
- Lee, H.; Yanilmaz, M.; Toprakci, O.; Fu, K.; Zhang, X. A review of recent developments in membrane separators for rechargeable lithium-ion batteries. Energy Environ. Sci. 2014, 7, 3857–3886. [Google Scholar] [CrossRef]
- Pan, S.; Chen, J.; Wei, Y.; Wu, C.; Jia, J.; Yao, K. Simulation Analysis of the Influence of Operating Parameters on the Pressure Profile in the Coating Bead. Coatings 2024, 14, 1413. [Google Scholar] [CrossRef]
- Wang, X.; Xu, B.; Guo, S.; Zhao, Y.; Chen, Z. Droplet impacting dynamics: Recent progress and future aspects. Adv. Colloid Interface Sci. 2023, 317, 102919. [Google Scholar] [CrossRef] [PubMed]
- Park, H.; Carr, W.W.; Zhu, J.; Morris, J.F. Single drop impaction on a solid surface. AIChE J. 2003, 49, 2461–2471. [Google Scholar] [CrossRef]
- Harlow, F.H.; Shannon, J.P. The Splash of a Liquid Drop. J. Appl. Phys. 1967, 38, 3855–3866. [Google Scholar] [CrossRef]
- Nepomnyashchy, A. Droplet on a liquid substrate: Wetting, dewetting, dynamics, instabilities. Curr. Opin. Colloid Interface Sci. 2021, 51, 101398. [Google Scholar] [CrossRef]
- Vafaei, S.; Podowski, M.Z. Analysis of the relationship between liquid droplet size and contact angle. Adv. Colloid Interface Sci. 2005, 113, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Vafaei, S.; Podowski, M.Z. Theoretical analysis on the effect of liquid droplet geometry on contact angle. Nucl. Eng. Des. 2005, 235, 1293–1301. [Google Scholar] [CrossRef]
- Yan, Z.; Li, Y.; Li, C. Numerical simulation study of droplet impact on various solid surfaces. J. Therm. Sci. Tech. 2018, 17, 8. [Google Scholar]
- Wijshoff, H. Drop dynamics in the inkjet printing process. Curr. Opin. Colloid Interface Sci. 2018, 36, 20–27. [Google Scholar] [CrossRef]
- Arogeti, M.; Sher, E.; Bar-Kohany, T. Drop Impact on Small Targets With Different Target-to-Drop Diameters Ratio. Chem. Eng. Sci. 2018, 193, 89–101. [Google Scholar] [CrossRef]
- Bennett, T.; Poulikakos, D. Splat-quench solidification: Estimating the maximum spreading of a droplet impacting a solid surface. J. Mater. Sci. 1993, 28, 963–970. [Google Scholar] [CrossRef]
- Chandra, S.; Avedisian, C.T. On the collision of a droplet with a solid surface. Proc. R. Soc. A Math. Phys. Eng. Sci. 1991, 432, 13–41. [Google Scholar] [CrossRef]
- Eggers, J.; Fontelos, M.A.; Josserand, C.; Zaleski, S. Drop dynamics after impact on a solid wall: Theory and simulations. Phys. Fluids 2010, 22, 062101. [Google Scholar] [CrossRef]
- Roisman, I.V.; Lembach, A.; Tropea, C. Drop splashing induced by target roughness and porosity: The size plays no role. Adv. Colloid Interface Sci. 2015, 222, 615–621. [Google Scholar] [CrossRef]
- Guan, C.; Lv, X.; Han, Z.; Chen, C. The wetting characteristics of aluminum droplets on rough surfaces with molecular dynamics simulations. Phys. Chem. Chem. Phys. 2020, 22, 2361–2371. [Google Scholar] [CrossRef] [PubMed]
- Shang, Y.; Zhang, Y.; Hou, Y.; Bai, B.; Zhong, X. Effects of surface subcooling on the spreading dynamics of an impact water droplet. Phys. Fluids 2020, 32, 123–309. [Google Scholar] [CrossRef]
- Sakakibara, B.; Inamuro, T. Lattice Boltzmann simulation of collision dynamics of two unequal-size droplets. Int. J. Heat Mass Transf. 2008, 51, 3207–3216. [Google Scholar] [CrossRef]
- Wei, Y.; Qian, Y. Coalescence of Two Colliding Liquid Droplets with Lattice Boltzmann Method. In Proceedings of the 65th Annual Meeting of the APS Division of Fluid Dynamics, San Diego, CA, USA, 18–20 November 2012. [Google Scholar]
- Deng, Z.; Zhang, C.; Chen, Y.; Zhang, L.; Shi, M. Study on Dynamics Behaviors of Droplet Coalescence. J. Eng. Thermophys. 2015, 36, 1321–1324. [Google Scholar]
- Li, P.; Huang, Y.; Yu, Y.; Ma, X.; Wang, Z.; Shao, G. Recent advances and future prospects for PVDF-based solid polymer electrolytes. J. Power Sources 2025, 628, 235855. [Google Scholar] [CrossRef]









| Symbol | Value | Property |
|---|---|---|
| k | 0.0929 | Consistency index (Pa·s) |
| n | 1.0681 | Flow behavior index |
| 4.6501 | Yield stress (Pa) | |
| 0.0910 | Yield viscosity (Pa·s) |
| Substrate Type | Roughness () |
|---|---|
| Al2O3 | 0.499 |
| PE | 0.735 |
| boehmite | 0.797 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, L.; Ma, Y.; Yu, K.; Xu, H.; Hao, J.; Li, Y.; Wang, K.; Sun, D. The Effect of Substrate Roughness and Impact Angle on Droplet Spreading in Spraying. Coatings 2025, 15, 242. https://doi.org/10.3390/coatings15020242
Ma L, Ma Y, Yu K, Xu H, Hao J, Li Y, Wang K, Sun D. The Effect of Substrate Roughness and Impact Angle on Droplet Spreading in Spraying. Coatings. 2025; 15(2):242. https://doi.org/10.3390/coatings15020242
Chicago/Turabian StyleMa, Li’e, Yijun Ma, Kanghui Yu, Hongli Xu, Jiaqi Hao, Yuan Li, Kaiyu Wang, and Dongyue Sun. 2025. "The Effect of Substrate Roughness and Impact Angle on Droplet Spreading in Spraying" Coatings 15, no. 2: 242. https://doi.org/10.3390/coatings15020242
APA StyleMa, L., Ma, Y., Yu, K., Xu, H., Hao, J., Li, Y., Wang, K., & Sun, D. (2025). The Effect of Substrate Roughness and Impact Angle on Droplet Spreading in Spraying. Coatings, 15(2), 242. https://doi.org/10.3390/coatings15020242






