Abstract
The process of normal (N) zone propagation in three superconducting YBaCuO thin films with different Pearl length values was theoretically studied. The point appearance of the N zone was found to result from powerful energy release caused by micro-sized magnetic cumulation. Solutions of the heat equation for hot electrons, diffusing to ~15 nm depth into the edge of the Pearl length, were obtained for the two length cases. The hot electron thermalization induced a transition to N state at the aforementioned depth due to fast exceeding of Tc, followed by flash high temperature growth. In the third case, we considered a process of crack branching when the superconducting current concentrated at the tips, followed by the transition to N state caused by exceeding jc. The superfast reaction of the superconductor allowed it to restore the energy loss at the Pearl length in all cases. This explains the step propagation process of the N zone with velocities up to 2.7 × 103 and 1.1 × 103 m/s in the first and second cases. In the third, the propagation can reach the detonation wave velocity of about 1 × 104 m/s. It is concluded that the process of the N zone propagation has the character of a combustion wave.
1. Introduction
There is special interest for researchers in the investigation of interphase border movement, especially in cases where the phase transition is accompanied by ample heat release. In such a case, a self-sustaining combustion-like wave can be formed. Examples include the freezing wave turning supercooled water into ice [1], the wave of condensation of steam in a shock tube [2,3], and the condensation of gaseous hydrocarbons [4,5].
A case of sufficient heat release is the propagation of the normal (N) phase zone in the superconductor with a flowing current from a small N area, which appears due to the Joule heating. The study of the propagation of the N zone began a long time ago, as this is of great importance for creating fast-acting detectors and current limiters [6,7]. The transition from a superconducting (S) to N state is commonly accepted as S-N switching. In the type II superconductor at the overcritical current values, the codependence between the Joule heating and the current’s magnetic field forms positive feedback. Due to nonlinear and dissipative effects during magnetic flux penetration, this feedback creates a medium where various stationary waves can propagate [8,9]. A thermomagnetic shock wave can be initiated by a local rapid increase in temperature with a simultaneous magnetic flux jump. However, such wave propagation is most likely a single event due to the consequent loss of the material’s S properties. As a result, such single S-N switching is currently not used widely, so experimenting with it is rare. However, studies of heat propagation after heating thin metal films with ultra-short power laser pulses are carried out quite intensively. The obtained results are used in various technological processes. When taking into account fast processes, a two-temperature model is used. The heat conduction equation is solved both for hot electron diffusion and for slower heat processes in the lattice [10,11,12,13].
In some applications, it is crucial to use current pulses of ns duration transmitting through a transmission line. The S section of the transmission line can be switched by the current pulse of overcritical value. During study of such switching of thin YBaCuO film strip sections, certain features of the S-N switching have been revealed. In thin-film strip-like samples, the current and expelled magnetic field were found to be concentrated at the Pearl length λeff [14]. After studying scanning electron microscope images of the damaged samples, it was unveiled that a strong counteraction of the Lorentz force and the Meissner force is manifested at the sub-nanosecond risetime of the pulse. Therefore, the propagation of the N zone occurs from both film edges to the center. The moving S-N border constantly changes shape because it is in bending instability [15]. Moreover, such S-N border movement is accompanied by the formation of coherent jets when the valleys of the unstable S-N border buckle during the retreating of the S state. The jets are formed due to the incompressibility property of Meissner currents [15]. A hint of the existence of unconventional repulsive interaction between paired electrons was published in [16].
According to the model, the N zone propagation slowdown due to the counteraction is compensated by the high velocity of the penetrating coherent jets [15]. At higher current densities in λeff, jets with magnetic flux can penetrate deeply into the S state, with subsequent narrowing and reconnection of current lines at the narrowing point. After that, the S state forms circle regions with a trapped magnetic flux [17]. The images show that dark, round spots of a micron radius remain on the damaged thin films. This means that the S state tends to compress and eliminate this possibility of the emergence of the small N areas, and magnetic cumulation takes place because of the magnetic flux conservation law.
It can be noted that the disappearance of the S state can be achieved in a very short time by exciting the pairs in a fulminant manner, breaking them apart into nonequilibrium electrons [18,19]. Therefore, theoretically, the N zone can propagate during S-N switching with a very high Fermi velocity [20]. However, S-N border movement with Fermi velocity will most likely be achieved when the border between the S state, as the macroscopic quantum state, and S-N locally retreats when maintaining the S state becomes energetically nonviable.
The regions with trapped magnetic flux are micro-sized, about 10–15 µm in diameter, and because of magnetic cumulation, this value decreases by an order of magnitude. After an instantaneous temperature increase, the Lorentz and Meissner force counteraction appears. However, the radius of the N area is too small, and the S-N border cannot enter the state of bending instability. The question of how the N zone propagates becomes non-trivial. So, an answer to this question is offered in this article. Magnetic cumulation by S current is rarely mentioned in scientific papers; therefore, some data are taken from a two-temperature heat propagation model after pulsed laser illumination of thin metal films [12,13,21].
2. Modeling of Micro-Sized Magnetic Cumulation Induced by S State of Type II Superconductor with Subsequent N Zone Propagation
The article is a continuation of the experimental [22] and theoretical [15] study of the N zone propagation induced by S-N switching in thin YBaCuO films caused by an overcritical nanosecond current pulse. The study revealed the compressive action of the S state on micro-sized areas with trapped magnetic flux. The least understood is the propagation of the N zone from the local switched area caused by the magnetic field cumulation when, due to the small size of the area, a bending instability cannot develop. Herein, we try to give the results more physical meaning, although these are still only estimates.
2.1. Initial Conditions of the Magnetic Cumulation by S Currents
Preliminary calculations of currents and magnetic fields of micro-sized magnetic cumulation were carried out in [15]. Here, we expand the number of values of λeff to three, namely 2.45, 1.64, and 1.16 μm. We also take their current density values from [15]. The greatest uncertainty is caused by determining the initial current encircling a trapped magnetic flux. Before the reconnection of current lines, the current density is close to the critical one, but after the reconnection, as follows from the experiment, there is a cumulation of area with trapped flux. This means that the number of normal electrons has decreased, and the S properties, especially critical current density, have increased. It is assumed that all initial critical current densities will be comparable to the largest critical current density 15.9 × 1011 A/m2, as in the case when λeff equals 1.16 μm.
We rewrite Formula (4) from [15] for calculating the magnetic field in a simpler form:
here, is the magnetic constant, j is S current density, d is film thickness, r is the encircled area radius, and indexes = 0, 1 correspond to beginning and end of the cumulation.
The data on the beginning of the cumulation are given in Table 1.

Table 1.
Initial data for the areas with trapped magnetic flux.
The calculations of the results of the end of the cumulation are based on the conservation of magnetic flux during compression of the encircled area.
2.2. Solution of the Heat Conduction Equation to Determine the Parameters of the Propagation of the N Zone in the Absence of Banding Instability
There are insufficient data on the local heating of YBaCuO thin films to high temperatures. For this reason, we used a two-temperature model describing the heating of metal films by a short laser pulse [10,11,23]. The model developers often use the hyperbolic type of heat conduction equation. Since our results are of an estimation nature, the usual parabolic equation is solved. In Section 2.2.1 and Section 2.2.2, the solutions presented are for the cases in which λeff equal to 2.45 and 1.64 μm. In the case when λeff is 1.16 μm, N zone propagation condition is introduced in the Section 2.2.3.
2.2.1. Solution of Heat Conduction Equation with the First-Order Boundary Condition
The heat equation written in polar coordinates without φ coordinate is reduced to a dependence on a single variable by introducing a self-similar one:
where a is temperature conductivity, and τ is time. The boundary conditions are U(r,0) = T0; U(r1 + λeff,τ) = T1, τ > 0.
After replacing the variables, the heat equation transforms:
The solution is in the following form:
where special function (x) is the exponential integral, is constant, and is the film temperature at beginning time moment. It should be noted that (x) = −(−x).
2.2.2. Solution of Heat Conduction Equation with the Second-Order (Neuman) Boundary Condition
Such condition is preferable for the diffusion of hot electrons induced by a high gradient of temperature. To find a solution for the spreading of hot electrons, temperature regulation, in addition to the scale interval of , with new variable η (see Equation (2)), is introduced by the scale temperature value θsc:
where is a constant heat flux density, and λ is heat conductivity. Temperature conductivity a = λ/ρ·c, where ρ is density, and c is specific heat of YBaCuO.
The transformed equation is obtained as follows:
A solution of Equation (6) could be obtained using Laplace transform, but here, the solution is presented as a power series. However, in this case, the numerators in the coefficients appear as prime numbers, and we write it in expanded form:
also, finding T(η) is possible by using the second solution of the Kummer equation √π· with additive constant equal to 7.
The resulting solution is in the following form:
The boundary condition is computes the derivative at the point close to zero. At our scale, 1 nm point is an acceptable value. Determining is more challenging than from the Equation (4). is calculated after determining the temperature of the hot electrons.
According to the concept of cumulative S-N switching, initially, the temperatures of the regions after cumulation, having a radius of r1 + λeff, are estimated. With the appearance of the large temperature gradient, due to delay caused by the opposition of the Meissner force to the Lorentz force, a diffusion of hot electrons into the λeff with high-density S current begins. At some diffusion depth, thermalization of the electrons occurs. However, all this occurs on a micro-scale, so due to inevitable losses, the total propagation of the N zone does not exceed the distance of 4–5 λeff. Here, we consider the process at single λeff without taking into account the inevitable losses.
2.2.3. N Zone Propagation in the Case When λeff Equals 1.16 μm
In this case, the heating temperature of a thin film after the cumulation exceeds half of its melting temperature, 700 K, and micro cracks appear in it. It is known that the top of a rapidly opening crack is in an unstable state. As a result of the instability, the top tip becomes the source of minute, microscopic side branches [24,25]. When current flows through the material, it concentrates at the tops of cracks, and the released heat provokes their further growth. The irreversible damage peculiarities in thin films with flowing current are sufficiently described in [26]. To explain N zone propagation when the thin film is in the S state, a schematic diagram is employed.
3. Results
Based on the law of magnetic flux conservation, the results of the central area with a radius r1 + λeff being heated were obtained and shown in Table 2.

Table 2.
Result data at the end of the magnetic cumulation calculated based on magnetic flux conservation.
The N current densities J1(N) after the S-N switching were determined based on the maximum density obtained experimentally for the entire film—1.08 × 1012 A/m2. As one can see, the cumulated magnetic fields do not have large values. In the third case, due to the pulsed action reducing the second critical field by one-third [27], the obtained field value is close to the second critical field for YBaCuO thin films. This cannot be said about the densities of S currents because their values exceed the values of the irreversible damage currents at λeff in all cases (see Table 1 in [15]). The heating-up time was estimated using Formula (3) from [15].
For defining the heat conductivity λel and heat capacity cel of hot electrons, the following relationships are used [11]:
where ρ is YBaCuO density of 6.3 × 103 kg/m3. Table 3 demonstrates these values:

Table 3.
Thermophysical parameters for hot electrons used in constructing the solution by Expression (8).
Constant in series for T(η) is equal to 3, (see Equation (7)), and is equal to 2 (see Equation (8)).
Figure 1a,b demonstrate the diffusion of hot electrons after the magnetic cumulation. The diffusion is a very fast, picosecond process. The values of the gradients and the heat fluxes are 1.8 × 108, 3.6 × 108 K/m and 0.8 × 1010, 1.5 × 1010 W/m2. The course of the curves in Figure 1a,b are similar, and as it follows from Table 2, Figure 1b demonstrates the diffusion at higher temperatures. To calculate N zone velocity, we take the diffusion distances δ as 16 nm from Figure 1a and 10 nm from Figure 1b. Then, to estimate the time, it is necessary to take the densities j1 (N) from Table 2. Since the volume parameters are not included in the evaluation formula, one obtains the same heating-up times for the same temperatures. As a result, one obtains velocity values such as 516.1 m/s and 256.4 m/s. In such relatively long times, the S state will be able to fully recover its S border by restoring the energy losses.
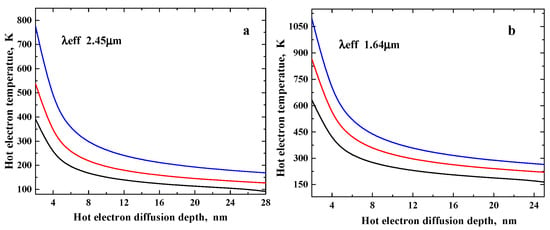
Figure 1.
(a,b) Hot electron diffusion depth after different time intervals. (a) For the film with λeff of 2.45 μm, the starting point is at 3.95 μm and initial temperature 80 K; (b) for the film with λeff of 1.64 μm, the starting point is at 2.84 μm and initial temperature 80 K. Curve lines indicate the hot electron diffusion: black after 1.4 ps, red after 2 ps, and blue after 3 ps for (a) and after 2.6 ps for (b).
The volume of the central cumulation areas, which are in Table 2, is about 30 times larger than the volume of the switched ring. The theoretical results show that the S current density tends to be infinity at the very edge of the S state border [28,29]. Formula (3) from [22] for calculating the current densities in a thin S film also works for nm distances. For our distances δ, this increases S current density by about one order of magnitude. These circumstances allow us to reduce the switching times in the evaluation approach. For calculating the N zone velocity switching times, let us take 6 ps and 9 ps, correspondingly. These are still acceptable times for restoring the S border of the S state. Let the first velocities be minimal and the second ones maximal. The obtained values are shown in Table 4.

Table 4.
Minimal and maximal S-N border step propagation velocities.
At some diffusion depth, thermalization of the electrons occurs. The temperature of the boundary increases with time when the boundary condition of the second kind is applied. Therefore, at a certain temperature and depth, the temperature after thermalization will rise by 8–10 degrees, which is sufficient for S-N switching. Given the high current density at the depth δ << λeff, the temperature of this depth after S-N switching can reach the initial high temperature. But, due to the S state ability to protect the S properties of the λeff, the energy loss upon S-N switching will be instantly restored, and the S-N border then retreats on the δ distance. This process will then begin to repeat. Based on these data, in thin, high-quality YBaCuO films, after micro-sized magnetic cumulation, the front of the N zone constantly replenishes energy ahead of itself while propagating. Such propagation corresponds to the qualities of the combustion wave.
Figure 2 demonstrates a slower process, namely the spreading of heat from the central areas of cumulation. In this case, the film is already heated by the fast propagation of the N zone with step-by-step S-N switching. The curve lines are obtained by using Solution (4). The heating-up temperatures of 313 K and 373 K are taken as examples. From Equation (4), with the boundary condition, one can obtain values of 28 and 44, correspondingly, using temperatures from Table 2. The YBaCuO film parameters for higher temperatures were used for the calculations, as in [15].
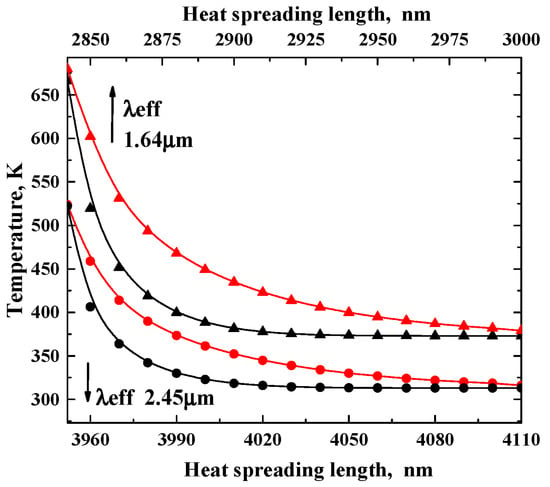
Figure 2.
Heat spreading across heated-up film after the N zone step propagation. Circles correspond to film with λeff of 2.45 μm, starting point is at 3.95 μm, and initial temperature is 313 K; triangles correspond to film with λeff of 1.64 μm, starting point is at 2.84 μm, and initial temperature is 373 K. Curved lines indicate diffusion: black after 300 ps; red after 2 ns.
The process of destructive propagation of the N zone in the case of the highest S current densities is demonstrated in the structural diagram in Figure 3. The central region, heated above 750 K by current and cumulated magnetic field, is shown in green and red. At such temperatures, gaps open in the film in the radial direction, and the circular current concentrating at their tops heats them, increasing the opening velocity. At high opening velocities, the tips of the tops enter a state of instability. This instability is characterized by the appearance of a destruction zone with many branching, minute gaps. Energy release turns the process explosive-like.
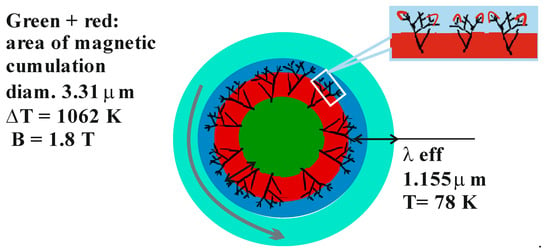
Figure 3.
Structure diagram of crack-branching phenomenon after cumulative S-N switching in the case when λeff is 1.16 μm. Blue ring—nanometric thickness domain of high density S currents. Teal ring—S state. On the zoomed-out area, branching, minute cracks from the top of the crack penetrate the domain. Meissner’s force cannot resist this. Arrow indicates current flow.
Now imagine that such minute cracks penetrate the very edge of the S border with very high-density currents (see inset in Figure 3). The S current concentrates at the tips of minute cracks, and its density immediately exceeds the critical density value. A narrow ring zone with very high resistance is formed, and the released heat is sufficient to melt it. If the S state restores the current density at its border, the N zone, as revealed in [26], can propagate with velocities close to the detonation velocity 1 × 104 m/s. Naturally, such propagation occurs over a small radius due to losses, leaving a micro-sized spot of melted film, as seen in the scanning electron microscope images. In the case when one of the cracks goes forward, a comparatively long micro-sized slit with melted edges will be visible in the images.
4. Discussion
A relatively simple model of N zone propagation after cumulative S-N switching is proposed. Cumulation results from compressing the areas with trapped magnetic flux by S state. Estimates of the N zone velocities for three λeff values are made using solutions of the heat equation and estimation formulas. There is a lack of experimental data on the damage to the S state by high-density currents of ns duration, that is, the irreversible damage of the films. We did not conduct experimental investigations with S films for objective temporal reasons. However, in [17], it was proposed to realize the same experiment with a Type I superconductor. To date, the authors have not found any experimental studies investigating the emergence of the cumulative effect at S-N border during N zone propagation when the S-N border is in the state of bending instability. Nowadays, carrying out the experiment would require the arrangement to include a high-speed camera capable of operating in a cryostat in tandem with an optical microscope as well as a modern scanning electron microscope to examine the damaged films.
On the other hand, the impact of short optical pulses on thin metal films has been studied experimentally and theoretically [10,11,13]. Some results from these works were herein used. It was impossible to cover all the physical phenomena in such fast and temperature-contrasting step propagation, the peculiarity of which is its iterative phase transition and micro size. With temperature gradients, the minimum of which is 1.8 × 108 K/m, it is necessary to estimate the contribution of magnetohydrodynamic effects to account for some of them making a noticeable contribution to the process.
The magnetic field’s cumulation depends on the magnetic flux compression kinematics, which requires working against the magnetic pressure and minimizing the loss of magnetic flux. For these purposes, an explosive was used in magneto-cumulative generators. How the S state evolves such a process remains unclear. The reverse process—the restoration of the S state when the current is abruptly removed—was not considered for some reason, even though the time-dependent Ginzburg–Landau equations could be applied to study the dynamics of this restoration [30]. But, when any single vortex, a quantum of magnetic flux, appears at the first critical magnetic field, it occurs cumulatively with a cumulation coefficient of 2, as follows from comparing formulas Hc1 = Φ0 ln(λ/ξ)/4πλ2 and for magnetic field in the center of vortex H = Φ0 ln(λ/ξ)/2πλ2, where Φ0 is magnetic flux quantum, and ξ is correlation length.
Turning to the cause of the formation of micro areas with trapped magnetic flux, that is, to the generation of coherent jets during the buckling, the following should be noted. When a cavity collapses, an incompressible liquid cumulatively penetrates by jet into another medium. For the S thin film, as we proposed, the Meissner currents on the borders of the S state serve as such incompressible medium. During the development of bending instability, the valleys buckle, bringing the S coherent jets into the S state [17]. The magnetic field then enters in the wake of the S jet, unlike the case of the integral liquid jet. Unconventional electron–electron repulsion influences the pairing that was considered in [16]. This can open a way to determine the incompressibility property of Meissner currents. However, while the charge 2e appears in the fundamental formulas, the calculations of the repulsion of such spatially separated boson electron pairs are unknown to the present authors. During the S-N switching of the thin films, a stepwise process of N-zone propagation was observed. However, the presence of bending instability at the S-N border and coherent jets made it challenging to classify this wave motion. In the absence of instability, it becomes clearer that the nature of N-zone propagation exhibits the characteristics of a combustion wave.
5. Conclusions
The little-studied dynamic phenomenon of compression by the S state of micro-sized areas with a trapped magnetic flux was theoretically investigated. Such compression occurs due to the unique properties of the S state, in which quantum properties manifest themselves on a macroscopic scale. In thin S films, the areas appear as a result of penetration of the S state by a coherent jet containing the magnetic field. The S state maintains its integrity by cutting off the upper part of the jet and encircling the area. Conservation of the magnetic flux leads to magnetic cumulation with subsequent local S-N switching. As a result of the appearance of high temperature, a considerable temperature gradient arises at the S-N border. The small radius of the cumulated point region does not allow for the development of bending instability of the S-N border. Using a two-temperature model of thermal propagation allowed us to estimate the depth of diffusion of hot electrons into the S state, which is at about 15–25 nm. At the same time, their thermalization occurs at this depth. These are fast, ps processes comparable with the reaction of the S state to the threat of decay. If thermalization leads to an increase in temperature by 8–10 degrees, S-N switching occurs. At the very edge of the S state, the current density is estimated to be of the order 1012 A/m2, so the temperature of the switched ring can rise to the initial temperature. While retreating, the S state restores the properties of its border. It follows that the N zone propagation becomes stepwise. During S-N switching of the thin films, a stepwise process of N zone propagation was also observed, but the presence of bending instability of the S-N border and coherent jets caused difficulties in classifying such a wave motion. Here, it is concluded that the nature of the N zone propagation has the properties of a combustion wave. The velocity range of such propagation is estimated to be from 0.26 × 103 to 2.66 × 103 m/s.
By applying the solutions of the heat conductivity equation, we allow ourselves some concessions to correspond to the experimental data. Indeed, the solutions obtained applying this equation to the cases for λeff equaling to 2.45 and 1.64 µm gave plausible results, and the authors decided to present them for publication.
Author Contributions
Conceptualization, O.K.; methodology, O.K. and L.A.; formal analysis, O.K. and L.A.; data curation, O.K. and L.A.; writing—original draft preparation, O.K.; writing—review and editing, O.K. and L.A.; visualization, O.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tavakoli, F.; Davis, S.H.; Kavehpour, H.P. Freezing of supercooled water drops on cold solid substrates: Initiation and mechanism. J. Coat. Technol. Res. 2015, 12, 869–875. [Google Scholar] [CrossRef]
- Courtney, W.G.; Forshey, D.R. Condensation of water via rarefaction wave. Phys. Fluids 1978, 21, 1086. [Google Scholar] [CrossRef]
- Gardiner, W.C. Shock tube studies of combustion chemistry. In Shock Waves; Takayama, K., Ed.; Springer: Berlin/Heidelberg, Germany, 1992; pp. 49–60. [Google Scholar] [CrossRef]
- Ferri, A. (Ed.) Fundamental Data Obtained from Shock-Tube Experiments; Pergamon Press: New York, NY, USA, 1961. [Google Scholar]
- Emelianov, A.V.; Eremin, A.V.; Fortov, V.E. Chemical condensation wave initiating oxygen-free combustion and detonation. Russ. J. Phys. Chem. B 2021, 15, 299–306. [Google Scholar] [CrossRef]
- Dresner, L. Normal zone propagation. In Stability of Superconductors, Selected Topics in Superconductivity; Springer: Boston, MA, USA, 2002; pp. 83–99. [Google Scholar] [CrossRef]
- Colangelo, D.; Dutoit, B. Analysis of the influence of the normal zone propagation velocity on the design of resistive fault current limiters. Supercond. Sci. Technol. 2014, 27, 124005. [Google Scholar] [CrossRef]
- Tailanov, N.A. Thermomagnetic shock waves in the vortex state in type-II superconductors. In Topics in Superconductivity Research; Martins, B.P., Ed.; Nova Science Publishers: Hauppauge, NY, USA, 2005; pp. 37–59. [Google Scholar]
- Taylanov, N.A. On the stability of thermomagnetic waves in type II superconductors. Supercond. Sci. Technol. 2001, 14, 326–328. [Google Scholar] [CrossRef]
- Oane, M.; Taca, M.; Tsao, S.L. Two Temperature Model for Metals: A New “Radical” Approach. Lasers Eng. 2013, 24, 105–113. [Google Scholar]
- Majchrzak, E.; Poteralska, J. Numerical analysis of short-pulse laser interactions with thin metal film. Arch. Foundry Eng. 2010, 10, 123–128. [Google Scholar]
- Zhang, Y.; Tzou, D.Y.; Chen, J.K. Micro- and Nanoscale Heat Transfer in Femtosecond Laser Processing of Metals. In High-Power and Femtosecond Lasers: Properties, Materials and Applications, Chapter 5; Barret, P.-H., Palmer, M., Eds.; Nova Science Publishers, Inc.: New York, NY, USA, 2009; pp. 159–206. [Google Scholar]
- Gaudio, P.; Montanari, R.; Pakhomova, E.; Richetta, M.; Varone, A. W-1% La2O3 Submitted to a Single Laser Pulse: Effect of Particles on Heat Transfer and Surface Morphology. Metals 2018, 8, 389. [Google Scholar] [CrossRef]
- Pearl, J. Current distribution in superconducting films carrying quantized fluxoids. Appl. Phys. Lett. 1964, 5, 65–66. [Google Scholar] [CrossRef]
- Kiprijanovič, O.; Ardaravičius, L. Descriptive model of the transition from superconducting to normal state in thin high quality YBaCuO films by nanosecond electrical pulses. Thin Solid Film. 2022, 748, 139159. [Google Scholar] [CrossRef]
- Krasnov, V.M.; Katterwe, S.-O.; Rydh, A. Signatures of the electronic nature of pairing in high-Tc superconductors obtained by non-equilibrium boson spectroscopy. Nat. Commun. 2013, 4, 2970. [Google Scholar] [CrossRef] [PubMed]
- Ardaravičius, L.; Kiprijanovič, O. Detailed look into the unstable S-N border during propagation of the N-zone into the thin YBaCuO film. Phys. Scr. 2023, 98, 055924. [Google Scholar] [CrossRef]
- Semenov, A.D.; Gol’tsman, G.N.; Sobolewski, R. Hot-Electron Effect in Superconductors and Its Applications for Radiation Sensors. Supercond. Sci. Tech. 2002, 15, R1. [Google Scholar] [CrossRef]
- Coslovich, G.; Giannetti, C.; Cilento, F.; Dal Conte, S.; Ferrini, G.; Galinetto, P.; Parmigiani, F. Evidence for a photoinduced nonthermal superconducting-to-normal-state phase transition in overdoped Bi2Sr2Ca0.92 Y0.08 Cu2O8+δ. Phys. Rev. B 2011, 83, 064519. [Google Scholar] [CrossRef]
- Gray, K.E.; Fowler, D.E. A superconducting fault-current limiter. J. Appl. Phys. 1978, 49, 2546–2549. [Google Scholar] [CrossRef]
- Anwar, M.S.; Latif, A.; Iqbal, M.; Rafique, M.S.; Khaleeq-Ur-Rahman, M.; Siddique, S. Theoretical model for heat conduction in metals during interaction with ultra short laser pulse. Laser Part. Beams 2006, 24, 347–353. [Google Scholar] [CrossRef]
- Kiprijanovič, O.; Ardaravičius, L.; Gradauskas, J.; Šimkevičius, Č.; Keršulis, S.; Ašmontas, S. Instability, magnetic flux trapping and cumulative effect during pulsed S-N switching of thin high quality YBaCuO films. Supercond. Sci. Technol. 2020, 33, 095013. [Google Scholar] [CrossRef]
- Majchrzak, E. Parabolic and hyperbolic two-temperature models of microscopic heat transfer. comparison of numerical solutions. In Materials Science Forum; Trans Tech Publications Ltd.: Wollerau, Switzerland, 2012; Volume 706–709, pp. 1454–1459. [Google Scholar] [CrossRef]
- Sharon, E.; Gross, S.; Fineberg, J. Local crack branching as a mechanism for instability in dynamic fracture. Phys. Rev. Lett. 1995, 74, 5096. [Google Scholar] [CrossRef]
- Naimark, O.; Barannikov, V.; Davydova, M.; Plekhov, O.; Uvarov, S. Crack propagation: Dynamic stochasticity and scaling. Tech. Phys. Lett. 2000, 26, 254–258. [Google Scholar] [CrossRef]
- Ardaravičius, L.; Keršulis, S.; Kiprijanovič, O.; Šimkevičius, Č.; Vengalis, B. Fast damaging processes in the TaN thin film absorbers under action of nanosecond electrical pulses. Intern. J. Struct. Integr. 2016, 7, 607–616. [Google Scholar] [CrossRef]
- Fujishiro, H.; Tateiwa, T.; Fujiwara, A.; Oka, T.; Hayashi, H. Higher trapped field over 5 T on HTSC bulk by modified pulse field magnetizing. Phys. C Supercond. Its Appl. 2006, 445–448, 334–338. [Google Scholar] [CrossRef]
- Rhoderick, E.; Wilson, E. Current Distribution in Thin Superconducting Films. Nature 1962, 194, 1167–1168. [Google Scholar] [CrossRef]
- Prokof’ev, D. Distribution of the magnetic field induced by a current passing through slabs in the superconducting and normal states. Tech. Phys. 2006, 51, 675–682. [Google Scholar] [CrossRef]
- Berdiyorov, G.; Harrabi, K.; Oktasendra, F.; Gasmi, K.; Mansour, A.I.; Maneval, J.P.; Peeters, F.M. Dynamics of current-driven phase-slip centers in superconducting strips. Phys. Rev. B 2014, 90, 054506. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).