Synchronous Measurement of Optical Transmission and Viscoelastic Properties of Polymer Optical Fibers
Abstract
1. Introduction
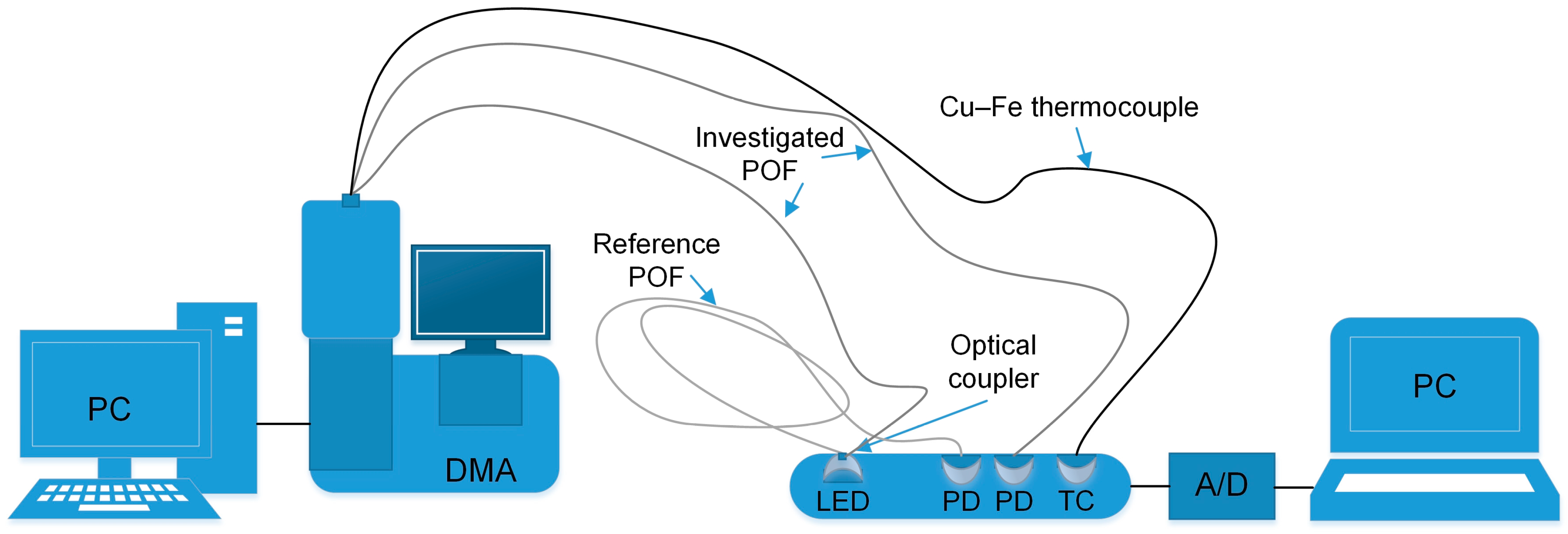
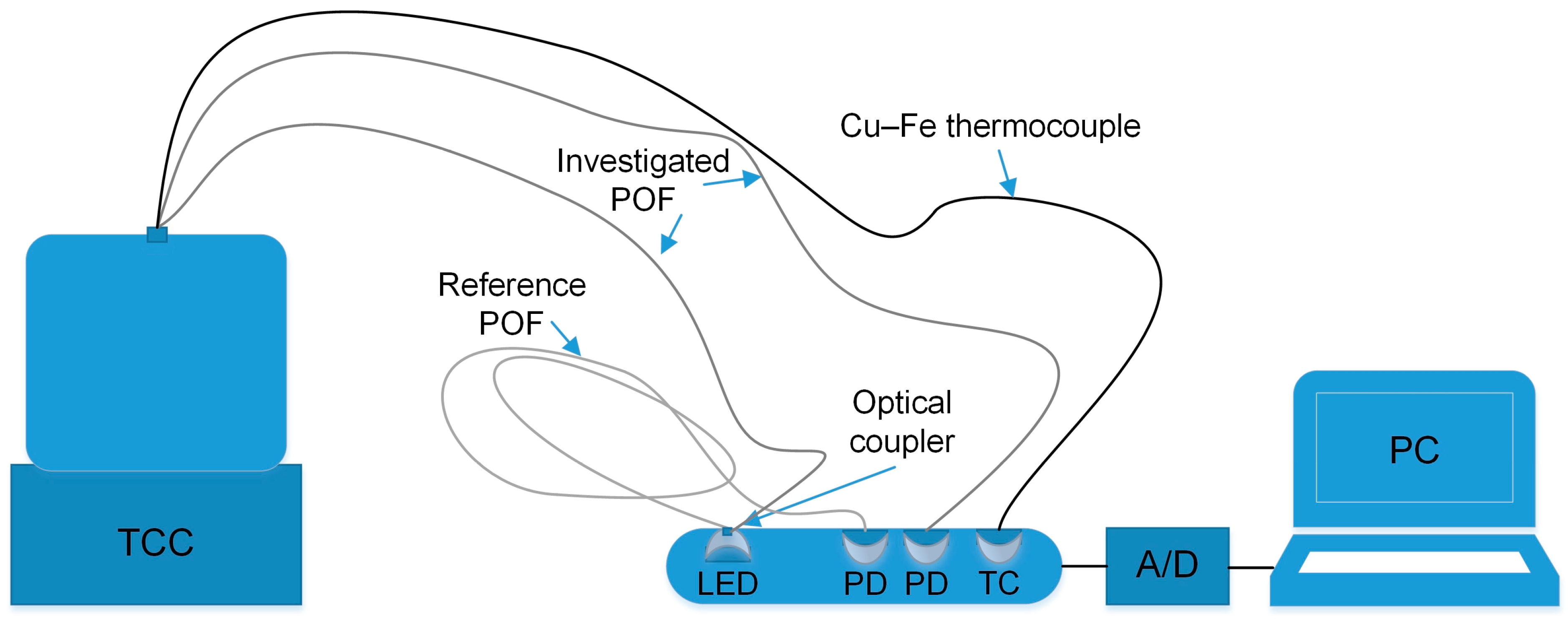
2. Materials and Methods
3. Results
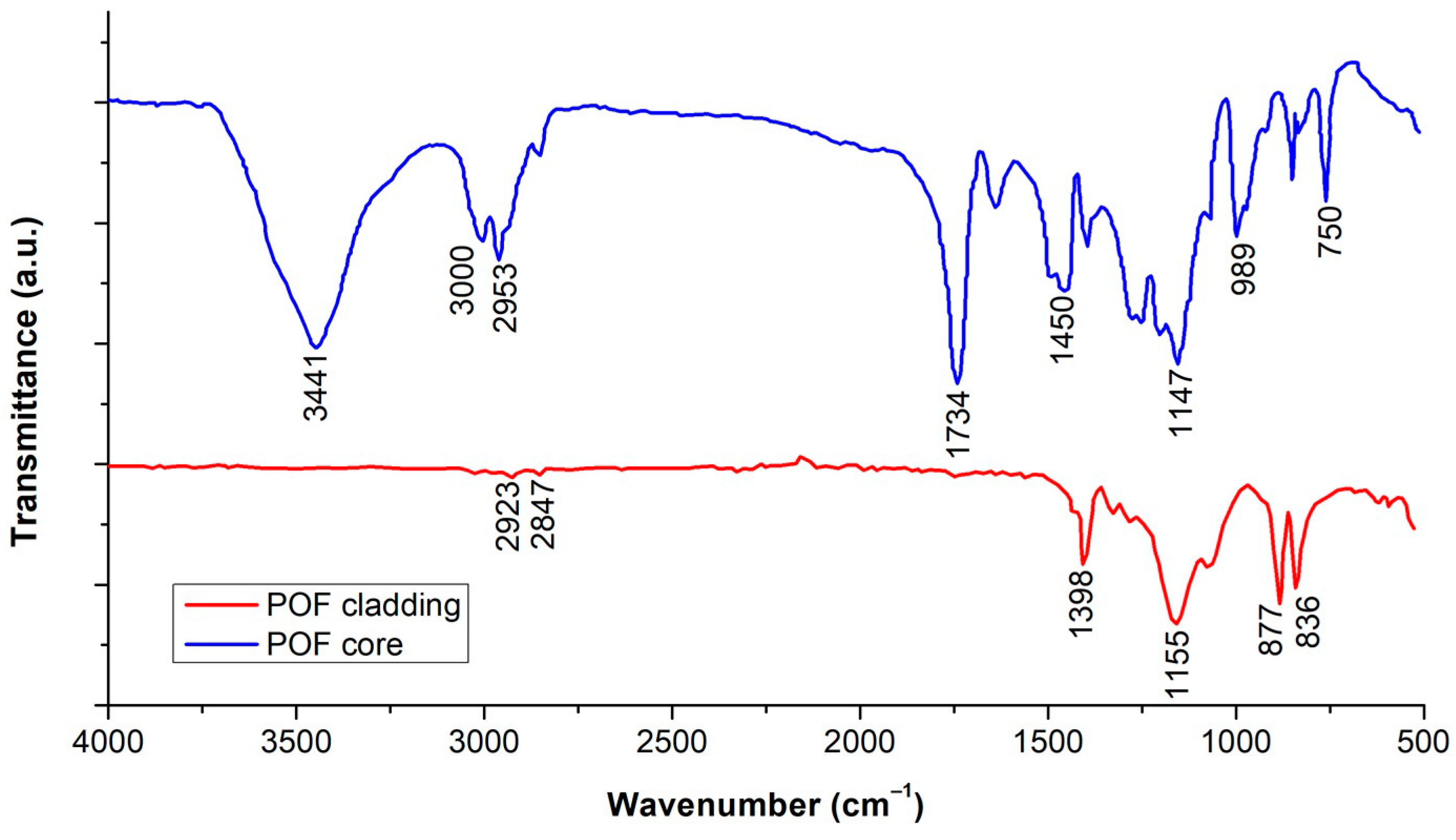
3.1. FTIR Measurements
3.2. DSC Measurements
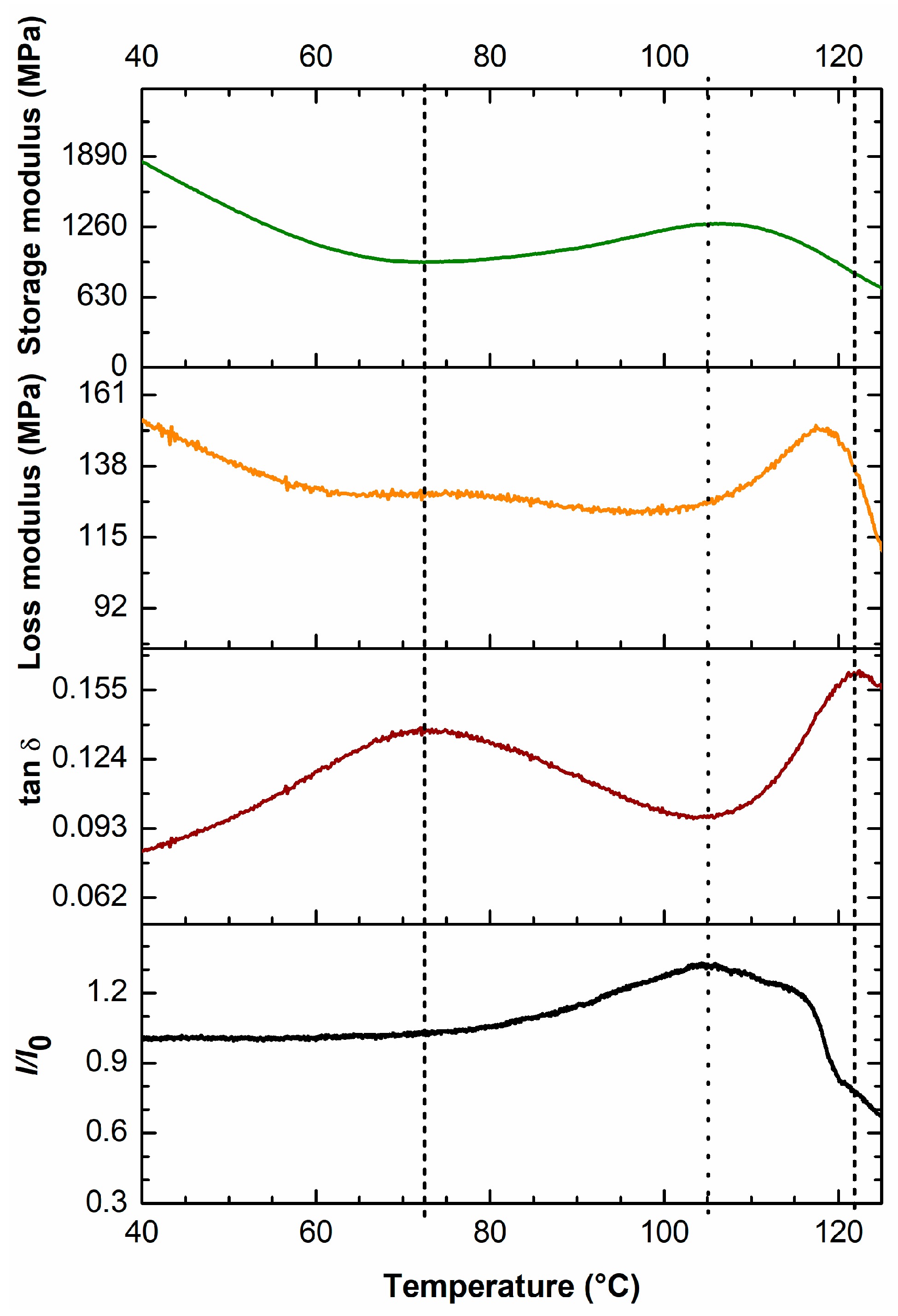
3.3. Dual Cantilever DMA on POF
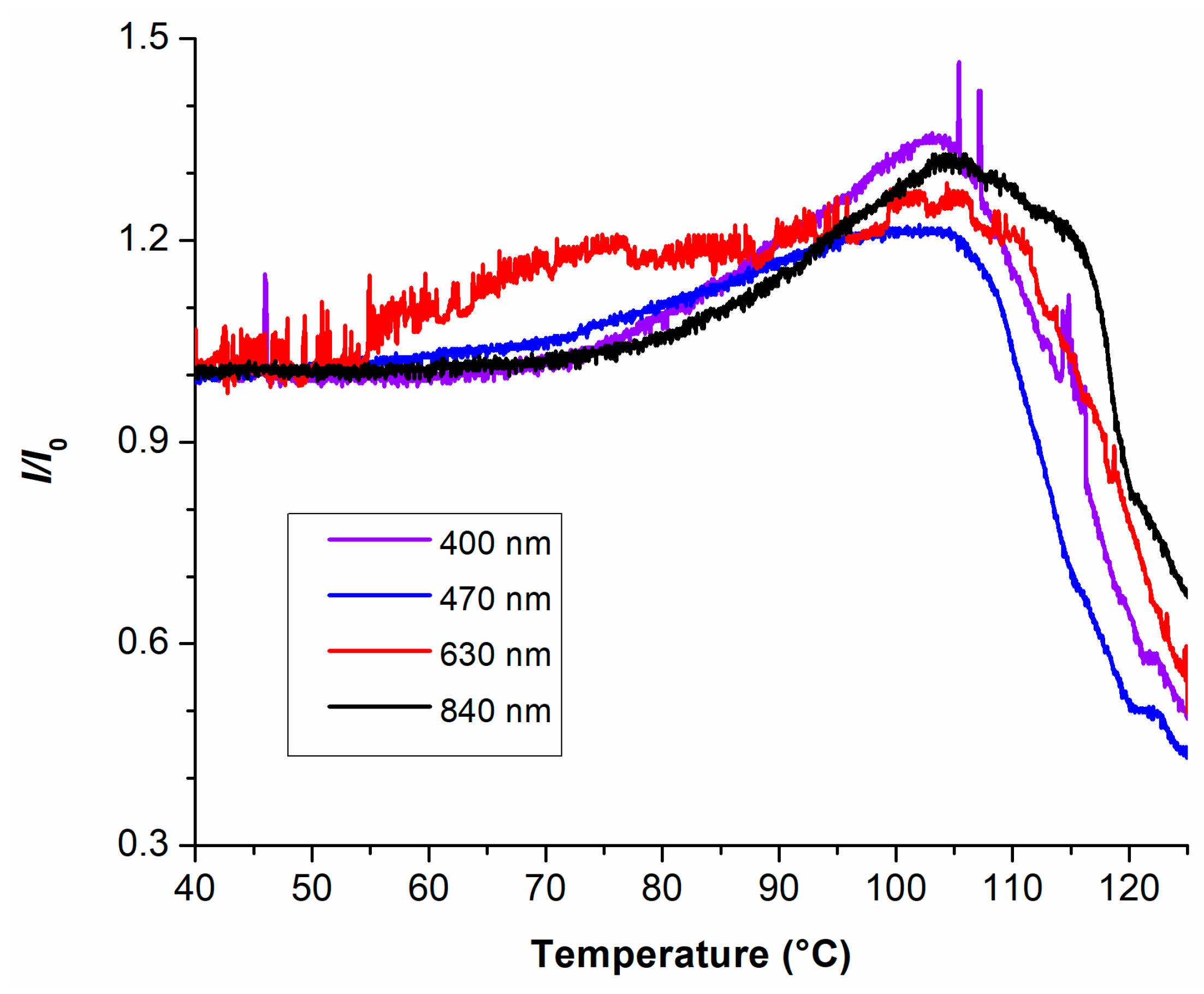
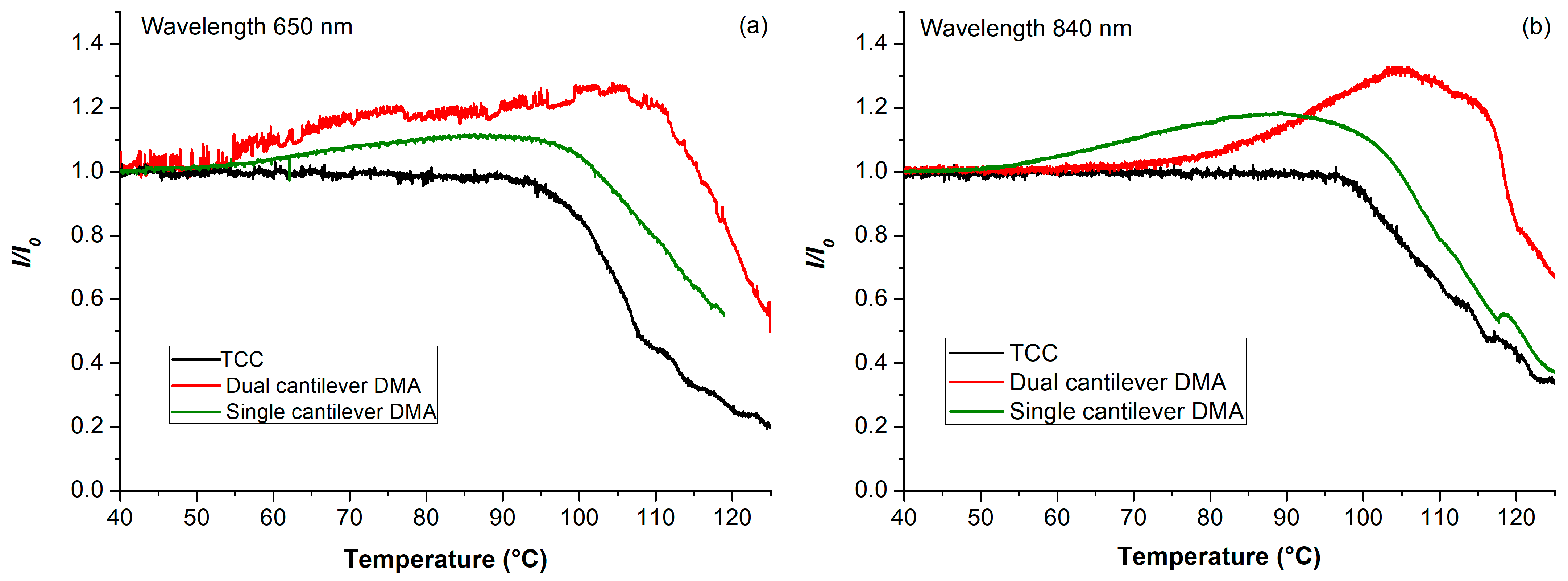
3.4. Measurements in the Temperature-Controlled Chamber (TCC)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Menard, K.P. Dynamic Mechanical Analysis: A Practical Introduction, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 978-0-429-19016-2. [Google Scholar]
- Groenewoud, W.M. Dynamic mechanical analisys. In Characterisation of Polymers by Thermal Analysis; Elsevier: Amsterdam, The Netherlands, 2001; pp. 94–122. ISBN 978-0-444-50604-7. [Google Scholar]
- Swaminathan, G.; Shivakumar, K. A Re-Examination of DMA Testing of Polymer Matrix Composites. J. Reinf. Plast. Compos. 2009, 28, 979–994. [Google Scholar] [CrossRef]
- Bilro, L.; Alberto, N.; Pinto, J.L.; Nogueira, R. Optical Sensors Based on Plastic Fibers. Sensors 2012, 12, 12184–12207. [Google Scholar] [CrossRef]
- Golovastikov, N.V.; Kazanskiy, N.L.; Khonina, S.N. Optical Fiber-Based Structural Health Monitoring: Advancements, Applications, and Integration with Artificial Intelligence for Civil and Urban Infrastructure. Photonics 2025, 12, 615. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Y.; Qi, L.; Zhang, Y. Soft Optical Fibers for Biomedical and Wearable Technologies: Current Trends and Future Prospects. Adv. Funct. Mater. 2025, 35, 2507712. [Google Scholar] [CrossRef]
- Appajaiah, A. Climatic Stability of Polymer Optical Fibers (POF). Ph.D. Thesis, Potsdam University, Berlin, Germany, 2004. [Google Scholar]
- Zubia, J.; Arrue, J. Plastic Optical Fibers: An Introduction to Their Technological Processes and Applications. Opt. Fiber Technol. 2001, 7, 101–140. [Google Scholar] [CrossRef]
- Savović, S.; Djordjevich, A. Mode Coupling in Strained and Unstrained Step-Index Plastic Optical Fibers. Appl. Opt. 2006, 45, 6775. [Google Scholar] [CrossRef]
- Ma, Y.; Fu, D.; Zhang, Z.-F. Solution Doping of PMMA-Based Step-Index Polymer Optical Fibers by Rhodamine B Near Glass Transition Temperature of PMMA. Photonics 2024, 11, 966. [Google Scholar] [CrossRef]
- Belkheir, M.; Rouissat, M.; Mokaddem, A.; Doumi, B.; Boutaous, A. Studying the Effect of Polymethyl Methacrylate Polymer Opticals Fibers (POFs) on the Performance of Composite Materials Based on the Polyether Ether Ketone (PEEK) Polymer Matrix. Emergent Mater. 2022, 5, 2075–2085. [Google Scholar] [CrossRef]
- Chen, Y.-C. Power Losses in Bent and Elongated Polymer Optical Fibers. Appl. Opt. 2007, 46, 4570. [Google Scholar] [CrossRef]
- Chen, L.-W.; Lu, W.-H.; Chen, Y.-C. An Investigation into Power Attenuations in Deformed Polymer Optical Fibers under High Temperature Conditions. Opt. Commun. 2009, 282, 1135–1140. [Google Scholar] [CrossRef]
- Musbah, S.; Brajovic, L. Simultaneous Measurement of Optical and Dynamic Mechanical Properties of Plastic Optical Fibers. Chem. Ind. Chem. Eng. Q. 2010, 16, 309–317. [Google Scholar] [CrossRef]
- Losada, M.Á.; Mazo, M.; López, A.; Muzás, C.; Mateo, J. Experimental Assessment of the Transmission Performance of Step Index Polymer Optical Fibers Using a Green Laser Diode. Polymers 2021, 13, 3397. [Google Scholar] [CrossRef]
- Mousavi, L.; Sabaeian, M.; Nadgaran, H. Thermally-Induced Birefringence in Solid-Core Photonic Crystal Fiber Lasers. Opt. Commun. 2013, 300, 69–76. [Google Scholar] [CrossRef]
- Leal-Junior, A.; Frizera, A.; Pontes, M.J.; Antunes, P.; Alberto, N.; Domingues, M.F.; Lee, H.; Ishikawa, R.; Mizuno, Y.; Nakamura, K.; et al. Dynamic Mechanical Analysis on Fused Polymer Optical Fibers: Towards Sensor Applications. Opt. Lett. 2018, 43, 1754. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, P.A.; Radford, D.W. A DMA-Based Approach to Quality Evaluation of Digitally Manufactured Continuous Fiber-Reinforced Composites from Thermoplastic Commingled Tow. J. Compos. Sci. 2022, 6, 61. [Google Scholar] [CrossRef]
- Senthilkumar, K.; Subramaniam, S.; Ungtrakul, T.; Kumar, T.S.M.; Chandrasekar, M.; Rajini, N.; Siengchin, S.; Parameswaranpillai, J. Dual Cantilever Creep and Recovery Behavior of Sisal/Hemp Fibre Reinforced Hybrid Biocomposites: Effects of Layering Sequence, Accelerated Weathering and Temperature. J. Ind. Text. 2022, 51, 2372S–2390S. [Google Scholar] [CrossRef]
- Henriques, I.R.; Borges, L.A.; Costa, M.F.; Soares, B.G.; Castello, D.A. Comparisons of Complex Modulus Provided by Different DMA. Polym. Test. 2018, 72, 394–406. [Google Scholar] [CrossRef]
- Stajcic, I.; Radojevic, V.; Lazarevic, Z.; Curcic, M.; Hadzic, B.; Kojovic, A.; Stajcic, A. Poly(Methyl Methacrylate)-Based Core-Shell Electrospun Fibers: Structural and Morphological Analysis. Coatings 2025, 15, 727. [Google Scholar] [CrossRef]
- Cruz, R.; Ataka, K.; Heberle, J.; Kozuch, J. Evaluating Aliphatic CF, CF2, and CF3 Groups as Vibrational Stark Effect Reporters. J. Chem. Phys. 2024, 160, 204308. [Google Scholar] [CrossRef]
- Mitsubishi Chemical Group. ESKA Polymer Optical Fiber. Available online: https://www.pofeska.com/pofeskae/download/02.html (accessed on 27 September 2025).
- Suzuki, Y.; Kano, T.; Tomii, T.; Tsuji, N.; Matsumoto, A. Relaxation and Amorphous Structure of Polymers Containing Rigid Fumarate Segments. Polymers 2022, 14, 4876. [Google Scholar] [CrossRef]
- Nikolaidis, A.K.; Achilias, D.S. Thermal Degradation Kinetics and Viscoelastic Behavior of Poly(Methyl Methacrylate)/Organomodified Montmorillonite Nanocomposites Prepared via In Situ Bulk Radical Polymerization. Polymers 2018, 10, 491. [Google Scholar] [CrossRef] [PubMed]
- Alzarrug, F.A.; Dimitrijević, M.M.; Jančić Heinemann, R.M.; Radojević, V.; Stojanović, D.B.; Uskoković, P.S.; Aleksić, R. The Use of Different Alumina Fillers for Improvement of the Mechanical Properties of Hybrid PMMA Composites. Mater. Des. 2015, 86, 575–581. [Google Scholar] [CrossRef]
- Stojanović, D.B.; Brajović, L.; Obradović, V.; Mijailović, D.; Dramlić, D.; Kojović, A.; Uskoković, P.S. Hybrid Acrylic Nanocomposites with Excellent Transparency and Hardness/Toughness Balance. Prog. Org. Coat. 2020, 139, 105437. [Google Scholar] [CrossRef]
- TA Instruments DMA Q800 Specifications. Available online: https://www.tainstruments.com/pdf/brochure/dma.pdf (accessed on 27 September 2025).
- Bashir, M.A. Use of Dynamic Mechanical Analysis (DMA) for Characterizing Interfacial Interactions in Filled Polymers. Solids 2021, 2, 108–120. [Google Scholar] [CrossRef]
- Stojanović, D.B.; Brajović, L.; Orlović, A.; Dramlić, D.; Radmilović, V.; Uskoković, P.S.; Aleksić, R. Transparent PMMA/Silica Nanocomposites Containing Silica Nanoparticles Coating under Supercritical Conditions. Prog. Org. Coat. 2013, 76, 626–631. [Google Scholar] [CrossRef]
- Geng, K.; Tsui, O.K.C. Effects of Polymer Tacticity and Molecular Weight on the Glass Transition Temperature of Poly(Methyl Methacrylate) Films on Silica. Macromolecules 2016, 49, 2671–2678. [Google Scholar] [CrossRef]
- Ionita, D.; Cristea, M.; Banabic, D. Viscoelastic Behavior of PMMA in Relation to Deformation Mode. J. Therm. Anal. Calorim. 2015, 120, 1775–1783. [Google Scholar] [CrossRef]
- Mohammadi, M.; Fazli, H.; Karevan, M.; Davoodi, J. The Glass Transition Temperature of PMMA: A Molecular Dynamics Study and Comparison of Various Determination Methods. Eur. Polym. J. 2017, 91, 121–133. [Google Scholar] [CrossRef]


| POF | Cladding Material | Core Material | |
|---|---|---|---|
| Tg | 119.17 °C | / | 119.93 °C |
| Tm | 127.09 °C | 127.04 °C | / |
| Light Wavelength (nm) | Tinc (°C) | Tmax (°C) | (%) |
|---|---|---|---|
| 400 | 65 | 102–106 | 35.0 |
| 470 | 55 | 99–104 | 21.5 |
| 650 | 55 | 100–106 | 25.4 |
| 840 | 65 | 103–105 | 31.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brajović, L.; Kojovic, A.; Stajcic, I.; Lazarevic, Z.; Curcic, M.; Gilic, M.; Stojanovic, D. Synchronous Measurement of Optical Transmission and Viscoelastic Properties of Polymer Optical Fibers. Coatings 2025, 15, 1295. https://doi.org/10.3390/coatings15111295
Brajović L, Kojovic A, Stajcic I, Lazarevic Z, Curcic M, Gilic M, Stojanovic D. Synchronous Measurement of Optical Transmission and Viscoelastic Properties of Polymer Optical Fibers. Coatings. 2025; 15(11):1295. https://doi.org/10.3390/coatings15111295
Chicago/Turabian StyleBrajović, Ljiljana, Aleksandar Kojovic, Ivana Stajcic, Zorica Lazarevic, Milica Curcic, Martina Gilic, and Dusica Stojanovic. 2025. "Synchronous Measurement of Optical Transmission and Viscoelastic Properties of Polymer Optical Fibers" Coatings 15, no. 11: 1295. https://doi.org/10.3390/coatings15111295
APA StyleBrajović, L., Kojovic, A., Stajcic, I., Lazarevic, Z., Curcic, M., Gilic, M., & Stojanovic, D. (2025). Synchronous Measurement of Optical Transmission and Viscoelastic Properties of Polymer Optical Fibers. Coatings, 15(11), 1295. https://doi.org/10.3390/coatings15111295






