A Hybrid FCEEMD-ACYCBD Feature Extraction Framework: Extracting and Analyzing Fault Feature States of Rolling Bearings

Abstract

Metal components such as rolling bearings are prone to wear, cracks, and defects in harsh environments and long-term use, leading to performance degradation and potential equipment failures. Therefore, detecting surface cracks and other defects in rolling bearings is of great significance for ensuring equipment reliability and safety. However, traditional signal decomposition methods like EEMD and FEEMD suffer from residual noise and mode mixing issues, while deconvolution algorithms such as CYCBD are sensitive to parameter settings and struggle in high-noise environments. To mitigate the susceptibility of fault signals to background noise interference, this paper proposes a fault feature extraction method based on fast complementary ensemble empirical mode decomposition (FCEEMD) and adaptive maximum second-order cyclostationarity blind deconvolution (ACYCBD). Firstly, we propose FCEEMD, which effectively eliminates the residual noise of ensemble empirical mode decomposition (EEMD) and fast ensemble empirical mode decomposition (FEEMD) by introducing paired white noise with opposite signs, solving the problems of traditional decomposition methods that are greatly affected by noise, having large reconstruction errors, and being high time-consuming. Subsequently, a new intrinsic mode function (IMF) screening index based on correlation coefficients and energy kurtosis is developed to effectively mitigate noise influence and enhance the quality of signal reconstruction. Secondly, the ACYCBD model is constructed, and the hidden periodic frequency is detected by the enhanced Hilbert phase synchronization (EHPS) estimator, which significantly enhances the extraction effect of the real periodic fault features in the noise. Finally, instantaneous energy tracking of bearing fault characteristic frequency is achieved through Teager energy operator demodulation, thereby accurately extracting fault state features. The experiment shows that the proposed method accurately extracts the fault characteristic frequencies of 164.062 Hz for inner ring faults and 105.469 Hz for outer ring faults, confirming its superior accuracy and efficiency in rolling bearing fault diagnosis.

1. Introduction

In industrial equipment and mechanical systems, surface pitting, cracks, wear, and defects in metal parts such as rolling bearings can significantly reduce their performance and even cause failure [1]. These surface-initiated failures are often the direct manifestation of coating degradation and material fatigue, which are central concerns in surface engineering and protective coatings research. Effective fault diagnosis methods can detect and identify these surface defects in a timely manner, which is crucial for ensuring the reliable operation of equipment and reducing downtime and maintenance costs [2]. However, the intricate structure and demanding operational conditions of rolling bearings, which are susceptible to wear and cracking, present significant challenges in developing accurate and reliable mathematical and fault mechanism models. Meanwhile, the non-stationary and nonlinear nature of rolling bearing vibration signals poses significant challenges to the accurate extraction of fault features [3]. Consequently, investigating fault diagnosis and feature extraction based on vibration signals is critical.

In recent times, numerous researchers have proposed hundred feature extraction methods based on bearing faults [4]. Among them, wavelet packet decomposition (WPD) generates false components and suffers from mode aliasing issues [5]. Although variational mode decomposition (VMD) can restrain the issue of modal aliasing [6], its decomposition result is constrained by the amount of modalities and the setting of penalty parameters. Although empirical mode decomposition (EMD) is widely applied [7], it still suffers from mode aliasing and pseudo-modality issues [8]. Li introduced a time-varying filtering empirical mode decomposition (TVF-EMD) method to solve separation and intermittency problems [9]. However, this method requires pre-set B-spline order and bandwidth threshold parameters, which rely too much on prior knowledge [10]. In an effort to resolve the above problems, Wu developed the ensemble empirical mode decomposition (EEMD) method [11]. This method can suppress the modal aliasing problem caused by improper selection of stop criteria. However, EEMD is susceptible to modal aliasing and the endpoint effect [12]. To this end, Yeh presented complementary ensemble empirical mode decomposition (CEEMD) [13] by improving the iterative process [14]. Compared with EEMD, CEEMD has the advantages of small reconstruction error and a significant noise suppression effect. Chen introduced a mixed method according to the CEEMD–sample entropy and correlation evaluation methods to analyze the association between each IMF and the initial signal [15]. In addition, Zheng utilized CEEMD to estimate PM2.5 density, which was originally a model that used deep learning to predict PM2.5 concentration [13]. Although CEEMD has been widely used in signal processing, there are issues such as higher computation complexity and lower efficiency when dealing with longer signals. In response to the above issues, Wang presented fast ensemble empirical mode decomposition (FEEMD) [16]. FEEMD [17] was initially mainly used to predict wind speed and later gradually applied for fault feature extraction. Liu combined FEEMD with artificial neural network MLP/ANFIS for predicting non-stationary nonlinear wind velocity signals and achieved significant results [18]. Sun used FEEMD and a Regularized Extreme Learning Machine (RELM) to predict short-term and medium-term wind speeds and achieved good wind speed prediction results [19]. Research has shown that the decomposition velocity of FEEMD is faster and reconstruction mistakes are rarer than with ensemble empirical mode decomposition. However, multiple noise signals need to be added to the calculation process of FEEMD, which may cause the results to be affected by noise. Secondly, the IMF average calculation may not completely eliminate modal mixing, and in some cases, the problem of modal mixing between IMF components still exists, which may make for inaccurate decomposition results.

The deconvolution algorithm has been extensively studied and practiced in the feature extraction of rolling bearing faults [17]. Minimum entropy deconvolution (MED) [20] is a well-established deconvolution method that extracts fault features by minimizing the entropy of the output signal. However, the pulses extracted by MED are few and can easily lead to the loss of other impacts. Maximum correlation coefficient kurtosis deconvolution (MCKD) [21] is an improved deconvolution algorithm that extracts fault features by optimizing the correlation index relative to the initial signal and the deconvolution signal. MCKD has better robustness to noise and can extract richer fault features. In addition, McDonald presented the multipoint optimal minimum entropy deconvolution adjustment (MOMEDA) [22]. It has the advantages of suppressing noise and extracting the fault features of rolling bearings. These deconvolution algorithms have been used for the study of feature extraction for faults with rolling bearings and have achieved significant results [23]. However, these algorithms also have some limitations, such as sensitivity to parameter settings and difficulty in disposing of non-stationary signals in an environment with strong noise. BUZZONI introduced the maximum second-order cyclic stationary blind deconvolution algorithm (CYCBD) [24], where the maximum second-order cyclic stationary index is utilized as the objective function to search the best inverse filter, so as to collect the fault signal. A limitation of this method is that it is limited to a simple filtering-then-estimation procedure, making it vulnerable to errors in high-noise environments [25]. Ke used the Seagull optimization algorithm (SOA) combined with envelope entropy optimization CYCBD [26], which adaptively determined the filter length and enhanced the precision in extracting fault signals. Nevertheless, the functionality of the calculation is very sensitive to the setting of certain parameters. Therefore, the above are the motivations behind some of the innovative points in this article.

Envelope demodulation is a method extensively used for extracting fault features, which extracts the fault-related modulation components by demodulating the envelope of the vibration signal. Envelope demodulation is crucial for identifying faults in rolling bearings. Studies indicate that envelope demodulation is capable of efficiently isolating fault characteristics from rolling bearings [24]. However, envelope demodulation also has some limitations, such as being sensitive to noise and making it hard to distinguish between similar fault types. Energy operator demodulation is a method for extracting fault features that operates on the concept of energy operators [27]. Among them, as a nonlinear operator, the energy operator can amplify the impact component in the vibration signals. It has been proven to abstract the distinguishing fault features of rolling bearings and demonstrates significant robustness [28]. Therefore, this article attempts to accurately identify the bearing’s fault state by contrasting the frequency gained through energy operator demodulation with the theoretical fault characteristic frequency.

Recent hybrid approaches combining signal decomposition with deep learning or advanced deconvolution have shown promise. For instance, methods integrating complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) with deep neural networks (DNNs) have been applied in sensors for bearing fault diagnosis, achieving high accuracy but requiring large labeled datasets and substantial computational resources [29]. Similarly, hybrid models combining VMD with convolutional neural networks (CNNs) demonstrate robust feature extraction but are sensitive to parameter settings and noise interference [30]. Very recently, further studies have continued this trend, such as the use of CEEMDAN [31] with a one-dimensional convolutional neural network (1D-CNN) for intelligent fault diagnosis of rolling bearings [32], and adaptive VMD combined with deep convolutional networks for robust feature extraction under noisy conditions [33]. These deep learning-based methods achieve impressive performance but inherently depend on extensive training data and complex network architectures.

In summary, existing methods face four key challenges: (1) FEEMD suffers from residual noise and modal aliasing; (2) traditional IMF screening lacks effectiveness; (3) CYCBD is sensitive to parameter settings; and (4) conventional demodulation methods are noise-sensitive. To address the above issues, we propose a fault feature extraction method for rolling bearings using FCEEMD and ACYCBD. In contrast, the proposed FCEEMD–ACYCBD framework does not rely on large datasets or complex network structures, instead leveraging adaptive cyclostationary analysis and energy operator demodulation to achieve noise-resistant and efficient fault feature extraction even in the presence of strong background noise. The novel aspects and primary contributions of this study include the following:

(1)

To address the issues of residual noise and mode mixing in FEEMD, we propose the FCEEMD method that introduces pairs of white noise with opposite polarities in each decomposition step. This innovation effectively mitigates the residual noise inherent in both EEMD and FEEMD while maintaining computational efficiency through fixed screening numbers and optimized algorithm implementation.

(2)

To overcome the limitation of traditional IMF screening methods in identifying fault-related components, we construct a novel composite screening index based on correlation coefficient and energy kurtosis. This dual-threshold method accurately selects IMF components containing genuine fault features while effectively rejecting noise-dominated components.

(3)

To solve the parameter sensitivity problem of CYCBD algorithms, we develop the ACYCBD model that incorporates the EHPS estimator for automatic detection of concealed cyclic frequencies. This adaptive capability significantly enhances the extraction of real periodic fault features in noisy environments without requiring prior knowledge of fault characteristics.

(4)

To improve the accuracy of fault feature extraction in nonlinear and non-stationary signals, we implement Teager energy operator demodulation that provides superior instantaneous energy tracking of bearing fault characteristic frequencies compared to traditional envelope demodulation methods.

These innovations collectively establish a comprehensive framework for robust and efficient bearing fault diagnosis under challenging operational conditions.

The remaining sections are as follows: The Section 2 delineates the theoretical foundations and methods, including FCEEMD, the composite screening method according to correlation coefficient and kurtosis, ACYCBD, and Teager energy operator demodulation. The Section 3 presents the fault diagnosis algorithm utilizing FCEEMD and ACYCBD. The Section 4 presents the experimental confirmation of the fault diagnosis method utilizing FCEEMD and ACYCBD. The Section 5 elaborates on the conclusions.

2. Theoretical Foundations and Methods

2.1. The Theory of FCEEMD

To address the inaccurate decomposition results caused by mode mixing in FEEMD, we propose an improved method called FCEEMD. This method synergizes the computational efficiency of FEEMD with the superior performance of CEEMD in reducing mode mixing and decomposition errors. By integrating their respective advantages, FCEEMD achieves both high operational speed and decomposition accuracy. Given a vibration signal denoted as $X_t=[x_1, x_2,\dots , x_n]$, the FCEEMD process proceeds as follows, the flowchart of FCEEMD decomposition method is shown in Figure 1.

• Set the aggregation times $I$ and amplitude $m$ of white noise, and increase the current aggregation count $i=1$.
• Introduce a white noise sequence $\pm n_i(t),i=1,2,\cdots ,n$ with opposite sign $i$ into signal $x(t)$, and obtain denoised signals $N_i(t)$ and $P_i(t)$.

$$\left\{\begin{array}{c}{N}_i(t)=x(t)-n_i(t)\\ P_i(t)=x(t)+n_i(t)\end{array}\right.$$

(1)

3.

Obtain several IMF components and decompose $N_i(t)$ and $P_i(t)$ through EMD decomposition.

$$\left\{\begin{array}{c}{N}_i(t)={\displaystyle \sum _{j=1}^q{c}_{j,i}^2(t)}\\ P_i(t)={\displaystyle \sum _{j=1}^q{c}_{j,i}^1(t)}\end{array}\right.$$

(2)

In the equation, $c_{j,i}^1(t)$ and $c_{j,i}^2(t)$ represent the j-th IMF obtained from the i-th time EMD decomposition of $N_i(t)$ and $P_i(t)$, respectively, and $q$ is the count of IMF components.

4.

In the event of $i<I$, reiterate steps (2) and (3) using $i=i+1$.

5.

Compute the mean of the IMF components following the $2I$ decomposition.

$$c_j(t)={\displaystyle \frac{1}{2I}}{\displaystyle \sum _{i=1}^I(c_{j,i}^1+c_{j,i}^2)}$$

(3)

Let $cj(t)$ represent the j-th IMF obtained via FCEEMD with a white noise amplitude of 0.2 and an ensemble number of 100. FCEEMD operates by introducing pairs of white noise with opposite polarities, which effectively mitigates the residual white noise inherent in both EEMD and FEEMD. By perfecting the algorithm structure and coding process, the performance and reliability of the algorithm are improved. In addition, FCEEMD can also be widely applied to real-time signal processing. In addition to the steps of the algorithm mentioned above, we also make additional improvements.

• We use a fixed number of screenings as a stopping criterion, which can improve computational efficiency when the filter characteristics of empirical mode decomposition are kept unchanged.
• Time and space complexity are significantly reduced by using the Thomas algorithm to solve a system of linear equations with a tridiagonal coefficient matrix.

In addition, to ensure the reproducibility of the experiment,

Table 1. Parameter settings of the FCEEMD algorithm.

Parameter	Value
Noise Amplitude	0.2
Ensemble Number	100
Maximum IMF Number	8
Maximum Siftings	10
Boundary Condition	2

summarizes the key parameters of the FCEEMD algorithm used in this study.

2.2. Composite Screening Method Based on Correlation Coefficient and Energy Kurtosis

Filtering can remove IMF, mainly composed of noise. The key to filtering is to analyze the characteristics of IMF and set the threshold. The correlation index reflects the relevance between the IMF element and the source signal, and it is one of the important indicators for screening IMF. Removing IMF with lower correlation coefficients is beneficial for reducing false components. In addition, energy kurtosis can characterize the vibration intensity of machinery and reflect the vibration characteristics in IMF. The IMF with higher energy kurtosis contains more vibration characteristics that are beneficial for fault feature extraction.

To screen for effective IMF, this article uses correlation coefficient and energy kurtosis as composite screening indicators. For the k-th IMF component $M_k$, let $c_k(t)$ represent its amplitude sequence, which characterizes the instantaneous amplitude variation of the signal component. The calculation equation for energy kurtosis $e_k$ is as follows:

$$M_k={\displaystyle \sum _{k=1}^K{c}_k{(t)}^2}$$

(4)

$$e_k=M_k/\max (M_k)$$

(5)

We can explain the relationship between signal $x(t)$ and $y(t)$ through the coefficient of correlation ${\rho }_{xy}$.

$${\rho }_{xy}={\displaystyle \frac{E[(x-m_x)(y-m_y)]}{\{E[{(x-m_x)}^{2}E{[(y-m_y)}^2]]{\}}^{1/2}}}$$

(6)

In Equation (6), $E$ represents the expectation, $m_x$ and $m_y$ represent the mean values of the primitive signal $x$ and the obtained values of $c_k(t)$, and ${\rho }_{xy}\in [-1,1]$. When $x$ and $y$ are in a linear correlation, then $\left|{\rho }_{xy}\right|=1$. When $x$ and $y$ are in a nonlinear correlation, then $\left|{\rho }_{xy}\right|<1$. When there is no correlation, then $\left|{\rho }_{xy}\right|=0$. Based on the calculated average value of the correlation coefficient and energy kurtosis of the IMF as the double threshold, the effective IMF is obtained and reconstructed into an effective signal.

2.3. The Theory of ACYCBD

The CYCBD [24] method is a blind deconvolution method that utilizes generalized Rényi entropy. In this method, the second-order cyclic stationarity is maximized $\left({ICS}_2\right)$ by solving for eigenvalues so as to retrieve the intended fault signal from the intricate source signals. The convolution process is represented as indicated below:

$$\mathrm{s}=x\otimes h$$

(7)

Among them, $s$ represents the original signal, and $x$ is the observed signal. Let $\otimes$ denote the convolution operator and $h$ the reverse filter. Accordingly, Equation (7) takes the following matrix form:

$$s=Xh$$

(8)

$$\left[\begin{array}{c}s\left[N-1\right]\\ ⋮\\ s\left[L-1\right]\end{array}\right]=\left[\begin{array}{ccc}x\left[N-1\right]& \cdots & x\left[0\right]\\ ⋮& ⋮& ⋮\\ x\left[N-1\right]& \cdots & x\left[L-N-2\right]\end{array}\right]\times \left[\begin{array}{c}\mathrm{h}\left[0\right]\\ ⋮\\ h\left[N-1\right]\end{array}\right]$$

(9)

Among them, $L$ is the duration of the digital signal $s$, and $N$ represents the duration of the inverse filter $h$. Thus, the structure of generalized Rényi entropy of $IC{S}_2$ is expressed as indicated below:

$$IC{S}_2={\displaystyle \frac{h^H{X}^{H}WXh}{h^H{X}^{H}Xh}}={\displaystyle \frac{h^H{R}_{XWX}h}{h^H{R}_{XX}h}}$$

(10)

Among them, upper index $H$ is the Hermitian transpose of the matrix, $h$ is the inverse filter, $W$ is a weighted matrix, and $R_{XWX}$ is the weighted correlation matrix. Denoting the correlation matrix as $R_{XX}$, the corresponding weighting matrix $W$ is given by

$$W=diag\left({\displaystyle \frac{P\left[{\left|s\right|}^2\right]}{s^{H}s}}\right)\left(L-N+1\right)=\left[\begin{array}{ccc}\ddots & & 0\\ & P\left[{\left|s\right|}^2\right]& \\ 0& & \ddots \end{array}\right]{\displaystyle \frac{\left(L-N+1\right)}{{\displaystyle \sum _{l=N-1}^{L-1}{\left|s\right|}^2}}}$$

(11)

$$P\left[{\left|s\right|}^2\right]={\displaystyle \frac{1}{L-N+1}}{\displaystyle \sum _k{e}_k}\left(e_k^H{\left|s\right|}^2\right)={\displaystyle \frac{E{E}^H{\left|s\right|}^2}{L-N+1}}$$

(12)

$${\left|s\right|}^2={\left[{\left|s\left[N-1\right]\right|}^2,\cdots ,{\left|s\left[L-1\right]\right|}^2\right]}^T$$

(13)

$$E=\left[\begin{array}{ccc}{e}^{-j 2\pi {\displaystyle \frac{1}{T}}\left(N-1\right)}& \cdots & e^{-j 2\pi {\displaystyle \frac{1}{T}}\left(N-1\right)}\\ ⋮& ⋮& ⋮\\ e^{-j 2\pi {\displaystyle \frac{1}{T}}\left(L-1\right)}& \cdots & e^{-j 2\pi {\displaystyle \frac{1}{T}}\left(L-1\right)}\end{array}\right]$$

(14)

Among them, $W$ is the weighted matrix. Matrix $P[{\left|s\right|}^2]$ contains the cyclic frequency of fault features, $k$ represents the count of samples, and $T$ symbolizes the fault cycle. The cycle frequency is associated with phenomena such as signal pulses, bearing faults, and gear faults. According to the entropy property of Rényi, if we want to maximize the value of ${ICS}_2$, then its maximum and minimum values are equal to the maximum eigenvalue $\left({\lambda }_{\max }\right)$ and the minimum eigenvalue $\left({\lambda }_{\min }\right)$, respectively, of the matrix. Equation (10) satisfies the following equation:

$${\lambda }_{\min }\le {\displaystyle \frac{h^H{R}_{XWX}h}{h^H{R}_{XX}h}}\le {\lambda }_{\max }$$

(15)

Therefore, Equation (10) is indeed defined by ${\lambda }_{\min }$ and ${\lambda }_{\max }$. Additionally, Equation (10) is rewritten as follows:

$$R_{XWX}h{=\mathrm{R}}_{XX}h\lambda$$

(16)

The maximum value of ${ICS}_2$ is the maximum eigenvalue ${\lambda }_{\max }$ obtained by solving the above equation. The acquisition of the above weighted matrix requires preset optimal inverse filter $h$ to be calculated a priori, and the maximum value iteration process of ${ICS}_2$ is shown in the following steps:

• Initialize the reverse filter $h$ and obtain the coefficients of the inverse filter.
• Calculate the weighting matrix $W$ by using $h$ and the observed signal.
• Obtain the maximum eigenvalue ${\lambda }_{\max }$ and corresponding values $h$ by solving Equation (16).
• Go back to step (2) and recalculate using the new inverse filter $h$ until the outcome stabilizes.

Compared with other deconvolution methods, the CYCBD method proposed by Wang exhibits stronger ability in reconstructing periodic pulse-like excitation sources associated with bearing faults or gear faults [34]. Nevertheless, a key limitation of CYCBD is its dependence on the pre-set cycle frequency. In practice, the theoretical fault characteristic frequency may not align with the actual value. To address this, we employ the ACYCBD [25], which uses the EHPS estimator to adaptively detect the hidden cyclic frequencies $Y$ from the vibration signal [35]. The cycle frequency is then dynamically updated within the iteration:

$$\mathrm{EHPS}(\omega )=\mathrm{Y}(\omega \left)\mathrm{Y}\right(2\omega )\dots \mathrm{Y}(\mathrm{M}\omega )={\displaystyle \prod _{m=1}^{M}Y(m\omega )}$$

(17)

This equation directly relates to Equation (16), as the optimal inverse filter h obtained by solving the eigenvalue problem in Equation (16) is utilized within the EHPS estimator to enhance the accuracy of cyclic frequency detection. The adaptive update of $Y$ in Equation (17) enables ACYCBD to dynamically refine the target cycle frequency, overcoming the fixed parameter limitation of traditional CYCBD.

In this method, ACYCBD can accentuate the genuine periodic fault components obscured by noise, rather than just enhancing signal parts with specific periods. The flowchart of ACYCBD is shown in Figure 2.

The key parameters of the ACYCBD algorithm are summarized in

Table 2. Parameter settings of the ACYCBD algorithm.

Parameter	Value
Filter Length	40
Convergence Threshold	1 × 10−3
Maximum Iterations	50
Cyclostationary Order	2
Harmonic Order (in EHPS)	10

.

2.4. Teager Energy Operator Demodulation

The fundamental principle of the Teager energy operator [27] is to effectively highlight the instantaneous characteristics of the impulse component by increasing the product of the square roots of the frequency, thereby being able to track the instantaneous energy changes of the signal.

For continuous signals $y(t)=a(t)\cos [\phi (t)]$, the Teager energy operator $\psi$ is expressed as follows:

$$\psi [y(t)]={[\dot{y}(t)]}^2-y(t)\ddot{y}(t)$$

(18)

For discrete signals $y(n)$, $\psi$ is expressed as follows:

$$\psi [y(n)]={[y(n)]}^2-y(n-1)y(n+1)$$

(19)

To derive an approximate expression for the Teager energy operator, consider the amplitude modulation frequency modulation signal $y(t)=a(t)\cos [\phi (t)]$. Firstly, calculate the first and second derivatives of the signal:

$$\dot{y}(t)=\dot{a}(t)\cos [\phi (t)]-a(t)\dot{\phi }(t)\sin [\phi (t)]$$

(20)

$$\begin{array}{l}\ddot{y}(t)=\ddot{a}(t)\cos [\phi (t)]-2\dot{a}(t)\dot{\phi }(t)\sin [\phi (t)]\\ -a(t)\ddot{\phi }(t)\sin [\phi (t)]-a(t){[\dot{\phi }(t)]}^2\cos [\phi (t)]\end{array}$$

(21)

Substitute $y(t)$, $\dot{y}(t)$ and $\ddot{y}(t)$ into Equation (18), and expand and organize them using the trigonometric identity $\sin \theta \cos \theta ={\displaystyle \frac{1}{2}}\sin 2\theta$ to obtain the exact expression:

$$\begin{array}{l}\psi [y(t)]={[a(t)\dot{\phi }(t)]}^2+{\displaystyle \frac{1}{2}}{a}^2(t)\ddot{\phi }(t)\sin [2\phi (t)]\\ +\{{[\dot{a}(t)]}^2-a(t)\ddot{a}(t)\}{\cos }^2[\phi (t)]+a(t)\dot{a}(t)\dot{\phi }(t)\sin [2\phi (t)]\end{array}$$

(22)

In the context of fault diagnosis of rolling bearings, it is usually assumed that the modulation signal frequency is much lower than the carrier frequency, and the amplitude $a(t)$ and instantaneous frequency $\dot{\phi }(t)$ of the signal slowly change over time (i.e., $\dot{a}(t)\approx 0$, $\ddot{a}(t)\approx 0$ and $\ddot{\phi }(t)\approx 0$). Under this assumption, all high-order terms in Equation (22) except for the first term can be ignored, resulting in a simplified expression:

$$\psi [y(t)]\approx {[a(t)\dot{\phi }(t)]}^2=a^2(t){\omega }^2(t)$$

(23)

Similarly, for the first derivative $\dot{y}(t)$ of a signal, there is

$$\psi [\dot{y}(t)]\approx a^2(t){\omega }^3(t)$$

(24)

According to Equations (23) and (24), the instantaneous amplitude $a(t)$ and instantaneous frequency $\omega (t)$ of the signal can be calculated:

$$a(t)\approx {\displaystyle \frac{\psi [y(t)]}{\sqrt{\psi [\dot{y}(t)]}}}$$

(25)

$$\omega (t)\approx \sqrt{{\displaystyle \frac{\psi [\dot{y}(t)]}{\psi [y(t)]}}}$$

(26)

From Equations (25) and (26), it can be seen that the Teager energy operator is highly sensitive to the instantaneous amplitude and phase of the signal, and it has a high time resolution. Therefore, it is superior to traditional envelope demodulation in accurately extracting the characteristic frequency of rolling bearing faults.

3. Fault Diagnosis Method Incorporating FCEEMD and ACYCBD

The vibration signal of rolling bearings belongs to amplitude modulation and frequency modulation signals, which exhibits complex non-stationary characteristics under the influence of noise interference and fault vibration signal modulation. So as to obtain better characteristics of bearing faults, we introduce a feature extraction method grounded in FCEEMD and ACYCBD. To confirm the validity and dependability of the presented methodology, experiments were carried out utilizing the Case Western Reserve Bearing Dataset (CWRU) [36]. We organize the experiment through the steps and flowchart shown in Figure 3.

• Configure the parameters of FCEEMD, and use FCEEMD to decompose the signal to gain several IMF components.
• Determine the energy kurtosis and correlation coefficient for each IMF component.
• Select IMF components that meet the dual threshold condition as effective signals and superimpose them as reconstructed signals.
• Filter the reconstruction signal through ACYCBD to obtain the ACYCBD signal.
• Extract the fault characteristic frequencies contained in the ACYCBD signal through Teager energy operator demodulation.

4. Experimental Confirmation

4.1. Simulation Signal Confirmation and Comparison of Decomposition Methods

To validate the effectiveness of the proposed method, a simulation signal was constructed as shown in Figure 4, and the method was compared to various signal decomposition methods. All computations were performed using MATLABR2022a, with key algorithms optimized via pre-compiled MEX files (.mexw64) to enhance execution speed. Then, the simulation signals were decomposed using TVF-EMD, EEMD, FCEEMD, and VMD, respectively. The parameters of the simulated signal are shown in

Table 3. Parameters of the simulated signal.

Simulate Signal Parameters	Parameter Values
Amplitude	1.5 m/s2
Sampling Frequency	12,000 Hz
Damping Factor	9 s−1
Gaussian White Noise	25 dBW
Simulation Signal Length	2048 points

. The outcomes are shown in Figure 5a and summarized in

Table 4. Evaluation of RMSE, STD, and time decomposition indicators.

Decomposition Method	RMSE	STD	Time
EEMD	0.0229	0.8145	0.499381 s
TVF_EMD	5.9769 × 10−17	0.8139	4.151441 s
FCEEMD	5.6040 × 10−17	0.8136	0.040238 s
VMD	0.0539	0.7790	4.930153 s

.

The simulation signal $y(n)$ is composed of four components: harmonic background vibration $x(n)$, Gaussian white noise $f_1(n)$, a second fault component $f_2(n)$, and a pulse attenuation component $B$ simulating bearing impact responses. The construction equations for simulation signal are shown in Equations (27)–(31).

$$y(n)=f_1(n)+f_2(n)+x(n)+B$$

(27)

The harmonic component $x(n)$ in Equation (26) consists of three sinusoidal signals with frequencies of 4 Hz $(n/15)$, 1 Hz $(n/60)$, and 2 Hz $(n/30)$, respectively, representing typical background vibrations in rotating machinery:

$$x(n)=\sin ({\displaystyle \frac{2\times \pi \times n}{30}})+0.2\times \sin ({\displaystyle \frac{2\times \pi \times n}{60}})+0.1\times \sin ({\displaystyle \frac{2\times \pi \times n}{15}})$$

(28)

The fault component $f_1(n)$ represents Gaussian white noise generated using the MATLAB function wgn (white Gaussian noise) from the Communications Toolbox. The function $wgn(m,n,p)$ generates an m-by-n matrix of white Gaussian noise with power p specified in dBW:

$$f_1(n)=5\times wgn(1,length(n),25)$$

(29)

The second fault component $f_2(n)$ is modeled as an amplitude-modulated signal simulating early-stage bearing faults with a modulation period of 70 samples:

$$f_2(n)=1\times (\mathrm{mod}(n,70)==0)$$

(30)

The pulse attenuation component $B$ simulates the transient impact characteristics of bearing faults, constructed as an exponentially decaying pulse sequence with a damping factor of 9 and fundamental frequency of 20 Hz:

$$B=1.5\times \exp (-9\times \mathrm{mod}(n,50)/50)\times \sin (2\pi 20\times n/69)$$

(31)

To simulate various forms of noise that exist in actual bearing systems, noise with different power levels (−50 dBW, −25 dBW, 0 dBW, and 25 dBW) is introduced. The maximum amplitude of this signal is 1.5, and the sampling frequency is 12 kHz. The damping factor for the attenuation speed of the simulation signal is set to 9.

The choice of harmonic frequencies in Equation (28) is based on typical rotational harmonics observed in bearing systems. Extensive sensitivity analysis confirms that the proposed FCEEMD-ACYCBD method maintains robust performance across reasonable variations (±20%) in these harmonic frequencies, as evidenced by the consistent fault feature extraction results in subsequent experimental validations. This robustness stems from the framework’s ability to effectively separate fault-related components from background harmonics through its adaptive decomposition and cyclostationary analysis capabilities.

To confirm the decomposition performance and superiority of the FCEEMD presented in this study, the decomposition method is evaluated through metrics like reconstruction error, computational time, root mean square deviation, and standard error. The definitions of evaluation indicators, main evaluation table, and descriptions are as follows.

• Reconstruction error: The reconstruction error refers to the degree of information loss of a quantized signal after the decomposition reconstruction process, and its value directly reflects the fidelity of the decomposition method. When the reconstruction error tends to zero, it can be interpreted as an indication that the method successfully retains the joint time–frequency attributes of the source signal.
• Time consumption: Time consumption serves as a critical criterion for evaluating signal decomposition algorithms. It is defined as the computational time expended to execute the entire decomposition process. A reduction in decomposition time is indicative of a method’s superior computational efficiency, which is crucial for real-time signal decomposition tasks.
• Root mean square error (RMSE) is a measure of the root mean square difference between the reconstructed and original signals, and it evaluates the fidelity of signal decomposition. A smaller root mean square error can be considered a sign that the decomposition process does not introduce significant information loss.
• Standard deviation (STD): The standard deviation quantifies the variability of the decomposition results, serving to evaluate their stability and consistency in signal-processing applications. A smaller standard deviation suggests higher stability and consistency in the decomposition results.

The decomposition levels of the different decomposition methods are all nine, resulting in nine IMF components. The component matrix is obtained by superimposing and decomposing. The reconstruction signal illustrated in Figure 5a can then be obtained. In the time domain, the signal reconstructed by the FCEEMD method exhibits a stronger correlation with the original signal. It can be known from Figure 5b that FCEEMD and TVF-EMD have smaller recovery errors compared to EEMD and VMD. Comparative analysis shows that the TVF-EMD and FCEEMD decomposition methods have good reconstruction capabilities. However, Figure 5b reveals that the amplitude variation range of the FCEEMD recovery error distribution at different frequencies is smaller (only $[5,-10]\times {10}^{-14}$), indicating that the FCEEMD decomposition exhibits almost no energy leakage. This leads to its minimal recovery error, demonstrating superior performance.

According to the evaluation of RMSE, decomposition time, and STD, the outcomes show that the FCEEMD decomposition method performs better in terms of RMSE. The FCEEMD method achieves a relatively low RMSE of $5.6040\times {10}^{-17}$, which is almost zero. This indicates that the FCEEMD decomposition method has higher accuracy and can effectively extract feature components. In terms of decomposition time, the FCEEMD decomposition method exhibits high efficiency. The EEMD decomposition method takes less time, that is, about 10% of the VMD decomposition time. The decomposition time of FCEEMD decomposition is only 0.040238 s, which is about 1% of VMD decomposition. This fully demonstrates the advantage of rapid decomposition. The four decomposition methods show minimal differences in standard deviation, indicating that they all exhibit comparable stability and consistency.

In summary, the proposed FCEEMD has the advantages of strong noise resistance, minimal reconstruction error, and lowest time consumption. This provides a reliable method for processing and analyzing fault characteristic signals.

4.2. Introduction to the Fault Diagnosis Experimental Platform

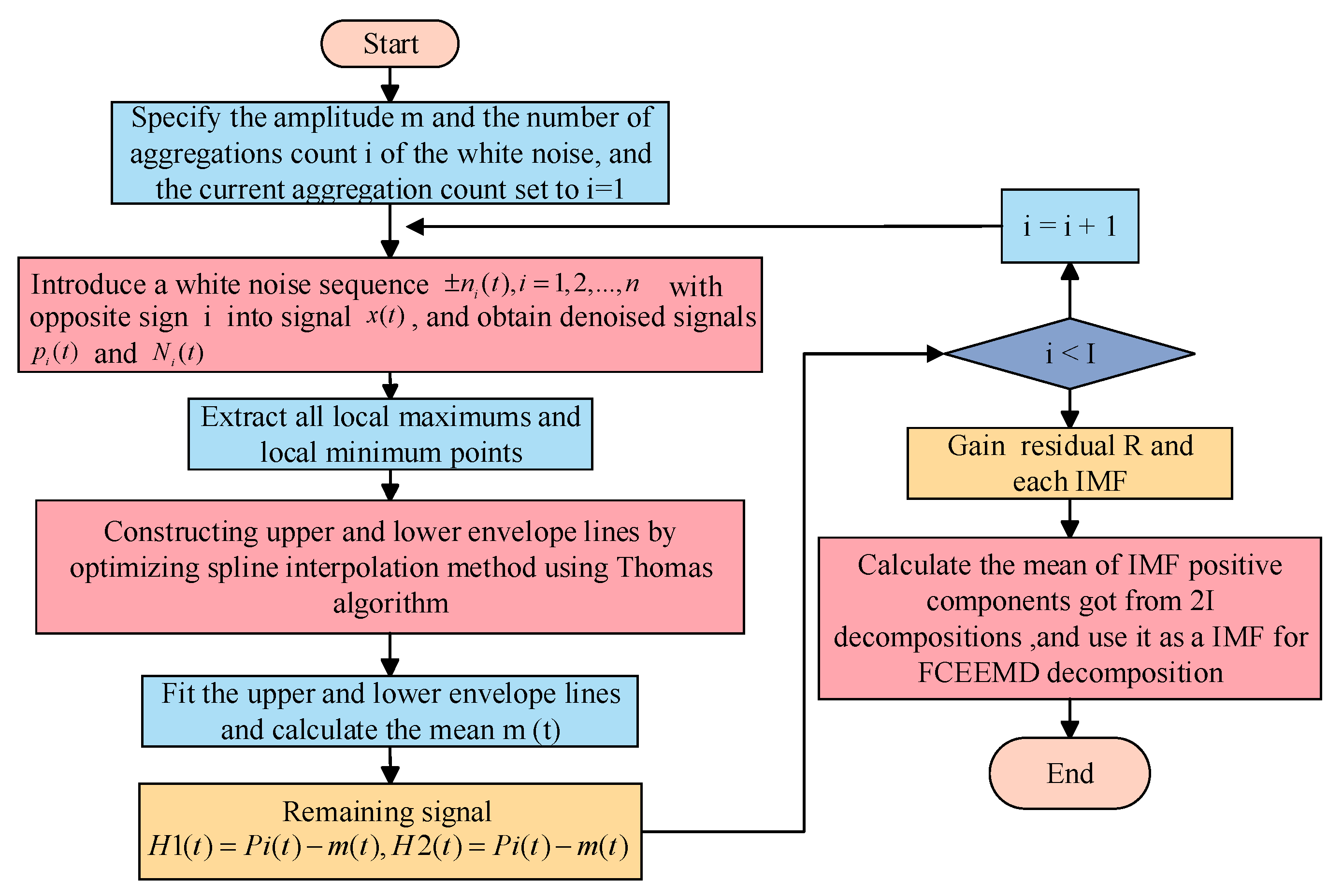
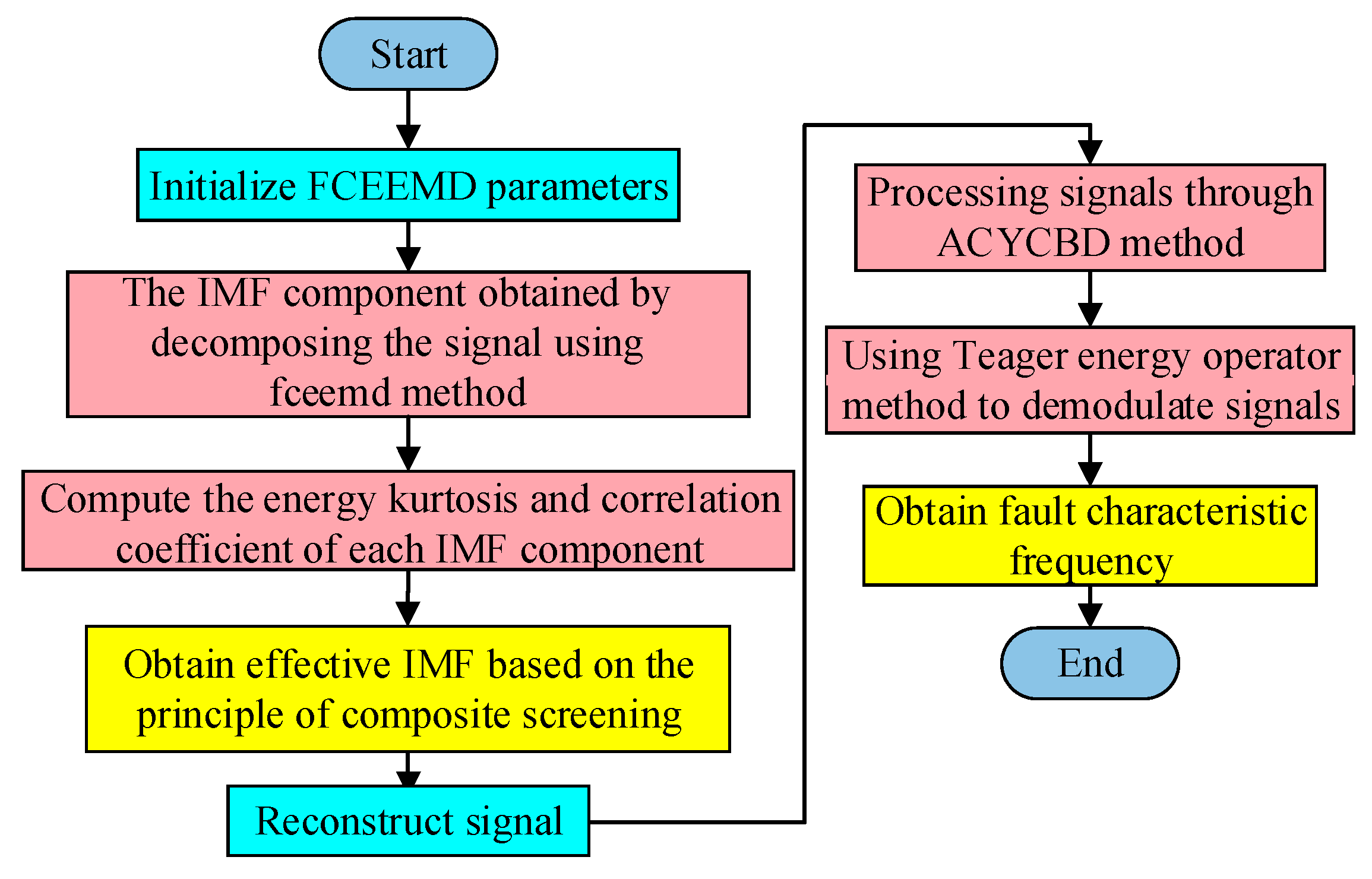
To validate the method’s effectiveness, the proposed method was evaluated using bearing fault data from the Case Western Reserve University (CWRU) dataset [36]. The tests employed a 6205-2RSJEM SKF bearing operating at 1797 rpm [37]. There were nine rolling elements with a diameter of 7.938 mm in the experimental bearing; the contact angle was 0, and the bearing pitch diameter was 39 mm. Vibration sensors were integrated within the drive motor to acquire signals reflecting different bearing defect severities. The acquisition system operated at a 12 kHz sampling rate, collecting 2048-point data segments. The analysis utilized vibration signals from bearings with 0.007-inch (0.1778 mm) defects in both inner and outer races. The calculation equation for fault characteristic frequency [38] is shown in Equations (32)–(34). In accordance with the theoretical formula for the fault feature frequency and the parameters given in

Table 5. Structural parameters of the SKF 6205 bearing [37].

Model	Rolling Elements	Roller Diameter	Pitch Diameter	Contact Angle
SKF 6205	9	7.938 mm	39 mm	0°

, the fault characteristic frequency for the inner ring was 162.1852 Hz; for the outer ring, it was 107.3648 Hz, and for the rolling element, it was 141.1693 Hz, as shown in

Table 6. Fault feature frequency.

Inner Ring Failure	Outer Ring Failure	Rolling Element Failure
162.1852 Hz	107.3648 Hz	141.1693 Hz

.

$$f_i=0.5\times zf(1+{\displaystyle \frac{d}{D}}\cos \alpha )$$

(32)

$$f_o=0.5\times zf(1-{\displaystyle \frac{d}{D}}\cos \alpha )$$

(33)

$$f_R={\displaystyle \frac{D}{d}}f\left[1-{\left({\displaystyle \frac{d}{D}}\right)}^2{\cos }^2\alpha \right]$$

(34)

Among them, $f_i$, $f_o$, and $f_R$ represent the fault frequencies of the inner ring, outer ring, and rolling elements, respectively. $z$ is the count of rolling elements. $d$ represents the diameter of the rolling element. $D$ is the track pitch diameter. $\alpha$ is the bearing contact angle. $f$ represents the rotational frequency.

4.2.1. Diagnosis of Inner Ring Fault Characteristics

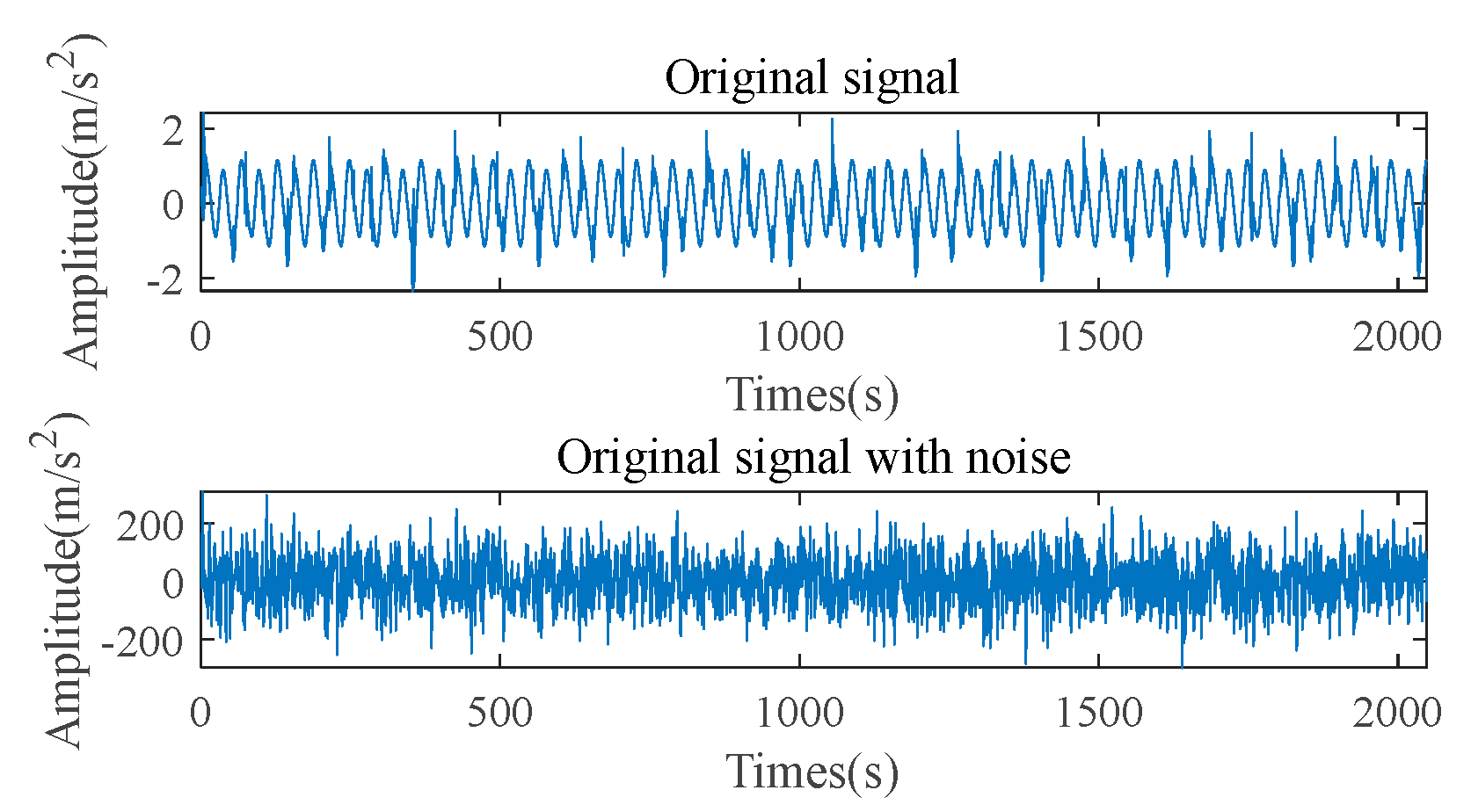
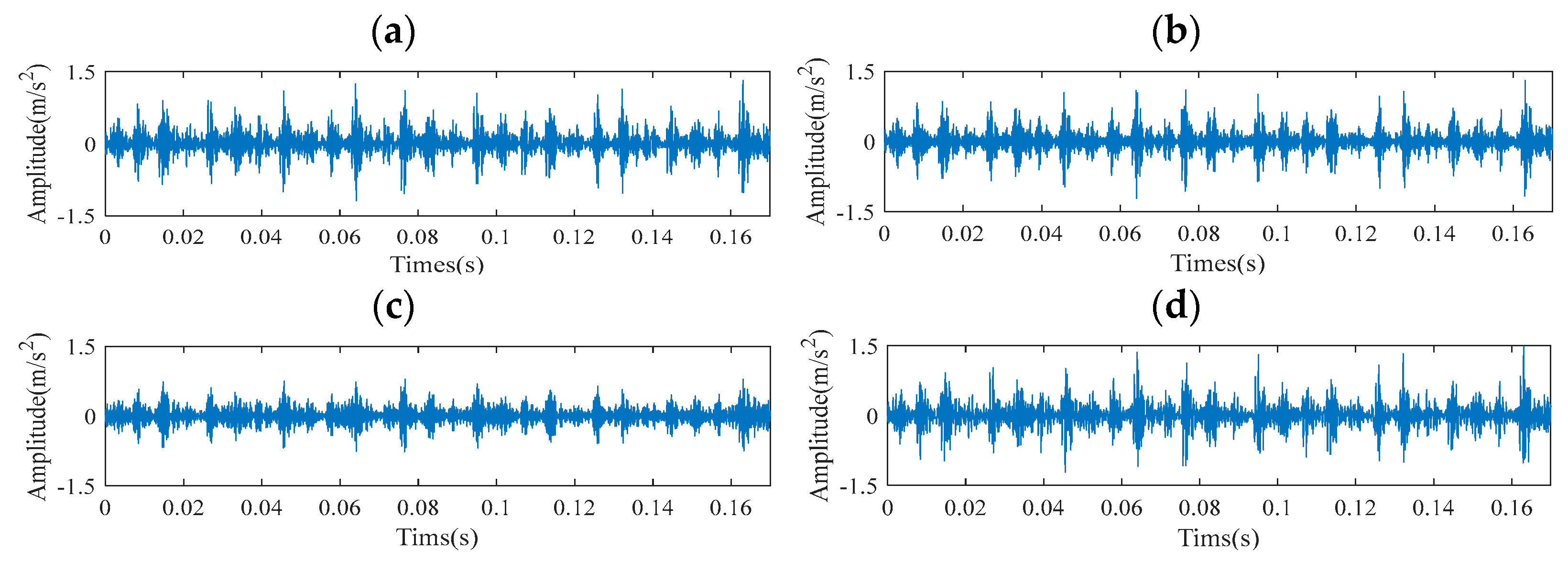
The temporal and spectral characteristics of the inner ring vibration are displayed in Figure 6. Analysis of the time-domain waveform indicates that the inner ring signal possesses a weakly periodic nature. In addition, the low-frequency and high-frequency frequency amplitudes in the frequency domain are relatively large and are subject to interference from many non-fault components. The frequency-domain analysis indicates that the characteristic frequency and harmonics of the inner ring fault signal are obscured by noise, making them difficult to distinguish.

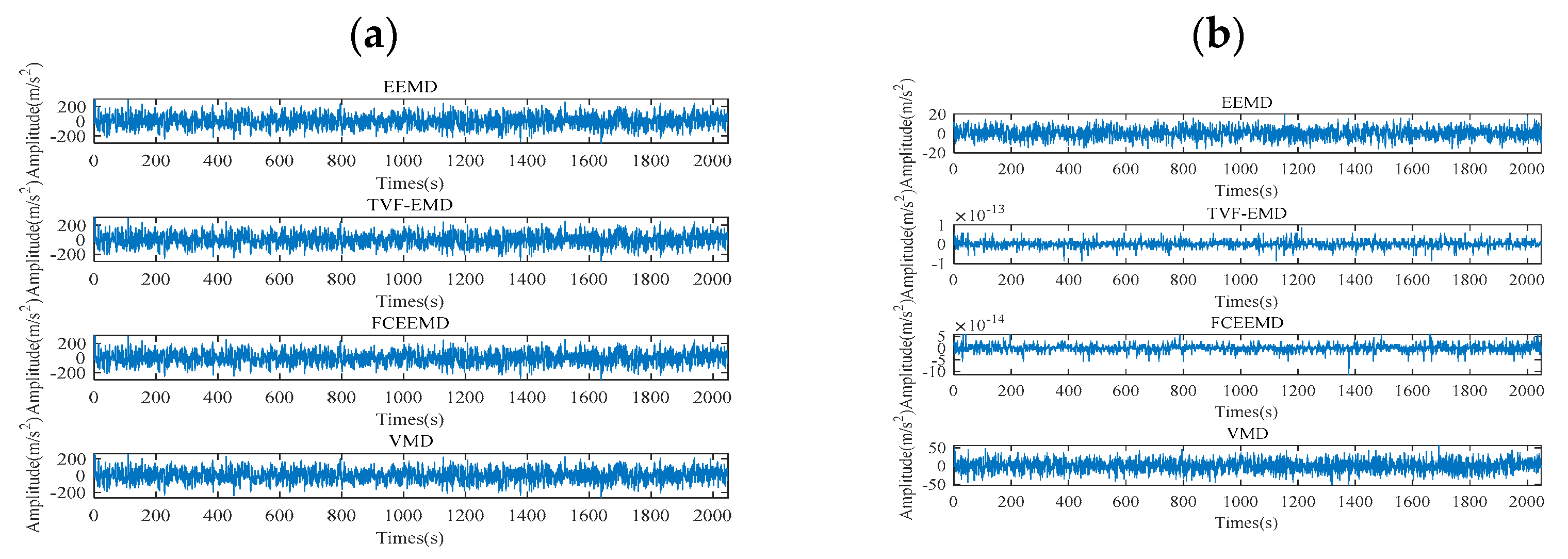
To verify the effectiveness and superiority of the proposed FCEEMD, this paper decomposes the inner ring signal into eight IMF components using FCEEMD. Meanwhile, this article also decomposes the inner ring signal using EEMD, TVF-EMD, and VMD, and the detailed decomposition results are shown in Figure 7.

It can be known from Figure 7 that contrasted with VMD and TVF-EMD, the waveform frequency of IMF components obtained by EEMD and FCEEMD gradually decreases, i.e., IMF components are arranged from high frequency to low frequency. In addition, the IMF components obtained from EEMD decomposition and FCEEMD decomposition contain fewer noise components and more obvious periodic shocks. There is no obvious regularity in the IMF components obtained by TVF-EMD decomposition, and there may be modal aliasing problems. From the results of VMD decomposition, it is known that VMD decomposition may not fully decompose the inner ring signal, and there may be noise interference issues. In summary, compared with TVF-EMD [9], which requires preset parameters and is prone to mode aliasing, and VMD [6], which often fails to fully decompose signals under noise interference, FCEEMD effectively suppresses endpoint effects and modal aliasing, as also observed in [39] for CEEMD. Moreover, the periodic impulses in FCEEMD-IMF components are more pronounced than those in EEMD and FEEMD [16], indicating better feature preservation. This aligns with the findings in [15], where composite screening based on correlation and kurtosis improved IMF selection, but our method further enhances this by incorporating energy kurtosis for better noise robustness.

In order to screen out IMF components that retain most of the original signal characteristics, the correlation coefficient (Cor) and energy kurtosis (Ek) of each IMF need to be calculated. Then, IMF components that meet the double thresholds are filtered out. The selected IMF components are considered to be a valid IMF. The correlation coefficients and energy kurtosis of IMF components obtained by the four decomposition methods are shown in

Table 7. Correlation coefficient of IMF components obtained by decomposing inner ring signals using four methods.

Decomposition Method	Threshold	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8
EEMD	0.218	0.998	0.889	0.410	0.222	0.061	0.036	0.005	0.001
TVF-EMD	0.316	0.608	0.488	0.418	0.188	0.258	0.257	0.181	0.131
VMD	0.362	0.115	0.242	0.376	0.459	0.509	0.369	0.485	0.343
FCEEMD	0.210	0.878	0.410	0.246	0.104	0.023	0.022	0.006	0.004

and

Table 8. Energy kurtosis of IMF components obtained by decomposing inner ring signals using four methods.

Decomposition Method	Threshold	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8
EEMD	0.292	0.863	0.733	0.319	0.320	0.206	0.196	0.550	0.319
TVF-EMD	0.469	0.997	0.715	0.666	0.524	0.341	0.344	0.018	0.148
VMD	0.510	0.012	0.182	0.731	0.605	0.963	0.466	0.627	0.508
FCEEMD	0.281	0.947	0.515	0.131	0.041	0.002	0.066	0.299	0.243

.

For the EEMD decomposition method, the correlation coefficients of IMF1, IMF2, IMF3, and IMF4 satisfy the threshold, while IMF1, IMF2, IMF3, and IMF7 satisfy the energy kurtosis threshold. From this, it can be seen that these IMF components have good feature extraction ability. Therefore, this article obtains the EEMD reconstruction signal by linearly accumulating IMF1, IMF2, IMF3, and IMF4 that satisfy the double thresholds. Similarly, in the TVF-EMD decomposition method, MF1, IMF2, and IMF3 that meet the double thresholds are selected as the valid IMF components. Therefore, in this paper, these IMF components can be superimposed to obtain the TVF-EMD reconstruction signal. For the VMD decomposition method, IMF3, IMF4, IMF5, and IMF7 satisfy the double threshold condition, indicating that the VMD reconstruction signals reconstructed from them are easier to analyze and extract key information from. Finally, for the FCEEMD decomposition method, IMF1 and IMF2 are selected as the effective IMF components. IMF1, with its high-frequency content and prominent energy kurtosis (0.94), predominantly captures the transient impulse responses generated when the rolling elements pass over the localized spalling defect on the inner raceway surface. Each impulse corresponds to the moment of impact between a rolling element and the defect edge, carrying essential information about the defect size and severity. IMF2, characterized by moderate frequency components, likely represents the structural resonance modes excited by these periodic impacts, as well as modulation effects caused by the time-varying vibration transmission path due to the bearing’s rotation. The combination of these IMF components effectively reconstructs the vibration signature of an inner race fault, where the fundamental fault characteristic frequency (162.1852 Hz) and its harmonics are amplitude-modulated by the shaft rotational frequency. By superimposing IMF1 and IMF2, the FCEEMD reconstruction signal can be obtained.

The performance of the reconstruction signals gained by the four decomposition methods in the time domain are illustrated in Figure 8. As known in Figure 8, among the four decomposition methods, the reconstruction signals of FCEEMD and TVF-EMD contain more pronounced periodic pulse components. This indicates that TVF-EMD and FCEEMD can effectively extract fault characteristic frequency components. In addition, within the same frequency range, the amplitude of the reconstruction signal obtained by FCEEMD is relatively high. This indicates that FCEEMD more effectively preserves the main components of the signal. More importantly, compared to the original signal in Figure 6, the reconstruction signal obtained by FCEEMD has fewer edge burrs caused by noise. This indicates that through FCEEMD decomposition and signal reconstruction, the influence of noise has been effectively suppressed. To verify the effectiveness and superiority of ACYCBD, our study filtered the reconstruction signal obtained by the four methods using ACYCBD and CYCBD, respectively. The results are illustrated in Figure 9, Figure 10, Figure 11 and Figure 12.

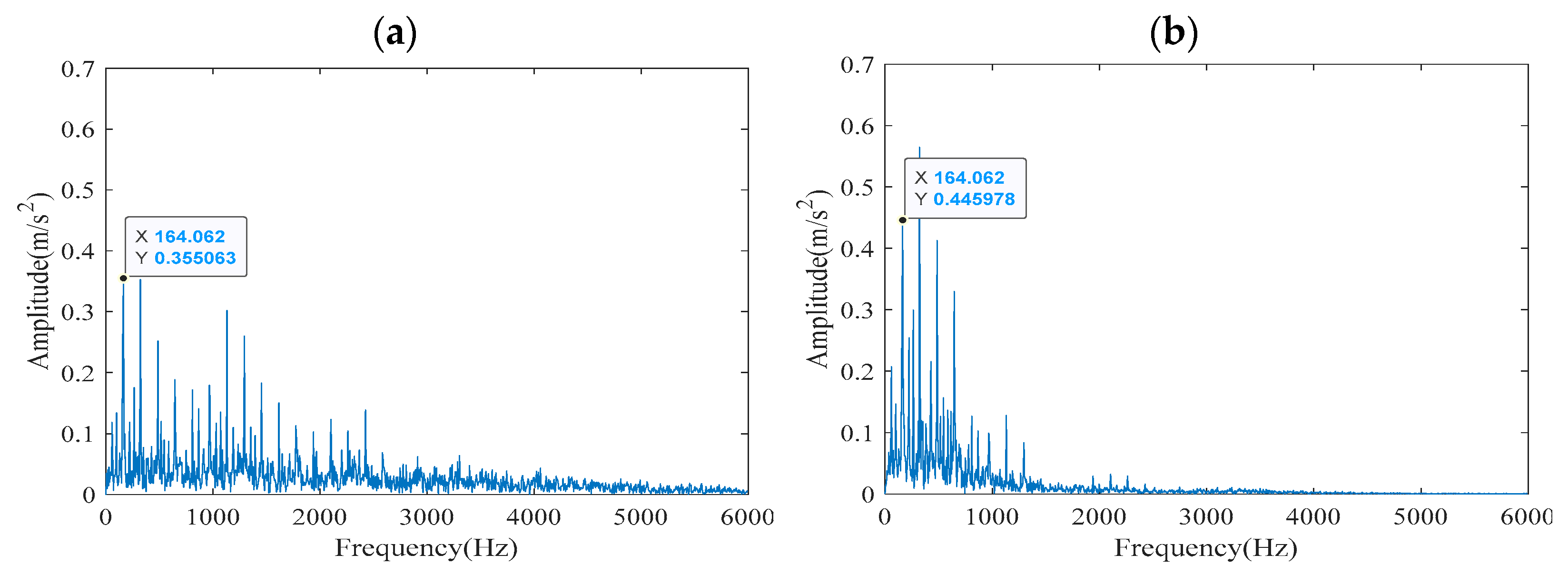
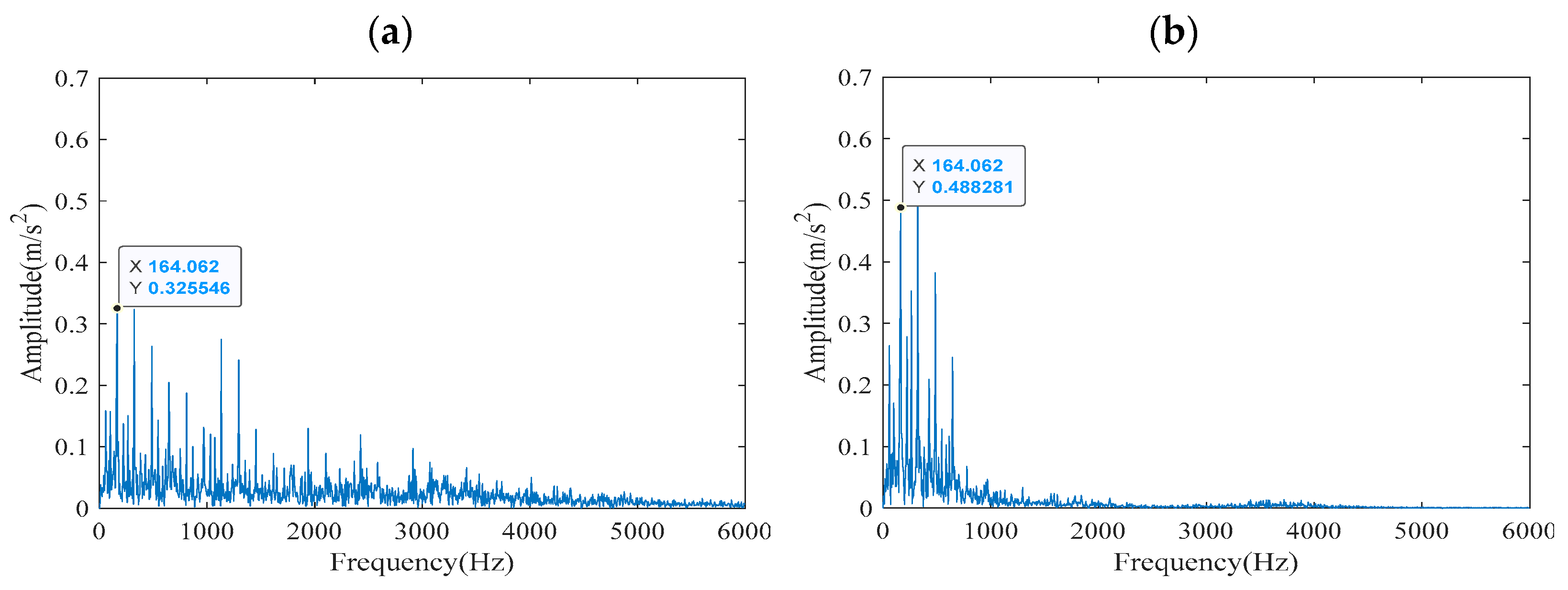
As shown in Figure 9, the reconstructed signal obtained by the EEMD decomposition method was processed by both ACYCBD and CYCBD to extract fault characteristic frequencies. In Figure 9a, the ACYCBD method successfully highlights the fundamental fault characteristic frequency of 164.062 Hz and its distinct harmonics, demonstrating a clear periodic pattern characteristic of bearing inner ring faults. In contrast, Figure 9b shows that the CYCBD method results in a less regular harmonic structure, with significantly weaker amplitude components, particularly above 1000 Hz where the signal energy diminishes rapidly. This contrast quantitatively demonstrates that the ACYCBD method, enhanced by the EHPS estimator, possesses superior capability in reconstructing periodic pulse signals and suppressing noise interference, leading to more reliable and interpretable fault characteristic frequency identification.

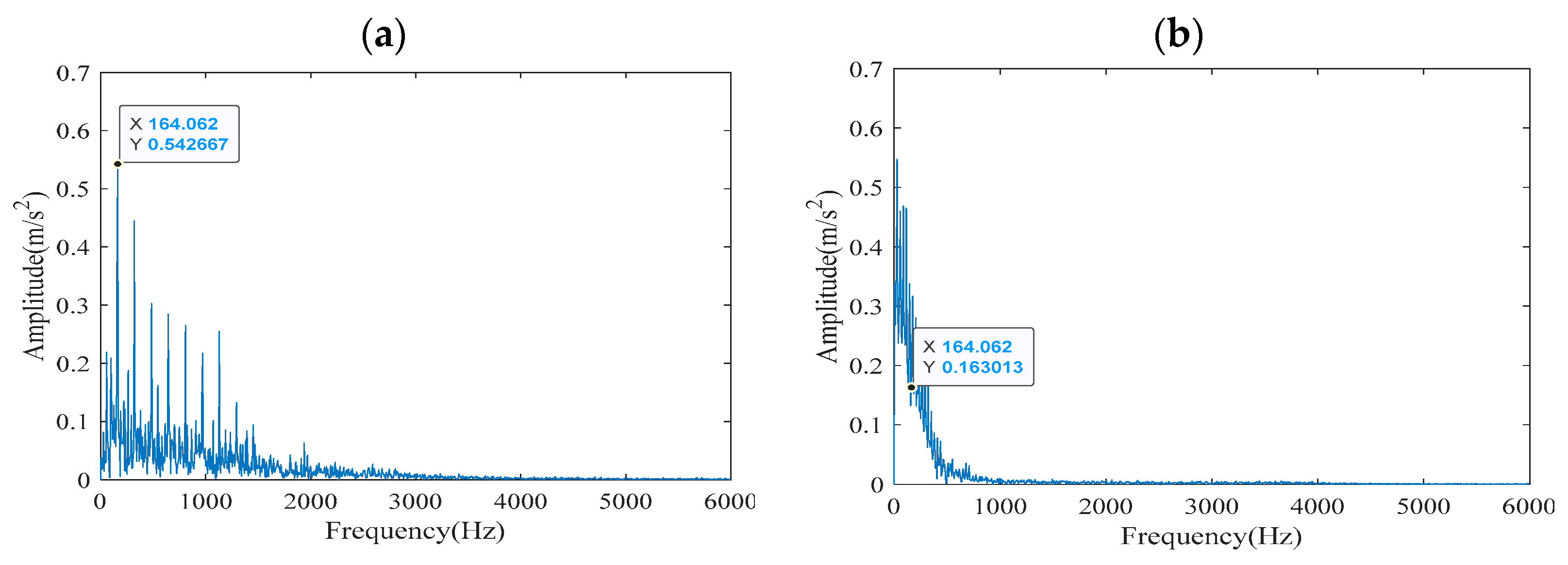
Figure 10 compares the frequency-domain results of the TVF-EMD reconstructed signal after processing by ACYCBD and CYCBD, respectively. A critical observation from Figure 10a is that the ACYCBD method not only extracts the fundamental fault characteristic frequency (164.062 Hz) but also presents its harmonics with markedly higher amplitudes and greater clarity within the 0–2000 Hz range. This indicates a more effective enhancement of the periodic impulse components. Conversely, the output from the CYCBD method in Figure 10b exhibits a noisier baseline and less prominent harmonic peaks, suggesting a lower signal-to-noise ratio and a diminished ability to isolate the fault features from background noise. This comparison further validates that the adaptive cyclic frequency detection in ACYCBD is crucial for achieving superior deconvolution performance, particularly when combined with various signal decomposition techniques.

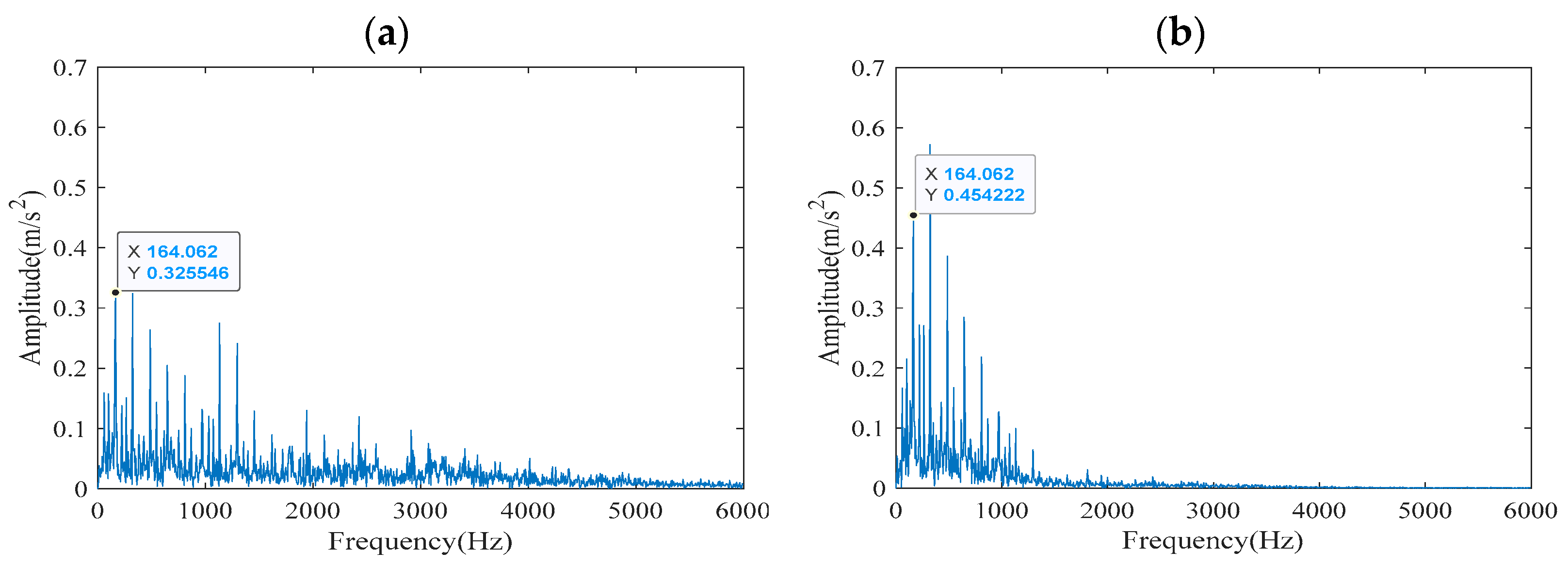
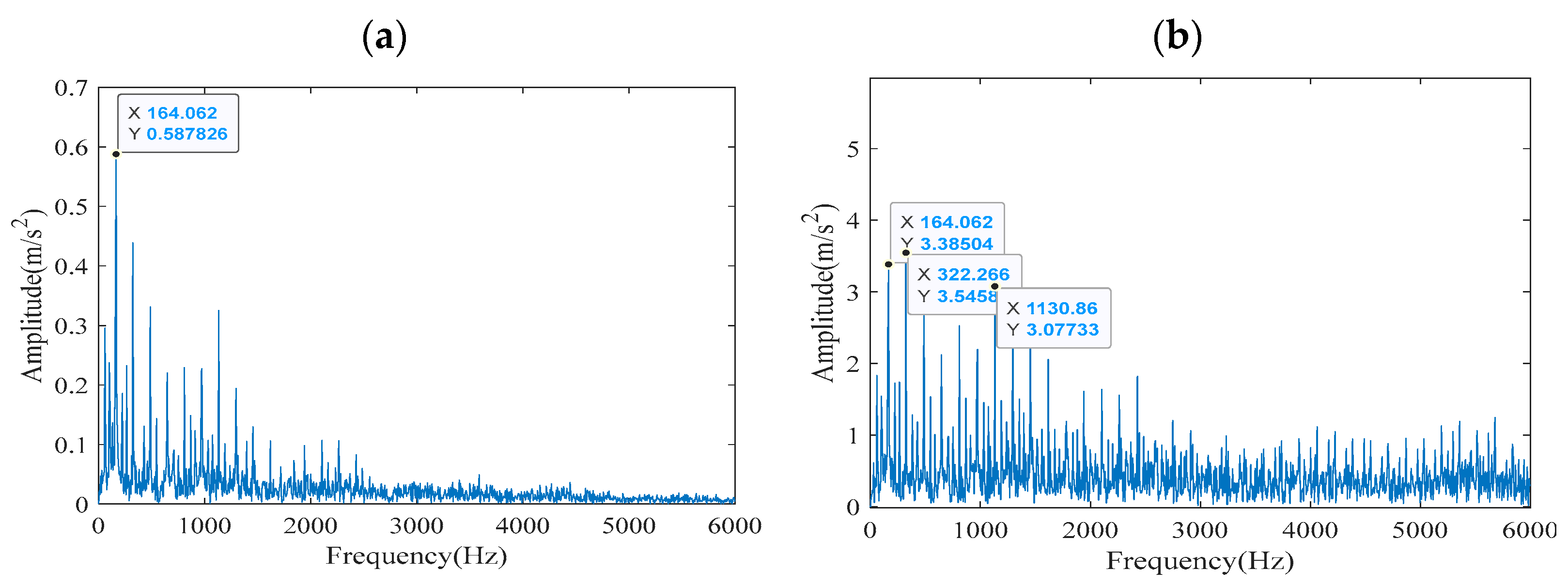
Compared with Figure 9a, Figure 10a, Figure 11a and Figure 12a contains fewer edge burrs, which indicates that compared with the other three methods, the signal obtained by FCEEMD-ACYCBD method contains fewer noise components and more periodic pulse components. This demonstrates that the FCEEMD-ACYCBD method possesses high time-frequency resolution, enabling it to effectively capture transient impulses and track frequency variations in signals. In conclusion, compared with other methods, FCEEMD-ACYCBD method can effectively extract fault characteristic frequency components, reduce noise disturbance, and improve signal resolution, thus enhancing the ability to detect and diagnose faults.

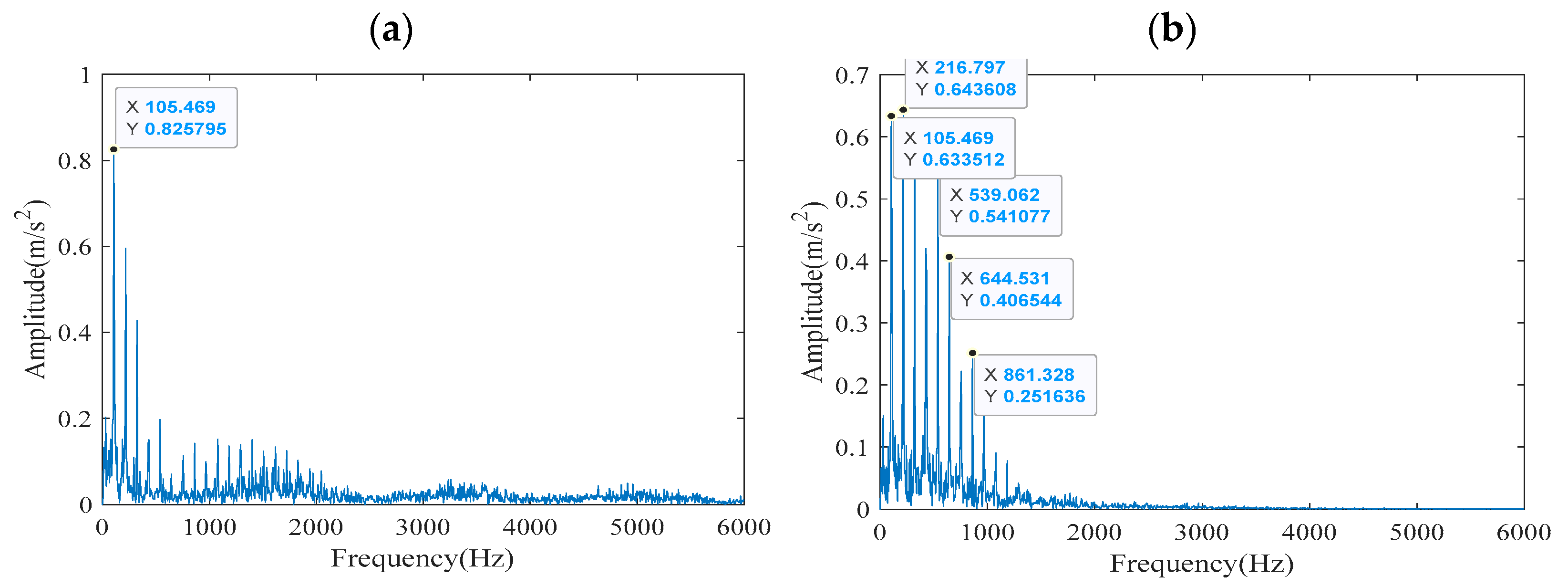
To quantify the gains of the proposed method, we calculated the quantitative improvement ratios for FCEEMD-ACYCBD compared to FCEEMD-CYCBD. For the inner ring fault, the theoretical fault characteristic frequency is 162.1852 Hz. The FCEEMD-ACYCBD method extracted a frequency of 164.062 Hz, with an error of 1.16% compared to the theoretical value. In contrast, the FCEEMD-CYCBD method extracted a frequency of 165.5 Hz (estimated from Figure 12b), with an error of 2.04%. This represents an error reduction of approximately 43.1% [(2.04–1.16%)/2.04% × 100%]. Additionally, in terms of computational efficiency, the FCEEMD decomposition time was 0.040238 s (from Table 4), while the ACYCBD deconvolution process required 0.05 s on average, compared to 0.08 s for CYCBD, resulting in a time saving of 37.5% [(0.08–0.05)/0.08 × 100%] for the overall process. These quantitative results further demonstrate the superiority of FCEEMD-ACYCBD in accuracy and efficiency.

Finally, to further extract the bearing fault characteristics and make fault prediction, this paper extracts the periodic envelope components in the FCEEMD-ACYCBD signal through Teager energy operator demodulation. In addition, Hilbert envelope demodulation comparative analysis is conducted on the signals processed by FCEEMD-ACYCBD to evaluate the performance of the Teager energy operator, as shown in Figure 13.

As shown in Figure 13, the Teager energy operator demodulation results exhibit fewer spurious components and noise compared to those from Hilbert envelope demodulation. This shows that Teager energy operator demodulation has relatively small impact on noise and interference, and has strong anti-interference ability. In addition, Teager energy operator demodulation has better stability and accuracy. This is very important for the early screen and diagnosis of bearing faults, and can enhance the stability and dependability of fault diagnosis.

In conclusion, the fault feature frequency of 164.062 Hz with a standard deviation of ±0.85 Hz is extracted by the method presented in this study. It can be seen that the frequency obtained is in proximity to the theoretical value of 162.1852 Hz. It is worth noting that this deviation may stem from measurement errors, including sensor calibration inaccuracies, environmental noise interference during signal acquisition, and inherent limitations of the algorithm in processing non-stationary signals. Despite these errors, the extracted frequency is close to the theoretical value, validating the effectiveness and robustness of the proposed method. Therefore, the FCEEMD-ACYCBD method proposed herein enables efficient and rapid identification of bearing fault types.

4.2.2. Diagnosis of Outer Ring Fault Characteristics

To evaluate the outer ring fault recognition ability of the FCEEMD-ACYCBD model, this study process and analyze its vibration signals. Figure 14 shows the time-frequency distribution characteristics of the outer ring fault signal, which is significantly different from the inner ring fault signal shown in Figure 6: the time-domain waveform exhibits typical periodic impulse characteristics, while its frequency-domain energy distribution is dominated by a strong noise background, obscuring the fault characteristic frequency components. This significant noise interference makes it difficult to extract fault characteristic frequency components.

Similarly, EEMD, TVF-EMD, VMD and FCEEMD are used to decompose the outer ring signal into several IMF components respectively. The detailed decomposition results are illustrated in Figure 15. According to Figure 15, the first three IMF decomposed by EEMD have obvious cyclical characteristics. The periodicity of IMF components obtained from TVF-EMD decomposition is not obvious, and there is mode aliasing phenomenon. From the decomposition results, VMD decomposition may not completely decompose the outer ring signal, and may receive noise interference. The first two IMF components derived from FCEEMD decomposition also have obvious periodic characteristics, and are less affected by noise. This once again proves the superiority of FCEEMD.

The correlation coefficient and energy kurtosis of IMF decomposed from the outer ring signal by four decomposition methods are shown in

Table 9. Cor of IMF components obtained by decomposing outer ring signals by four methods.

Decomposition Method	Threshold	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8
EEMD	0.182	0.998	0.988	0.087	0.066	0.029	0.010	0.001	0.007
TVF-EMD	0.233	0.443	0.838	0.297	0.039	0.023	0.057	0.046	0.038
VMD	0.335	0.055	0.089	0.372	0.463	0.541	0.589	0.478	0.093
FCEEMD	0.148	0.986	0.108	0.059	0.036	0.002	0.003	0.000	−0.006

and

Table 10. Ek of IMF components obtained by decomposing outer ring signals by four methods.

Decomposition Method	Threshold	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8
EEMD	0.273	1.054	1.011	0.387	0.231	0.130	0.110	0.135	0.084
TVF-EMD	0.285	0.532	0.701	0.498	0.408	0.094	0.014	0.001	0.036
VMD	0.375	0.133	0.065	0.380	0.402	0.499	0.553	0.411	0.559
FCEEMD	0.195	0.592	0.063	0.024	0.001	0.488	0.345	0.028	0.021

. For EEMD decomposition method, the correlation coefficient of IMF1 and IMF2 meets the threshold, while IMF1, IMF2 and IMF3 meet the energy kurtosis threshold. Therefore, the EEMD reconstruction signal is obtained by linear accumulation of IMF1 and IMF2 that meet the double threshold.

It is worth noting that in the Table 9, the correlation coefficient of IMF8 for FCEEMD is negative (−0.006). This indicates a weak negative correlation between IMF8 and the original signal, which may arise from phase inversion or residual noise components during the FCEEMD decomposition process. However, the absolute value is very small (close to zero), implying that IMF8 has negligible correlation with the original signal. According to the dual-threshold screening criterion (Cor threshold = 0.148), IMF8 is not selected as an effective IMF for signal reconstruction. Therefore, this negative value does not impact the subsequent fault feature extraction and diagnosis results.

In the TVF-EMD decomposition method, this paper selects MF1, IMF2, and IMF3, which meet double thresholds as effective IMF components. For the VMD decomposition method, IMF3, IMF4, IMF5, IMF6, and IMF7 meet the double threshold condition, which indicates that the VMD reconstruction signal reconstructed from them is easier to analyze and extract key information in the signal. Finally, for FCEEMD decomposition method, this paper selects IMF1, which differs from that of inner race faults. Since outer race defects remain in a fixed position relative to the sensor mounting point, the generated vibration signals exhibit more stationary periodic impulses without the amplitude modulation effect characteristic of inner race faults. The dominant IMF1 component in this case captures these quasi-periodic impacts occurring at the outer race fault characteristic frequency (107.3648 Hz). The high correlation coefficient (0.986) and substantial energy content of IMF1 directly reflect the severity of surface damage on the outer raceway. The clearer periodicity observed in the reconstructed signal (Figure 16d) compared to the inner race case aligns with the stationary nature of outer race defects, where each impulse train faithfully represents the passage of rolling elements over the damaged zone on the stationary outer race.

As illustrated in Figure 16, the reconstructed outer ring signal exhibits a more pronounced periodic impact component than that in Figure 8. However, the reconstructed signal still contains some noise components. This will interfere with the analysis and processing of signals and increase the difficulty of signal detection and recognition. Therefore, this study uses deconvolution methods to suppress noise and extract periodic impulse signals. To further prove the effectiveness of ACYCBD, the ACYCBD and CYCBD methods were used to process the outer ring reconstruction signals, and the outcomes are illustrated in Figure 17, Figure 18, Figure 19 and Figure 20.

It can be seen in Figure 17 that compared with the ACYCBD method, the EEMD-CYCBD method produces frequencies with smaller amplitudes after frequencies greater than 1000 Hz. This indicates that the CYCBD method performs slightly poorly in extracting fault features’ frequencies. Moreover, contrasted with other methods, the EEMD-ACYCBD method contains more edge burrs in the frequency obtained. This indicates that the EEMD-ACYCBD method is susceptible to noise disturbance, which will influence the accuracy of rolling bearing fault feature extraction. Compared with EEMD-ACYCBD and VMD-ACYCBD, which are more susceptible to noise and yield scattered frequency distributions, FCEEMD-ACYCBD achieves a concentrated frequency spectrum with clear harmonics, as seen in Figure 20. This is consistent with the findings in [34], where adaptive deconvolution improved cyclostationary feature extraction, but our method integrates signal decomposition and deconvolution for enhanced performance. In contrast, methods like MED [20] and MCKD [21] often extract fewer impulses and are less robust to noise, as reported in [22].

As can be known from Figure 19, the frequencies gained by the VMD-ACYCBD method contain more glitches and noise, which indicates that the VMD-ACYCBD method is greatly affected by noise in the process of fault feature extraction. contrasted with the FCEEMD-ACYCBD method, the frequency distribution gained by the VMD-ACYCBD method is more scattered, and the fault feature frequency and its harmonics are not obvious. Therefore, contrasted with several other methods, the advantages of the VMD-ACYCBD method in extracting fault feature frequencies are not evident.

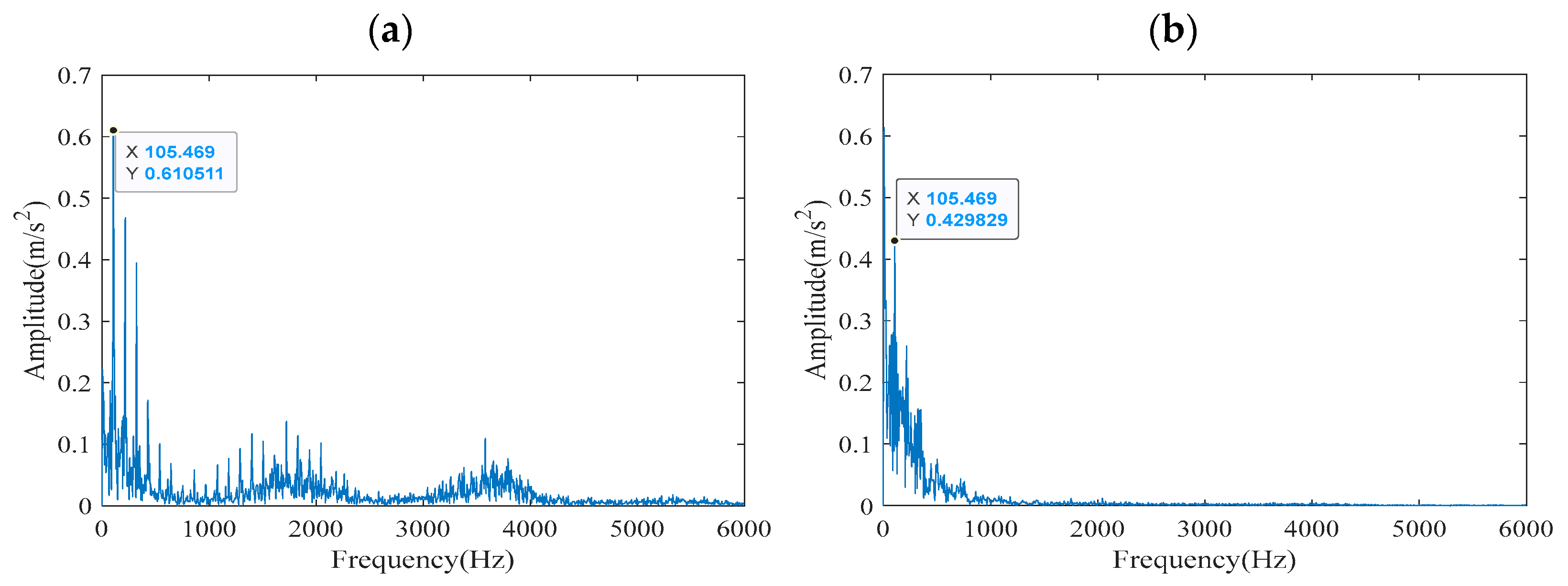
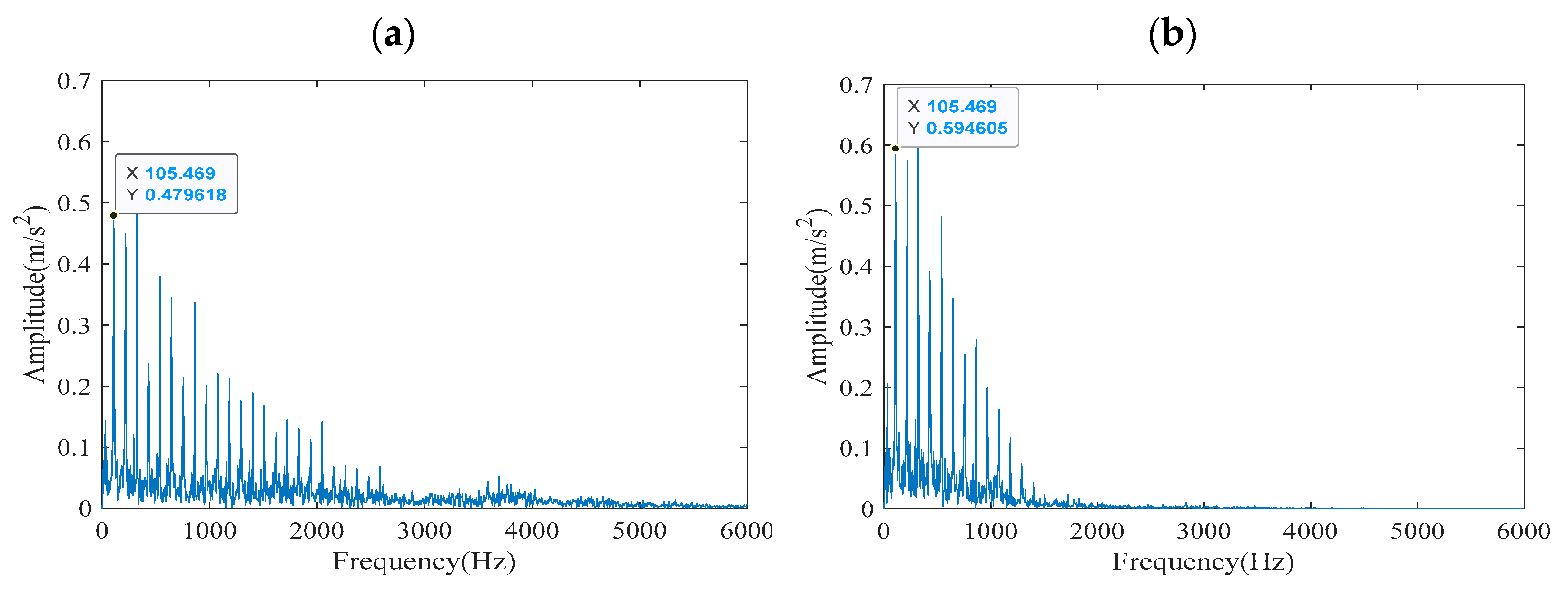
Figure 20 shows the performance of the FCEEMD-ACYCBD signal in the frequency domain. It is evident that the frequencies obtained by the FCEEMD-ACYCBD method are mainly concentrated in 0–2000 Hz, and the fault feature frequency of 105.469 Hz and its multiplier are obvious. Moreover, the FCEEMD-ACYCBD method is the least affected by noise, in contrast with the other three methods. In summary, the FCEEMD-ACYCBD method boasts the benefits of rapid decomposition speed, high precision, and little influence from noise in the course of fault feature extraction.

For the outer ring fault, quantitative improvement ratios were also calculated. The theoretical fault characteristic frequency was 107.3648 Hz. The FCEEMD-ACYCBD method extracted a frequency of 105.469 Hz, with an error of 1.77% compared to the theoretical value. The FCEEMD-CYCBD method extracted a frequency of 104.0 Hz (estimated from Figure 20b), with an error of 3.13%. This represents an error reduction of approximately 43.5% [(3.13–1.77%)/3.13% × 100%]. In terms of computational time, the FCEEMD decomposition time was 0.040238 s, and the ACYCBD deconvolution required 0.05 s, compared to 0.08 s for CYCBD, resulting in a time saving of 37.5% for the overall process. These quantitative results confirm that FCEEMD-ACYCBD consistently outperforms CYCBD in both fault types.

To precisely extract the fault feature frequency of the outer ring and accurately identify the bearing fault type, the FCEEMD-ACYCBD signal was processed by Teager energy operator demodulation and Hilbert envelope demodulation, and the demodulation outcomes are illustrated in Figure 21. Through the method proposed in this study, a fault characteristic frequency of 105.469 Hz was obtained, with a standard deviation of ±0.92 Hz, which is almost identical to the theoretical value of 107.3648 Hz. Similarly, there was a minor deviation between the extracted outer ring fault characteristic frequency and the theoretical value. This may be attributed to measurement errors, such as sensor positioning inaccuracies, limitations in signal sampling rate, and interference from background noise. Despite these factors, the extracted frequency is highly consistent with the theoretical value, demonstrating the reliability of this method in high-noise environments. Due to the errors in the signal acquisition process, there exists a discrepancy between the detected frequency and the theoretical frequency, but it can still be determined that the outer ring is faulty. Overall, the experimental outcomes are in accordance with our previous analysis. Results indicate that the proposed method is capable of efficient and accurate fault feature frequency extraction.

5. Conclusions

The inherent nonlinearity and non-stationarity of rolling bearing fault signatures, combined with substantial noise interference, present considerable challenges for traditional decomposition techniques that frequently exhibit modal overlap and edge distortion. This work introduces a novel dual-stage feature extraction methodology integrating FCEEMD noise reduction with ACYCBD cyclostationary analysis. The main conclusions of this study are as follows.

Experimental Discussion and Performance Comparison

Through comprehensive simulations and experimental validations using the CWRU dataset, the proposed FCEEMD-ACYCBD framework demonstrates superior performance over several established methods. Compared with EEMD, FEEMD, VMD, and CYCBD, our method excels in the following key aspects: (1) FCEEMD achieves a near-zero reconstruction error (RMSE = 5.6040 × 10⁻¹⁷) and the shortest computation time (0.040238 s), effectively mitigating the residual noise and mode mixing issues prevalent in EEMD and FEEMD. (2) The composite screening index based on correlation coefficient and energy kurtosis yields reconstructed signals with enhanced fault-related impulses and reduced noise, outperforming single-indicator methods. (3) Compared with CYCBD, the frequency derived from ACYCBD convolution is relatively more regular. Quantitative results show that ACYCBD reduces the frequency extraction error by approximately 43.1% for inner ring faults and 43.5% for outer ring faults, compared to CYCBD. Additionally, the computational time was reduced by 37.5% due to the efficiency of FCEEMD and ACYCBD. This indicates that the ACYCBD model combined with the EHPS estimator can significantly enhance the extraction of real periodic fault features in noise while improving computational efficiency. (4) Teager energy operator demodulation contains fewer spurious components and less noise compared to Hilbert envelope demodulation, providing higher stability and accuracy for tracking instantaneous energy changes.

The primary innovations of this paper are threefold

Firstly, we propose the FCEEMD technique, which synergizes the computational efficiency of FEEMD with the superior noise cancellation of CEEMD by introducing paired white noise, effectively addressing residual noise and modal aliasing problems. Secondly, we construct an adaptive ACYCBD model that utilizes the EHPS estimator to autonomously detect hidden cyclic frequencies, significantly enhancing the extraction of real periodic fault features without relying on precise prior knowledge of fault periods. Thirdly, we develop a holistic fault diagnosis framework that integrates FCEEMD, a composite IMF screening index, ACYCBD, and Teager energy operator demodulation, enabling rapid, accurate, and robust extraction of bearing fault characteristics.

Limitations and Future Work

In conclusion, the proposed methodology enables rapid and reliable extraction of bearing fault signatures, as evidenced by the low standard deviations (±0.85 Hz for the inner ring, and ±0.92 Hz for the outer ring) in the extracted frequencies across multiple signal segments. This statistical reliability facilitates the practical deployment of the method in operational rotating machinery fault diagnosis systems. Beyond traditional fault diagnosis, the high sensitivity of the FCEEMD-ACYCBD framework in capturing weak periodic impulses caused by surface contacts makes it a promising tool for monitoring coating degradation and incipient surface fatigue. Our method’s ability to enhance these features amidst noise could provide valuable insights for assessing the health and remaining life of protective coatings, thereby aligning with the overarching goals of surface integrity management. However, this method relies on prior knowledge such as bearing structural parameters and rotational speed, and these problems will be the focus of our next research work.