A CFD-DEM Simulation of Droplets in an Airless Spray Coating Process of a Square Duct
Abstract
1. Introduction
2. Governing Equations
2.1. Gas Phase Equations
2.2. Motion Equation of Droplets
2.3. Motion of Rotary Sprayer
2.4. Boundary and Calculation Conditions
3. Selections of Discrete Element Parameter and Gas Turbulence Model
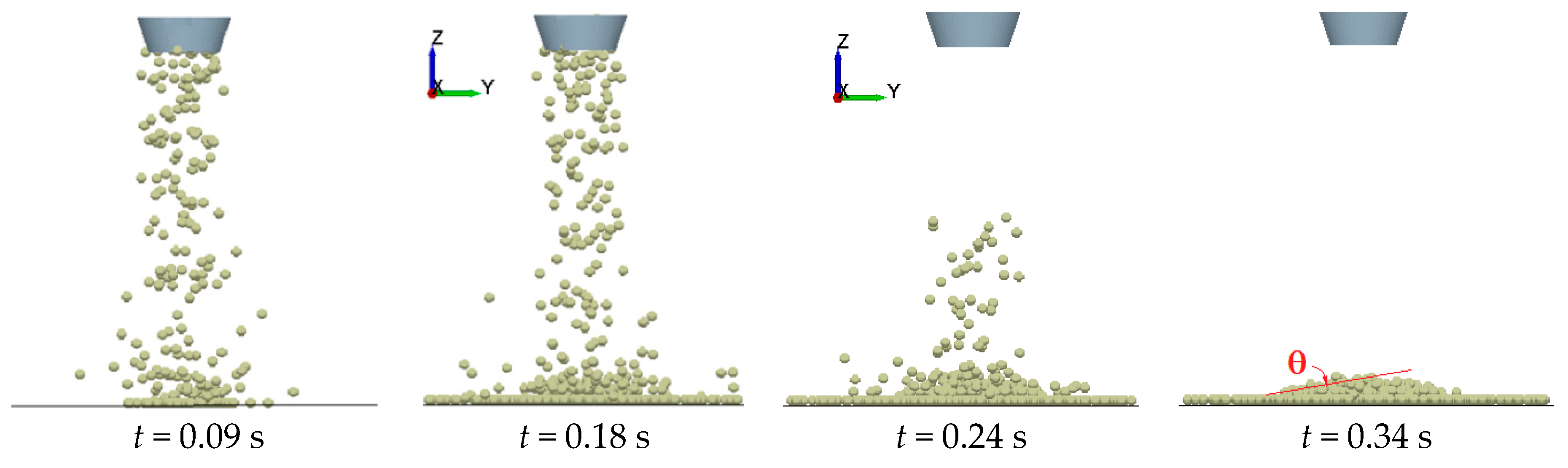
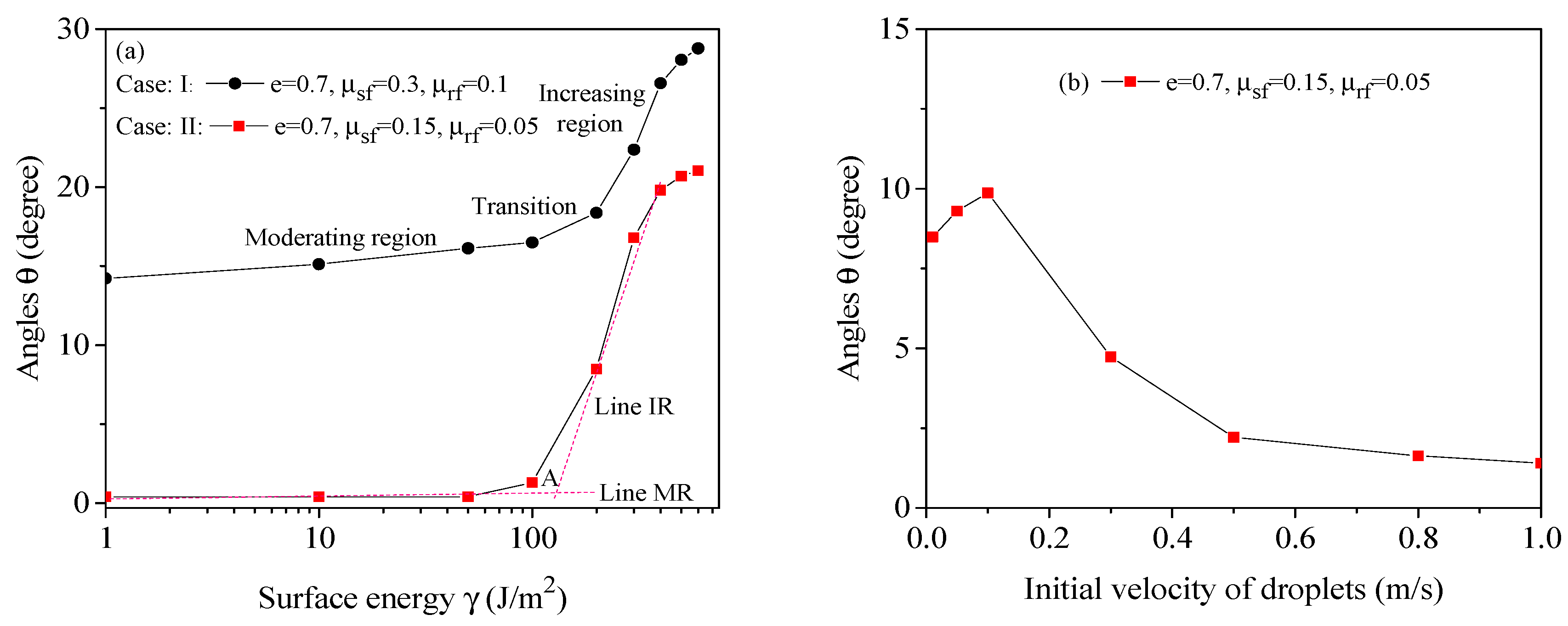
3.1. Virtual Calibration Test of Surface Energy
3.2. Selection of Gas Turbulent Model
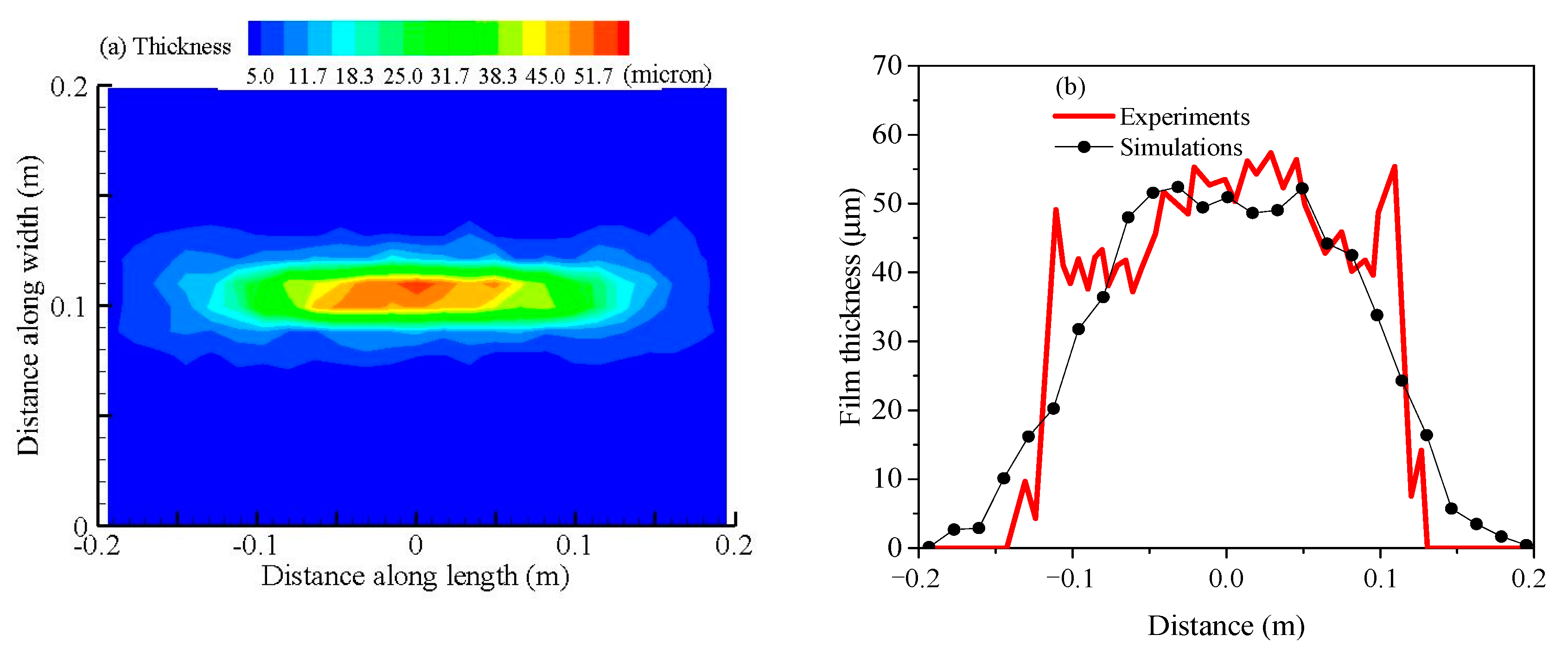
4. Comparison with Experimental Data in a Panel Using an Airless Sprayer
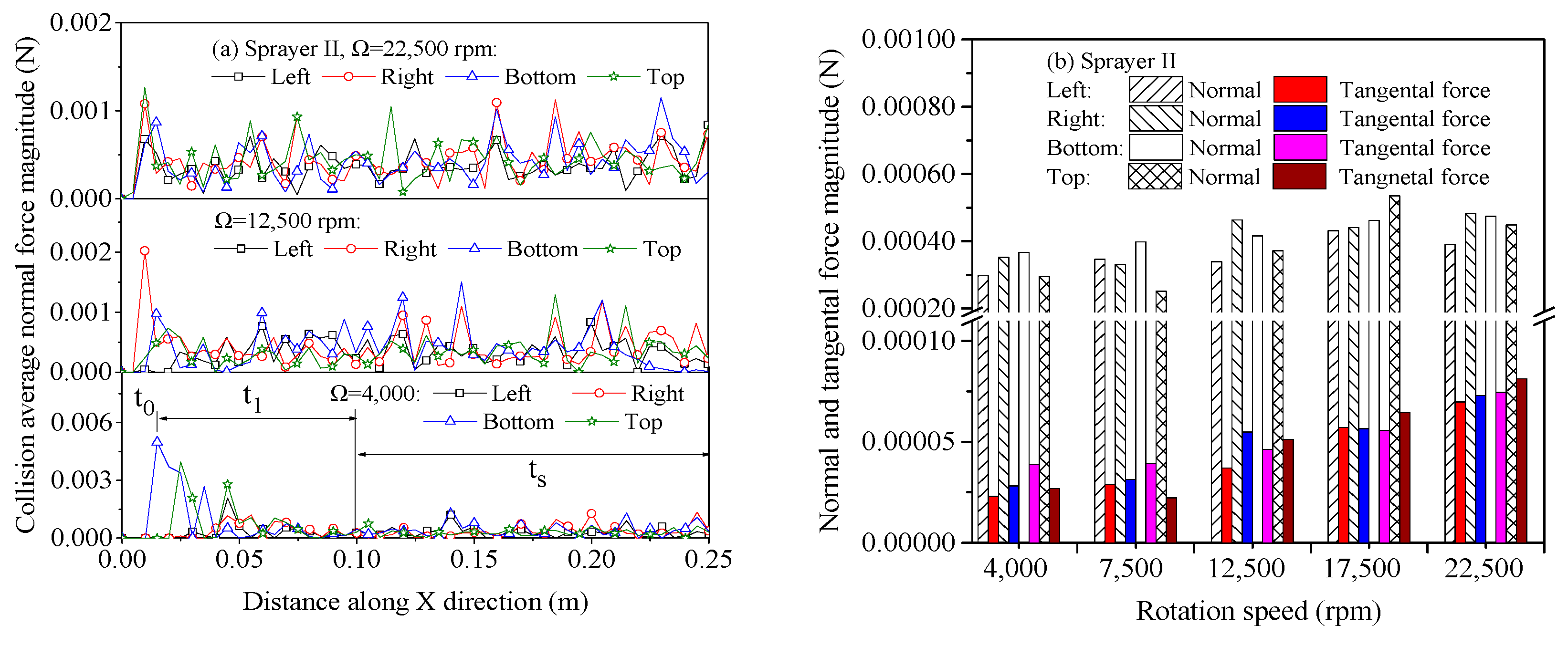
5. Discussions and Analyses
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | contact radius, m |
| Cd | drag coefficient |
| Ch | discharge coefficient |
| d | droplet diameter, m |
| e | coefficient of restitution |
| E | modulus, Pa |
| fc,n | normal contact force, N |
| fc,t | tangential contact force, N |
| Fr | Fr number |
| Ii | moment of inertia of droplet i, kg·m2 |
| g | gravitational acceleration, m/s2 |
| Gk | generation of kinetic energy, kg/m·s3 |
| m | mass of droplet, kg |
| n | number fraction |
| nik | unit vector between the droplet i and k |
| nm | mean number fraction |
| N | droplet number |
| Nm | mean droplet number |
| pf | fluid pressure, Pa |
| R | radius, m |
| Re | Re number |
| T | torque, N·m |
| u | velocity, m/s |
| vd | discharge velocity, m/s |
| vi | droplet velocity, m/s |
| vn,ik | normal relative velocity between droplet i and k, m/s |
| vt,ik | tangential relative velocity between droplet i and k, m/s |
| Greek symbols | |
| ω | angular velocity, rad/s |
| δn | normal displacement, m |
| δt | tangential displacement, m |
| ρf | gas density, kg/m3 |
| μf | gas viscosity, kg/s·m |
| μs | friction coefficient |
| μt | turbulent viscosity, kg/s·m |
| σ | Prandtl number |
| σn | variance |
| τ | gas phase stress, Pa |
| Ω | rotation speed, rpm |
| ν | Poisson ratio |
| γ | surface energy, J/m2 |
| ΓA | surface energy at the intersection A, J/m2 |
| θ | accumulation angle, degree |
References
- Lambourne, R.; Strivens, T.A. Paint and Surface Coatings: Theory and Practice; Woodhead Publishing: Sawston, UK, 1999. [Google Scholar]
- Mohamed, M.G.; Ahmed, N.M.; M. El-Gawad, A.W. Corrosion protection performance of reinforced steel coated with paints based on waste materials. Anti-Corros. Methods Mater. 2018, 65, 368–374. [Google Scholar] [CrossRef]
- Sathiyanarayanan, S.; Muthukrishnan, S.; Venkatachari, G.; Trivedi, D.C. Corrosion protection of steel by polyaniline (PANI) pigmented paint coating. Prog. Org. Coat. 2005, 53, 297–301. [Google Scholar] [CrossRef]
- Plesniak, M.W.; Sojka, P.E.; Singh, A.K. Transfer efficiency for airless painting systems. J. Coat. Technol. Res. 2004, 1, 137–145. [Google Scholar] [CrossRef]
- Gad, H.M.; Baraya, E.A.; Farag, T.M.; Ibrahim, I.A. Effect of geometric parameters on spray characteristics of air assisted pressure swirl atomizer. Alex. Eng. J. 2022, 61, 5557–5571. [Google Scholar] [CrossRef]
- Ye, Q.; Domnick, J. Analysis of droplet impingement of different atomizers used in spray coating processes. J. Coat. Technol. Res. 2017, 14, 467–476. [Google Scholar] [CrossRef]
- Bayrel, L.; Orzechowski, Z. Liquid Atomization; Taylor & Francis: Washington, DC, USA, 1993. [Google Scholar]
- Kamoun, O.; Gassoumi, A.; Shkir, M.; Gorji, N.E.; Turki-Kamoun, N. Synthesis and characterization of highly photocatalytic active Ce and Cu co-doped novel spray pyrolysis developed MoO3 films for photocatalytic degradation of eosin-Y dye. Coatings 2022, 12, 823. [Google Scholar] [CrossRef]
- Williams, A. Combustion of Liquid Fuel Sprays; Butterworth-Heinemann: London, UK, 1990. [Google Scholar]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ye, Q.; Shen, B.; Tiedje, O.; Bauernhansl, T.; Domnick, J. Numerical and experimental study of spray coating using air-assisted high pressure atomizers. At. Sprays 2015, 25, 643–656. [Google Scholar] [CrossRef]
- Shen, B.; Ye, Q.; Guettler, N.; Tiedje, O.; Domnick, J. Primary breakup of a non-Newtonian liquid using a high-speed rotary bell atomizer for spray-painting processes. J. Coat. Technol. Res. 2019, 16, 1581–1596. [Google Scholar] [CrossRef]
- Fogliati, M.; Fontana, D.; Garbero, M.; Vanni, M.; Baldi, G.; Donde, R. CFD simulation of paint deposition in an air spray process. J. Coat. Technol. Res. 2006, 3, 117–125. [Google Scholar] [CrossRef]
- Li, J.; Xiao, J.; Huang, Y.; Lou, H.H. Integrated process and product analysis: A multiscale approach to paint spray. AIChE J. 2007, 53, 2841–2857. [Google Scholar] [CrossRef]
- Baytok, Y.M.; Erek, A.; Saf, O. Numerical estimation of film thickness with an air-assisted spray gun. Eng. Trans. 2023, 71, 241–263. [Google Scholar]
- Yang, G.; Chen, Y.; Chen, S.; Zhang, F. Modeling of film formation in airless spray. J. Phys. Conf. Ser. 2022, 2179, 012024. [Google Scholar] [CrossRef]
- Venkatachalam, P.; Sahu, S.; Anupindi, K. Numerical investigation on the role of a mixer on spray impingement and mixing in channel cross-stream airflow. Phys. Fluids 2022, 34, 033316. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, X.; Yang, Q.; Zhao, R.; Jin, Y. Experimental and numerical investigations on the spray characteristics of liquid-gas pintle injector. Aerosp. Sci. Technol. 2022, 121, 107354. [Google Scholar] [CrossRef]
- Chen, S.M.; Chen, W.Z.; Chen, Y.; Jiang, J.Z.; Wu, Z.J.; Zhou, S. Research on film-forming characteristics and mechanism of painting V-shaped surfaces. Coatings 2022, 12, 658. [Google Scholar] [CrossRef]
- Yang, G.; Wu, Z.; Chen, Y.; Chen, S.; Jiang, J. Modeling and characteristics of airless spray film formation. Coatings 2022, 12, 949. [Google Scholar] [CrossRef]
- Wu, Z.; Chen, Y.; Liu, H.; Hua, W.; Duan, J.; Kong, L. A review of the developments of the characteristics and mechanisms of airless spraying on complex surfaces. Coatings 2023, 13, 2095. [Google Scholar] [CrossRef]
- Fries, L.; Antonyuk, S.; Heinrich, S.; Palzer, S. DEM-CFD modeling of a fluidized bed spray granulator. Chem. Eng. Sci. 2011, 66, 2340–2355. [Google Scholar] [CrossRef]
- Heine, M.; Antonyuk, S.; Fries, L.; Niederreiter, G.; Heinrich, S.; Palzer, S. Modeling of the spray zone for particle wetting in a fluidized bed. Chem. Ing. Tech. 2013, 85, 280–289. [Google Scholar] [CrossRef]
- Darabi, P.; Pougatch, K.; Salcudean, M.; Grecov, D. DEM investigations of fluidized beds in the presence of liquid coating. Powder Technol. 2011, 215, 365–374. [Google Scholar] [CrossRef]
- Pasternak, L.; Sommerfeld, M.; Muramulla, P.; Yuan, F.L.; Gopireddy, S.; Urbanetz, N.; Profitlich, T. Tablet coating in lab-scale drum coaters: Combining DEM simulations and spray experiments to predict tablet coating. Powder Technol. 2023, 427, 118683. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Madlmeir, S.; Radl, S. A coarse-grained parcel method for heat and mass transfer simulations of spray coating processes. Adv. Powder Technol. 2022, 33, 103590. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Speziale, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: La Canada, CA, USA, 2004. [Google Scholar]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles; Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Hamid, R.N.; Reza, Z.; Rahmat, S.G.; Navid, M. Coupled CFD-DEM Modeling: Formulation, Implementation and Application to Multiphase Flows; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Mikami, T.; Kamiya, H.; Horio, M. Numerical simulation of cohesive powder behavior in a fluidized bed. Chem. Eng. Sci. 1998, 53, 1927–1940. [Google Scholar] [CrossRef]
- Feng, Y.Q.; Xu, B.H.; Zhang, S.J.; Yu, A.B.; Zulli, P. Discrete particle simulation of gas fluidization of particle mixtures. AIChE J. 2004, 50, 1713–1728. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: New York, NY, USA, 1985. [Google Scholar]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1971, 324, 301–321. [Google Scholar]
- Gilabert, F.; Roux, J.N.; Antonio, C. Computer simulation of model cohesive powders: Influence of assembling procedure and contact laws on low consolidation states. Phys. Rev. E 2007, 75, 011303. [Google Scholar] [CrossRef]
- Fluent. FLUENT User’s Guide; Fluent Inc.: Lebanon, NH, USA, 2019. [Google Scholar]
- EDEM. EDEM Theory Guide; Altair Engineering Inc.: Troy, MI, USA, 2020. [Google Scholar]
- Zhou, Z.Y.; Pinson, D.; Zou, R.P.; Yu, A.B. Discrete particle simulation of gas fluidization of ellipsoidal particles. Chem. Eng. Sci. 2011, 66, 6128–6145. [Google Scholar] [CrossRef]
- Grima, A.P.; Wypych, P.W. Development and validation of calibration methods for discrete element modelling. Granul. Matter 2011, 13, 127–132. [Google Scholar] [CrossRef]
- Asaf, Z.; Rubinstein, D.; Shmulevich, I. Determination of discrete element model parameters required for soil tillage. Soil Tillage Res. 2007, 92, 227–242. [Google Scholar] [CrossRef]
- Ucgul, M.; Fielke, J.M.; Saunders, C. Three-dimensional discrete element modelling (DEM) of tillage: Accounting for soil cohesion and adhesion. Biosyst. Eng. 2015, 129, 298–306. [Google Scholar] [CrossRef]
- Keppler, I.; Hudoba, Z.; Oldal, I.; Csatar, A.; Fenyvesi, L. Discrete element modeling of vibrating tillage tools. Eng. Comput. 2015, 32, 308–328. [Google Scholar] [CrossRef]
- Barr, J.B.; Ucgul, M.; Desbiolles, J.M.A.; Fielke, J.M. Simulating the effect of rake angle on narrow opener performance with the discrete element method. Biosyst. Eng. 2018, 171, 1–15. [Google Scholar] [CrossRef]
- Hoshishima, C.; Ohsaki, S.; Nakamura, H.; Watano, S. Parameter calibration of discrete element method modelling for cohesive and non-spherical particles of powder. Powder Technol. 2021, 386, 199–208. [Google Scholar] [CrossRef]
- Yarin, A.L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Shi, Q.; Wang, B.; Mao, H.; Liu, Y. Calibration and measurement of micrometre-scale pollen particles for discrete element method parameters based on the Johnson-Kendal-Roberts model. Biosyst. Eng. 2024, 237, 83–91. [Google Scholar] [CrossRef]
- Xia, R.; Li, B.; Wang, X.; Li, T.; Yang, Z. Measurement and calibration of the discrete element parameters of wet bulk coal. Measurement 2019, 142, 84–95. [Google Scholar] [CrossRef]
- Ajmal, M.; Roessler, T.; Richter, C.; Katterfeld, A. Calibration of cohesive DEM parameters under rapid flow conditions and low consolidation stresses. Powder Technol. 2020, 374, 22–32. [Google Scholar] [CrossRef]
- Zhu, J.; Zou, M.; Liu, Y.; Gao, K.; Su, B.; Qi, Y. Measurement and calibration of DEM parameters of lunar soil simulant. Acta Astronaut. 2022, 191, 169–177. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ε eddy-viscosity model for high Reynolds number turbulent flows-Model development and validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Orszag, S.A.; Yakhot, V.; Flannery, W.S.; Boysan, F.; Choudhury, D.; Maruzewski, J.; Patel, B. Renormalization group modeling and turbulence simulations. In Proceedings of the International Conference on Near-Wall Turbulent Flows, Tempe, AZ, USA, 15–17 March 1993. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ye, Q.; Shen, B.; Tiedje, O.; Domnick, J. Investigations of spray painting processes using an airless spray gun. In Proceedings of the 24th European Conference on Liquid Atomization and Spray Systems, Estoril, Portugal, 5–7 September 2011. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Greenspan, H.P. The Theory of Rotating Fluid; Cambridge University Press: New York, NY, USA, 1968. [Google Scholar]
- Teoman, B.; Potanin, A.; Armenante, P.M. The discharge of complex fluids through an orifice: A review. Chem. Eng. Res. Des. 2022, 179, 346–364. [Google Scholar] [CrossRef]
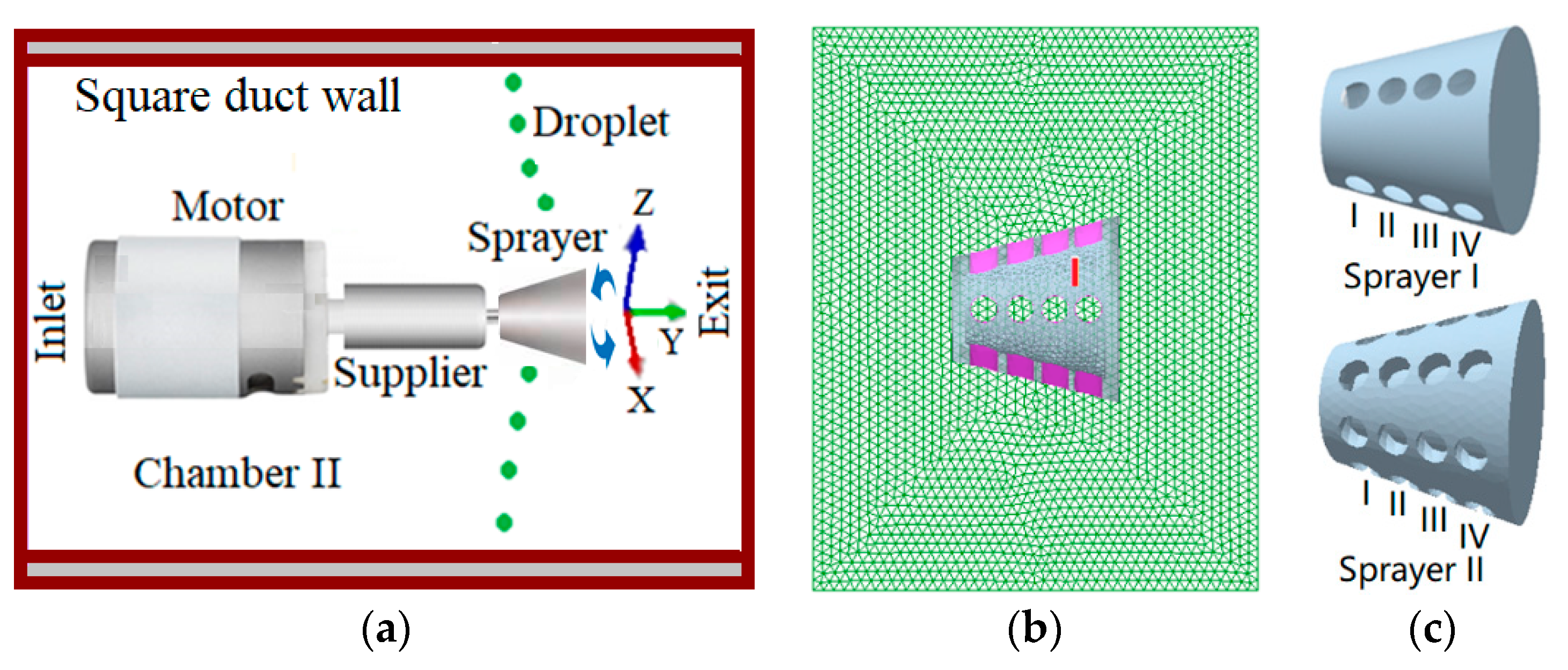



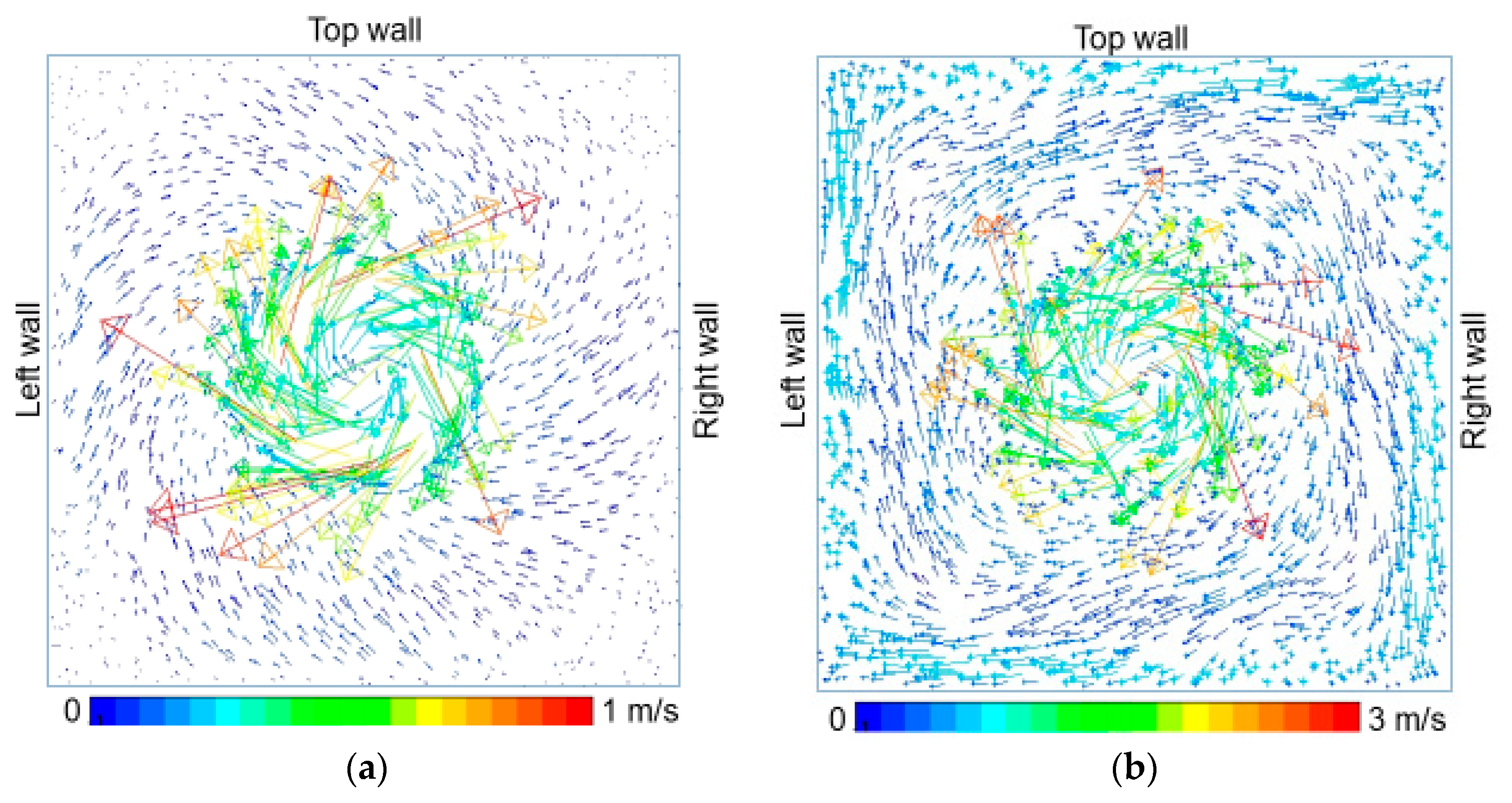



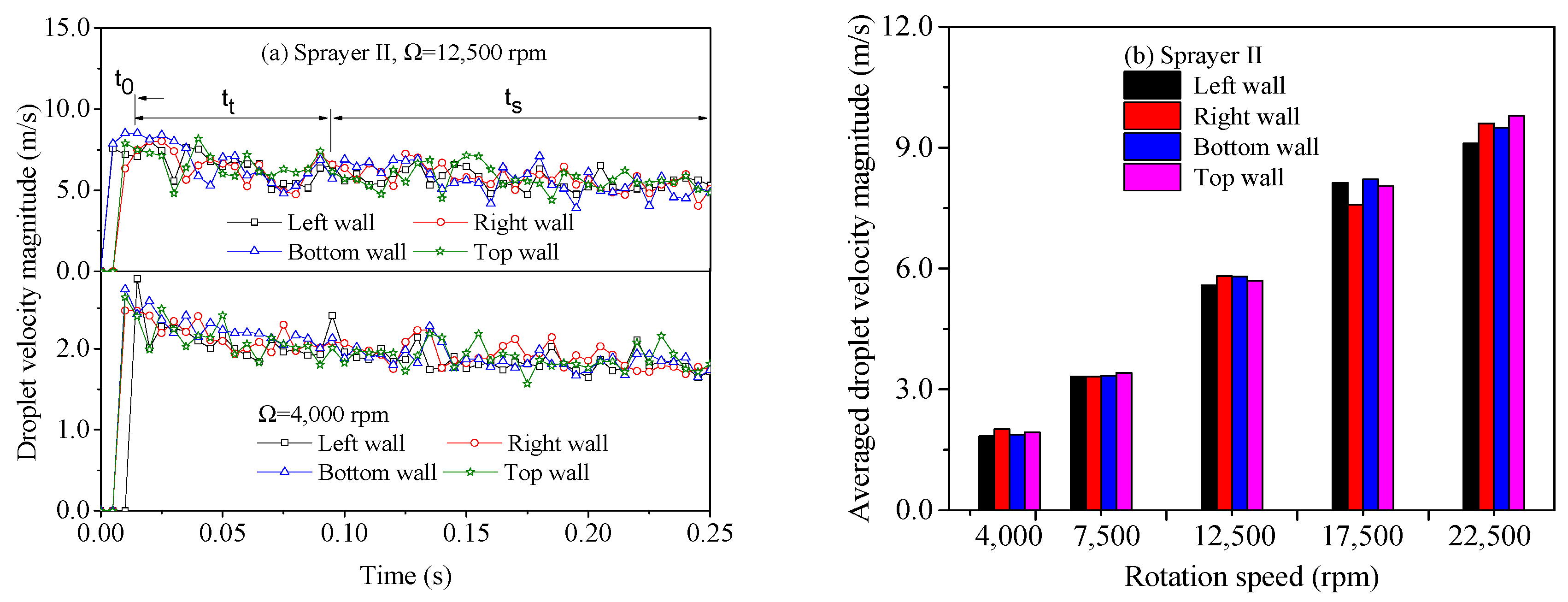
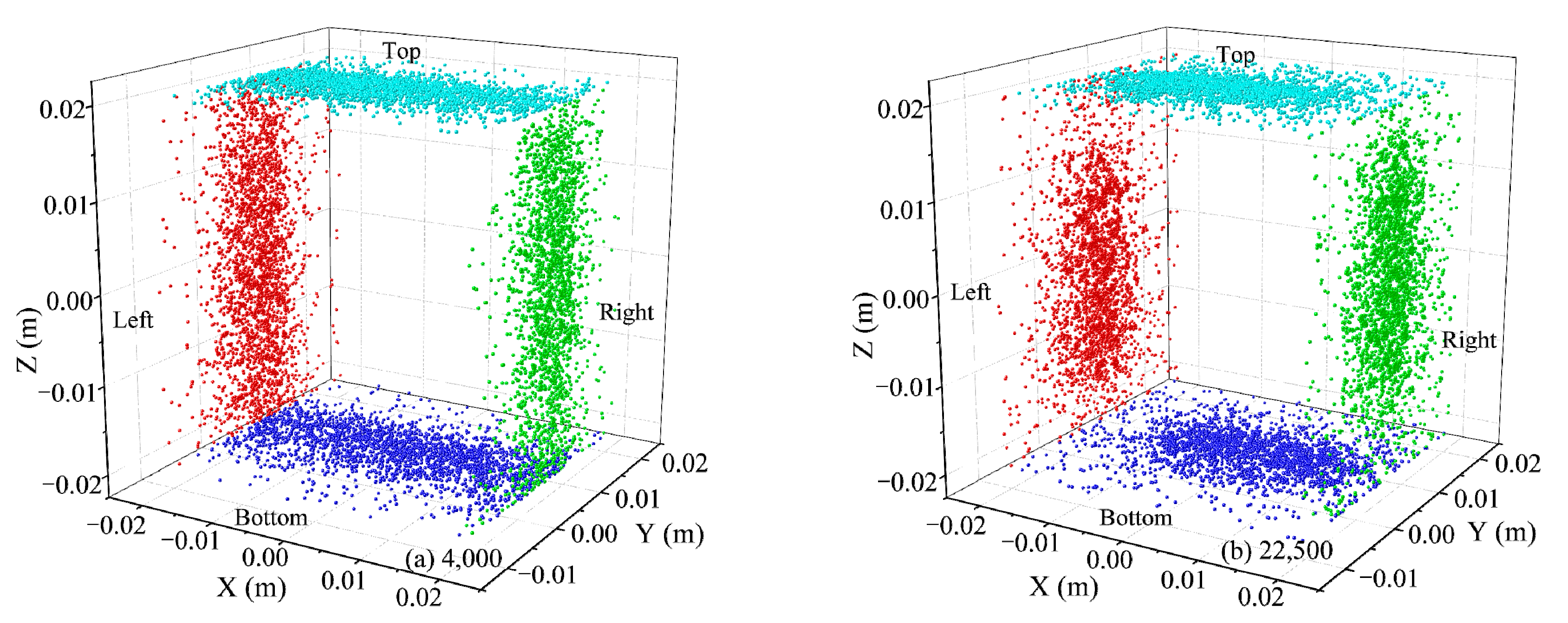
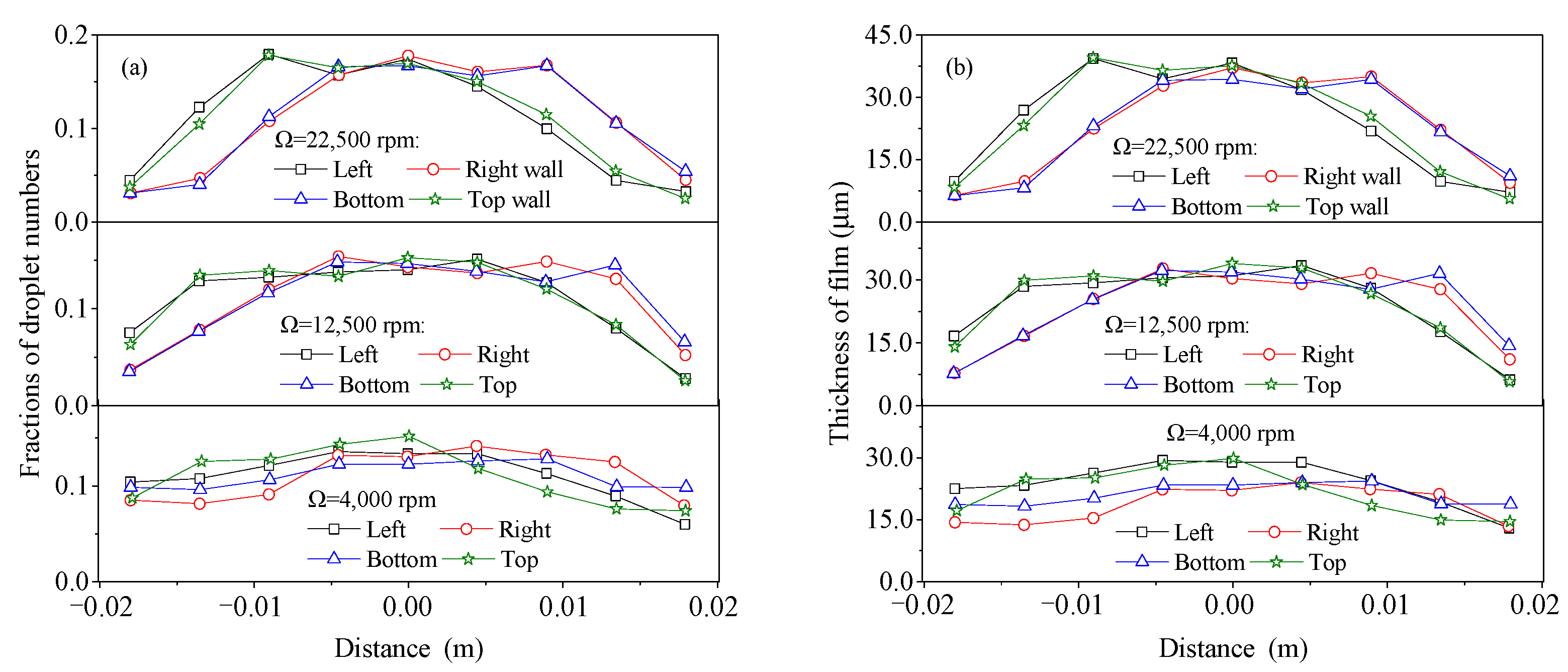


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Horizontal duct size | 40.5 × 40.5 mm | Large diameter of sprayer | 12.5 mm |
| Small diameter of sprayer | 7.5 mm | Length of rotary sprayer | 12.0 mm |
| Gas density | 1.2 kg/m3 | Gas viscosity | 1.8 × 10−5 Pa s |
| Droplet diameter | 0.2 mm | Droplet density | 1060 kg/m3 |
| Diameter of holes | 2.0 mm | Hole number of sprayer I and II | 16, 32 |
| Mass flux of droplets | 0.0044 kg/s | Number of droplets | 100,000 1/s |
| Wall Young modulus | 2.5 × 108 Pa | Young modulus of droplets | 1.2 × 107 Pa |
| Wall Poisson ratio | 0.23 | Droplet Poisson ratio | 0.25 |
| Restitution coefficient of wall | 0.7 | Restitution coefficient of droplets | 0.7 |
| Wall static friction coefficient | 0.5 | Droplet static friction coefficient | 0.15 |
| Wall rolling friction coefficient | 0.05 | Droplet rolling friction coefficient | 0.05 |
| Sprayer restitution coefficient | 0.7 | Sprayer static friction coefficient | 0.5 |
| Poisson ratio of sprayer | 0.23 | Surface energy of wall–droplet | 100.0 J/m2 |
| Surface energy of droplets | 0.03 J/m2 | Surface energy of wall | 0.04 J/m2 |
| Source | Particles | Size, μm | Density, kg/m3 | Poisson’s Ratio | Elastic Modulus, Pa | Friction Coefficient | Restitution Coefficient | Surface Energy, J/m2 | AoR, Degree |
|---|---|---|---|---|---|---|---|---|---|
| Shi et al. [47] | Pollen | 19.56 | 1259.76 | 0.1–0.5 | 5.25 × 106 | 0.466 | 0.14 | 5.06 × 10−4 | 56.6 |
| Hoshishima et al. [45] | Lactose | 210 | 1700 | 0.25 | 10 × 106 | 0.5 | 0.35 | 0.09 | 46.1 |
| Xia et al. [48] | Wet coal | 6–8 mm | 1500 | 0.3 | 2 × 108 | 0.198 | 0.54 | 0.008 | 27.82–39.94 |
| Ajmal et al. [49] | Wet sand | 2.8 mm | 2083 | 0.3 | 1 × 108 | 0.41 | 0.3 | 5.0 | 11.25–40.35 |
| Zhu et al. [50] | Lunar soil simulant | 40 | 1360 | 0.2–0.3 | (2.5–7.2) × 107 | 0.1–0.9 | 0.3–0.7 | 0.02–0.06 | 23.2–49.2 |
| Present study | Droplets | 200 | 1060 | 0.23 | 1.2 × 107 | 0.15 | 0.7 | 0.03 | 0.42–28.78 |
| Realizable k-ε Model | RNG k-ε Model | SST k-ω Model | |
|---|---|---|---|
| Gas velocity magnitude | Unlike RNG and SST models | Like SST model | Like RNG model |
| Droplet velocity magnitude | Low | Medium | High |
| Standard deviation of ni | High | Medium | Low |
| Skewness of ni | Small | Medium | Large |
| Parameters | Experimental Values | Simulation Values |
|---|---|---|
| Droplet diameter | 81.0 µm | 81.0 µm |
| Droplet density | 1317 kg/m3 | 1317 kg/m3 |
| Inlet droplet mass flux | 0.02733 kg/s at p = 200 bar | 0.02733 kg/s |
| Inlet droplet velocity | 110–80 m/s at z = 50 and 100 mm | 140 m/s |
| Effective orifice diameter | 0.48–0.53 mm | A rectangular inlet of 8 × 2 mm |
| Spray angle | 45 degree | 45 degree |
| Sprayer-to-target distance | 300 mm | 300 mm |
| Robot velocity | 900 mm/s | 900 mm/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Chen, X.; Hong, N.; Li, Q.; Xu, Z.; Sheng, M.; Wang, R. A CFD-DEM Simulation of Droplets in an Airless Spray Coating Process of a Square Duct. Coatings 2024, 14, 282. https://doi.org/10.3390/coatings14030282
Li X, Chen X, Hong N, Li Q, Xu Z, Sheng M, Wang R. A CFD-DEM Simulation of Droplets in an Airless Spray Coating Process of a Square Duct. Coatings. 2024; 14(3):282. https://doi.org/10.3390/coatings14030282
Chicago/Turabian StyleLi, Xiang, Xing Chen, Niancheng Hong, Qianzheng Li, Zenghui Xu, Ming Sheng, and Rui Wang. 2024. "A CFD-DEM Simulation of Droplets in an Airless Spray Coating Process of a Square Duct" Coatings 14, no. 3: 282. https://doi.org/10.3390/coatings14030282
APA StyleLi, X., Chen, X., Hong, N., Li, Q., Xu, Z., Sheng, M., & Wang, R. (2024). A CFD-DEM Simulation of Droplets in an Airless Spray Coating Process of a Square Duct. Coatings, 14(3), 282. https://doi.org/10.3390/coatings14030282






