Abstract
This study contributes to the understanding of the adhesive properties in normal contacts, providing valuable information on the influence of various factors on adhesive strength and energy dissipation. The adhesive normal contact between a steel spherical indenter and a soft sheet of elastomer is studied experimentally. The dependencies of contact strength and mechanical energy dissipation in the complete indentation–detachment cycle on the indentation depth, the velocity of the indenter, its radius, thickness, and elastic modulus of the elastomer, the specific work of adhesion, as well as the roughness of the indenter surface, were analyzed. Experimental results are compared with simulations using the boundary element method (BEM), and the reasons leading to discrepancies between experiments and simulations are analyzed. It is shown that over a wide range of experimental parameters, the rate of mechanical energy dissipation can be estimated with sufficient accuracy using a simple empirical relation.
1. Introduction
In many technological processes in industry as well as in living nature, adhesive interactions between contacting surfaces play an important role [1,2,3]. Adhesive and mechanical properties can be modified by coating contact surfaces. Depending on the needed outcome, the use of a suitable coating can modify adhesive properties by changing surface energy [4,5,6,7]. In small-scale devices, such as MEMS (micro-electromechanical systems), adhesion becomes especially important, and “stiction”, an unintentional adhesion of a compliant microstructure surface, becomes a problem [6,8,9,10]. Chemical and physical modification of the surface, e.g., electrostatic deposition of microparticles to create a silicon layer, can influence both mechanical properties and the work of adhesion and thus change the adhesion and friction forces [4,11]. By reducing friction and wear, material and energy in moving components can be saved [8,12,13]. On the contrary, in other situations, adhesion and friction are required. Examples of such processes include soldering, welding, fertilizer packaging, fine particle transporting, etc. In nature, adhesion is successfully used by some living organisms to move on inclined surfaces [14,15], by bacteria to attach living organs [16,17,18], etc. As a rule, easily deformable bodies with a small elastic modulus are prone to good adhesion. This is due to the fact that all natural objects have rough and usually fractal surfaces [19,20]. The presence of roughness prevents the formation of good contact between objects composed of rigid materials because the adhesive forces are insufficient to deform the contacting surfaces in the areas of roughness. However, if at least one of the contacting bodies is soft, it can be easily deformed, and the material fills the space between the roughnesses. This is precisely the situation considered in the present experimental work: a contact between a rigid steel indenter and a soft elastomer with well-defined adhesive properties. It is known that contact properties are dependent on material properties. To determine these properties, experimental studies can be performed, where an indenter of known geometry is indented into the test material. Nanoindentation methods are used to measure the mechanical properties of materials with higher accuracy because the measurement takes place on a smaller scale [21]. Especially the elastic modulus of the test material can be measured with the methods of nanoindentation. As this method only requires small forces and indentation depths, it is particularly suitable for measuring the mechanical properties of thin film coatings with minimal contribution from the substrate beneath [22]. Despite the many advantages of nanoindentation, measuring the elastic modulus from the unloading curve remains a complicated task. This is due to several reasons: if the coating is fractured, the measured elastic modulus may be the same as the elastic modulus of the substrate alone. Due to the small scale of the contact, the measured values of indentation depth and force can be affected by the roughness or contamination of the contact surfaces [22]. Additionally, since high-precision tools are needed, the cost of conducting nanoindentation tests is very high in comparison to indentation experiments where bigger indenters are used. To avoid these problems, experimental data can be supported by computer simulations of the indentation process. In the present work, the boundary element method (BEM) was used to determine the adhesive and mechanical properties of the contact. As we have used BEM modification for coated half-space, this method can also be applied for the investigation of the properties of thin coatings.
In the present work, two parameters are experimentally studied: the adhesive strength of the contact (the minimum external force that must be applied to completely destroy the contact) and the dissipation of mechanical energy in the full indentation–detachment cycle. The dependencies of these values on experimental parameters were estimated within the framework of the classical Johnson–Kendall–Roberts (JKR) theory of adhesive contact [23,24], where the dependence of the elastic force on the indentation depth F(d) is defined. In deriving the basic JKR relations, it is assumed that the adhesion forces are short-ranged and small compared to the characteristic contact dimensions such as contact radius, indentation depth, etc. Although there are other approaches to describe adhesion, such as the case of long-range adhesive forces in the framework of the Derjaguin–Muller–Toporov (DMT) theory [25,26], numerous experimental works have shown that it is the JKR approach that agrees well with experiments studying the contact between a solid and a soft elastomer [27,28]. It is worth noting that in [29], with the use of the Dugdale model [30], it was shown that both JKR and DMT are limited cases of the general theory of adhesion.
In JKR, the control parameters are the radius of a spherical indenter and indentation depth (geometric properties), the elastic modulus and Poisson’s ratios of the contacting bodies (material parameters), as well as the specific work of adhesion, which is a function of the surface energies of the contacting bodies (chemical properties).
When considering the complete indentation–detachment adhesion cycle, many experimental works show that at the indentation stage, adhesion usually has a weak effect [31]. At the pull-off stage, however, adhesion plays a determining role. This is a well-known but not fully explained fact [32]. It leads to an additional adhesion hysteresis, which is discussed, for example, in our previous work [33]. Both stages (immersion of the indenter into the elastomer and subsequent detachment) can be satisfactorily described using the JKR approach by assuming that the specific work of adhesion in the indentation stage is significantly smaller than in the detachment stage.
It follows from JKR that as the indenter radius and specific work of adhesion increase, the adhesive contact strength and mechanical energy dissipation also increase. However, in reality, some other parameters that are not present in JKR—such as indenter velocity (due to viscoelasticity), contact time (due to interface hardening effects), indenter surface roughness (due to changes in real contact area and appearance of elastic instabilities), elastomer thickness (deviation from half-space approximation), etc.—can have a significant effect on the contact mechanics. The present work is undertaken to experimentally study the effect of parameters such as indentation depth, velocity of motion of the indenter, its radius, thickness, and elastic modulus of the elastomer, specific work of adhesion, roughness of the indenter surface, on the energy dissipation in the adhesive contact, and its pull-off adhesive strength.
2. Materials and Methods
2.1. Methodology of the Experiment
Figure 1 shows a photograph of a device that was produced by us to conduct all the experiments described in this paper.

Figure 1.
(a) external view of the experimental setup; (b) close-up view of the contact area between indenter (4) and elastomer (6) with all-round LED illumination (5).
The left panel of the figure shows the general view of the device; the right panel represents a close view of the measuring unit. Here, the spherical steel indenter (4) is attached to a three-axis K3D40 force sensor (ME-Meßsysteme GmbH, Hennigsdorf, Germany) (3). The indenter is moved in the normal direction by the high-precision linear stage L-511.24AD00 (Physik Instrumente (PI) GmbH & Co. KG, Karlsruhe, Germany) (1) that is controlled by the C-863 Mercury Servo Controller (Physik Instrumente (PI) GmbH & Co. KG, Karlsruhe, Germany) (10). A GSV-1A4 SubD37/2 four-channel analog amplifier (ME-Meßsysteme GmbH, Hennigsdorf, Germany) is used to amplify the electrical signal received from the force sensor. The amplifier is paired with a computer via the NI USB-6211 16-bit ADC (National Instruments, Austin, TX, USA). In the experiment, the indenter (4) is pressed into the elastomer (6) to a fixed indentation depth dmax. Subsequently, the indenter is moved in the opposite direction until the contact is completely broken. In the figure, the elastomer (6) is a sheet of transparent rubber TANAC CRG N3005 (Innovation company TANAC Co., Ltd., Gifu City, Japan) with a thickness h = 5 mm. Rubber is lying on a silicate glass plate (7). The evolution of the contact region is monitored from below the contact through glass and elastomer using a Conrad USB digital video camera (9) with a physical resolution of 1600 × 1200 pixels. Coordinated control of all electronic devices is carried out using a computer program developed in LabVIEW Full Development System ver. 2019 (National Instruments, Austin, TX, USA). Throughout the experiment, at a fixed time interval Δt, the values of the three components of the contact force are recorded, and photographs of the contact area are saved. The contact area is illuminated by a surrounding LED lighting system (5) consisting of 80 LEDs. A tilting mechanism (8) allows for changing the spatial position of the rubber sheet into which the indentation takes place. The described device has been used in previous experiments, as outlined in our earlier works, such as [33,34].
2.2. Numerical Modeling Methodology
We have previously performed experiments similar to those described in the present work, for example, in [33,34,35]. All experiments, which are carried out under different conditions, have shown that adhesion is much weaker at the stage of indentation of the indenter into the elastomer than at the stage of subsequent withdrawal of the indenter. This behavior always leads to secondary adhesion hysteresis, meaning that the loading and unloading curves F(d) do not coincide even at the stage of a formed adhesive contact. The resulting hysteresis leads to additional dissipation of mechanical energy in the complete indentation–detachment cycle [35]. However, additional hysteresis can cause increased dissipation in more complex tangential contacts (friction) in various tribological systems [36,37].
In some works, secondary adhesion hysteresis is attributed to the influence of roughness, moisture, viscoelasticity, plasticity, or the presence of chemical inhomogeneities on the surfaces of the contacting bodies [32,34,35]. This hysteresis is even observed in experiments with mirror-polished surfaces (minimization of roughness effects), extremely low velocity of the indenter (minimization of viscoelastic effects), when using a hard indenter and soft elastomer as contacting bodies (no plastic deformation), and thorough chemical cleaning of the indenter surface (no chemical inhomogeneities) [34]. Therefore, the true causes leading to hysteresis still remain unclear. This does not prevent the formulation of phenomenological approaches that are able to describe the experimentally observed behavior. The experimentally measured dependencies of the normal force on the indentation depth F(d) can often be represented by two JKR curves [23], assuming that the indentation stage corresponds to a significantly lower value of the specific work of adhesion γ12 than the detachment stage.
The indentation process is simulated using the boundary element method (BEM). This method has recently been modified for adhesive contacts between a rigid indenter and an elastic half-space with elastic modulus E2 and Poisson’s ratio ν2 that is covered by an elastic layer with thickness h having elastic parameters E1 and ν1 [38]. To solve the contact problem of an arbitrarily shaped rigid indenter with an elastic layer, a square area of the layer surface of size L x L is considered, which is partitioned into N square cells with the size Δx = Δy = Δ in the x and y directions in the plane. It is assumed that the contact pressure in each cell is constant. If the pressure distribution p is known, the matrix u of displacement of the surface in the normal direction can be calculated using the forward FFT and inverse IFFT Fourier transform procedures [38]
where uz is the Fourier transform of the fundamental solution, given in analytical form in [38]. The contact problem is solved iteratively. At each step, the displacement matrix u is calculated for a given pressure distribution p according to (1). The inverse problem of finding the pressure p at given displacements u is solved using the conjugate gradient method [39,40]. To consider adhesion, a detachment criterion is used: the contact gets lost at the critical pressure
where γ12 (J/m2) is the specific work of adhesion in the contact between the indenter and the substrate. For non-adhesive contacts, the detachment criterion is that the normal pressure becomes p > 0. For adhesive contacts, the criterion used is p > −σc. More detailed information on the features of the method is given in [38]. It is worth noting that the BEM modification described above has been successfully tested experimentally (see [41]).
Figure 2 shows typical dependencies of force F and contact area A on indentation depth d obtained in the simulation, where a significantly lower value of specific work of adhesion was chosen for the indentation phase than for the detachment phase. Here, at the point of first contact O, the contact area propagates only slightly due to adhesion (see Figure 2b), leading to the appearance of a small negative normal force F with the jump to the point A (see inset in Figure 2a). At further indentation, the force and contact area increase monotonically according to AB dependences. At point B, the indenter reaches the maximum indentation depth, dmax = 0.15 mm, after which it moves in the opposite direction (detachment phase). Since the detachment phase corresponds to a substantially higher value of specific work of adhesion, immediately after reversing the indenter, the contact area remains constant over some interval BC, and the dependence of F(d) is linear over this interval due to the constant contact stiffness. At point C, the contact area begins to decrease. The next labeled point in the figure is point D, which corresponds to the minimum of the dependence F(d). The absolute value of the normal force F corresponding to point D indicates the minimum external force that must be applied to completely detach the indenter from the substrate. Hereinafter, we will call this absolute value of the force |Fmin| the adhesive strength of the contact. Further withdrawing of the indenter out of the substrate at point E results in complete detachment.
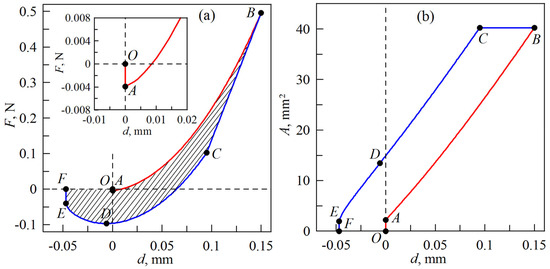
Figure 2.
Typical dependencies of the normal force F (a) and contact area A (b) on the indentation depth d for the indenter indentation phase (section OAB, colored in red) and the detachment phase (section BCDEF, colored in blue) obtained as a result of BEM simulations.
The dissipation of mechanical energy ΔW in a complete indentation-detachment cycle is determined by the area of the shaded figure OABCDEFO shown in Figure 2a. The dependencies shown in Figure 2 are obtained with the following parameters: indenter radius R = 50 mm, elastic modulus of the indented substrate E1 = 0.324 MPa, its Poisson’s ratio ν = 0.47, substrate thickness h = 5 mm. The role of the half-space on which the elastic layer is located is performed by a rigid substrate. The computer program assigns the elastic modulus E2 = 10100 MPa to ensure that only the elastic layer undergoes deformation during the indentation. The specific work of adhesion γ12 = 0.0175 J/m2 corresponds to the indentation phase, and much bigger γ12 = 0.4 J/m2 to the detachment. The parameters mentioned above are not randomly chosen, as they correspond to the properties of the materials used in the experiment.
From the technical details, we mention the fact that the simulation area L × L was partitioned by a grid with N × N = 1024 × 1024 = 1,048,576 cells that provided sufficiently high accuracy of calculations. The linear size of the simulation area L in each numerical experiment was chosen based on the value of the maximum indentation depth, dmax. Namely, in each specific case, for a known set of parameters and the value of dmax, the contact radius aJKR corresponding to the JKR theory for the half-space was calculated [23,24]. The size of the simulation area was L = 6aJKR, which corresponds to three contact diameters at the maximum indentation depth. The required computing speed was ensured by using the NVIDIA Tesla P100 16 GB PCI-E GPU graphic card paired with an Intel Core i5-8600K CPU that operated stably at 4.6 GHz. The use of a GPU allows for a greatly increased speed of calculating the forward and inverse Fourier transforms in Equation (1), which is the procedure requiring the most CPU time in the method used.
3. Results
The main purpose of the present work is to identify the factors influencing the value of mechanical energy dissipation as well as contact pull-off strength. Several series of experiments were conducted where the radii of spherical indenters, the elastic parameters of the elastomer and its thickness, the surface properties of the indenter, its velocity of motion, etc. were varied. All experiments consisted of indenting the indenter into the elastomer to a fixed depth dmax and then pulling it away from the elastomer until the contact completely broke. Below, we describe the results obtained.
3.1. Effect of Indentation Depth dmax
In this series of experiments, a mirror-polished steel indenter with radius R = 50 mm was used. The roughness amplitude of the surface of such an indenter was only several micrometers, as it was measured in our previous work [34]. In the experiments, the indenter was plunged into a sheet of TANAC CRG N3005 rubber with a thickness h = 5 mm to a depth of dmax at a velocity of v = 1 µm/s. After reaching the maximum depth, it was moved in the opposite direction at the same velocity until detachment. Figure 3 shows the results of five experiments for indentation depths dmax = 0.1, 0.2, 0.3, 0.4, and 0.5 mm. For each indentation depth value, three experiments were performed in a sequence; thus, the figure contains data from 15 complete indentation–detachment cycles. Figure 3a shows the dependence of the normal force on the displacement. In Figure 3b, an enlarged excerpt of these dependences is depicted (the dependences corresponding to different dmax are shown in different colors).
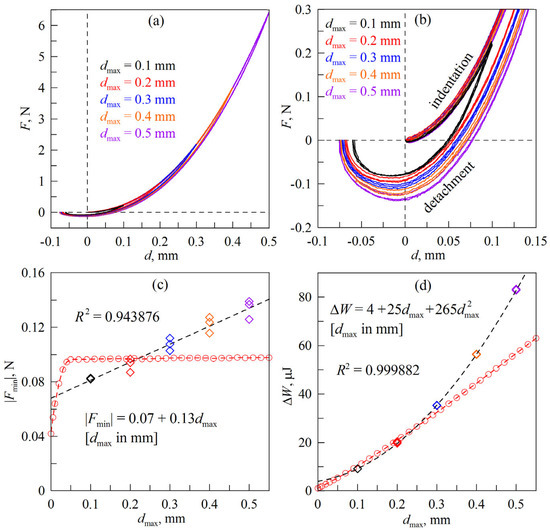
Figure 3.
(a) dependencies of the normal force F on the indentation depth d at different values of the maximum indentation depth dmax; (b) enlarged excerpt of the dependencies shown in panel (a); (c) dependencies of the adhesive strength of the contact |Fmin| on the maximum indentation depth dmax, diamonds correspond to the experiment; circles correspond to the simulation; (d) dependencies of the energy dissipation in the complete indentation–detachment cycle ΔW on the indentation depth dmax. The dependencies calculated on the basis of all the experiments performed are shown in diamonds; the circles show the results of modeling.
From panels (a) and (b), it follows that all three indentation cycles for each fixed value of dmax show a satisfactory agreement of results. Indentation occurs according to F(d) dependencies, labeled “indentation” in Figure 3b; detachment occurs according to “detachment” curves. In the indentation phase, the influence of adhesion is very small, so that the contact propagates almost adhesion-free. During the detachment, all F(d) dependencies show noticeable negative values for the normal force F (see Figure 3b), which are only realized in the adhesive contacts as an additional force must be applied to break the contact. In the previous Section 2.2 of the paper, we agreed to call the absolute value of the minimum negative force |Fmin| on the F(d) dependencies in the contact failure phase the “adhesive strength of the contact”, since it is the minimum value of the external force required for complete breakage of the adhesive contact. Figure 3b shows that the adhesive strength |Fmin| increases with increasing indentation depth dmax. The dependency of the adhesive strength on the dmax for all indentation–detachment cycles carried out is shown in Figure 3c, where the diamonds show the experimental results. The dashed line through these symbols shows the result of the least-squares approximation (the equation is shown in the figure panel). The approximation shows that in the considered case, there is a linear growth of |Fmin| with increasing dmax. The figure also shows the value of the coefficient of determination, R2, being close to one. The proximity suggests the correctness of choosing the linear dependence |Fmin|(dmax) as an approximation function. The reasons for the observed increase in adhesive strength |Fmin| with rising indentation depth are that as dmax increases, the contact pressure and the time t, during which the indenter is in contact with the rubber, increase. Both of these factors lead to the strengthening of the adhesive contact, as experimentally shown in [33].
In Figure 3d, the calculated dependence of energy dissipation ΔW in the full indentation–detachment cycle on the indentation depth dmax is shown by the diamonds. The dissipation value ΔW is defined as the area of the figure made of the dependencies F(d) corresponding to indentation and indenter detachment, which are closed by the abscissa axis. In the figure, the calculated results of all 15 indentation cycles (three cycles for each dmax) are shown by diamonds. The dashed line that runs through the symbols illustrates the second-order polynomial approximation found by the least-squares method (the equation is shown in the figure panel). The approximation, according to the value of the coefficient of determination R2, describes the experimentally found dependence ΔW(dmax) in the range of experimental dmax with high accuracy.
In Figure 3c,d in addition to the experimental data discussed above, circles show the results of the BEM simulations. The procedure is described in Section 2.2 of this paper, where the parameters used for the simulation are also specified. In this case, during different indentation–detachment cycles, only the indentation depth dmax changes in the simulation, which is consistent with the experiment. The remaining parameters of the model are fixed, except for the space discretization parameters and the quantities that depend on them (for details, see Section 2.2). From Figure 3c,d it can be seen that the simulation provides a satisfactory numerical match with the experiment. However, there are also differences that we will describe. Among the differences, two main ones can be emphasized:
- (A)
- Figure 3c shows that the adhesive strength |Fmin| obtained in the simulation first increases with the increase of dmax and reaches a constant value when the depth dmax exceeds some critical value. This feature has already been discussed in our previous work [35]. The observed effect is easily understood by referring to Figure 2a, where the complete indentation–detachment cycle is represented by two JKR curves AB and CDE, which are connected by a straight line BC. The point is that at small dmax in the detachment phase, the F(d) dependency (or more precisely, its rectilinear section BC) shifts to the second JKR curve to the left of point D, i.e., points D and C on the F(d) dependency change places in the direction of the abscissa axis. Therefore, in the detachment phase, the normal force F does not reach its minimum value, corresponding to point D. The physical reason is that in the indentation phase at low dmax, insufficient contact propagation occurs to provide the adhesive strength |Fmin|, given by the second JKR curve CDE in the detachment phase. The lowest values of adhesive strength |Fmin| and mechanical energy dissipation ΔW occur at dmax = 0 mm. This minimal ΔW was called in [42] the “depth-independent” part of dissipation, and this part of ΔW is always included in the value of the full energy dissipation. In the case with dmax = 0 mm, after the contact has reached an equilibrium value, determined by the specific work of adhesion γ12 = 0.0175 J/m2, the indenter immediately enters the detachment phase, where in simulations γ12 = 0.4 J/m2. As dmax increases (see Figure 3c), point C, which is to the left of point D, will approach it until, at some critical value of dmax, points C and D coincide. It is at this point in Figure 3c that the |Fmin|(dmax) dependency obtained in the simulation comes to a constant value. With further growth of dmax, the adhesive strength does not increase, as it is already determined by the value of force F at point D, which does not depend on the indentation depth.
In the experiment, the summarized results are presented in Figure 3c with diamonds. The adhesive strength |Fmin| monotonically increases with rising depth dmax, resulting in contact strengthening due to increasing contact pressure and contact duration with increasing dmax that we discussed in detail in [33,43]. The increase in |Fmin| observed in the experiment with increasing dmax leads to additional dissipation of mechanical energy in the complete indentation–detachment cycle. Therefore, the experimental curve ΔW(dmax) in Figure 3d shows a faster increase in dissipation ΔW with increasing dmax (diamonds) than predicted by theoretical modeling (circles).
- (B)
- In the simulation, the indenter detachment under the instability conditions occurs abruptly along the EF path shown in Figure 2, where at point E there is still contact and at point F we have complete contact failure. In the experiment, as evident in Figure 3b, the detachment is carried out more smoothly. This is due to the viscoelastic properties of the elastomer into which the indentation is made. To ensure quasi-static conditions in the experiment, the indenter motion was carried out with a very low velocity v = 1 μm/s. However, once contact instability occurs, rubber breakaway at the edges of the contact does not occur instantaneously but at some finite velocity that is set by the current contact configuration and rubber properties. Therefore, it takes some time for the rubber to detach from the indenter, even if we are in the instability zone, whereas in the simulation, detachment would occur instantaneously. As a result, the force F in the detachment region of the dependency decreases smoothly, resulting in additional energy dissipation, which is calculated as the area between the F(d) curves for indentation and detachment phases.
The characteristics described above in (A) and (B) lead to additional dissipation of mechanical energy in the experiment compared to the simulation, which is well observed by comparing the experimental (diamonds) and theoretical (circles) dependencies of ΔW(dmax) that are plotted in Figure 3d.
3.2. Effect of the Indenter Radius R
Figure 4 shows the results of experiments on the indentation of mirror-polished steel indenters with radii R = 11, 22, 30, 40, 50, and 100 mm. For each radius, three indentation cycles were performed in a row. Other experimental parameters: elastomer—TANAC CRG N3005 rubber sheet with thickness h = 5 mm, indentation depth dmax = 0.3 mm, indenter velocity in the indentation and detachment phases v = 1 µm/s.
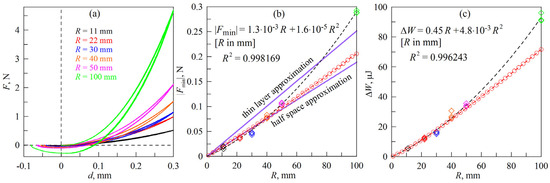
Figure 4.
(a) dependencies of normal force F on indentation depth d at different values of indenter radius R; (b) dependencies of adhesive contact strength |Fmin| on indenter radius R, diamonds—experiment, circles—simulation; (c) dependencies of energy dissipation in the complete indentation-detachment cycle ΔW on indenter radius R, calculated for all experiments (diamonds) and obtained in simulations (circles).
The analysis of experimental results showed that with increasing indenter radius R, the adhesive strength |Fmin| and dissipation ΔW in the complete indentation–detachment cycle increase according to quadratic relationships, the equations of which are given in the corresponding panels of the figure. Note that the approximation functions do not include a free term due to the fact that at zero indenter radius R = 0 mm, the force |Fmin| and dissipation ΔW should also take zero values since R = 0 mm formally corresponds to the case when there is no indenter and, consequently, no contact. The BEM method used for modeling is based on the adhesive interaction of the JKR-type, and in this case, the theoretical dependencies |Fmin|(R) are known. Thus, in the case of a parabolic indenter in the thin layer limit (h → 0) located on a rigid substrate, the adhesive strength of the contact is defined as [44,45]
At the same time, for the half-space limit (h → ∞), the value of the adhesive strength of the contact is given by a different relation from the above, following directly from the JKR theory [23]
In the simulation at the detachment stage, γ12 = 0.4 J/m2 is assumed, determining dependencies (3) and (4), illustrated in Figure 4b as solid lines. It can be seen that at small indenter radii R, the dependency |Fmin|(R) obtained in the simulation (circles) coincides with the half-space case (4). However, as R increases, it deviates towards the thin layer solution (3).
From the comparison of experiments with simulations, it follows that visible deviation is observed only for the indenter of the largest radius, R = 100 mm, both for the dependence of adhesive strength |Fmin|(R) and dissipation ΔW(R). The observed deviation may be related to the strengthening of the contact. As the indenter radius increases, the experimental conditions approach the contact with a thin layer where the contact pressure is higher. The increase in contact pressure leads to the strengthening of the contact and an increase in its adhesive strength, as was shown in [33,43]. An increase in adhesive strength also leads to an increase in energy dissipation ΔW, as discussed above in Section 3.1 in paragraph (A). In addition, within the described series of experiments, several indenters with potentially different surface energies were used. This variation could provide different values of the specific work of adhesion γ12, which may also be the reason for the observed discrepancies for the indenter with the largest radius, R = 100 mm.
3.3. Effect of the Elastomer Thickness h
In the experiments described above, a sheet of TANAC CRG N3005 rubber with a thickness of h = 5 mm was used as an elastomer, into which the indentation is made. This subsection describes experiments with elastomers with different thicknesses. Elastomer samples were composed of sheets with a thickness of 5 mm each by placing them on top of each other. When layered, the sheets were firmly bonded by adhesion, suggesting that there was no displacement at the interface between the sheets during normal indentation. Therefore, the elastomer composed of individual sheets can be considered homogeneous in terms of its mechanical properties under the conditions of the conducted experiments. Experiments were performed with thicknesses: h = 5, 10, 15, 20, and 25 mm. Other experimental parameters: indentation depth dmax = 0.3 mm, radius of the steel mirror-polished indenter R = 50 mm, indenter velocity in the indentation and detachment phases v = 1 µm/s. The results obtained are shown in Figure 5, with three consecutive indentation–detachment cycles for each elastomer thickness.
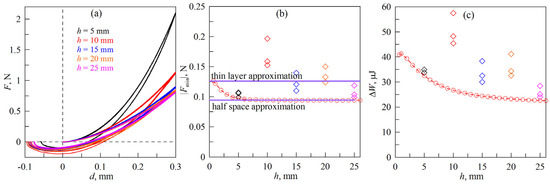
Figure 5.
(a) dependencies of normal force F on indentation depth d at different values of elastomer thickness h; (b) dependencies of adhesive contact strength |Fmin| on elastomer thickness h; diamonds correspond to experiments; circles show simulation results; (c) dependence of energy dissipation in the full indentation–detachment cycle ΔW on elastomer thickness h, calculated for all experiments (diamonds) and obtained from simulation (circles).
Figure 5a shows that as the elastomer thickness h increases, the contact stiffness decreases, which can be seen from the decrease in the value of the normal force F at the maximum indentation depth dmax = 0.3 mm. It is also worth noting that with each further increase of the elastomer thickness h, by 5 mm, the difference between the two nearby F(d) dependencies (e.g., at h = 15 mm and 20 mm) becomes less and less pronounced. This is because as the elastomer thickness increases, we approach the half-space limit h >> a, where a is the contact radius. Therefore, when the thickness h exceeds a certain value, further increases in h no longer lead to any noticeable changes in the contact properties, which was also experimentally observed in [41].
Figure 5b,c show the dependence of the adhesive contact strength |Fmin| and energy dissipation in the complete indentation–detachment cycle ΔW on the elastomer thickness h. Let us first note the simulation results shown by the circles. In Figure 5b, the solid horizontal lines correspond to the half-space (4) and thin layer (3) solutions. It can be seen that at large elastomer thicknesses h the dependence |Fmin|(h) obtained in the simulations coincides with the half-space limit, and with decreasing thickness, h approaches the thin layer limit, which is expected. However, the experimental data do not show such a dependence. Moreover, they do not fit into any dependence but rather present arbitrarily scattered values, albeit near the expected solution. Therefore, approximation of experimental data by mathematical functions |Fmin|(d) and ΔW(d) was not carried out in the considered case. We believe that such a significant range of values is due to the variation in the value of the specific work of adhesion γ12 in different experiments. As described above, elastomers with different thicknesses were obtained by overlapping sheets of TANAC CRG N3005 material with thicknesses h = 5 mm each. In this case, each successive sheet of elastomer was superimposed on top of the previous one. Therefore, in each new experiment, the indenter contacted the surface of a new elastomer sheet. Although all sheets represented the same material, their individual properties may have differed. With this method of producing elastomers of various thicknesses, the specific work of adhesion γ12 is a much more sensitive parameter than, for example, the elastic modulus E, which showed stable values when the elastomer was composed of individual sheets [41]. Moreover, the solutions for the boundary cases of thin layer (3) and half-space (4) show similar values of adhesive strength |Fmin|, which can be visually seen in Figure 5b. Determining such differences in an experiment can be challenging due to the influence of many different factors that are difficult to control. However, despite the existing problems, the values of |Fmin| and ΔW obtained in experiments for thicknesses h = 5 mm and h = 25 mm are in good agreement with the simulation data. Therefore, to evaluate the general picture in the considered case, we will rely on the dependencies |Fmin|(d) and ΔW(d) obtained in the simulation. In particular, the simulations show a decrease in the dissipation value ΔW with increasing elastomer thickness h, asymptotically yielding some constant value, since with increasing h we approach the half-space limit.
3.4. Influence of the Surface Energy of Contacting Bodies (Specific Work of Adhesion γ12)
The specific work of adhesion γ12 in the contact of two bodies is determined by the energies of the contacting surfaces Δγ1 and Δγ2, as well as by the energy of the interfacial layer in the contact Δγ12 [46]:
According to expression (5), when γ12 > 0, the bodies in contact will “stick” to each other due to adhesion, since this is an energetically favorable process. This is precisely the situation we consider in the present paper. The purpose of this paragraph is to clarify the effect of the specific work of adhesion γ12 on the adhesive strength of the contact |Fmin| and the dissipation of mechanical energy ΔW. In order to change γ12, the indenter surface was treated. In the experiments, a mirror-polished steel indenter with radius R = 50 mm was used. The thickness of the TANAC CRG N3005 elastomer was h = 5 mm, the indentation depth was dmax = 0.3 mm, and the indenter velocity in the indentation and detachment phases was v = 1 µm/s. Three experiments were performed, the results of which are shown in Figure 6. In the first experiment, the indenter surface was not treated in any way, and three indentation cycles were performed in a row. Figure 6a illustrates this experiment with three coincident black curves with the lowest value of adhesive strength |Fmin|. Before the next experiment, the indenter surface was cleaned in an EMMI-05P ultrasonic bath in an aqueous solution of EMAG EM-404 cleaner for 16 min at room temperature. In the previous work [43], it was shown that such cleaning leads to an increase in the adhesive strength of the contact.
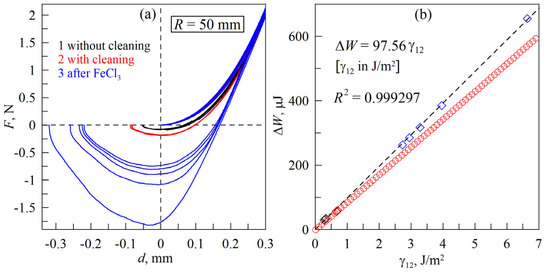
Figure 6.
(a) dependencies of normal force F on indentation depth d for different types of steel indenter treatment; (b) dependence of energy dissipation in the complete indentation–detachment cycle ΔW on specific work of adhesion γ12, calculated for all experiments (diamonds) and obtained from modeling (circles).
The results of the experiment conducted after cleaning the indenter are shown in Figure 6a by the following three red overlapping curves (three indentation cycles). Notice the increased value of adhesive strength |Fmin| compared to the first case where the indenter was used without cleaning.
In the third and final series of experiments, prior to the experiment, the indenter surface was treated for ≈ 1 min with a 40% aqueous ferric chloride solution FeCl3. Such treatment leads to a significant increase in adhesive strength. The bottom five F(d) curves in Figure 6a show the results of five consecutive indentation cycles. Compared to the case of an untreated indenter (upper curves in the figure), the first indentation cycle after treating the indenter surface with a FeCl3 solution (lower curve in the figure) shows an increase in the adhesive contact strength |Fmin| by more than 19 times. With such a high adhesive force |Fmin| at contact failure, the surface characteristics of the contacting bodies change significantly, as each subsequent indentation cycle shows a significant decrease in adhesive strength. Moreover, the trend of decreasing adhesive strength is maintained for all five indentation cycles performed. We assume that the value of |Fmin| decreases due to the fact that in such a strong contact, the adhesion forces are sufficient to pull the polymer molecules out of the elastomer volume when the indenter is withdrawn from the elastomer. The elongated molecules remain on the indenter surfaces, contaminating them, resulting in reduced contact strength. In support of this hypothesis, we point out that in experiments with the softer material CRG N0505, after interaction of the indenter with the elastomer and detachment, an oily spot becomes visually noticeable on the indenter surface.
The F(d) dependencies shown in Figure 6a correspond to different values of adhesive strength |Fmin|, due to variations in the specific work of adhesion γ12. Therefore, for further analysis, it is reasonable to represent the dependence |Fmin| as a function of γ12. It is difficult to measure the value of γ12 directly in the experiment due to the rapid change of this value. Therefore, it is reasonable to determine the work of adhesion by comparing the experimental dependencies F(d) with known analytical solutions or with the results of computer simulations. To find the necessary dependence of |Fmin|(γ12), modeling with BEM was performed. The procedure is described in Section 2.2 of the paper, where the parameters used for the modeling are also specified. A series of 100 numerical experiments on indenter detachment from the elastomer were performed, where the specific work of adhesion γ12 was varied from 0.1 J/m2 to 10 J/m2 in steps of 0.1 J/m2. Modeling showed that the dependence of the adhesive strength of contact |Fmin| on the specific work of adhesion γ12 in the considered case is given by the expression.
The necessity of modeling is that an elastomer of fixed thickness h = 5 mm is used in the experiment. For the limits of a half-space (elastomer of infinite thickness) and a thin layer (elastomer of zero thickness), analytical solutions of (4) and (3) exist. If we consider the formula in the form |Fmin| = απRγ12 for the general case of elastomer of arbitrary thickness, then the limiting case of half-space will correspond to the value α = 3/2, and for the thin layer limit we will have α = 2. In modeling, in fact, the value of the parameter α is found. Thus, in the case shown in Figure 6 (see Equation (6)), with an indenter with radius R = 50 mm, we obtain α ≈ 1.757. Note that in the other series of experiments shown in Figure 7, an indenter with a smaller radius, R = 22 mm, was used, and for these experiments, we obtained a lower value of α ≈ 1.541 (see also Equation (7)). The obtained values of the parameter α align with the general concepts of layer adhesion (see Equations (3) and (4)). According to these expressions, α decreases as the system approaches the half-space limit, i.e., indicating an increase in elastomer thickness h or a decrease in indenter radius R. However, Section 3.5 of the paper shows that, in fact, the overall picture of layer adhesion is more complex, since the force |Fmin| also depends on the elastic modulus of the layer.
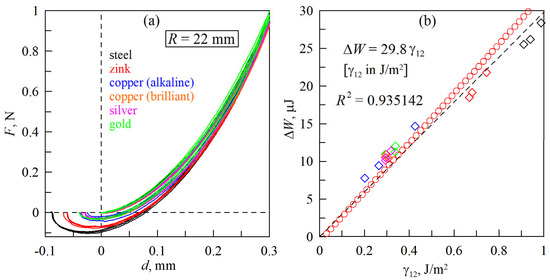
Figure 7.
(a) dependencies of the normal force F on the indentation depth d for different metals with which the surface of the steel indenter was coated (uncoated steel indenter, zinc, copper (2 types), silver, gold); (b) dependence of the energy dissipation in the complete indentation–detachment cycle ΔW on the specific work of adhesion γ12, calculated for all the experiments performed (diamonds) and obtained from modeling (circles).
The linear function (6) above is an approximation of the discrete dependence |Fmin|(γ12) obtained in BEM modeling by the least squares method. The coefficient of determination for this approximation was R2 = 0.999371. Using Equation (6), the value of the specific work of adhesion γ12 was assigned to each of the 11 experimental |Fmin| values (a total of 11 indentation cycles are shown in Figure 6a). These obtained values of γ12 are used to represent the experimental dependence of ΔW(γ12), shown in Figure 6b by the diamonds. The dashed line in Figure 6b is an approximation of ΔW(γ12) by a linear function, the expression for which is given in the figure. Thus, as the specific work of adhesion γ12 increases, the adhesive strength of contact |Fmin| and the dissipation of mechanical energy ΔW in a complete indentation–detachment cycle increase linearly.
As discussed above, Figure 6 presents the results of experiments where the surface energy of the indenter was modified by chemical treatment. Another possibility to vary the specific work of adhesion is to use different materials from which the substrate (elastomer) and the indenter are made. However, all other parameters (including the indenter radius R, the elastic characteristics of the elastomer E and ν, and its thickness h) must remain constant in order to be able to compare the experimental results so that the effect of the specific work of adhesion γ12 can be analyzed. In the series of experiments described below, in order to change the surface properties of the indenter, the indenter was coated with thin layers of various metals by electrolytic deposition. Since the same indenter was used, its radius remained constant in all experiments. The indenter (cathode) was placed in the electrolyte, and an electric current was passed through the electrolyte for several minutes, the value of which was calculated based on the electrolyte used and the surface area of the indenter. After another coating was applied to the indenter, a series of experiments of three indentation cycles were performed, after which another metal was applied and the next series of experiments was carried out. The results of the experiments are shown in Figure 7.
It should be noted that here an indenter with radius R = 22 mm was used, while in all the experiments described above, another indenter with radius R = 50 mm was utilized. This is due to the fact that the indenter we had at our disposal with radius R = 50 mm was made of stainless steel (unlike the indenter R = 22 mm), and the electrolytes used do not allow the coating of stainless steel. Apart from using an indenter with a different radius and surface coatings made of various metals, all other experimental parameters were similar to those under which the data shown above in Figure 6 were obtained.
Figure 7a shows the results of experiments using an uncoated steel indenter as well as one coated with thin layers of zinc, copper, silver, and gold. In the case of the copper layer, two experiments were carried out with different coatings. These were a matte copper coating applied using an alkaline electrolyte and a coating with a pronounced metallic luster obtained using an acidic electrolyte. Thus, a series of six experiments were conducted, each using an indenter with a different surface chemistry. In all cases, three indentation cycles were performed consecutively, and all measured F(d) dependencies are shown in Figure 7a. The dependencies shown in Figure 7b were obtained in the same way as those shown in Figure 6b. In the case of an indenter with a radius R = 22 mm (Figure 7), the dependence |Fmin|(γ12) found as a result of BEM simulations of the indentation process is as follows:
Function (7) is the least squares approximation of the discrete dependence |Fmin|(γ12) obtained in the simulation; the coefficient of determination for this approximation is R2 = 0.999902. From the comparison of Figure 6 and Figure 7, it can be observed that there is no qualitative difference between them. This means that the macroscopic adhesive properties of the contact do not depend on exactly how the indenter was treated to change its surface energy Δγ, but depend only on the value of Δγ itself. The quantitative differences between the results shown in Figure 6 and Figure 7 are primarily due to the different radii R of the indenters used, 50 mm and 22 mm, which differ by more than a factor of two.
In a series of experiments with the results displayed in Figure 7 showed that the highest adhesive strength had the contact between the elastomer and the steel indenter, prior to coating. The second-highest strength is demonstrated by the zinc-coated indenter. Gold, silver, and two types of copper plating provide the lowest (approximately equal) adhesive strength. Given that the dissipation of mechanical energy ΔW, while all other conditions being constant, increases with increasing adhesive strength of the contact |Fmin|, the metals were ranked in terms of the influence of the coating type on the ΔW value. Specifically, the highest value is provided by the steel indenter, followed by zinc, then copper, gold, and silver. The experimental data obtained, however, cannot be treated as accurate results, which are provided by pure metals, because we did not perform chemical analysis of the obtained coatings. The purpose of the described study was to vary the surface energy of the indenter to find out its effect on the adhesive properties of normal contact. The surface energy was changed in two ways: by treating the indenter with chemical solutions (see Figure 6), and by electrolytically depositing metal coatings on its surface (see Figure 7). Both methods showed qualitatively similar results.
In Figure 6b and Figure 7b, the circles show the dependencies ΔW(γ12) obtained in the BEM simulations; the procedure is described in Section 2.2 of the paper. It is evident from the figures that the simulation results are slightly different from the experimental results. In this case, it is difficult to point out the reasons for this discrepancy because the γ12 values used to represent the experimental ΔW(γ12) dependencies were determined indirectly by BEM simulations rather than directly in the experiment. With this method of determining γ12, the “experimental” dependencies of adhesive strength, |Fmin|(γ12) will perfectly match the simulation since they are in fact the results of simulations (6) and (7) (this is why the experimental dependencies of |Fmin|(γ12) are not shown in Figure 6 and Figure 7). This hybrid way of constructing “experimental” ΔW(γ12) dependencies should bring an error into the interpretation of experimental results due to the idealization of the system in the simulation, since the form of ΔW(γ12) strongly depends on |Fmin|(γ12).
3.5. Effect of Elastomer Elastic Modulus E
The next series of experiments was conducted to investigate the effect of the elastic modulus of the elastomer on the contact properties. The thickness of the elastomer in all experiments was h ≈ 5 mm, indentation depth dmax = 0.3 mm, radius of steel mirror-polished indenter R = 50 mm, speed of indenter movement at indentation and detachment v = 1 µm/s. The variation of the elastic modulus of the elastomer in the described series of experiments was carried out by using several elastomers with different properties. Two of them are different grades of TANAC rubber: CRG N3005 and CRG N0505. In our previous work [33], it was experimentally found that the elastic moduli of these elastomers are E ≈ 0.324 MPa (CRG N3005) and E ≈ 0.054 MPa (CRG N0505). In this case, Poisson’s ratio was not directly measured in the experiments. Instead, the value ν = 0.47, which is close to incompressible materials and characteristic of elastomers, was used.
In addition to the experiments with these rubbers, several experiments were conducted using layers of solidified aqueous solution of food gelatin, each with a thickness of 5 mm, serving as an elastomer. The first elastomer from gelatin was made as follows: Four grams of gelatin were added to 96 mL of water. After its complete dissolution with thorough stirring, the solution was placed in a square-bottomed dish with side dimensions of 140 mm × 140 mm. The amount of the required solution was calculated assuming that the thickness of the elastomer after gelatin solidification must be h ≈ 5 mm. Thus, the volume of liquid required to produce the elastomer was 14 × 14 × 0.5 = 98 cm3. The solution was placed in the refrigerator for 2 h, and after that, the solidified gelatin was kept at room temperature for one hour. Then an experiment was carried out on the indentation into the resulting elastomer (three indentation cycles in a row). After the experiment, the gelatin elastomer was dissolved in a microwave. An additional portion of dry gelatin (weighing 4 to 5 g) was added, and the above procedure was repeated. Four samples of gelatin elastomer were produced with this method. A total of six elastomers—four gelatins and two varieties of rubber—were investigated in the described series of experiments.
An important aspect of the discussed series of experiments is the use of different elastomer samples, the values of the specific work of adhesion γ12 for which may differ significantly. These differences could be one of the reasons for the different values of adhesive strength |Fmin| for all experiments. However, the actual value of the specific work of adhesion γ12 can also depend on the elastic modulus [47]. We have previously observed repeatedly that stiffer materials provide higher values of adhesive strength |Fmin|, although according to the theoretical Equations (3) and (4), there should be no such dependence. When describing the conducted series of experiments, we will speak about the dependence of the adhesive strength of the contact |Fmin| precisely on the elastic modulus of the elastomer E, since this was the only material parameter that could be controlled in the experiment. The experimental results obtained are shown in Figure 8, with 3 indentation cycles shown for each elastomer.
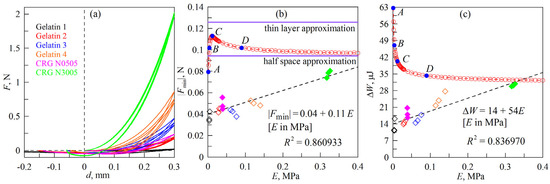
Figure 8.
(a) dependencies of the normal force F on the indentation depth d for 6 different elastomers with different elastic moduli E; (b) dependencies of the adhesive contact strength |Fmin| on the elastic modulus of elastomer E; the diamonds correspond to the experiment; the circles show the simulation results; (c) dependencies of energy dissipation in the full indentation–detachment cycle ΔW on the elastic modulus of elastomer E, calculated for all the experiments performed (diamonds) and obtained from simulation (circles).
To determine the values of the elastic modulus E of the used elastomers, modeling of indentation using BEM was conducted. A spherical indenter with a radius R = 50 mm was used to indent in an elastic layer of elastomer with a thickness h = 5 mm, the procedure of which is described in Section 2.2 of the paper. All experimentally measured F(d) dependencies shown in Figure 8a demonstrate the maximum normal force Fmax at indentation depth d = dmax = 0.3 mm. This value of Fmax was used to determine the modulus of elasticity. The numerical BEM was used to determine a value of E at which the contact configuration calculated at d = dmax corresponded to the normal force equal to the experimentally determined value of Fmax, separately for each of the indentation cycles performed. In the dependences |Fmin|(E) and ΔW(E) shown in Figure 8b,c, the values of the determined elastic modulus E for all experiments performed are plotted on the abscissa axis. Note that each indentation cycle shows slightly different elastic modulus values even for the same elastomer, which leads to an additional scatter of experimental values in the direction of the abscissa axis, as can be seen in Figure 8b,c. The point is that for each indentation cycle, modeling was performed to find the elastic modulus, and since even for the same elastomer, the values of maximum forces Fmax in different cycles are slightly different, the calculated values of modulus E will also differ. The variation in Fmax in different indentation cycles (as a rule, a decrease in force in each subsequent cycle) when using hardened gelatin solution as an elastomer is due to partial destruction of the gelatin surface after indenter detachment, since gelatin is much less stable compared to rubber samples. The change in elastic modulus in different indentation cycles is also associated with the heating process of gelatin, since it was not heated to equilibrium room temperature before the experiment. In this case, it is justified, since the purpose of the discussed series of experiments was to establish the dependences of the values |Fmin| and ΔW on the elastic modulus E, which does not necessarily have to be constant in different indentation cycles.
The experimental results shown in Figure 8 indicate that the values of |Fmin| and ΔW increase with increasing elastic modulus E, which was previously experimentally observed in [33]. In this case, the experimental dependences |Fmin|(E) and ΔW(E) can be approximated by linear functions; the expressions are given in the corresponding panels of the figure. In Figure 8b,c, the filled diamonds show the results corresponding to the rubber samples, while the empty diamonds show the cases in which jelly was used as elastomer. The circles in the figure represent the results of the computer simulation. It is evident that in the case under consideration, there is both quantitative and qualitative inconsistency with the experiment. As stated above, one of the reasons for this discrepancy may be the significant difference in the values of specific work of adhesion γ12 for the different elastomers prepared for the experiment, while in the simulations the value of γ12 was assumed constant in all cases (see Section 2.2 of the paper). Furthermore, in certain experiments, a solidified gelatin solution (unfilled diamonds in Figure 8b,c) acted as an elastomer, and its surface could be partially destroyed in the process of indenter detachment. In addition, the surface of the solidified gelatin becomes progressively more uneven with increasing elasticity (higher concentration of gelatin in water), and this will also lead to a deviation of the system behavior from what is theoretically predicted. To identify the real reasons for this mismatch, it is necessary to conduct an additional series of experiments and simulations, which is beyond the scope of this study.
Let us discuss the simulation results shown in Figure 8b,c with circles, as they show a number of interesting features. First, the obtained dependence of the adhesive strength |Fmin|(E) is non-monotonic. At the same time, analytical solutions for the limiting cases of thin layer (3) and half-space (4) show that there is no dependence of the adhesive strength |Fmin| on the elastic modulus E. In order to compare the results obtained in the simulation with the analytical estimates, two solid horizontal lines are added to Figure 8b, the lower one representing the solution for the half-space (4) and the upper one showing the solution for the thin layer (3). The dependence of |Fmin|(E) obtained in the simulations shows that the value of |Fmin| approaches the half-space solution as the elastic modulus E increases. This is a logical result because, as the elastic modulus increases, the adhesive contact radius decreases. The contact radius corresponding to the minimum of the F(d) dependence at the detachment stage, i.e., the radius at force F = Fmin, which exists only due to adhesion, is also significantly reduced. As a result, the values of |Fmin| should approach the half-space limit (4) with increasing E, as demonstrated by Figure 8b. It is also interesting that, for small values of E, the adhesive strength |Fmin| becomes even smaller than the corresponding thin layer limit (3). For example, in Figure 8b, the |Fmin|(E) dependence starts at point A, corresponding to the value E = 0.001 MPa (or 1 kPa). And point A shows less adhesive strength than the half-space limit (4). In general, the dependence |Fmin|(E) has non-monotonic behavior, leading to the fact that there is some optimal value of the elastic modulus E where the maximum adhesive strength of the contact is realized. In our previous work [48], it was shown that the adhesive strength |Fmin| depends non-monotonically on the elastomer thickness h, leading to the existence of an optimal thickness h at which the adhesive strength |Fmin| is maximized. In order to clarify the general picture, it is necessary to study accurately the three-dimensional dependence |Fmin|(E, h). However, a detailed study of this requires additional analysis, which is beyond the scope of this study.
The second interesting feature of the considered case is that the ΔW(E) dependence in Figure 8c shows a monotonic decrease in energy dissipation with increasing elastic modulus, despite the non-monotonicity of the |Fmin|(E) function in Figure 8b. Although, based on the shape of the curves in Figure 2a showing the typical F(d) dependencies obtained in the simulations, it can be assumed that as |Fmin| increases, the energy dissipation ΔW should also increase. This increase in dissipation must occur since the value of the force |Fmin| corresponds to point D in Figure 2a, and as point D descends in the negative direction of the ordinate axis, the area of the shaded figure determining the dissipation ΔW must increase. Therefore, at first glance, the non-monotonicity of the |Fmin|(E) dependence should also lead to the non-monotonicity of ΔW(E), which is not observed in Figure 8c. To ascertain the reasons for this non-trivial behavior, Figure 9 is additionally provided.
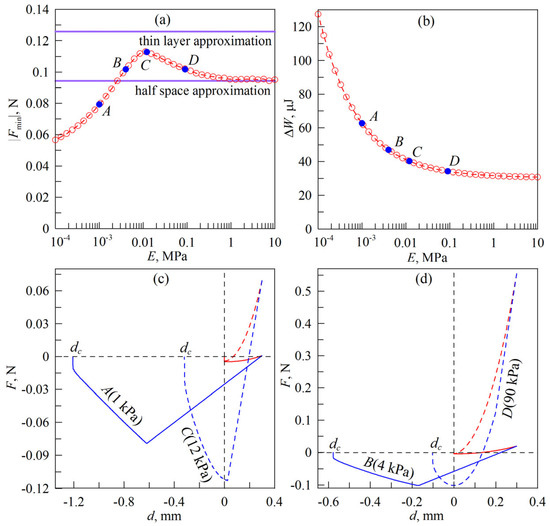
Figure 9.
(a) dependence of the adhesive strength |Fmin| on the elastic modulus E; (b) dependence of the mechanical energy dissipation ΔW in the complete indentation–detachment cycle on the elastic modulus E; (c,d) dependencies of the normal forces F on the indentation depth d corresponding to points A, B, C, D shown in panels (a,b) of the figure, where red colored lines indicate the indenting phase and blue colored lines the pull-off phase. Different line styles correspond to different points shown in panels (a,b).
Figure 9a,b shows the dependencies |Fmin|(E) and ΔW(E) similar to those presented in Figure 8b,c. The difference is that in Figure 9, these dependencies are shown for a wider range of values of the elastic modulus, so for convenience, the abscissa axis is presented here on a logarithmic scale. In the dependencies shown in Figure 9a,b, points A, B, C, and D are labeled, corresponding to a monotonic increase in elastic modulus E. Namely, these points correspond to the values of elastic modulus E = 1, 4, 12, and 90 kPa, with the increase of which the energy dissipation ΔW monotonically decreases (the same points are labeled in Figure 8b,c). The points A and C are chosen so that the adhesive strength |Fmin|A < |Fmin|C, but ΔWA > ΔWC, i.e., here a lower adhesive strength |Fmin| corresponds to a higher dissipation value ΔW. The reason for this behavior can be seen in Figure 9c, which shows the force-displacement dependencies F(d) corresponding to points A and C. The figure shows that the dissipation ΔW can increase not only by increasing the adhesive strength |Fmin|, but also by increasing the contact duration. Here, the curve corresponding to point A shows the complete breakage of the contact at a significantly greater distance of the indenter from the elastic layer, which leads to an increase in the dissipation value, despite the fact that the contact is characterized by a lower adhesive strength |Fmin| than at the parameters of point C.
Since the dependence |Fmin|(E) shows non-monotonic behavior, it becomes possible to provide the same values of adhesive strength |Fmin| at different values of elastic modulus E, as demonstrated by points B and D. The corresponding dependencies F(d) are shown in Figure 9d. Both curves depicted in Figure 9d show the same |Fmin| minima, although at the parameters of point B, the indenter must be pulled further away from the elastomer to break the contact. This feature opens up new technological possibilities in applications requiring precise control over adhesive contact strength |Fmin|, because the same adhesive strength can be achieved at two different values of the elastomer elastic modulus E. This allows for the adjustment of other contact properties, such as the critical distance of the indenter from the elastic layer dc at which contact failure occurs (see Figure 9c,d), energy dissipation ΔW in a complete indentation–detachment cycle, contact stiffness K = ∂F/∂d, contact area A, etc. This interesting feature requires a more detailed study as well as experimental verification, which we plan to do in future works.
3.6. Effect of Velocity of Indenter
Numerous experimental studies show that viscoelastic effects have a significant influence on adhesive forces as the velocity of the indenter increases [49,50]. In this subsection, we will analyze how the velocity of the indenter affects the dissipation of mechanical energy in the complete indentation–detachment cycle and the adhesive strength of the contact. To study the effect of the velocity of the indenter, a series of experiments were conducted where a steel indenter with a radius R = 50 mm and a mirror smooth surface was indented into a sheet of TANAC CRG N3005 rubber with a thickness of h = 5 mm to a depth of dmax = 0.3 mm. The velocities of indenter motion in the indentation and detachment phases were the same. Experiments were performed for velocities v = 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, and 1024 µm/s, with three indentation cycles for each velocity value. Figure 10 shows the results of the experiments.
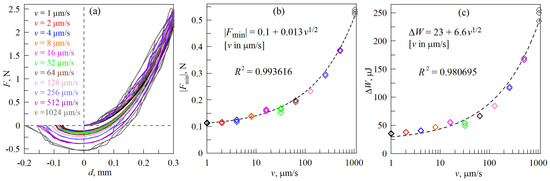
Figure 10.
(a) dependencies of normal force F on indentation depth d at different values of velocities of indenter v; (b) dependencies of contact adhesive strength |Fmin| on indenter velocity v; (c) dependence of energy dissipation in the complete indentation–detachment cycle ΔW on indenter velocity v, calculated for all experiments shown in panel (a).
Figure 10a shows the experimentally measured dependencies of the normal force F on the indentation depth d at different indenter velocities v. Curves corresponding to different velocities are shown in different colors. From the experiment, it can be observed that the value of adhesive strength |Fmin| increases as the velocity of the indenter increases (see Figure 10b). The |Fmin|(v) approximation, whose equation is shown in Figure 10b, contains a v1/2 term, i.e., it represents a root dependence. Whereas, the adhesive strength of the contact |Fmin| depended linearly on the indentation depth dmax (see Figure 3c). Figure 10c demonstrates the dependence of mechanical energy dissipation ΔW(v) in full indentation–detachment cycles, also representing the root dependence. Note that the obtained approximation of ΔW(v) is qualitatively different from the ΔW(dmax) dependence shown in Figure 3d, which represents a quadratic function.
It is worth mentioning that the adhesive strength of the contact is strongly influenced by the nature of contact propagation in the indentation phase. Figure 10 shows the effect of indenter velocity in the case where the indenter was moved at the same velocities for both indentation and subsequent detachment (contact failure). When moving at high velocities during the indentation phase, the contact does not have time to acquire the maximum adhesive strength, which is achieved during indentation at low velocities in the quasi-static case. Additionally, we conducted a series of experiments where the indenter was plunged into the elastomer at a constant velocity of v = 1 µm/s, ensuring quasi-static conditions of contact propagation. The indenter detachment was performed at various velocities similar to those shown in Figure 10. The results obtained in the series of experiments are shown in Figure 11. Comparing the results shown in Figure 10 and Figure 11, it is evident that in the case of quasi-static contact propagation in the indentation phase (Figure 11), significantly higher values of the contact adhesive strength |Fmin| and mechanical energy dissipation ΔW are realized. For a more detailed comparative analysis of contact properties in experiments with quasi-static contact propagation during the indentation phase and with the same indenter velocities in both phases, panel (d) is additionally demonstrated in Figure 11. In Figure 11d, the triangles show the velocity dependence of the ratio of the contact adhesive strengths |Fmin| given in Figure 11b to the corresponding values illustrated in Figure 10b. The circles in Figure 11d show the dependence of the ratio of energy dissipations in the discussed experiments. The dashed lines in Figure 11d show the ratios of the corresponding approximation functions, whose mathematical expressions are given in Figure 10 and Figure 11 in panels (b) and (c).
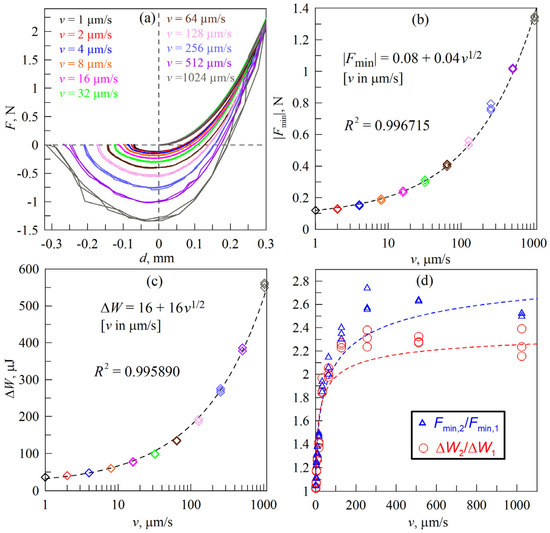
Figure 11.
(a) Dependencies of the normal force F on the indentation depth d at different values of the indenter velocity v in the contact failure phase, in the indentation phase the indenter velocity is always the same and is v = 1 µm/s; (b) dependencies of the adhesive strength of the contact |Fmin| on the indenter velocity in the detachment phase; (c) dependence of energy dissipation in the complete indentation–detachment cycle ΔW on the indenter velocity in the detachment phase, calculated for all experiments shown in panel (a); (d) dependencies of the ratios of adhesive strengths (triangles) and energy dissipation (circles) in the experiments shown in Figure 11, to the analogous values shown in Figure 10.
Figure 11d shows that with increasing indenter velocity v, the adhesive contact strength |Fmin|, and mechanical energy dissipation ΔW in the experiment with quasi-static contact propagation first show increasingly larger values compared to the experiment where the indenter velocity in both phases was the same. However, starting from the value v = 256 µm/s, the growth of the considered magnitude ratios stops, after which they remain approximately constant. From the figure, however, it is clearly evident that quasi-static contact propagation in the indentation phase makes the contact stronger compared to the case where the indenter is displaced with equal velocities in the indentation and detachment phases. This effect is observed in the whole range of investigated velocities, and at indenter detachment velocities v > 32 µm/s, the contact under quasi-static propagation becomes two and more times stronger.
Note that in this subsection, we have not performed computer simulations of the indentation process. This is due to the fact that indentation experiments are carried out with different indenter velocities, many times higher than the values at which the contact can be considered quasi-static. In this case, viscoelastic effects are manifested, and the influence of these effects is studied by experiments, as depicted in Figure 10 and Figure 11. Consideration of viscoelastic effects is not possible within the BEM method, as described in Section 2.2 of this paper. Note, however, that there are BEM modifications that allow viscoelasticity to be taken into account [51,52,53]. Moreover, in a recent work [54], a simple method for modeling indentation considering the viscoelasticity of the elastomer based on the method of dimensionality reduction (MDR) was proposed considering the finite thickness of the elastomer. Therefore, modeling the situation shown in Figure 10 and Figure 11 should not be a problem. However, it requires additional elastomer parameters to be known, which require further experiments to determine. This aspect is beyond the scope of the present work.
3.7. Effect of Indenter Surface Roughness
In a previous study [34], we investigated the effect of indenter surface roughness on adhesive strength and mechanical energy dissipation in the indentation–detachment cycles. In [34], experiments with indenters with radii R = 30, 40, 50, and 100 mm were carried out. Sandpaper with different grit sizes of P2000 (10.3 µm), P1500 (12.6 µm), P1000 (18.3 µm), P800 (21.8 µm), P400 (35 µm), P320 (46.2 µm), P180 (82 µm), P80 (201 µm), P60 (269 µm), and P40 (425 µm) were used to create roughness. For each roughness and indenter, three consecutive indentation cycles were performed. Figure 12 shows experimental data for an indenter with a radius R = 50 mm (see [34] for a more detailed description of the experiments as well as results for all indenters). Here, the case “P0” corresponds to the largest roughness of the indenter that was not created with sandpaper but by additional scratching the surface with a metal hacksaw.
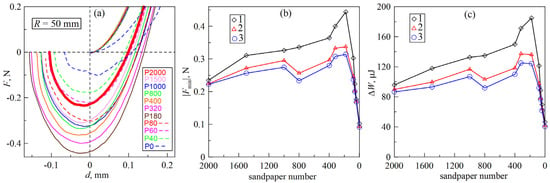
Figure 12.
(a) dependencies of the normal force F on the indentation depth d for indenters with different surface roughness for the first indentation cycle; (b) dependencies of the adhesive contact strength |Fmin| on the number of sandpaper used to create the indenter roughness; different symbols correspond to different indentation cycles; (c) calculated dependencies of energy dissipation in the complete indentation–detachment cycle ΔW on the number of sandpaper; different symbols correspond to different indentation cycles.
Figure 12a displays the F(d) dependencies in the first indentation cycle, which are cut off from above to emphasize the contact failure region. The red bold curve corresponds to the case of a mirror polished indenter (P2000). All curves can be identified using the legend given in the figure panel. The general trend in the experiments was that, initially, the adhesive strength |Fmin| and the dissipation of mechanical energy ΔW increased as the amplitude of the indenter roughness increased, and with further increases in roughness, these values decreased, i.e., the contact became less strong. This can easily be seen in Figure 12b,c, where the above-mentioned trend is maintained in all three indentation cycles (the values of |Fmin| and ΔW decrease in each subsequent indentation cycle). This behavior is due to the fact that at low roughness amplitude, the elastomer material fills the gaps between neighboring irregularities on the indenter surface, which leads to an increase in the real contact area and, consequently, an increase in the adhesive strength of the contact. If the roughness exceeds a critical value, the actual contact area decreases as the elastomer becomes unable to fill the gaps between the roughnesses. In both cases, the dependencies F(d) are satisfactorily described by the JKR theory when the effective specific work of adhesion γ12, dependent on the indenter roughness, is considered. At extremely large roughnesses, the contact becomes topologically non-simply connected, and non-monotonicities appear in the F(d) dependences due to the emergence of stable contact configurations at the indenter detachment stage (see the upper dashed curve in Figure 12a corresponding to the contact failure stage at F < 0 N). In this case, the dependencies F(d) can no longer be satisfactorily described using the classical JKR theory [23], but it remains possible to perform computer simulations, for example, in the framework of the boundary element [55] or finite element [56] methods. Note that the simulations performed in [55] also showed an increase and then a decrease in the adhesive strength of the contact with increasing indenter surface roughness.
In experimental work [34], an increase and a subsequent decrease of adhesive strength with increasing indenter surface roughness were observed for indenters with radii R = 40, 50, and 100 mm, while no such dependence on roughness was observed for an indenter with radius R = 30 mm. We attribute this to the fact that for indenters with small radii, the adhesive strength |Fmin| due to the small size of the contact spot depends not on the averaged roughness parameters but on the individual properties of the roughness directly in the center of the contact zone. That is, for contacts of small sizes, the problem loses its statistical meaning, and the establishment of general regularities with decreasing indenter radius becomes impossible. In real mechanisms, surface roughness is formed as a result of wear and complex physico-chemical processes, so the contacting surfaces have much more pronounced heterogeneous properties, further complicating the analysis.
Simulations of the indentation process for the case of a rough indenter surface are not carried out in this paper since such modeling is a separate, difficult task, primarily due to the complexity of measuring the real indenter profile. Therefore, there are many unresolved issues in modeling the adhesive contact of real rough surfaces. For example, in [34], we never managed to experimentally establish a parameter characterizing the roughness of the indenter surface, on which the adhesive strength of the contact would depend. Although both experiments [34] and computer simulations [55] suggest that such a parameter exists.
4. Discussion
The dependencies of |Fmin| and ΔW on the sandpaper number, with the decrease of which the amplitude of the indenter surface roughness increases, are visually similar to each other. This implies the existence of some regularity between |Fmin| and ΔW. To explain this pattern, Figure 13 is shown in panels (a) and (b), where the dependences of adhesive strength |Fmin| and ΔW in the first indentation cycles for indenters of different radii R from [34] are shown.
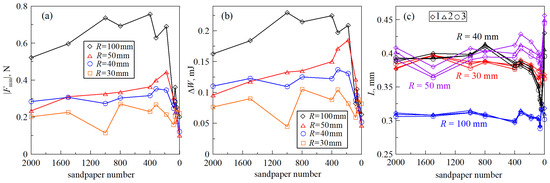
Figure 13.
(a) dependencies of the adhesive strength of contact |Fmin| on the sandpaper number used to create the indenter roughness. Dependences marked with different symbols correspond to the first indentation cycles for indenters with different radii R, the values of which are shown in the figure; (b) calculated dependencies of energy dissipation corresponding to the dependences shown in panel (a); (c) dependencies of the ratio of energy dissipation ΔW to the adhesive strength of contact |Fmin| (8).
As discussed earlier in the description of Figure 12, the above dependencies initially show an increase in the values of |Fmin| and ΔW with increasing roughness amplitude, followed by a decrease. This tendency, however, is violated in the case of the indenter with the smallest radius, R = 30 mm, the reasons for which are described above. Figure 13c shows the ratios of energy dissipation ratios ΔW to adhesive strength |Fmin|, where for each indenter the results of all three indentation cycles are plotted; the results of the first indentation cycles are displayed in Figure 13a,b. Since the ratio ΔW/|Fmin| has the dimension of length, let us introduce some “characteristic length” L:
From Figure 13c, it can be observed that the value of L (8) does not depend on the indenter roughness as well as on the indentation cycle number and remains approximately constant at moderate roughnesses: for an indenter with radius R = 100 mm, we have L ≈ 0.3 mm; for all other cases, L ≈ 0.4 mm. These values of L correspond exactly to the maximum indentation depths dmax in the corresponding experiments (see [35]). The smaller value of L for the indenter with radius R = 100 mm was chosen to reduce the value of the normal force F at d = dmax, as it increases with the indenter radius. It follows that L in (8) corresponds to the maximum indentation depth dmax, but only when the indenter roughness is not extremely large. When the roughness exceeds a critical value, the F(d) dependencies are no longer described by JKR curves since the contact becomes non-simply connected and stable contact configurations appear in the process of indenter detachment (see curve “P0” in Figure 12a). In total, Figure 13c shows the results for 4 different indenters, each showing the results of 11 experiments with different roughnesses, with 3 indenting cycles in each case. Thus, the figure shows the results of 4 × 11 × 3 = 132 experiments that confirm the empirical relationship (8). The validity of formula (8) is also proved by the results of [33], in which the effect of contact duration on its adhesive strength was studied. At the same time, the maximum indentation depth in the experiments described in [33] was dmax = 0.2 mm. Thus, the study has shown that the value of mechanical energy dissipation in a complete indentation–detachment cycle can be estimated using a simple empirical relationship [33]
if the maximum indentation depth dmax and the adhesive strength of the contact |Fmin| are known.
To analyze the applicability region of the phenomenological Equation (9), the relations L = ΔW/|Fmin| (8) were determined for all experiments described in this paper. The results obtained are shown in Figure 14.
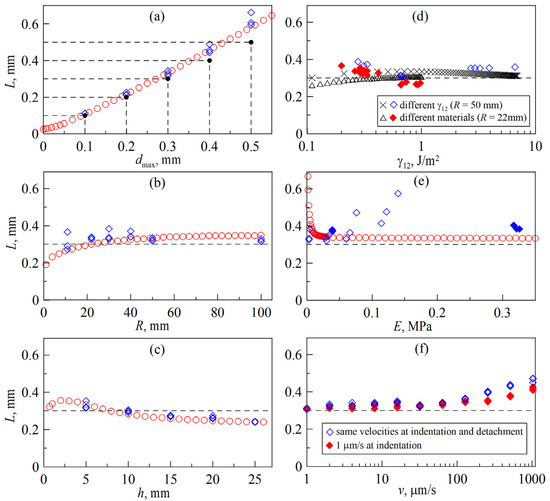
Figure 14.
Dependencies of energy dissipation ratio ΔW to adhesive strength |Fmin| (characteristic lengths L = ΔW/|Fmin| (8)) on indentation depth dmax (a), indenter radius R (b), elastomer thickness h (c), specific work of adhesion γ12 (d), elastomer elastic modulus E (e), and indenter velocity v (f). Diamonds (empty and shaded) show the experimental results; other symbols (circles, crosses, triangles) show the simulation results.
Figure 14a shows the dependence of the parameter L on the indentation depth dmax corresponding to the experiment, the results of which are demonstrated in Figure 3. Here, the diamonds show the experimental results, and the circles show the BEM simulation results. At the intersection of each pair of horizontal and vertical dashed lines shown in the figure, there are points that satisfy Equation (9), since at these points L = dmax. From the dependencies L(dmax) shown in Figure 14a, it is evident that the validity of the approximation (9) diminishes as dmax increases. Figure 14a shows that the experimental results agree with the simulation results over the entire range of dmax depths, while the empirical relation (9) is applicable at dmax ≤ 0.3 mm. Note that all other panels of Figure 14 show experimental results in which the indentation depth is dmax = 0.3 mm.
Figure 14b,c show the dependencies of the value of L on the indenter radius R (corresponding to the experimental dependences in Figure 4) and the elastomer thickness h (corresponding to Figure 5). Here, the approximation (9) works satisfactorily for all cases considered. However, in both figures, the experimental results show much better agreement with the simulation results than with the approximation (9); the same is realized in Figure 14a.
Figure 14d (see also Figure 6 and Figure 7) shows the dependencies of the characteristic length L on the specific work of adhesion γ12, where the abscissa axis is presented in logarithmic coordinates for easy visualization of the results. In the figure, empty diamonds show the results of an experiment in which chemical treatment of the indenter surface was performed in order to vary γ12 (see Figure 6). The filled diamonds correspond to a series of experiments in which thin layers of different metals were deposited on the indenter surface. All experimental data presented in Figure 14d (all 29 experiments) show both satisfactory performance of approximation (9) and agreement with the simulation results (crosses and triangles). The crosses correspond to the simulation of the indentation of an indenter with a radius R = 50 mm, and the triangles corresponding to an indenter with a radius R = 22 mm. Exactly such indenters were used in the two series of experiments presented in the article.
From Figure 14e (see experimental Figure 8), it can be seen that the experimental data (diamonds) deviate significantly from both the empirical expression (9) and the BEM simulation results (circles). The reasons for this deviation were discussed above in the descriptions of Figure 8 and Figure 9, where the mismatch between the experimental and simulation results is analyzed. The point is that in experiments with fixed indentation depth dmax according to the phenomenological relations (8) and (9), the ratio ΔW/|Fmin| must be conserved since we take ΔW/|Fmin| = dmax. Therefore, as |Fmin| increases, the energy dissipation ΔW must increase. However, as Figure 9 demonstrates, increasing the adhesive strength |Fmin| does not always lead to an increase in the dissipation of mechanical energy ΔW, at least, this is what the results of the computer simulations show. The question of the relationship between adhesive strength and mechanical energy dissipation in a complete indentation–detachment cycle under variation of the elastic modulus of the elastomer requires a more thorough study, which is beyond the scope of the present work.
And the last Figure 14f shows the values of the ratio L corresponding to experiments in which the effect of indenter velocity was studied (see Figure 10 and Figure 11). Here, the empty diamonds show the results corresponding to the case of indenter motion in the indentation and detachment phases with the same velocities (see Figure 10), and the filled diamonds indicate the values of L in the experiments in which the indenter velocity in the indentation phase was always v = 1 µm/s, i.e., quasi-static contact propagation (see Figure 11). Both cases demonstrate that the empirical Equation (9) is satisfactorily satisfied for velocities v < 64 µm/s.
From the analysis of Figure 14 presented in this subsection, we can conclude that Equation (9) holds at low indenter velocities v and indentation depths dmax. However, there are ranges of elastomer thickness h, indenter radius R, and elastic modulus E at which (9) is valid. For example, if R and E become less than some critical values, Equation (9) becomes inapplicable. Note also that in all cases considered in Figure 14, the experimental results match much better with the BEM simulation results than with the approximation (9). Therefore, if in the study of a particular system there is no information about the range of parameters in which the relation (9) is valid, it is advisable to perform BEM simulations to estimate the magnitude of dissipation and adhesive strength. However, BEM may also require unknown parameters, such as the specific work of adhesion γ12, which can vary significantly between different indentation cycles while keeping the other experimental parameters (indenter radius, indentation depth, elastomer modulus, etc.) constant.
5. Conclusions
This paper describes the results of a series of experiments in which the adhesive properties of normal contact between a spherical steel indenter and a much softer elastomer sheet were studied. The dependences of adhesive strength of contact and mechanical energy dissipation in the complete indentation–detachment cycle on the geometrical parameters of the experiment (maximum indentation depth, elastomer thickness, contact radius, indenter roughness), elastic parameters (elastomer elastic modulus), chemical properties of the contacting bodies (surface energies, which set the specific work of adhesion), and the velocity of indenter motion were analyzed. It was shown that, in a wide range of experimental parameters, the dissipation of mechanical energy is determined with sufficient accuracy by the product of the maximum indentation depth and the adhesive strength of the contact. The adhesive strength is understood here as the maximum absolute value of the negative normal force |Fmin| on the force-depth F(d) dependences in the contact failure region. With the empirical relationship found, it is possible to accurately estimate the rate of energy dissipation, which facilitates the optimization of materials and processes in applications that require precise control of dissipated energy, such as damping devices or shock absorption systems. It was found that the dependence of the adhesive strength on the elastic modulus of the elastomer is nonlinear, and there is some optimal value of the elastic modulus that provides the maximum adhesive strength of the contact. This feature, however, is realized only for the contact of the indenter with an elastic layer of finite thickness, since for the half-space there is no dependence of the adhesive strength on the elastic modulus.
Author Contributions
Conceptualization, scientific supervision, project administration, writing—review and editing, V.L.P.; methodology, hardware, software, conducting experiments, simulations, experimental and theoretical data analysis, visualization, validation, writing—original draft preparation, I.A.L.; analysis of literary sources for the introduction section, writing—original draft preparation, T.H.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deutsche Forschungsgemeinschaft (Project DFG PO 810-55-3).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated for this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kinloch, A.J. Adhesion and Adhesives. Science and Technology, 1st ed.; Springer: Dordrecht, The Netherlands, 1987; 442p, ISBN 978-0-412-27440-4. [Google Scholar] [CrossRef]
- Gorb, S. Adhesion and Friction in Biological Systems; Springer: Dordrecht, The Netherlands, 2012; 280p, ISBN 9789400714441. [Google Scholar]
- Dening, K.; Heepe, L.; Afferrante, L.; Carbone, G.; Gorb, S.N. Adhesion control by inflation: Implications from biology to artificial attachment device. Appl. Phys. 2014, 116, 567–573. [Google Scholar] [CrossRef]
- Zhang, Y.; Sundararajan, S. Adhesion and friction studies of silicon surfaces processed using a microparticle-based method. Tribol. Lett. 2006, 23, 1–5. [Google Scholar] [CrossRef]
- Kennedy, F.E.; Lidhagen, D.; Erdemir, A.; Woodford, J.B.; Kato, T. Tribological behavior of hard carbon coatings on steel substrates. Wear 2003, 255, 854–858. [Google Scholar] [CrossRef]
- Maboudian, R.; Ashurst, W.R.; Carraro, C. Self-assembled monolayers as anti-stiction coatings for MEMS: Characteristics and recent developments. Sens. Actuators A Phys. 2000, 82, 219–223. [Google Scholar] [CrossRef]
- Cammarano, A.; De Luca, G.; Amendola, E. Surface modification and adhesion improvement of polyester films. Cent. Eur. J. Chem. 2013, 11, 35–45. [Google Scholar] [CrossRef]
- Maboudian, R.; Ashurst, W.R.; Carraro, C. Tribological challenges in micromechanical systems. Tribol. Lett. 2002, 12, 95–100. [Google Scholar] [CrossRef]
- Yapu, Z. Stiction and anti-stiction in MEMS and NEMS. Acta Mech. Sin. 2003, 19, 1–10. [Google Scholar] [CrossRef]
- Tas, N.; Sonnenberg, T.; Jansen, H.; Legtenberg, R.; Elwenspoek, M. Stiction in surface micromachining. J. Micromech. Microeng. 1996, 6, 385–397. [Google Scholar] [CrossRef]
- Bose, S.; Robertson, S.F.; Bandyopadhyay, A. Surface modification of biomaterials and biomedical devices using additive manufacturing. Acta Biomater. 2018, 66, 6–22. [Google Scholar] [CrossRef]
- Yazawa, S.; Minami, I.; Prakash, B. Reducing Friction and Wear of Tribological Systems through Hybrid Tribofilm Consisting of Coating and Lubricants. Lubricants 2014, 2, 90–112. [Google Scholar] [CrossRef]
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Autumn, K.; Gravish, N. Gecko adhesion: Evolutionary nanotechnology. Philos. Trans. R. Soc. 2008, 366, 1575–1590. [Google Scholar] [CrossRef]
- Shirtcliffe, N.J.; McHale, G.; Newton, M.I. Wet Adhesion and Adhesive Locomotion of Snails on Anti-Adhesive Non-Wetting Surfaces. PLoS ONE 2012, 7, e36983. [Google Scholar] [CrossRef]
- Hori, K.; Matsumoto, S. Bacterial adhesion: From mechanism to control. Biochem. Eng. J. 2010, 48, 424–434. [Google Scholar] [CrossRef]
- Straub, H.; Bigger, C.M.; Valentin, J.; Abt, D.; Qin, X.-H.; Eberl, L.; Maniura-Weber, K.; Ren, Q. Bacterial Adhesion on soft Materials: Passive Physicochemical Interactions or Active Bacterial Mechanosensing. Adv. Healthc. Mater. 2019, 8, 1801323. [Google Scholar] [CrossRef]
- Quirynen, M.; Bollen, C.M.L. The influence of surface roughness and surface-free energy on supra- and subgingival plaque formation in man. J. Clin. Periodontol. 1995, 22, 1–14. [Google Scholar] [CrossRef]
- Aghababaei, R.; Brodsky, E.E.; Molinari, J.F.; Chandrasekar, S. How roughness emerges on natural and engineered surfaces. MRS Bull. 2022, 47, 1229–1236. [Google Scholar] [CrossRef]
- Pogrebnjak, A.D.; Borisyuk, V.N.; Bagdasaryan, A.A.; Maksakova, O.V.; Smirnova, E.V. The multifractal investigation of surface microgeometry of (Ti-Hf-Zr-V-Nb)N nitride coatings. J. Nano Electron. Phys. 2014, 6, 04018. [Google Scholar]
- Schuh, C.A. Nanoindentation studies of materials. Mater. Today 2006, 9, 32–40. [Google Scholar] [CrossRef]
- Bull, S.J. Nanoindentation of coatings. J. Phys. D Appl. Phys. 2005, 38, R393–R413. [Google Scholar] [CrossRef]
- Johnson, K.L.; Kendall, K.; Roberts, A.D. Surface energy and the contact of elastic solids. Proc. R. Soc. Lond. A 1971, 324, 301–313. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A. Adhesive Contact of Elastic Bodies: The JKR Theory. In Encyclopedia of Tribology; Wang, Q.J., Chung, Y.W., Eds.; Springer: Boston, MA, USA, 2013; pp. 43–49. [Google Scholar] [CrossRef]
- Derjaguin, B.V.; Muller, V.M.; Toporov, Y.P. Effect of contact deformations on the adhesion of particles. J. Colloid Interface Sci. 1975, 53, 314–326. [Google Scholar] [CrossRef]
- Greenwood, J.A. Derjaguin and the DMT Theory: A Farewell to DMT? Tribol. Lett. 2022, 70, 61. [Google Scholar] [CrossRef]
- Woerdeman, D.L.; Amouroux, N.; Ponsinet, V.; Jandeau, G.; Hervet, H.; Léger, L. Characterization of glass-epoxy adhesion using JKR methods and atomic force microscopy. Compos. Part A Appl. Sci. Manuf. 1999, 30, 95–109. [Google Scholar] [CrossRef]
- Prokopovich, P.; Perni, S. Comparison of JKR- and DMT-based multi-asperity adhesion model: Theory and experiment. Colloids Surf. A Physicochem. Eng. Asp. 2011, 383, 95–101. [Google Scholar] [CrossRef]
- Maugis, D. Adhesion of spheres: The JKR-DMT-transition using a Dugdale model. J. Colloid Interface Sci. 1992, 150, 243–269. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Baek, D.; Hemthavy, P.; Saito, S.; Takahashi, K. Evaluation of energy dissipation involving adhesion hysteresis in spherical contact between a glass lens and a PDMS block. Appl. Adhes. Sci. 2017, 5, 4. [Google Scholar] [CrossRef]
- Greenwood, J.A. Reflections on and extensions of the Fuller and Tabor theory of rough surface adhesion. Tribol. Lett. 2017, 65, 159. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L. Hysteresis in an adhesive contact upon a change in the indenter direction of motion: An experiment and phenomenological model. Tech. Phys. 2021, 66, 611–629. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Pohrt, R. Adhesion between rigid indenter and soft rubber layer: Influence of roughness. Front. Mech. Eng. 2020, 6, 49. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L. Dissipation of mechanical energy in an oscillating adhesive contact between a hard indenter and an elastomer. Tech. Phys. Lett. 2020, 46, 1092–1095. [Google Scholar] [CrossRef]
- Hsu, C.P.; Mandal, J.; Ramakrishna, S.N.; Spencer, N.D.; Isa, L. Exploring the roles of roughness, friction and adhesion in discontinuous shear thickening by means of thermo-responsive particles. Nat. Commun. 2021, 12, 1477. [Google Scholar] [CrossRef] [PubMed]
- Park, J.Y.; Salmeron, M. Fundamental Aspects of Energy Dissipation in Friction. Chem. Rev. 2014, 114, 677–711. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Pohrt, R.; Lyashenko, I.A.; Popov, V.L. Boundary element method for nonadhesive and adhesive contacts of a coated elastic half-space. Proc. Inst. Mech. Eng. J J. Eng. Tribol. 2020, 234, 73–83. [Google Scholar] [CrossRef]
- Polonsky, I.A.; Keer, L.M. A numerical method for solving rough contact problems based on the multi-level multi-summation and conjugate gradient techniques. Wear 1999, 231, 206–219. [Google Scholar] [CrossRef]
- Pohrt, R.; Li, Q. Complete boundary element formulation for normal and tangential contact problems. Phys. Mesomech. 2014, 17, 334–340. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L.; Borysiuk, V. Experimental verification of the boundary element method for adhesive contacts of a coated elastic half-space. Lubricants 2023, 11, 84. [Google Scholar] [CrossRef]
- Deng, W.; Kesari, H. Depth-dependent hysteresis in adhesive elastic contacts at large surface roughness. Sci. Rep. 2019, 9, 1639. [Google Scholar] [CrossRef]
- Lyashenko, I.A.; Popov, V.L. The effect of contact duration and indentation depth on adhesion strength: Experiment and numerical simulation. Tech. Phys. 2020, 65, 1695–1707. [Google Scholar] [CrossRef]
- Papangelo, A. Adhesion between a power-law indenter and a thin layer coated on a rigid substrate. Facta Univ. Ser. Mech. Eng. 2018, 16, 19–28. [Google Scholar] [CrossRef]
- Yang, F. Asymptotic solution to axisymmetric indentation of a compressible elastic thin film. Thin Solid Films 2006, 515, 2274–2283. [Google Scholar] [CrossRef]
- Liu, J.-L.; Xia, R. A unified analysis of a micro-beam, droplet and CNT ring adhered on a substrate: Calculation of variation with movable boundaries. Acta Mech. Sin. 2013, 29, 62–72. [Google Scholar] [CrossRef]
- Wang, H.; Jacobi, F.; Waschke, J.; Hartmann, L.; Löwen, H.; Schmidt, S. Elastic modulus dependence on the specific adhesion of hydrogels. Adv. Funct. Mater. 2017, 27, 1702040. [Google Scholar] [CrossRef]
- Li, Q.; Lyashenko, I.A.; Pohrt, R.; Popov, V.L. Influence of a Soft Elastic Layer on Adhesion of Rough Surfaces. In Contact Problems for Soft, Biological and Bioinspired Materials; Springer: Berlin/Heidelberg, Germany, 2022; pp. 93–102. [Google Scholar] [CrossRef]
- Violano, G.; Chateauminois, A.; Afferrante, L. A JKR-Like solution for viscoelastic adhesive contacts. Front. Mech. Eng. 2021, 7, 664486. [Google Scholar] [CrossRef]
- Gent, A.N.; Petrich, P.R. Adhesion of viscoelastic materials to rigid substrates. Proc. R. Soc. A 1969, 310, 433–448. [Google Scholar] [CrossRef]
- Kusche, S. The boundary element method for viscoelastic material applied to the oblique impact of spheres. Facta Univ. Ser. Mech. Eng. 2016, 14, 293–300. [Google Scholar] [CrossRef][Green Version]
- Putignano, C.; Carbone, G. A Review of Boundary Elements Methodologies for Elastic and Viscoelastic Rough Contact Mechanics. Phys. Mesomech. 2014, 17, 321–333. [Google Scholar] [CrossRef]
- Kang, H. Using the Boundary Element Method to Simulate Visco-Elastic Deformations of Rough Fractures. In Recent Developments in the Solution of Nonlinear Differential Equations; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Forsbach, F. A Simple Semi-Analytical Method for Solving Axisymmetric Contact Problems Involving Bonded and Unbonded Layers of Arbitrary Thickness. Machines 2023, 11, 474. [Google Scholar] [CrossRef]
- Li, Q.; Pohrt, R.; Popov, V.L. Adhesive strength of contacts of rough spheres. Front. Mech. Eng. 2019, 5, 7. [Google Scholar] [CrossRef]
- Bugnicourt, R.; Sainsot, P.; Dureisseix, D.; Gauthier, C.; Lubrecht, A.A. FFT-Based Methods for Solving a Rough Adhesive Contact: Description and Convergence Study. Tribol. Lett. 2018, 66, 29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).