Residual Stresses of 316L Stainless Steel Laser Direct Metal During Pulsed-Wave and Continuous-Wave Laser Additive Manufacturing: A Comparative Study

Abstract

Continuous-wave laser (CW) and pulsed-wave laser (PW) are the two laser modes in direct energy deposition (DED). This paper mainly reports on a study into the effects of the two laser modes on residual stresses with a given energy input. The contour method (CM) with non-uniform spatial distribution of inspection points was used to capture residual stress distributions in DED of Fe3000 on a substrate made of 316L stainless steel. Residual stresses in the transition zone between the deposit and the substrate were carefully examined to gain an understanding of cracks frequently observed at the connection between the substrate and the deposit. Furthermore, X-ray diffraction, along with successive material removal, was used to reveal residual stresses at various depths in the substrate. The results showed that significant tensile longitudinal stresses developed at the substrate–deposit junction for both CW and PW laser modes. It increased sharply (about 64%) with the increase in energy input for CW mode, while it showed the opposite trend for PW mode; the longitudinal residual stress decreased 13.2% with the increase in energy input. PW, however, introduced lower residual stress than that of CW under the condition of high-energy input; the maximum longitudinal residual stress decreased by about 10.4% compared to CW mode. This was due to stress relaxation at high-energy inputs in PW mode. In addition, residual stresses were found to be higher than the initial yield stress, and yielding occurred in the deposited part. The results determined by the CM and X-ray diffraction depth profiling were found to be consistent.

1. Introduction

Direct energy deposition (DED) uses a high-energy-density laser beam as a heat source to form a molten pool by laser action on a substrate and powder material, which is then solidified and formed in a single layer and then formed into a three-dimensional solid part by a “layer-by-layer” build-up manufacturing method. In the DED process, the thermal mechanism between the heat source and the material is extremely complex, and the thermophysical process is difficult to control and has many influencing factors, resulting in large residual stresses within the molded part. Tensile residual stresses in deposited structures compromise structural integrity and service performance due to the formation and initiation of cracks [1,2]. Especially in the heat-affected zone, the large tensile residual stress at the connection between the substrate and the deposit along the laser scanning direction can cause cracking at the deposited material’s root. This phenomenon has been recorded in Figure 1. Figure 1a is the cracking phenomenon of the deposited materials during DED. Figure 1b is a scanning electron microscope (SEM) image of 200 times magnification at the transverse section of the substrate and deposit after DED. At the connection between the substrate and the deposit, there exist a large number of micro-cracks. Therefore, accurate characterization of the residual stress of the substrate and the deposit is of great significance to determine how to eliminate micro-cracks in the workpiece. Reducing and homogenizing the residual stress at the connection between the substrate and the deposit is a key measure to eliminate micro-cracks in the workpiece.

Many scholars have proposed methods to reduce residual stress from the perspectives of reducing temperature gradients and releasing stress through post-processing. You et al. [3] eliminated some of the residual stresses by reducing the laser power and increasing the scanning speed. At the same time, they also investigated the effect of process parameters such as laser incidence angle and cladding material on residual stresses. Amandas et al. [4] concluded that the line energy density is inversely correlated with the residual stress. He also investigated the effect of scanning path on residual stress, and the continuous scanning strategy significantly reduced the residual stress by 39% compared to the island scanning strategy. However, Michael et al. [5] concluded that the island scanning path in tool steels is more effective (about 30%) in reducing residual stresses. Denlinger [6] investigated the effect of interlayer residence time on residual stresses in Ti6Al4V and Inconel 625. In the case of Inconel 625, increasing the residence time was beneficial in reducing the residual stresses, whereas in the case of Ti6Al4V, reducing the interlayer residence time reduced the residual stress. A dimensionless model for predicting the temperature gradient during additive manufacturing was proposed by Michelle [7], who used the model to investigate the relationship between laser power, scanning speed, preheating process, and temperature gradient. At the same time, the study found that the residual stress could be reduced by up to 20% by varying the process parameters of the laser itself (laser power and scanning speed). The preheating process is the most important means of reducing residual stresses, as it can reduce the involved tensile stresses to 60% of the original peak value. Shiomi et al. [8] performed heat treatment and laser repetitive scanning of chromium–molybdenum steel laser additively fabricated specimens to reduce the residual stresses by about 70% and 55%, respectively. Pruk [9] and Martina [10] used a localized preheating process and a rolling technique to reduce the residual stresses in rectangular thin-walled 304 stainless steel parts by 30% and 50%. However, most researchers have controlled the residual stresses of laser additively manufactured specimens by controlling the laser processing parameters (e.g., laser power and scanning speed) and some external processing techniques (e.g., laser scanning strategy, preheating, etc.). Few articles have investigated the effect of changes in laser modulation mode on residual stress.

Pulsed-wave (PW) laser mode with periodic heating–cooling circulation heat process (hot scheduling) performs better compared to continuous wave (CW) laser mode, which causes the temperature of the molten pool to change periodically [11,12]. PW can effectively reduce the temperature gradient in the heat-affected zone during laser processing. At the same time, it can lead to lower heat accumulation and a higher cooling rate, forming residual stresses that are different from those in the traditional CW processing of deposited parts [12]. The main aim of this work was to study the deformation and residual stress fields using CW and PW modes with constant total energy input. The longitudinal residual stress in the depth direction of the substrate was characterized using a contour method introduced by DED. This is a well-known method for measuring residual stress in the cutting section of the workpiece [13,14], where the cutting section deforms due to the release of residual stress perpendicular to the cutting surface [15,16]. The results were compared to X-ray diffraction (the most common nondestructive method of measuring residual stress) at the same locations from the substrate centerline. Meanwhile, the residual stress in the vertical direction was measured by CM as well.

The results of this work show that PW can effectively reduce the residual stress of additively manufactured deposits through continuous remelting to release tensile stress. It provides a new idea for the reduction and elimination of residual stress in additively manufactured deposits and lays a foundation for the improvement of its service performance.

2. Materials and Methods

2.1. Materials and Samples

This experiment employed 316L stainless steel as the substrate material, with the substrate measuring 60 × 60 × 10 mm. The material was Fe3000, and the composition of the powder is presented in

Table 1. The composition of the powder.

Element	B	Cr	Fe	Si	Cu	Mo	Nb	Ni
Percentage	20%	9%	8.5%	3%	7.2%	3%	5%	44.3%

. Prior to the experiments, the powder was processed in a vacuum drying chamber. The temperature of the chamber needed to be adjusted to 100 degrees centigrade within 20 min to guarantee that the moisture within the powder was entirely eliminated. Eight samples were fabricated on a laser direct deposition system. The system was mainly composed of a YLS-4000-CL fiber laser (laser wavelength is 1070 nm), an IRB2400/16 six-axis robot system, a powder feeding system (high-precision powder feeder, coaxial nozzle), and an atmosphere control system.

The formula Q = P × t, in which Q stands for energy input, P denotes laser power, and t indicates laser exit time, was used with the aim of studying the influence of PW scheduling on residual stress under the circumstance of the same energy input. PW pulse cycle time and duty ratio were determined to be 0.1 s (10 Hz pulse frequency) and 50%, respectively. The laser power of PW (600 W for low-energy input/1200 W for high-energy input) was identified as 2 times greater than that of CW (300 W for low-energy input/600 W for high-energy input) to ensure the same energy input. The other conditions were the same. Eight samples were divided into two groups, with each group containing four samples. The process parameters are shown in

Table 2. Laser processing parameters.

Number	CW/PW	Power (W)	Total Energy Input (J)	Scanning Speed (mm/s)	Powder Feeding Rate (g/min)	Number of Layers	Pulse Frequency (HZ)	Duty Ratio
1	CW	300	300	6	10.3	20	/	/
2	CW	600	600	6	10.3	20	/	/
3	PW	600	300	6	10.3	20	10	50%
4	PW	1200	600	6	10.3	20	10	50%

. Each sample generated 20 layers. Each layer was uplifted by 0.1 mm, used a single track, and resulted in 2 mm wide, 4 mm tall, and 60 mm long samples. The rest of the process parameters were as follows: the spot diameter was 1 mm, the protective gas was pure argon, and the control flow rate was 8 L/min.

For the first group, the deposited plate was divided into two parts, with each part providing for the two residual stress measurement methods (contour method (CM) and X-ray diffraction), which were used to measure the longitudinal residual stress of the substrate. CM could achieve a cross-sectional (2-D) map of the residual stress that was normal to the cross section. X-ray diffraction was used to measure and verify the CM results of longitudinal residual stress of the substrate along the depth direction at the same locations from the deposited material’s centerline, as shown in Figure 2. The second group used CM to measure the residual stress in the vertical direction of the deposited materials.

2.2. Residual Stress Measurement

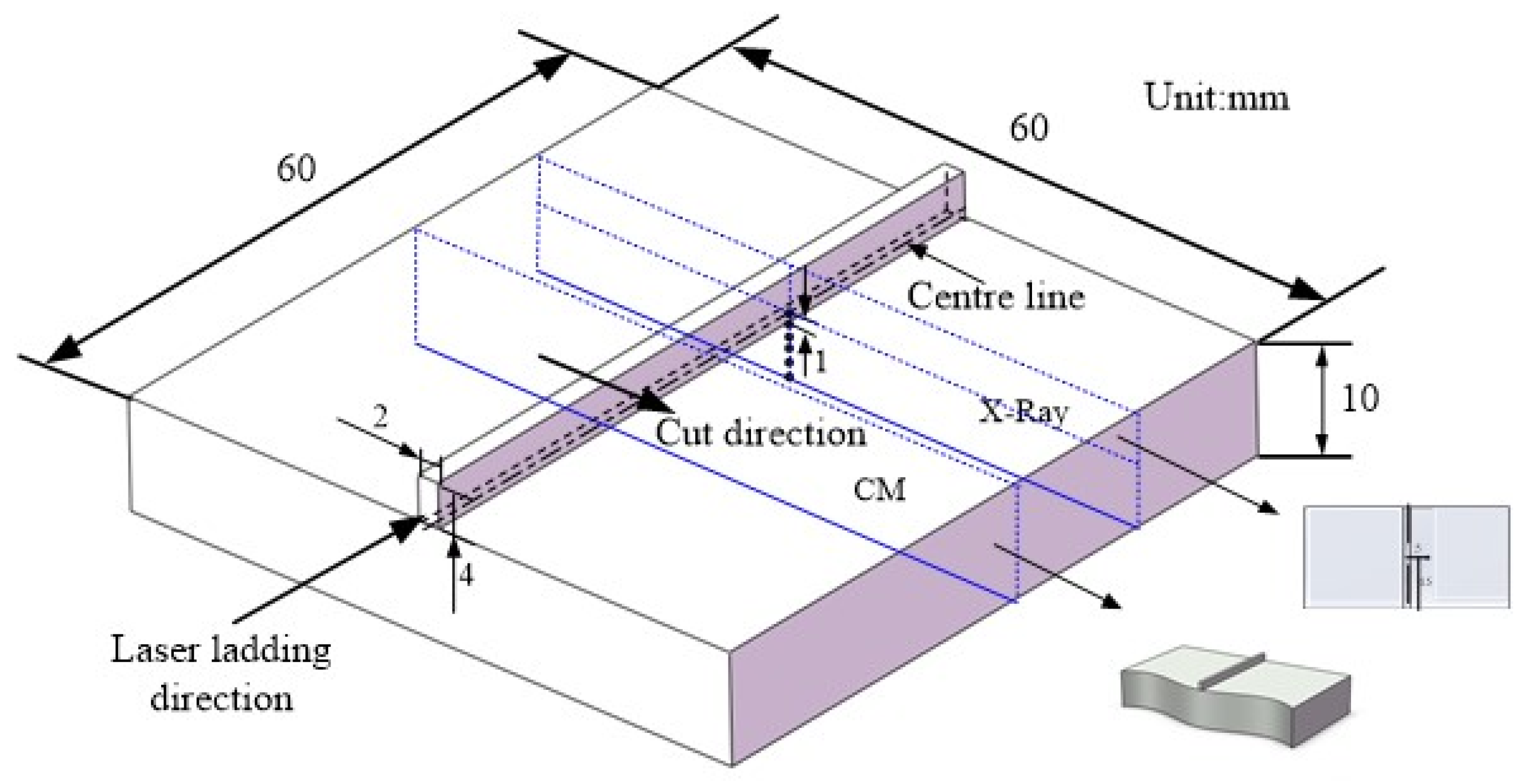
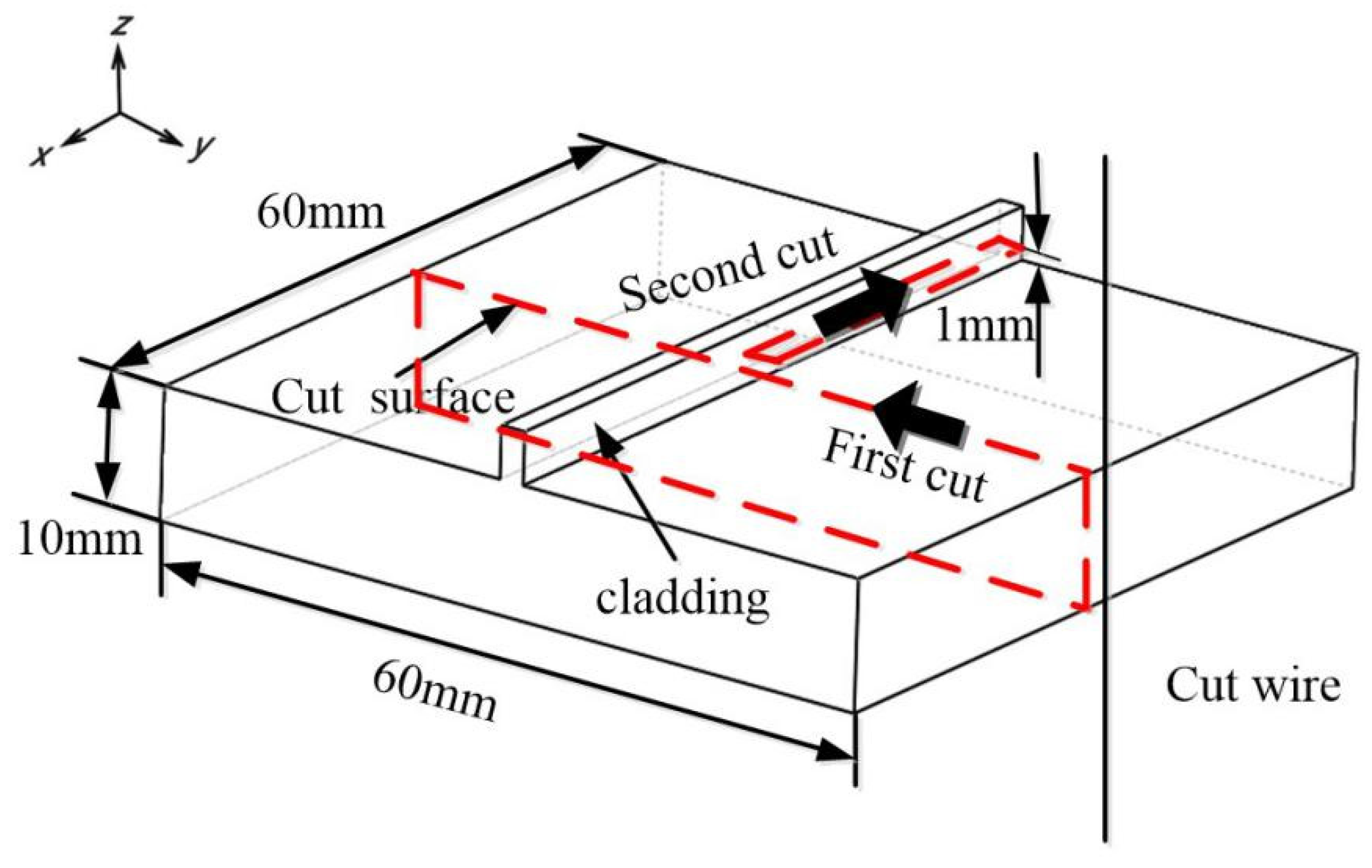
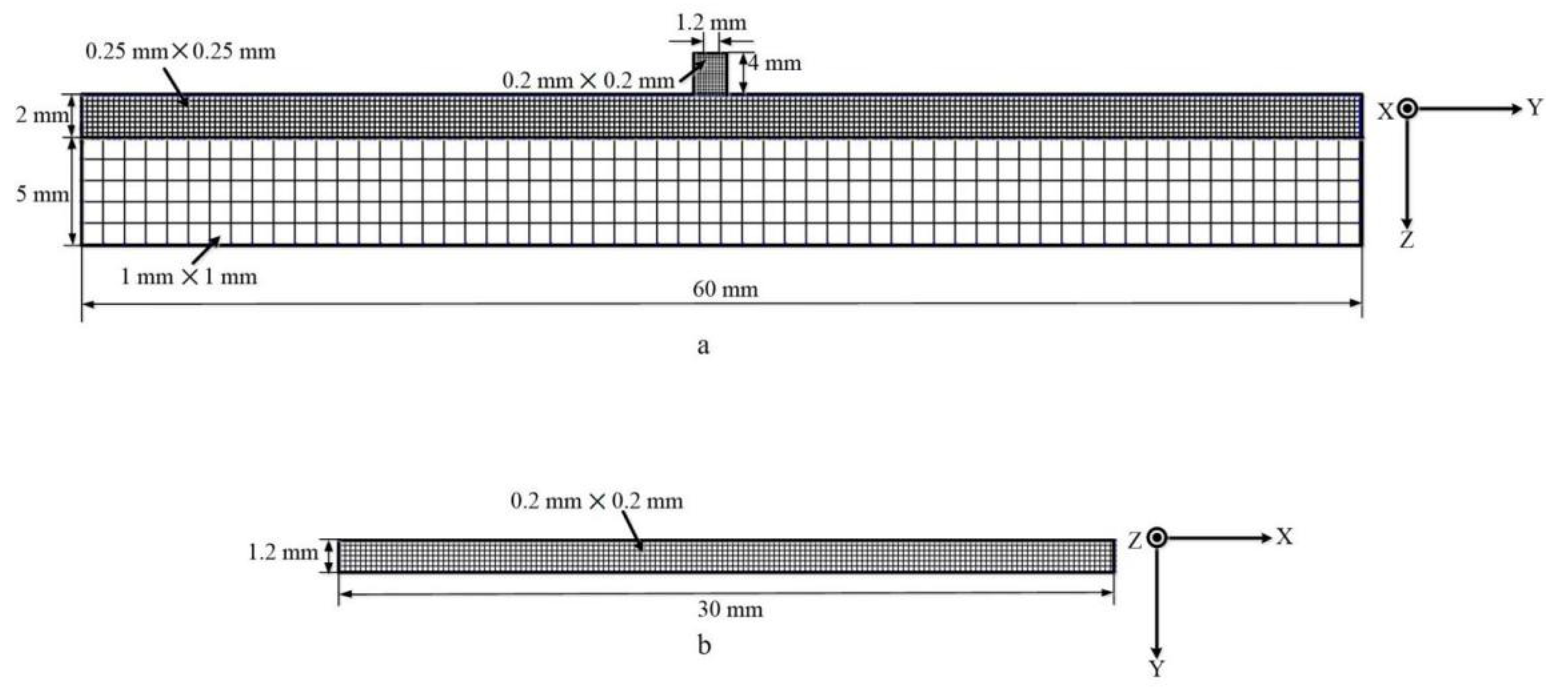
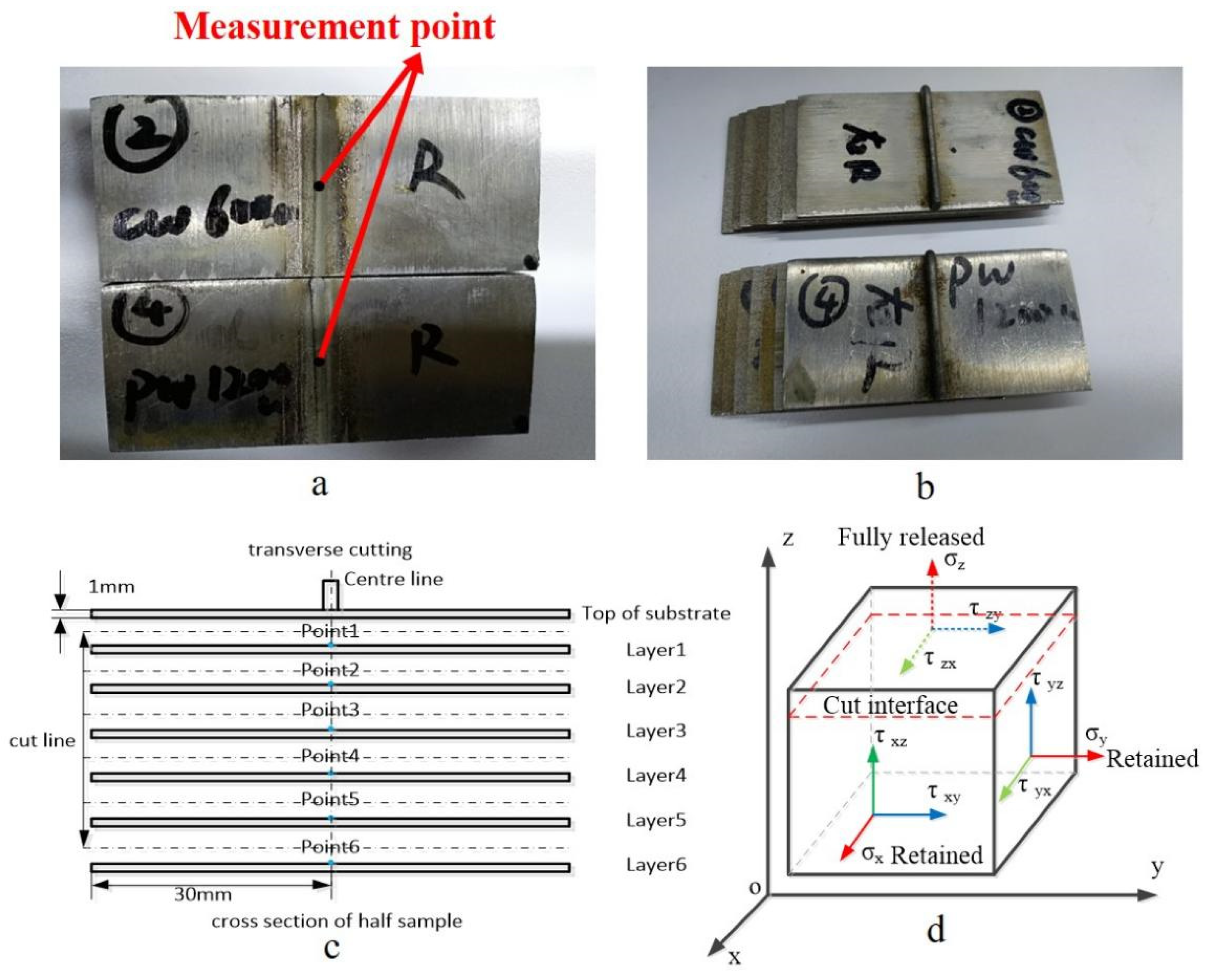
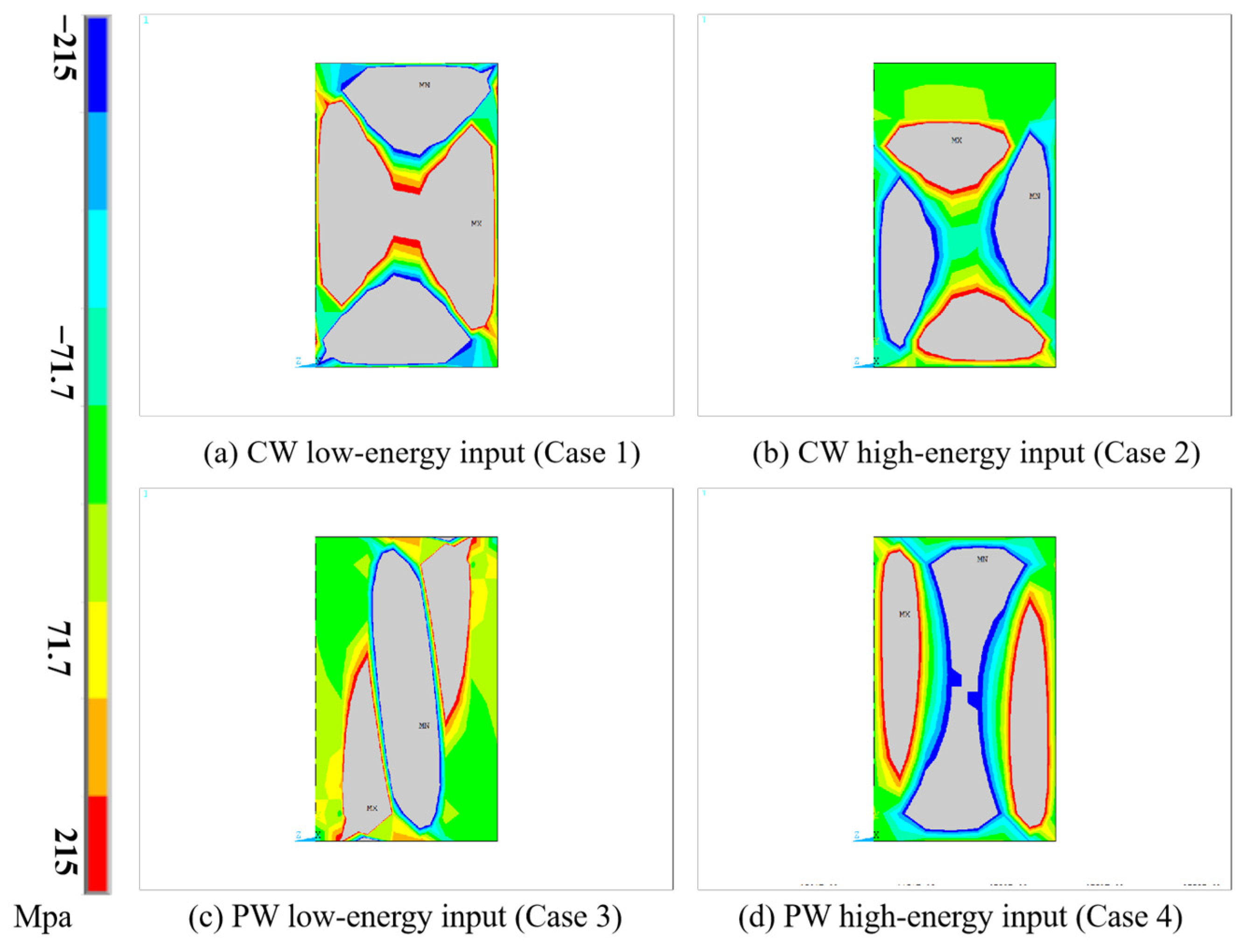
Contour Method

A cross-sectional (2-D) map of the residual stresses perpendicular to the cross section can be furnished using the contour method, which is a workable technique for mapping residual stress. It is based on an elastic superposition principle, according to which residual stresses can be relaxed when slitting the material. CM performs the displacements of the cut surface (the surface contour) compared to an assumed flat surface contour. Then, an opposite of the measured contour displacements is imposed on a finite element model. This process can be divided into three stages: (1) making the cut, (2) measuring the surface, and (3) calculating stress. A detailed description is given in Refs. [17,18].

(1)

Making the cut

Each plate was cut in half using wire EDM with a 100 µm diameter brass wire. The first cut was at the mid-length position, and the whole sample was cut in half. The second cut was at 1 mm above the root of the deposited materials, and half of the sample’s deposited materials were cut, as shown in Figure 3. The specimen was clamped on two sides to prevent specimen movement. A “skim cut” model was selected to minimize any cutting-induced stresses [17].

(2)

Measuring the Surface

The normal displacements of the cutting surfaces of two parts after wire cutting were measured using a coordinate measuring machine manufactured by Hexagon Metrology-EXPLORER-10.21.08 (Hexagon AB Company, Stockholm, Sweden). For the first cut, in order to capture the residual stress at the joint of the substrate and the deposited materials, a non-uniform distribution of inspection points, as shown in Figure 4a, was applied on the cross section to take into account differences in dimensions between the deposited material component and the substrate as well as drastic change in stress near the joint. Measurement spacing between the two inspection points was 0.2 mm. Two resolutions were applied to measure the cross section of the substrate, and the entire measurement areas were set to 60 mm × 7 mm. From the top surface down to 2 mm deep, the measurement spacing was 0.25 mm. Below that, a coarse resolution with the measurement spacing of 1 mm was used. For the second cut, the size of the measure area was set to 1.2 mm × 30 mm, and the measurement spacing was 0.2 × 0.2 mm, as shown in Figure 4b. After measuring the cut surface, the first step in data processing was to make each side of the “cut data” aligned to the same coordinate frame so that the two cut surfaces appeared as mirror images. Therefore, we needed to mirror the data of one of them and then average it. This minimized deviations caused by improper operation of the wire EDM, including surface slanting. By using the smooth method to fit the averaged data, the noise and surface roughness were filtered [18]. Unavoidably, the measured data contain errors on the edge of the surface from cutting and can be ignored.

(3)

Calculating Stress

A 3-D FE model for stress calculation was established for one half of the substrate using ANSYS 15.0. The material was assumed to be homogeneous, isotropic, and linearly elastic with a Young’s modulus of 200 GPa and a Poisson’s ratio of 0.3. The sample model used was brick 8 node 185 meshed with hexahedral elements. The final displacements, after averaging and filtering with opposite signs, were input to an FE model on the finite element surface as displacement boundary conditions. Three additional point boundary conditions were applied to the model to restrain rigid-body motion.

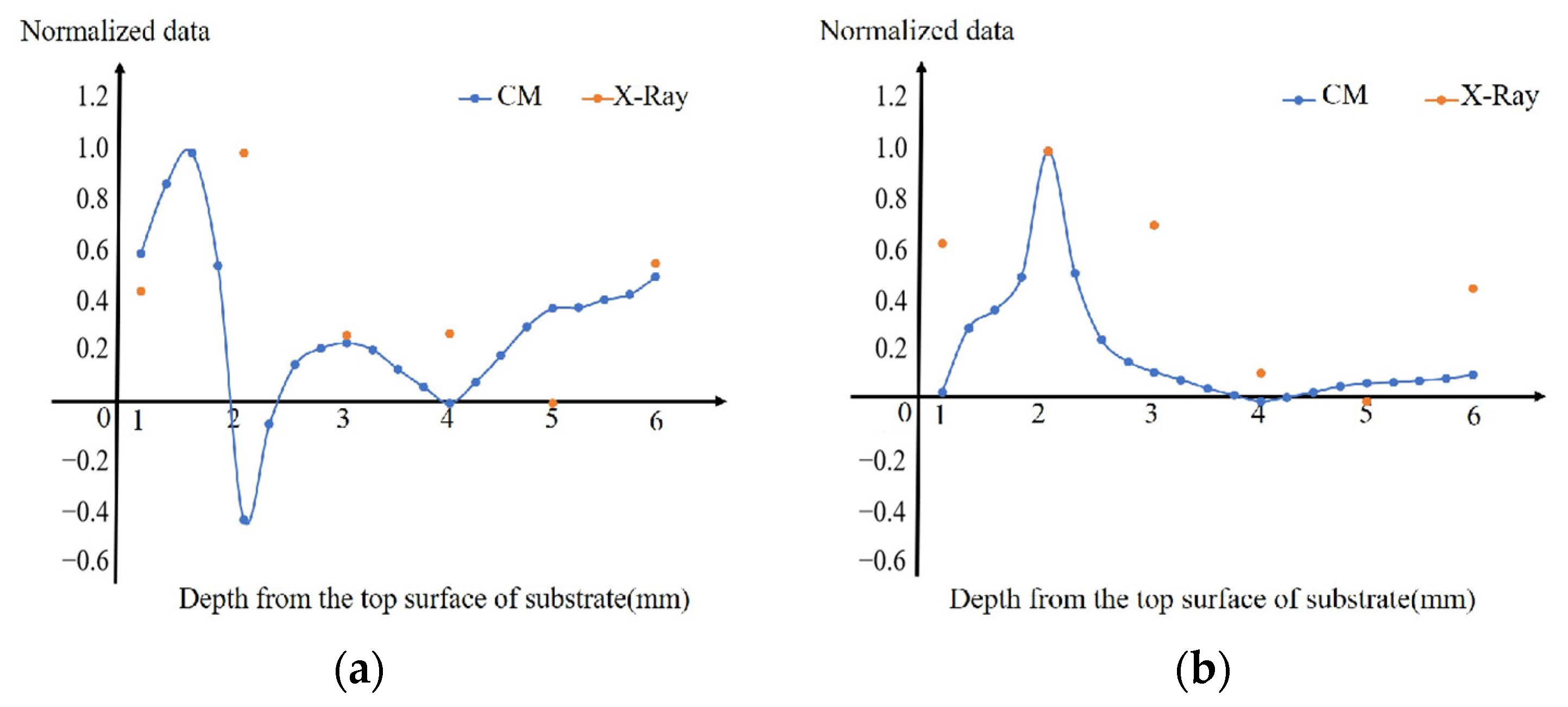
2.3. X-Ray Diffraction

The residual stress was measured using X-ray diffraction as well, which was conducted on the Proto IXRD instrument using Cr Ka radiation. Electropolishing, a method commonly used in successive material removal X-ray diffraction depth profiling, was also used to minimize the introduction of new stresses like wire electrode cutting, which can result in measurement errors in X-ray diffraction experiments. In order to ensure that the error sources introduced by CM and X-ray diffraction were the same, wire electric discharge machining was used to cut half of two samples (Case 2/Case 4) in 6 cross sections, on average, along the longitudinal direction (at 1, 2, 3, 4, 5, and 6 mm from the top surface of the plate). Then, on each section, a point (in the centerline) was measured using X-ray diffraction. Because the measurement point on the top surface of the substrate was too rough, which caused considerable errors when using X-ray diffraction measurement (Figure 5a), we started the measurement point from the second-level cutting surface. The physical map of the samples after transverse cutting is shown in Figure 5b. The schematic diagram measuring the points is identified in Figure 5c. The stress state of the measuring points on the cutting surface is shown in Figure 5d. According to the principle of CM [18], after transverse cutting, the vertical principal stress perpendicular to the cutting surface (σz) can be completely released, and the remaining two directions of principal stress (transverse principal stress (σx) and longitudinal principal stress (σy)) can be preserved. Therefore, the longitudinal residual stress (σx) along the vertical direction of the substrate was measured by X-ray diffraction with transverse cutting.

3. Results

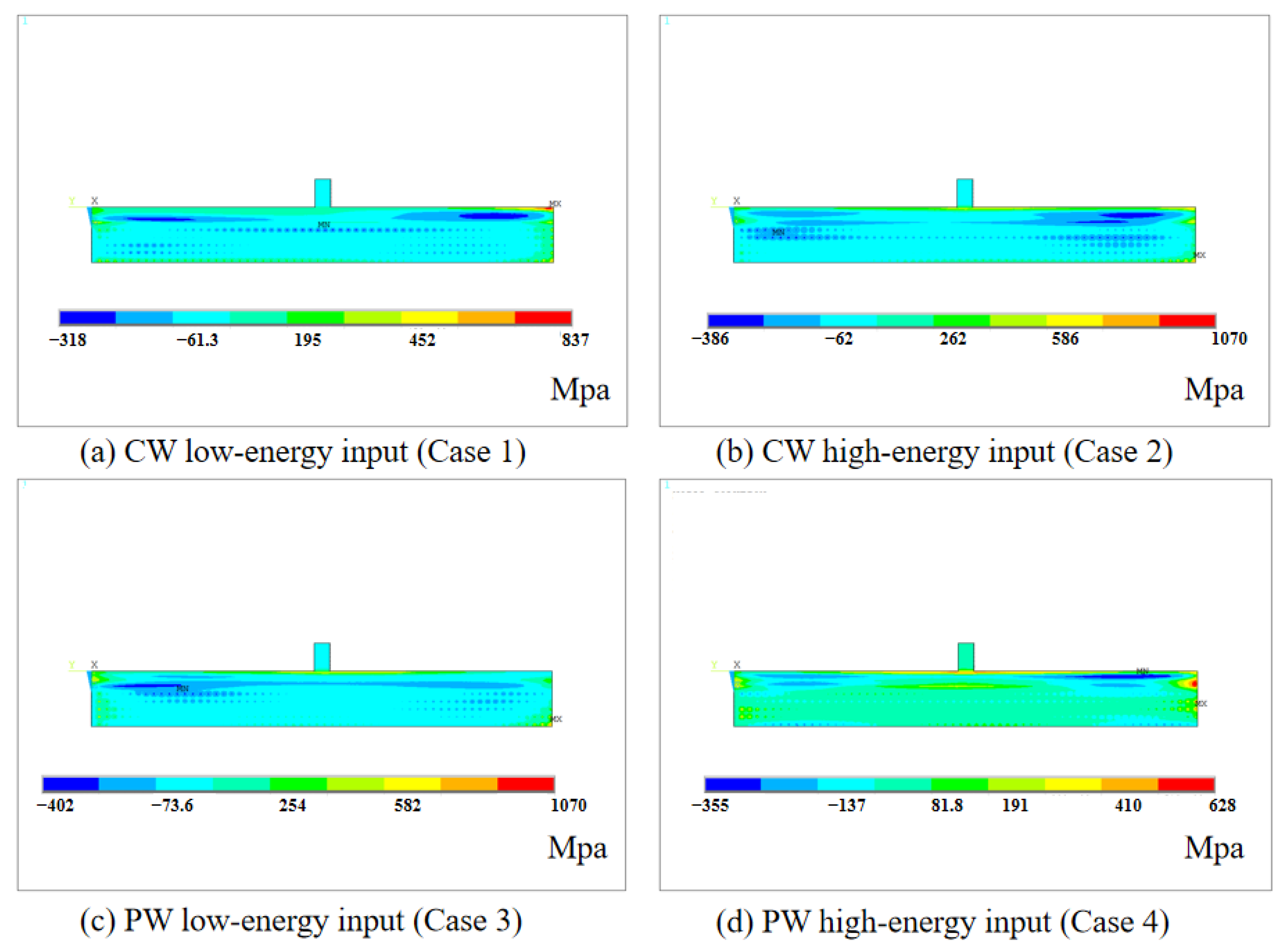
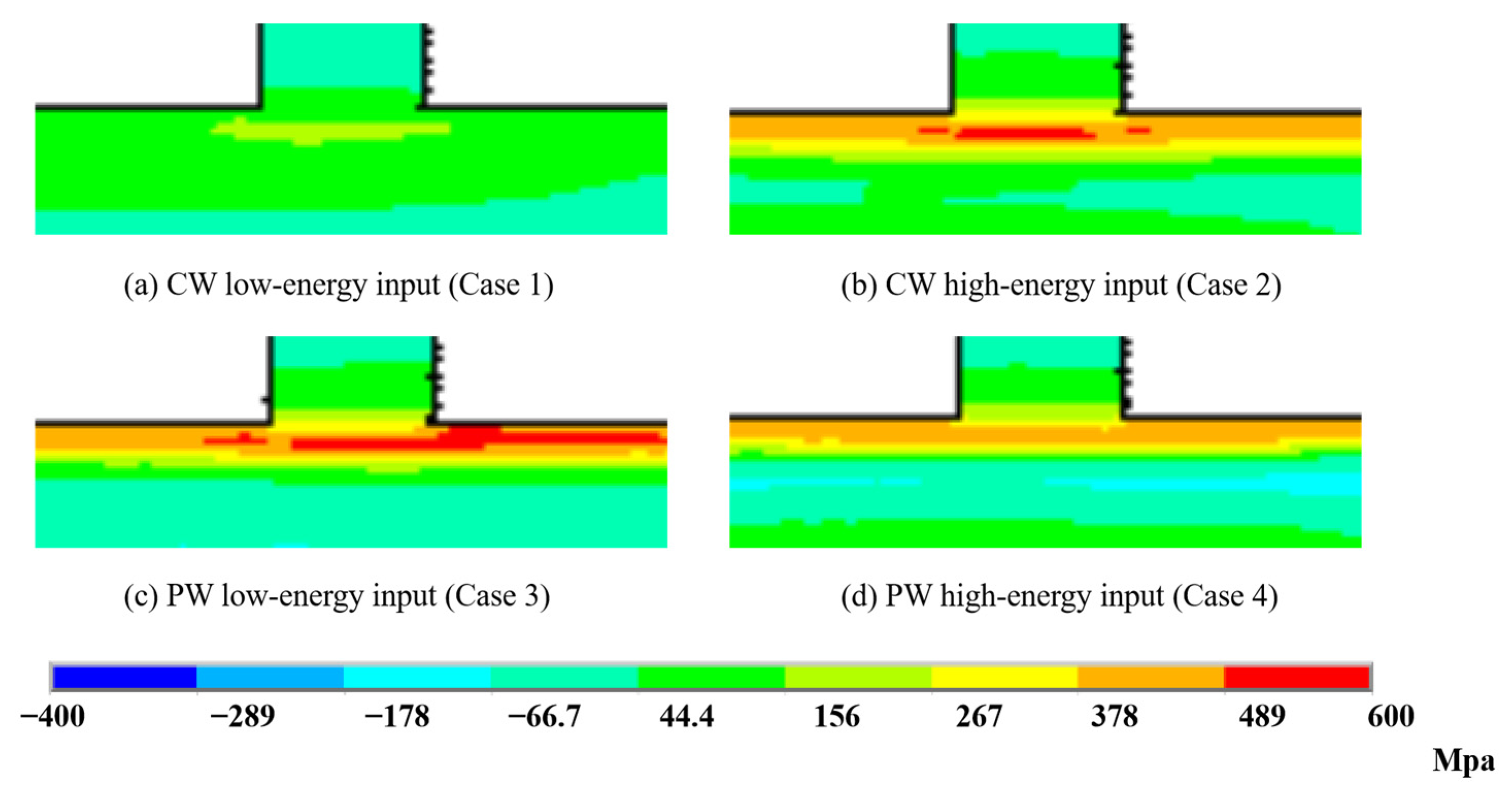
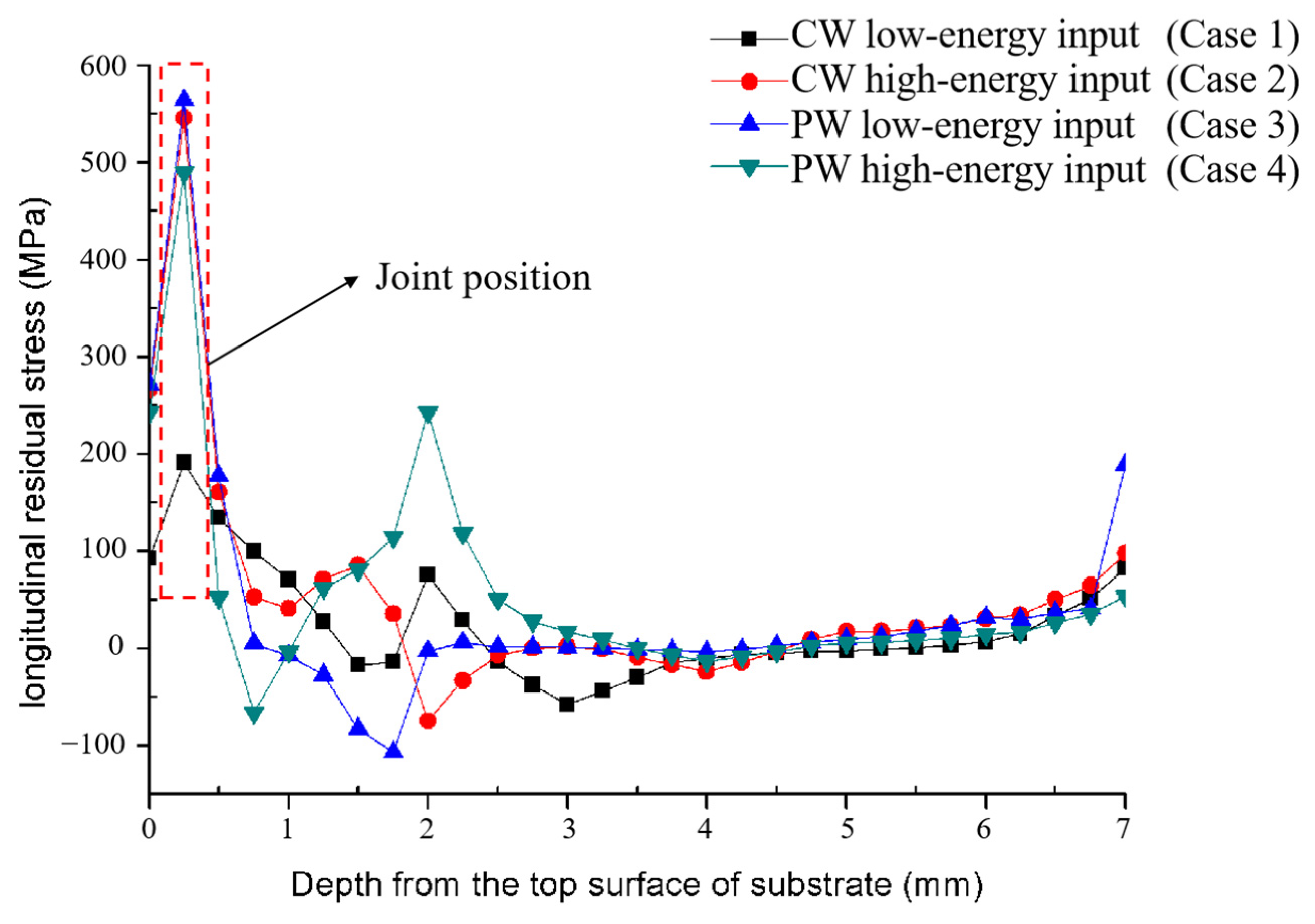
3.1. Residual Stresses in Substrate

The four samples underwent residual stress analysis in the substrate by means of CM, and the results are presented in the form of contour maps in Figure 6. The distribution of longitudinal residual stress near the top of the substrate approximated a parabolic one with the horizontal direction. It was observed that it was tensile at the mid-length and compressive at both ends, which is in line with the stress balance at a free surface. Significant variation occurred in the value of longitudinal residual stress with the depth direction at the connection between the substrate and the deposit (0.5 mm from the top of the substrate in depth direction) and the heat-affected zone (HAZ). The maximum tensile stress was attained in this area. It got increasingly compressive as it approached closer to the bottom of the substrate.

Based on Figure 6, Case 2 and Case 4 data were extracted separately. The CM results were compared to those of X-ray diffraction on specimens with two laser modes (CW/PW) under high-energy input conditions along the vertical direction, as seen in Figure 7. The stress values obtained can be corrected using the following layer-by-layer correction formula [19]:

$$\sigma (z_1)={\sigma }_m(z_1)+\left\{\begin{array}{l}-4{\sigma }_m(H)\left({\displaystyle \frac{H-Z_1}{H}}\right)+\left[{\sigma }_m(H)+2H{\sigma }_m^{\prime }(H)\right]\times {\left({\displaystyle \frac{H-Z_1}{H}}\right)}^2+\\ {\displaystyle \frac{1}{3}}\left[2{\sigma }_m(H)+H{\sigma }_m^{\prime }(H)-2H^2{\sigma }_m^{″}(H)\right]\times {\left({\displaystyle \frac{H-Z_1}{H}}\right)}^3\cdots \end{array}\right\}$$

(1)

where ${\sigma }_m(z_1)$ is the residual stress measured in the current layer, ${\sigma }_m(H)$ is the residual stress measured in the front layer, $H$ is the original plate thickness, $Z_1$ is the plate thickness after layer removal, and $\sigma (z_1)$ is the corrected stress in the current layer.

However, our experiments only met a few requirements of this formula because X-ray diffraction can only be measured by points, which leads to the discontinuity of this method, and it is difficult to calculate the higher-order derivative of residual stress (${\sigma }_m^{\prime }(H)$/${\sigma }_m^{″}(H)$). Therefore, normalized data of the two methods was used to compare the trend, as shown in Figure 7. The figure shows the distribution trend of longitudinal residual stress at six positions along the vertical direction with Case 2 and Case 4 specimens (at 1, 2, 3, 4, 5, and 6 mm from the top surface of the plate). As can be seen, both substrates had measurements at the centerline, as described in Section 2.3. The blue dots and the red dots represent the normalized data measured by CM and X-ray diffraction, respectively. Overall, it can be seen that using the two residual stress testing methods, the trend of the results was similar, with the contour measurement values being slightly lower than the X-ray diffraction results. This is because, in X-ray diffraction, the number and type of material phases, the surface treatment, the material grain size, and other factors have an impact on the X-ray diffraction peak capture, and the deviation of the diffraction peak and post-processing on the fitting of the diffraction peak will cause certain errors in the X-ray diffraction results.

3.2. Residual Stresses in Deposited Materials

Residual stress analysis in the deposited materials obtained from CM was performed on these four samples. The longitudinal residual stresses are plotted in the form of contour maps in Figure 8, with CW/PW low-energy input specimens shown in Figure 8a/Figure 8c and high-energy input specimens shown in Figure 8b/Figure 8d. To find the locations with residual stress exceeding the yield stress in the cross section of the deposited materials, the range of contour was set to +/−215 MPa, which was the yield stress of the material at room temperature. As can be seen from Figure 8, a significant portion of the cross section was yield. Similar observations have been made previously [17,20,21]. It is also worth noting that the profile of the yield area was different for CW and PW modes. A possible reason for this is that periodic thermal cycles under different laser modes are different. Further investigation will be carried out to study the mechanics, such as the thermal histories, leading to the differences.

The residual stress in the vertical direction is plotted in the form of contour maps in Figure 9, with CW/PW low-energy input specimens shown in Figure 9a/Figure 9c and high-energy input specimens shown in Figure 9b/Figure 9d. On the cross section, most areas showed compressive stress, while local areas exhibited tensile stress. Considering the same energy input, the maximum value of residual stress in the vertical direction increased with the PW mode low-energy input sample compared with the CW mode low-energy input sample (~186 MPa for Case 1 and ~248 MPa for Case 3). However, for high-energy input specimens, pulsed-wave laser mode actually reduced the value of residual stress in the vertical direction (412 MPa for Case 2 and 224 MPa for Case 4). Considering the same laser beam mode, there was a significant difference with varying energy inputs in CW mode. The maximum value of residual stress in the vertical direction increased remarkably from 186 MPa for Case 1 to 412 MPa for Case 3. However, there was no obvious distinction in PW mode (248 MPa for Case 3 and 224 MPa for Case 4).

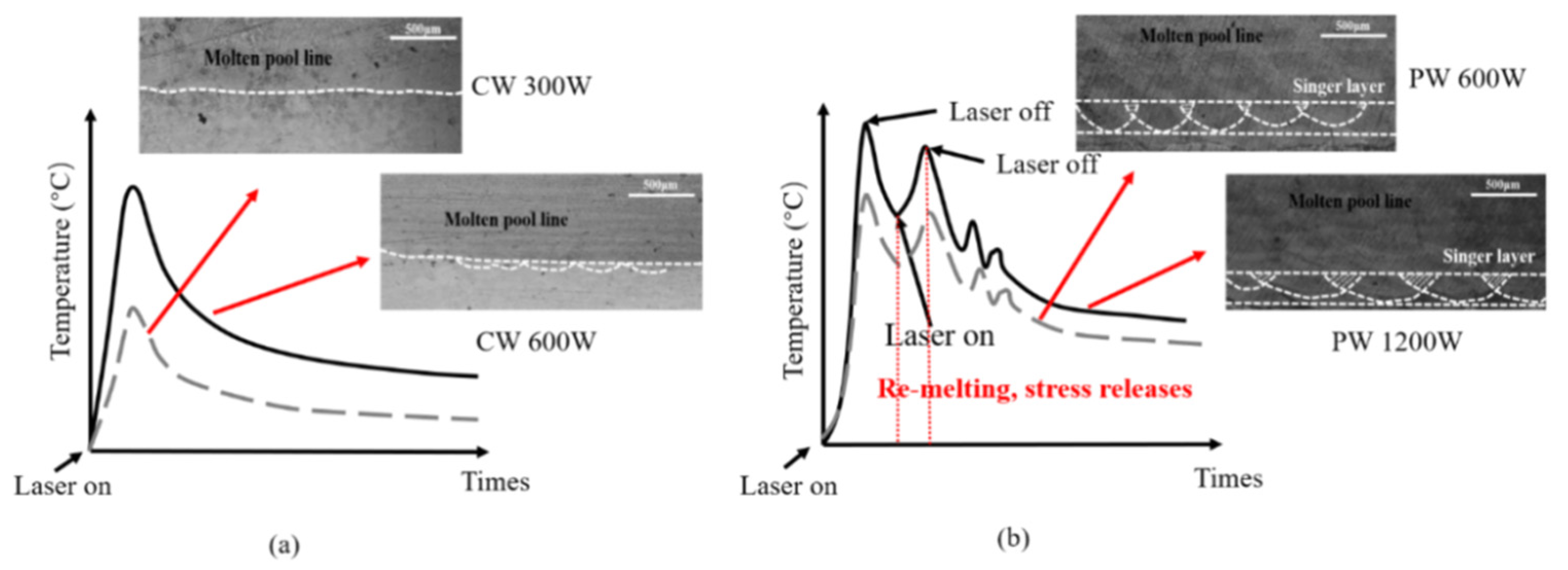
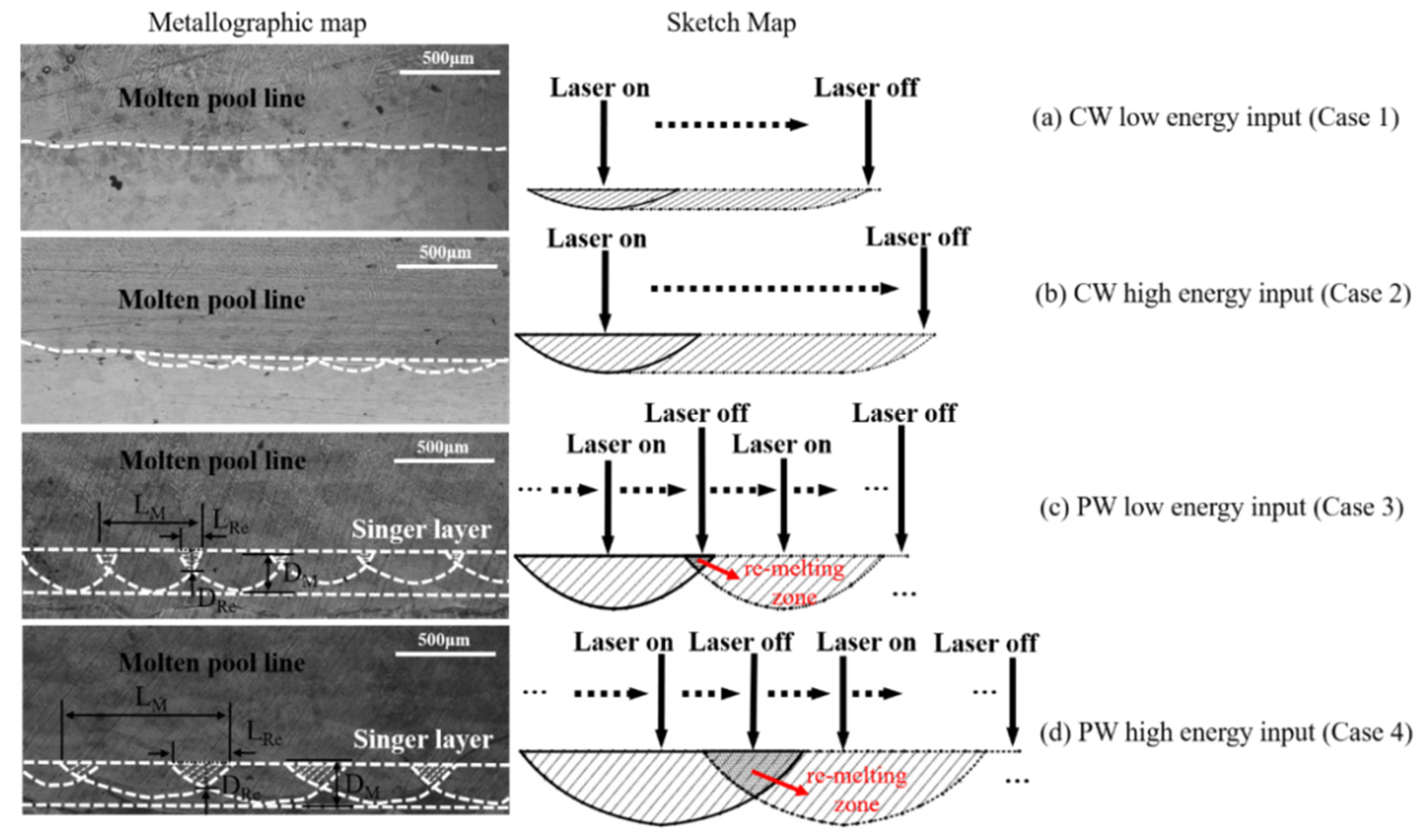
4. Discussion

The junction area between the substrate and the deposited materials was magnified, and the lower and upper limits of the color bar were set to −400 and 600 MPa, as shown in Figure 10. The longitudinal residual stress data with the vertical direction was extracted on the midline of the cross section from Figure 6 and is displayed in Figure 11.

Considering the same laser beam mode, the results with varying energy inputs in CW mode showed obvious differences. A larger stress gradient occurred with the high-energy input specimen (44.4~267 MPa for Case 1 and −66.7~600 MPa for Case 2), as can be seen in Figure 10a,b. The maximum longitudinal residual stress of the specimen with low-energy input reached roughly 195 MPa at the point of junction where the substrate interfaced with the deposited materials. Meanwhile, the specimen with high-energy input attained a maximum value of approximately 546 MPa (Figure 11), corresponding to twice the yield strength of the base material. This can be explained by the strain hardening effect of the material and the triaxial state of residual stress [17,22]. Moreover, The properties of the materials changed under high-energy input, and their yield strength decreased from brittle to ductile. Due to the instability of the melting process, some alloy elements with lower boiling temperatures were vaporized and evaporated. This vaporization phenomenon affected the material composition, thereby affecting the mechanical and chemical properties of the produced parts. These parts presented extensive residual stress [23]. Thus, for CW samples, the longitudinal residual stress at the joint increased with the increase in laser energy input. This trend is consistent with what is mentioned in the literature [3]. As the laser power increases, the heat input gradually increases, and the temperature gradient becomes larger, causing a significant increase in residual stress [24]. For PW samples, the stress gradient was analogous between the two energy input specimens (−66.7~600 MPa for Case 3 and −178~489 MPa for Case 4), as shown in Figure 10c,d. The longitudinal residual stress at the connection between the substrate and the deposit decreased 13.2% when the laser energy input doubled (about 564 MPa for Case 3 and about 489 MPa for Case 4), as shown in Figure 11. Thus, the increase in laser energy input had little effect on the magnitude of longitudinal residual stress with PW mode. This is because PW mode may cause more stress release, and the residual stress increase caused by the increase in heat input is not significant, which is consistent with the description in reference [25] and will be explained in detail in the analysis below.

Considering the same energy input, a similar stress gradient appeared at the connection between the substrate and the deposit in CW mode compared with PW mode with low-energy input (about −66.7~600 MPa for Case 2 and about −178~489 MPa for Case 4), as can be seen in Figure 10b,d. The maximum value of longitudinal residual stress at the connection between the substrate and the deposit declined by 10.3% with the PW high-energy input specimen than with the CW high-energy input specimen (~546 MPa for Case 2 and ~489 MPa for Case 4), as indicated in Figure 11. Therefore, compared with CW mode, PW mode reduced longitudinal residual stress by about 10% with high-energy input. This may be due to the frequent thermal expansion and cooling contraction caused by the cyclical switching light in PW mode, resulting in a smaller temperature gradient at the connection between the substrate and the deposit. However, for low-energy input specimens, pulsed-wave laser did not homogenize longitudinal residual stress at the joint (195 MPa for Case 1 and 564 MPa for Case 3), as shown in Figure 11. Instead, it brought a higher stress gradient (44.4~267 MPa for Case 1 and −66.7~600 MPa for Case 3), as shown in Figure 10a,c. The occurrence of this phenomenon was mentioned in reference [25] and may be related to the size of the re-melting areas under high or low heat input, which will be explained in detail below.

The values of longitudinal residual stress at the connection between the substrate and the deposit and at 0.25 mm from the top of the substrate under different laser modes with varying energy inputs were extracted from Figure 11 and are shown in Figure 12. The longitudinal residual stress increased significantly with the increase in laser power at low-energy input with CW mode. With the same peak power, the longitudinal residual stress was weakly dependent on the laser mode. On the contrary, for PW mode, a remarkable increase in laser power caused a slight decrease in the longitudinal residual stress.

This phenomenon can be explained by Figure 13 and Figure 14 and

Table 3. Dimensions of longitudinal section of molten pool and area of re-melting zone.

Case	Molten Pool			Re-Melting Zone			Percentage
	LM (mm)	DM (mm)	AM (mm2)	LRe (mm)	DRe (mm)	ARe (mm2)	AreaRe/AreaM
1	/	/	/	/	/	/	/
2	/	/	/	/	/	/	/
3	0.5	0.187	0.047	0.111	0.083	0.0046	9.7%
4	0.875	0.23	0.100	0.333	0.119	0.0198	19.8%

. Based on the literature [26], the temperature history at the midpoint of the substrate surface in the manufacturing process of direct laser deposition with CW and PW modes is shown in Figure 13, which shows a schematic temperature history curve with these two modes under varying energy inputs at any point on the surface of the substrate on the laser scanning path. The abscissa represents the time, the starting point is the time when the laser illuminates the point, and the longitudinal coordinate represents the temperature. The left side of Figure 14 is a metallographic map for the four cases, where the white dotted line is the boundary line of the molten pool. The right side of Figure 14 is a sketch map of the molten pool based on the left side. It describes the state of the molten pool under different laser modes and different heat input conditions. The CW mode low-/high-energy input specimen is shown in Figure 14a/Figure 14b (Case 1/Case 2) and the PW mode low-/high-energy input specimen is shown in Figure 14c/Figure 14d (Case 3/Case 4). In CW mode, the propulsive line of the molten pool is almost a straight line, and a clear arc molten pool line can be seen in PW mode. Table 3 represents the dimensions of the longitudinal section of the molten pool and the area of the re-melting zone under different laser modes and varying energy input conditions. It is worth noting that the area of the molten pool area and re-melting area was simply calculated by the equivalent triangle, i.e., (length × depth)/2. LM, DM, and AM represent the length, depth, and area of the molten pool, and L_Re, D_Re, and A_Re represent the length, depth, and area of the re-melting zone, respectively.

With low-energy input conditions, CW mode produced lower cooling rates compared with PW mode [27] and became responsible for lower residual stress [28]. With high-energy input conditions, although PW mode brought a higher cooling rate, the higher laser power produced a molten pool measuring 0.875 mm in length and 0.23 mm in depth during the multiple temperature rise processes caused by the periodic switching laser (case 4), resulting in a 19.8% re-melting zone. This re-melting phenomenon regenerated phase transition (solid to liquid). The stress produced by thermal expansion and solidification shrinkage in the previous cycle was released due to this phenomenon. Compared to CW mode with high-energy input specimens, which only had a transition from liquid to solid phase, the PW mode high-energy input samples continuously underwent such a liquid–solid–liquid process, endlessly releasing the stress produced in the previous cycle and leading to lower final residual stress. Therefore, PW mode displayed smaller residual stress with high-energy input.

For CW specimens, high laser energy input can significantly increase heat accumulation in the molten pool, resulting in high values of residual stress and a large stress gradient. For PW samples, they all experienced a periodic process of the lasers switching on and off during the process. The time for the laser to turn on and off was the same, and the distance the laser traveled on the substrate was also equal during this period. However, the high-energy input specimen led to a longer and deeper molten pool than that of the low-energy input sample (0.875 mm length and 0.23 mm depth for Case 4 and 0.5 mm length and 0.187 mm depth for Case 3), resulting in greater re-melting areas (19.8% and 9.7% for Case 4 and Case 3, respectively). As described above, larger re-melting areas release more stress rapidly, contributing to lower residual stress, while smaller re-melting areas do not have the ability to release more stress, resulting in a high residual stress deposit.

In other studies, methods such as reducing the temperature gradient during the laser additive manufacturing process (e.g., changing the laser power, scanning speed, preheating, and other measures) and using post-processing (e.g., heat treatment, tumbling treatment, etc.) after the workpiece has been deposited are commonly used to reduce the residual stresses of the deposited parts. However, these methods are time-consuming and have limited effect on the reduction of residual stresses. This work provides a new idea for the reduction and elimination of residual stress in additively manufactured deposits. In the future, we will further optimize the PW process and explore the effect of the pulsed laser process on the residual stress of additively manufactured deposited parts in order to lay the foundation for manufacturing low-stress, high-performance additively manufactured workpieces.

5. Conclusions

The residual stresses induced during DED with two distinct laser modes, namely CW and PW, were investigated in this work. CM and X-ray diffraction were used to assess the distributions of residual stresses in the metal depositions, the substrate, and the junction. The detailed summary of the findings of this paper is as follows:

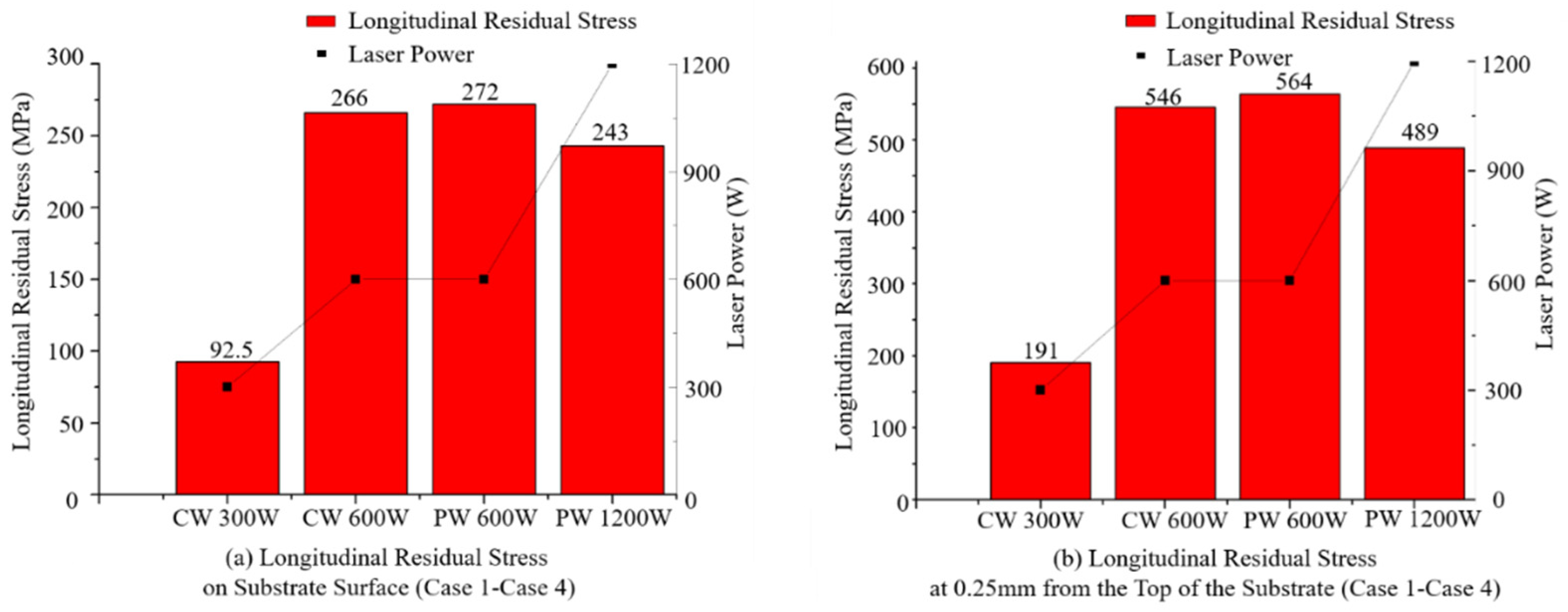
• For low-energy input, in the substrate, the longitudinal residual stress increased significantly for the PW specimen compared to the CW specimen. A similar trend was observed in the deposited materials.
• For high-energy input, in the substrate, the longitudinal residual stress was smaller for the PW specimen than the CW specimen. In the deposited materials, an analogous trend was found.
• For CW mode, the longitudinal residual stress increased sharply with the increase in energy input.
• For PW mode, the longitudinal residual stress decreased by 13.2% with the increase in energy input.
• At the substrate–component junction, where micro-cracks and even delamination are prone to occur, it was found that PW mode could reduce the longitudinal residual stress by about 10.3% in the high-energy input sample.