Interface Leakage Theory of Mechanical Seals Considering Microscopic Forces
Abstract
1. Introduction
2. Void Characteristics of the Sealing Interface
2.1. Contact Mechanics Model of the Sealing Interface
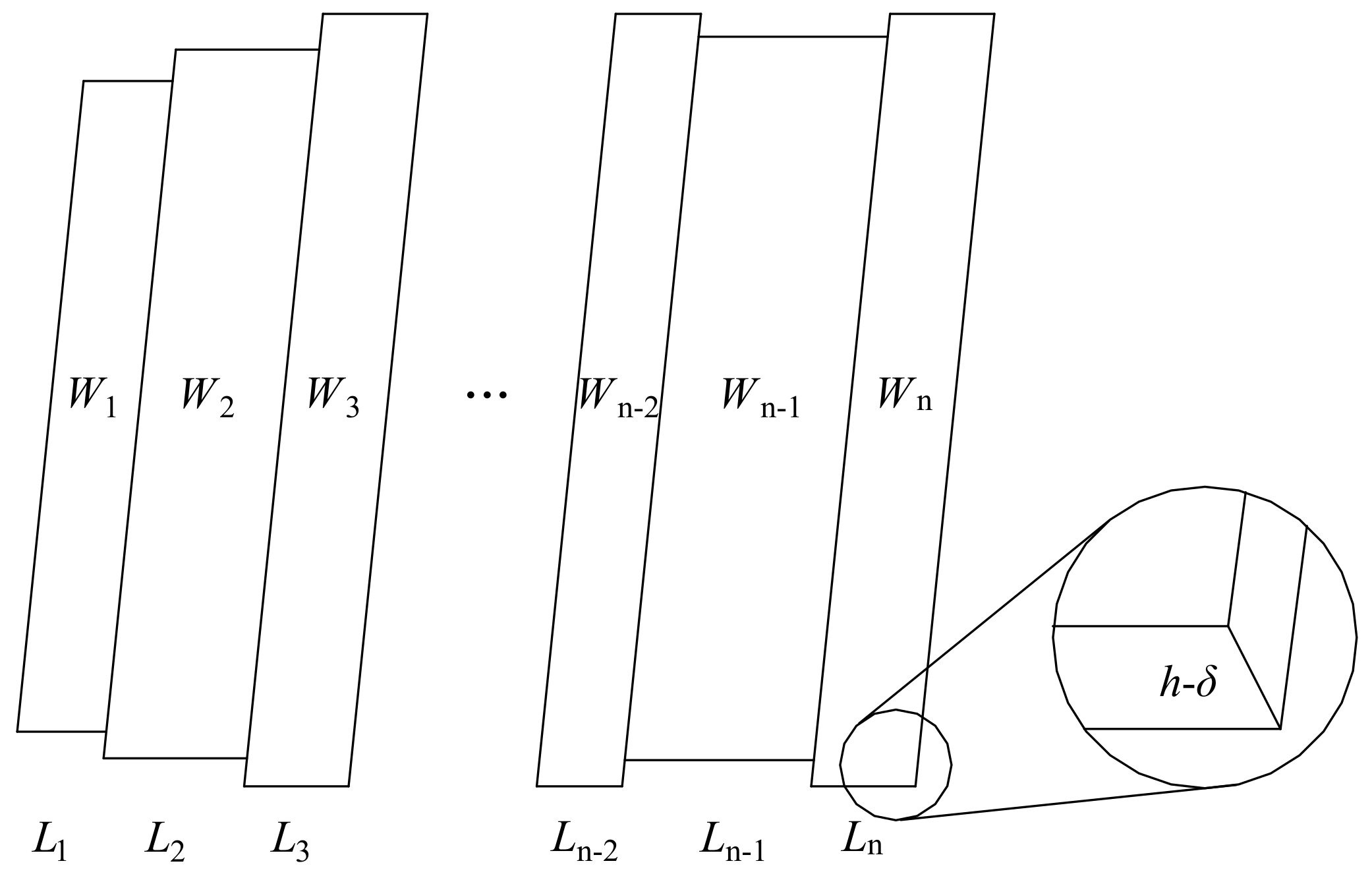
2.2. Void State
3. Microscopic Force
3.1. Function and Classification
3.1.1. Van der Waals Force
3.1.2. Electrostatic Force
3.1.3. Spatial Configuration Force
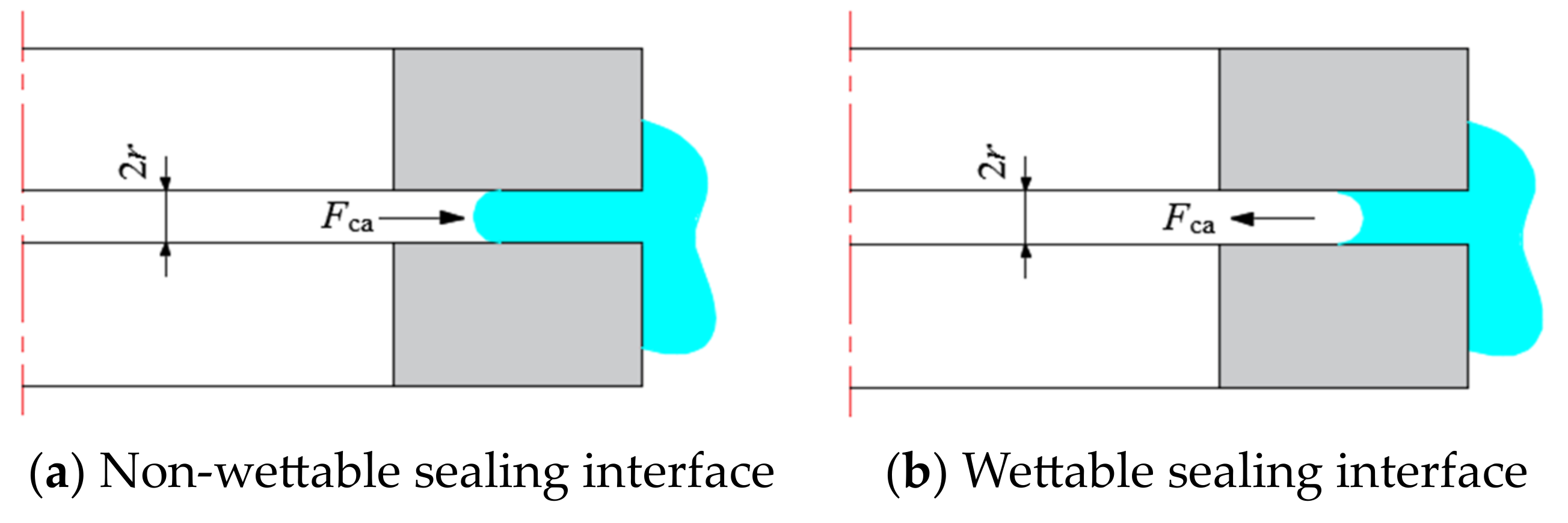
3.1.4. Surface Tension
3.2. Critical Void Radius
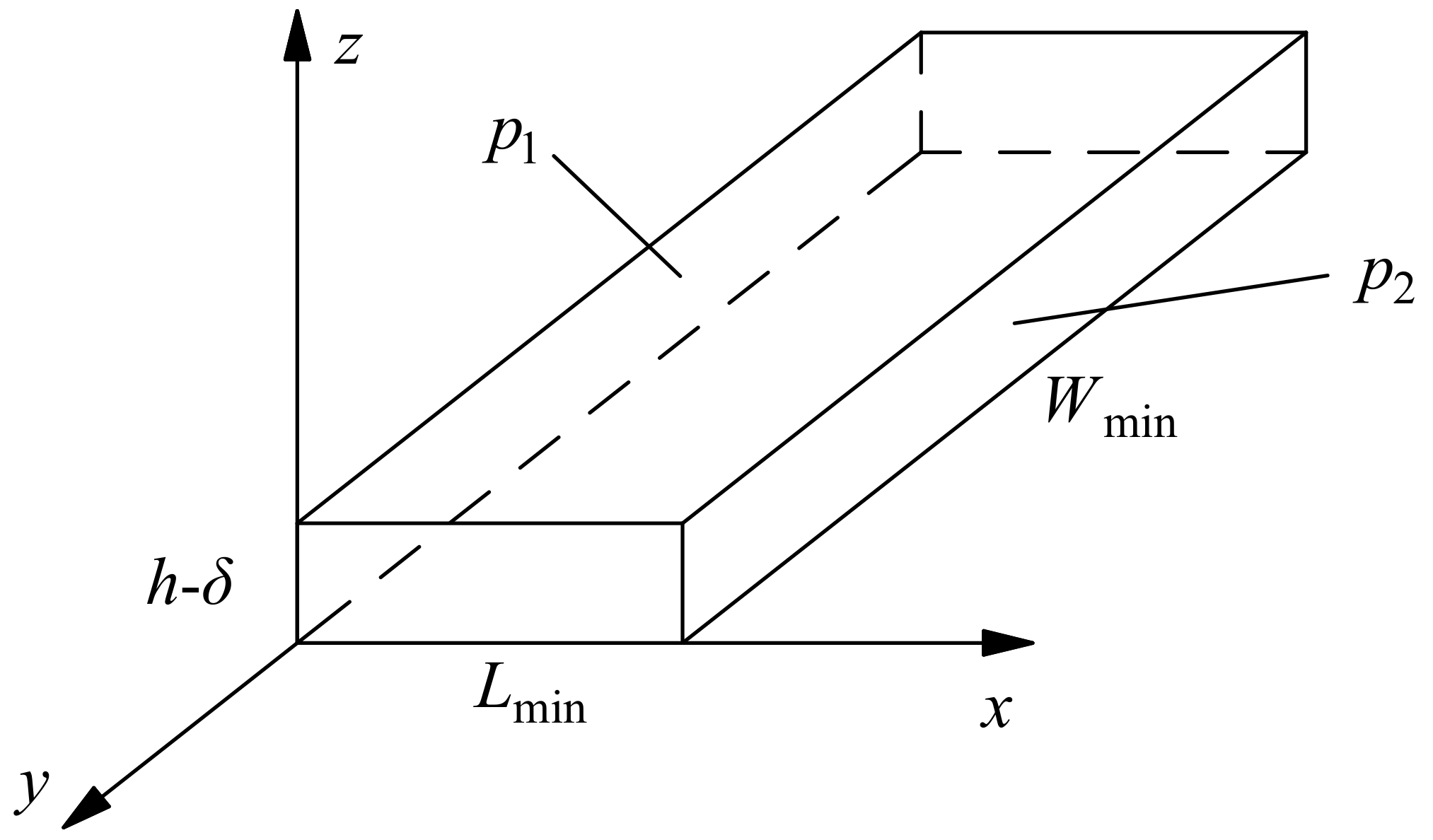
3.3. Fluid Flow Resistance
4. Leakage Rate Calculation Model
5. Leakage Theory Verification
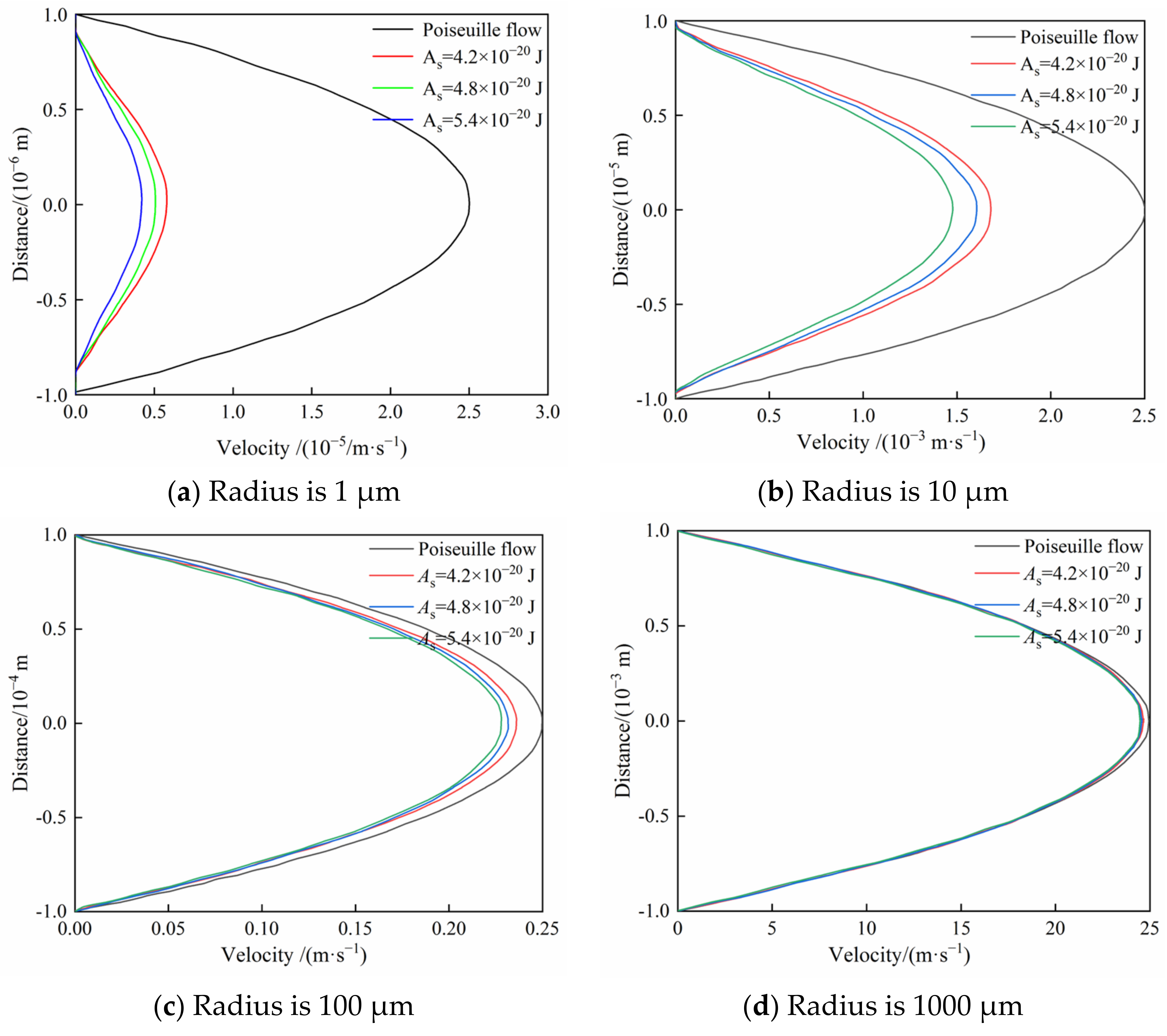
5.1. The Influence of Microscopic Forces on Fluid Flow
5.2. Calculation Example
5.3. Leakage Rate Experiment
5.3.1. Test Rig
5.3.2. Experimental Procedure
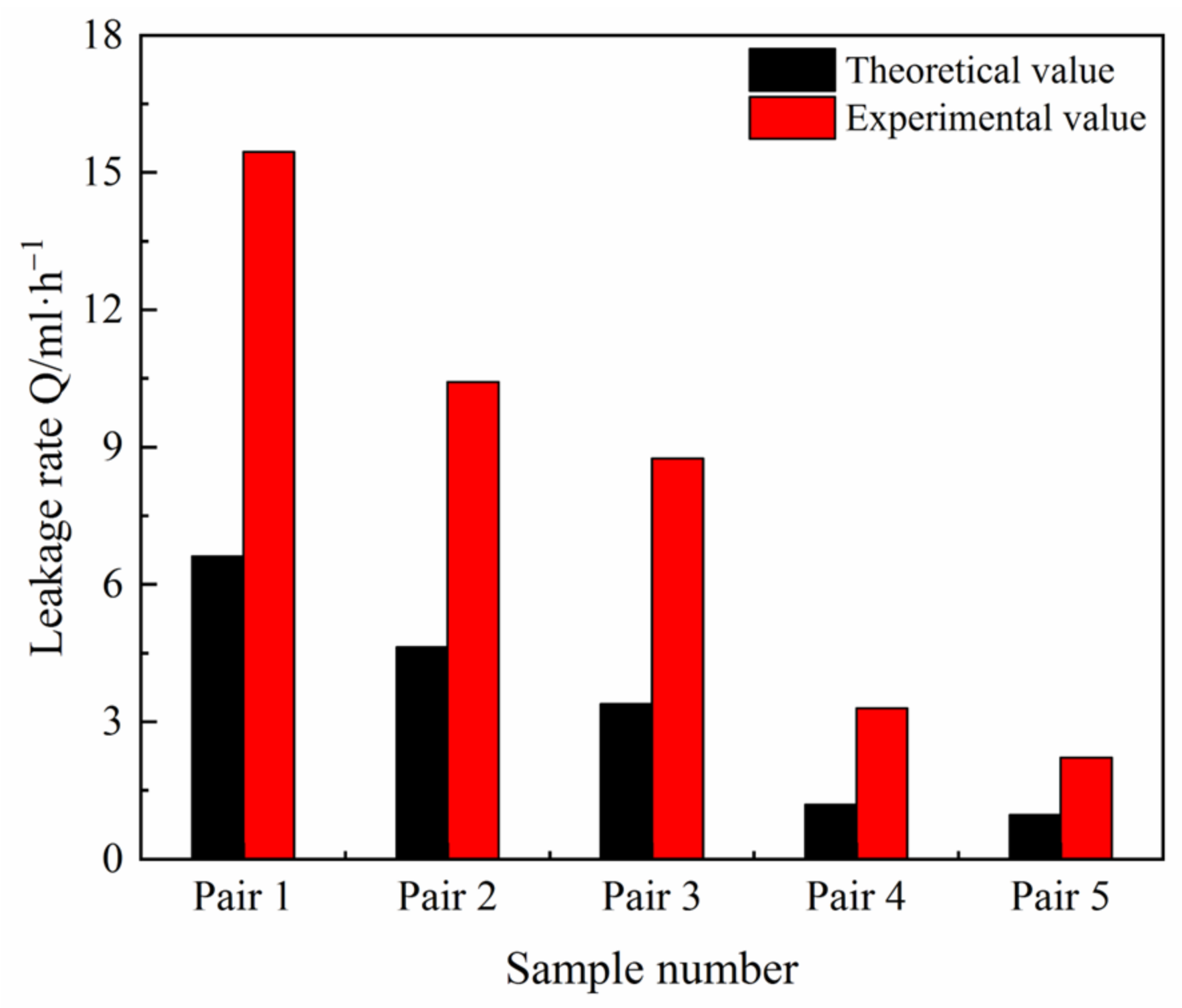
5.3.3. Experimental Results
6. Leak Judgment Criterion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lebeck, A.O. Principles and Design of Mechanical Face Seals, 1st ed.; A Wiley-Interscience Publication John Wiley & Sons, Inc: New York, NY, USA, 1991; pp. 13–18. [Google Scholar]
- Li, K.; Jia, X.; Guo, F. A model for breakaway distance and maximum static friction to study the static frictional behavior of the secondary seal in non-contacting mechanical seals. Tribol. Int. 2019, 135, 219–229. [Google Scholar] [CrossRef]
- Wang, Y.; He, Y.; Xie, X.; Huang, Z.; Xu, H.; Hu, Q.; Ma, C. Design and Simulation of a New Near Zero-Wear Non-Contact Self-Impact Seal Based on the Tesla Valve Structure. Lubricants 2023, 11, 102. [Google Scholar] [CrossRef]
- Stefanko, D.; Jerald, N.J.; Leishear, R. Relationship between vibrations and mechanical seal life in centrifugal pump. J. Nerv. Ment. Dis. 2007, 164, 122–128. [Google Scholar]
- Mayer, E. Mechanical Seals, 3rd ed.; Newness-Butterworth Publications: London, UK, 1977; pp. 45–48. [Google Scholar]
- Lebeck, A.O. Hydrodynamic lubrication in wavy contacting face seals: A two-dimensional model. J. Tribol.-T ASME 1981, 103, 578–586. [Google Scholar] [CrossRef]
- Lorenz, B.; Persson, B. Leak rate of seals: Effective-medium theory and comparison with experiment. Eur. Phys. J. E 2010, 31, 159–167. [Google Scholar] [CrossRef]
- Persson, B.; Albohr, O.; Creton, C.; Peveri, V. Contact area between a viscoelastic solid and a hard, randomly rough, substrate. J. Chem. Phys. 2004, 120, 8779–8793. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Persson, B. Contact mechanics: Contact area and interfacial separation from small contact to full contact. J. Phys. Condens. Matter 2008, 20, 4656–4658. [Google Scholar] [CrossRef]
- Persson, B. Fluid leakage in static rubber seals. Tribol. Lett. 2022, 70, 31. [Google Scholar] [CrossRef]
- Persson, B. Comments on the theory of fluid flow between solids with anisotropic roughness. Tribol. Lett. 2021, 69, 2. [Google Scholar] [CrossRef]
- Fischer, F.; Schmitz, K.; Tiwari, A.; Persson, B. Fluid leakage in metallic seals. Tribol. Lett. 2020, 68, 125. [Google Scholar] [CrossRef]
- Sun, J.J.; Ma, C.B.; Lu, J.H.; Yu, Q.P. A leakage channel model for sealing interface of mechanical face seals based on percolation theory. Tribol. Int. 2018, 118, 108–119. [Google Scholar]
- Ji, Z.B.; Sun, J.J.; Lu, J.H.; Ma, C.B.; Yu, Q.P. A prediction method for static leakage at the interface of mechanical seals based on percolation theory. J. Tribol. 2017, 37, 734–742. [Google Scholar]
- Zheng, W.; Sun, J.J.; Ma, C.B.; Yu, Q.P. Percolation interpretation of film pressure forming mechanism of mechanical seal and calculation method of film pressure coefficient. Tribol. Int. 2022, 173, 107664. [Google Scholar] [CrossRef]
- Anikin, Y.A.; Derbakova, E.P.; Dodulad, O.I.; Kloss, Y.Y.; Martynov, D.V.; Rogozin, O.A.; Shuvalov, P.V.; Tcheremissine, F.G. Computing of gas flows in micro- and nanoscale channels on the base of the boltzmann kinetic equation. Procedia Comput. Sci. 2010, 1, 735–744. [Google Scholar] [CrossRef]
- Zheng, W.; Sun, J.; Ma, C.; Yu, Q. The theoretical basis of face contact pressure design of the zero-leakage mechanical seal. Coatings 2022, 12, 536. [Google Scholar] [CrossRef]
- Zhang, H.; Etsion, I. An advanced efficient model for adhesive wear in elastic—Plastic spherical contact. Friction 2022, 10, 1276–1284. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol.-T ASME 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Majumder, A.; Tien, C.T. Fractal characterization and simulation of rough surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Etsion, I. Discussion of the Paper: Optical in situ micro tribometer for analysis of real contact area for contact mechanics, adhesion, and sliding experiments. Tribol. Lett. 2012, 46, 205. [Google Scholar] [CrossRef][Green Version]
- Majumdar, A.; Bhushan, B. Role of fractal geometry in roughness characterization and contact mechanics of surfaces. J. Tribol.-T ASME 1990, 112, 205–216. [Google Scholar] [CrossRef]
- ANSI/ASME B46.1; Surface. Texture (Surface Roughness, Waviness, and Lay), An American National Standards. ASME: New York, NY, USA, 2020.
- Greenwood, J.A.; Tripp, J.H. The elastic contact of rough spheres. J. Appl. Mech.-T ASME 1967, 34, 153–159. [Google Scholar] [CrossRef]
- Sun, J.J.; Ji, Z.B.; Ma, C.B. Reanalysis of contact mechanics problems on rough surfaces. CIESC J. 2018, 50, 68–77. [Google Scholar]
- Wang, S.; Komvopoulosk, K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: Part I elastic contact and heat transfer analysis. J. Tribol.-T ASME 1994, 116, 812–823. [Google Scholar] [CrossRef]
- Bottiglione, F.; Carbone, G.; Mantriota, G. Fluid leakage in seals: An approach based on percolation theory. Tribol. Int. 2009, 42, 731–737. [Google Scholar] [CrossRef]
- Deng, Q.J.; Zhu, W.Y.; Wang, X.F.; Sui, X.G.; Wang, X.J. The role of microscopic forces and seepage models in porous media. J. Beijing Univ. Sci. Technol. 2014, 36, 415–423. [Google Scholar]
- Zhang, L.J.; Zheng, Z. Colloid and Interfacial Chemistry, 1st ed.; South China University of Technology Press: Guangzhou, China, 2006; pp. 34–37. [Google Scholar]
- Zhang, X.L.; Zhu, W.Y.; Cai, Q.; Liu, Q.P.; Wang, X.F.; Lou, Y. Flow analysis of microcompressible fluid in nanomicron circular tubes considering solid wall forces. J. Beijing Univ. Sci. Technol. 2014, 36, 569–575. [Google Scholar]
- Sun, J.J.; Chen, G.Q.; Ji, Z.B. Analysis of interface leakage mechanism of contact mechanical seals. CIESC J. 2018, 69, 282–290. [Google Scholar]
- Yuan, T.; Chen, Z.; Liu, W.J.; Zhou, X.H.; Tu, W.P.; Wang, F. Application and mechanical model of capillary mechanics in super hydrophilic membrane separation process. J. South China Univ. Technol. (Nat. Sci. Ed.) 2014, 42, 82–89. [Google Scholar]
- Xia, Q.; Chen, C.G. Principles of Chemical Engineering (Volume I), 1st ed.; Tianjin University Press: Tianjin, China, 2009; pp. 25–29. [Google Scholar]
- Gh Mohiuddin, M.; Li, D.Q. Flow characteristics of water in microtubes. Int. J. Heat Fluid Flow 1999, 20, 142–148. [Google Scholar] [CrossRef]
- Huon, C.; Tiwari, A.; Rotella, C.; Persson, B. Air, helium and water leakage in rubber O-ring seals with application to syringes. Tribol. Lett. 2022, 70, 35. [Google Scholar] [CrossRef]
- Xu, L.S.; Liu, Y.Y.; Wu, J.H.; Yuan, X.Y.; Hao, M.M.; Wang, Y.L.; Liu, F.Y.; Li, Z.T. Transient dynamic analysis and experimental verification on lubrication regime transition during startup period of non-contacting mechanical seal in liquid oxygen turbopump. Tribol. Int. 2022, 176, 107932. [Google Scholar] [CrossRef]








| Physical Parameters | Hard Ring | Soft Ring | |
|---|---|---|---|
| Material | YG8 | M106K | |
| Elastic modulus E (Gpa) | 600 | 20 | |
| Yield strength σy (Mpa) | / | 50 | |
| Poisson’s ratio | 0.24 | 0.29 | |
| Fractal dimension D, Scale coefficient G (m) | Pair 1 (P600) | 2.607, 2.27 × 10−11 | 2.326, 5.34 × 10−10 |
| Pair 2 (P1000) | 2.350, 4.30 × 10−10 | ||
| Pair 3 (P1500) | 2.394, 3.69 × 10−10 | ||
| Pair 4 (P2000) | 2.424, 3.07 × 10−10 | ||
| Pair 5 (P2500) | 2.426, 2.48 × 10−10 | ||
| Inner diameter ri (mm) | 62 | 68 | |
| Outer diameter ro (mm) | 82 | 79 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, W.; Sun, J.; Ma, C.; Yu, Q. Interface Leakage Theory of Mechanical Seals Considering Microscopic Forces. Coatings 2023, 13, 1435. https://doi.org/10.3390/coatings13081435
Zheng W, Sun J, Ma C, Yu Q. Interface Leakage Theory of Mechanical Seals Considering Microscopic Forces. Coatings. 2023; 13(8):1435. https://doi.org/10.3390/coatings13081435
Chicago/Turabian StyleZheng, Wei, Jianjun Sun, Chenbo Ma, and Qiuping Yu. 2023. "Interface Leakage Theory of Mechanical Seals Considering Microscopic Forces" Coatings 13, no. 8: 1435. https://doi.org/10.3390/coatings13081435
APA StyleZheng, W., Sun, J., Ma, C., & Yu, Q. (2023). Interface Leakage Theory of Mechanical Seals Considering Microscopic Forces. Coatings, 13(8), 1435. https://doi.org/10.3390/coatings13081435






