Theoretical and Numerical Constant Mean Curvature Surface and Liquid Entry Pressure Calculations for a Combined Pillar–Pore Structure
Abstract
:1. Introduction
2. Mathematical Background
3. Numerical Methods
4. Results
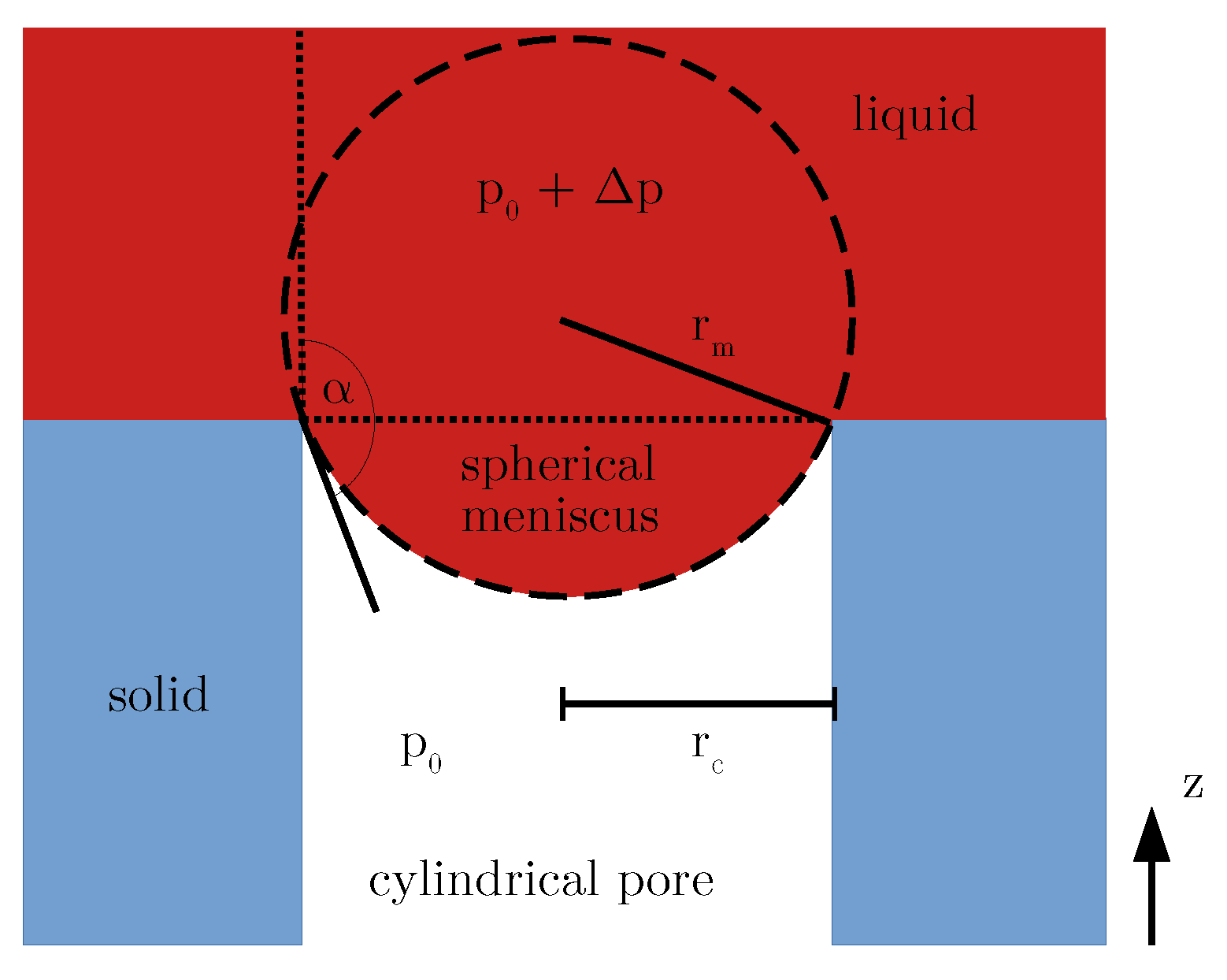
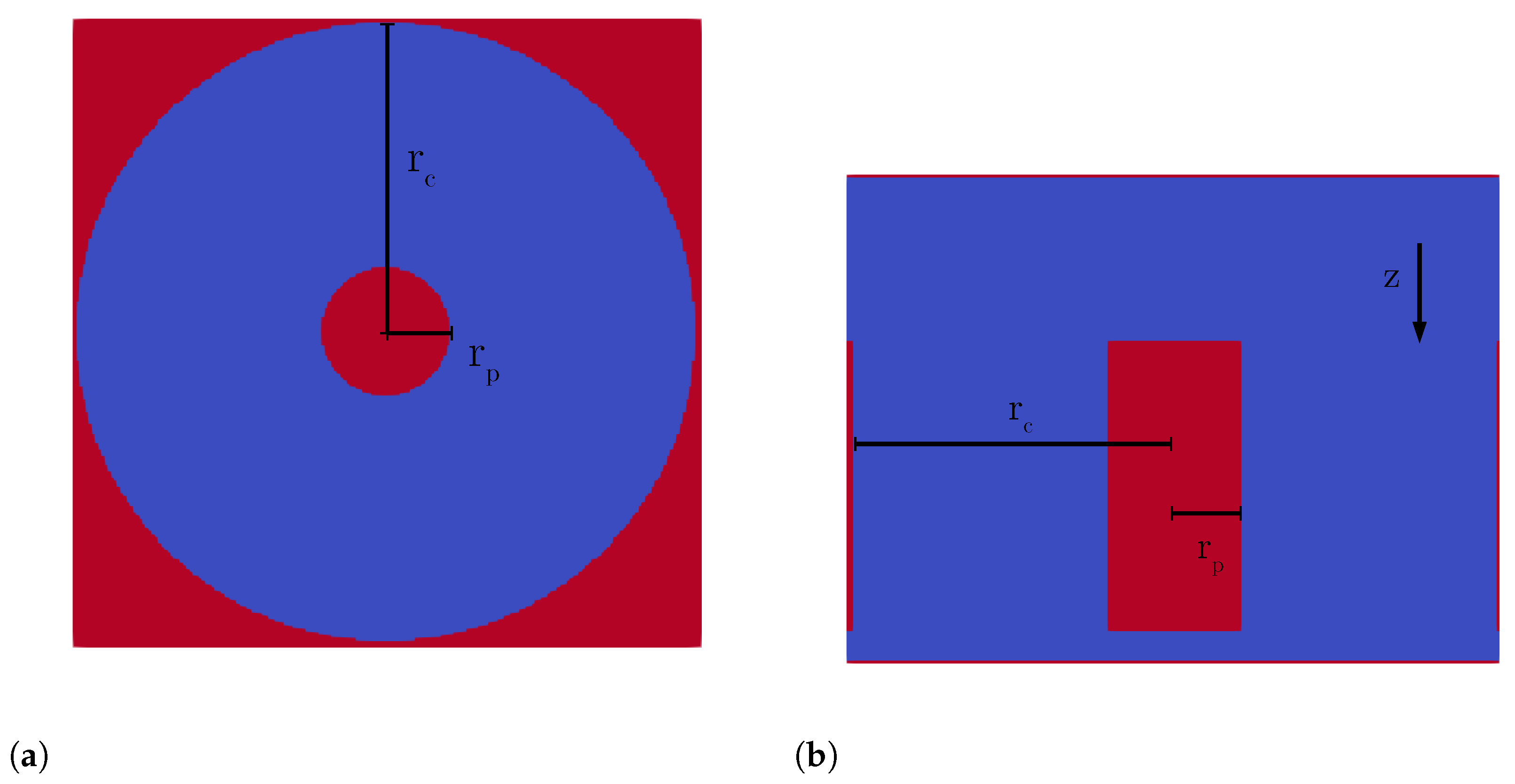
4.1. Theoretical Analysis of the Constant Mean Curvature Surface for a Combined Pillar–Pore Structure

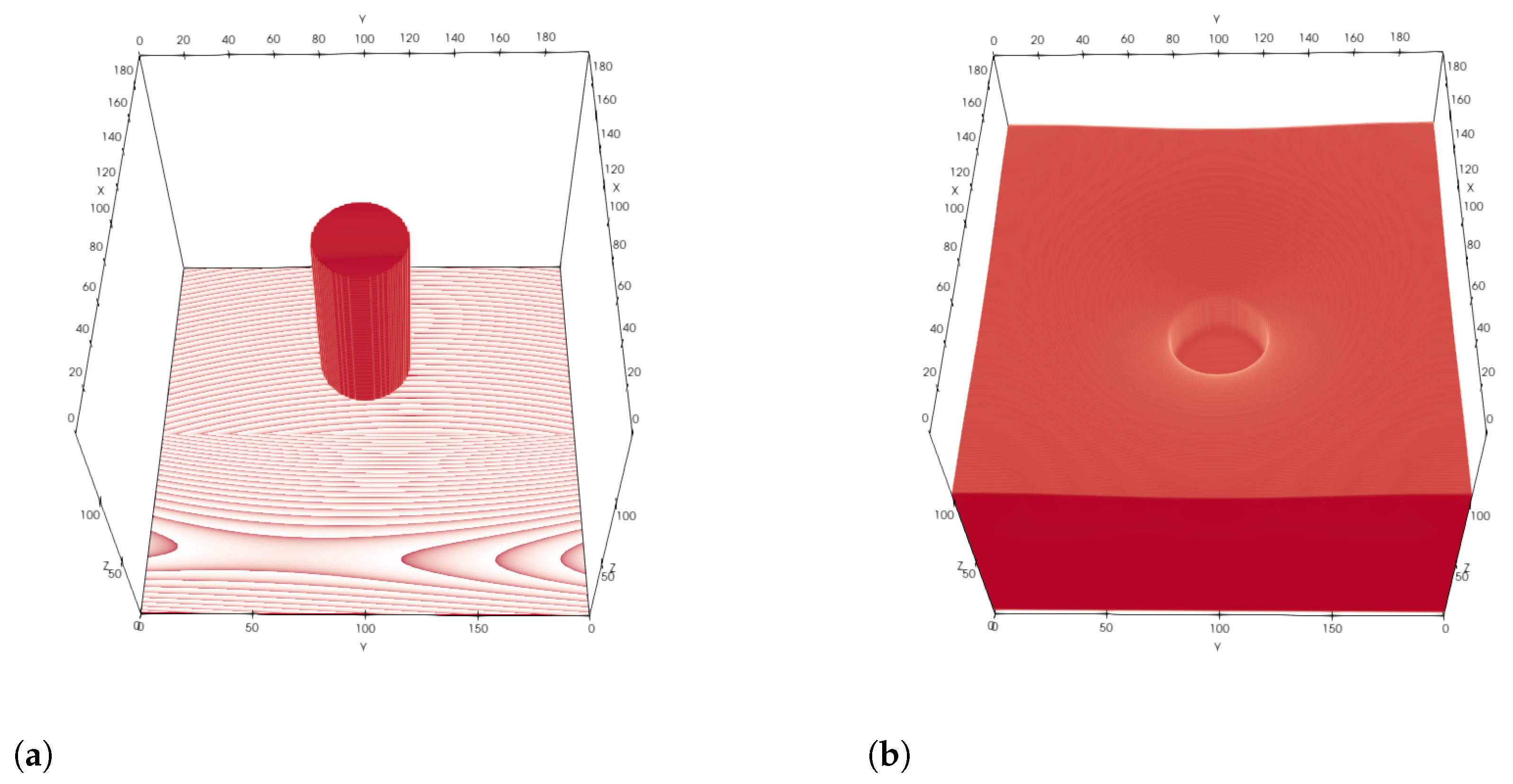
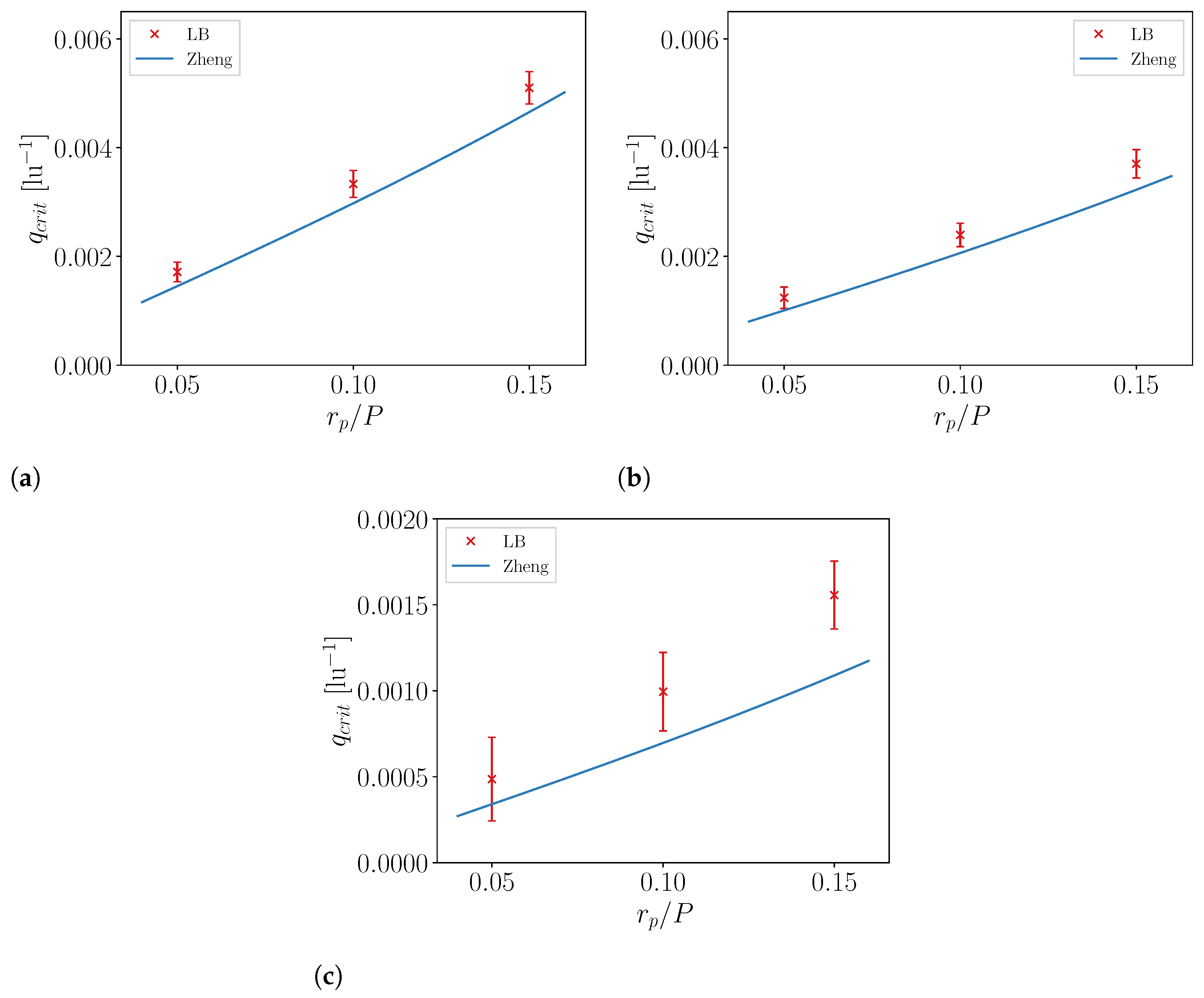
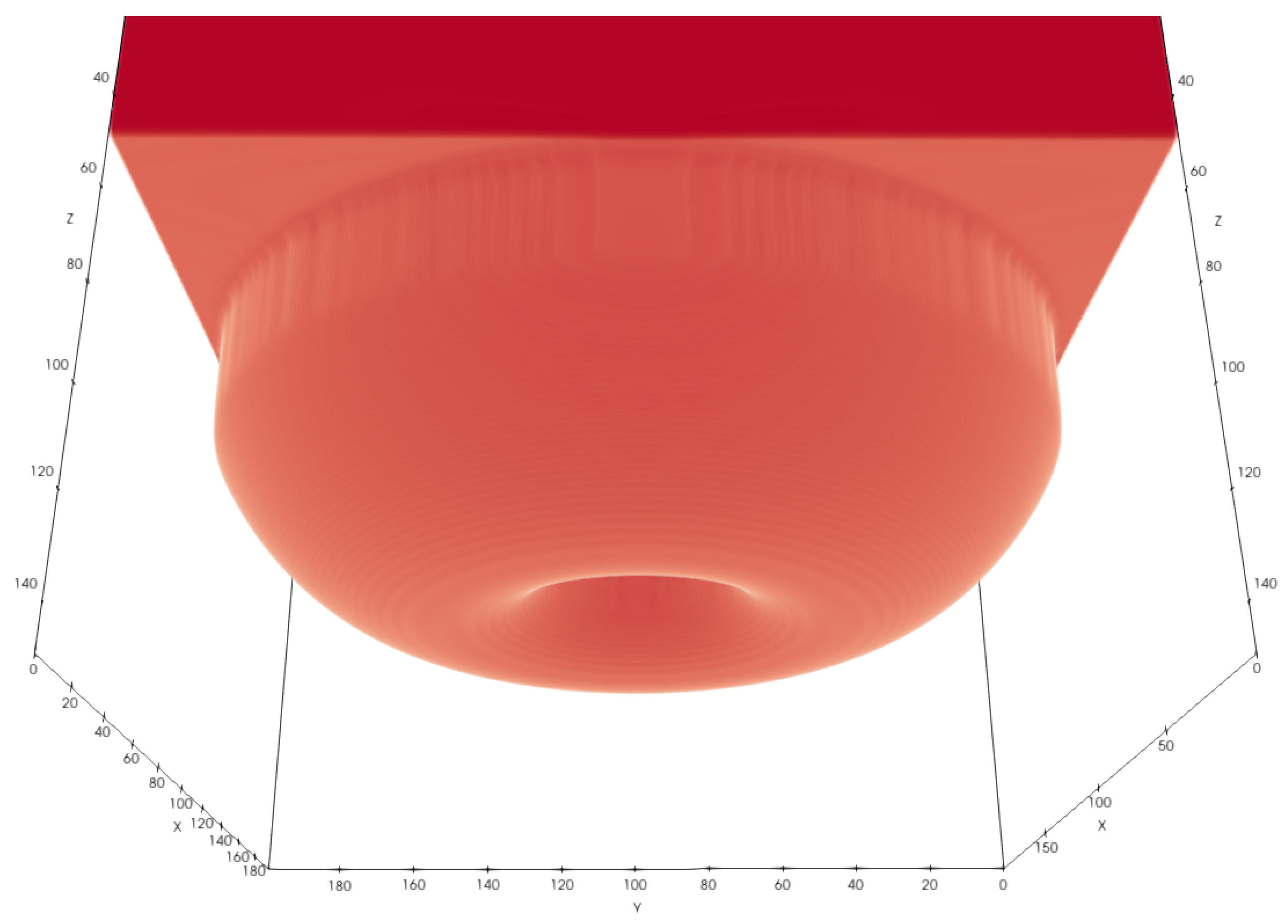
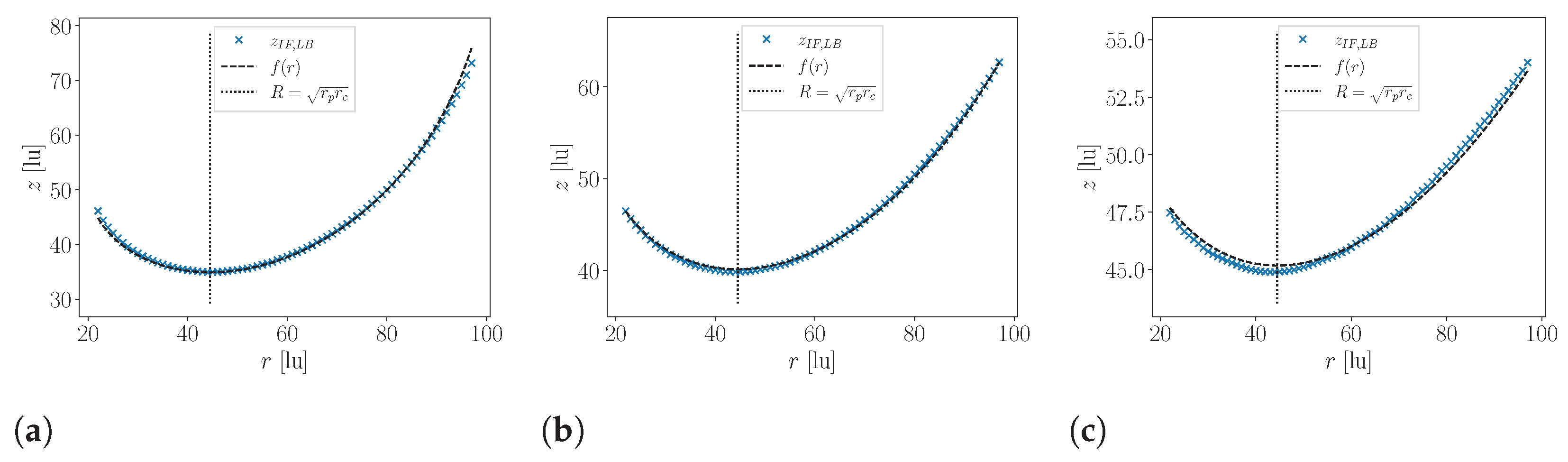
4.2. Numerical Calculation of the Constant Mean Curvature Surface and the Liquid Entry Pressure with the Lattice Boltzmann Method
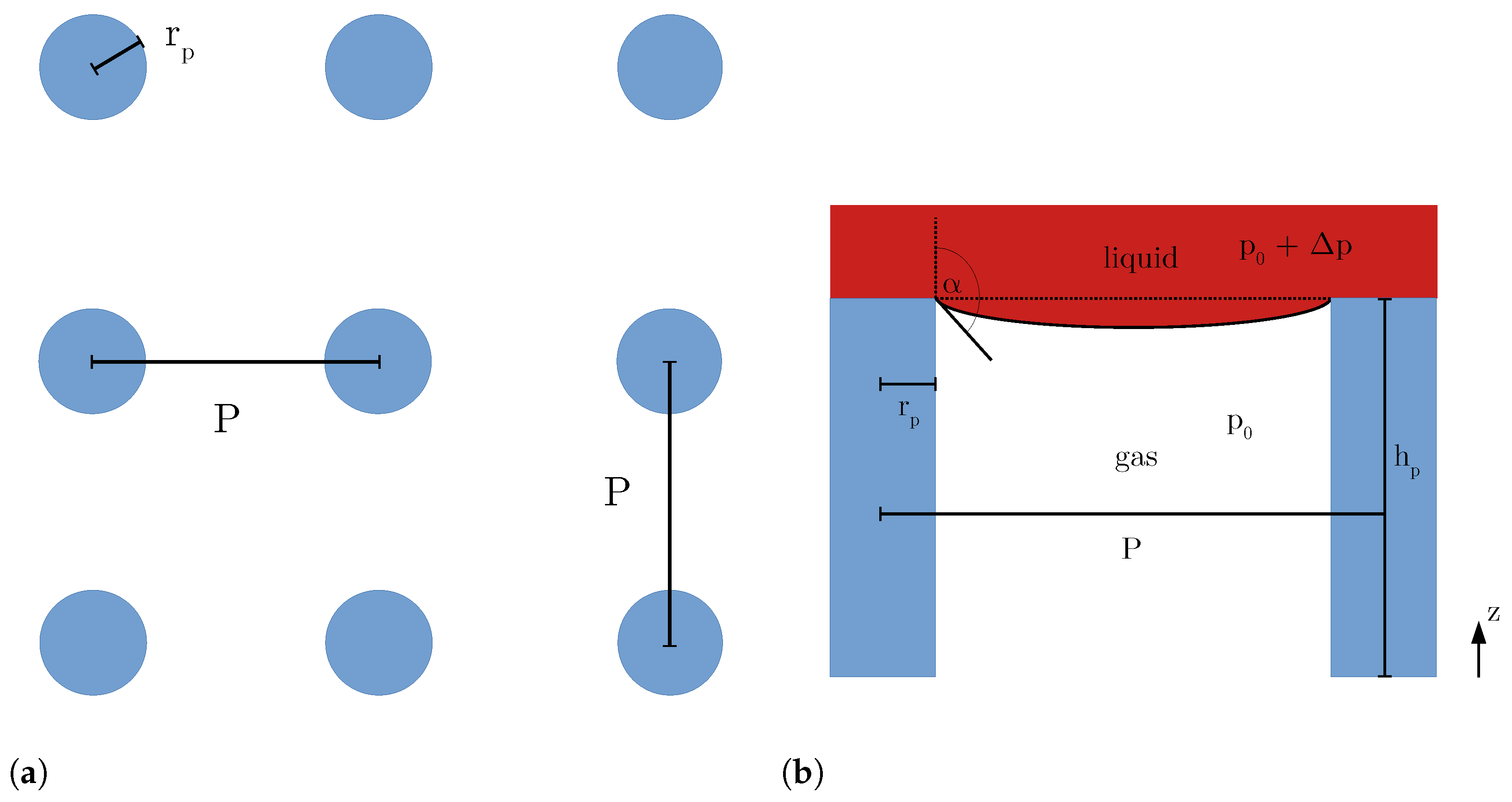
4.2.1. Single Circular Pillar with Periodic Boundary Conditions
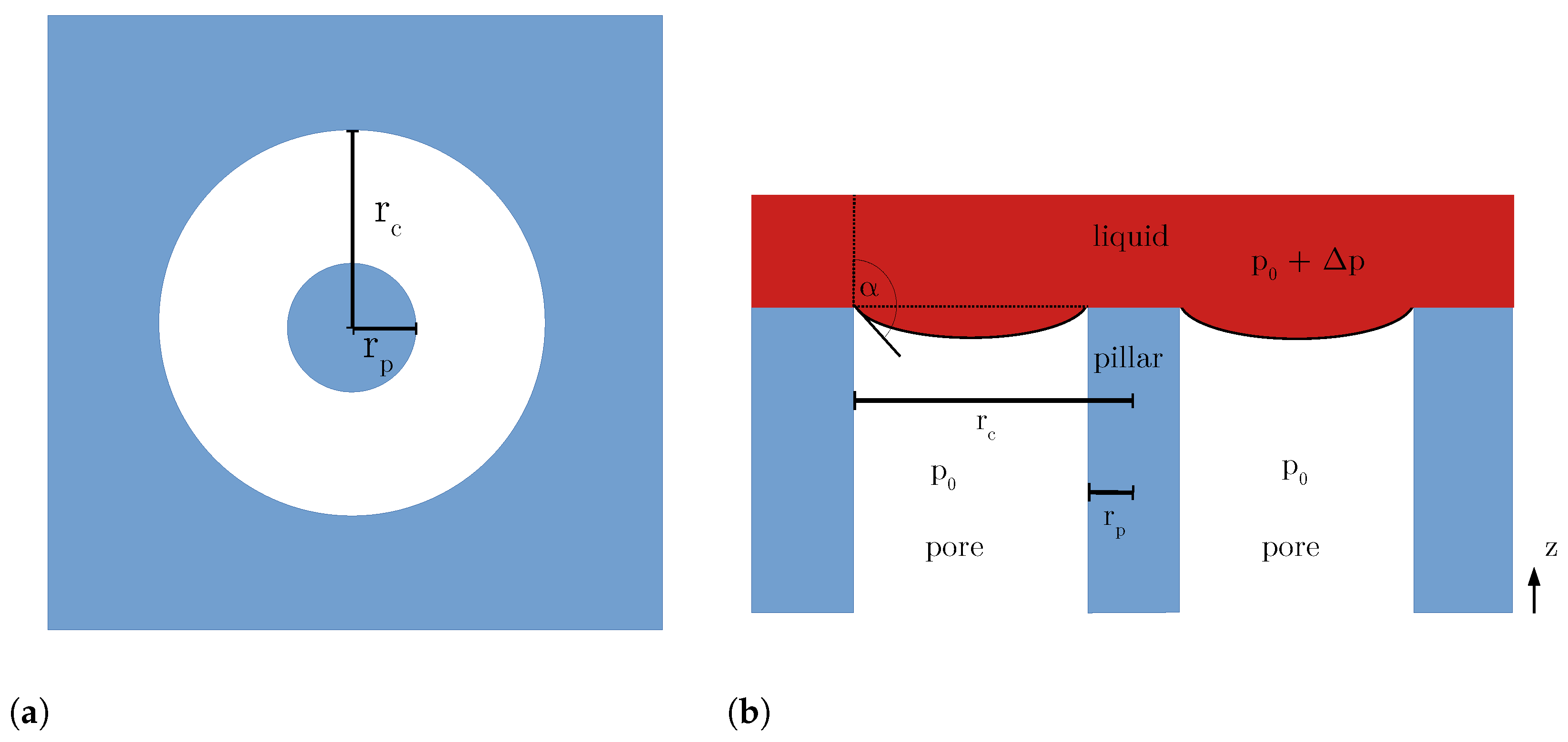
4.2.2. Combined Pillar–Pore Structure
5. Discussion
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMC | Constant mean curvature |
| PDE | Partial differential equation |
| Liquid entry pressure (LEP) | |
| Surface tension | |
| q | |
| Pillar radius | |
| Pore radius | |
| R | Location of the minimum |
| Contact angles between the liquid and the pillar wall | |
| Contact angles between the liquid and the pore wall | |
| Equilibrium contact angle between liquid and solid | |
| P | Pitch pillar (periodicity in x- and y-directions) |
| Area of the periodically repeated cell () | |
| A | Top area of the pillar () |
| l | Perimeter of the pillar () |
| Unit normal vector of the liquid–gas interface | |
| LB | lattice Boltzmann |
| NRMSD | normalised root mean square deviation |
| p | Pressure |
| Density | |
| Liquid density | |
| Gas density | |
| Force | |
| Lattice spacing | |
| Time step | |
| m | Fluid particle mass |
| LB parameter to tune the equilibrium contact angle | |
| G | LB parameter to control the fluid–fluid interaction strength |
| Relaxation time | |
| Kinematic viscosity | |
| Speed of sound | |
| g | Gravitation acceleration |
| Velocity | |
| Discrete lattice velocity |
References
- Jung, Y.; Bhushan, B. Wetting behaviour during evaporation and condensation of water microdroplets on superhydrophobic patterned surfaces. J. Microsc. 2008, 229, 127–140. [Google Scholar] [CrossRef] [PubMed]
- Gogolides, E.; Ellinas, K.; Tserepi, A. Hierarchical micro and nano structured, hydrophilic, superhydrophobic and superoleophobic surfaces incorporated in microfluidics, microarrays and lab on chip microsystems. Microelectron. Eng. 2015, 132, 135–155. [Google Scholar] [CrossRef]
- Xiao, Z.; Zheng, R.; Liu, Y.; He, H.; Yuan, X.; Ji, Y.; Li, D.; Yin, H.; Zhang, Y.; Li, X.M.; et al. Slippery for scaling resistance in membrane distillation: A novel porous micropillared superhydrophobic surface. Water Res. 2019, 155, 152–161. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agonafer, D.D.; Lee, H.; Vasquez, P.A.; Won, Y.; Jung, K.W.; Lingamneni, S.; Ma, B.; Shan, L.; Shuai, S.; Du, Z.; et al. Porous micropillar structures for retaining low surface tension liquids. J. Colloid Interface Sci. 2018, 514, 316–327. [Google Scholar] [CrossRef]
- Yao, X.; Gao, J.; Song, Y.; Jiang, L. Superoleophobic Surfaces with Controllable Oil Adhesion and Their Application in Oil Transportation. Adv. Funct. Mater. 2011, 21, 4270–4276. [Google Scholar] [CrossRef]
- Xue, Z.; Wang, S.; Lin, L.; Chen, L.; Liu, M.; Feng, L.; Jiang, L. A Novel Superhydrophilic and Underwater Superoleophobic Hydrogel-Coated Mesh for Oil/Water Separation. Adv. Mater. 2011, 23, 4270–4273. [Google Scholar] [CrossRef] [PubMed]
- Field, R.W. Separation by reconfiguration. Nature 2012, 489, 41–42. [Google Scholar] [CrossRef]
- Sridhar, A.; Ong, C.L.; Paredes, S.; MicheL, B. Thermal Design of a Hierarchical Radially Expanding Cavity for Two-Phase Cooling of Integrated Circuits. In Proceedings of the International Electronic Packaging Technical Conference and Exhibition, Changsha, China, 11–14 August 2015; Volume 1. [Google Scholar] [CrossRef]
- Kim, B.S.; Harriott, P. Critical entry pressure for liquids in hydrophobic membranes. J. Colloid Interface Sci. 1987, 115, 1–8. [Google Scholar] [CrossRef]
- Rahimpour, M.R.; Esmaeilbeig, M.A. Chapter 6—Membrane Wetting in Membrane Distillation. In Current Trends and Future Developments on (Bio-) Membranes; Basile, A., Curcio, E., Inamuddin, Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 143–174. [Google Scholar] [CrossRef]
- Lobaton, E.; Salamon, T. Computation of constant mean curvature surfaces: Application to the gas–liquid interface of a pressurized fluid on a superhydrophobic surface. J. Colloid Interface Sci. 2007, 314, 184–198. [Google Scholar] [CrossRef]
- Laplace, P.S. Supplément au dixième livre du Traité de Mécanique Céleste. J.B.M. Duprat 1805, 4, 1–79. [Google Scholar]
- Racz, G.; Kerker, S.; Kovács, Z.; Vatai, G.; Ebrahimi, M.; Czermak, P. Theoretical and Experimental Approaches of Liquid Entry Pressure Determination in Membrane Distillation Processes. Period. Polytech. Chem. Eng. 2014, 58, 81–91. [Google Scholar] [CrossRef] [Green Version]
- Young, T. III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Kwok, D.; Neumann, A. Contact angle measurement and contact angle interpretation. Adv. Colloid Interface Sci. 1999, 81, 167–249. [Google Scholar] [CrossRef]
- Ruiz-Cabello, F.J.M.; Rodríguez-Valverde, M.A.; Marmur, A.; Cabrerizo-Vílchez, M.A. Comparison of Sessile Drop and Captive Bubble Methods on Rough Homogeneous Surfaces: A Numerical Study. Langmuir 2011, 27, 9638–9643. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Luo, K.H.; Kang, Q.J.; Chen, Q. Contact angles in the pseudopotential lattice Boltzmann modeling of wetting. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2014, 90, 053301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jäger, T.; Mokos, A.; Prasianakis, N.I.; Leyer, S. Pore-Level Multiphase Simulations of Realistic Distillation Membranes for Water Desalination. Membranes 2022, 12, 1112. [Google Scholar] [CrossRef]
- Zheng, Q.S.; Yu, Y.; Zhao, Z.H. Effects of hydraulic pressure on the stability and transition of wetting modes of superhydrophobic surfaces. Langmuir 2005, 21, 12207–12212. [Google Scholar] [CrossRef]
- Schiller, U.D.; Krüger, T.; Henrich, O. Mesoscopic modelling and simulation of soft matter. Soft Matter 2018, 14, 9–26. [Google Scholar] [CrossRef] [Green Version]
- Xiong, W.; Cheng, P. Mesoscale simulation of a molten droplet impacting and solidifying on a cold rough substrate. Int. Commun. Heat Mass Transf. 2018, 98, 248–257. [Google Scholar] [CrossRef]
- Prasianakis, N.I.; Rosén, T.; Kang, J.; Eller, J.; Mantzaras, J.; Büichi, F.N. Simulation of 3D Porous Media Flows with Application to Polymer Electrolyte Fuel Cells. Commun. Comput. Phys. 2013, 13, 851–866. [Google Scholar] [CrossRef] [Green Version]
- Rosen, T.; Eller, J.; Kang, J.; Prasianakis, N.I.; Mantzaras, J.; Büchi, F.N. Saturation dependent effective transport properties of PEFC gas diffusion layers. J. Electrochem. Soc. 2012, 159, F536. [Google Scholar] [CrossRef]
- Luo, K.; Xia, J.; Monaco, E. Multiscale modelling of multiphase flow with complex interactions. J. Multiscale Model. 2009, 1, 125–156. [Google Scholar] [CrossRef]
- Qin, F.; Del Carro, L.; Mazloomi Moqaddam, A.; Kang, Q.; Brunschwiler, T.; Derome, D.; Carmeliet, J. Study of non-isothermal liquid evaporation in synthetic micro-pore structures with hybrid lattice Boltzmann model. J. Fluid Mech. 2019, 866, 33–60. [Google Scholar] [CrossRef]
- Afra, B.; Amiri Delouei, A.; Mostafavi, M.; Tarokh, A. Fluid-structure interaction for the flexible filament’s propulsion hanging in the free stream. J. Mol. Liq. 2021, 323, 114941. [Google Scholar] [CrossRef]
- Afra, B.; Karimnejad, S.; Amiri Delouei, A.; Tarokh, A. Flow control of two tandem cylinders by a highly flexible filament: Lattice spring IB-LBM. Ocean Eng. 2022, 250, 111025. [Google Scholar] [CrossRef]
- Prasianakis, N.I.; Karlin, I.V.; Mantzaras, J.; Boulouchos, K.B. Lattice Boltzmann method with restored Galilean invariance. Phys. Rev. E 2009, 79, 066702. [Google Scholar] [CrossRef] [Green Version]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. (EPL) 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Peng, C.; Tian, S.; Li, G.; Sukop, M.C. Single-component multiphase lattice Boltzmann simulation of free bubble and crevice heterogeneous cavitation nucleation. Phys. Rev. E 2018, 98, 023305. [Google Scholar] [CrossRef] [Green Version]
- Kunes, J. Dimensionless Physical Quantities in Science and Engineering; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 2012. [Google Scholar]
- Safi, M.A.; Mantzaras, J.; Prasianakis, N.I.; Lamibrac, A.; Büchi, F.N. A pore-level direct numerical investigation of water evaporation characteristics under air and hydrogen in the gas diffusion layers of polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2019, 129, 1250–1262. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [Green Version]
- Shan, X.; Chen, H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Safi, M.A.; Prasianakis, N.I.; Mantzaras, J.; Lamibrac, A.; Büchi, F.N. Experimental and pore-level numerical investigation of water evaporation in gas diffusion layers of polymer electrolyte fuel cells. Int. J. Heat Mass Transf. 2017, 115, 238–249. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization. In Visualization Handbook; Elesvier: Amsterdam, The Netherlands, 2005; ISBN 978-0123875822. [Google Scholar]
- Weisstein, E.W. Elliptic Integral. From MathWorld—A Wolfram Web Resource. 2023. Available online: https://mathworld.wolfram.com/EllipticIntegral.html (accessed on 9 March 2023).
- Wolfram Inc. Mathematica, Version 13.2; Wolfram Inc.: Champaign, IL, USA, 2022. [Google Scholar]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.L.; Tao, W.Q. A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, J.; He, X.; Wang, Y. Thermal pseudo-potential lattice Boltzmann method for simulating cavitation bubbles collapse near a rigid boundary. Comput. Fluids 2021, 217, 104817. [Google Scholar] [CrossRef]
- Mazloomi M., A.; Chikatamarla, S.S.; Karlin, I.V. Entropic lattice Boltzmann method for multiphase flows: Fluid-solid interfaces. Phys. Rev. E 2015, 92, 023308. [Google Scholar] [CrossRef] [PubMed]
- Varrette, S.; Cartiaux, H.; Peter, S.; Kieffer, E.; Valette, T.; Olloh, A. Management of an Academic HPC & Research Computing Facility: The ULHPC Experience 2.0. In Proceedings of the 6th ACM High Performance Computing and Cluster Technologies Conference (HPCCT 2022), Fuzhou, China, 8–10 July 2022; Association for Computing Machinery (ACM): Fuzhou, China, 2022. [Google Scholar]

| () | |||
| (lu−1) | |||
| Equation (36) (lu−1) | |||
| deviation (lu−1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jäger, T.; Keup, J.; Prasianakis, N.I.; Leyer, S. Theoretical and Numerical Constant Mean Curvature Surface and Liquid Entry Pressure Calculations for a Combined Pillar–Pore Structure. Coatings 2023, 13, 865. https://doi.org/10.3390/coatings13050865
Jäger T, Keup J, Prasianakis NI, Leyer S. Theoretical and Numerical Constant Mean Curvature Surface and Liquid Entry Pressure Calculations for a Combined Pillar–Pore Structure. Coatings. 2023; 13(5):865. https://doi.org/10.3390/coatings13050865
Chicago/Turabian StyleJäger, Tobias, Jemp Keup, Nikolaos I. Prasianakis, and Stephan Leyer. 2023. "Theoretical and Numerical Constant Mean Curvature Surface and Liquid Entry Pressure Calculations for a Combined Pillar–Pore Structure" Coatings 13, no. 5: 865. https://doi.org/10.3390/coatings13050865
APA StyleJäger, T., Keup, J., Prasianakis, N. I., & Leyer, S. (2023). Theoretical and Numerical Constant Mean Curvature Surface and Liquid Entry Pressure Calculations for a Combined Pillar–Pore Structure. Coatings, 13(5), 865. https://doi.org/10.3390/coatings13050865






