Abstract
Mechanical properties are among the crucial parameters for multilayer hybrid perovskite-based devices. Here, the mechanical properties of the high-quality single-crystalline MAPbX3 (MA = CH3NH3, X = Cl, Br, I), including the hardness (H) and Young’s modulus (E), are systematically studied using the three-dimensional nanoindentation (3D nanoindentation) method. In the sequence of Cl, Br, and I, the hardness and Young’s modulus of MAPbX3 decrease gradually. The hardness of MAPbX3 ranges from 0.31 to 0.57 GPa, and Young’s modulus values are less than 30 GPa. The low hardness and Young’s modulus are attributed to the weak lattice framework composed of Pb-X and the weak hydrogen bond between CH3NH3+ and the octahedron. The relationship between the hardness and Young’s modulus of MAPbX3 is also described. Generally, this work provides the favorable parameters required to further support the design and modification of investigations regarding perovskite-based devices.
1. Introduction
The application of renewable energy is of great significance to the protection of the environment and the sustainable development of society [1,2]. Among various kinds of renewable energy, solar energy is regarded as a low-cost and pollution-free energy that is widely used on a global scale. Photovoltaic cells are devices that can convert solar energy into electricity, but they require a high energy conversion efficiency [3,4]. Organic–inorganic perovskites are appealing materials for novel thin-film solar cells due to their extraordinary photoelectric performance, high-absorption coefficients and lower fabricating costs [5,6,7], long carrier diffusion length [8,9,10], and low trap densities [4,11]. MAPbX3 (MA = CH3NH3, X = Cl, Br, I) is a kind of widely investigated organic–inorganic hybrid perovskite material that has been actively applied in optoelectronic devices such as solar cells [12,13,14], lasers [15,16], light-emitting diodes [17,18], photodetectors [19,20,21,22], as well as solar thermoelectric devices [23], such as detectors, water electrolysis devices, luminescence devices, and memristors [24,25]. In order to further improve photoelectric conversion efficiency, an increasing number of scholars have devoted time to studying carrier transport and optical properties, electronic structures, and interface engineering [8,12,26,27,28,29]. In particular, the power conversion efficiency rate of perovskite solar cells has, in the last few years, been improved to an impressive rate of 25.6% due to their high absorption coefficient, fast carrier mobility, and long carrier lifetime [30,31].
Additionally, the mechanical properties and parameters that must be considered in practical design and commercialized applications include long-term material service, extended device-life, and the preservation of resources [32]. Perovskite photovoltaic cells generally have a multilayer structure [33,34], and the matching between each layer needs to be considered since it may influence the transmission efficiency and even degrade the perovskite layer [35]. In particular, the hardness and Young’s modulus help gauge the resistance of materials to plastic deformation and elastic deformation, respectively [36,37]. Thus, these mechanical properties are important for designing the multilayer structure of photovoltaic cells. Unfortunately, valuable and accurate mechanical property parameters such as the hardness (H) and Young’s modulus (E) seem to be widely neglected, and very few works covering the mechanical properties of MAPbX3 have been reported systematically [38]. Moreover, few have investigated the mechanical properties of MAPbX3 [39,40], and those that have done so have provided dispersed results. The hardness trends of MAPbX3 (MA = CH3NH3, X = Cl, Br, I) are different from the experiment values that our group obtained from reproducible experimental data. Therefore, well-documented validations of H and E values for MAPbX3 are needed.
Without noise from grain boundaries, secondary phases, tiny grains, etc., near-natural performance can be reflected by single-crystal-based macro measurements. Compared to polycrystalline samples, single-crystalline perovskites exhibit better performance [3,4,17,41]. Additionally, procedures such as indentation experiments are considered to be improved techniques for accurately determining the hardness and elastic modulus by using load and displacement sensing [42]. Multiple data points can be measured by using nanoindentation methods on single crystals with flat faces.
Consequently, the mechanical properties are accurately obtained on the high-quality, centimeter-scale single crystal of MAPbX3 (X = Cl, Br, I) by using the 3D nanoindentation method described in our work, the growth of which is facilitated by antisolvent vapor-assisted crystallization (AVC) [4] and inverse temperature crystallization (ITC) methods [7].
2. Experiments
2.1. Crystal Growth of CH3NH3PbX3 (X = Cl, Br, I)
For MAPbI3, a high-quality and suitable-sized single-crystal sample was rapidly grown via ITC, as shown in Figure 1. The solubility of MAPbI3 in certain solvents tended to decrease with increasing temperature—a trend which has been observed in only a few materials [43]. Therefore, choosing a proper solvent is important for the ensuing crystallization. The solvent used for MAPbI3 was dimethylformamide (DMF). The solution concentration was 1.2 M for MAPbI3. The molar ratio of MAI and PbI2 was 1.1:1. The solution was dissolved at an ambient temperature for 2~6 h and then filtered with 0.22 μm pore size polytetrafluoroethylene (PTFE). The filtered solution was put into a Bunsen beaker and then kept in an ambient atmosphere (60 °C) in an oil bath for 5 h. This meant that we could approximately obtain high-quality single crystals with a size of 1–20 mm, after the above solution was placed in an ambient atmosphere (90 °C) for 12 h. Large single crystals (7–20 mm in size) with a regular shape, smooth surface, and sufficient size were used for mechanical and thermal property characterization. Moreover, the crystals dissolved in the solution as the temperature decreased. It was found that the solution could be reused for the growth of a single crystal.
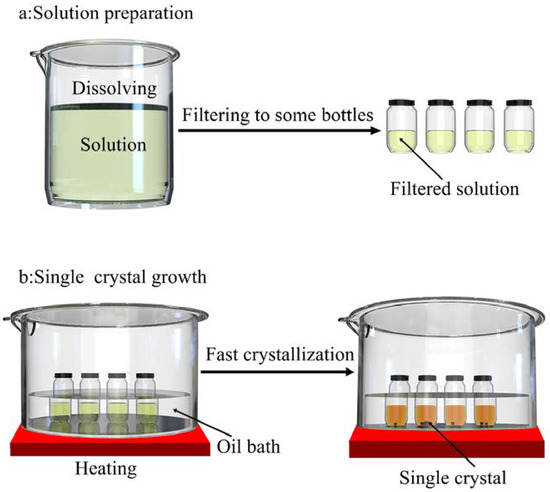
Figure 1.
Crystal growth process for MAPbI3 (a) the process of solution preparation (b) the process of single crystal growth.
For MAPbCl3 and MAPbBr3, a single crystal is grown via AVC method. The diagram of preparation process is shown in Figure 2. PbCl2 (PbBr2) and MACl (MABr) (1:1 by molar PbCl2: 2M) were dissolved in dimethylsulfoxide (DMSO) (or DMF). MAPbCl3 and MAPbBr3 single crystals were grown along with slow diffusion of the antisolvent DCM. We obtained suitable single crystals for approximately a week. The seed crystal growth method is the same as ITC.
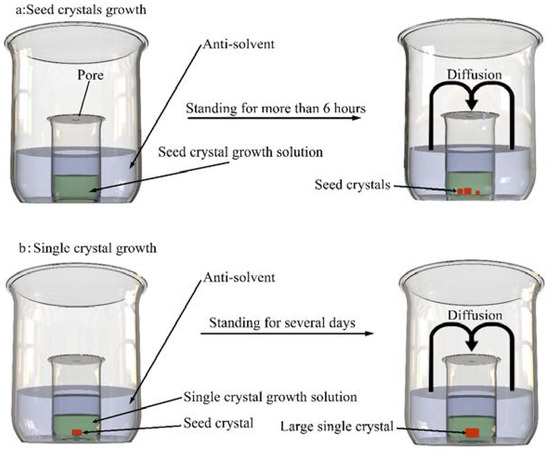
Figure 2.
Crystal growth process for MAPbX3 X = Cl, Br (a) the process of seed crystal growth (b) the process of single crystal growth.
2.2. Single-Crystal and Powder X-ray Diffraction Characterization
Powder and single-crystal X-ray diffraction (XRD) were performed on a MiniFlex 600 with Cu-Kα radiation (λ = 1.54186 Å). Powder samples were operated at 40 kV, 15 mA, whereas for single crystals, it was 20 kV, 2 mA. CH3NH3PbX3 (X = Cl, Br, I) powders were made by grinding our single crystal into fine powders with an agate mortar. Single crystals of CH3NH3PbX3 (X = Cl, Br, I) were made according to our solution crystallization method.
2.3. Nanoindentation Measurements
The hardness and Young’s modulus were measured by using the 3D nanoindentation (iMicro KLA., Milpitas, CA, USA) release method on an iNano instrument [44]. A Berkovinch tip (trigonal geometry) with a radius of curvature of 20 nm was used. The constant force was 5 mN, and the test matrix was a 30 × 30 array including 900 nanoindentation points in total within a square area of 20 μm × 20 μm on the microstructure of the single crystal.
In order to obtain more accurate test results, the flatness of the sample needed to be higher when nanoindentation was used. During the test, the error of the upper and lower surface thickness of the sample was generally required to be less than 10 microns. When the sample surface was treated, different types of sandpaper were used to grind it step by step. Then, a polishing cloth with different levels of roughness and polishing pastes for different particle size was used for polishing on a polishing machine with a speed of 600 r/min to make the sample suitable for measurement. The flatness of the style could be measured automatically by the test instrument. If the flatness exceeded the range specified by the test instrument, the test process could not be carried out.
2.4. Thermal Properties Measurements
Thermogravimetric analysis (TGA) and differential scanning calorimetry (DSC) were executed on a synchronous thermal analyzer (DSC-TG404, NETZSCH, Berlin, Germany). A small amount of broken crystals (<20 mg) were placed in Al2O3 crucible. For DSC and TGA, the sample was heated from room temperature to 600 °C with a speed of 5 K/min.
3. Results and Discussion
XRD analysis was conducted for MAPbX3 powders and the single crystal samples. The XRD patterns of MAPbX3 powders and the single crystal samples, together with Rietveld profile refinement patterns, are shown in Figure 3a–c [45]. Rietveld profile refinement results are listed in Table 1, and the data reported in previous references are also listed for comparison [46,47,48,49]. The Rietveld refinement parameters sig and RWP (%) are below 15%, indicating that the refinement results are credible. The macro sample picture of the single crystal of MAPbBr3 is shown in Figure 3d. Similar to other reports at room temperature [4,6,7,17], MAPbCl3 and MAPbBr3 single crystals exhibit the same crystal structure that belongs to the cubic system with space group Pm3m (lattice parameters equal to 5.69 Å and 5.93 Å, respectively), while MAPbI3 single crystals are perfectly assigned to the tetragonal system with space group I4/m (a = 8.88 Å, c = 12.69 Å) [50]. Meanwhile, it can be seen from the single-crystal XRD patterns that the facets of MAPbCl3 and MAPbBr3 are (001) crystal planes. For MAPbI3, the eight exposed crystal faces (112) lead to the disappearance of the (001) crystal planes, which are different from the (100) and (010) crystal planes in the tetragonal system. The macro sample diagram of the MAPbBr3 crystal is prepared by the liquid phase method. As shown in the picture, the sample is red and translucent, and the sample size can reach 10 mm.
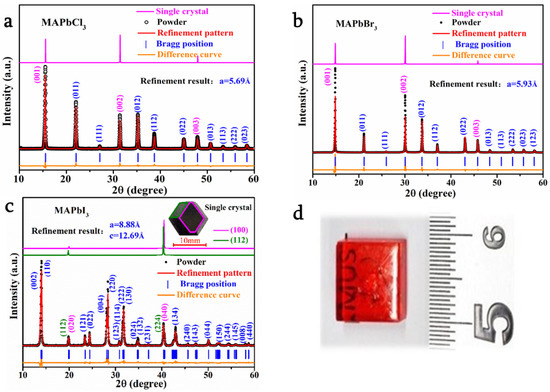
Figure 3.
X-ray diffraction (XRD) analysis of MAPbX3 (a) MAPbCl3; (b) MAPbBr3; (c) MAPbI3; (d) the macro sample diagram of MAPbBr3.

Table 1.
Crystal system, space group, lattice parameters (a, c/Å), and Rietveld refinement parameters sig and RWP (%) of MAPbX3 (X = Cl, Br, I).
From the figure, it can be observed that the XRD pattern of the MAPbX3 (X = Cl, Br, I) powder sample is highly consistent with the refined XRD pattern. The two sets of spectra are almost coincident. The fluctuation of the difference curve is also very small. This proves the phase purity and high quality of the single-crystal samples.
The thermal stability is critical for solar cell materials since it determines the service temperature and working stability of the solar cells. The thermal stability of MAPbX3 (X = Cl, Br, I) single crystal samples are also investigated by TGA and DSC measurements, as shown in Figure 4a–c. From the decline of the TGA curve and the right peak of the DSC, it turns out that the weight loss of the MAPbX3 (X = Cl, Br, I) samples started at about 245 °C, 347 °C, and 311 °C, respectively, indicating that the single-crystal perovskites were more stable than the thin-film perovskites, which experience thermal decomposition at about 150 °C [16,17]. Furthermore, when the temperature continues to rise to 450 °C, the weight loss of all the samples stops. There are about 74%~83% mass fractions in the product remaining, proving that the residual product is mainly PbX2 (X = Cl, Br, I) [51,52].
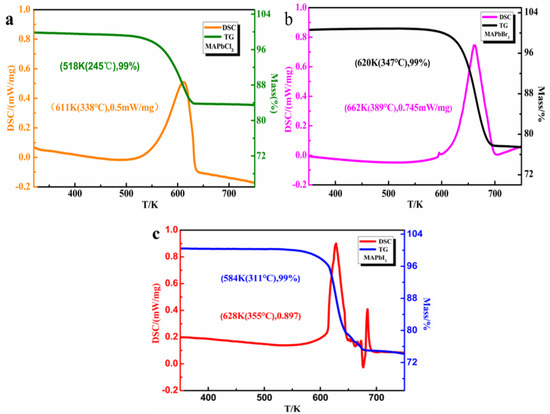
Figure 4.
Differential scanning calorimetry (DSC) and weight loss (TG) of MAPbX3 (a) for MAPbCl3, (b) for MAPbBr3, and (c) for MAPbI3.
By merit of the high-quality bulk single crystal that we have grown, the mechanical properties of MAPbX3, such as the hardness and Young’s modulus, were accurately measured by the 3D nanoindentation method. High-resolution maps of the mechanical properties of MAPbCl3 are shown in Figure 5. Figure 5a,b are the plane projections of the hardness and Young’s modulus of MAPbCl3, respectively. It can clearly be seen that the hardness distribution of each position in the microregion of the MAPbCl3 sample is uniform, indicating a higher quality of samples. At the same time, mechanical parameters such as the hardness and modulus have a higher reliability. The average hardness value of MAPbCl3 is 0.57 GPa, and for Young’s modulus, it is 27.96 GPa.
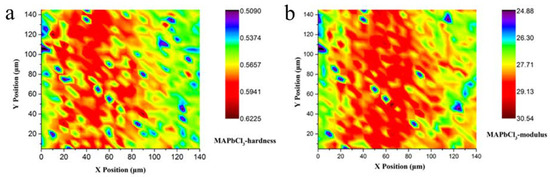
Figure 5.
Mechanical properties mapping of MAPbCl3 (a) Plane projections of hardness; (b) Plane projections of Young’s modulus.
The detected hardness and Young’s modulus distribution along the Y direction at each X position of the MAPbCl3 sample are shown in Figure 6. The Y direction of the MAPbCl3 sample is the (100) test surface.
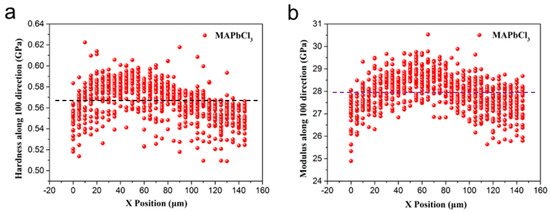
Figure 6.
The results of each test point (a) Hardness along the Y direction dependent on the X positions accompanied (dotted line: average hardness is 0.57 GPa); (b) Young’s modulus along the Y direction dependent on the X positions accompanied (dotted line: average strength is 28 GPa).
Visibly, further details prove that the hardness is basically concentrated in the region of 0.54–0.60 GPa (average hardness is 0.57 GPa). The Young’s modulus is concentrated in the 27–29 GPa band region (average strength is 28 GPa). The overall distribution is more evenly concentrated. The data away from the scope may be attributed to the microdefects in the single crystal.
After linear fitting, the overall detected hardness and Young’s modulus data and the relationship between the micro Young’s modulus and hardness of MAPbCl3 are shown in Figure 7. Obviously, within the range of hardness distribution for MAPbCl3, Young’s modulus is proportional to the hardness. The relationship between the hardness and Young’s modulus can be expressed as E = 10.6 + 30.7 × H (the hardness and modulus data are basically distributed between E = 11.615 + 30.7 × H and E = 9.615 + 30.7 × H). The hardness can be characterized more easily by common instruments, such as the Vickers hardness tester. However, the detection of Young’s modulus requires relatively complicated devices. Therefore, using the fitting expression, the Young’s modulus can be found as long as we can obtain the hardness of the sample.
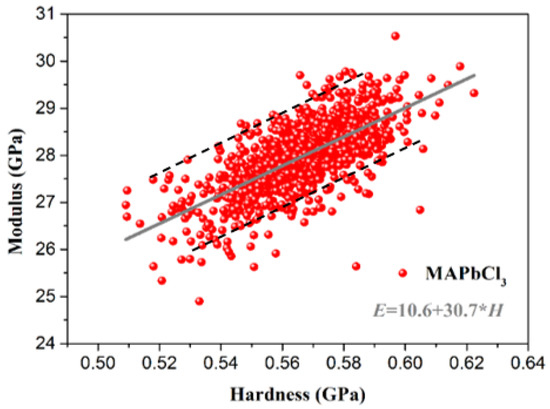
Figure 7.
The relationship between the micro Young’s modulus and hardness of MAPbCl3.
Figure 8a,b exhibit the plane projections of hardness and Young’s modulus for MAPbBr3. Despite a small color difference within the area, the value difference is small. Apparently, the hardness distribution of each position in the microregion of the MAPbBr3 sample is uniform. Thus, mechanical parameters such as the hardness and Young’s modulus still have a higher reliability. Considering that the differences are caused by solute diffusion during the crystal growth process, errors in this method are inevitable. After calculating the overall data, the average hardness value of MAPbBr3 is deemed to be 0.48 GPa, and for the Young’s modulus, it is 22.89 GPa.
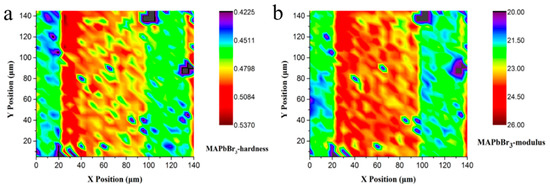
Figure 8.
Mechanical properties mapping of MAPbBr3 (a) Plane projections of hardness; (b) Plane projections of Young’s modulus.
Figure 9a,b show the detected hardness and Young’s modulus value distribution along the Y direction at different X positions of the MAPbBr3 samples, respectively. The Y direction of MAPbBr3 is the same as it was in [100], which is the same as that of MAPbCl3. MAPbBr3 single crystals untreated with smooth flat surfaces were used. The hardness is distributed over the region of 0.46–0.52 GPa. Simultaneously, the Young’s modulus is mainly concentrated in the 21–25 GPa band region for MAPbBr3.
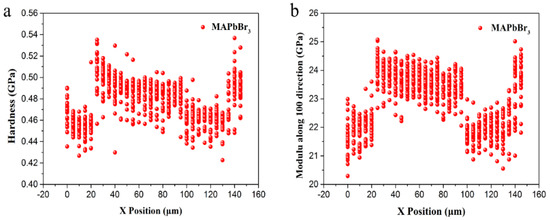
Figure 9.
The results of each test point: Hardness along Y direction dependent on the X positions accompanied. (a) Hardness along Y direction dependent on the X positions accompanied. (b) Young’s modulus along Y direction dependent on the X positions accompanied.
Similarly, linear fitting was used to fit the relationship between the hardness and elastic modulus for MAPbBr3. As shown in Figure 10, the Young’s modulus is proportional to the hardness within the hardness distribution range for MAPbBr3. The relationship between the hardness and Young’s modulus follows the formula E = 3.2 + 41.4 × H (the hardness and modulus data are basically distributed between E = 4.3 + 41.4 × H and E = 1.8 + 41.4 × H). In contrast, the slope is closed to the MAPbCl3. Accordingly, we can use this relationship to predict the Young’s modulus of the sample. This prediction can help facilitate the selection of materials in device design.
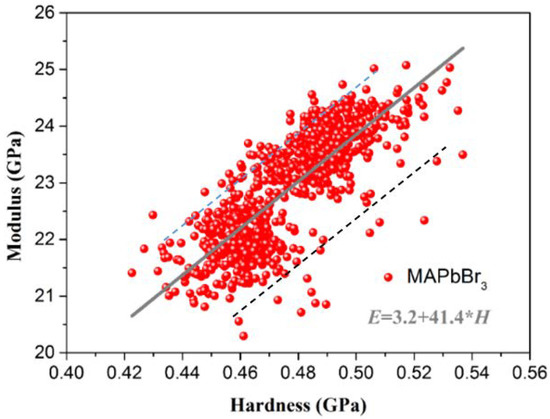
Figure 10.
The relationship between the micro Young’s modulus and hardness of MAPbBr3.
For MAPbI3, we also give the corresponding plane projections of the hardness and Young’s modulus for MAPbI3 in Figure 11a and Figure 11b, respectively.
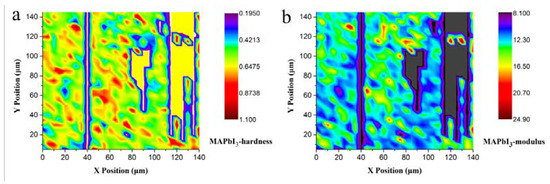
Figure 11.
Mechanical properties mapping of MAPbI3 (a) Plane projections of hardness; (b) Plane projections of Young’s modulus.
Regarding the nanoindentation test, the requirement for the flatness of the sample surface is extremely high. Therefore, we selected high-quality single crystals whose surfaces were visibly exceedingly smooth and flat in order to execute the correlated test. The unhappy paradox here is that the graph stemming from the test data is not perfect. On the right side of Figure 11a,b, there are a few blocky yellow and gray areas that indicate the unpressed positions due to the tiny height inconsistency of the sample surface. Because of the long test time (about 30 min), our test data are still highly credible in terms of the mechanical parameters such as hardness and modulus. As the repositioning of close mechanical property values is ideal, it is worth mentioning that, for MAPbX3 themselves, compared with MAPbCl3 and MAPbBr3, the surface of MAPbI3 may appear a little matte. By calculating all of the data, we can observe that the average hardness value of MAPbI3 is 0.31 GPa, and for the Young’s modulus, it is 13.35 GPa.
Figure 12 shows the value distribution of the hardness and Young’s modulus at different X positions. The test surface of the MAPbI3 sample is the (100) surface. It can be seen from the figure that the hardness and modulus values of the sample are relatively concentrated. The hardness is basically distributed in the region of 0.2–0.7 GPa, and the Young’s modulus is centralized in the range of 10–15 GPa. The test results are as expected.
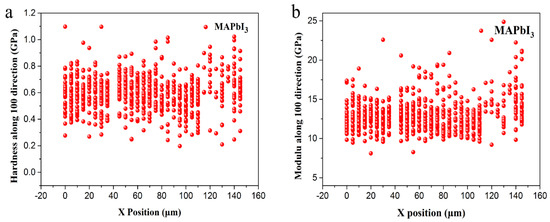
Figure 12.
The results of each test point: Hardness along Y direction dependent on the X positions accompanied. (a) Hardness along Y direction dependent on the X positions accompanied; (b) Young’s modulus along Y direction dependent on the X positions accompanied.
Similarly, as shown in Figure 13, the hardness and Young’s modulus of MAPbI3 are concentrated on a straight line, and the relationship between the hardness and elastic modulus is fitted by a simple linear fit. The hardness and Young’s modulus of MAPbI3 follow a relationship of E = 6.5 + 10.98 × H. The hardness of the samples can be obtained by the simple Vickers hardness tester. We can use this relationship to predict the Young’s modulus of the samples. This provides convenience for material design and provides a theoretical basis for finding the relationship between the hardness and modulus of hybrid perovskite materials. This is also conducive to providing ideas for subsequent modification studies, such as doping, to improve material performance.
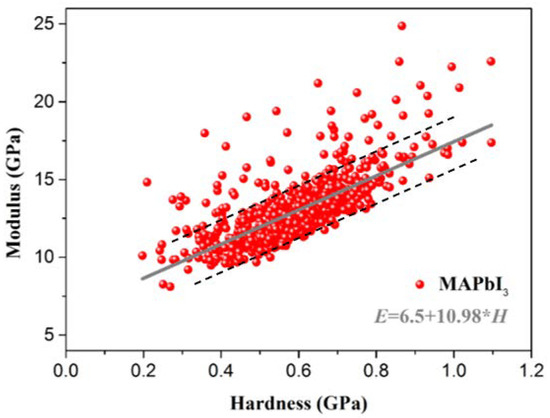
Figure 13.
The relationship between the micro Young’s modulus and hardness of MAPbI3.
The Young’s modulus (E) and bulk modulus (B) of MAPbX3 in each direction are obtained via first-principles calculations based on density of functional theory (DFT), which are conducted using the plane wave basis in Cambridge Sequential Total Energy Package (CASTEP, v7.0) code. More details surrounding the calculation method are mentioned in the literature, for example, as in [53]. The calculated results are shown in Table 2. The elastic constants Cij can be obtained by calculating the total energy as a function of appropriate lattice deformation. The elastic strain energy follows the formula U = ∆U/V0 = . Here, ΔU is the difference in energy and V0 is the volume of the original cell. According to the calculated elastic constants, the bulk modulus (B) and Young’s modulus (E) of polycrystalline materials are evaluated by the Voigt-Reuss–Hill (VRH) approximation.

Table 2.
Calculated Young’s modulus and bulk modulus in different directions.
The calculated Young’s modulus agrees well with the experimental Young’s modulus measured for the single crystals. Our experimental Young’s modulus values are in agreement with a previous report [38,54], albeit just approximately 5% higher than their data, and exhibit the same trend of ECl > EBr > EI. From a micro perspective, Young’s modulus shows the bonding strength between atoms, ions, or molecules. According to the linear expansion coefficient research of CH3NH3PbX3 [38], the Pb–X bond plays a dominant role in the elasticity of these materials [27]. In the sequence of Cl, Br, I, Pb–X strength decreases gradually. Thus, Young’s modulus of MAPbX3 decreases in accordance with the order of Cl, Br, and I. From a macro perspective, Young’s modulus is a measure of the ability of an object to resist elastic deformation. In other words, within the limits of flexibility, under a certain stress, a smaller elastic deformation occurs in MAPbCl3.
However, for the hardness of other mechanical properties, there are some differences between our data and their reports. Regarding data values, on the whole, the hardness is ultralow. Our data are only approximately 0.1 higher than their respective data. The ability of a material to locally resist the intrusion of hard objects into its surface is called hardness, from which the resistance of a material to plastic deformation can be determined. Consequently, plastic deformation may readily occur in device applications due to the low hardness of MAPbX3. More positively, this may cater to device designs that require some plastic deformation to take place during the working period.
However, the changing trend of MAPbX3 (X = Cl, Br, I) (H…Cl > H…Br > H…I) is exactly opposite to what is reported in the literature [38,54]. MAPbI3 still exhibits the weakest resistance to plastic deformation. This is consistent with the macro observations in our experiments. For external conditions, the number of our data tests times is huge (900 times for each sample), and the average value of data is directly derived from computer statistics. For the internal mechanism, we can assert that the stronger the chemical bond strength between the atoms, ions, or molecules, the greater the hardness. Therefore, the results of H…Cl > H…Br > H…I in our report may be more reliable.
Generally, lower amounts of hardness and Young’s modulus have been inextricably linked to weaker chemical bonding in MAPbX3 between the atoms, ions, and molecules. Not only does the weak lattice framework composed of Pb-X but also the weak hydrogen bond between CH3NH3+ and the Pb-X octahedron play a part. On account of the reduced trend of bond strength in Pb-X in the sequence of Cl, Br, and I, the ability to resist external stress for the octahedral framework composed of Pb-X (X = Cl, Br, I) is gradually weakened. Simultaneously, the hardness and Young’s modulus gradually decrease.
4. Conclusions
In this work, centimeter-sized and high-quality MAPbX3 single crystals are grown. Using the high-resolution three-dimensional nanoindentation (3D nanoindentation) method, on the whole, the mechanical properties, including the hardness and Young’s modulus, of MAPbX3 (X = Cl, Br, I) are investigated systematically and accurately. The ultra-low hardness of MAPbX3 ranges from 0.31 to 0.57 GPa, and Young’s modulus ranges from 13.35 to 27.96 GPa. As the X in MAPbX3 changes in the sequence of Cl, Br, and I, the hardness and Young’s modulus decrease gradually (that is H…Cl > H…Br > H…I and ECl > EBr > EI). These results are attributed to the weak lattice framework composed of Pb-X and the bonding of methylamine ions (CH3NH3+) to the octahedron, which depends only on the weak hydrogen bond. We also summarize the relationship between the hardness and Young’s modulus of MAPbX3. Consequently, there are laws to follow in the subsequent modification research. In fact, our work provides a more accurate and reliable mechanical property parameter of MAPbX3 (X = Cl, Br, I) for reference.
Author Contributions
Software, C.G.; Validation, F.Q.; Formal analysis, J.L., Z.Z., M.H. and J.F.; Investigation, J.L., C.G., M.H. and J.W.; Resources, J.L. and X.C.; Data curation, J.L.; Writing—original draft, C.G.; Writing—review & editing, J.L., Z.Z. and J.F.; Visualization, J.L.; Project ad-ministration, J.F.; Funding acquisition, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Key R&D Program of China (No. 2019YFB1503200), the Natural Science Foundation of China (No. 51762028; No. 91960103), Materials Genome Engineering of Rare and Precious Metal of Yunnan Province (2019, 202002AB080001-1), and the Scientific re-search project of basic scientific research funds of provincial colleges in Heilongjiang Province (No. 2020-KYYWF-0255).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Madaleno, M.; Nogueira, M.C. How Renewable Energy and CO2 Emissions Contribute to Economic Growth, and Sustainability—An Extensive Analysis. Sustainability 2023, 15, 4089. [Google Scholar] [CrossRef]
- Saeed, S.; Makhdum, M.S.A.; Anwar, S.; Yaseen, M.R. Climate Change Vulnerability, Adaptation, and Feedback Hypothesis: A Comparison of Lower-Middle, Upper-Middle, and High-Income Countries. Sustainability 2023, 15, 4145. [Google Scholar] [CrossRef]
- Rocha, Q.S.; Munis, R.A.; da Silva, R.B.G.; Aguilar, E.W.Z.; Simões, D. Photovoltaic Solar Energy in Forest Nurseries: A Strategic Decision Based on Real Options Analysis. Sustainability 2023, 15, 3960. [Google Scholar] [CrossRef]
- Hannan, M.A.; Al-Shetwi, A.Q.; Mollik, M.S.; Ker, P.J.; Mannan, M.; Mansor, M.; Al-Masri, H.M.K.; Mahlia, T.M.I. Wind Energy Conversions, Controls, and Applications: A Review for Sustainable Technologies and Directions. Sustainability 2023, 15, 3986. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef]
- Wolf, S.D.; Holovsky, J.; Moon, S.-J.; Löper, P.; Niesen, B.; Ledinsky, M.; Haug, F.-J.; Yum, J.-H.; Ballif, C. Organometallic Halide Perovskites: Sharp Optical Absorption Edge and Its Relation to Photovoltaic Performance. J. Phys. Chem. Lett. 2014, 5, 1035–1039. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, Y.; Yang, M.; Choi, S.; Zhu, K.; Luther, J.M.; Beard, M.C. Low surface recombination velocity in solution-grown CH3NH3PbBr3 perovskite single crystal. Nat. Commun. 2015, 6, 7961. [Google Scholar] [CrossRef]
- Shi, D.; Adinolfi, V.; Comin, R.; Yuan, M.; Alarousu, E.; Buin, A.; Chen, Y.; Hoogland, S.; Rothenberger, A.; Katsiev, K.; et al. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science 2015, 347, 519–522. [Google Scholar] [CrossRef]
- Dong, Q.F.; Fang, Y.J.; Shao, Y.C.; Mulligan, P.; Qiu, J.; Cao, L.; Huang, J.S. Electron-hole diffusion lengths > 175 μm in solution-grown CH3NH3PbI3 single crystals. Science 2015, 347, 967–970. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Z.; Cui, D.; Ren, X.; Sun, J.; Liu, X.; Zhang, J.; Wei, Q.; Fan, H.; Yu, F.; et al. Two-Inch-Sized Perovskite CH3NH3PbX3(X = Cl, Br, I) Crystals: Growth and Characterization. Adv. Mater. 2015, 27, 5176–5183. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Abdelhady, A.L.; Murali, B.; Alarousu, E.; Burlakov, V.M.; Peng, W.; Dursun, I.; Wang, L.; He, Y.; Maculan, G.; et al. High-quality bulk hybrid perovskite single crystals within minutes by inverse temperature crystallization. Nat. Commun. 2015, 6, 7586. [Google Scholar] [CrossRef] [PubMed]
- Docampo, P.; Ball, J.M.; Darwich, M.; Eperon, G.E.; Snaith, H.J. Efficient organometal trihalide perovskite planar-heterojunction solar cells on flexible polymer substrates. Nat. Commun. 2013, 4, 2761. [Google Scholar] [CrossRef] [PubMed]
- Nie, W.; Tsai, H.; Asadpour, R.; Blancon, J.-C.; Neukirch, A.J.; Gupta, G.; Crochet, J.J.; Chhowalla, M.; Tretiak, S.; Alam, M.A.; et al. High-Efficiency Solution-Processed Perovskite Solar Cells with Millimeter-Scale Grains. Science 2015, 347, 522–525. [Google Scholar] [CrossRef] [PubMed]
- Stranks, S.D.; Eperon, G.E.; Grancini, G.; Menelaou, C.; Alcocer, M.J.P.; Leijtens, T.; Herz, L.M.; Petrozza, A.; Snaith, H.J. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 2013, 342, 341–344. [Google Scholar] [CrossRef]
- Xing, G.; Mathews, N.; Lim, S.S.; Yantara, N.; Liu, X.; Sabba, D.; Grätzel, M.; Mhaisalkar, S.; Sum, T.C. Low-temperature solution-processed wavelength-tunable perovskites for lasing. Nat. Mater. 2014, 13, 476–480. [Google Scholar] [CrossRef]
- Deschler, F.; Price, M.; Pathak, S.; Klintberg, L.E.; Jarausch, D.-D.; Higler, R.; Hüttner, S.; Leijtens, T.; Stranks, S.D.; Snaith, H.J.; et al. High photoluminescence efficiency and optically pumped lasing in solution-processed mixed halide perovskite semiconductors. J. Phys. Chem. Lett. 2014, 5, 1421–1426. [Google Scholar] [CrossRef]
- Tan, Z.-K.; Moghaddam, R.S.; Lai, M.L.; Docampo, P.; Higler, R.; Deschler, F.; Price, M.; Sadhanala, A.; Pazos, L.M.; Credgington, D.; et al. Bright light-emitting diodes based on organometal halide perovskite. Nat. Nanotechnol. 2014, 9, 687–692. [Google Scholar] [CrossRef]
- Seo, H.K.; Kim, H.; Lee, J.; Park, M.H.; Jeong, S.H.; Kim, Y.H.; Kwon, S.J.; Han, T.H.; Yoo, S.; Lee, T.W. Efficient Flexible Organic/Inorganic Hybrid Perovskite Light-Emitting Diodes Based on Graphene Anode. Adv. Mater. 2017, 29, 1605587. [Google Scholar] [CrossRef]
- Dou, L.; Yang, Y.M.; You, J.; Hong, Z.; Chang, W.H.; Li, G.; Yang, Y. Solution-processed hybrid perovskite photodetectors with high detectivity. Nat. Commun. 2014, 5, 5104. [Google Scholar] [CrossRef]
- Ding, J.; Du, S.; Zhao, Y.; Zhang, X.; Zuo, Z.; Cui, H.; Zhan, X.; Gu, Y.; Sun, H. High-quality inorganic-organic perovskite CH3NH3PbI3 single crystals for photo-detector applications. J. Mater. Sci. 2017, 52, 276–284. [Google Scholar] [CrossRef]
- Maculan, G.; Sheikh, A.D.; Abdelhady, A.L.; Saidaminov, M.I.; Haque, M.A.; Murali, B.; Alarousu, E.; Mohammed, O.F.; Wu, T.; Bakr, O.M. CH3NH3PbCl3 single crystals: Inverse temperature crystallization and visible-blind UV-photodetector. J. Phys. Chem. Lett. 2015, 6, 3781–3786. [Google Scholar] [CrossRef] [PubMed]
- Rao, H.-S.; Li, W.-G.; Chen, B.-X.; Kuang, D.-B.; Su, C.-Y. In Situ Growth of 120 cm2 CH3NH3PbBr3 Perovskite Crystal Film on FTO Glass for Narrowband-Photodetectors. Adv. Mater. 2017, 29, 1602639. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Galli, G. Perovskites for Solar Thermoelectric Applications: A First Principle Study of CH3NH3AI3 (A = Pb and Sn). Chem. Mater. 2014, 26, 5394–5400. [Google Scholar] [CrossRef]
- Xiao, Z.; Huang, J. Energy-Efficient Hybrid Perovskite Memristors and Synaptic Devices. Adv. Electron. Mater. 2016, 2, 1600100. [Google Scholar] [CrossRef]
- Sadhanala, A.; Ahmad, S.; Zhao, B.; Giesbrecht, N.; Pearce, P.; Deschler, F. Blue-green color tunable solution processable organoleadchloride–bromide mixed halide perovskites for optoelectronicapplications. Nano Lett. 2015, 15, 6095–6101. [Google Scholar] [CrossRef]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient Planar Heterojunction Perovskite Solar Cells by Vapour Deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Q.; Li, G.; Hong, Z.; You, J.; Liu, Y.; Yang, Y. Interface engineering of highly efficient perovskite solar cells. Science 2014, 345, 542–546. [Google Scholar] [CrossRef]
- Qin, P.; Tanaka, S.; Ito, S.; Tetreault, N.; Manabe, K.; Nishino, H.; Nazeeruddin, M.K.; Gratzel, M. Inorganic hole conductor-based lead halide perovskite solar cells with 12.4% conversion efficiency. Nat. Commun. 2014, 5, 3834. [Google Scholar] [CrossRef]
- Xing, G.; Mathews, N.; Sun, S.; Lim, S.S.; Lam, Y.M.; Gratzel, M.; Mhaisalkar, S.; Sum, T.C. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 2013, 342, 344–347. [Google Scholar] [CrossRef]
- Yang, W.S.; Park, B.-W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S.; Seo, J.; Kim, E.K.; Noh, J.H.; et al. Iodide Management in Formamidinium-Lead-Halide-Based Perovskite Layers for Efficient Solar Cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, M.; Seo, J.; Lu, H.; Ahlawat, P.; Mishra, A.; Yang, Y.; Hope, M.A.; Eickemeyer, F.T.; Kim, M.; et al. Pseudo-halide anion engineering for α-FAPbI3 perovskite solar cells. Nature 2021, 592, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Alomayri, T.; Vickers, L.; Shaikh, F.U.A.; Low, I.-M. Mechanical properties of cotton fabric reinforced geopolymer composites at 200–1000 °C. J. Adv. Ceram. 2014, 3, 184–193. [Google Scholar] [CrossRef]
- Lee, M.M.; Teuscher, J.; Miyasaka, T.; Murakami, T.N.; Snaith, H.J. Efficient hybrid solar cells based on meso-superstructuredorganometal halide perovskites. Science 2012, 338, 643–647. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Shi, G. Two-Dimensional Materials for Halide Perovskite-Based Optoelectronic Devices. Adv. Mater. 2017, 29, 1605448. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Deng, Y.; Wei, H.; Zheng, X.; Yu, Z.; Shao, Y.; Shield, J.E.; Huang, J. Strained hybrid perovskite thin films and their impact on the intrinsic stability of perovskite solar cells. Sci. Adv. 2017, 3, 5616. [Google Scholar] [CrossRef] [PubMed]
- Dong, X.; Li, X.; Chen, H.; Dong, Q.; Wang, J.; Wang, X.; Pan, Y.; Chen, X.; Zhou, H. Realizing enhanced energy storage and hardness performances in 0.90NaNbO3−0.10Bi(Zn0.5Sn0.5)O3 ceramics. J. Adv. Ceram. 2022, 11, 729–741. [Google Scholar] [CrossRef]
- Zhao, Z.F.; Xiang, H.M.; Dai, F.Z.; Peng, Z.J.; Zhou, Y.C. Preparation and mechanical properties of β-Zr2O(PO4)2: A soft and damage tolerant ceramic with machinability and good thermal shock resistance. J. Eur. Ceram. Soc. 2020, 40, 155–164. [Google Scholar] [CrossRef]
- Feng, J. Mechanical properties of hybrid organic-inorganic CH3NH3BX3 (B = Sn, Pb; X = Br, I) perovskites for solar cell absorbers. APL Mater. 2014, 2, 081801. [Google Scholar] [CrossRef]
- Rakita, Y.; Cohen, S.R.; Kedem, N.K.; Hodes, G.; Cahen, D. Mechanical properties of APbX3 (A = Cs or CH3NH3; X = I or Br) perovskite single crystals. MRS Commun. 2015, 5, 623–629. [Google Scholar] [CrossRef]
- Sun, Y.F.S.; Kieslich, G.; White, T.J.; Cheetham, A.K. Mechanical Properties of Organic-Inorganic Halide Perovskites, CH3NH3PbX3 (X=I, Br and Cl), by Nanoindentation. J. Mater. Chem. A 2015, 3, 18450–18455. [Google Scholar] [CrossRef]
- Hu, M.Y.; Ge, C.; Wu, P.; Tan, Q.; Chen, Z.; Wang, Y.; Shi, J.; Feng, J. Ultralow thermal conductivity and ultrahigh thermal expansion of single-crystal organic–inorganic hybrid perovskite CH3NH3PbX3 (X= Cl, Br, I). J. Phys. Chem. C 2018, 122, 15973–15978. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Saidaminov, M.I.; Abdelhady, A.L.; Maculan, G.; Bakr, O.M. Retrograde solubility of formamidinium and methylammonium lead halide perovskites enabling rapid single crystal growth. Chem. Commun. 2015, 51, 17658–17661. [Google Scholar] [CrossRef] [PubMed]
- Chong, X.Y.; Hu, M.Y.; Feng, J. Elaborating the phases and mechanical properties of multiphase alloy: Experimental two-dimensional mapping combined with theoretical calculations. Mater. Charact. 2017, 134, 347–353. [Google Scholar] [CrossRef]
- Lutterotti, L. Total pattern fitting for the combined size–strain–stress–texture determination in thin film diffraction. Nucl. Instrum. Meth. B 2010, 268, 334–340. [Google Scholar] [CrossRef]
- Yin, W.J.; Yang, J.H.; Kang, J.; Yan, Y.; Wei, S.-H. Halide perovskite materials for solar cells: A theoretical review. J. Mater. Chem. A 2015, 3, 8926–8942. [Google Scholar] [CrossRef]
- Zunger, A.; Wei, S.H.; Ferreira, L.G.; Bernard, J.E. Special quasirandom structures. Phys. Rev. Lett. 1990, 65, 353–356. [Google Scholar] [CrossRef]
- Kitazawa, N.; Watanabe, Y.; Nakamura, Y. Optical properties of CH3NH3PbX3 (X = halogen) and their mixed-halide crystals. J. Mater. Sci. 2002, 17, 3585–3587. [Google Scholar] [CrossRef]
- Colella, S.; Mosconi, E.; Fedeli, P.; Listorti, A.; Gazza, F.; Orlandi, F.; Ferro, P.; Besagni, T.; Rizzo, A.; Calestani, G.; et al. MAPbI3-xClx mixed halide perovskite for hybrid solar cells: The role of chloride as dopant on the transport and structural properties. Chem. Mater. 2013, 25, 4613–4618. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. (Eds.) NIST Chemistry Webbook; NIST Standard Reference Database No. 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017.
- Elbaz, G.A.; Straus, D.B.; Semonin, O.E.; Hull, T.D.; Paley, D.W.; Kim, P.; Owen, J.S.; Kagan, C.R.; Roy, X. Unbalanced Hole and Electron Diffusion in Lead Bromide Perovskites. Nano Lett. 2017, 17, 1727–1732. [Google Scholar] [CrossRef]
- Feng, J.; Xiao, B. Crystal Structures, Optical Properties, and Effective Mass Tensors of CH3NH3PbX3 (X = I and Br) Phases Predicted from HSE06. J. Phys. Chem. Lett. 2014, 5, 1278–1282. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Wei, W.; Li, L.; Tan, Y.; Tang, Y. Mechanical Properties of a 2D Lead-Halide Perovskite, (C6H5CH2NH3)2PbCl4, by Nanoindentation and First-Principles Calculations. J. Phys. Chem. C 2020, 124, 19204–19211. [Google Scholar] [CrossRef]
- Laamari, M.E.; Cheknane, A.; Benghia, A.; Hilal, H.S. Optimized opto-electronic and mechanical properties of orthorhombic methylamunium lead halides (MAPbX3) (X = I, Br and Cl) for photovoltaic applications. Sol. Energy 2019, 182, 9–15. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).